First off, let me say that you can find the answer to this question in Sage using the nauty generator. If you’re going to be a serious graph theory student, Sage could be very helpful.
count = 0
for g in graphs.nauty_geng("20 180:180"):
count = count+1
print count
The answer is 4613. But, this isn’t easy to see without a computer program.
At this point, perhaps it would be good to start by thinking in terms of of the number of connected graphs with at most 10 edges. Then, all the graphs you are looking for will be unions of these. You should be able to figure out these smaller cases. If any are too hard for you, these are more likely to be in some table somewhere, so you can look them up.
Connected graphs of order n and k edges is:
n = 1, k = 0: 1
n = 2, k = 1: 1
n = 3, k = 2: 1
n = 3, k = 3: 1
n = 4, k = 3: 2
n = 4, k = 4: 2
n = 4, k = 5: 1
n = 4, k = 6: 1
n = 5, k = 4: 3
n = 5, k = 5: 5
n = 5, k = 6: 5
n = 5, k = 7: 4
n = 5, k = 8: 2
n = 5, k = 9: 1
n = 5, k = 10: 1
.
.
.
n = 10, k = 9: 106
n = 10, k = 10: 657
n = 11, k = 10: 235
I used Sage for the last 3, I admit. But, I do know that the Atlas of Graphs contains all of these except for the last one, on P7.
В полном графе с 6 вершинами имеется 15 рёбер, поэтому дополнение графа из условия задачи будет иметь 4 ребра. Графы изоморфны тогда и только тогда, когда изоморфны их дополнения, поэтому достаточно перечислить все попарно неизоморфные графы с 6 вершинами и 4 рёбрами.
Если граф имеет простой цикл, то длина такого цикла равна 3 или 4. Для цикла длиной 4 все рёбра использованы, то есть получается цикл и две изолированные вершины. Пусть есть цикл длиной 3. Тогда четвёртое ребро к нему можно добавить двумя способами. Получится или треугольник с «ножкой» и двумя изолированными вершинами, или треугольник с отрезком и отдельной точкой.
Итак, графов с циклами имеется три. Остальные графы — объединения деревьев. В каждом дереве рёбер на единицу меньше, чем вершин. Поэтому деревьев должно быть два. Варианты (по числу вершин): 5+1, 4+2, 3+3. Дерево с двумя вершинами одно. С тремя вершинами — также одно. Деревьев с четырьмя вершинами два: это цепь, а также «трилистник». Добавляя к таким деревьям ещё одно ребро, чтобы снова получилось дерево, мы видим, что с пятью вершинами имеется три дерева: цепь, четырёхполюсник, и ещё одно дерево, получаемое из трилистника (понятно, какое). Итого у нас имеется три случая графов типа 5+1, два случая типа 4+2, и один случай типа 3+3; итого шесть.
Вместо получается ровно 9 попарно неизоморфных графов.
|
1 0 0 |
1 1 1 |
0 0 0 |
|||||||||
|
0 1 2 |
|||||||||||
|
1 1 1 |
A |
= |
1 0 0 |
. |
|||||||
|
0 11 |
|||||||||||
|
1 2 1 |
2 2 0 |
||||||||||
|
Решая это матричное уравнение, будем иметь |
|||||||||||
|
1 0 0 |
−1 0 0 0 |
1 1 1 |
−1 0 0 0 |
||||||||
|
0 1 2 |
= |
||||||||||
|
A = 1 1 1 |
1 0 0 |
1 1 0 |
. |
||||||||
|
0 1 1 |
|||||||||||
|
1 2 1 |
2 2 0 |
0 2 2 |
Это означает, что f = x + xy + 2x2 y + 2x2 y2 .
§2.1. Основные определения
Определение. Пусть V – произвольное множество, V2 – множество всех его двухэлементных подмножеств, т.е. множество неупорядоченных пар {а, b}, где а, b V. Пара (V, E), где Е – произвольное подмножество V2, называется графом (неориентированным графом). При этом элементы множества V называются вершинами графа, элементы множества E – ребрами. Множества вершин и ребер графа G обозначаются символами V(G) и E(G) соответственно. Вершины и ребра графа называются его
элементами.
В дальнейшем рассматриваются только конечные графы, т.е. множество E предполагается конечным. Число | V(G) | вершин называется его порядком и обозначается через |G|. Если |G| = п, |E(G)| = т, то G называют (п, т)-графом.
Говорят, что две вершины u и v смежны, если множество {u, v} является ребром, и не смежны в противном случае. Если е = {u, v} – ребро, то вершины u и v называют его концами. В этом случае также

говорят, что ребро е соединяет вершины u и v. Такое ребро обозначается символом uv .
Два ребра называются смежными, если они имеют общий конец. Вершина е и ребро v называются инцидентными, если v является концом ребра е, и не инцидентными в противном случае.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии – ребрам. В качестве иллюстрации рассмотрим граф G, изображенный на
|
5 |
4 |
||||||||
|
1 |
2 |
3 |
|||||||
|
Рис. 2.1 |
Рис. 2.2 |
Рис. 2.3 |
|||||||
|
рис. 2.1. |
|||||||||
|
Это (5, 6)-граф, V(G) |
= {1, 2, 3, 4, 5}, E(G) = {{1, 2}, {1, 5}, {2,3}, {2, 4}, |
{2, 5}, {4, 5}}. Вершины 1и 2 смежны, а 1 и 3 не смежны. Вершина 1 и ребро {1, 2} инцидентны.
Иногда в графах допускается наличие петель, т.е. ребер {а, а} (рис. 2.2),
|
и кратных ребер, т.е. ребро {а, b} учитывается несколько раз (рис. 2.3). |
||
|
Мы будем рассматривать графы без петель и |
||
|
кратных ребер. |
||
|
Ориентированный граф – это пара (V, А), где V |
||
|
– множество вершин, А – множество |
||
|
ориентированных ребер (или дуг), т.е. |
||
|
упорядоченных пар (u, v), где u, v V. При этом |
||
|
и называется началом дуги, v – концом. На |
||
|
рисунке дуги отмечаются стрелками, |
Рис. 2.4 |
|
|
указывающими направление от начала к концу |
||
|
(рис. 2.4). |
Графы специального вида
Приведем примеры некоторых графов специального вида.
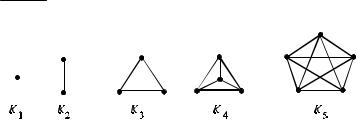
Граф G называется полным, если любые две его вершины смежны, т.е. E(G) = (V(G))(2). Полный граф порядка п обозначается символом Кп, в
нем n(n2−1) ребер. На рис. 2.5 изображены графы Кп, n ≤ 5 .
Рис. 2.5
Граф называется пустым, если в нем нет ребер. Пустой граф порядка п обозначается Оп.
Красивыми примерами являются графы пяти платоновых тел (т.е.
правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра (рис. 2.6).
Ниже неоднократно используются термины “разбиение” и “покрытие”. Набор подмножеств множества S называется покрытием множества S, если объединение этих множеств совпадает с S. Покрытие называется разбиением, если никакие два из входящих в него множеств не пересекаются.
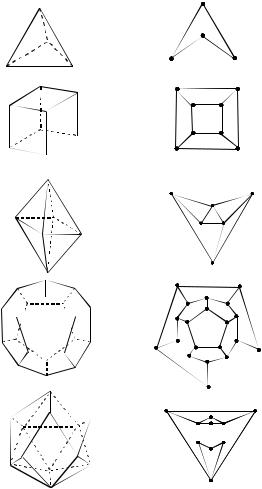
Тетраэдр
Куб
Октаэдр
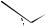
Икосаэдр
Рис. 2.6
Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и

из q вершин обозначается символом K p,q при р = 1 получаем звезду
K1,q . На рис. 2.7 изображены звезда K1,5 и полный двудольный граф
K3,3 .
|
Заметим, что одна из долей двудольного |
||
|
графа может быть пустой. Так, О1 – |
||
|
двудольный граф с одной пустой долей, |
||
|
О2 можно трактовать как двудольный |
||
|
граф с двумя одновершинными долями |
||
|
или как двудольный граф, одна из долей |
Рис. 2.7 |
|
|
которого содержит две вершины, а |
||
|
другая является пустым множеством. |
Изоморфизм графов
Легко подсчитать число графов с фиксированным множеством вершин V. Эти графы различаются своими ребрами, и поэтому их число равно
количеству подмножеств множества V V, т.е. C2 , где п = | V |. Однако
× 2 n
эти графы на всегда следует различать. Как в применении теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа), и связи между объектами (ребра графа). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать. Такие графы называются
изоморфными.
Определение. Пусть G и Н – графы, а ϕ:V (G) →V (H ) – биекция. Если для любых вершин и и v графа G их образы ϕ(u) и ϕ(v) смежны в Н
тогда и только тогда, когда и и v смежны в G, то эта биекция называется изоморфизмом графа G на граф Н. Если такой изоморфизм существует, то мы пишем G H и говорим, что графы G и Н
изоморфны.
Пример 1. Графы, представленные на рис. 2.8 изоморфны, указана
|
1 |
2 |
3 |
1 |
4 |
1 |
4 |
соответствующая |
|||
|
изоморфизмам |
||||||||||
|
нумерация вершин. |
||||||||||
|
5 |
2 |
5 |
2 |
|||||||
|
Графы на рис. 2.9 |
||||||||||
|
неизоморфны |
||||||||||
|
4 |
5 |
6 |
3 |
6 |
6 |
3 |
(например, вследствие |
|||
|
того, что в первом |
||||||||||
Рис. 2.8

Рис. 2.9
графе есть циклы из трех ребер, а во втором их нет).
Очевидно, что отношение изоморфизма графов является
эквивалентностью, т.е. оно симметрично, рефлексивно и транзитивно. Следовательно, все графы разбивается на классы так, что графы из одного класса попарно
изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игнорируется при введении понятия графа. Класс изоморфных графов принято называть
абстрактным графом.
В некоторых случаях приходится различать изоморфные графы. Граф
|
порядка п называется |
||||||
|
1 |
2 |
3 |
помеченным, если его |
|||
|
вершинам присвоены |
||||||
|
некоторые метки, например, |
||||||
|
номера 1, 2, …, п. Отождествив |
||||||
|
2 |
3 |
1 |
3 |
1 |
2 |
каждую из вершин графа с ее |
|
Рис. 2.10. |
номером (а, следовательно, |
|||||
|
множество вершин – с |
множеством чисел {1, 2, …, п}), определим равенство графов G и Н одного и того же порядка: G = Н тогда, когда ЕG = ЕН. На рис. 2.10 изображены три разных помеченных графа.
Число gn помеченных графов порядка п определяется сложно. Известна
формула Пойа
C2
gn ~ 2 n / n! ,
дающая асимптотику числа gn. Эта формула означает, что две функции
C2
g(п)=gn и f(n)= 2 n / n! асимптотически равны, т.е. lim g(n) / f (n) =1.
n→∞
Операции над графами
Граф Н называется подграфом (или частью) графа G, если VH VG, ЕH ЕG. Подграф Н называется остовным подграфом, если VH = VG. Если множество вершин подграфа Н есть U, а множество его ребер
совпадает с множеством всех ребер графа G, оба конца которых принадлежат U, то Н называется подграфом, порожденным множеством U. На рис.2.11 изображены граф G и три его подграфа Н1, Н2 и Н3 , среди которых Н3 является остовным, а Н2 – порожденным. Граф Н называется объединением графов F и G, если V(H) = V(G) V(F) и E(H)= E(G) E(F). В этой ситуации пишут Н = F G.
|
G |
H1 |
H2 |
H3 |
||||||||||||||||
|
4 |
5 |
4 |
5 |
4 |
5 |
4 |
5 |
||||||||||||
|
1 |
2 |
3 |
1 |
2 |
1 |
2 |
1 |
2 |
3 |
||||||||||
|
Рис. 2.11 |
|||||||||||||||||||
|
Объединение F G называется дизъюнктным, если V(G) ∩ V(F) = . |
|||||||||||||||||||
|
Введем операцию произведения графов. Пусть задано два графа |
G1 = |
(V1, E1), G2 = (V2, E2). Произведением графов G1 ×G2 = G называется граф, для которого VG =V1 ×V2 – декартово произведение множеств
вершин исходных графов, а E(G) определяется следующим образом: вершины (и1, и2) и (v1, v2) в графе G смежны тогда и только тогда, когда
или и1 = v1, а и2 и v2 смежны в G2, или и2 = v2, а и2 и v2 смежны в G1 (рис. 2.12).
|
u1 |
(u1 ,v1) (u1 ,v2) (u1 ,v3) |
|||||||||
|
v1 |
v2 |
v3 |
||||||||
|
(u2 |
||||||||||
|
u2 |
,v1) (u2 |
,v2) (u2 ,v3) |
||||||||
|
Рис. 2.12 |
Очевидно, что | V (G1 ×G2 ) |=| V (G1) | | V (G2 ) | ,
| E(G1 ×G2 ) |=|V (G1) | | E(G2 ) | + | E(G1) | |V (G2 ) | .
С помощью операции произведения можно определить п-мерный куб Bn рекуррентно: B1 = K2 , Bn = K2 × Bn−1 .

Покажем, что это определение совпадает с данным ранее. Действительно, V (Bn ) = 2n . Вершины графа Bn можно представить
векторами длины п из 0 и 1 таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются в одной координате.
Для произвольного графа G
следующим образом определяется
дополнительный граф (или дополнение) G : V (G) =V (G) , и
две несовпадающие вершины
|
Рис. 2.13 |
||||
|
смежны в G тогда и только тогда, |
||||
когда они не смежны в G: E(G) =V 2 E(G) (рис. 2.13).
Граф, изоморфный своему дополнению, называется самодопол-
нительным.
Степень вершины
Число ребер, инцидентных некоторой вершине v, называется степенью вершины и обозначается deg v. В полном графе Кп степень каждой вершины равна п – 1. максимальная и минимальная степени вершин графа G обозначаются символами ∆(G) и δ(G) соответственно:
|
∆(G) = max deg v, |
δ (G) = min deg v . |
|
v VG |
v VG |
Вершина степени 0 называется изолированной, вершина степени 1
–концевой (висячей). Ребро, инцидентное концевой вершине, также называется концевым. Вершина графа, смежная с каждой другой его вершиной, называется доминирующей.
Пример 2. В графе Н3 на рис 2.11 вершина 3 – висячая, вершина 2
–доминирующая, ∆(G) = 4, δ (G) =1 .
Пути в графах
Чередующаяся последовательность
|
v1, e1, v2 , e2 , …, vl , el , vl +1 |
(2.1) |
вершин и ребер графа, такая что ei = vivi+1 (i = 1, 2, …, l), называется
путем, соединяющим вершины v1 и vl +1 (или ( v1 , vl +1 )-путем).
Очевидно, что путь можно задать последовательностью
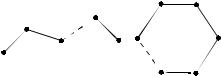
Рис. 2.14
v1, v2 , …, vl , vl +1
его вершин, а также последовательностью его ребер e1, e2 , …, el .
Граф называется связным, если любые две несовпадающие вершины в нем соединены маршрутом.
Путь называется простым, если все его вершины, кроме, может быть, крайних, различны. Путь называется
цепью, если все его ребра различны, и простой цепью, если все его вершины различны. Путь (2. 1) называется циклическим, если
v1 = vl+1 . Циклическая цепь называется циклом, а циклическая
простой путь – простым циклом. Простую цепь, имеющую п вершин, будем обозначать Cn, простой цикл – Zn ( рис.2.14).
Число l ребер в пути (2.1) называется его длиной.
Пример 3. В графе G на рис 2.11 (1, 4, 5, 2, 4) – цепь; (1, 4, 5, 2, 3) –
простая цепь; (1, 4, 5, 2, 4, 1) – циклический путь, не являющийся циклом; (4, 3, 2, 4) – цикл.
Метрические характеристики графа
Пусть G – граф, а и и v – две его несовпадающие вершины. Длина кратчайшего (и, v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинами и и v и обозначается через d(u, v). Положим еще d(u, и) = 0. Очевидно, что введенное таким образом расстояние удовлетворяет аксиомам метрики:
1)d(u, v) ≥ 0,
2)d(u, v) = 0 тогда и только тогда, когда u = v,
3)d(u, v) = d(v, u),
4)d(u, v) + d(v, w) ≥ d(u, w) (неравенство треугольника).
Для фиксированной вершины и величина
e(u) = max d(u, v)
v VG
называется эксцентриситетом вершины и. Максимальный из всех эксцентриситетов вершин графа называется диаметром графа G и обозначается через d(G). Тем самым,
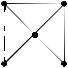
d(G) = max e(u) .
u VG
Вершина v называется периферийной, если e(v) = d(G) .
Простая цепь длины d(G), расстояние между концами которой равно d(G), называется диаметральной цепью.
|
Пример 4. В графе на рис. 2.15 d(1,2) = 1, d(1, 3) = |
4 |
5 |
||
|
2; е(1) = 2; d(G) = 2. Все вершины, кроме вершины |
2 |
|||
|
2 являются периферийными, (1, 2, 3) – |
||||
|
диаметральная цепь. |
||||
|
Минимальный из эксцентриситетов вершин |
||||
|
связного графа называется его радиусом и |
||||
|
обозначается r(G): |
1 |
3 |
||
|
r(G) = min e(u) = min max d(u, v) . |
Рис. 2.15 |
|||
|
u VG |
u VG v VG |
Очевидно, что радиус графа не больше его диаметра.
Вершина v называется центральной, если e(v) = r(G) . Множество
всех центральных вершин графа называется его центром. Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин.
Решение типовых задач
1.Доказать, что сумма степеней всех вершин графа равно удвоенному числу ребер (лемма о рукопожатиях).
Решение. Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 1 два раза (оно учитывается в степенях двух вершин). Поэтому сумма степеней всех вершин графа равно удвоенному числу ребер.
2.Найти все неизоморфные графы четвертого порядка.
Решение. У графа четвертого порядка число ребер может быть от 0 в пустом графе О4 до 6 в полном графе K4.
Если | E(G) |= 0 , получаем единственный граф О4.
Если | E(G) |=1 – тоже единственный граф с двумя изолированными
вершинами, и двумя смежными друг другу.
При | E(G) |= 2 получаем два графа: ребра смежные и нет.

4
При | E(G) |= 3 , имеем ∑deg(vi ) = 2 | E(G) |=6 . Если изолированных
i=1
вершин нет, то возможные наборы степеней вершин: 1, 1, 2, 2 и 1, 1, 1, 3. Если изолированная вершина одна, то нет вершины со степенью 3, и возможный набор степеней вершин 2, 2, 2, т.е. цикл. Двух изолированных вершин быть не может.
Если | E(G) | = 4 , получаем, что из полного графа удалены два ребра:
либо смежные, либо нет. Получаем два графа.
Если | E(G) | = 5 получаем единственный граф удалением из полного
графа одного ребра.
Все неизоморфные графа порядка 4 представлены на рис. 2.16.
Рис. 2.16
3. Доказать, что если число ребер графа порядка п > 2 больше, чем
Cn2−1 , то он связен.
Решение. Предположим, что он не связен. Тогда существуют две вершины а и b, не связанные между собой. Обозначим через 1 множество вершин, достижимых из а, через V2 – множество вершин, достижимых из b. Тогда ни одна вершина из V2 не связана ни с какой вершиной из V1 . Пусть |V1| = k < n, k > 0. Тогда |V2| = n – k > 0. Если k
|
= 1, то |V2| = n – 1 и наибольшее значение |E| равно |
(n−1)(n−2) |
(когда |
|
|
2 |
|||
подграф, порожденный V2 – полный), что противоречит условию. При k ≥ 2 наибольшее значение достигается, если подграфы, порожденные V1
|
и V2 |
– полные. Тогда, | E |
|= |
k(k −1) |
, |
| E |
2 |
|= |
(n − k)(n − k −1) |
, и для |
|
1 |
2 |
2 |
|||||||
всего графа имеем
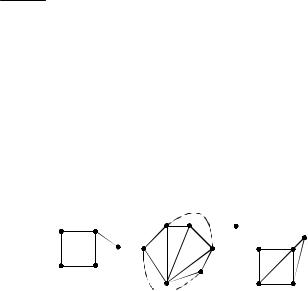
|
| |
E |=| E |
| + | E |
2 |
|= |
k(k −1) |
+ |
(n − k)(n − k −1) |
= |
n2 − 2nk + 2k 2 − n |
= |
||
|
1 |
2 |
2 |
2 |
|||||||||
|
= |
(n −1)(n − 2) + 2(n −1− nk + k 2 ) |
= Cnk−1 + (n −1)(1− k) < Cnk−1 , |
||||||||||
|
2 |
что противоречит условию, следовательно, исходный граф связен.
4. Доказать, что в связном графе любые две простые цепи максимальной длины имеют общую вершину.
Решение. Предположим, что у двух простых цепей u1, u2 , …, uk и v1, v2 , …, vk максимальной длины нет общих вершин. Возьмем произвольно по одной вершине из каждой цепи ui и v j . Так как граф
связный, то существует путь из ui в v j . Выберем из отрезков цепей от u1 до ui и отui до uk тот, длина которого не меньше k / 2 . Аналогично для v j . Составим новую простую цепь из этих отрезков и простой цепи,
соединяющей ui и v j , ее длина больше k , что противоречит тому, что
исходные цепи максимальны.
Задачи для самостоятельного решения
1.Доказать, что число ребер в полном графе Кп порядка п равно
n(n −1) . 2
2.Найти |V(Bn)|, |E(Bn)|, где Bn – п-мерный куб.
3.Найти количество неизоморфных графов, имеющих 7 вершин и 20 ребер.
4.Найти количество неизоморфных графов, имеющих 10 вершин и 43 ребра.
5.Найти все попарно неизоморфные графы пятого порядка.
6.Найти число помеченных графов, имеющих п вершин и т ребер.
7.Доказать, что если порядок самодополнительного графа равен п, то
п ≡ 0 (mod 4) или п ≡ 1 (mod 4).
8.Найти самодополнительный граф с минимальным, отличным от 1 числом вершин.
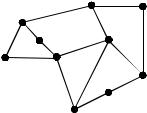
9.Изобразить граф, являющийся дополнением графа G (рис. 2.17).
а)

Рис. 2.17
10.Доказать, что не существует графа, степени всех вершин которого попарно различны.
11.Существует ли граф со следующим набором степеней вершин:
а)1, 1, 1, 3, 3, 4, 4;
б)1, 1, 2, 2, 2, 3, 3, 4?
Определяется ли граф однозначно набором степеней вершин?
12.Построить граф с данным набором степеней вершин:
а)1, 1, 2, 2, 2; б) 1, 2, 2, 2, 3, 4.
13.Доказать, что в любом графе число вершин нечетной степени четно.
14.Существует ли граф с шестью вершинами, у которого степени всех вершин равны 3?
15.Доказать, что любой путь, соединяющий вершины u и v, содержит простую цепь, соединяющую те же вершины.
16.Сколько существует путей длины 3 из вершины (0, 0, 0) в (1, 1, 1) в графе В3?
17.Доказать, что в двух простых цепях максимальной длины связного графа совпадают средние вершины, если k – четное, и одна из двух средних вершин одной цепи совпадает с одной из двух средних вершин другой цепи, если k – нечетное.
18.Привести пример цикла, не являющегося простым.
19.Доказать, что всякий цикл содержит простой цикл.
20.Доказать, что объединение двух несовпадающих простых (u, v)- цепей содержит простой цикл.
21.Пусть С и D – два несовпадающих простых цикла, имеющих общее ребро е. Доказать, что граф (С D) e содержит простой цикл.
22.Показать, что расстояние между вершинами графа удовлетворяет аксиомам метрики.
23.Доказать, что если δ(G) ≥ (п – 1)/2, то граф G связен.
24.Построить граф, центр которого
а) состоит ровно из одной вершины; б) состоит ровно из трех вершин и
не совпадает с множеством всех вершин; в) совпадает с множеством всех вершин.
Рис.2.18
25.Доказать, что диаметр графа не превосходит его удвоенного радиуса.
26.Привести пример графа, диаметр и радиус которого равны.
27.Найти расстояние d(u, v) в графе, изображенном на рис. 2.18.
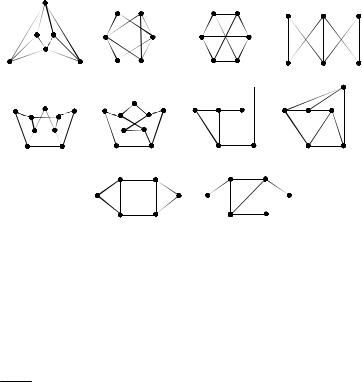
28.Какие из пар графов на рис. 2.19 изоморфны?
29.Докажите, что отношение изоморфизма графов является отношением эквивалентности.
|
a) |
б) |
|||||
в)
д)
Рис. 2.19
Ответы
1.Указание. Степень каждой вершины равна п – 1. Сумма степеней вершин равна удвоенному числу ребер. 2. |V(Bn)| = 2п, |E(Bn)| = п2п – 1.
3.1. Указание: посчитать, сколько ребер удалено из полного графа. 4.
2.5. Указание: рассмотреть возможные наборы степеней вершин.
6. Cm( −1) . Указание: рассмотреть полный граф и выяснить, скольким
n n
2
способами можно выбрать из него те ребра, которые остаются в искомом. 7. Указание: удвоенная сумма числа ребер графа равна числу ребер полного графа. 8. Указание: рассмотрев наборы степеней вершин, доказать, что среди графов порядка 4 самодополнительных нет
подсчёт кол-ва неизоморфных графов
, все варианты попарно неизоморфных графов
- Подписаться на тему
- Сообщить другу
- Скачать/распечатать тему
|
|
|
|
Во первых приветсвую всех юзеров,профи программеров и админов сего ресура, ну и поздравляю с праздниками. Написать программу на любом языке программирования (желательно на С, подсчитывающюю количество попарно НЕ изоморфных графов с n вершинами и 4мярёбрами. тоесть надо написать программу , где вводиться кол-во вершин и выводиться количество попарно неизоморфных графов (графы неориентированы и не имеют петель). Сообщение отредактировано: VzLOM — 06.01.05, 13:51 |
vk |
|
|
Рейтинг (т): 39 |
В каких конкретно местах встал? Давай свою эту пару мест. Если успею и смогу, помогу. Хотя скорее всего, кто-нибудь более умный и быстрый раньше поможет. |
|
VzLOM |
|
|
фурмулировка и определения связанные с изоморфностью ясны, как сравнивать 2 графа тоже понятно (просто сравниваюца степени вершин — т.е. кол-во единиц в столбцах и строках матрицы смежностти), больше пугают слова «попарно» и «кол-во» |
|
mo3r |
|
|
А не проще ли просто строить неизморофные — их всего-то ничего. Добавлено 06.01.05, 18:03 |
|
VzLOM |
|
|
да, но варианты должен разбирать комп, и ещё я не очень понял почему при n>8 такойже ответ что и при 8 |
vk |
|
|
Рейтинг (т): 39 |
Цитата mo3r,6.01.05, 20:57 @ 07.01.70, 13:33 А не проще ли просто строить неизморофные — их всего-то ничего. Безусловно, проще. А как найти количество всех неизоморфных? Неужели только перебором? Ну, в конце концов, можно и перебором. Это же курсовой, а не оптимизационная задача. Цитата mo3r,6.01.05, 20:57 @ 07.01.70, 13:33 Во-первых, если n>=8, то, по-моему, ответ будет такой же, как и при n=8. Да, мне тоже так показалось. Ведь ребер всего четыре, так? Значит, на 8 вершинах мы получаем последний раз увеличение числа неизоморфных — вариант, когда ни одно ребро не смежно другому. Для n>8 новых вариантов не появится. Цитата VzLOM,6.01.05, 21:52 @ 07.01.70, 13:34 да, но варианты должен разбирать комп Оно конечно, но никто тебе не мешает решение первых двух (а то и трех) вариантов (0 и 1 вершина) задать жестко. Чтобы зря алгоритм не гонять. Сообщение отредактировано: vk — 06.01.05, 19:36 |
|
VzLOM |
|
|
может ктонить накидает пример такого алгоритма, потомучто мне в мою, необременённую большими мозговыми ресурсами, голову ничё пока не приходит на ум |
|
mo3r |
|
|
Суть алгоритма: Проверку изоморфности делаем так: считаем степень каждой вершины, сортируем их в порядке возрастания. Два графа изоморфны тогда и только тогда, когда они (отсортированные массивы степеней) равны. (По поводу этого я не совсем уверен, но должно быть так). По A граф строится так: есть матрица смежности C[1..n,1..n]. Она строится так (нас интересует только часть выше главной диагонали): для каждого i = 1..4: увеличиваем на единицу C[A[2*i-1],A[2*i]]. |
0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)
0 пользователей:
- Предыдущая тема
- Алгоритмы
- Следующая тема
[ Script execution time: 0,0348 ] [ 15 queries used ] [ Generated: 28.05.23, 08:54 GMT ]
Другой предмет 10-11 класс
50 баллов
сколько существует попарно неизоморфных графов с 10 вершинами и 43 ребрами
Ирина Каминкова
22.09.2020 21:54:01
Предполагаем граф без петель и кратных ребер.
В полном графе с 10 вершинами имеется 10*9/2 = 45 ребер.
Дополнением к данному графу будет граф с 2-мя ребрами.
Графы изоморфны тогда и только тогда, когда изоморфны их дополнения, поэтому достаточно перечислить все попарно неизоморфные графы с 10 вершинами и 2 ребрами.
В графе с 2 ребрами циклов нет.
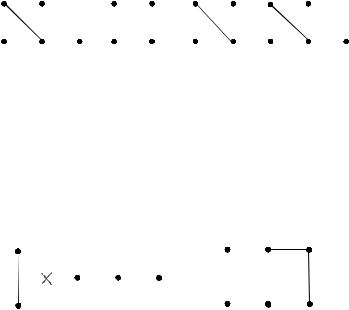
Неизоморфных графов с 2 ребрами 2:
1) «уголок», в котором двумя ребрами соединены 3 точки
2) две «палки», в которых двумя ребрами соединены 2*2=4 точки
Ответ: 2
Ответ эксперта
Все предметы
Рейтинг пользователей
















 тоесть надо както прогнать вначале все возможные графы (матрицы), потом их попарно сравнить и подсчитать неизоморфные.
тоесть надо както прогнать вначале все возможные графы (матрицы), потом их попарно сравнить и подсчитать неизоморфные. 


