Как найти количество листьев в дереве - Avtoru.top

ВНИМАНИЕ

Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru

Иногда мне приходится находить количество листьев в поисковом двоичном дереве. Решил ( в первую очередь для себя ) написать эту заметку-шпаргалку, чтобы при необходимости быстро вспомнить алгоритм.

Хочу рассмотреть следующее анонимное двоичное дерево поиска:

Рисунок — стандартное анонимное бинарное дерево поиска

➡ Очевидно, чтобы найти количество листьев в бинарном дереве, необходимо знать определения термина «лист», чтобы понимать, а что, собственно, ищем-то.

Лист — узел поискового двоичного дерева, который не имеет потомков.

Тогда я отмечу все листовые узлы на рассматриваемом анонимном дереве красным цветом:

Рисунок — двоичное дерево поиска, у которого листовые вершины закрашены красным цветом

Моя задача — понять, каким образом найти все эти «красные» вершины, являющиеся листьями. То есть мне нужна функция, которая в качестве результата вернет количество листьев двоичного дерева.

Я хочу посмотреть на это анонимное поисковое бинарное дерево со всеми связями, на котором выделены красным цветом все листовые узлы с их связями:

Рисунок — бинарное дерево поиска со всеми связями его вершин

Внимательно изучив топологию этого дерева стало понятно, что листовые узлы прекращают порождение новых узлов, так как у них нет потомков ( кстати, в соответствии с их определением ). Следовательно, если встретился лист, то сразу можно делать возврат. Нет никакого смысла спускаться ниже, доходя до NULL-указателей.

Поскольку искомая программная функция должна в качестве результата возвращать количество листьев в бинарном дереве поиска, то я буду возвращать «$+1$», когда встретится лист. Понятно, что мне потребуется запустить обход вершин всего поискового дерева.

В итоге я написал следующую мощную функцию, которая считает количество листов:

//——————————————————————————

// нахождение количества листьев в двоичном дереве поиска

//——————————————————————————

int Get_leafs_count( const Node* const node )

{

Node_status status = Get_status_node( node );

if ( status == NONE )

{

return 0;

}

if ( status == LEAF )

{

return 1;

}

return Get_leafs_count( node -> left ) + Get_leafs_count( node -> right );

}

//——————————————————————————

Также напомню, что собой представляет пользовательский тип данных Node_status:

//——————————————————————————

// статус узла бинарного дерева поиска

//——————————————————————————

typedef enum Node_status

{

NONE, // нет узла ( NULL-указатель )

LEAF, // пустой узел ( лист — не имеет сыновей )

HALF, // половинчатый ( имеет одного сына: левого или правого )

FULL // полный ( имеет обоих сыновей )

} Node_status;

//——————————————————————————

Функция Get_leafs_count является максимально универсальной. Даже, если на вход этой функции передать пустое дерево, то она корректно обработает такую ситуацию и в качестве ответа вернет $0$. При этом данная функция является достаточно сложной для понимания, так как использует каскадную рекурсию.

➡ Думаю, что теперь я легко смогу брать алгоритм и программную функцию для своих проектов, связанных с обработкой бинарного дерева поиска.

В комментариях пишите, что непонятно в рамках этой функции. Если непонятно, что это за функция Get_status_node, которая вызывается внутри функции Get_leafs_count, то попробуйте реализовать ее самостоятельно. Цель этой функции — определение статуса узла поискового дерева. Кстати, в одной из своих заметок, я детально рассказываю об этой функции и привожу ее программную реализацию.

ВНИМАНИЕ

Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru

Источник

I am trying to write a function that calculates the number of leaves of a binary tree by incorporating my BinaryTree class:

This is my BinaryTree class:

class BinaryTree:

def __init__(self, data):
    self.data = data
    self.left = None
    self.right = None

def insert_left(self, new_data):
    if self.left == None:
        self.left = BinaryTree(new_data)
    else:
        t = BinaryTree(new_data)
        t.left = self.left
        self.left = t

def insert_right(self, new_data):
    if self.right == None:
        self.right = BinaryTree(new_data)
    else:
        t = BinaryTree(new_data)
        t.right = self.right
        self.right = t

def get_left(self):
    return self.left

def get_right(self):
    return self.right

def set_data(self, data):
    self.data = data

def get_data(self):
    return self.data

And this the function that I wrote: at the moment its not outputting the right values. I think there is something wrong with my recursion but I cannot figure it out:

def num_leaves(my_tree):
    count = 0
    if my_tree.get_left() and my_tree.get_right() is None:
        count += 1
    if my_tree.get_left():
        num_leaves(my_tree.get_left())
    if my_tree.get_right():
        num_leaves(my_tree.get_right())

    return count

an example of an input and output would be:

a = BinaryTree(1)
a.insert_left(2)
a.insert_right(3)
print(num_leaves(a))

output:

instead of 2.

The idea behind my function is that it recurs until it finds a node where the left and right subtree are None, then it adds one to count. This way it finds each leaf.

What am I doing wrong?

Источник

Подсчёт листьев бинарного дерева

20.04.2021, 21:28. Показов 4375. Ответов 10

Здравствуйте, такое задание:
Создать сбалансированное дерево поиска с числами от -50 до 50 и распечатать информацию прямым, обратным обходом и по возрастанию. Сделать функции добавления нового значения, удаления значения и поиска. Всю память надо освободить.
а) Посчитать число листьев в дереве.
б) удалить элементы кратные X.
В общем-то практически всё сделала, но функция подсчёта листьев печатает пустой результат, всё остальное, вроде, работает. (Хотя не уверена в том, что моё дерево сбалансированное, хотя код из методички)
Вот код:

C++

#include <iostream>
#include <Windows.h>
 
using namespace std;
 
struct tree
{
    int inf;
    tree* left;
    tree* right;
}; tree *proot;
 
tree* addtree(tree* proot, int inf) //Добавление нового элемента
{
    tree* nl, * pr = NULL, * ps;
    bool b;
    nl = new tree;
    nl->inf = inf;
    nl->left = NULL;
    nl->right = NULL;
    if (proot == NULL)
        return nl;
    ps = proot;
    while (ps != NULL)
    {
        pr = ps;
        b = (inf < ps->inf);
        if (b)
            ps = ps->left;
        else
            ps = ps->right;
    }
    if (b)
        pr->left = nl;
    else
        pr->right = nl;
    return proot;
}
 
void uptodowntree(tree* p) //Обход всего дерева в прямом порядке сверху вниз
{
    if (NULL == p) return;
        uptodowntree(p->left);
        cout << p->inf << "t";
        uptodowntree(p->right);
}
 
void downtouptree(tree* p) // Обход всего дерева в обратном порядке снизу вверх
{
    if (NULL == p) return;
        downtouptree(p->right);
        cout << p->inf << "t";
        downtouptree(p->left);
}
 
tree* findtree(tree* p, int key)
{
    if (p == NULL)
    {
        return NULL;  // не найден
    }
    if (p->inf == key)
    {
        return p; // нашли!!!
    }
 
    if (key <= p->inf)
    {
        // left
        if (p->left != NULL)
            return findtree(p->left, key); // рекурсивный поиск влево
        else
        {
            return NULL; // не найден
        }
    }
    else
    {
        //right
        if (p->right)
            return findtree(p->right, key);// рекурсивный поиск вправо
        else
        {
            return NULL; // не найден
        }
    }
}
 
tree* deletetree(tree* p) // Удаление всего дерева
{
    if (p == NULL)
        return NULL;
    deletetree(p->left);
    deletetree(p->right);
    delete(p);
    p = NULL;
    return NULL;
}
 
tree* deletelist(tree* proot, int inf) //Удаление элемента с заданным ключом
{
    tree* ps = proot, * pr = proot, * w, * v = NULL;
    while ((ps != NULL) && (ps->inf != inf)) // Поиск удаляемого узла
    {
        pr = ps;
        if (inf < ps->inf)
            ps = ps->left;
        else
            ps = ps->right;
    }
    if (ps == NULL) //Если узел не найден
        return proot;
    if ((ps->left == NULL) && (ps->right == NULL)) //Если узел не имеет дочерей
    {
        if (ps == pr) //Если это был последний элемент
        {
            delete(ps);
            return NULL;
        }
        if (pr->left == ps) //Если удаляемый узел слева
            pr->left = NULL;
        else //Если удаляемый узел справа
            pr->right = NULL;
        delete(ps);
        return proot;
    }
    if (ps->left == NULL) // Если узел имеет дочь только справа
    {
        if (ps == pr) // Если удаляется корень
        {
            ps = ps->right;
            delete(pr);
            return ps;
        }
        if (pr->left == ps) // если удаляемый узел слева
            pr->left = ps->right;
        else // если удаляемый узел справа
            pr->right = ps->right;
        delete(ps);
        return proot;
    }
    if (ps->right == NULL) // если узел имеет дочь только слева
    {
        if (ps == pr) // если удаляется корень
        {
            ps = ps->left;
            delete (pr);
            return ps;
        }
        if (pr->left = ps) //если удаляемый узел слева
            pr->left = ps->left;
        else // Если удаляемый узел справа
            pr->right = ps->left;
        delete(ps);
        return proot;
    }
    w = ps->left; //Если узел имеет двух дочерей
    if (w->right == NULL) //Если максимальный следует за ps
        w->right = ps->right;
    else //Если максимальный не следует за ps
    {
        while (w->right != NULL)
        {
            v = w;
            w = w->right;
        }
        v->right = w->left;
        w->left = ps->left;
        w->right = ps->right;
    }
    if (ps == pr) // если удаляется корень
    {
        delete(ps);
        return w;
    }
    if (pr->left = ps)  //если удаляемый узел слева
        pr->left = w;
    else  //если удаляемый узел справа
        pr -> right = w;
    delete(ps);
    return proot;
}
 
void freemem(tree* p)
{
    if (p != NULL)
    {
        freemem(p->left);
        freemem(p->right);
        delete (p);
    }
}
 
size_t CoutTerminal(tree* proot) //подсчёт листьев
{
    size_t result;
    if ((proot->left == NULL) && (proot->right == NULL))
    {
        result = 1;
    }
    else
    {
        result = 0;
    }
    if (proot->left)
    {
        result += CoutTerminal(proot->left);
    }
    if (proot->right)
    {
        result += CoutTerminal(proot->right);
    }
    return result;
}
 
tree* del_leaves(tree* root, int x) { //Функция удаления листьев бинарного дерева кратных Х
    if (!root)
        return 0;
    if (!root->left && !root->right && !(root->inf % x)) {
        delete(root);
        return 0;
    }
    root->left = del_leaves(root->left, x);
    root->right = del_leaves(root->right, x);
    return root;
}
 
int main()
{
    SetConsoleCP(1251);
    SetConsoleOutputCP(1251);
 
    int ch; int a, b, k; char del;
    int kolvo;
    int delel;
    struct tree* starttree = 0;
    struct tree* q = NULL;
 
    while (1)
    {
        ch = Choice();
 
        if (ch == 1)
        {
            cout << "Введите количество ветвей: ";
            cin >> kolvo;
            cout << endl;
            if (kolvo > 0)
            {
                for (int i = 0; i < kolvo; i++)
                {
                    do
                    {
                    cout << "Введите значение " << i + 1 << " узла: ";
                    cin >> a;
                    starttree = addtree(starttree, a);
                    } while ((a > 50) || (a < -50));
                }
            }
                else
                  cout << "Повторите ввод!" << endl;
        }
        else if (ch == 2)
        {
            cout << "Введите значение нового узла: ";
            cin >> b;
            addtree(starttree, b);
        }
        else if (ch == 3)
        {
            cout << "Введите элемент, который нужно найти: ";
            cin >> k;
            cout << endl;
            q = findtree(starttree, k);
            if (q)
            {
                cout << "Найденный элемент: " << q->inf;
                cout << endl;
                cout << "Вы хотите удалить элемент (y,n): ";
                cin >> del;
                if (del == 'y')
                {
                    deletelist(starttree, q->inf);
                    cout << endl;
                    cout << "Запись успешно удалена!" << endl;
                }
            }
            else
            {
                cout << endl;
                cout << "Элемент не найден!";
            }
        }
 
        else if (ch == 4)
        {
            uptodowntree(starttree);
        }
 
        else if (ch == 5)
        {
            downtouptree(starttree);
        }
 
        else if (ch == 6)
        {
            cout << "Число листьев в дереве: ";
            CoutTerminal(starttree);
            cout << endl;
        }
 
        else if (ch == 7)
        {
            cout << "Введите элемент X, кратно которому нужно удалить элементы: ";
            cin >> delel;
            del_leaves(starttree, delel);
        }
 
        else if (ch == 8)
        {
            system("cls");
        }
 
        else if (ch == 9)
        {
            exit(0);
        }
    }
    return 0;
}

Добавлено через 2 минуты
Ещё не уверена в правильности удаления, в принципе, в задании не уточняется, как его правильно делать. Но, когда я ввожу числа: 4, 3, 5, 1, 7, 8, 6, 2, 9, 12, то удаляется только 6 и 12, оно и понятно, в принципе, 3 и 9 не удаляется, потому что есть листья дальше, а у 6 и 12 указатели на left и right = NULL. В принципе, я думаю, что меня устраивает, но, можно ли как-то сделать удаление прям всех кратных элементов и вывод оставшихся, чтоб ветви соединялись как-то

Источник

Здравствуйте, у меня вроде все получилось сделать, только, почему всегда ответ получается 0, как это можно исправить

#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h> 
 
//структура, описывающая узел бинарного дерева 
typedef struct node
{   
    char str[200];
    int kol;
    node *left;
    node *right;
} tree; 
 
void create(tree **root);
void add(tree **root, char word[], int i);
void print(tree *root);//Обход в прямом порядке
void print2(tree *root);//Симметричное отображение
void print3(tree *root);//реверсивный вывод
int list_count(tree *root);
 
int main() 
{ 
        int result = 0;
        tree *root = NULL; 
        create(&root);//создание
        print(root);//вывод прямой
//      print2(root); //симметричный
//      print3(root); //реверсивный
        list_count(root);
        printf("n%dn", result);
        return 0;
}

void create(tree **root)
{
    FILE *in;
    int i = 0;
    char word[20];
    char a;
 
    if((in = fopen("C:\text.txt", "r")) == NULL)
    {
        printf("nError opening filen");
    }
    else
    {
        while(!feof(in))
        {
            fread(&a, sizeof(char), 1, in);
            if(a != ' ')
            {
                if(a != 'n')
                {
                    word[i] = a;
                    word[i + 1] = '';
                    i++;
                }
            }
            if(( a == ' ') || (a == 'n'))
            {
                add(root, word, i);
                i = 0;
            }
        }
    }
    fclose(in);
}
 
void add(tree **root, char word[], int i)
{
    if((*root) == NULL)
    {
        (*root) = (tree *)malloc(sizeof(node));
        strncpy((*root)->str, word, sizeof(char) * (i + 1));
        (*root)->kol = 1;
        (*root)->right = NULL;
        (*root)->left = NULL;
        return;
    }
    if(strcmp(word, (*root)->str) > 0)
    {
        add(&(*root)->right, word, i);
    }
    else if(strcmp(word, (*root)->str) < 0)
    {
        add(&(*root)->left, word, i);
    }
    else
        (*root)->kol++;
}
void print(tree *root) //в прямом порядке
{ 
 
    if (root!=NULL) 
    {  
        printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
        print(root->left);
        print(root->right);
    } 
}
void print2(tree *root)//симметричный порядок
{
        
    if (root!=NULL) 
    {  
        print2(root->left);
        printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
        print2(root->right);
    } 
 
}
void print3(tree *root)//реверсивный вывод
{
    
    if (root!=NULL) 
    {  
        print3(root->left);
        print3(root->right);
        printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
    } 

}
int list_count(tree *root)
{
        int result;
         if ((root->left==NULL)&&(root->right==NULL))
        {
            result = 1;
        }
        else
        {
            result = 0;
        }
        if (root->left)
        {
            result += list_count(root->left);
        }
        if (root->right)
        {
            result += list_count(root->right);
        } 
        return result;
 
}

Найдите ошибку или как посоветуете исправить

Люди, это же должно быть просто

Код к задаче: «Найти количество листьев в дереве»

Источник

В
приведенных ниже алгоритмах предполагается,
что узел (элемент) дерева декларирован
сл

Type

PNode
= ^TNode;

TNode
= record

Data
: integer; {информационное
поле}

left,right
: PNode;

end;

едующей записью:

А1. Вычисление суммы значений информационных полей элементов

Алгоритм
реализован в виде функции, возвращающей
значение суммы информационных полей
всех элементов. Тривиальным считается
случай, когда очередной узел – пустой,
и, следовательно, не имеет информационного
поля.

function
Sum(Root : PNode) : integer;

begin

if
Root=Nil then
{узел
— пустой}

Sum
:= 0

else

Sum
:= Root^.Data + Sum(Root^.left)

+
Sum(Root^.right);

{end
if}

end;

Для
нетривиального случая результат
вычисляется как значение информационного
элемента в корне (Root^.Data)
плюс суммы информационных полей левого
и правого поддеревьев.

А
выражение Sum(Root^.left)представляет
собой рекурсивный вызов левого поддерева
для данного корня Root.

А2. Подсчет количества узлов в бинарном дереве

function
NumElem(Tree:PNode):integer;

begin

if
Tree = Nil then

NumElem
:= 0

else

NumElem
:= NumElem(Tree^.left)

+
NumElem(Tree^.right) + 1;

{end
if}

end;

А3. Подсчет количества листьев бинарного дерева

function
Number(Tree:PNode):integer;

begin

if
Tree = Nil then

Number := 0 {дерево
пустое – листов нет}

else
if (Tree^.left=Nil)
and (Tree^.right=Nil) then

Number
:= 1 {дерево
состоит из одного узла — листа}

else

Number
:= Number(Tree^.left) + Number(Tree^.right);

{end
if}

end;

Анализ
приведенных алгоритмов показывает, что
для получения ответа в них производится
просмотр всех узлов дерева. Ниже будут
приведены алгоритмы, в которых порядок
обхода узлов дерева отличается. И в
зависимости от порядка обхода узлов
бинарного упорядоченного дерева, можно
получить различные результаты, не меняя
их размещения.

Примечание:
Просмотр
используется не сам по себе, а для
обработки элементов дерева, а просмотр
сам по себе обеспечивает только некоторый
порядок выбора элементов дерева для
обработки. В приводимых ниже примерах
обработка не определяется; показывается
только место, в котором предлагается
выполнить обработку текущего

А4. Алгоритмы просмотра дерева

Самой
интересной особенностью обработки
бинарных деревьев является та, что при
изменении порядка просмотра дерева, не
изменяя его структуры, можно обеспечить
разные последовательности содержащейся
в нем информации. В принципе возможны
всего четыре варианта просмотра:
слева-направо, справа-налева, сверху-вниз
и снизу-вверх. Прежде чем увидеть, к
каким результатам это может привести,
приведем их.

а.
Просмотр дерева слева – направо

procedure
ViewLR(Root:PNode); {LR -> Left – Right }

begin

if
Root<>Nil then

begin

ViewLR(Root^.
left); {просмотр
левого поддерева}

{Операция
обработки корневого элемента –

вывод
на печать, в файл и др.}

ViewLR(Root^.right);
{
просмотр правого поддерева
}

end;

б.
Просмотр справа налево

procedure
ViewRL(Root:PNode); {LR -> Right – Left}

begin

if
Root<>Nil then

begin

ViewRL(Root^.right);
{просмотр
правого поддерева}

{Операция
обработки корневого элемента –

вывод
на печать, в файл и др.}

ViewRL(Root^.left);
{
просмотр левого поддерева
}

end;

в.
Просмотр сверху – вниз

procedure
ViewTD(Root:PNode); {TD –> Top-Down}

begin

if
Root<>Nil then

begin

{Операция
обработки корневого элемента –

вывод
на печать, в файл и др.}

ViewTD(Root^.left);
{просмотр
левого поддерева}

ViewTD(Root^.right);
{
просмотр правого поддерева
}

end;

г.
Просмотр снизу-вверх

procedure
ViewDT(Root:PNode); {DT –> Down — Top}

begin

if
Root<>Nil then

begin

ViewDT(Root^.left);
{просмотр
левого поддерева}

ViewDT(Root^.right);
{
просмотр правого поддерева
}

{Операция
обработки корневого элемента –

вывод
на печать, в файл и др.}

end;

Пример
1. Рассмотрим
результаты просмотра для приведенных
алгоритмов, при условии, что обработка
корневого элемента сводится к выводу
значения его информационного поля, а
дерево в этот момент имеет следующие
узлы:

Результаты
просмотра:

Алгоритм «Слева направо»	1, 3, 7, 10, 70, 96, 98
Алгоритм «Справа налево»	98, 96, 70, 10, 7, 3, 1
Алгоритм «Сверху вниз»	10, 3, 1, 7, 96, 70, 98

Из
приведенной таблицы видно, что, просто
изменяя порядок просмотра дерева
(слева-направо и справа-налево), можно
получить отсортированные по возрастанию
или по убыванию числа.

Пример
2. Пусть в
узлах дерева расположены элементы
арифметического выражения:

Р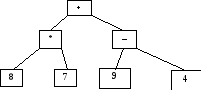езультаты
просмотра:

«Слева направо»	8 * 7 + 9 – 4	инфиксная форма записи выражения
«Сверху вниз»	+ * 8 7 – 9 4	префиксная форма записи выражения
«Снизу вверх»	8 7 * 9 4 – +	постфиксная форма записи выражения

{
Определить
существование значения SearchValue

и
вернуть указатель на элемент, содержащий
его,

или
вернуть Nil,
если
элемент не найден}

function
Search(SearchValue:integer;Root:PNode):PNode;

begin

if
(Root=Nil) or
(Root^.Data=SearchValue) then

Search
:= Root

else
if
(Root^.Data > SearchValue) then

Search
:= Search(SearchValue,Root^.left)

else

Search
:= Search(SearchValue,Root^.right);

{end
if}

end;

5. Поиск элемента
в двоичном упорядоченном дереве

Вывод.
Тексты приведенных алгоритмов очень
компактны и просты в понимании.

В
заключение отметим, что рекурсивные
алгоритмы широко используются в базах
данных и при построении компиляторов,
в частности для проверки правильности
записи арифметических выражений,
синтаксис которых задается с помощью
синтаксических диаграмм.

Для
закрепления материала предлагается
решить следующую задачу:

Данные
о студентах содержат фамилию и три
оценки, полученные на экзаменах. Занести
их с клавиатуры или из текстового файла
в бинарное дерево поиска, упорядоченное
по значению средней оценки. Затем вывести
на экран список студентов, упорядоченный
по убыванию средней оценки. Кроме фамилий
вывести все три оценки и их среднее
значение с точностью до одного знака
после запятой.

Соседние файлы в папке лекции