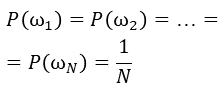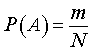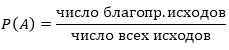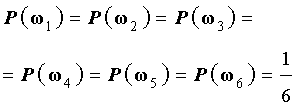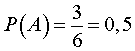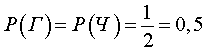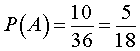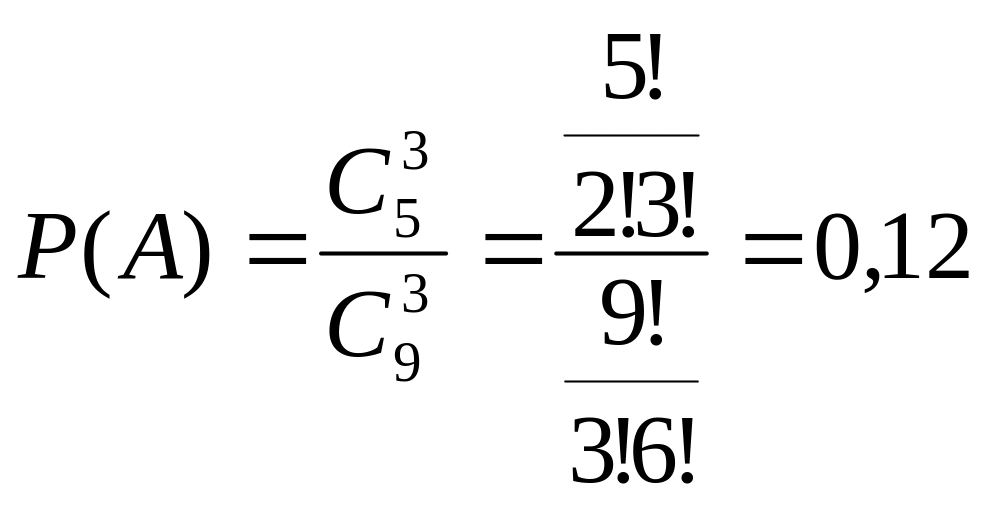Лучшее спасибо — порекомендовать эту страницу
Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами или элементарными событиями. Исход называется благоприятствующим появлению события $А$, если появление этого исхода влечет за собой появление события $А$.
Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 
Вероятностью события $A$ называют отношение числа $m$ благоприятствующих этому событию исходов к общему числу $n$ всех равновозможных несовместных элементарных исходов, образующих полную группу
$$P(A)=frac{m}{n}. quad(1)$$
Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству $0 le P(A) le 1$ .
Полезные материалы
Онлайн-калькуляторы
Большой пласт задач, решаемых с помощью формулы (1) относится к теме гипергеометрической вероятности. Ниже по ссылкам вы можете найти описание популярных задач и онлайн-калькуляторы для их решений:
- Задача про шары (в урне находится $k$ белых и $n$ черных шаров, вынимают $m$ шаров…)
- Задача про детали (в ящике находится $k$ стандартных и $n$ бракованных деталей, вынимают $m$ деталей…)
- Задача про лотерейные билеты (в лотерее участвуют $k$ выигрышных и $n$ безвыигрышных билета, куплено $m$ билетов…)
Обучающие статьи с примерами
- Как найти вероятность в задачах про подбрасывания монеты?
- Как найти вероятность в задачах про игральные кости?
Примеры решений на классическую вероятность
Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. Событие А достоверное.
Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?
Решение. Вынуть два шара из десяти можно следующим числом способов: 
Число случаев, когда среди этих двух шаров будут два белых, равно 
Искомая вероятность 
Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?
Решение. Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. Событие, заключающееся в вынимании синего шара, невозможное.
Пример. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?
Решение. Количество элементарных исходов (количество карт) n=36. Событие А = (Появление карты червовой масти). Число случаев, благоприятствующих появлению события А, m=9. Следовательно,

Пример. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.
Решение. Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е. 
Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех 


Искомая вероятность 
Еще больше примеров решений
Классическое определение вероятности
Содержание
Случайный эксперимент. Множество элементарных исходов. Случайные события
Теория вероятностей — это раздел математики, посвященный изучению математических моделей случайных экспериментов, то есть таких экспериментов, результаты которых заранее неизвестны.
Например, одним из случайных экспериментов, часто используемых в теории вероятностей, является подбрасывание игральной кости. Результатом этого случайного эксперимента будет количество выпавших очков.
Напомним, что игральная кость – это кубик из однородного материала, грани которого пронумерованы числами 1, 2, 3, 4, 5, 6 при помощи нанесенных на грани кубика точек.
Множество всех возможных результатов случайного эксперимента называют множеством элементарных событий. Это множество принято обозначать заглавной греческой буквой Ω . Элементы множества Ω называют элементарными событиями.
Элементарные события часто называют элементарными исходами или, просто, исходами, а множество всех элементарных событий называют пространством элементарных событий, множеством элементарных исходов или пространством элементарных исходов.
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω . Например, в классическом определении вероятности событием является каждое подмножество множества элементарных событий Ω. В более сложных вероятностных моделях событиями являются не все подмножества Ω, а только часть из них.
Случайные события часто для простоты называют событиями.
Классическое определение вероятности
Если в результате случайного эксперимента может реализоваться один из нескольких равновозможных вариантов, то используют классическое определение вероятности.
Классическое определение вероятности является краеугольным камнем теории вероятностей и вводится в соответствии со следующей схемой.
-
Определяется множество элементарных событий (результаты случайного эксперимента).
В классическом определении вероятности в качестве множества элементарных событий Ω используют произвольное множество, состоящее из конечного числа элементов. Элементы множества Ω (элементарные события) обозначают
ω1 , ω2 , … , ωN ,
где N – число элементов множества Ω .
-
Вероятность каждого элементарного события полагают равной
и обозначают буквой P . Таким образом,
-
Определяются случайные события.
Пустым множеством
называют множество, в котором нет ни одного элемента. Пустое множество содержится в любом множестве, то есть является подмножеством любого множества.
В классическом определении вероятности в качестве случайных событий используются всевозможные подмножества множества Ω , включая пустое множество
и все множество Ω .
Случайные события принято обозначать буквами A , B , C , …
-
Определяется вероятность каждого случайного события.
Если A – случайное событие, то вероятность события A полагают равной числу
где через m обозначено количество элементарных событий, входящих в множество A .
Вероятность случайного события A принято обозначать P (A).
Таким образом, справедливо равенство
(1)
причем, поскольку числитель в правой части формулы (1) не превосходит знаменателя, то вероятность любого случайного события A заключена в пределах
(2)
В частности, если
или A = Ω , то справедливы равенства
(3)
ЗАМЕЧАНИЕ. При вычислении вероятности события A элементарные события, входящие в событие A , называют благоприятными исходами и формулу (1) записывают в виде
|
|
(4) |
Примеры решения задач
ПРИМЕР 1. Эксперимент состоит в подбрасывании игральной кости один раз. Описать схему введения классического определения вероятности для этого эксперимента.
РЕШЕНИЕ. Обозначим через ωk событие, состоящее в том, что при подбрасывании игральной кости выпадает число k . Тогда элементарные события
| ω1 , ω2 , ω3 , ω4 , ω5 , ω6 | (5) |
составляют множество элементарных событий Ω :
| Ω = {ω1 , ω2 , ω3 , ω4 , ω5 , ω6 }. | (6) |
Поскольку множество Ω состоит из 6 элементов, то вероятность каждого элементарного события равна :
Каждое случайное событие является подмножеством Ω и состоит из нескольких элементарных событий. Так, например, случайное событие
A = { выпало нечетное число }
состоит из трех элементарных событий
A = {ω1 , ω3 , ω5 } .
В силу формулы (4) справедливо равенство
ПРИМЕР 2. Эксперимент состоит в подбрасывании монеты один раз. Описать схему введения классического определения вероятности для этого эксперимента.
РЕШЕНИЕ. Обозначим русскими буквами Г и Ч элементарные события, состоящие в том, что при подбрасывании монеты выпадают герб ( Г ) или число ( Ч ) соответственно. Тогда
Ω = { Г , Ч } ,
ПРИМЕР 3. Найти вероятность того, что при однократном подбрасывании двух игральных костей сумма выпавших чисел будет больше, чем 8 .
РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны всевозможные суммы чисел, выпавших при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании первой кости, а первый столбец таблицы – это числа, выпавшие при бросании второй кости. На пересечении строки и столбца указана сумма чисел, выпавших на двух костях.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
В этой таблице все возможные результаты эксперимента представлены в 36 клетках. При этом в 10 клетках, выделенных в таблице желтым цветом, результаты превышают число 8 . Поэтому искомая вероятность
ОТВЕТ.
Геометрическая
вероятность
§ 1. Пространство элементарных исходов.
Каждый эксперимент
заканчивается каким-то определенным
результатом, который не всегда возможно
заранее предугадать. Для того, чтобы
формально описать некоторый эксперимент,
нужно указать все возможные варианты
результатов, которыми этот эксперимент
может закончиться. В теории вероятностей
такие результаты называются исходами.
Множество
всех возможных исходов эксперимента
называется пространством элементарных
исходов.
Предполагается, что эксперимент может
закончиться одним и только одним
элементарным исходом. В наиболее простом
случае все эти исходы можно перечислить:
= 1
, 2,
… n,
или =
1,
2
, ….
Такое пространство
элементарных исходов называется
дискретным.
Простейшим
пространством элементарных исходов
является такое пространство, в котором
все указанные исходы рассматриваемого
эксперимента
-
равновозможны;
-
взаимно несовместны
(т.е. в результате эксперимента может
произойти один и только один из указанных
исходов), -
все исходы образуют
полную группу событий (т.е . никакие
другие исходы, кроме перечисленных, не
могут произойти).
Такое пространство
конечно и называется пространством
равновозможных исходов (или симметричным
пространством).
ПРИМЕР 1. При
бросании симметричной монеты возможны
два исхода – выпадение решки или герба.
Они удовлетворяют всем трем указанным
выше условиям и потому в этом случае
пространство элементарных исходов
представляется так (здесь буквами Р и
Г обозначены решка и герб соответственно):
ПРИМЕР 2. При
одновременном бросании двух монет
исходы представляют собой упорядоченные
пары, состоящих из символов Р и Г. Первый
элемент этой пары – результат, выпавший
на первой монете, второй элемент –
результат на второй монете. Очевидно,
что таких пар – четыре:
ПРИМЕР 3.
В случае бросания игральной кости может
выпасть любое из чисел 1, 2, 3, 4, 5, 6. Поэтому
пространство элементарных исходов
ПРИМЕР 4. При
одновременном бросании двух игральных
костей элементарные исходы представляют
собой пары (x,
y),
где x
– число очков, выпавшее на первой кости,
а y
– число очков на второй кости. Всего
таких пар – 36:
§ 2. Событие и его вероятность.
В дискретном
пространстве вероятность каждого
элементарного исхода считается заданной
и обозначается Р(i),
или просто рi
, причем
всегда
-
рi
0 -
(или
),
т.е. сумма (конечная
или бесконечная) вероятностей всех
элементарных исходов равна единице.
Элементарные исходы мы называем
элементарным
событием.
Событием
называется
любое подмножество, состоящее из
элементарных исходов пространства
элементарных событий .
Говорят, что «событие А произошло», если
эксперимент закончился одним из
элементарных исходов iА.
Вероятностью
события А называется сумма вероятностей
всех элементарных исходов, входящих в
А, то есть Р(А)=
.
Из этого определения вероятности события
следует, что всегда 0
Р(А)
1.
В случае равновозможных
исходов вероятность элементарного
события А определяется формулой
,
где
– число элементов во множестве ,
которое обычно называется «общее число
исходов», а
– число элементов во множестве A,
называемое «числом благоприятствующих
исходов».
Событие
А,
состоящее из всех элементарных исходов,
не входящих в А, называется противоположным
событием к событию А. Оно происходит
тогда и только тогда, когда событие A
не произошло. Очевидно что Р(А) + Р(А)
= 1. Это равенство используется для
вычисления вероятности события А в
случае, когда вероятность противоположного
события известна или легко может быть
найдена, тогда Р(А) = 1 — Р(А).
Таким образом, для
вычисления вероятности в каждой задаче
важно определить, в чем состоит
эксперимент, правильно построить
соответствующее пространство элементарных
событий
и выделить в нем требуемое событие A.
Затем, используя методы комбинаторики,
подсчитать число элементов в
и A.
Задача 1.
В ящике 5 апельсинов и 4 яблока. Наудачу
выбираются 3 фрукта. Какова вероятность,
что все три фрукта – апельсины?
Решение.
Элементарными исходами здесь являются
выборки, включающие 3 фрукта.
Решение.
Так как порядок здесь безразличен, будем
считать выборки неупорядоченными (и,
разумеется, бесповторными). Общее число
элементарных исходов
равно числу способов выбрать 3 элемента
из 9, т.е. числу сочетаний n=
.
Число благоприятных исходов m=
будет равно числу способов выбора трех
апельсинов из имеющихся 5, т.е. числу
сочетаний трех элементов из 5, т.е.
.
Тогда вероятность
.
Задача 2.
Преподаватель
предлагает каждому из трех студентов
задумать любое число от 1 до 10. Считая,
что выбор каждым из студентов любого
числа из заданных равновозможен, найти
вероятность того, что у кого-то из них
задуманы числа совпадут.
Решение.
Подсчитаем сначала общее количество
исходов. Элементарными исходами будем
считать упорядоченные совокупности
задуманных чисел: N1,
N2,
N3,
где N1
— число, задуманное первым студентом,
N2
— вторым и N3
— третьим Первый из них выбирает одно
из 10 чисел — 10 возможностей, второй
делает то же самое — 10 возможностей,
наконец, выбор третьего также 10
возможностей. Согласно основной теоремы
комбинаторики общее число способов
будет равно:
n=
N1N2N3=103
= 1000 элементарных исходов.
Подсчет количества
благоприятных исходов более сложен.
Заметим, что совпадение задуманных
чисел может произойти у любой пары
студентов (или даже одновременно у всех
троих). Чтобы не разбирать отдельно все
эти случаи, удобно перейти к противоположному
событию, т.е. подсчитать количество тех
случаев, когда все три студента задумывают
разные числа. Первый из них по-прежнему
имеет 10 способов выбора числа. Второй
студент теперь имеет лишь 9 возможностей
(поскольку ему приходится заботиться
о том, чтобы его число не совпало с
задуманным числом первого студента N2
N1.
Третий студент еще более ограничен в
выборе — у него всего 8 возможностей
(из 10 возможных для N3
исключаются два числа: N3
N1
, N3
N2).
Поэтому общее число комбинаций задуманных
чисел, в которых нет совпадений, равно
в силу той же основной теоремы m=10
9
8 = 720. Остальные случаи 1000 — 720 = 280
характеризуются наличием хотя бы одного
совпадения. Следовательно, искомая
вероятность совпадения равна Р=280/1000=
0,28.
Задача 3.
Найти вероятность того, что в 8-значном
числе ровно 4 цифры совпадают, а остальные
различны.
Решение.
Событие А={8-значное число содержит 4
одинаковые цифры}. Из условия задачи
следует, что в числе 5 различных цифр,
одна из них повторяется — число способов
её выбора — любая из 10 цифр, и эта цифра
занимает любые 4 места в числе – число
способов
.
Оставшиеся 4 места занимают различные
цифры из неиспользованных 9, и так как
число зависит от порядка расположения
цифр, то число способов выбора четырех
цифр равно
. Тогда число благоприятствующих исходов
.
Всего же способов составления 8-значных
чисел равно ||=108.
Искомая вероятность равна
.
Задача 4.
Шесть клиентов случайным образом
обращаются в 5 фирм. Найти вероятность
того, что хотя бы в одну фирму никто не
обратится.
Решение.
Рассмотрим обратное событие
,
состоящее в том, что в каждую из 5 фирм
обратился клиент, тогда в какую-то из
них обратились два человека, а в остальные
4 фирмы – по одному клиенту. Таких
возможностей
.
А всего способов распределить 6 клиентов
по 5 фирмам
.
Отсюда
,
следовательно
.
Задача 5.
Среди 25 экзаменационных билетов имеется
5 «счастливых» и 20 «несчастливых».
Студенты подходят за билетами один за
другим по очереди. У кого больше
вероятность вытащить «счастливый»
билет: у того, кто подошел первым, или у
того, кто подошел вторым?
Решение.
Пусть «счастливые» билеты имеют номера
1,2,3,4,5. Обозначим через i1
номер
билета, взятого первым студентом, через
i2
— номер билета, взятого вторым студентом,
тогда элементарным исходом будет пара
,
а пространство элементарных исходов
здесь все элементарные
исходы равновероятны. Событие А={первый
студент взял «счастливый» билет} имеет
вид
а событие В={второй
студент взял «счастливый» билет} имеет
вид:
Каждое из событий
А и В содержит
элементов, а все пространство
содержит
элементов.
Следовательно, Р(А)=Р(В)=1/5.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #