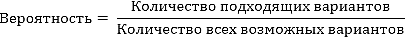Как найти количество битов необходимое для кодирования

Задачи, связанные с определением количества информации, занимают довольно большое место как в общем курсе 9-11 классов, так и при итоговой аттестации разного типа.

Обычно решение подобных задач не представляет трудности для учащихся с хорошими способностями к анализу ситуаций. Но большинство учеников поначалу путаются в понятиях и не знают, как приступить к решению.

Тем не менее, к 9-му классу учащиеся уже имеют определенный опыт решения задач по другим предметам (более всего – физика) с применением формул. Определить, что в задаче дано, что необходимо найти, и выразить одну переменную через другую – действия довольно привычные, и с ними справляются даже слабые ученики. Представляется возможным ввести некоторые дополнительные формулы в курсе информатики и найти общий стиль их применения в решении задач.

Оттолкнемся от одной из главных формул информатики – формулы Хартли N=2ⁱ. При ее использовании учащиеся могут еще не знать понятия логарифма, достаточно вначале иметь перед глазами, а затем запомнить таблицу степеней числа 2 хотя бы по 10-й степени.

При этом формула может применяться в решении задач разного типа, если правильно определить систему обозначений.

Выделим в системе задач на количество информации задачи следующих типов:

1. Количество информации при вероятностном подходе;
2. Кодирование положений;
3. Количество информации при алфавитном подходе (кодирование текста);
4. Кодирование графической информации;
5. Кодирование звуковой информации

Все задачи группы A (в случае, если мы имеем дело с равновероятными событиями) решаются непосредственно по формуле Хартли с ее привычными обозначениями:

• N – количество равновероятных событий;
• i – количество бит в сообщении о том, что событие произошло,

Причем в задаче может быть определена любая из переменных с заданием найти вторую. В случае если число N не является непосредственно числом, представляющим ту или иную степень числа 2, количество бит нам необходимо определить «с запасом». Так для гарантированного угадывания числа в диапазоне от 1 до 100 необходимо задать минимально 7 вопросов (27=128).

Решение задач для случаев неравновероятных событий в этой статье не рассматривается.

Для решения задач групп B-E дополнительно введем еще одну формулу:

Q=k*i

и определим систему обозначений для задач разного типа.

Для задач группы B значение переменных в формуле Хартли таково:

• i – количество «двоичных элементов», используемых для кодирования;
• N – количество положений, которые можно закодировать посредством этих элементов.

Так:

• два флажка позволяют передать 4 различных сообщения;
• с помощью трех лампочек можно потенциально закодировать 8 различных сигналов;
• последовательность из 8 импульсов и пауз при передаче информации посредством электрического тока позволяет закодировать 256 различных текстовых знаков;

и т.п.

Рассмотрим структуру решения по формуле:

Задача 1: Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно в пять символов?

Дано: i = 5

Найти: N

Решение: N = 2⁵

Ответ: 5

Каждый элемент в последовательности для кодирования несет один бит информации.

Очевидно, что при определении количества элементов, необходимых для кодирования N положений, нас всегда интересует минимально необходимое для этого количество бит.

При однократном кодировании необходимого количества положений мы определяем необходимое количество бит и ограничиваемся формулой Хартли. Если кодирование проводится несколько раз, то это количество мы обозначаем как k и, определяя общее количество информации для всего кода (Q), применяем вторую формулу.

Задача 2: Метеорологическая станция ведет наблюдение за влажностью воздуха, результатом которых является целое число от 1 до 100%, которое кодируется посредством минимально возможного количества бит. Станция сделала 80 измерений. Какой информационный объем результатов наблюдений.

Дано: N = 100; k = 80

Найти: Q

Решение:

По формуле Хартли i = 7 (с запасом); Q = 80 * 7 = 560

Ответ: 560 бит

(Если в задаче даны варианты ответов с использованием других единиц измерения количества информации, осуществляем перевод: 560 бит = 70 байт).

Отметим дополнительно, что, если для кодирования используются нe «двоичные», а скажем, «троичные» элементы, то мы меняем в формуле основание степени.

Задача 3: Световое табло состоит из лампочек. Каждая из лампочек может находиться в одном из трех состояний («включено», «выключена» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов.

В данном случае N = 18, основание степени – 3. Необходимо найти i. Если логарифмы еще не знакомы, определяем методом подбора – 5. Ответ: 5 лампочек

Далее рассмотрим решение задач на кодирование текстовой, графической и звуковой информации.

Здесь важно провести параллели:

Информация, которая обрабатывается на компьютере, должна быть представлена в виде конечного множества элементов (символ для текста, точка – для графики, фрагмент звуковой волны – для звука), каждый из которых кодируется отдельно с использованием заданного количества бит. Зависимость количества элементов, которые могут быть закодированы, от количества бит, отводимых, на кодирование одного элемента, как и раньше, определяем по формуле Хартли.

А путем умножения количества элементов (k) на «информационный вес» одного из них, определяем общее количество информации в текстовом, графическом, звуковом фрагменте (Q).

Каждую задачу можно решить, обозначив заданными переменными известные данные, и выразив одну переменную через другую. Только необходимо помнить, что непосредственно расчеты чаще всего производятся в минимальных единицах измерения (битах, секундах, герцах), а потом, если необходимо, ответ переводится в более крупные единицы измерения.

Рассмотрим конкретные примеры:

Алфавитный подход позволяет определить количество информации, заключенной в тексте. Причем под «текстом» в данном случае понимают любую конечную последовательность знаков, несущую информационную нагрузку. Поэтому обозначения переменных для задач группы C одинаково применимы как для задач на передачу обычной текстовой информации посредством компьютера (i = 8, N = 256 или i = 16, N = 16256) так и для задач на передачу сообщений посредством любых других алфавитов (здесь и далее используются разные названия, встречающиеся в задачах):

• i – количество бит, используемое для кодирования одного текстового знака, равнозначно: количество информации (в битах), в нем содержащееся, информационный «вес», информационный «объем» одного знака;
• N – полное количество знаков в алфавите, используемом для передачи сообщения, мощность алфавита;
• k – количество знаков в сообщении;
• Q – количество информации в сообщении (информационный «вес», «объем» сообщения), количество памяти, отведенное для хранения закодированной информации;

Задача 4: Объем сообщения – 7,5 кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?

Дано:

Q = 7,5 Кбайт = 7680 байт ( в данном случае нет необходимости перевода в биты);

k = 7680

Найти: N

Решение: i = Q / k = 1 байт = 8 бит; N = 2⁸ = 256

Ответ: 256 знаков

Задача 5: Дан текст из 600 символов. Известно, что символы берутся из таблицы размером 16 на 32. Определите информационный объем текста в битах.

Дано:

k = 600; N = 16 * 32

Найти: Q

Решение:

N = 2⁴ * 2⁵ = 2⁹; i = 9; Q = 600 * 9 = 5400 бит;

Ответ: 5400 бит

Задача 6: Мощность алфавита равна 64. Сколько кбайт памяти потребуется, чтобы сохранить 128 страниц текста, содержащего в среднем 256 символов на каждой странице?

Дано:

N = 64; k = 128 * 256

Найти: Q

Решение:

64 = 2ⁱ; i = 6; Q = 128 * 256 * 6 = 196608 бит = 24576 байт = 24 Кбайт;

Ответ: 24 Кбайт

Задача 7: Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?

Дано:

N = 7; k = 180

Найти: Q

Решение:

7 = 2ⁱ; i = 3 (с запасом); Q = 180 * 3 = 540 бит;

Ответ: 540 бит

Рассматривая задачи групп D и E, вспоминаем, что при кодировании графики и звука производится дискретизация, то есть разбиение изображения на конечное множество элементов (пикселей) и звуковой волны на конечное множество отрезков, количество которых зависит от количества измерений в секунду уровня звука (частоты дискретизации) и времени звучания звукового файла.

То есть –

• общее количество элементов в графическом файле (k) равно разрешению изображения или разрешению экрана монитора, если изображение формируется на весь экран,
• общее количество элементов в звуковом файле (k) равно произведению частоты дискретизации на время звучания (важно при этом использовать в качестве единиц измерения минимальные единицы – герцы и секунды).

Рассмотрим всю систему обозначений для данного типа задач:

• i – количество бит, используемое для кодирования одного элемента изображения или звукового фрагмента, равнозначно: глубина цвета, звука;
• N – насыщенность цвета, равнозначно: количество цветов в палитре изображения, цветовое разрешение изображения; насыщенность звука (в задачах обычно не используется);
• k – количество точек в изображении, равнозначно: разрешение изображения (или экрана) или количество фрагментов дискретной звуковой волны (равно произведению частоты дискретизации на время звучания);
• Q – количество информации, содержащееся в графическом (звуковом) файле, равнозначно: информационный «объем», «вес» графического (звукового) файла, объем памяти (видеопамяти), необходимый для хранения заданного файла.

Задача 8: Для хранения растрового изображения размером 64 на 64 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?

Дано:

k = 64 * 64 = 212; Q = 512 байтов = 29 * 23 = 212 бит;

Найти: N

Решение:

i = Q / k = 2¹² / 2¹² = 1; N = 21 = 2

Ответ: 2 цвета

Задача 9: Сколько памяти нужно для хранения 64-цветного растрового графического изображения размером 32 на 128 точек?

Дано:

N = 64; k = 32 * 128;

Найти: Q

Решение:

i = 6 (по формуле Хартли); Q = 32 * 128 * 6 = 24576 бит = 3072 байт = 3 Кбайт

Ответ: 3 Кбайт

Задача 10: Оцените информационный объем моноаудиофайла длительностью звучания 1 минута, если глубина кодирования равна 16 бит при частоте дискретизации 8 кГц

Дано:

k = 60 * 8000; i = 16;

Найти: Q

Решение:

Q = 60 * 8000 * 16 = 7680000 бит = 960000 байт = 937,5 Кбайт

Ответ: 937,5 Кбайт

(Если файл стерео, Q будет больше в 2 раза).

Задача 11: Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 625 Кбайт

Дано:

i = 16; k = 32000 * t; Q = 625 кбайт = 640000 байт = 5120000 бит;

Найти: t

Решение:

k = Q / i; k = 5120000 / 16 = 320000; t = 320000 / 32000 = 10 сек

Ответ: 10 секунд

В эту же схему укладывается решение задач на скорость передачи информации любого типа, если в хорошо известной учащимся формуле:

S = V * t принять S = Q (количество переданной информации вместо расстояния).

Задача 12: Сколько секунд потребуется обычному модему, передающему сообщения со скоростью 28800 бит/сек, чтобы передать цветное растровое изображение размером 640 на 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами?

Дано:

V = 28800 бит/сек; k = 640 * 480; i = 3 байт = 24 бит;

Найти: t

Решение:

t = S (Q) / V; Q = k * i = 640 * 480 * 24 = 7372800 бит; t = 7372800 / 28800 = 256 сек.

Ответ: 256 сек

В заключение отметим, что после определенной тренировки решения задач по формулам, многие учащиеся перестают нуждаться в их прописывании в задаче, сразу определяя порядок необходимых арифметических действий для ее решения.

Информация и ее кодирование

Различные подходы к определению понятия «информация». Виды информационных

процессов. Информационный аспект в деятельности человека

Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:

• информация — это новые факты, новые знания;
• информация — это сведения об объектах и явлениях окружающей среды, которые повышают уровень осведомленности человека;
• информация — это сведения об объектах и явлениях окружающей среды, которые уменьшают степень неопределенности знаний об этих объектах или явлениях при принятии определенных решений.

Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.

Основными социально значимыми свойствами информации являются:

• полезность;
• доступность (понятность);
• актуальность;
• полнота;
• достоверность;
• адекватность.

В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.

Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.

Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).

Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.

Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.

Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.

Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.

Язык как способ представления и передачи информации

Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.

В зависимости от способа восприятия знаки делятся на:

• зрительные (буквы и цифры, математические знаки, музыкальные ноты, дорожные знаки и др.);
• слуховые (устная речь, звонки, сирены, гудки и др.);
• осязательные (азбука Брайля для слепых, жесты-касания и др.);
• обонятельные;
• вкусовые.

Для долговременного хранения знаки записывают на носители информации.

Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).

По способу связи между формой и значением знаки делятся на:

• иконические — их форма похожа на отображаемый объект (например, значок папки «Мой компьютер» на «Рабочем столе» компьютера);
• символы — связь между их формой и значением устанавливается по общепринятому соглашению (например, буквы, математические символы ∫, ≤, ⊆, ∞; символы химических элементов).

Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.

Языки делятся на:

• естественные (разговорные) — русский, английский, немецкий и др.;
• формальные — встречающиеся в специальных областях человеческой деятельности (например, язык алгебры, языки программирования, электрических схем и др.)

Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.

Методы измерения количества информации: вероятностный и алфавитный

Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.

Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:

N = 2^I.

Например, пусть шарик находится в одной из четырех коробок. Таким образом, имеется четыре равновероятных события (N = 4). Тогда по формуле Хартли 4 = 2^I. Отсюда I = 2. То есть сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.

Алфавитный подход

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:

I = log₂ N.

Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:

I = log₂ 32 = 5 битов.

Если N не является целой степенью 2, то число log₂N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log₂N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.

Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:

N = 26; N’ = 32; I = log₂N’ = log₂(2⁵) = 5 битов.

Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:

I = M · log₂N.

Примеры решения задач

Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение. С помощью n лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2ⁿ сигналов. 2⁵ < 50 < 2⁶, поэтому пяти лампочек недостаточно, а шести хватит.

Ответ: 6.

Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log₂101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log₂128 = 7 битов. Для 80 измерений общий информационный объем равен:

80 · 7 = 560 битов = 70 байтов.

Ответ: 70 байтов.

Вероятностный подход

Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

$I=-∑↙{i=1}↖{N}p_ilog_2p_i$,

где $I$ — количество информации;

$N$ — количество возможных событий;

$p_i$ — вероятность $i$-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

$p_1={1}/{2}, p_2={1}/{4}, p_3={1}/{8}, p_4={1}/{8}$.

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

$I=-({1}/{2}·log_2{1}/{2}+{1}/{4}·log_2{1}/{4}+{1}/{8}·log_2{1}/{8}+{1}/{8}·log_2{1}/{8})={14}/{8}$ битов $= 1.75 $бита.

Единицы измерения количества информации

Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).

Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.

В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.

Производные единицы измерения количества информации:

1 байт = 8 битов

1 килобайт (Кб) = 1024 байта = 2¹⁰ байтов

1 мегабайт (Мб) = 1024 килобайта = 2²⁰ байтов

1 гигабайт (Гб) = 1024 мегабайта = 2³⁰ байтов

1 терабайт (Тб) = 1024 гигабайта = 2⁴⁰ байтов

Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче

Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.

В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.

Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).

Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.

Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.

Примеры решения задач

Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.

Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 0100₂ = В4₁₆.

Ответ: В4₁₆.

Скорость передачи информации и пропускная способность канала связи

Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.

Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.

Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.

Примеры решения задач

Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.

Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:

Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2⁸ ⋅ 10³ : 2³ : 2¹⁰) ⋅ (3 ⋅ 15 ⋅ 2²) = (2⁸ ⋅ 125 ⋅ 2³ : 2³ : 2¹⁰) ⋅ (3 ⋅ 15 ⋅ 2²) = 125 ⋅ 45 = 5625 Кбайт.

Ответ: 5625 Кбайт.

Технология обработки графической и звуковой информации

Растровая графика. Растровые графические объекты и операции над ними

Растровые графические изображения формируются в процессе сканирования рисунков и фотографий, а также при использовании цифровых фото- и видеокамер. С помощью графического редактора можно создать растровое графическое изображение непосредственно на компьютере.

Растровое графическое изображение состоит из отдельных точек — пикселей, образующих строки и столбцы. Основные свойства пикселя — расположение и цвет. Значения свойств кодируются двоичным кодом и сохраняются в видеопамяти компьютера.

Качество изображения на экране монитора зависит от пространственного разрешения и глубины цвета.

Пространственное разрешение определяется как произведение количества строк изображения на количество точек в строке. Глубина цвета измеряется в битах на точку и определяет количество цветов, в которые могут быть окрашены точки изображения. Чем больше пространственное разрешение и глубина цвета, тем выше качество изображения и тем больше объем его файла. В операционных системах предусмотрена возможность выбора необходимого пользователю и технически возможного графического режима.

Растровые изображения чувствительны к масштабированию. При уменьшении изображения несколько соседних точек преобразуются в одну, поэтому теряется четкость мелких деталей изображения. При его увеличении увеличивается размер каждой точки и появляется ступенчатый эффект (пикселизация изображения).

Для графических изображений могут использоваться различные палитры (наборы) цветов. Количество цветов N в палитре и количество информации I, необходимое для кодирования цвета каждой точки, связаны соотношением N = 2^I.

Например, для черно-белого изображения палитра состоит из двух цветов. Тогда с помощью этой формулы можно вычислить, какое количество информации необходимо, чтобы закодировать цвет каждой точки: 2 = 2^I ⇒ 2¹ = 2^I ⇒ I = 1 бит.

Информационный объем IП требуемой видеопамяти рассчитывается по формуле Iп = I · X · Y,

где I — глубина цвета в битах на точку,

Х — количество точек изображения по горизонтали,

Y — количество точек изображения по вертикали.

Цветовые модели

Для кодирования цветов изображения в компьютере используются цветовые модели. Цветовая модель (система цветопередачи) — это способ представления различных цветов спектра в виде набора числовых характеристик определенных базовых компонентов.

Цветовая модель RGB. С экрана монитора человеческий глаз воспринимает цвет как сумму излучения трех базовых цветов: красного (Red), зеленого (Green) и синего (Blue). Эти цвета называются основными. Цвета палитры RGB формируются путем сложения базовых цветов, имеющих различную интенсивность. Цвет Color в палитре можно определить с помощью формулы Color = R + G + B.

Если все базовые цвета имеют максимальную интенсивность, получается белый цвет, если минимальную — черный. Серый цвет — промежуточный между черным и белым. В нем есть все цветовые составляющие, но они одинаковы и нейтрализуют друг друга. Красный цвет получается при максимальной интенсивности красного и минимальной интенсивности зеленого и синего цветов. Аналогично, зеленый и синий цвета получаются при максимальной интенсивности соответствующего базового цвета и минимальной интенсивности остальных цветов. При глубине цвета в 24 бита (трехбайтная кодировка) значение интенсивности каждого базового компонента задается целым десятичным числом от 0 до 255 или двоичным числом от 00000000 до 11111111. В этом случае красный цвет, например, будет закодирован последовательностью 255 0 0 (или 11111111 00000000 00000000); белый — 255 255 255 (11111111 11111111 11111111); желтый — 255 255 0 (или 11111111 11111111 00000000); голубой — 0 255 255 (или 00000000 11111111 11111111); черный — 0 0 0 (или 00000000 00000000 00000000). Последовательности 127 0 0 и 235 0 0 будут означать оттенки красного цвета, но в первом случае цвет будет более темный. Данная цветовая модель используется для компьютерных изображений, предназначенных для просмотра на экране монитора или телевизора.

Цветовая модель CMYK. Палитра цветов формируется путем наложения базовых цветов: голубого (Cyan), пурпурного (Magenta), желтого (Yellow) и черного (Black). Доля каждого базового компонента задается в процентах (целым числом от 0 до 100). Цвет Color в палитре можно определить с помощью формулы Color = C + M + Y.

Голубой, пурпурный и желтый цвета называются дополнительными, т. к. они дополняют основные цвета до белого: голубой дополняет красный, пурпурный — зеленый, а желтый — синий.

Данная палитра используется при печати изображений на принтере и основана на восприятии отражаемого света. Изображение на бумаге человек воспринимает в отраженном свете. Если на бумагу краски не нанесены, то падающий белый свет полностью отражается, и мы видим белый лист бумаги (White = (C = 0, M = 0, Y = 0)). Если краски нанесены, то они поглощают определенные цвета. Цвета в палитре формируются путем вычитания из белого цвета определенных цветов. Например, нанесенная на бумагу голубая краска поглощает красный свет и отражает зеленый и синий (Cyan = W – R = G + B); желтая краска поглощает синий свет и отражает красный и зеленый (Yellow = W – B = G + R).

Цветовая модель HSB. Палитра цветов формируется путем установки значений трех базовых компонентов: оттенка (Hue), насыщенности (Saturation) и яркости (Brightness). Оттенок Н определяет цвет в спектре и задается целым числом от 0 до 360 (0 — красный цвет, 360 — фиолетовый). Насыщенность S характеризует долю белого цвета, добавленного к выбранному оттенку, и задается в процентах от 0 до 100. При минимальной насыщенности какой-либо оттенок цвета становится серым. Яркость В определяется примесью черного цвета к выбранному оттенку и задается в процентах от 0 до 100. Любой оттенок при минимальной яркости становится черным. Эту модель используют художники при создании компьютерных изображений, моделируя нужный цвет на «виртуальном мольберте» графического редактора.

Форматы растровых графических файлов

При сохранении графического изображения на внешнем носителе могут использоваться различные способы упорядочивания данных в файле, каждый из которых определяет формат (тип) графического файла.

За счет большого количества пикселей в изображении и соответственно большого количества данных, которые надо сохранять, размеры файлов растровых изображений достаточно велики. Поэтому для растровых графических файлов применяется сжатие. Алгоритм сжатия включается непосредственно в формат графического файла.

BMP (Bit MaP image) — универсальный формат растровых графических файлов. Изображение в этом формате сохраняется попиксельно, без сжатия. Стандартное расширение имени файла — bmp. Этот формат поддерживается многими графическими редакторами и рекомендуется для хранения и обмена данными с другими приложениями.

JPEG (Joint Photographic Expert Group) — использует эффективные алгоритмы сжатия данных, которые значительно уменьшают размеры файлов. Но это достигается за счет необратимой потери части данных и ухудшения качества изображения. Стандартные расширения имени файла — jpg или jpeg. Данный формат целесообразно использовать для хранения многоцветных изображений с плавными переходами между цветами, где потеря качества малозаметна. Формат поддерживается приложениями для различных операционных систем и часто используется для размещения графических изображений на Web-страницах в Интернете.

GIF (Graphics Interchange Format) — самый «плотный» из графических форматов, не имеющих потери информации. Файлы этого формата имеют расширение gif. В этом формате хранятся и передаются малоцветные (до 256 цветов) изображения, например рисованные иллюстрации. У этого формата есть интересные особенности, позволяющие создавать необычные эффекты: прозрачность фона и анимацию изображения.

TIFF (Tagged Image File Format) — формат, поддерживаемый всеми основными графическими редакторами, включает в себя алгоритм сжатия без потерь информации. Файлы этого формата имеют расширение tif. Они сохраняют изображения с высоким качеством, поэтому широко используются в полиграфии. Формат обеспечивает не очень большую степень сжатия, но дает возможность сохранять в одном файле дополнительную информацию в невидимых вспомогательных слоях — каналах (например, наложение аннотаций и примечаний на рисунок).

PNG (Portable Network Graphic) — формат, аналогичный формату GIF, но позволяет использовать значительно больше цветов в изображении. Стандартное расширение имени файла — png.

Существуют и другие форматы растровых файлов, такие как PCX, IFF, LBM, IMG, MAC, MSP, PGL.

Среди всего разнообразия форматов нет идеального, удовлетворяющего всем требованиям пользователя. Поэтому графические редакторы предоставляют пользователю возможность самостоятельно выбирать формат графического файла в зависимости от целей работы с ним и последующего использования.

Графические редакторы

Для создания, редактирования и просмотра графических изображений используются специальные программы — графические редакторы.

С помощью растровых графических редакторов можно обрабатывать цифровые фотографии и отсканированные изображения, повышая при этом их качество путем изменения яркости, контрастности, цветовой палитры, а также удаления дефектов изображения. Кроме того, растровые графические редакторы позволяют создавать новые изображения и применять к ним различные эффекты преобразования. Необходимо помнить, что после окончания рисования нарисованный объект перестает существовать как самостоятельный элемент и становится лишь группой пикселей на рисунке.

Существуют простые растровые графические редакторы, например Paint — стандартное приложение операционной системы Windows, и мощные графические системы, например Adobe Photoshop. Основные возможности растровых графических редакторов:

• cоздание изображения:

— определение области рисования (размер, поля, ориентация холста);

— рисование стандартных графических примитивов (линии, прямоугольники, многоугольники, овалы);

— рисование традиционными методами с помощью инструментов рисования, таких как карандаш, кисть, распылитель, заливка, ластик;

— добавление текста и его форматирование;

— управление цветом: выбор цвета из стандартной и расширенной палитры, копирование цвета, определение цвета пикселя;

• редактирование изображения:

— выделение области изображения для обработки специальными инструментами;

— копирование, перемещение, удаление выделенных областей изображения;

— геометрическое преобразование выделенных областей изображения: изменение размера, поворот, наклон, отражение.

Примеры решения задач

Пример 1. В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Как уменьшился его информационный объем?

Решение.

2^I1 = 65536; 2^I1 = 2¹⁶ ⇒ I1 = 16 .

2^I2 = 16; 2^I2 = 2⁴ ⇒ I2 = 4.

${I1}/{I2}= {16}/{4} = 4$.

Ответ: информационный объем уменьшился в 4 раза.

Пример 2. Черно-белое растровое графическое изображение имеет размер 10 $×$ 10 точек. Какой информационный объем имеет изображение?

Решение. В палитре 2 цвета, следовательно, глубина цвета I = 1 бит (2 = 2^I ; 2¹ = 2^I ⇒ I = 1).

Информационный объем I_П найдем по формуле: I_П = I · X · Y = 1 · 10 · 10 = 100 битов.

Ответ: 100 битов.

Пример 3. Растровое графическое изображение с палитрой из 256 цветов имеет размер 10 $×$ 10 точек. Какой информационный объем имеет изображение?

Решение. Найдем глубину цвета: 256 = 2^I; 28 = 2^I ⇒ I = 8 . Информационный объем I_П найдем по формуле: I_П = I ∙ X ∙ Y = 8 ∙ 10 ∙ 10 = 800 битов = 800 : 8 = 100 байтов.

Ответ: 100 байт.

Пример 4. Для хранения растрового изображения размером 64 $×$ 64 пикселя отвели 1,5 килобайта памяти. Каково максимально возможное число цветов в палитре изображения?

Решение. По условию I_П =1,5 Кбайт или 1,5 · 2¹⁰ байт = 1,5 · 2¹⁰ · 8 бит.

X · Y = 64 · 64 = 2⁶ · 2⁶ = 2¹². Из формулы I_П = I · X · Y найдем глубину цвета I:

$I={I_П}/{X·Y}={1.5·2^{10}·8}/{2^{12}}=1.5·2^1=3$.

Из формулы N = 2^I найдем число цветов N: N = 2³ = 8 цветов.

Ответ: максимально возможное количество цветов в палитре — 8.

Пример 5. Каков минимальный объем памяти, достаточный для хранения любого растрового изображения размером 256 × 256 пикселей, если в изображении используется палитра из 216 цветов? (Саму палитру хранить не нужно).

Решение. Из формулы N = 2^I найдем глубину цвета I: 2¹⁶ = 2^I; I = 16. Тогда объем памяти I_П = I · X · Y = 16 · 256 · 256 = 2⁴ · 2⁸ · 2⁸ = 2²⁰ бита = 2²⁰ : 8 = 2¹⁷ байта = 2⁷ Кбайтт.

Ответ: 2⁷ Кбайт = 128 Кбайт.

Пример 6. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor = » = «# XXXXXX » , где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели. Какой цвет будет у страницы, заданной командой языка HTML < body bgcolor = «# FFFFFF » > ?

Решение. В 24-битной RGB-модели каждая цветовая составляющая (красная, зеленая, синяя) может принимать значение от 0 до 255 и кодируется одним байтом (двумя шестнадцатеричными цифрами). FF₁₆ = 255₁₀. Т. е. FF FF FF = 255 255 255 . Это означает, что все цветовые составляющие имеют максимальную интенсивность. В RGB-модели это соответствует белому цвету.

Ответ: белый цвет.

Векторная графика. Векторные графические объекты и операции над ними

В векторной графике основным элементом изображения является линия. В растровой графике тоже существует линия, но там она рассматривается как комбинация точек. Для каждой точки отводится одна или несколько ячеек памяти. Следовательно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде нескольких параметров. Что бы мы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.

Линия — это элементарный объект векторной графики. Простейшие объекты объединяются в более сложные. Например, объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб — либо как 12 связанных линий, либо как 6 связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.

Как и все объекты, линии имеют свойства: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т. п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Незамкнутая линия имеет вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.

Хотя объекты векторной графики хранятся в памяти в виде набора параметров, на экран все изображения все равно выводятся в виде точек. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изображении объекта. Аналогичные вычисления производятся и при выводе объектов на принтер.

Достоинства векторной графики:

• Небольшой информационный объем файлов. Достаточно сложные композиции, насчитывающие тысячи объектов, расходуют лишь десятки и сотни килобайтов.
• Легко решаются вопросы масштабирования. Если линии задана толщина, равная 0,15 мм, то, сколько бы мы ни увеличивали или ни уменьшали рисунок, эта линия все равно будет иметь только такую толщину, поскольку это одно из свойств объекта, жестко за ним закрепленное. Распечатав чертеж на большом или на малом листе бумаги, мы всегда получим линии одной и той же толщины. Это свойство векторной графики широко используется в картографии, в конструкторских системах автоматизированного проектирования (САПР) и в автоматизированных системах архитектурного проектирования. При увеличении рисунка можно более подробно рассмотреть сложный объект.

Программы, предназначенные для работы с векторными изображениями, называют векторными графическими редакторами. Их применяют в тех случаях, когда основным требованием к изображению является высокая точность формы. Такая задача возникает при разработке логотипов компаний, при художественном оформлении текста (например, журнальных заголовков или рекламных объявлений), а также во всех случаях, когда иллюстрация является чертежом, схемой или диаграммой, а не рисунком. Векторная графика также лежит в основе flash-анимации. Примеры редакторов: Adobe Illustrator, Macromedia Freehand, CorelDraw.

Основные возможности векторных графических редакторов:

1) создание изображения:

• определение области рисования (размер, поля, ориентация холста);
• рисование стандартных графических примитивов (линий, прямоугольников, многоугольников, овалов);
• добавление текстовых областей и выносок;
• изменение видимости объектов путем изменения порядка размещения их слоев (каждый графический объект рисуется в своем слое, а весь рисунок состоит из множества слоев);
• градиентная заливка объектов;
• задание степени прозрачности объекта;

2) редактирование изображения:

• выделение отдельного объекта в рисунке или группы объектов;
• группировка нескольких объектов в один новый объект;
• выравнивание объектов с помощью сетки, которую можно настраивать;
• копирование, перемещение, удаление выделенных объектов;
• геометрическое преобразование выделенных объектов: изменение размера, поворот, наклон, отражение.

Форматы векторных графических файлов

Разнообразие форматов векторной графики значительно меньше, чем растровой графики, и практически каждый векторный редактор использует свой собственный формат сохранения данных.

WMF (Windows MetaFile) — универсальный формат векторных графических файлов для приложений Windows. Используется для хранения коллекции графических изображений Microsoft Clip Gallery. Возможные расширения файлов WMF, EMF, WMZ, EMZ:

CGM (Computer Graphic Metafile) — широко используется как стандартный формат векторных графических данных в сети Интернет.

EPS (Encapsulated PostScript) — формат, поддерживаемый программами для различных операционных систем. Рекомендуется для создания иллюстраций в настольных издательских системах.

CDR (CorelDRaw files) — оригинальный формат файлов векторного графического редактора CorelDraw. Изображение в файле может состоять из нескольких страниц. Формат позволяет сохранять не только векторную графику, но и текст и растровые изображения. Максимальный размер рисунка 45 × 45 м. Возможные расширения файлов CDR или CDТ.

AI (Adobe Illustrator files) — оригинальный формат файлов векторного графического редактора Adobe Illustrator. Сохраняет в файле только одну страницу, максимальный размер рисунка 3 × 3 м.

SVG (Scalable Vector Graphics) — универсальный формат двумерной графики. Позволяет сохранять в файле текст, графические изображения и анимацию. Файлы могут дополнительно сжиматься программами-архиваторами. Формат обрабатывается практически всеми векторными графическими редакторами. Широкое применение получил в инженерной графике и при разработке Web-сайтов.

Информационный объём сообщения

Алфавитный подход к количеству информации

Единица измерения информации — байт

Компьютеры обычно работают в двоичной системе счисления, состоящей из двух цифр: 0 и 1.

Один двоичный знак — 0 или 1 — называется бит —(англ. bit — сокращение от английских слов binary digit, что означает двоичная цифра). Бит представляет наименьшую единицу информации. Однако компьютер имеет дело не с отдельными битами, а с байтами.

8 бит является настолько характерной величиной, что ей присвоили свое название — байт.

Байт = 8 бит = является единицей измерения информации.

Последовательностью битов можно закодировать текст, изображение, звук или какую — либо другую информацию. Такой метод представления информации называется двоичным кодированием (binary encoding).

Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (звуки, изображения, показания приборов и т. д.) для обработки на компьютере должна быть предварительно преобразована в числовую форму при помощи соответствующих компьютерных программ.

Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста.

Таблица байтов

1 байт = 8 бит

1 Кб (1 Килобайт) = 2¹⁰ байт = 2*2*2*2*2*2*2*2*2*2 байт == 1024 байт (примерно 1 тысяча байт — 10³ байт)

1 Мб (1 Мегабайт) = 2²⁰ байт = 1024 килобайт (примерно 1 миллион байт — 10⁶ байт)

1 Гб (1 Гигабайт) = 2³⁰ байт = 1024 мегабайт (примерно 1 миллиард байт — 10⁹ байт)

1 Тб (1 Терабайт) = 2⁴⁰ байт = 1024 гигабайт (примерно 10¹² байт). Терабайт иногда называют тонна.

Алфавитный подход к измерению информации

Представим, что нам надо закодировать латинский алфавит, который содержит 26 символов. Сколько бит потребуется для кодирования каждого символа? А какой объем информации будет нужен для хранения слова из 10 закодированных нами букв? Давайте попробуем посчитать. Кодировка предполагает, что каждому символу алфавита мы ставим в соответствие уникальный набор битов, т.е. у всех символов эти наборы разные. Количество комбинаций N, которое можно составить из i битов (каждый их них может быть либо 0, либо 1), будет равно:

К = 2ⁱ

В нашем случае K = 26. Получаем 26 = 2ⁱ. 26 не является степенью двойки, но это не страшно — нам надо найти такое минимальное i, чтобы 2ⁱ точно было больше 26. 2⁴ = 16 — не подходит (получается, что с помощью 4 бит мы можем закодировать только 16 символов). 2⁵ = 32 — подходит. Нашли, что i = 5, т.е. вес одного символа — 5 бит. Вернемся ко второму вопросу: какой объем будет занимать слово из 10-ти букв? Одна буква весит 5 бит, значит, 10 букв будут весить 5×10 = 50 бит.

В данном примере мы вычислили количество бит, необходимое для кодирования одного символа буквенного алфавита. Я думаю, вы уже догадались, что данная формула:

К = 2ⁱ будет справедлива не только для кодирования алфавита, но и для кодирования комбинаций любых других параметров (например, количества цветов в изображении или уровней звука музыкального файла).

Изученный нами подход к измерению информации называется алфавитным. Он применяется для кодирования и определения занимаемого объема любых цифровых файлов — как текстовых, так и медиа. Данный подход сам по себе необходимо очень хорошо понимать для решения задания №11 в ЕГЭ. Кроме того, на нем основаны принципы кодирования медиафайлов — этому вопросу посвящено задание №7.

В компьютере также используется свой алфавит, который можно назвать компьютерным. Количество символов, которое в него входит, равно 256 символов. Это мощность компьютерного алфавита. А закодировать 256 разных символов можно с помощью 8 битов (1 байта).

Вероятностный подход к измерению информации

В ЕГЭ в задании №11 может встретиться весьма специфический прототип с вероятностным подходом к измерению информации. Для него необходимо ознакомиться с такой наукой, как Теория вероятностей.

Теория вероятности (ТВ) — это раздел математики, изучающий случайные события. Основным понятием в ТВ является вероятность события. Когда мы говорим о вероятности события, в обычной жизни мы подразумеваем некоторую меру возможности его возникновения. В ТВ есть четкое определение вероятности, которого нужно придерживаться.

Допустим, у вас есть несколько исходов какого-то события — например, вы подбрасываете монету. Может выпасть орел, а может — решка. Для простоты не будем брать в расчет очень редкие случаи (например, когда монета упала ребром, или вы подкинули ее так сильно, что она улетела в космос). Также будем считать, что наша монета идеальна и симметрична, и вероятность выпадения орла и решки одинакова (в ТВ тогда говорят, что эти события «равновероятны»). Все эти уточнения важны, ведь математика — точная наука. В описанном нами случае вероятность каждого исхода равна 50% (1/2). Интуитивно мы это понимаем, а с точки зрения ТВ это число получилось из определения вероятности события. По определению вероятность события равна количеству «нужных» исходов, деленному на количество всех возможных:

Конечно, такая простая формула работает только тогда, когда у нас есть фиксированное количество заранее известных равновероятных исходов. В реальной жизни все иначе и намного сложнее. Например, вы когда-нибудь видели идеально симметричную монету? Вряд ли. В этом случае вероятность двух исходов события (выпадение орла или же решки) будет неодинаковым, и наша формулы не сработает. К счастью, в ЕГЭ такие сложные ситуации не встретятся, поэтому вам достаточно запомнить только формулу для вероятности, которая дана выше. Ниже приведено несколько примеров вычисления вероятности исходов простых событий.

Вероятность нескольких событий

Пускай есть не одна монета, а три. И мы подбрасываем их одновременно. Мы уже знаем, что для каждой монеты вероятность выпадения орла или решки равна 1/2. А чему равна вероятность того, что на всех трех монетах сразу выпадет орел? А хотя бы на одной? Можем просто посчитать по известной нам формуле. При подбрасывании трех монет возможно всего 8 исходов: ооо, оор, оро, орр, роо, рор, рро, ррр (кстати, посчитать количество способов очень быстро поможет комбинаторика, но об этом дальше). Выпадение на всех трех монетах орла — это 1 исход. Получается, вероятность равна 1/8. А выпадение хотя бы на одной орла — это 7 исходов (все ситуации, кроме ррр). Как видите, такой способ считать вероятность составных событий не очень удачный. В теории вероятности есть правила, которые позволяют избежать таких сложностей.

События происходят одновременно

Если необходимо найти вероятность И первого, И второго, И третьего … событий (т.е. вероятность одновременного выполнения исходов), то вероятности перемножаются. Вернемся к примеру с подбрасыванием трех монет. Вероятность выпадения орла на каждой монете отдельно равна 1/2, значит, вероятность одновременного выполнения этих трех событий равна 1/2 × 1/2 × 1/2 = 1/8.

Должно произойти хотя бы одно из нескольких событий

Если необходимо найти вероятность ИЛИ первого, ИЛИ второго, ИЛИ третьего … событий (т.е. вероятность выполнения хотя бы исходов), то вероятности складываются. Это правило хорошо иллюстрируется тем, как мы считали вероятность того, что орел выпадет хотя бы на одной монете. Вероятность каждого из исходов (ооо, оор, оро, орр, роо, рор, рро, ррр) была равна 1/8, а всего их 7. Складываем 1/8 7 раз и получаем 7/8.

Теперь же поговорим о самом вероятностном подходе к измерению информации.

Вероятностный подход к измерению информации

Выше было сказано, что теория вероятности и теория информации тесно связаны. На самом деле, когда мы узнаем о выполнении какого-то события, мы получаем определенную информацию, которую можно измерить. Чем менее вероятно событие, тем более «ценно» оно с точки зрения информации. Редкое событие несет больше информации, и наоборот, частое, вероятное событие — меньше. Более подробно вам расскажут об этом в вузе на любом техническом направлении, а для решения задания ЕГЭ достаточно знать только одну формулу, которая связывает вероятность события с количеством информации, которое оно несет:

(2^{i} = frac{1}{p})

Здесь p — вероятность события, а i — количество информации (в бит). Такой подход к изменению информации называется вероятностным. В дополнение к нему есть другой подход, называемый алфавитным (про алфавитный подход см. теорию «Хранение и передача информации в компьютере»).