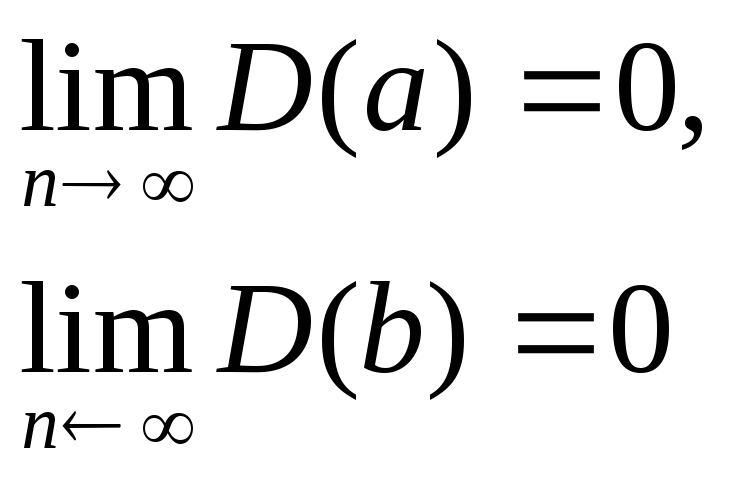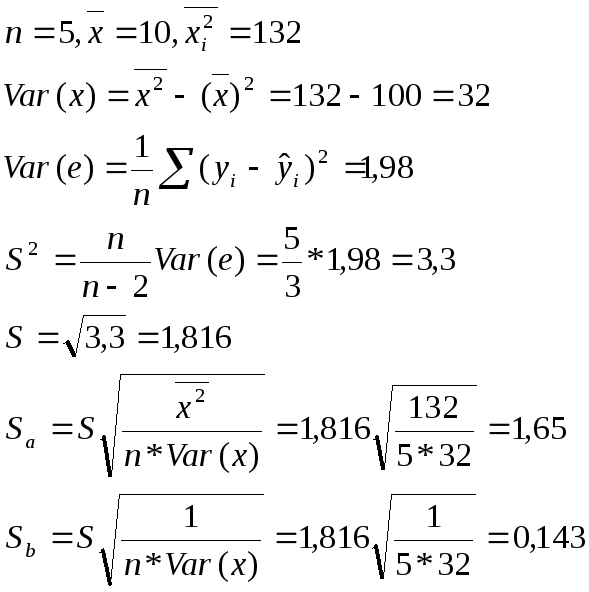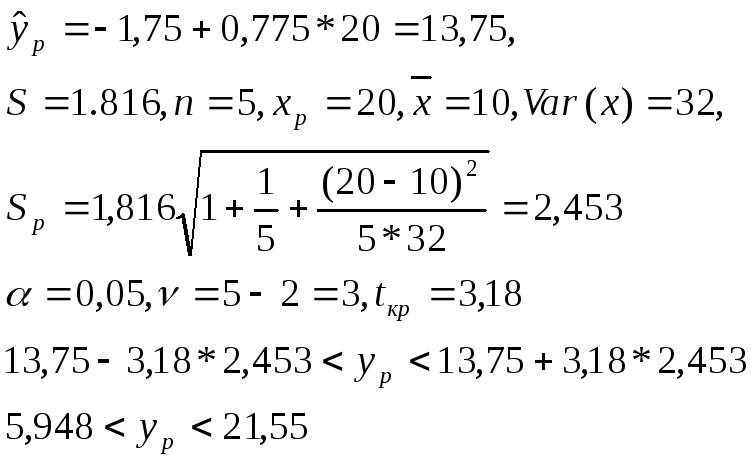Парная линейная регрессия и метод наименьших квадратов (МНК)
Краткая теория
Простейшей системой
корреляционной связи является линейная связь между двумя признаками — парная
линейная корреляция. Практическое значение ее в том, что есть системы, в
которых среди всех факторов, влияющих на результативный признак, выделяется
один важнейший фактор, который в основном определяет вариацию результативного
признака. Измерение парных корреляций составляет необходимый этап в изучении
сложных, многофакторных связей. Есть такие системы связей, при изучении которых
следует предпочесть парную корреляцию. Внимание к линейным связям объясняется
ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные
формы связей для выполнения расчетов преобразуются в линейную форму.
Уравнение парной линейной
корреляционной связи называется уравнением парной регрессии и имеет вид:
где
–
среднее значение результативного признака
при
определенном значении факторного признака
;
– свободный
член уравнения;
– коэффициент
регрессии, измеряющий среднее отношение отклонения результативного признака от
его средней величины к отклонению факторного признака от его средней величины
на одну единицу его измерения – вариация
, приходящаяся на единицу вариации
.
Параметры уравнения
находят
методом наименьших квадратов (метод решения систем уравнений, при котором в
качестве решения принимается точка минимума суммы квадратов отклонений), то
есть в основу этого метода положено требование минимальности сумм квадратов
отклонений эмпирических данных
от
выровненных
:
Для нахождения минимума
данной функции приравняем к нулю ее частные производные.
В результате получим
систему двух линейных уравнений, которая называется системой нормальных
уравнений:
Решая эту систему в общем
виде, получим:
Параметры уравнения парной
линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же
результат:
или
Если
коэффициент линейной корреляции
уже
рассчитан, то легко может быть найден коэффициент
парной
регрессии:
где
,
– стандартные
отклонения.
Примеры решения задач
Задача 1
Имеются следующие данные о
цене на нефть
(ден.
ед.) и индексе акций нефтяных компаний
(усл.
ед.).
| Цена на нефть (ден. ед.) | 17,28 | 17,05 | 18,30 | 18,80 | 19,20 | 18,50 |
| Индекс акций (усл. ед.) | 537 | 534 | 550 | 555 | 560 | 552 |
- Построить
корреляционное поле. - Предполагая, что между
переменными x и y существует линейная зависимость, найти уравнение линейной
регрессии - Оценить тесноту связи.
Решение
Построим корреляционное
поле, для этого отметим в системе координат
6 точек, соответствующих данным парам значений этих признаков.
Корреляционное поле и линия регрессии
Расположение точек на
рисунке показывает, что зависимость между компонентами
и
двумерной дискретной случайной величины может
выражаться линейным уравнением регрессии
.
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
|
|
|
|
|
|
|
| 1 | 17,28 | 537 | 298,5984 | 288369 | 9279,36 |
| 2 | 17,05 | 534 | 290,7025 | 285156 | 9104,7 |
| 3 | 18,3 | 550 | 334,89 | 302500 | 10065 |
| 4 | 18,8 | 555 | 353,44 | 308025 | 10434 |
| 5 | 19,2 | 560 | 368,64 | 313600 | 10752 |
| 6 | 18,5 | 552 | 342,25 | 304704 | 10212 |
| Сумма | 109,13 | 3288 | 1988,521 | 1802354 | 59847,06 |
Коэффициенты
уравнения регрессии
можно найти методом наименьших квадратов,
решив систему нормальных уравнений:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Подставляя
в систему уравнений числовые значения, получаем:
Решая
систему уравнений, получаем:
Уравнение
парной линейной регрессии:
Коэффициент линейной корреляции
вычислим по формуле:
Вывод
Таким
образом уравнение линейной регрессии, устанавливающее зависимость между ценой
на нефть и индексом акций имеет вид
— с увеличением цены на нефть на 1 ден.ед.
цена акций увеличивается на 12,078 ед. Коэффициент корреляции очень близок к
единице — между исследуемыми величинами существует очень тесная связь.
Задача 2
По
территории региона приводятся данные за 2011 г.
Требуется:
-
Построить линейное уравнение парной регрессии
от
.
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку
аппроксимации.
Оценить статистическую значимость параметров регрессии и корреляции с помощью
–критерия Фишера и
–критерия Стьюдента.
Выполнить прогноз заработной платы
при прогнозном значении среднедушевого
прожиточного минимума
, составляющем
107% от среднего уровня.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный
интервал.
На одном графике построить исходные данные и теоретическую прямую.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение линейной парной регрессии
1)
Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
Получено
уравнение линейной регрессии
Вывод
С
увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная
заработная плата возрастает в среднем на 1.012 руб.
Коэффициент линейной корреляции
2)
Теснота линейной связи оценивается с помощью
коэффициента корреляции
:
Коэффициент
детерминации:
Вывод
Это
означает, что 69.2% вариации заработной платы
объясняется вариацией фактора
–среднедушевого прожиточного минимума.
Средняя ошибка аппроксимации
Качество
модели можно оценить с помощью средней ошибки аппроксимации:
Вывод
Качество
построенной модели оценивается как хорошее, так как средняя ошибка
аппроксимации не превышает 8-10%.
F-критерий
3)
Рассчитаем
– критерий.
По таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=1 и k2=12-2=10, критическое значение:
Вывод
– гипотеза о статистической незначимости
уравнения регрессии отклоняется.
Статистическая значимость параметров регрессии
Оценку
статистической значимости параметров регрессии проведем с помощью
t–статистики Стьюдента
и путем расчета
доверительного интервала каждого из показателей.
Выдвигаем
гипотезу
о статистически незначимом отличии показателей
от нуля:
для числа степеней свободы
и
составит 2,23
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Определим
случайные ошибки
Тогда:
Фактическое значение превосходит
табличное значение t–статистики.
Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Рассчитаем
доверительные интервалы для параметров регрессии
и
. Для этого
определим предельную ошибку для каждого показателя:
Доверительные
интервалы:
или
или
Точечный прогноз
4)
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение прожиточного минимума составит
руб., тогда прогнозное значение среднедневной
заработной платы составит:
Интервальный прогноз
5)
Ошибка прогноза составит:
Предельная
ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный
интервал прогноза:
6) Построим исходные данные
и теоретическую прямую:
Корреляционное поле и прямая уравнения регрессии
Вопросы:
-
Истинное и
выборочное уравнения регрессии. -
Метод наименьших
квадратов. -
Геометрическая
интерпретация метода наименьших
квадратов. -
Экономическая
интерпретация коэффициентов парной
линейной регрессии. -
Основные предпосылки
регрессионного анализа. Теорема
Гаусса-Маркова. -
Расчет стандартных
ошибок коэффициентов регрессии. -
Проверка значимости
коэффициентов регрессии. -
Построение
доверительных интервалов для параметров
теоретической регрессии. -
Проверка общего
качества уровня регрессии. Коэффициент
детерминации. -
Проверка значимости
коэффициента детерминации. -
Оценка тесноты
связи между переменными. Коэффициент
корреляции. -
Проверка значимости
коэффициента корреляции. -
Прогнозирование.
1.
Пусть исследуется
статистическая зависимость экономического
показателя У (объясняемая зависимая
переменная) от экономического показателя
Х (фактора, объясняющей или независимой
переменной). Предположим, что зависимость
носит линейный характер, тогда ее можно
описать уравнением.
У=+
Х+Е
(1),
где Х – неслучайная
величина, У и Е – случайные величины.
Случайная величина
Е отражает воздействие на зависимую
переменную У неучтенных и случайных
факторов и называется ошибкой регрессии.
Уравнение (1) называют истинным
(теоретическим) уравнением
регрессии или линейной регрессионной
моделью. На основе реальных статистических
данных об экономических показателях
Х и У (выборке данных из генеральной
совокупности) оцениваются параметры
регрессии α и β и строится выборочное
уравнение регрессии
,
(2)
а, в,
— коэффициенты регрессии. Уравнение (2)
называют еще эмпирическим уравнением
регрессии.
Одним из методов
нахождения коэффициентов регрессии а
и в
является метод
наименьших квадратов (МНК).
2.
Пусть из генеральной
совокупности выбраны данные об
экономических показателях У: ( у,
у,
…, у)
и Х: ( х,
х,…,
х)
.
Если в (2) подставить наблюдаемое
(выборочное значение хi,
то получим расчетное значение
зависимой переменной у:
(3)
Разность между
фактическими и расчетными значениями
зависимой переменной обозначим ei
и назовем
остатком, т.е.:
(4)
Суть МНК заключается
в следующем: коэффициенты а
и в
должны быть такими, чтобы сумма квадратов
остатков была минимальна
(5)
в (5) уi
и xi
– известные величины, а а
и в
– неизвестные.
Запишем необходимые
условия экстремума функции S
относительно а и в:

Система (6) является
системой двух уравнений относительно
двух неизвестных а
и в.
Она легко преобразовывается в систему
(7):

Разделим оба
уравнения системы на n:

3.
начертим оси
координат Х ,У и изобразим в первой
четверти точки (хi,уi)
Полученное
изображение называется диаграммой
рассеяния или полем корреляции.
Проведем линию
регрессии
Согласно МНК, а
и в должны
быть такими, чтобы построенная линия
была ближайшей к точкам поля корреляции
по их совокупности.
Сумма квадратов
расстояний от точек поля корреляции до
линии регрессии должна быть минимальной.
Пример1: исследуется
зависимость прибыли предприятия от
затрат на приобретение нового оборудования
и техники. Собранны статистические
данные по пяти однотипным предприятиям.
Данные в млн. ден.ед. представлены в
таблице 1.
Таблица
1
|
№ предприятия |
Затраты |
Прибыль, |
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
Построить уравнение
регрессии.
Данные таблицы
представим графически, т.е. построим
поле корреляции:
Из полученной
диаграммы рассеяния видно, что зависимость
статистическая и ее можно представить
линейной регрессией
.
Для оценки коэффициентов регрессииа
и в воспользуемся
формулами (8), для этого построим рабочую
таблицу 2.
Таблица2
е нового оборудования
и техники. в была минимальна00000000
|
№ предприятия |
|
|
|
|
|
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
4 36 100 196 324 |
2 12 40 154 216 |
1 4 16 121 144 |
|
Итого: |
50 |
30 |
660 |
424 |
286 |
|
Среднее |
10 |
6 |
132 |
84,8 |
57,2 |
|
|
|
|
|
|
Подставим результаты,
полученные в таблице 2 в формулы (8):
испр.
Таким образом,
уравнение регрессии, описывающее
зависимость прибыли предприятия от
затрат на новое оборудование и технику
имеет вид:
Выбрав с помощью
диаграммы рассеяния для описания
зависимости линейную регрессию мы
выполнили этап спецификации (подбора
функции), а рассчитав коэффициенты а
и в,
т.е. оценив параметры теоретической
регрессии, мы выполнили этап параметризации.
4.
Коэффициент парной
линейной регрессии в
показывает, как в среднем изменяется
зависимый экономический показатель у
с изменением независимого фактора х на
единицу. Так в примере 1 коэффициент
в=0,775
показывает, что при увеличении расходов
на приобретение нового оборудования и
техники на 1 ден.ед. прибыль предприятия
в среднем увеличится на 0,775 ден. ед.
Коэффициент а
парной
линейной регрессии экономического
смысла не имеет.
5.
Для того, чтобы
оценки параметров теоретической
регрессии, полученные на основе МНК
были лучшими по сравнению с оценками,
найденными с помощью других методов,
должны выполнятся определенные условия,
которые называются основными
предпосылками регрессионного анализа.
Для того, чтобы их
сформулировать, вспомним что теоретическая
регрессия описывается уравнением
,
или для i-го
наблюдения
Предпосылки:
1. Математическое
ожидание случайного члена ε в любом
наблюдении должно быть равно 0:
2. Дисперсия
случайного члена ε должна быть постоянной
для всех наблюдений:
3. Случайные члены
должны быть статистически независимы
друг от друга:
4. Объясняющая
переменная хi
– неслучайная величина
Теорема Гаусса-Маркова:
Если выполняются
предпосылки 1-4 регрессионного анализа,
то оценки параметров теоретической
регрессии а и в есть наилучшие линейные
оценки, обладающие следующими свойствами:
1. Они являются
несмещенными:
2. Они являются
эффективными, т.е. имеют наименьшую
дисперсию в классе всех несмещенных
оценок.

3. Они являются
состоятельными, т.е.
Это значит, что
при достаточно большом объеме выборки
n,
оценки а и в близки к истинным параметрам
линейной регрессионной модели α и β.
6.
Для расчета
дисперсий D(a)
и D(в)
коэффициентов регрессии а
и в
в формулах (9) использовалась дисперсия
σ2
случайного члена ε. Эта дисперсия
неизвестна, но ее можно оценить, используя
выборочные данные. Можно доказать, что
несмещенной оценкой дисперсии σ2
является величина S2,
где:
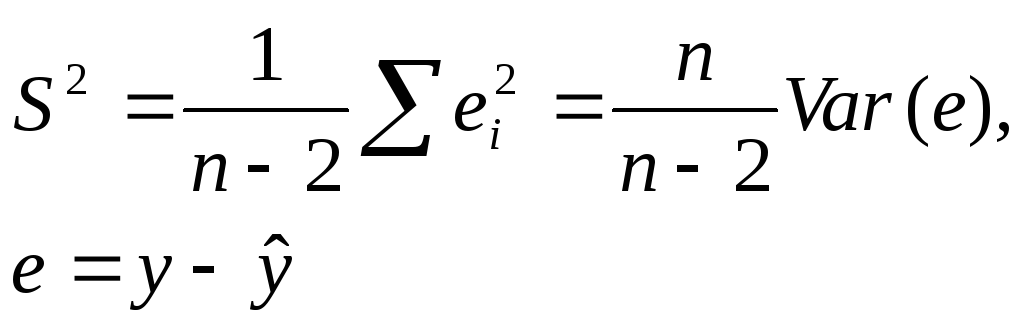
Величина S
называется стандартной ошибкой регрессии.
Она служит мерой разброса зависимой
переменной около линии регрессии.
Запишем в формулах (9) дисперсию σ2
ее оценкой S2:

и
называют
оценками дисперсии коэффициентов
регрессии, а величинаSa
и Sв
– стандартными ошибками коэффициентов
регрессии. Они
используются для построения доверительных
интервалов, которым принадлежат параметры
истинной регрессии и для проверки
значимости коэффициентов регрессии.
Вернемся в Примеру
1 и рассчитаем стандартные ошибки
коэффициентов регрессии:
7.
Коэффициента
регрессии получены на основании
выборочных данных, отобранных случайным
образом. Следовательно, коэффициенты
регрессии а и в являются случайными
числами и их значение может быть лишь
случайно оказались отличными от нуля.
Поэтому проводят проверку значимости
коэффициентов регрессии, т.е. проверку
того, значимо ли они отличны от нуля.
Для этого используют процедуру проверку
гипотез. Проверим значимость коэффициента
в.
Для этого:
1. Сформулируем
гипотезу Н0:
.
Она состоит в том,
что истинный коэффициент β=0,
2. В качестве
критерия проверки гипотезы принимают
случайную величину t:
. (12)
Эта случайная
величина имеет распределение Стьюдента
с ν = n-2
степенями свободы. Подставим в формулу
(12) оцененное по выборке значение
коэффициента в и его стандартную ошибку
Sв,
получим наблюдаемое или расчетное
значение t-критерия
tрасч.
3. Выбирают уровень
значимости проверки гипотезы. Как
правило α= 0,05 или α=0,01, т.е. пятипроцентный
или однопроцентный уровень значимости.
4. По таблице
распределения Стьюдента для выборочного
уровня значимости α/2 и ν = n-2
находят t
кр.
(критическое).
5. Если | tрасч.|
> t
кр.,
то гипотеза Н0
о равенстве параметра β=0 отвергается,
параметр β существенно отличен от нуля,
коэффициент в
значим, а переменная х оказывает
существенное влияние на зависимую у
(Н0
считается неверной с вероятностью 1- α)
6. Если | tрасч.|
< t
кр.,
гипотеза Н0
принимается, коэффициент в
незначим и переменная х не оказывает
существенного влияния на зависимую
переменную у.
Замечание: аналогично
проверяется значимость коэффициента
а
в уравнении регрессии, однако проверка
значимости коэффициента в
имеет гораздо большее значение в
регрессионном анализе.
Вернемся в примеру
1 и проверим значимость коэффициента
в.
Зависимость прибыли предприятия от
расходов на новое оборудование и технику
описывается регрессией:
(1,65) (0,143).
-
Формулируем
гипотезу Н0,
состоящую в том, что истинный коэффициент
β=0,
.
-
Определим tрасч.
.
-
Выбираем уровень
значимости проверки гипотезы
α= 0,05.
-
По таблице
распределения Стьюдента для α/2=0,025 и
числа степеней свободы
ν = 5-2=3
определим t
кр.
= 3,182.
5. | tрасч.|=5,4
> t
кр.=3,182,
поэтому гипотеза Н0
не верна с вероятностью
1-α= 1-0,05 = 0,95, параметр
β существенно отличен от нуля, коэффициент
в
значим и затраты на новое оборудование
и технику оказывают существенное влияние
на прибыль предприятия.
8.
Вспомним, что
линейная регрессионная модель (истинная
или теоретическая регрессия) имеет вид:
(13)
На основании
выборки строится выборочное уравнение
регрессии:
Также на основании
выборки рассчитывается стандартные
ошибки регрессии Sa
и Sв.
Можно доказать,
что с вероятностью 1-α (α – выбранный
уровень значимости) значения параметра
β лежат внутри интервала:
(14)
и с вероятностью
1-α (α – выбранный уровень значимости)
значение параметра α истинной регрессии
лежит внутри интервала:
(15)
Вернемся к Примеру
1 и построим доверительный интервал
для параметра β в регрессионной модели,
описывающей зависимость прибыли
предприятия от затрат на новое
оборудование и технику. Выберем уровень
значимости α= 0,05. т.к. в данном примере
ν = 5-2=3 , то t
кр.
= 3,182, в
= 0,775,
Тогда с вероятностью
1-α= 1-0,05 = 0,95 параметр β истинной регрессии
попадает в интервал
или 0,32<b<1,23
с вероятностью 95%.
9.
Выборочное уравнение
регрессии имеет вид:
тогда
Рассчитаем
выборочную дисперсию (вариацию) Var(y):
.
Из основных
предпосылок регрессионного анализа
следует, что
,
следовательно
т.е. дисперсия
зависимой переменной у (Var(y))
распадается на 2 части:
—
часть, объясняемая уравнением регрессии,
и часть
—
необъяснимая часть, зависящая от неученых
и случайных факторов.
Коэффициентом
детерминации называют отношение R2:
, (16)
которое характеризует
долю вариации зависимой переменной,
объясненную уравнением регрессии. Из
(16) следует что R2
меняется от 0 до 1:
,
чем ближе R2
к единице, тем меньше
,
т.е. доля вариации зависимой переменной,
объясняемая случайными и неучеными
факторами, тем лучше качество уравнения
регрессии. Если=0,
тоR2=1,
имеем функциональную зависимость. Чем
ближе R2
к 0, тем больше,
т.е. больше доля вариации, объясненная
случайными и неучеными факторами, тем
хуже качество регрессии. Т.к.

Вернемся к примеру
1, можно посчитать, что:
Коэффициент
детерминации близок к 1, качество
регрессии хорошее.
Можно утверждать,
что вариация (изменчивость) прибыли
предприятия на 90,7% объясняется затратами
на новое оборудование и технику и на
9,3% — прочими неучтенными и случайными
факторами.
10.
Т.к. R2
оценивается на основании выборочных
данных, то его отличие от 0 может оказаться
случайным. Поэтому проводят проверку
его значимости:
1. Формулируется
гипотеза Н0:
R2=0,
состоящая в том, что истинный коэффициент
детерминации равен 0.
2. В качестве
критерия проверки гипотезы применяют
случайную величину F:
. (18)
Величина F
имеет распределение Фишера с двумя
степенями свободы ν1=1,
ν2=n-2.
-
Выберем уровень
значимости проверки гипотезы значимости:
.
-
На основании α,
ν1, ν2
в таблице
распределения Фишера выбираем Fкр.
(критическое) -
Сравниваем Fрасч
и Fкр..
если Fрасч
> Fкр.,
то с вероятностью 1-α гипотезу Н0
считаем неверной, т.е. истинный коэффициент
детерминации существенно отличен от
нуля, уравнение регрессии значимо и
переменные, включенные в уравнение
регрессии достаточно объясняют поведение
зависимой переменной. Если Fрасч
< Fкр.,
то принимаемая гипотеза Н0,
уравнение регрессии считается незначимым.
Проверим значимость
коэффициента детерминации в примере
1:
-
Формулируем
гипотезу Н0:
R2=0. -
Находим Fрасч..
В (18) подставим значение коэффициента
детерминации, оцененное по выборке:
.
3.Выбираем уровень
значимости α=0,005.
4. В таблице
распределения Фишера на основании
α=0,05 и для степеней свободы ν1=1,
ν2
=5-2=3 найдем
Fкр.
.
-
Fрасч
=29,2> Fкр.=10,13,
поэтому Н0
не верна в вероятностью 1-0,05=0,95, коэффициент
детерминации значим, значимо построенное
в Примере 1 уравнение регрессии.
11.
Уравнение регрессии
всегда дополняется показателем тесноты
связи между переменными. При использовании
линейной регрессии в качестве такого
показателя выступает линейный коэффициент
корреляции:
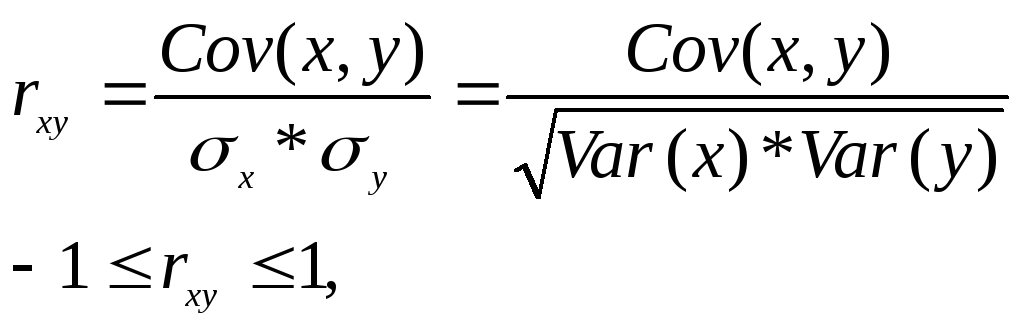
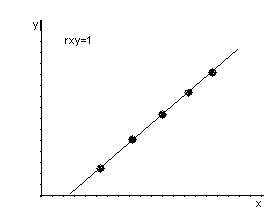
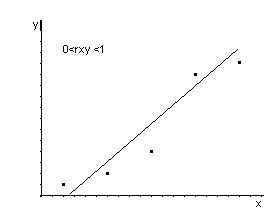
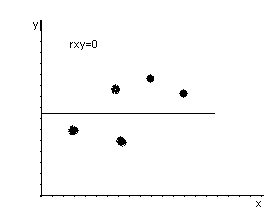
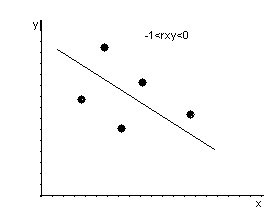
rxy
– безразмерная величина, показывает
степень линейной зависимости между
переменными. Чем ближе rxy
к ±1, тем сильнее линейная зависимость.
Чем ближе rxy
к 0, тем линейная зависимость слабее.
Если rxy
= ±1, то имеет место функциональная
линейная зависимость. Если rxy
= 0, то линейная зависимость отсутствует.
Если rxy
>0, то связь между переменными
положительная, если rxy
<0 – отрицательная.
Рассчитаем
коэффициент корреляции в примере 1:
rxy
>0 и близок к 1 следовательно линейная
зависимость между прибылью предприятия
и затратами на новое оборудование –
положительная и тесная.
12.
Осуществляется
аналогично проверки значимости
коэффициентов регрессии и детерминации,
используется t-статистика:
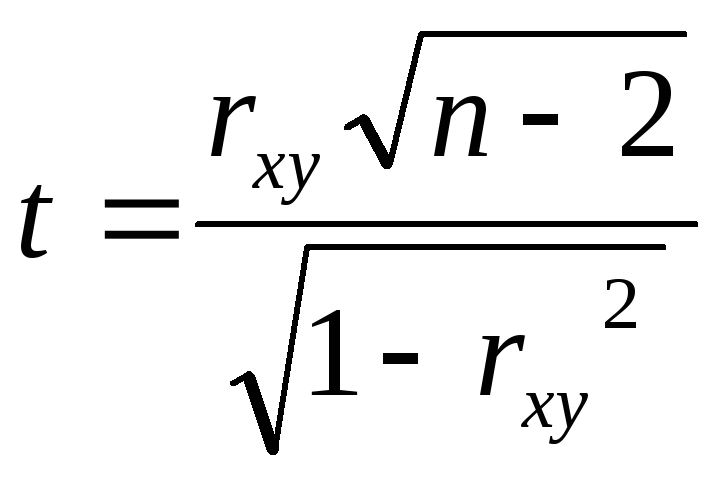
Проведем проверку
значимости коэффициента корреляции в
примере 1:
-
Формулируем
гипотезу, состоящую в том, что истинный
коэффициент корреляции равен нулю:
.
-
Подставим значение
коэффициента корреляции, вычисленное
по выборке в (20):
-
Выбираем уровень
значимости α=0,05. -
Для α/2=0,025 и для
ν=n-2=3
в таблице распределения Стьюдента
находим tкр.:
Следовательно,
истинный коэффициент корреляции
существенно отличен от 0, линейная
зависимость между прибылью предприятия
и затратами на новое оборудование и
технику действительно тесная..
Замечание 1:
В парном линейном
регрессионном анализе проверка значимости
коэффициента в, коэффициента корреляции
и коэффициента детерминации являются
эквивалентными.
Замечание 2:
Легко показать,
что коэффициент детерминации равен
квадрату коэффициента корреляции,
,
13.
Прогнозирование
на основе эконометрических моделей
является одной из основных задач
эконометрики.
Под прогнозированием
в эконометрике понимают построение
оценки зависимой переменной для таких
значений независимых переменных, которых
нет в исходных наблюдениях.
Различают точечное
прогнозирование и интервальное.
.
Точечный прогноз
это число, значение зависимой переменной,
вычисляемое для заданных значений
независимых переменных.
Интервальный
прогноз это интервал, в котором с заданным
уровнем значимости ( с заданной
вероятностью) находится истинное
значение зависимой переменной для
заданных значений независимых переменных.
Рассмотрим парную
линейную регрессионную модель
и соответствующее выборочное уравнение
регрессии.
Обозначим через ур
истинное значение переменной у для
заданного значения независимой переменной
хр,
т.е.
.
Точечным прогнозом
для ур
является
,
т.е. чтобы получить точечный прогноз
нужно в построенное уравнение регрессии
подставить заданное значение независимой
переменной.
Ошибкой
предсказания
()
называют разность между прогнозным и
истинным значениями независимой
переменной.
Можно доказать,
что дисперсия ошибки предсказания
. (21)
Из (21) следует, что
чем ближе заданное значение независимой
переменной
к
тем
меньше дисперсия прогноза и чем больше
объем выборкиn,
тем меньше дисперсия прогноза.
Заменив в (21)
дисперсию
на
ее оценку,
извлечем, квадратный корень и получим
стандартную ошибку предсказания.
(22)
Выберем уровень
значимости α и по таблице распределения
Стьюдента найдем tкр.
Тогда с вероятностью 1- α истинное
значение переменной ур
будет находится внутри интервала:
(23)
Очевидно, что чем
ближе
к
и чем большеn,
тем уже доверительный интервал (тем
точнее прогноз). Это надо учитывать,
выбирая прогнозные значения для
независимой переменной.
Вернемся в Примеру
1 и найдем точечный и интервальный
прогнозы для прибыли предприятия для
затрат на новое оборудование и технику
в размере 20 млн. денежных единиц.
Вывод:
с вероятностью 0,95 истинное значение
прибыли попадет в полученный интервал.
Парная линейная регрессия. Задачи регрессионного анализа
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Уравнение парной линейной регрессии и метод наименьших квадратов
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:
- прямая парной линейной регрессии проходит через точку ;
- среднее значение отклонений равна нулю: ;
- значения и не связаны: .
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,
— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
—
остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .
Можем убедиться, что выполняется закономерность SSR = SST — SSE :
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.
Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .
Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .
Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Задачи регрессионного анализа
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,
где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
Уравнение регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: . Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 | ||
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
| 8,4988 | 11,1431 | х | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
| 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х | |
| 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | ||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
| 8,4988 | 11,1431 | 0,000640820 | х | х | х | |
| 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
http://math.semestr.ru/corel/corel.php
http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html