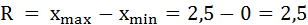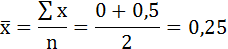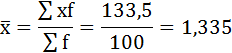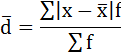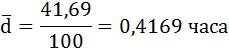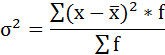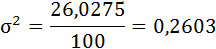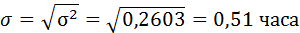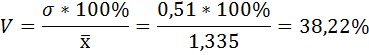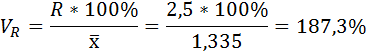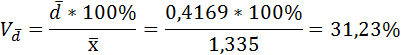Имеются следующие данные выборочного обследования студентов одного из вузов:
| Затраты времени на дорогу до института, час | Число студентов, % к итогу |
|---|---|
| До 0,5 | 7 |
| 0,5 – 1,0 | 18 |
| 1,0 – 1,5 | 32 |
| 1,5 – 2,0 | 37 |
| Свыше 2,0 | 6 |
| Всего | 100 |
Вычислите абсолютные и относительные показатели вариации.
Решение:
Проанализируем исходные данные.
Данный ряд распределения содержит открытые интервалы, которые предварительно необходимо закрыть. Величина интервала второй группы равна 0,5 следовательно, и величина первой группы также равна 0,5. Величина интервала предпоследней группы равна 0,5, значит, и последний интервал будет иметь величину, равную 0,5.
Найдём абсолютные показатели вариации:
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации затрат времени на дорогу до института равен 2,5 часа.
2) Средние затраты времени определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
Занесём результаты вычислений в таблицу:
| Затраты времени на дорогу до института, час | Закрытые интервалы | Середина интервала, (х) | Число студентов, % к итогу, (f) | хf |
|---|---|---|---|---|
| До 0,5 | 0 – 0,5 | 0,25 | 7 | 1,75 |
| 0,5 – 1,0 | 0,5 – 1,0 | 0,75 | 18 | 13,5 |
| 1,0 – 1,5 | 1,0 – 1,5 | 1,25 | 32 | 40 |
| 1,5 – 2,0 | 1,5 – 2,0 | 1,75 | 37 | 64,75 |
| Свыше 2,0 | 2,0 – 2,5 | 2,25 | 6 | 13,5 |
| Всего | – | – | 100 | 133,5 |
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
| Затраты времени на дорогу до института, час | Середина интервала, (х) | Число студентов, % к итогу, (f) | хf | 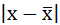 |
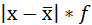 |
|---|---|---|---|---|---|
| До 0,5 | 0,25 | 7 | 1,75 | 1,085 | 7,595 |
| 0,5 – 1,0 | 0,75 | 18 | 13,5 | 0,585 | 10,53 |
| 1,0 – 1,5 | 1,25 | 32 | 40 | 0,085 | 2,72 |
| 1,5 – 2,0 | 1,75 | 37 | 64,75 | 0,415 | 15,355 |
| Свыше 2,0 | 2,25 | 6 | 13,5 | 0,915 | 4,49 |
| Всего | — | 100 | 133,5 | — | 41,69 |
Среднее линейное отклонение затрат времени составляет 0,4169 часа.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Построим вспомогательную таблицу:
| Затраты времени на дорогу до института, час | Середина интервала, (х) | Число студентов, % к итогу, (f) | 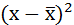 |
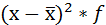 |
|---|---|---|---|---|
| До 0,5 | 0,25 | 7 | 1,17723 | 8,24058 |
| 0,5 – 1,0 | 0,75 | 18 | 0,34223 | 6,16005 |
| 1,0 – 1,5 | 1,25 | 32 | 0,00722 | 0,2312 |
| 1,5 – 2,0 | 1,75 | 37 | 0,17223 | 6,37233 |
| Свыше 2,0 | 2,25 | 6 | 0,83723 | 5,02335 |
| Всего | — | 100 | 2,53613 | 26,0275 |
5) Среднее квадратическое отклонение затрат времени определяется как корень квадратный из дисперсии:
Найдём относительные показатели вариации:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значения признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Поскольку V > 33%, следовательно, вариация значительная, а совокупность не однородна.
7) Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и определяется по формуле:

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
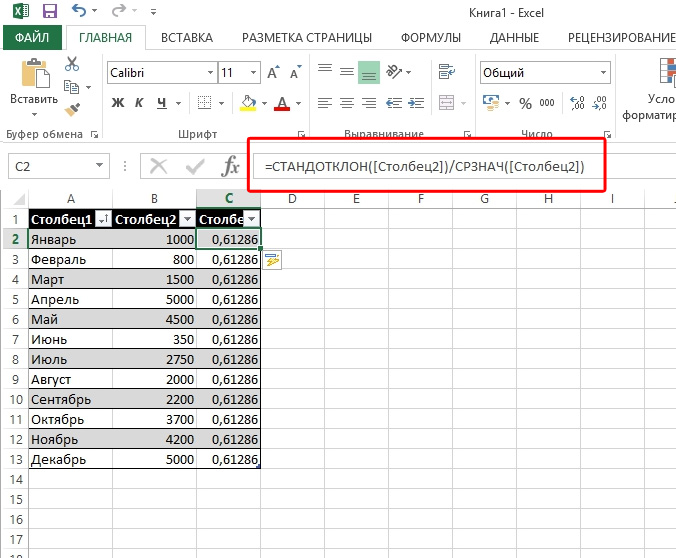
Вставьте формулу и укажите диапазон данных
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
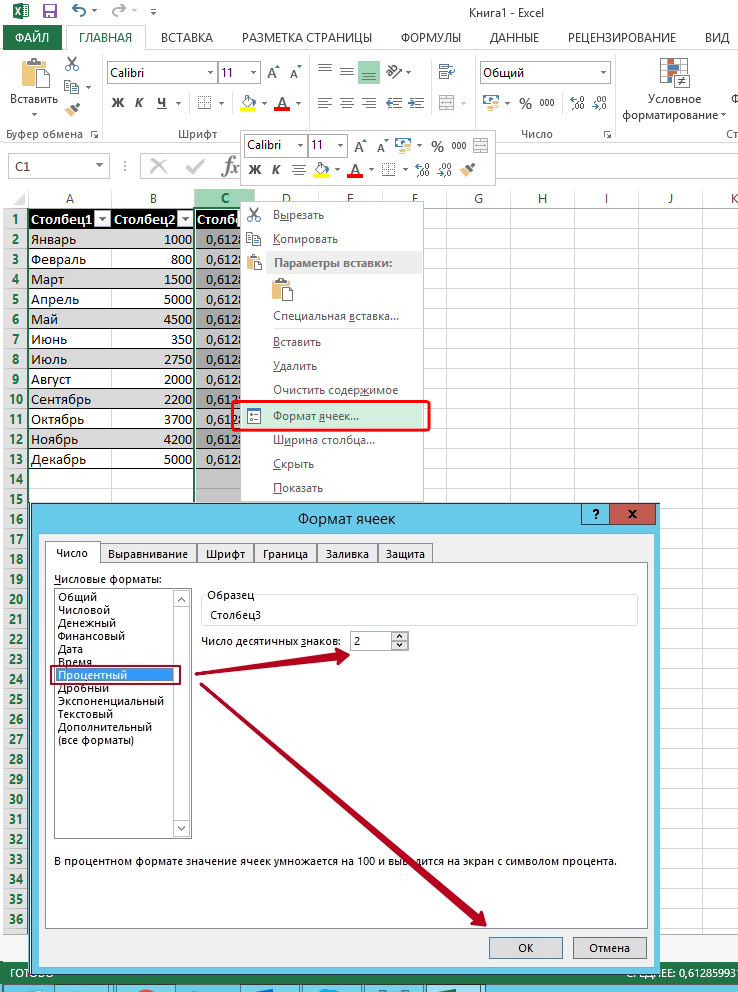
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
- Откройте вкладку «Главная».
- Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.
Коэффициент вариации — это статистическая метрика, которая может помочь специалистам зарегистрировать изменения в данных с течением времени. Эта метрика также может быть эффективным методом расчета финансового риска и вознаграждения за инвестиционную деятельность. Вы можете рассчитать коэффициент вариации с помощью простой формулы.
В этой статье мы обсудим, что такое коэффициент вариации и как его рассчитать, а также приведем несколько примеров применения этого статистического измерения к различным инвестиционным сценариям.
Основные выводы:
-
Коэффициент вариации — это эффективная метрика для быстрой оценки относительной дисперсии точек данных вокруг среднего значения выборки.
-
Финансовые аналитики и инвесторы могут часто оценивать коэффициент вариации для анализа риска и волатильности в зависимости от ожидаемой доходности инвестиций.
-
Более низкое соотношение между стандартным отклонением и средним значением может указывать на более высокий коэффициент доходности, в то время как более высокое соотношение может указывать на более низкий коэффициент доходности.
Что такое коэффициент вариации?
Коэффициент вариации (CV) измеряет разброс точек данных вокруг среднего значения. Отношение стандартного отклонения к среднему значению делает CV ценным ресурсом при сравнении вариаций одного ряда данных с другим. Он показывает, насколько сильно варьируются данные в выборке по сравнению со средним значением популяции.
Когда вы оцениваете CV, вы можете представить значение в процентах, где более низкий процент может указывать на более низкий CV, а более высокий процент может означать более высокий CV. В финансовом и инвестиционном анализе, где волатильность и риск могут влиять на потенциальную доходность, более низкий CV означает более низкое соотношение риска и доходности, что указывает на лучший компромисс между потенциальной доходностью и риском, присущим конкретному инвестиционному инструменту.
Какова формула для коэффициента вариации?
Формула CV использует стандартное отклонение и среднее значение данных вашей выборки для расчета коэффициента, отражающего дисперсию ваших значений вокруг среднего. В статистическом анализе основной формулой для расчета коэффициента вариации является:
CV = стандартное отклонение выборочного среднего x 100
При применении формулы в бизнесе, например, в финансовых расчетах, многие специалисты упрощают формулу CV, чтобы она соответствовала таким финансовым показателям, как доходность инвестиций, прирост капитала, риск и волатильность инвестиций. Поэтому многие аналитики могут также использовать следующую формулу для расчета CV с точки зрения финансового риска и вознаграждения:
CV = прогнозируемая доходность волатильности x 100
Использование коэффициента вариации
Вы можете использовать КВ для определения соотношения риска и доходности, а также для определения того, превышает ли вознаграждение риск инвестиций. КВ также иногда может привести к неточному или непригодному для использования значению. Например, вычисление отрицательного значения или нуля может указывать на то, что измерение коэффициента неточно отражает ваш коэффициент. Нахождение коэффициента вариации в данных относится не только к сфере бизнеса и финансов.
Например, биологи и исследователи часто используют его в своих наблюдениях для расчета повторяемости результатов данных. Педагоги также могут применять CV для сравнения методик преподавания, выясняя, что приводит к повышению среднего балла. Метеорологи используют его для измерения временной изменчивости осадков. Однако существуют некоторые споры относительно точности CV в этих ситуациях. При широком диапазоне переменных и условий возрастает вероятность неточности.
Как рассчитать коэффициент вариации
Чтобы рассчитать коэффициент вариации, выполните следующие шаги, используя вышеупомянутую формулу:
1. Определите волатильность
Чтобы найти волатильность или стандартное отклонение, вычтите среднюю цену за период из каждой ценовой точки. Чтобы преобразовать разницу в дисперсию, возведите в квадрат, просуммируйте и усредните ответ. Квадратный корень из дисперсии становится приемлемым процентом для волатильности.
2. Определение ожидаемой доходности
Чтобы найти ожидаемую доходность, умножьте потенциальные исходы или доходность на вероятность их наступления. Сумма всех собранных ответов становится ожидаемой доходностью. На данном этапе оба показателя готовы для формулы.
3. Разделить
Рассчитав показатели волатильности и ожидаемой доходности, разделите их друг на друга. Большинство ответов дается в виде десятичных дробей. Вы также можете преобразовать CV в проценты.
4. Умножить на 100
Чтобы перевести в проценты, умножьте десятичные числа на 100. При этом десятичный знак сдвигается на две цифры, создавая либо целое число, либо десятичный процент. Окончательный ответ — коэффициент вариации.
Как рассчитать коэффициент вариации в электронной таблице
Некоторые предприятия и частные лица используют электронные таблицы для записи больших объемов данных за длительные периоды времени. Они выбирают электронные таблицы не только для того, чтобы успевать за огромным количеством собранных данных, но и для того, чтобы легко рассчитать коэффициент вариации в своих данных. Электронные таблицы могут записывать расчеты вместе с данными и продолжать их по мере добавления новых данных. Вы можете рассчитать коэффициент вариации с помощью электронной таблицы, выполнив следующие три шага:
1. Используйте функцию стандартного отклонения для набора данных
Программы для работы с электронными таблицами должны иметь определенную функцию для стандартного отклонения. Для того чтобы расчет работал, набор данных должен содержать эту функцию. Во многих распространенных программах электронных таблиц для вычисления стандартного отклонения можно ввести команду =STDEVP. Введите формулу в пустую ячейку рядом с соответствующим набором данных, который вы оцениваете.
2. Рассчитайте среднее значение
Вычисление среднего значения в электронных таблицах требует специальных формул. Например, в большинстве приложений электронных таблиц вы можете использовать =AVERAGE для применения программной функции. При вводе команды среднего значения поместите его в ячейку рядом с соответствующим набором данных, чтобы легче его увидеть.
3. Разделите стандартное отклонение на среднее значение
Разделите ячейки, содержащие стандартное отклонение и среднее значение. Например, чтобы разделить стандартное отклонение в ячейке A3 и среднее значение в ячейке A5, вы можете использовать функцию =A3A5 в пустой ячейке для вычисления коэффициента и отображения коэффициента вариации.
Некоторые программы обработки электронных таблиц могут вычислять коэффициент вариации с помощью команды =STDEV.P, что устраняет необходимость в нескольких шагах. В зависимости от программы, вы можете просто ввести команду в пустую ячейку и обозначить диапазон данных, которые вы хотите рассчитать. После этого в выбранной ячейке появится значение CV.
Пример расчета
Чтобы принять обоснованное решение между акциями и облигациями, Джамиля применяет формулу коэффициента вариации для определения соотношения риска и доходности для обоих инвестиционных инструментов. Сначала она оценивает инвестиции в акции, волатильность которых составляет 5%, а прогнозируемая доходность — 13%. Используя эти значения в формуле, Джамиля находит:
-
CV = среднее стандартное отклонение выборки x 100 =
-
CV = прогнозируемая доходность волатильности x 100 =
-
CV = (0.05) (0.13) x 100 = 0.38 x 100 = 38%
Чтобы рассчитать коэффициент вариации облигации для сравнения, Джамиля делит волатильность в 3% на прогнозируемую доходность в 15%. Используя формулу, она оценивает:
-
CV = стандартное отклонение выборочного среднего x 100 =
-
CV = прогнозируемая доходность волатильности x 100 =
-
CV = (0.03) (0.15) x 100 = 0.2 = 20%
Джамиля сравнивает инвестиции в облигации и акции и приходит к выводу, что CV инвестиций в облигации в размере 20% указывает на более низкое соотношение риска и доходности, чем CV акций в размере 38%. Теперь, когда Джамиля понимает, какой инвестиционный инструмент представляет наименьшее соотношение риска и доходности, она может выбрать наиболее подходящий вариант для достижения своих финансовых целей.