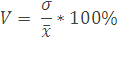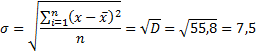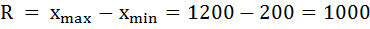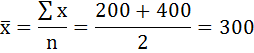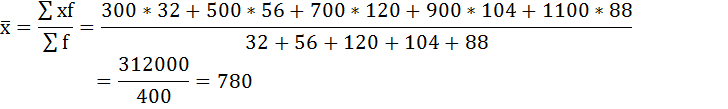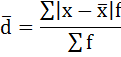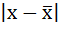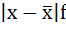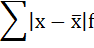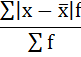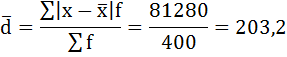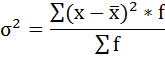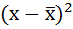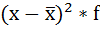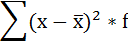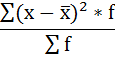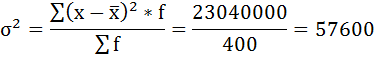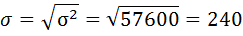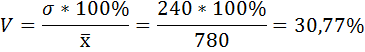Коэффициент вариации
Из
всех показателей вариации среднеквадратическое
отклонение в наибольшей степени
используется для проведения других
видов статистического анализа. Однако
среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности
значений и чтобы понять, насколько она
велика относительно самих значений,
требуется относительный показатель.
Такой показатель называется он коэффициент
вариации.
Формула
коэффициента вариации:
Данный
показатель измеряется в процентах (если
умножить на 100%).
В
статистике принято, что, если коэффициент
вариации
меньше
10%, то степень рассеивания данных
считается незначительной,
от
10% до 20% — средней,
больше
20% и меньше или равно 33% — значительной,
значение
коэффициента вариации не превышает
33%, то совокупность считается однородной,
если
больше 33%, то – неоднородной.
Средние,
рассчитанные для однородной совокупности
– значимы, т.е. действительно характеризуют
эту совокупность, для неоднородной
совокупности – незначимы, не характеризуют
совокупность из-за значительного
разброса значений признака в совокупности.
Возьмем
пример с расчетом среднего линейного
отклонения.
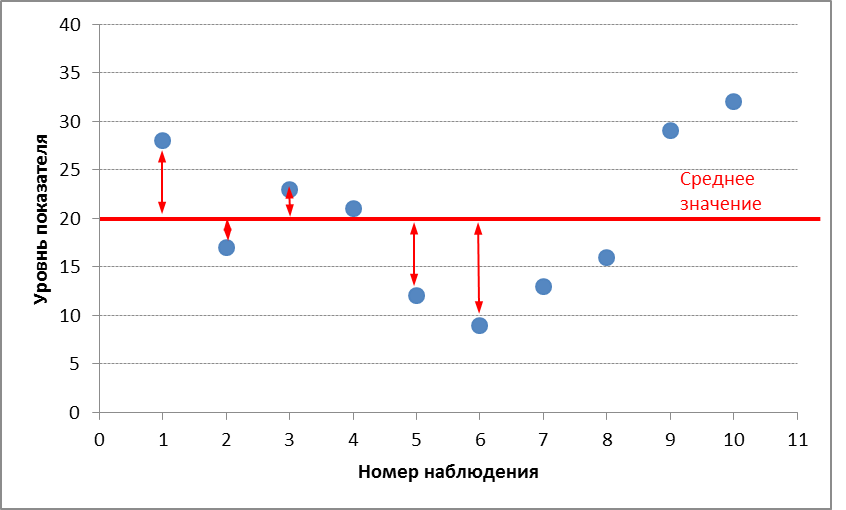
И
график для напоминания
По
этим данным рассчитаем: среднее значение,
размах вариации, среднее линейное
отклонение, дисперсию и стандартное
отклонение.
Среднее
значение – это обычная средняя
арифметическая.
Размах
вариации – разница между максимумом и
минимумом:
Среднее
линейное отклонение считается по
формуле:
Дисперсия
считается по формуле:
Среднеквадратическое
отклонение – квадратный корень из
дисперсии:
Расчет
сведем в табличку.
Вариация
показателя отражает изменчивость
процесса или явления. Ее степень может
измеряться с помощью нескольких
показателей.
-
Размах
вариации –
разница между максимумом и минимумом.
Отражает диапазон возможных значений. -
Среднее
линейное отклонение –
отражает среднее из абсолютных (по
модулю) отклонений всех значений
анализируемой совокупности от их
средней величины. -
Дисперсия –
средний квадрат отклонений. -
Среднеквадратическое
отклонение –
корень из дисперсии (среднего квадрата
отклонений). -
Коэффициент
вариации –
наиболее универсальных показатель,
отражающий степень разбросанности
значений независимо от их масштаба и
единиц измерения. Коэффициент вариации
измеряется в процентах и может быть
использован для сравнения вариации
различных процессов и явлений.
Таким
образом, в статистическом анализе
существует система показателей,
отражающих однородность явлений и
устойчивость процессов. Часто показатели
вариации не имеют самостоятельного
смысла и используются для дальнейшего
анализа данных. Исключением является
коэффициент вариации, который характеризует
однородность данных, что является ценной
статистической характеристикой.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
В статистике под вариацией понимают количественные
изменения величины исследуемого признака в пределах однородной совокупности,
обусловленные взаимодействием различных факторов. Причины, порождающие вариацию социально-экономических
явлений, очень сложны и многообразны. Они лежат в коренных особенностях
исследуемого явления, в его сущности, а также в методологии сбора исходной
информации. Социально-экономические явления, как правило, обладают большой
вариацией. Если исследуются результаты целенаправленной человеческой
деятельности, то вариация будет выражать вмешательство многочисленных факторов,
природу которых не всегда можно установить. Однако, в большинстве теоретических
исследований и практических применений статистики необходимы наряду со средней
показатели вариации, характеризующие группировку значений признака вокруг
средней, т. е. степень упорядоченности
статистической совокупности.
В соответствии с определением вариация измеряется
степенью колеблемости вариантов признака от уровня их
средней величины. Именно на этом и основано большинство показателей,
применяемых в статистике для измерения вариации значений признака в
совокупности. К показателям вариации относятся: размах вариации, среднее
линейное отклонение, дисперсия, среднее квадратическое
отклонение, коэффициент вариации.
Простейшим показателем вариации является размах вариации, определяемый как разность между максимальным и минимальным значениями
признака:
Размах вариации выражается в тех же единицах
измерений, что в варианты ряда. По величине его можно определить, например,
передовое и отстающее в достижении какой-либо цели. Величина вариации служит
также и для характеристики средней. Размах вариации имеет и самостоятельное
значение. Например, в промышленности для измерения точности изделий
устанавливают определенные пределы, соответствующие иногда величине размаха
вариации их признаков.
Однако показатель размаха вариации не может в полной
мере охарактеризовать колеблемость ряда, поскольку он
не учитывает промежуточных значений вариантов внутри этих пределов, а по этому
не отражает колеблемость ряда в целом, кроме того, он
полностью зависит от максимального и минимального значений, которые могут
оказаться не достаточно характерными.
Таким образом, размах вариации отражает иногда
случайную, а не типичную для данного ряда величину колеблемости.
По этому необходимы другие показатели вариации, основанные на всех значениях
признака в данной совокупности, а именно: среднее линейное отклонение,
дисперсия и среднее квадратическое отклонение.
Среднее линейное отклонение представляет среднюю
арифметическую из абсолютных значений отклонений отдельных вариантов от их
среднего значения.
Для данных, где частота каждого варианта равна
единице, среднее линейное отклонение определяется по формуле:
Для вариационных рядов
определяется с учетом частот по формуле:
Среднее линейное отклонение по сравнению с размахом
вариации дает более полную характеристику колеблемости
признака в совокупности.
Средний квадрат отклонений вариантов от их средней
величины называют дисперсией
.
Дисперсия рассчитывается по формуле:
Для негруппированных
данных, где частота каждого варианта равна единице, дисперсия рассчитывается по
формуле простой средней:
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
либо при равенстве весов:
Среднее квадратическое
отклонение является также обобщающим показателем колеблемости
признака и характеризует средний показатель отклонения вариантов ряда от их
общей средней. Выражается s в тех же именованных числах, в которых выражены
варианты совокупности и средняя величина.
Дисперсия и среднее квадратическое отклонение — наиболее широко применяемые
показатели вариации. Объясняется это тем, что они входят в большинство теорем
теории вероятностей, служащих фундаментом математической статистики. Кроме
того, дисперсия может быть разложена на составные элементы, позволяющие оценить
влияние различных факторов, обусловливающих вариацию признака. Порядок расчета
среднего квадратического отклонения следующий:
1) Определяется средняя
величина:
2) Рассчитывается
отклонения вариантов от средней:
3) Отклонение каждого
варианта от средней возводится в квадрат:
4) Квадрат отклонений
взвешивается по частотам:
5) Взвешенные по
частотам квадраты отклонений суммируются:
6) Полученная сумма
делится на сумму частот, и из нее извлекается квадратный корень.
Среднее квадратическое
отклонение можно вычислить, составив следующую расчетную таблицу:
| № п/п |
|
Линейные отклонения от средней
|
Квадрат линейных отклонений
|
Взвешенные квадраты
|
| … | … | … | … | … |
|
Итого |
Среднее квадратическое
отклонение можно вычислить на основании математических преобразований значений
варьирующего признака, применяя способ условных моментов:
где первый условный
момент:
второй условный момент:
Среднее квадратическое
отклонение по способу условных моментов определяется по формуле:
Система условных
моментов различных порядков, в частности, третьего
и
четвертого
используется при расчете различных
статистических характеристик (например, коэффициентов асимметрии и эксцесса).
Чем больше σ, тем разнообразнее состав
совокупности по величине изучаемого признака, и, наоборот, чем меньше σ, тем
состав совокупности по величине изучаемого признака более одинаков. Однако
оценка величины σ
как качественной характеристики ряда в конечном итоге определяется сущностью
изучаемых явлений. Среднее квадратическое отклонение
используется для сопоставления вариации по однородным совокупностям, а также
для одной совокупности за разные годы. Среднее квадратическое
отклонение является критерием надежности средней. Чем меньше оно, тем лучше
средняя арифметическая отражает всю представляемую совокупность.
Коэффициент осцилляции – процентное отношение размаха
вариации к средней
Линейный
коэффициент вариации (относительное линейное отклонение) измеряют через
соотношение среднего линейного отклонения и средней:
Коэффициент вариации представляет собой отношение
среднего квадратического отклонения к средней
арифметической:
Характеризуя степень колеблемости
признака, коэффициент вариации позволяет давать сравнительную характеристику
этой колеблемости одного и того же признака в
различных совокупностях.
Коэффициент вариации используется также, если
сравнивается степень вариации одного и того же признака в двух совокупностях,
имеющих разные по величине средние. Как относительные величины коэффициенты
вариации могут сопоставляться не только для одинаковых одноименных показателей,
но и для различных показателей, выраженных в разных единицах измерения. Таким
образом, коэффициент вариации в отличие от среднего квадратического
отклонения позволяет сопоставить глубину вариации неоднородных совокупностей.