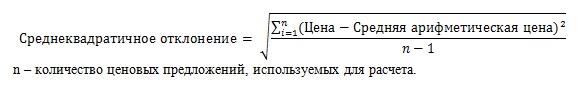Как найти коэффициент вариации примеры

Коэффициент вариации — это статистическая метрика, которая может помочь специалистам зарегистрировать изменения в данных с течением времени. Эта метрика также может быть эффективным методом расчета финансового риска и вознаграждения за инвестиционную деятельность. Вы можете рассчитать коэффициент вариации с помощью простой формулы.

В этой статье мы обсудим, что такое коэффициент вариации и как его рассчитать, а также приведем несколько примеров применения этого статистического измерения к различным инвестиционным сценариям.

Основные выводы:

• Коэффициент вариации — это эффективная метрика для быстрой оценки относительной дисперсии точек данных вокруг среднего значения выборки.

• Финансовые аналитики и инвесторы могут часто оценивать коэффициент вариации для анализа риска и волатильности в зависимости от ожидаемой доходности инвестиций.

• Более низкое соотношение между стандартным отклонением и средним значением может указывать на более высокий коэффициент доходности, в то время как более высокое соотношение может указывать на более низкий коэффициент доходности.

Что такое коэффициент вариации?

Коэффициент вариации (CV) измеряет разброс точек данных вокруг среднего значения. Отношение стандартного отклонения к среднему значению делает CV ценным ресурсом при сравнении вариаций одного ряда данных с другим. Он показывает, насколько сильно варьируются данные в выборке по сравнению со средним значением популяции.

Когда вы оцениваете CV, вы можете представить значение в процентах, где более низкий процент может указывать на более низкий CV, а более высокий процент может означать более высокий CV. В финансовом и инвестиционном анализе, где волатильность и риск могут влиять на потенциальную доходность, более низкий CV означает более низкое соотношение риска и доходности, что указывает на лучший компромисс между потенциальной доходностью и риском, присущим конкретному инвестиционному инструменту.

Какова формула для коэффициента вариации?

Формула CV использует стандартное отклонение и среднее значение данных вашей выборки для расчета коэффициента, отражающего дисперсию ваших значений вокруг среднего. В статистическом анализе основной формулой для расчета коэффициента вариации является:

CV = стандартное отклонение выборочного среднего x 100

При применении формулы в бизнесе, например, в финансовых расчетах, многие специалисты упрощают формулу CV, чтобы она соответствовала таким финансовым показателям, как доходность инвестиций, прирост капитала, риск и волатильность инвестиций. Поэтому многие аналитики могут также использовать следующую формулу для расчета CV с точки зрения финансового риска и вознаграждения:

CV = прогнозируемая доходность волатильности x 100

Использование коэффициента вариации

Вы можете использовать КВ для определения соотношения риска и доходности, а также для определения того, превышает ли вознаграждение риск инвестиций. КВ также иногда может привести к неточному или непригодному для использования значению. Например, вычисление отрицательного значения или нуля может указывать на то, что измерение коэффициента неточно отражает ваш коэффициент. Нахождение коэффициента вариации в данных относится не только к сфере бизнеса и финансов.

Например, биологи и исследователи часто используют его в своих наблюдениях для расчета повторяемости результатов данных. Педагоги также могут применять CV для сравнения методик преподавания, выясняя, что приводит к повышению среднего балла. Метеорологи используют его для измерения временной изменчивости осадков. Однако существуют некоторые споры относительно точности CV в этих ситуациях. При широком диапазоне переменных и условий возрастает вероятность неточности.

Как рассчитать коэффициент вариации

Чтобы рассчитать коэффициент вариации, выполните следующие шаги, используя вышеупомянутую формулу:

1. Определите волатильность

Чтобы найти волатильность или стандартное отклонение, вычтите среднюю цену за период из каждой ценовой точки. Чтобы преобразовать разницу в дисперсию, возведите в квадрат, просуммируйте и усредните ответ. Квадратный корень из дисперсии становится приемлемым процентом для волатильности.

2. Определение ожидаемой доходности

Чтобы найти ожидаемую доходность, умножьте потенциальные исходы или доходность на вероятность их наступления. Сумма всех собранных ответов становится ожидаемой доходностью. На данном этапе оба показателя готовы для формулы.

3. Разделить

Рассчитав показатели волатильности и ожидаемой доходности, разделите их друг на друга. Большинство ответов дается в виде десятичных дробей. Вы также можете преобразовать CV в проценты.

4. Умножить на 100

Чтобы перевести в проценты, умножьте десятичные числа на 100. При этом десятичный знак сдвигается на две цифры, создавая либо целое число, либо десятичный процент. Окончательный ответ — коэффициент вариации.

Как рассчитать коэффициент вариации в электронной таблице

Некоторые предприятия и частные лица используют электронные таблицы для записи больших объемов данных за длительные периоды времени. Они выбирают электронные таблицы не только для того, чтобы успевать за огромным количеством собранных данных, но и для того, чтобы легко рассчитать коэффициент вариации в своих данных. Электронные таблицы могут записывать расчеты вместе с данными и продолжать их по мере добавления новых данных. Вы можете рассчитать коэффициент вариации с помощью электронной таблицы, выполнив следующие три шага:

1. Используйте функцию стандартного отклонения для набора данных

Программы для работы с электронными таблицами должны иметь определенную функцию для стандартного отклонения. Для того чтобы расчет работал, набор данных должен содержать эту функцию. Во многих распространенных программах электронных таблиц для вычисления стандартного отклонения можно ввести команду =STDEVP. Введите формулу в пустую ячейку рядом с соответствующим набором данных, который вы оцениваете.

2. Рассчитайте среднее значение

Вычисление среднего значения в электронных таблицах требует специальных формул. Например, в большинстве приложений электронных таблиц вы можете использовать =AVERAGE для применения программной функции. При вводе команды среднего значения поместите его в ячейку рядом с соответствующим набором данных, чтобы легче его увидеть.

3. Разделите стандартное отклонение на среднее значение

Разделите ячейки, содержащие стандартное отклонение и среднее значение. Например, чтобы разделить стандартное отклонение в ячейке A3 и среднее значение в ячейке A5, вы можете использовать функцию =A3A5 в пустой ячейке для вычисления коэффициента и отображения коэффициента вариации.

Некоторые программы обработки электронных таблиц могут вычислять коэффициент вариации с помощью команды =STDEV.P, что устраняет необходимость в нескольких шагах. В зависимости от программы, вы можете просто ввести команду в пустую ячейку и обозначить диапазон данных, которые вы хотите рассчитать. После этого в выбранной ячейке появится значение CV.

Пример расчета

Чтобы принять обоснованное решение между акциями и облигациями, Джамиля применяет формулу коэффициента вариации для определения соотношения риска и доходности для обоих инвестиционных инструментов. Сначала она оценивает инвестиции в акции, волатильность которых составляет 5%, а прогнозируемая доходность — 13%. Используя эти значения в формуле, Джамиля находит:

• CV = среднее стандартное отклонение выборки x 100 =

• CV = прогнозируемая доходность волатильности x 100 =

• CV = (0.05) (0.13) x 100 = 0.38 x 100 = 38%

Чтобы рассчитать коэффициент вариации облигации для сравнения, Джамиля делит волатильность в 3% на прогнозируемую доходность в 15%. Используя формулу, она оценивает:

• CV = стандартное отклонение выборочного среднего x 100 =

• CV = прогнозируемая доходность волатильности x 100 =

• CV = (0.03) (0.15) x 100 = 0.2 = 20%

Джамиля сравнивает инвестиции в облигации и акции и приходит к выводу, что CV инвестиций в облигации в размере 20% указывает на более низкое соотношение риска и доходности, чем CV акций в размере 38%. Теперь, когда Джамиля понимает, какой инвестиционный инструмент представляет наименьшее соотношение риска и доходности, она может выбрать наиболее подходящий вариант для достижения своих финансовых целей.

Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.

Понимание коэффициента вариации

Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.

Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.

Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.

Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.

Обычно данный коэффициент
используют в таких целях как:

• Для сравнения
  нескольких различных рядов данных или
  показателей;
• Для оценки потенциальных
  объектов инвестирования;
• Для проведения
  XYZ-анализа.

КЛЮЧЕВЫЕ МОМЕНТЫ

• CV — это статистическая
  мера дисперсии в ряду данных вокруг
  среднего значения;
• В финансах CV
  позволяет инвесторам определить,
  насколько велика волатильность, или
  риск, по сравнению с величиной ожидаемой
  прибыли от инвестиций;
• Чем ниже величина
  отношения стандартного отклонения к
  средней доходности,тем лучше соотношение
  риска и доходности.

Формула CV

Ниже приведена формула для расчета коэффициента вариации:

Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.

Коэффициент вариации в Excel и Open Office

Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.

В Open
Office данный показатель
рассчитывается аналогично. Функция
стандартного отклонения здесь — STDEV,
а функция среднего значения
— AVERAGE.

Давайте
рассмотрим пример расчёта коэффициента
вариации в Open Office.
Предположим, что у нас
есть три потенциальных объекта для
инвестиций — объект А, объект Б и объект
В. Прибыль по каждому из этих проектов
за последние 6 лет занесена в таблицу
представленную ниже:

Давайте
рассчитаем значение CV
для каждого из этих
объектов. Начнём с расчёта стандартных
отклонений. Для этого применим к ряду
значений прибыли отдельно по каждому
объекту функцию STDEV:

Аналогичным
образом рассчитаем среднее значение
для каждого ряда данных:

Наконец
рассчитаем CV. Для
этого разделим полученные значения
отклонений на средние значения. В
результате получим следующую таблицу:

Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.

Пример использования коэффициента вариации для выбора объекта инвестиций

Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.

Для принятия решения инвестором используется следующая 15-летняя историческая информация:

Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.

Одной из ключевых стадий подготовки закупочной документации становится расчет начальной максимальной цены контракта (НМЦК). Законодательно предусмотрено несколько способов, с помощью которых можно производить расчеты. Чаще всего используется метод сопоставимых рыночных цен. При этом итоговая НМЦК должна определяться с учетом коэффициента вариации. Поэтому всем заказчикам необходимо понять, что включает в себя этот показатель и как его правильно определить.

Что такое коэффициент вариации

Размер НМЦК определяется еще на этапе планирования. Эта сумма должна быть отражена в плане и план-графике. Непосредственно перед подготовкой извещения она корректируется с учетом сложившейся на тот момент экономической обстановки. Вопросы, связанные с НМЦК рассматриваются в статье 22 44-ФЗ. Методики ее расчета описаны в Приказе Министерства экономики и развития № 567 от 02 октября 2013 года. В этом же документе приводятся правила определения коэффициента вариации.

Разработано несколько методик выявления НМЦК: нормативная, тарифная, проектно-сметная, затратная. Самым приоритетным считается метод сопоставимых рыночных цен. Именно его рекомендуется использовать при определении стартовой цены. Он предполагает сравнение коммерческих предложений, предоставляемых потенциальными поставщиками по запросу заказчика. Для проведения такого анализа и применяется коэффициент вариации. Он выражается в процентах.

Под коэффициентом вариации понимается мера относительного разброса предлагаемых цен. Он показывает, какую долю занимает средний разброс цен от среднего значения цены. Этот показатель может принимать следующие значения:

1. Меньше 10%. В таком случае разница в ценах признается незначительной.
2. От 10% до 20%. Разброс считается средним.
3. От 20% до 33%. Разница признается значительной, но допустимой.
4. Свыше 33%. Данные неоднородны. При расчете НМЦК не допускается использовать данные с коэффициентом вариации свыше 33%.

Для определения коэффициента разработана специальная формула. По ней легко подсчитать параметр, подставив соответствующие данные. Упростить себе задачу можно, используя калькуляторы, которые сегодня широко представлены в интернете. 

Что делать, если коэффициент завышен

Если при расчете коэффициента вариации получилось значение меньше 33%, то выборка признается однородной. Следовательно, полученное значение можно использовать для определения НМЦК. 

Если возникла такая ситуация, что значение коэффициента оказывается выше 33 процентов, тогда потребуется внесение корректировок в используемые данные. Для этого проводится дополнительное исследование рынка. Необходимо собрать коммерческие предложения от большего количества поставщиков и повторить расчет на основе новых данных. Если собрать дополнительные предложения не получается, можно воспользоваться сведениями из ранее заключенных договоров, которые хранятся в реестре контрактов. 

В крайней ситуации, когда никак не получается добиться нужного коэффициента вариации можно исключить из выборки неподходящие предложения. Вы также можете попросить поставщика указать в своем предложении нужную вам сумму. 

Правила расчета

Методика расчета коэффициента вариации прописана в приказе Минэкономразвития № 567. Согласно действующим нормам заказчик должен направить не менее пяти запросов коммерческих предложений потенциальным поставщикам. Для расчета используются не менее трех предложений, полностью соответствующих требованиям заказчика. 

Стоит отметить, что приказ № 567 не является нормативным актом, следовательно, его исполнение не обязательно. За его нарушение никаких штрафных санкций не предусматривается. Однако во избежание спорных ситуаций заказчика рекомендуется пользоваться именно этими правилами расчета.

Для определения коэффициента вариации применяется следующая формула:

Среднеквадратичное отклонение позволяет определить разброс данных. Для его определения выбирают среднюю цену и меру разброса. Вычислить среднеквадратичное отклонение удается по следующей формуле:

В ситуациях, когда закупка включает в себя одновременно несколько позиций, расчет ведется по каждой из них. Это позволяет выявить товары с наибольшим разбросом цен. 

Пример расчета

Предположим, что государственное учреждение проводит закупку принтеров для собственных нужд. Потенциальным поставщикам были отправлены соответствующие запросы. Было получено четыре коммерческих предложения цен: 2500 рублей, 2800 рублей, 2450 рублей и 2600 рублей.

В первую очередь необходимо рассчитать среднеарифметическое значение цены

Следующим шагом становится расчет среднеквадратичного отклонения

Осталось только рассчитать коэффициент вариации

Полученное значение коэффициента меньше 33%, следовательно, все собранные данные подходят для расчета стартовой цены контракта. Расчет НМЦК и коэффициента вариации оформляются в форме отчета, который становится обязательной частью закупочной документации. 

Коэффициент вариации – важный инструмент, позволяющий оценить правильность ценовых предложений, полученных от поставщиков. Поэтому при составлении документации заказчикам необходимо учитывать правила расчета этого показателя и особенности его применения.

Коэффициент вариации и стандартное отклонение: разница