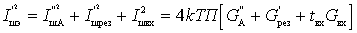Как найти коэффициент шума

From Wikipedia, the free encyclopedia

Noise figure (NF) and noise factor (F) are figures of merit that indicate degradation of the signal-to-noise ratio (SNR) that is caused by components in a signal chain. These figures of merit are used to evaluate the performance of an amplifier or a radio receiver, with lower values indicating better performance.

The noise factor is defined as the ratio of the output noise power of a device to the portion thereof attributable to thermal noise in the input termination at standard noise temperature T₀ (usually 290 K). The noise factor is thus the ratio of actual output noise to that which would remain if the device itself did not introduce noise, or the ratio of input SNR to output SNR.

The noise factor and noise figure are related, with the former being a unitless ratio and the latter being the same ratio but expressed in units of decibels (dB).^[1]

General[edit]

The noise figure is the difference in decibels (dB) between the noise output of the actual receiver to the noise output of an “ideal” receiver with the same overall gain and bandwidth when the receivers are connected to matched sources at the standard noise temperature T₀ (usually 290 K). The noise power from a simple load is equal to kTB, where k is the Boltzmann constant, T is the absolute temperature of the load (for example a resistor), and B is the measurement bandwidth.

This makes the noise figure a useful figure of merit for terrestrial systems, where the antenna effective temperature is usually near the standard 290 K. In this case, one receiver with a noise figure, say 2 dB better than another, will have an output signal to noise ratio that is about 2 dB better than the other. However, in the case of satellite communications systems, where the receiver antenna is pointed out into cold space, the antenna effective temperature is often colder than 290 K.^[2] In these cases a 2 dB improvement in receiver noise figure will result in more than a 2 dB improvement in the output signal to noise ratio. For this reason, the related figure of effective noise temperature is therefore often used instead of the noise figure for characterizing satellite-communication receivers and low-noise amplifiers.

In heterodyne systems, output noise power includes spurious contributions from image-frequency transformation, but the portion attributable to thermal noise in the input termination at standard noise temperature includes only that which appears in the output via the principal frequency transformation of the system and excludes that which appears via the image frequency transformation.

Definition[edit]

The noise factor F of a system is defined as^[3]

${displaystyle F={frac {mathrm {SNR} _{text{i}}}{mathrm {SNR} _{text{o}}}}}$

where SNR_i and SNR_o are the input and output signal-to-noise ratios respectively. The SNR quantities are unitless power ratios.
The noise figure NF is defined as the noise factor in units of decibels (dB):

${displaystyle mathrm {NF} =10log _{10}(F)=10log _{10}left({frac {mathrm {SNR} _{text{i}}}{mathrm {SNR} _{text{o}}}}right)=mathrm {SNR} _{text{i, dB}}-mathrm {SNR} _{text{o, dB}}}$

where SNR_i, dB and SNR_o, dB are in units of (dB).
These formulae are only valid when the input termination is at standard noise temperature T₀ = 290 K, although in practice small differences in temperature do not significantly affect the values.

The noise factor of a device is related to its noise temperature T_e:^[4]

${displaystyle F=1+{frac {T_{text{e}}}{T_{0}}}.}$

Attenuators have a noise factor F equal to their attenuation ratio L when their physical temperature equals T₀. More generally, for an attenuator at a physical temperature T, the noise temperature is T_e = (L − 1)T, giving a noise factor

${displaystyle F=1+{frac {(L-1)T}{T_{0}}}.}$

Noise factor of cascaded devices[edit]

If several devices are cascaded, the total noise factor can be found with Friis’ formula:^[5]

$F=F_{1}+{frac {F_{2}-1}{G_{1}}}+{frac {F_{3}-1}{G_{1}G_{2}}}+{frac {F_{4}-1}{G_{1}G_{2}G_{3}}}+cdots +{frac {F_{n}-1}{G_{1}G_{2}G_{3}cdots G_{{n-1}}}},$

where F_n is the noise factor for the n-th device, and G_n is the power gain (linear, not in dB) of the n-th device. The first amplifier in a chain usually has the most significant effect on the total noise figure because the noise figures of the following stages are reduced by stage gains. Consequently, the first amplifier usually has a low noise figure, and the noise figure requirements of subsequent stages is usually more relaxed.

Noise factor as a function of additional noise[edit]

The source outputs a signal of power $S_{i}$ and noise of power $N_{i}$ . Both signal and noise get amplified. However, in addition to the amplified noise from the source, the amplifier adds additional noise to its output denoted $N_{a}$ . Therefore, the SNR at the amplifier’s output is lower than at its input.

The noise factor may be expressed as a function of the additional output referred noise power $N_{a}$ and the power gain of an amplifier.

${displaystyle F=1+{frac {N_{a}}{N_{i}G}}}$

Derivation[edit]

From the definition of noise factor^[3]

${displaystyle F={frac {mathrm {SNR} _{text{i}}}{mathrm {SNR} _{text{o}}}}={frac {frac {S_{i}}{N_{i}}}{frac {S_{o}}{N_{o}}}},}$

and assuming a system which has a noisy single stage amplifier. The signal to noise ratio of this amplifier would include its own output referred noise $N_{a}$ , the amplified signal ${displaystyle S_{i}G}$ and the amplified input noise ${displaystyle N_{i}G}$ ,

${displaystyle {frac {S_{o}}{N_{o}}}={frac {S_{i}G}{N_{a}+N_{i}G}}}$

Substituting the output SNR to the noise factor definition,^[6]

${displaystyle F={frac {frac {S_{i}}{N_{i}}}{frac {S_{i}G}{N_{a}+N_{i}G}}}={frac {N_{a}+N_{i}G}{N_{i}G}}=1+{frac {N_{a}}{N_{i}G}}}$

In cascaded systems $N_{i}$ does not refer to the output noise of the previous component. An input termination at the standard noise temperature is still assumed for the individual component. This means that the additional noise power added by each component is independent of the other components.

Optical noise figure[edit]

The above describes noise in electrical systems. Electric sources generate noise with a power spectral density equal to kT, where k is the Boltzmann constant and T is the absolute temperature. However, there is also noise in optical systems. In these, the sources have no fundamental noise. Instead the energy quantization causes notable shot noise in the detector, corresponding to a noise power spectral density of hf where h is the Planck constant and f is the optical frequency.

In the 1990s, an optical noise figure has been defined.^[7] This has been called F_pnf for photon number fluctuations.^[8] The powers needed for SNR and noise factor calculation are the electrical powers caused by the current in a photodiode. SNR is the square of mean photocurrent divided by variance of photocurrent. Monochromatic or sufficiently attenuated light has a Poisson distribution of detected photons. If, during a detection interval the expectation value of detected photons is n then the variance is also n and one obtains SNR_pnf,in = n²/n = n. Behind an optical amplifier with power gain G there will be a mean of Gn photons. In the limit of large n the variance of photons is Gn(2n_sp(G-1)+1) where n_sp is the spontaneous emission factor. One obtains SNR_pnf,out = G²n²/(Gn(2n_sp(G-1)+1)) = n/(2n_sp(1-1/G)+1/G). Resulting optical noise factor is F_pnf = SNR_pnf,in / SNR_pnf,out = 2n_sp(1-1/G)+1/G.

F_pnf is in conceptual conflict compared to the electrical noise factor, which is now called F_e:

Photocurrent is proportional to optical power. Optical power is proportional to squares of a field amplitude (electric or magnetic). So, the receiver is nonlinear in amplitude. The power needed for SNR_pnf calculation is proportional to the 4th power of the signal amplitude. But for F_e in the electrical domain the power is proportional to the square of the signal amplitude.

At a certain electrical frequency, noise occurs in phase (I) and in quadrature (Q) with the signal. Both these quadratures are available behind the electrical amplifier. The same holds in an optical amplifier. But the direct detection photoreceiver needed for measurement of SNR_pnf takes mainly the in-phase noise into account whereas quadrature noise can be neglected for highn. Also, the receiver outputs only one quadrature. So, one quadrature is lost.

For an optical amplifier with large G it holds F_pnf ≥ 2 whereas for an electrical amplifier it holds F_e ≥ 1.

Moreover, today’s long-haul optical fiber communication is dominated by coherent optical I&Q receivers but F_pnf does not describe the SNR degradation observed in these.

The above conflicts are resolved by the optical in-phase and quadrature noise figure F_o,IQ.^[9] It can be measured using a coherent optical I&Q receiver. In these, power of the output signal is proportional to the square of an optical field amplitude because they are linear in amplitude. They pass both quadratures. For an optical amplifier it holds F_o,IQ = n_sp(1-1/G)+1/G ≥ 1. Quantity n_sp(1-1/G) is the input-referred number of added noise photons per mode.

F_o,IQ and F_pnf can easily be converted into each other. For large G it holds F_o,IQ = F_pnf/2 or, when expressed in dB, F_o,IQ is 3 dB less than F_pnf.

Unified noise figure[edit]

Total noise power spectral density per mode is kT + hf. In the electrical domain hf can be neglected. In the optical domain kT can be neglected. In between, say, in the low THz or thermal domain, both will need to be considered. It is possible to blend between electrical and optical domains such that a universal noise figure is obtained.

This has been attempted by a noise figure F_fas^[10] where the subscript stands for fluctuations of amplitude squares. At optical frequencies F_fas equals F_pnf and involves detection of only 1 quadrature. But the conceptual difference to F_e cannot be overcome: It seems impossible that for increasing frequency (from electrical to thermal to optical) 2 quadratures (in the electrical domain) gradually become 1 quadrature (in optical receivers which determine F_fas or F_pnf). The ideal noise factor would need to go from 1 (electrical) to 2 (optical), which is not intuitive. For unification of F_pnf with F_e, squares of signal amplitudes (powers in the electrical domain) must also gradually become 4th powers of amplitudes (powers in optical direct detection receivers), which seems impossible.

A consistent unification of optical and electrical noise figures is obtained for F_e and F_o,IQ. There are no contradictions because both these are in conceptual match (powers proportional to squares of amplitudes, linear, 2 quadratures, ideal noise factor equal to 1). Thermal noise kT and fundamental quantum noise hf are taken into account. The unified noise figure is F_IQ = (kTF_e + hfF_o,IQ) / (kT + hf) = (kT(T + T_e)) + hf(n_sp(1-1/G)+1/G)) / (kT + hf).^[9]

References[edit]

^ «Noise temperature, Noise Figure and Noise Factor».
^ Agilent 2010, p. 7
^ ^a ^b Agilent 2010, p. 5.
^ Agilent 2010, p. 7 with some rearrangement from T_e = T₀(F − 1).
^ Agilent 2010, p. 8.
^ Aspen Core. Derivation of noise figure equations (DOCX), pp. 3–4
^ E. Desurvire, „Erbium doped fiber amplifiers: Principles and Applications“, Wiley, New York, 1994
^ H. A. Haus, «The noise figure of optical amplifiers,» in IEEE Photonics Technology Letters, vol. 10, no. 11, pp. 1602-1604, Nov. 1998, doi: 10.1109/68.726763
^ ^a ^b R. Noe, «Consistent Optical and Electrical Noise Figure,» in Journal of Lightwave Technology, 2022, doi: 10.1109/JLT.2022.3212936, https://ieeexplore.ieee.org/document/9915356
^ H. A. Haus, «Noise Figure Definition Valid From RF to Optical Frequencies,» in IEEE JOURNAL OF SELECTED TOPICS IN QUANTUM ELECTRONICS, VOL. 6, NO. 2, MARCH/APRIL 2000, pp. 240-247

Keysight, Fundamentals of RF and Microwave Noise Figure Measurements (PDF), Application Note, 57-1, Published September 01, 2019., archived (PDF) from the original on 2022-10-09

External links[edit]

Noise Figure Calculator 2- to 30-Stage Cascade
Noise Figure and Y Factor Method Basics and Tutorial
Mobile phone noise figure

This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).

Источник

Коэффициент шума
— одна из основных характеристик приемника
СВЧ. Он показывает насколько собственные
шумы приемника влияют на усиливаемый
полезный сигнал. Коэффициент шума
—
это мера собственных (внутренних) шумов
приемника. Обычно качество приема
принято оценивать отношением мощности
сигналак мощности шумана выходе приемника, т.е..
Чем больше это отношение, тем качество
приема выше. Однако это отношение
зависит от мощности входного сигнала
и внешних шумов, поэтому в качестве
коэффициента шума принимают выражение:

Предполагается
при этом, что внешние шумы пересчитаны
на вход приемника, т.е. к
,
где— выходное сопротивление источника
сигнала приемника, т.е. антенны (см.
рисунок 2.1).

Рисунок 2.1

Таким образом,
величина
обусловлена тепловым шумом,
при этом принято считать, чтоимеет стандартную температуру.

Выходной шум
приемника
представляет собой сумму усиленного
входного шумаи внутреннего шума приемника. Из — за
добавления внутреннего шума
знаменатель в выражение дляменьше числителя, поэтому для коэффициента
шума можно дать следующее определение:

коэффициент шума
— это число, показывающее, во сколько
раз уменьшается отношение
на выходе приемника по сравнению с
отношениемна его входе.

Выражение для
можно упростить, исключив из него
мощность сигнала, т.к.

где
— коэффициент усиления приемника
(коэффициент передачи) по мощности,
тогда

На основании
последнего выражения можно дать второе
определение коэффициенту шума:

коэффициент шума
— это отношение полной мощности шума на
выходе приемника к той ее части (на
выходе), которая обусловлена только
внешним шумом (шумом источника сигнала).

Знаменатель
последнего выражения можно рассматривать
как выходной шум идеального нешумящего
приемника, который по всем показателям
аналогичен данному реальному приемнику
(но без внутренних шумов). Тогда получим

(2.1)

при этом можно
дать третье определение коэффициенту
шума:

коэффициент шума
— это число, показывающее, во сколько
раз мощность шума на выходе реального
приемника больше мощности шума на выходе
идеального приемника.

В основу всех трех
определений положено допущение о том,
что сигнал, входной шум и собственный
шум приемника проходят по одним и тем
же цепям приемника, не влияя друг на
друга, т.е. справедлив принцип суперпозиции.
Это позволяет определить мощность
сигнала на выходе независимо от мощности
шума, а выходной шум — как результат
суммирования собственных шумов
приемника с усиленными внешними
шумами. Поэтому все определения
коэффициента шума справедливы лишь
для линейной части приемника, т.е.
для додетекторной его части.

2.2 Выражение коэффициента шума через номинальные мощности

Расчеты коэффициента
шума упрощаются, если пользоваться
понятием номинальной мощности.

Выразим реальные
мощности через номинальные, т.е.

;

Для сигнала и шума
коэффициенты

и
одинаковы, т.к. сигнал и шум проходят
одни и те же цепи приемника. Подставим
эти значения в формулу для,
получим

т.е. можно формально
заменить реальные мощности номинальными
во всех трех формулах:

;
.

Из рассуждений не
следует, что коэффициент шума не зависит
от условий согласования. При
рассогласовании уменьшается выходной
сигнал
.
Выходной шум тоже уменьшается, но в
меньшей мере, т.к. основную его долю
составляет собственный шум
приемника, который не зависит от
согласования на входе.
Таким
образом, ухудшение согласования на
входе приводит к росту коэффициента
шума приемника.

Соседние файлы в папке Раздел №2 ПРМУ

Источник

Введение

Чем более слабые сигналы приходится обрабатывать в цифровых системах связи, тем большее значение приобретают такие параметры, как уровень бит-ошибок, который непосредственно зависит от чувствительности тракта обработки сигнала и, конечно, коэффициента шума. Из перечисленных параметров коэффициент шума интересен в том плане, что его можно использовать не только как критерий оценки работы всей приемной системы в целом, но и как ключевую характеристику отдельных СВЧ-компонентов, таких как усилители и смесители, которые образуют эту систему. Если разработчик контролирует коэффициент шума и усиление отдельных каскадов приемной системы, то это означает, что он контролирует всю систему в целом. Если величина коэффициента шума известна, то рассчитать чувствительность всей системы, зная полосу обработки сигнала, не составит труда. Именно коэффициент шума — это зачастую тот параметр, который выгодно отличает одно приемное устройство от другого, один усилитель от другого, один транзистор от другого. Тот факт, что без использования понятия коэффициента шума сегодня сложно представить спецификацию на приемное устройство, подразумевает, что точность и повторяемость измерения данного параметра особенно важны при разработках и производстве СВЧ-устройств.

Измерение шумов некого электронного устройства — важная процедура для минимизации шума, генерируемого этим устройством в приемных системах. Основным способом снижения вероятности бит-ошибок при приеме и обработке цифровых потоков является усиление полезного сигнала электронными устройствами, которые имеют низкий уровень собственных шумов. Традиционные методы увеличения соотношения полезного сигнала к шуму заключаются, с одной стороны, в увеличении мощности сигнала, передаваемого в направлении приемника, а с другой — в увеличении усиления приемной антенны. Подобные способы связаны с известными трудностями, поскольку увеличение мощности сигнала передатчика ограничивается законодательно соответствующими контрольными органами, а увеличение усиления в антенне обычно связано с необходимостью разработки более дорогой и более громоздкой антенной системы. Альтернативным способом увеличения соотношения полезного сигнала к шуму является минимизация коэффициента шума приемной системы и ее компонентов. Таким образом, измерения коэффициента шума абсолютно необходимы, чтобы иметь уверенность в том, что шум, вносимый элементами приемной системы, допустимый.

Основная задача данной статьи — рассмотрение способов оценки коэффициента шума электронных устройств при помощи современных измерительных приборов. При этом мы покажем возможность измерения коэффициента шума при помощи анализатора спектра «СК4-БЕЛАН 32», который укомплектован соответствующей опцией.

Для четкого понимания смысла подобных измерений и правильной интерпретации их результатов необходимо напомнить, что скрывается под термином «коэффициент шума», а также что подразумевают связанные с ним понятия (эффективная шумовая температура, Y-фактор, избыточный коэффициент шума и т. д.).

Теория

Шум, с которым мы имеем дело на практике, состоит из многих составляющих. Основные из них — это тепловой и дробовой шумы. Тепловой шум возникает при флуктуациях электронов в проводниках, имеющих некую конечную температуру. Некоторые из таких флуктуаций могут иметь спектральные составляющие в той же полосе частот, что и полезные сигналы, то есть их маскировать и затруднять их обработку. Шумовой спектр, генерируемый тепловым шумом, по своей природе однороден на всех частотах. Дробовой шум возникает из-за квантовой стохастической природы электрического тока. Ток не представляет собой непрерывного и предсказуемого движения электронов, а скорее является хаотическим потоком со случайным их распределением. Статистический анализ стохастического потока электронов показывает, что вариации тока имеют широкополосный характер (распределены в широкой полосе частот). Есть и другие природные феномены, которые имеют квантовую структуру и генерируют случайный шум. Примером может служить шум генерации и рекомбинации основных носителей, возникающий в транзисторах при распределении тока эмиттера между базой и коллектором. Несмотря на многообразие источников шума, у всех механизмов генерации шума есть одно свойство, общее с тепловым шумом: они имеют однородный спектр, равномерно распределенный в полосе частот до 5000 ГГц. Поэтому при оценке шума все его источники принято рассматривать как тепловой шум. Мощность теплового шума определяется как:

где P_A — доступная мощность (Дж/с или Вт); k — постоянная Больцмана (1,38×10^–23 Дж/К); T — абсолютная температура (К); B — полоса частот (Гц).

Важно помнить, что k×T×B — это «доступная» мощность. То есть она «доступна» только при оптимальной (согласованной) нагрузке (если нет отражения энергии).

Определение k×T×B позволяет интуитивно лучше понять природу шума. Постоянная Больцмана k характеризует среднюю величину выделяемой кинетической энергии на единицу температуры. Присутствие в формуле температуры T предполагает, что с ее ростом выделяется больше мощности. Ну, и поскольку шум имеет широкополосную природу, в формуле мощности шума фигурирует B — используемая полоса частот.

Абсолютную температуру в 290 К (обычно обозначается как T₀) принято считать опорной величиной источников шума при измерениях коэффициента шума. Эта величина соответствует 16,8 °С и 62,3° по Фаренгейту. Спектральная плотность тепловых шумов k×T, генерируемая резистором на согласованную нагрузку в каждом герце электромагнитного спектра при данной температуре, равна 4×10^–21 Вт или –174 дБ·м.

Неотъемлемой частью определения коэффициента шума является понятие «соотношение сигнал/шум». Этот термин интуитивно понятен, особенно если перейти к логарифмическим соотношениям. Поясним данный термин на простом примере. Допустим, мы имеем сигнал (S) с уровнем 10 мВт (+10 дБ·м). Чему равно теоретическое соотношение «сигнал/шум», измеряемое в децибелах, для данного сигнала в полосе 1 МГц при температуре 290 К? Сначала рассчитаем мощность шума (N) в полосе 1 МГц:

Теперь вычислим соотношение «сигнал/шум»: S/N = (+10–(–114)) = 124 дБ.

Заметим, что соотношение «сигнал/шум» выражается просто в дБ. Хотя и мощность шума, и сигнал первоначально были в логарифмическом масштабе относительно 1 мВт.

Уяснив термин «соотношение сигнал/шум». мы можем перейти к определению понятия «коэффициент шума». Этот коэффициент описывает уменьшение соотношения «сигнал/шум» по мере прохождения сигнала через приемное устройство или его отдельный каскад (усилитель, смеситель). Фундаментальное определение коэффициента шума следующее:

где S_in / N_in — соотношение «сигнал/шум» на входе устройства; S_out / N_out — соотношение «сигнал/шум» на выходе устройства.

Поскольку все электронные устройства «шумят» и, соответственно, добавляют некое количество шума к сигналу, величина F всегда больше единицы. Хотя величина F исторически называлась коэффициентом шума, современный термин «коэффициент шума» (децибельная величина NF) обычно подразумевает логарифмический масштаб величины F, равный 10 log₁₀F (дБ). В зарубежной специальной литературе, публикуемой ведущими производителями измерителей коэффициента шума (Agilent Technologies, Anritsu, Rohde & Schwarz) последовательно разграничиваются два термина: «фактор шума», или F, и, собственно, коэффициент шума NF. Итак,

NF = 10 log₁₀×F (3).

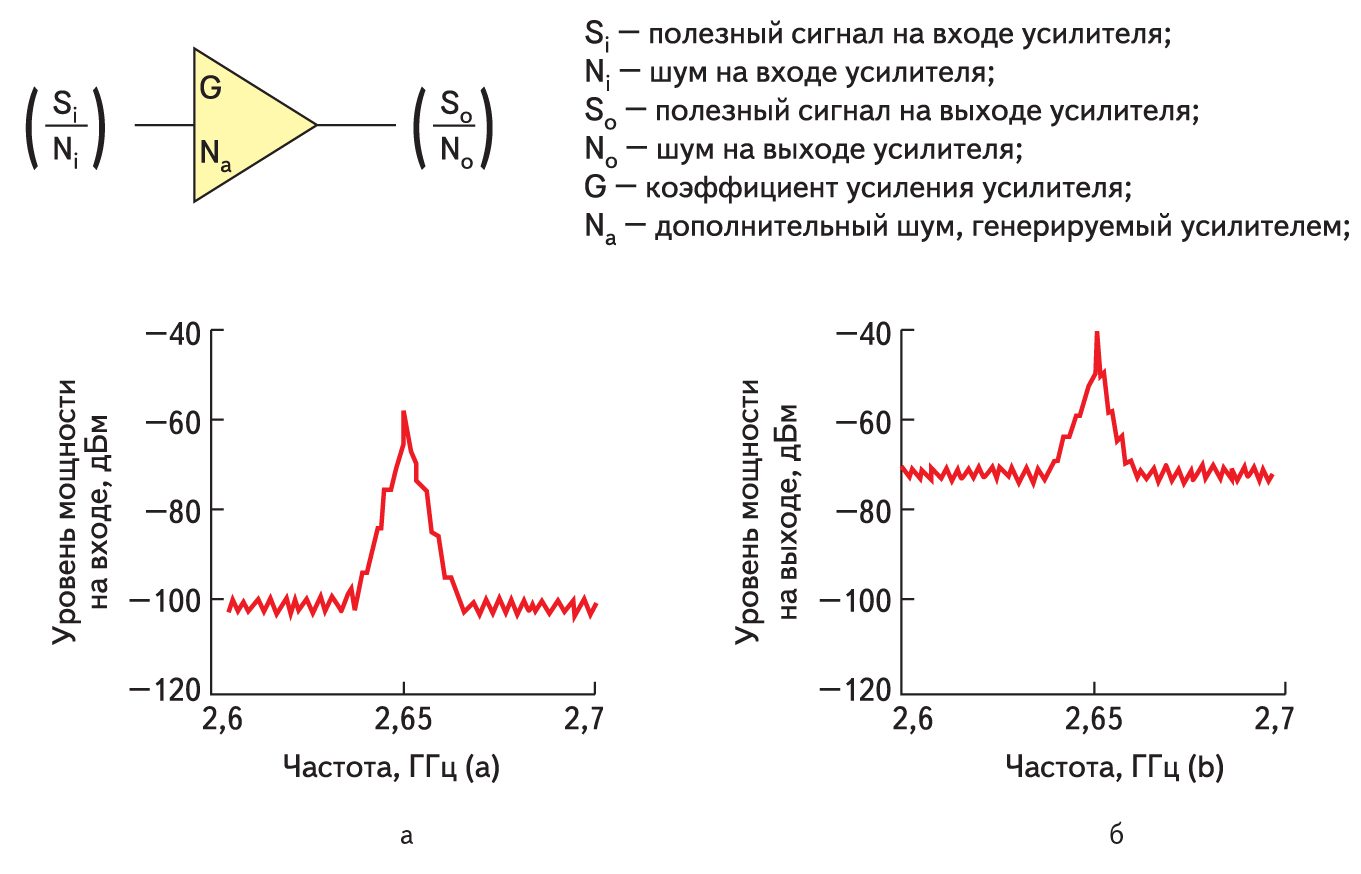
Рассмотрим коэффициент шума некоего известного усилителя. На рис. 1 показана его условная схема, а также сигналы на его входе и выходе.

Рис. 1. Условная схема усилителя. Сигналы на его входе и выходе

Если мы подключим к входу усилителя согласованную нагрузку при температуре 290 К, то она будет генерировать на входе усилителя шум k×T₀×B. На выходе этот шум усилится и превратится в k×T₀×B×G (G — коэффициент усиления усилителя) плюс к нему добавится некое количество шума, генерируемого в самом усилителе N_A. Тогда выражение (2) можно переписать следующим образом:

отсюда:

или

Выражение (4) является определением коэффициента шума, которое официально принято международным Институтом Радиоинженеров (сейчас Institute of Electrical and Electronics Engineers (IEEE)).

Если опираться на уравнения (4) и (5), то видно, что измерения коэффициента шума сводятся к измерениям уровня шума, коэффициента усиления и полосы. Однако, несмотря на понятность данных величин, в практических измерениях формулами (4) и (5) пользуются не так уж часто (хотя использовать их можно, о чем мы расскажем ниже). Это связано с тем, что измерить с большой точностью усиление в заданной полосе — зачастую не тривиальная задача. Большинство систем измерения коэффициента шума элегантно обходят задачу прямого измерения уровня шума и усиления, основывая алгоритмы своей работы на использовании, в первую очередь, линейных свойств тепловых шумов.

Дело в том, что тепловой шум (P_A = k×T×B) в постоянной полосе частот имеет линейные характеристики. На рис. 2 представлен график функции мощности теплового шума от абсолютной температуры. Очевидно, что мощность шума — это линейная функция вида ƒ (x) = m×x+b, где ƒ (x) — это P_A , x — абсолютная температура T, m — переменная k×B, а b — это точка пересечения с осью Y, где при абсолютной температуре в 0 К мощность шума будет равна 0.

Рис. 2. График функции мощности теплового шума от абсолютной температуры

Таким образом, P_A(T) = k×B(T)+0 = k×B(T). При постоянной величине полосы, которая нам известна, это уравнение позволяет рассчитать мощность теплового шума для любой абсолютной температуры, то есть полностью описывает характеристики теплового шума. Поскольку прямая определяется двумя точками, то для описания характеристик теплового шума нам фактически лишь нужно взять две температурные точки и провести в них два измерения мощности шума. Если мы произведем измерение мощности на выходе некоего устройства (например усилителя), подключив к его входу согласованную нагрузку (генератор шума) при температуре T₀ = 290 K, то уравнение для мощности P₁ можно записать в таком виде:

Затем предположим, что мы нагрели согласованную нагрузку (включили генератор шума) до значения T_HOT = T₀+T_EX и снова измерили мощность P₂ на выходе усилителя. Уравнение для мощности P₂ будет иметь вид:

Отношение мощностей P₂ / P₁ исторически называется «Y-фактором» или Y (по-видимому, в связи с тем, что значения мощностей графически откладываются на оси Y — рис. 2).

Используя (4), получаем:

Или:

откуда находим, что фактор шума равен:

Величину T_EX/T₀ или (T_HOT–T₀)/T₀ обычно называют избыточным коэффициентом шума, или ENR (excess noise ratio), и производители источников шума нормируют ее в дБ. Формула (8) чаще записывается как:

в логарифмическом виде выражение для коэффициента шума имеет вид:

Часто при измерениях коэффициента шума может использоваться другое понятие, которое также является фундаментальным, — понятие «эффективной температуры шума». Любой инженер, занимающийся измерением коэффициента шума, должен четко понимать взаимосвязь понятий «коэффициент шума» и «температура шума».

Рис. 3. Условная схема идеального приемника с согласованной нагрузкой 50 Ом на входе

Что же такое температура шума? Если 50-омный резистор с температурой 290 К подключен к входу идеального (не имеющего шумов) приемника с сопротивлением входа 50 Ом (рис. 3), то мощность шума на входе такого виртуального приемника составит:

А теперь представьте себе тестируемое устройство, например усилитель, подключенный в разрыв между 50-омным резистором и идеальным приемником (рис. 4).

Рис. 4. Условная схема измерения шума с объектом измерения, включенным в разрыв между приемником и согласованной нагрузкой 50 Ом

Шум на выходе тестируемого устройства теперь включает две составляющие. Одна из них — это усиленный шум резистора с температурой 290 К. Другая составляющая — это шум, генерируемый самим тестируемым устройством. Обратите внимание, что приемник не может различить эти две составляющие шума. Для приемника результат измерения был бы тем же, если бы тестируемое устройство было идеально и не генерировало шума, а резистор, подключенный к входу устройства, был нагрет до некоторой более высокой температуры (290+T_e ) К. В сущности, реальное тестируемое устройство может быть промоделировано как идеальное устройство, не вносящее шума, но имеющее на входе дополнительный источник шума с эквивалентной температурой T_e. Это — эффективная температура шума тестируемого устройства (или эквивалентная температура шума тестируемого устройства).

Преимущество понятия эффективной температуры шума заключается в том, что это понятие подводит общее основание под измерения случайного электрического шума, генерируемого любым источником: от транзистора на основе технологии GaAs до галактики. Есть много разновидностей электрического шума, и большинство из них не имеют тепловой природы. Однако все виды случайного шума можно выразить как эквивалентное количество теплового шума, который генерировался бы при температуре T_e. Обычно слово «эффективная» или «эквивалентная» в сочетании с «температурой шума» опускается и традиционно употребляется выражение «температура шума».

Поскольку мощность теплового шума P_А прямо пропорциональна температуре T (что следует из уравнения (1)), то значения температуры шума можно складывать, точно так же, как значения мощности шума при условии, что полоса B не меняется.

Дополнительно прояснить понятие температуры шума можно при помощи графического представления функции мощности шума от температуры (рис. 5).

Рис. 5. Графическое представление понятия эффективной шумовой температуры

График 1 (рис. 5) представляет собой функцию мощности шума некоего реального усилителя. Обратите внимание, что T_e — это экстраполированная в минус точка пересечения графика с температурной осью, а также что усилитель вносит собственный шум N_A . На выходе данного усилителя при температуре T₀ можно будет детектировать мощность, равную N₁. Теперь сместим график 1 вправо на величину T_e и получим график 2 (рис. 5). График 2 — это график мощности на выходе идеального усилителя, не вносящего собственных шумов (мощность шума при нулевой температуре равна нулю) с неизменным значением переменной k×B×G (усиление и полоса константны, так же, как и постоянная Больцмана). Однако видно, что данный усилитель имеет на выходе ту же самую мощность шума N₁. Таким образом, на выходе идеального усилителя можно получить ту же самую мощность, что и у реального усилителя, если источник шума на входе идеального усилителя «нагреть» на величину T_e. Обратите внимание, что увеличение мощности на выходе идеального усилителя, вызванное «нагревом» источника шума, точно соответствует вносимому шуму N_A исходного реального усилителя. Следовательно:

Связь между фактором шума (коэффициентом шума) и температурой шума описывается следующим выражением:

или

В таблице даны некоторые значения для F, NF и T_e. Можно запомнить, что 0,1 дБ приблизительно соответствует 7–7,5 K.

Таблица. Некоторые значения для F, NF и T_e

Коэффициент шума NF, дБ	Фактор шума F	Температура шума Te, К
0	1	0 (абсолютный ноль)
0,5	1,122	35,4
0,6	1,148	43,0
0,7	1,175	50,7
0,8	1,202	58,7
0,9	1,230	66,8
1,00	1,259	75,1
1,1	1,288	83,6
1,2	1,318	92,3
3	2,00	290
10	10	2610
20	100	28 710

Перед тем как перейти к практике измерений коэффициента шума, совершенно необходимо коснуться еще одного теоретического аспекта — определения коэффициента шума и температуры шума в многокаскадных системах. На рис. 6 показано, как генерируется шум в многокаскадной системе.

Рис. 6. Схема генерации шума в многокаскадной системе

Шум на входе показан как резистор с температурой T₀. Каждый каскад характеризуется своей полосой B, усилением G и вносимым шумом N_А. Фактор шума системы задается следующим уравнением:

и для двухкаскадной системы:

Выражения (13) и (14) обычно называются каскадной формулой Харальда Фриса. Обратите внимание на то, что полоса B не фигурирует в уравнениях (13) и (14). Это демонстрирует преимущество методов, основывающихся на понятиях коэффициента шума и температуры шума: они не зависят от полосы.

Величина [(F₂–1)/G₁] в уравнении (13) часто называется эффектом второго каскада. Если усиление в первом каскаде большое, то эффект второго каскада будет минимальным, так что общий фактор шума F₁₂ будет определяться фактором шума первого каскада F₁. Вот почему приемник с высокой чувствительностью практически всегда начинается с малошумящего усилителя с малым коэффициентом шума (с предварительного усилителя).

Уравнение (14) можно переписать таким образом, чтобы найти F₁, если другие значения известны:

Это же уравнение, выраженное через температуру шума, имеет вид:

Уравнения (15) и (16) являются основой для большинства автоматических анализаторов коэффициента шума и прочих подобных приборов. Тестируемое устройство всегда является первым каскадом, а прибор, к входу которого подключается тестируемое устройство, является вторым каскадом.

Окончание статьи

Литература

Friis H. T. Noise Figures of Radio Receivers. Proc. of the IRE, July, 1944.
Agilent. Fundamentals of RF and Microwave Noise Figure Measurements. Application note 57-1.
Agilent. Noise Figure Measurement Accuracy — The Y-Factor Method. Application note 57-2.
Vondran D. Vector Corrected Noise Figure Measurements // Microwave Journal, March 1999.
Anritsu. Noise Figure Accuracy. Application Note No. 11410-00227

Источник

Сразу хочу сказать, что здесь никакой воды про коэффициент шума входного устройства, и только нужная информация. Для того чтобы лучше понимать что такое
коэффициент шума входного устройства, коэффициент шума входного устройства , настоятельно рекомендую прочитать все из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов.

Следует различать коэффициент шума собственно входного устройства и

коэффициент шума входного устройства и первого каскада приемника, определяемый совместно. Рассмотрим вначале последний случай как более общий, а затем в качестве частного случая определим коэффициент шума собственно входного устройства.

Коэффициент шума входной цепи с учетом первого каскада приемника.

При расчете коэффициента шума учитываются шумы антенны как источника сигнала, шумы собственно входного устройства и шумы первого каскада, пересчитанные на его вход.

Предположим, что пересчитанная ко входу первого каскада проводимость источника сигнала составляет

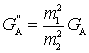
а ее собственные шумы характеризуются шумовым током

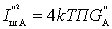
Проводимость резонансного контура

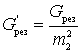
персчитанная ко входу первого каскада, обуславливает появление шумового тока

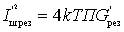
Шумы электронного прибора, стоящего на входе, пересчитываются к его входу и характеризуется источником шума

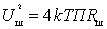
где 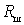— сопротивление шума.

Очевидно, надо учесть еще шумы, влзникающие во входной проводимости электронного прибора, причем эти шумы представляются шумовым током

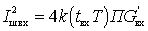
где 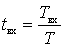— относительная шумовая температура шума, показывающая во сколько раз шумы реальной входной проводимости больше шумов соотвнтствующего омического сопротивления.

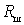
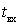
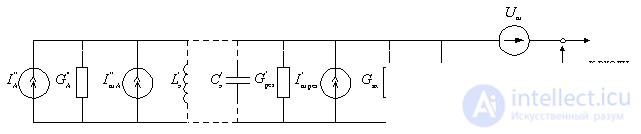
Величины и приводится в справочной литературе или рассчитываются по известным из курса электронных приборов формулам. Величина П представлчет собой эффективную шумовую полосу пропускания приемника. С учетом вышесказанного об источниках шумов, эквивалентная шумовая схема может быть представлена следующим образом.

Pисунок 6.6.

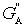
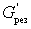
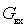
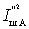
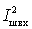
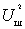
Как видно из рисунка проводимости , , являются соответственно источниками шумов , , а усилительный прибор — источником шумов

Коэффициент шума системы в соответствии с определением можно представить в виде отношения мощностей сигнала и шума в антенне и на выходе схемы, т.е.

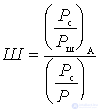
Соотношение сигнал/шум в антенне как источнике обуславливается ее данными. В частности, номинальные мощности антенны как источника сигналов и источника шумов

; .

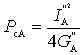
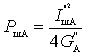
Их отношение составляет

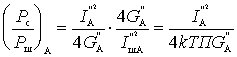
Найдем теперь отношение сигнал/шум на выходе.

Номинальные мощности сигнала и шума на выходе соответственно равны

; ,

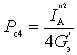
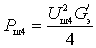
где

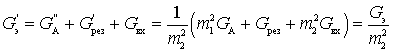
— результирующая проводимость шумящих источников.

Найдем напряжение шумов на зажимах 4-4′

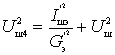
где

или

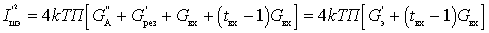
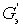
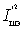
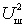
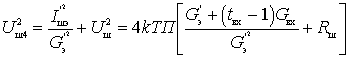
Учитывая значения , , , общее напряжение шумов на выходе схемы

Выражение, стоящее в квадратных скобках, является результирующим сопротивлением шума входного устройства и первого каскада:

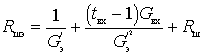
Три члена этой суммы характеризуют шумовые свойства следующих источников:

а) собственно входного устройства, шумовые свойства которого определяются сопротивлением, пересчитанным ко входу первого каскада, т.е . Об этом говорит сайт https://intellect.icu . величиной

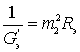
б) входа первого каскада, шумовые свойства которого определяются дополнительными шумами во входном сопротивлении электронного прибора

;

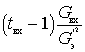
в) усилительного прибора, шумовые свойства которого определяются сопротивлением шума .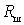

Определим теперь отношение сигнал/шум на выходе схемы

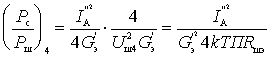
Тогда коэффициент шума

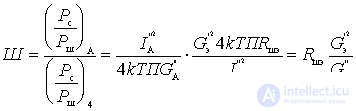
Обеспечение требуемых режимов при выборе связи между антенной, контуром и входом первого каскада.

Рассмотрим более подробно выражение для коэффициента шума, подставив в него значение результирующего сопротивления шума:

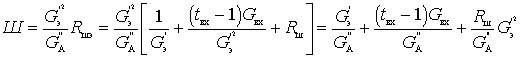
Принимая во внимание, что

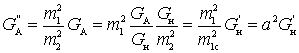
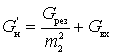
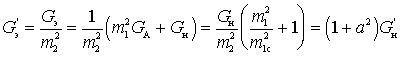
где — пересчитанная ко входу первого каскада проводимость нагрузки.

Коэффициент шума можно записать

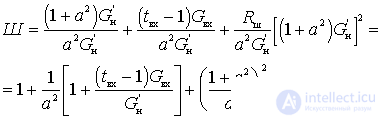
Второй член характеризует дополнительную величину Ш за счет шумов контура и входа первого каскада.

Третий член характеризует дополнительное значение Ш за счет электронного прибора.

Анализируя последнее выражение, рассмотрим 3 частных случая выбора связи между антенной, входным контуром и входом первого каскада:

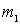
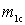
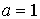
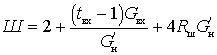
а) первый частный случай — режим согласования по мощности, при котором на входе приемника осуществляется согласование, т.е. коэффициент трансформации (включения) берется равным согласующему значению Т.к. в режиме согласования , то коэффициент шума определяется

В области относительно высоких частот, когда

, ,

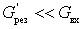
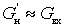
коэффициент шума

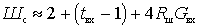
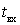
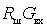
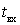
т.е. определяется величинами и . Из этого следует, что с целью уменьшения коэффициента шума надо выбирать электронные приборы с возможно меньшими значениями и .

б) второй частный случай — режим оптимального согласования по шумам.

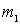
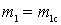
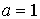
Этот случай характеризуется тем, что коэффициент включения со стороны антенны ,как и в предыдущем случае берется равным согласующему значению, т.е. и коэффициент рассогласования.

Вместе с тем контур присоединяется ко входу первого каскада не произвольно, а вполне определенным образом, выбором некоторого оптимального значения коэффициента включения 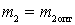с целью уменьшения коэффициента шума.

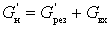
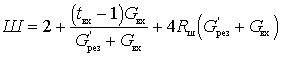
Выражение для коэффициента шума с учетом того, что примет вид

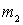
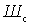
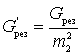
Чтобы найти оптимальную с точки зрения коэффициента шума величину коэффициента включения , возьмем производную по и приравняем ее нулю.

Отсюда

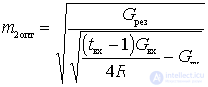
Тогда

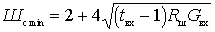
т.е. коэффициент шума определяется только параметрами электронного прибора.

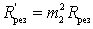
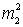
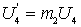
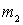
Уменьшение коэффициента шума при неполном подключении контура ко входу первого каскада обусловлено действием двух факторов: уменьшением пересчитанного значения резонансного сопротивления контура , вследствие чего резко уменьшается уровень шума (пропорционально ), и одновременно уменьшением уровня снимаемого с контура полезного сигнала (пропорционально ).

в) третий частный случай — режим оптимального рассогласования по шумам.

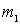
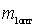
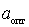
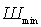
В данном случае коэффициент со стороны антенны не берется равным согласующему значению, а находится такое его оптимальное значение (или ), при котором коэффициент шума приобретает минимальное значение.

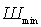
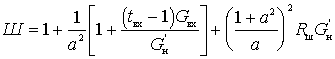
Для определения запишем Ш в виде

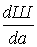
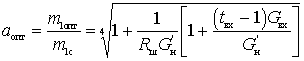
Берем производную от этого выражения по а , приравниваем ее к нулю и находим

Тогда

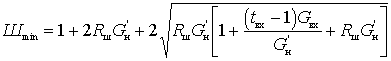
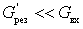
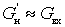
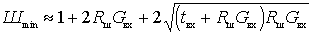
В области относительно высоких частот, когда , величина и

т.е. коэффициент шума определяется только параметрами электронного прибора.

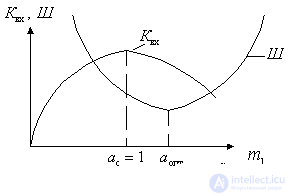
Уменьшение коэффициента шума при достигается за счет уменьшения влияния шумов резонансного контура и входа каскада.

Pисунок 6.7.

Коэффициент шума входного устройства без учета влияния первого каскада.

Как уже было показано

; .

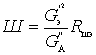
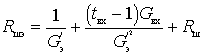
Для входного устройства без учета влияния первого каскада

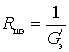
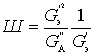
Отношение

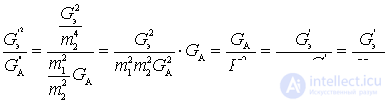
Статью про коэффициент шума входного устройства я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое коэффициент шума входного устройства, коэффициент шума входного устройства
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов

Источник

General[edit]

Definition[edit]

Noise factor of cascaded devices[edit]

Noise factor as a function of additional noise[edit]

Derivation[edit]

Optical noise figure[edit]

Unified noise figure[edit]

See also[edit]

References[edit]

External links[edit]

2.2 Выражение коэффициента шума через номинальные мощности

Введение

Теория

Не пропустите также: