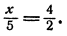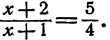Как найти коэффициент пропорциональности
5 части:Линейный коэффициент пропорциональностиКоэффициент пропорциональности периметраКоэффициент пропорциональности площадиКоэффициент пропорциональности объемаКоэффициент пропорциональности в химии
Вычисление коэффициента пропорциональности является довольно простой задачей. Вот как его вычислить.
Шаги
Часть 1 из 5: Линейный коэффициент пропорциональности
-
1
Разделите длину большей стороны на длину меньшей стороны. Посмотрите на две подобные фигуры. У них должна быть, по крайней мере, одна пара соответствующих сторон. Запишите эти две стороны в виде дроби, у которой в числителе поместите большую сторону, а в знаменателе – меньшую сторону. - Иначе говоря, вы делите длинную сторону на короткую сторону.
- Пример: даны два подобных прямоугольника. Первый прямоугольник имеет длину 4 см и ширину 2 см. Второй прямоугольник имеет длину 16 см и ширину 8 см. Найдите коэффициент пропорциональности этих прямоугольников.
- Длина меньшего прямоугольника соответствует длине большего прямоугольника.
- Длина меньшего прямоугольника равна 4 см. Длина большего прямоугольника равна 16 см.
- Коэффициент пропорциональности = длина большей стороны/ длина меньшей стороны = 16/4.
-
2
Упростите. Либо разделите числитель на знаменатель и представьте ответ в виде целого или десятичного числа, либо сократите дробь, разделив числитель и знаменатель на наибольший общий делитель. - Пример: коэффициент пропорциональности = 16/4
- Разделите числитель на знаменатель и представьте ответ в виде целого числа: 16/4 = 4.
- Сократите дробь и представьте ответ в виде дроби: 16/4 = 4/1.
- Представьте ответ в виде пропорции: 4:1.
-
3
Проверьте и запишите ответ. Проверьте ответ, применив описанный метод к другим соответствующим сторонам (если даны их значения). Разделите (как было описано выше) значения других соответствующих сторон и сравните полученные ответы. Если они совпадают, то вы правильно решили задачу. - Пример: ширина большего прямоугольника 8 см. Ширина меньшего прямоугольника 2 см. Чтобы проверить, что коэффициент пропорциональности 4:1, разделите большую ширину на меньшую ширину:
- 8/2 = 4/1
- Этот ответ также может быть записан в виде 4:1.
Часть 2 из 5: Коэффициент пропорциональности периметра
-
1
Найдите линейный коэффициент пропорциональности. У двух подобных фигур определите пару соответствующих сторон. Разделите большую сторону на меньшую и упростите результат. - Пример: даны два подобных прямоугольника. Первый прямоугольник имеет длину 15 см и ширину 5 см. Второй прямоугольник имеет длину 20 см и неизвестную ширину. Найдите коэффициент пропорциональности этих прямоугольников, ширину второго прямоугольника и его периметр.
- Линейный коэффициент пропорциональности: 20/15 =4/3.
- Этот ответ также может быть представлен в виде 4:3 или 1,3.
-
2
Умножьте соответствующую сторону на линейный коэффициент пропорциональности.[1]Если вам нужно найти неизвестное значение стороны, умножьте данное вам значение соответствующей стороны на коэффициент пропорциональности. - Обратите внимание, что для этого способа вам понадобится известное значение соответствующей стороны.
- Пример: ширина меньшего прямоугольника равна 5 см. Умножьте это значение на коэффициент пропорциональности 4/3.
- 5*(1,3) = 6,5
-
3
Запишите ответ. Вы получили неизвестное значение ширины. Запишите его и используйте далее для вычисления периметра (запишите величину периметра с соответствующими единицами измерения). - Пример: ширина второго прямоугольника равна 6,5 см.
- Пример: вычислите периметр по формуле: 2L+2W=Р.
- (2*20)+(2*6,5)=40+13=53 см.
Часть 3 из 5: Коэффициент пропорциональности площади
-
1
Найдите линейный коэффициент пропорциональности. У двух подобных фигур определите пару соответствующих сторон. Разделите большую сторону на меньшую и упростите результат. - Пример: даны два подобных прямоугольника. Первый прямоугольник имеет длину 8 см и ширину 3 см. Второй прямоугольник имеет длину 12 см и неизвестную ширину. Найдите коэффициент пропорциональности площадей этих прямоугольников и площадь второго прямоугольника.
- Линейный коэффициент пропорциональности: 12/8 =3/2.
- Этот ответ также может быть представлен в виде 3:2 или 1,5.
-
2
Возведите в квадрат линейный коэффициент пропорциональности.[2] Так как площадь прямоугольника равна произведению двух сторон, то для вычисления коэффициента пропорциональности площади нужно возвести в квадрат линейный коэффициент пропорциональности. - Пример: для вычисления коэффициента пропорциональности площади возведите в квадрат линейный коэффициент пропорциональности 1,5:
- 1,5*1,5=2,25
-
3
Умножьте коэффициента пропорциональности площади на площадь меньшей фигуры. Если дана площадь меньшей фигуры, вы можете найти площадь большей фигуры, умножив площадь меньшей фигуры на коэффициент пропорциональности площади. - Пример: найдите площадь меньшего прямоугольника, умножив его длину на ширину: 8*3=24 см^2
- Найдите площадь большего прямоугольника, умножив площадь меньшего прямоугольника на коэффициента пропорциональности площади: 24*2,25=54 см^2
-
4
Запишите ответ (с соответствующими единицами измерения). - Пример: коэффициент пропорциональности площадей этих прямоугольников равен 2,25. Площадь второго прямоугольника равна 54 см^2.
Часть 4 из 5: Коэффициент пропорциональности объема
-
1
Найдите линейный коэффициент пропорциональности. У двух подобных фигур определите пару соответствующих сторон. Разделите большую сторону на меньшую и упростите результат. - Пример: даны два подобных прямоугольных параллелепипеда. Первый параллелепипед имеет длину 10 см, высоту 8 см и ширину 4 см. Второй параллелепипед имеет длину 15 см и неизвестную ширину и высоту. Найдите коэффициент пропорциональности объемов этих параллелепипедов и объем второго параллелепипеда.
- Линейный коэффициент пропорциональности: 15/10 =3/2.
- Этот ответ также может быть представлен в виде 3:2 или 1,5.
-
2
Возведите в куб линейный коэффициент пропорциональности. Так как объем параллелепипеда равен произведению трех сторон, то для вычисления коэффициента пропорциональности объема нужно возвести в куб линейный коэффициент пропорциональности. - Пример: для вычисления коэффициента пропорциональности объема возведите в куб линейный коэффициент пропорциональности 1,5:
- 1,5*1,5*1,5=3,375
-
3
Умножьте коэффициента пропорциональности объема на объем меньшей фигуры. Если дан объем меньшей фигуры, вы можете найти объем большей фигуры, умножив объем меньшей фигуры на коэффициент пропорциональности объема. - Пример: найдите объем меньшего параллелепипеда, умножив его длину на ширину на высоту: 10*4*8 = 320 см^3
- Найдите объем большего параллелепипеда, умножив объем меньшего параллелепипеда на коэффициент пропорциональности объема: 320*3,375=1080 см^3
-
4
Запишите ответ (с соответствующими единицами измерения). - Пример: коэффициент пропорциональности объемов этих параллелепипедов равен 3,375. Объем второго параллелепипеда равен 1080 см^3.
Часть 5 из 5: Коэффициент пропорциональности в химии
-
1
Разделите молярную массу соединения на его молярную массу согласно эмпирической формуле.[3]Если вам дана эмпирическая формула химического соединения и вам нужно найти его молекулярную формулу, то вы можете найти нужный коэффициент пропорциональности, разделив молярную массу соединения на его молярную массу согласно эмпирической формуле. - Пример: найдите молекулярную формулу соединения Н2О с молярной массой 54,05 г/моль.
- Молярная масса H2O равна 18,0152 г/моль.
- Найдите коэффициент пропорциональности, разделив молярную массу соединения на его молярную массу согласно эмпирической формуле.
- Коэффициент пропорциональности: 54,05/18,0152 = 3
-
2
Умножьте эмпирическую формулу на коэффициент пропорциональности. Умножьте индекс каждого элемента в эмпирической формуле на найденный коэффициент пропорциональности. Таким образом, вы получите молекулярную формулу химического соединения. - Пример: чтобы найти молекулярную формулу соединения, данного в задаче, умножьте индексы Н20 на коэффициент пропорциональности 3.
- H2O*3 = H6O3
-
3
Запишите ответ. Вы нашли молекулярную формулу химического соединения, данного в задаче. - Пример: коэффициент пропорциональности равен 3. Молекулярная формула соединения: H6O3.
Загрузить PDF
Загрузить PDF
Коэффициент пропорциональности (линейный коэффициент пропорциональности) равен отношению двух соответствующих сторон подобных фигур. Подобные фигуры – это фигуры одинаковой формы, но разных размеров. Коэффициент пропорциональности используется для решения основных геометрических задач. Коэффициент пропорциональности можно использовать для вычисления длин неизвестных сторон. С другой стороны, по соответствующим сторонам можно вычислить коэффициент пропорциональности. Такие вычисления связаны с операцией умножения или с упрощением дробей.
-
1
Убедитесь, что фигуры подобны. У таких фигур все углы равны, а стороны соотносятся в некой пропорции. Подобные фигуры имеют одинаковую форму, но одна фигура больше другой.[1]
- В задаче должно быть сказано, что фигуры подобны, или что у них равные углы, или что стороны пропорциональны, или что одна фигура пропорциональна другой.
-
2
Найдите соответствующие стороны обеих фигур. Возможно, понадобится повернуть или зеркально отразить одну из фигур, чтобы выровнять обе фигуры и определить соответствующие стороны. Как правило, в задачах даются длины соответствующих сторон; в противном случае измерьте их.[2]
Если не знать значений хотя бы пары соответствующих сторон, нельзя найти коэффициент пропорциональности.- Например, дан треугольник, основание которого равно 15 см, и подобный треугольник с основанием, равным 10 см.
-
3
Запишите отношение. У каждой пары подобных фигур есть два коэффициента пропорциональности: один используется при увеличении размера, а другой – при уменьшении. Если размер меньшей фигуры увеличивается до размера большей фигуры, используйте отношение: коэффициент пропорциональности = (сторона большей фигуры)/(сторона меньшей фигуры). Если размер большей фигуры уменьшается до размера меньшей фигуры, используйте отношение: коэффициент пропорциональности = (сторона меньшей фигуры)/(сторона большей фигуры).[3]
- Например, если треугольник с основанием 15 см уменьшается до треугольника с основанием 10 см, используйте отношение: коэффициент пропорциональности = (сторона меньшей фигуры)/(сторона большей фигуры).
Подставив соответствующие значения, вы получите: коэффициент пропорциональности =.
- Например, если треугольник с основанием 15 см уменьшается до треугольника с основанием 10 см, используйте отношение: коэффициент пропорциональности = (сторона меньшей фигуры)/(сторона большей фигуры).
-
4
Упростите отношение. Упрощенное отношение (дробь) является коэффициентом пропорциональности. При уменьшении размера коэффициент пропорциональности представляет собой правильную дробь.[4]
При увеличении размера коэффициент пропорциональности представляет собой целое число или неправильную дробь, которую можно преобразовать в десятичную дробь.Реклама
-
1
Найдите значения сторон фигуры. Значения сторон одной из подобных фигур будут даны; в противном случае измерьте их. Если стороны одной из подобных фигур неизвестны, нельзя вычислить стороны второй фигуры.
- Например, дан прямоугольный треугольник, катеты которого равны 4 см и 3 см, а гипотенуза равна 5 см.
-
2
Выясните, будет ли подобная фигура больше или меньше данной. Если больше, стороны будут больше, а коэффициент пропорциональности представляет собой целое число, неправильную или десятичную дробь. Если подобная фигура меньше данной, стороны будут меньше, а коэффициент пропорциональности представляет собой правильную дробь.
- Например, если коэффициент пропорциональности равен 2, подобная фигура больше данной.
-
3
Умножьте значение одной стороны на коэффициент пропорциональности. Коэффициент пропорциональности должен быть дан. Если умножить сторону на коэффициент пропорциональности, можно найти значение соответствующей стороны подобной фигуры.[5]
- Например, если гипотенуза прямоугольного треугольника равна 5 см, а коэффициент пропорциональности равен 2, гипотенуза подобного треугольника вычисляется так:
. Таким образом, гипотенуза подобного треугольника равна 10 см.
- Например, если гипотенуза прямоугольного треугольника равна 5 см, а коэффициент пропорциональности равен 2, гипотенуза подобного треугольника вычисляется так:
-
4
Найдите значения остальных сторон подобной фигуры. Для этого умножьте известные значения сторон на коэффициент пропорциональности. Вы получите значения соответствующих сторон подобной фигуры.
Реклама
-
1
Задача 1. Найдите коэффициент пропорциональности следующих подобных фигур: прямоугольник с шириной 6 см и прямоугольник с шириной 54 см.
-
2
Задача 2. Сторона неправильного многоугольника равна 14 см. Сторона подобного многоугольника равна 8 см. Найдите коэффициент пропорциональности.
-
3
Задача 3. Стороны прямоугольника ABCD равны 8 см и 3 см. Прямоугольник EFGH является большим и подобным прямоугольником. Найдите площадь прямоугольника EFGH, если коэффициент пропорциональности равен 2,5.
Реклама
-
1
Молярную массу соединения разделите на молярную массу по эмпирической формуле. Если эмпирическая формула химического соединения известна и нужно найти молекулярную формулу того же химического соединения, коэффициент пропорциональности равен отношению молярной массы соединения к молярной массе по эмпирической формуле.
- Например, найдите молярную массу соединения H2O, молекулярная масса которого равна 54,05 г/моль.
- Молярная масса Н2О равна 18,0152 г/моль.
- Молярную массу соединения разделите на молярную массу по эмпирической формуле:
- Коэффициент пропорциональности равен 54,05/18,0152 = 3
- Например, найдите молярную массу соединения H2O, молекулярная масса которого равна 54,05 г/моль.
-
2
Эмпирическую формулу умножьте на коэффициент пропорциональности. В эмпирической формуле индексы элементов умножьте на вычисленный коэффициент пропорциональности. Вы найдете молекулярную формулу химического соединения, данного в задаче.
- Например, чтобы найти молекулярную формулу данного соединения, умножьте индексы соединения Н20 на коэффициент пропорциональности, равный 3.
- H2O * 3 = H6O3
- Например, чтобы найти молекулярную формулу данного соединения, умножьте индексы соединения Н20 на коэффициент пропорциональности, равный 3.
-
3
Напишите ответ. Найдены эмпирическая и молекулярная формулы химического соединения, которое дано в задаче.
- Например, коэффициент пропорциональности равен 3. Молекулярная формула соединения: H6O3.
Реклама
Об этой статье
Эту страницу просматривали 63 614 раз.
Была ли эта статья полезной?
Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Отношение площадей подобных треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»
Площади подобных треугольников
Средняя оценка: 4.8
Всего получено оценок: 107.
Средняя оценка: 4.8
Всего получено оценок: 107.
Подобные треугольники – это следующий шаг в изучении треугольников после равенства. Нужно в полной мере понимать возможности подобия треугольников, чтобы правильно использовать все свойства в решении задач. Разберемся в отличиях равенства, подобия и равновеличия, а также поговорим о свойствах сторон и определении площадей подобных треугольников.
Подобные треугольники
Подобными треугольниками называют треугольники, соответственные стороны которых пропорциональны, а углы равны. Равные треугольники также являются подобными с коэффициентом подобия равным 1.
Рис. 1. Подобные треугольники
Коэффициент пропорциональности (подобия) – это отношение длин сторон одного треугольника к соответствующим длинам сторон другого треугольника. Важно при подсчете коэффициента строго соблюдать какая сторона к какой относится.
Например, если вы начали расчет делением сторон большего треугольника на стороны меньшего, то стоит придерживаться такого подхода и далее.
Признаки подобия
Признаки подобия в чем-то похожи на признаки равенства треугольников. Всего их тр:
- По двум углам. Если два угла одного треугольника равны соответствующим углам другого треугольника, то такие треугольники подобны.
- По трем сторонам. Если три стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, то такие треугольники подобны.
- По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
Рис. 2. Признаки подобия треугольников
Свойства подобных треугольников
- Стороны подобных треугольников пропорциональны и относятся друг к другу в отношении, равном коэффициенту подобия.
- Углы подобных треугольников равны.
- Площади подобных треугольников относятся друг к другу в отношении, равном квадрату коэффициента подобия.
Остановимся подробнее на последнем свойстве. Почему все стороны соотносятся ,как коэффициент в первой степени, а площади в квадрате? Потому что площадь это половина произведения основания на высоту.
Пропорциональны друг другу не только стороны, но и характерные отрезки: медианы, высоты, биссектрисы.
Получается, что обе части произведения площади пропорциональны, но в произведении участвуют как высота, так и основание. Значит коэффициент пропорциональности должен быть возведен в квадрат.
Нужно четко различать понятие подобных и равновеликих треугольников. Подобные треугольники имеют коэффициент подобия, в соответствие с которым соотносятся стороны треугольника. А равновеликие треугольники могут, как угодно разнится по значениям сторон, важно лишь, чтобы площади треугольников были равны.
Что мы узнали?
Мы узнали, что такое подобные треугольники, поговорили об их свойствах. Поговорили об отношении площадей подобных треугольников и вывели это отношение на практике для лучшего запоминания формулы.
http://interneturok.ru/lesson/geometry/8-klass/podobnye-treugolniki/otnoshenie-ploschadey-podobnyh-treugolnikov
http://obrazovaka.ru/geometriya/ploschadi-podobnyh-treugolnikov-opredelenie.html
Определение пропорции:
Связь между четырьмя алгебраическими выражениями А, В, С и D, имеющая вид
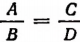
называется пропорцией.
(Равенство 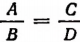
Примеры пропорции:
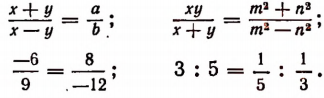
В пропорции 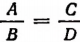
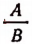
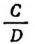
Главное свойство пропорции
Умножив левую и правую части пропорции
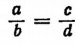
на произведение bd, получим ad = be, т. е. во всякой пропорции произведение крайних членов равно произведению средних.
Составление пропорции по данному равенству двух произведений
Пусть pq = ху. Разделив левую и правую части этого равенства на qx, получим
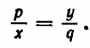
Этот результат можно сформулировать следующим образом.
Если произведение двух чисел равно произведению двух других, то из этих четырех чисел можно составить пропорцию, беря множители одного произведения за крайние, а множители другого произведения за средние члены пропорции. (При этом дополнительно требуется, чтобы оба последующих члена пропорции не оказались равными нулю.)
Перестановка членов пропорции
Пусть ad = be и числа а, b, с, d — все отличны от нуля. Разделив левую и правую части равенства ad = bc первый раз на bd, второй на ab, третий на ас и четвертый на cd, получим соответственно четыре пропорции:
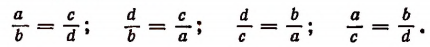
Поменяв местами отношения в этих равенствах, получим еще четыре пропорции:
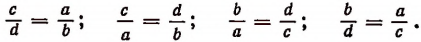
Этот результат показывает, что в пропорции можно менять местами средние и крайние члены и ставить оба крайних члена на места средних, а оба средних на места крайних.
Производные пропорции
1. Прибавив к левой и правой частям пропорции 
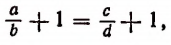
или
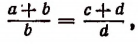
т. е. во всякой пропорции сумма членов первого отношения так относится к своему последующему, как сумма членов второго отношения — к своему последующему.
2. Вычтя из левой и правой частей пропорции 
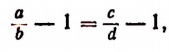
или
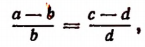
т. е. во всякой пропорции разность членов первого отношения так относится к своему последующему, как разность членов второго отношения — к своему последующему.
3. Разделив левую часть равенства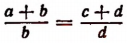
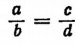
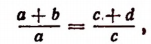
т. е. во всякой пропорции сумма членов первого отношения так относится к своему предыдущему, как сумма членов второго отношения — к своему предыдущему.
4. Разделив левую часть равенства 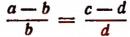

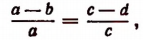
т. е. во всякой пропорции разность членов первого отношения так относится к своему предыдущему, как разность членов второго отношения —к своему предыдущему.
5. Разделив левую часть равенства 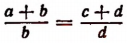
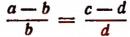
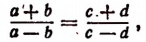
т. е. во всякой пропорции сумма членов первого отношения так относится к их разности, как сумма членов второго отношения — к их разности.
Из пропорции 

Например, умножив обе части пропорции 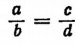
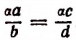
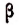
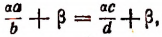
или
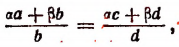
т. е. получим новую производную пропорцию.
Определение неизвестного члена пропорции
Пусть в пропорции 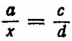
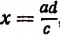
Примеры:
1. Найти неизвестное число х из пропорции 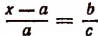
Составим производную пропорцию по правилу: сумма членов первого отношения так относится к своему последующему члену, как сумма членов второго отношения к своему последующему:
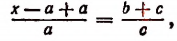
т. е.
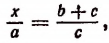
откуда
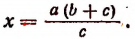
2. Найти неизвестное х из пропорции 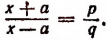
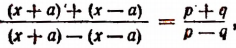
или
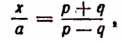
отсюда
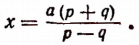
Ряд равных отношений
Иногда бывает удобно вместо различных букв употреблять для обозначения чисел одну и ту же букву, снабженную дополнительными значками — индексами. Например 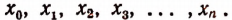
Основное свойство ряда равных отношений
Пусть имеется ряд равных отношений:
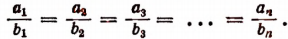
Обозначим общее значение всех этих отношений буквой k. Тогда
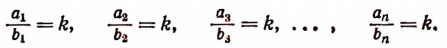
Отсюда
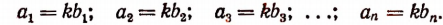
Складывая левые и правые части этих равенств, получим:
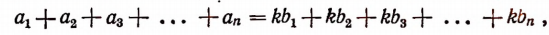
или
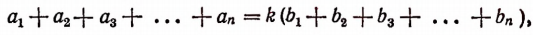
или
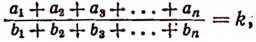
т.е.
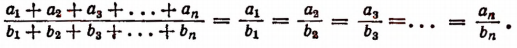
Итак, доказано следующее:
если несколько отношений равны друг другу, то отношение суммы их предыдущих членов к сумме последующих равно каждому из этих отношений.
Пример:
Пусть длины 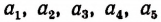
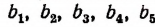
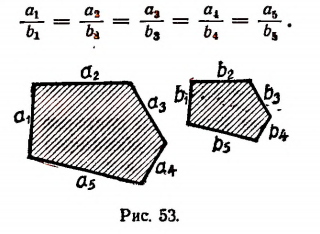
По свойству ряда равных отношений получим:
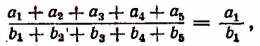
или
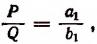
где Р и Q периметры многоугольников.
Прямая пропорциональность
Сначала рассмотрим несколько примеров.
Пример:
Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.
Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения 
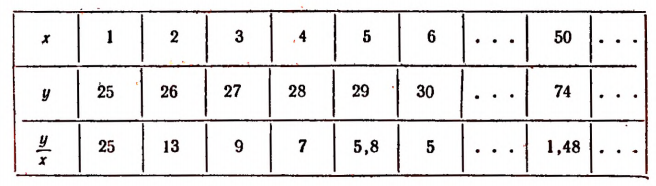
В этом примере отношение 
Пример:
Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.
Составим таблицу, подобную предыдущей.
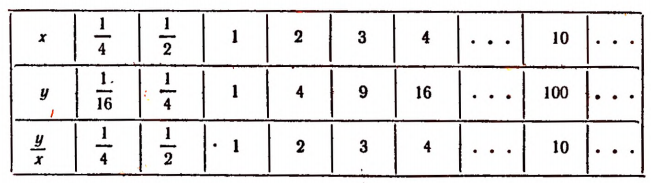
Отношение 
Пример:
Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.
Опять составим таблицу значений х, у и 

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение 
Определение:
Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение 
Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.
Возраст отца и возраст сына не пропорциональны.
Также не пропорциональны сторона квадрата и его площадь.
Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение 
Обозначая это постоянное число буквой k, получим:
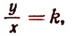
или
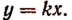
Следовательно, если величины у и х пропорциональны и отношение 
Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).
Теперь докажем обратное положение. Пусть
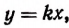
где k — постоянное число.
Отсюда следует, что при х = 0 и у = 0 и что 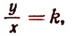
Из того что 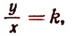
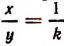
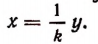
Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число 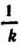
Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.
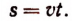
Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).
Сделаем еще два замечания.
Замечание:
Если имеется два ряда чисел:

и

и если
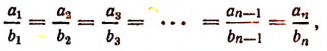
то числа одного из этих рядов называются пропорциональными числам другого ряда.
Замечание:
Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.
В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.
В заключение решим две простые задачи на пропорциональные величины.
Задача:
На карте в масштабе 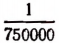
Решение:
Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:
С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)
Решение:
Обозначив искомое изменение (в мм) буквой х, получим:
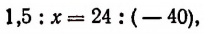
откуда
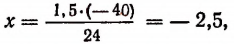
т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.
Обратная пропорциональность
Сначала приведем примеры.
1. Рассмотрим изменяющийся прямоугольный параллелепипед с квадратным основанием, имеющий неизменный объем, равный 3600 куб. см (рис. 54).
Пусть буква х обозначает в сантиметрах изменяющуюся сторону основания, а буква у — изменяющуюся высоту параллелепипеда.
Рассматривая таблицу:
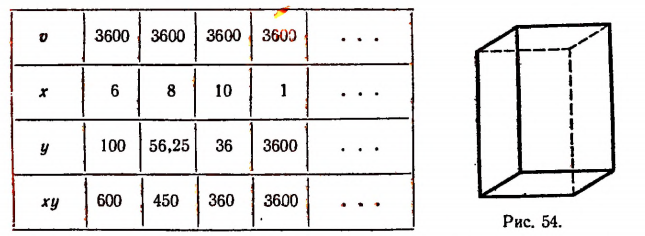
легко видеть, что произведение ху не остается неизменным при постоянстве объема.
2. Рассмотрим изменяющийся прямоугольник, имеющий неизменную площадь, равную 100 кв. см.
Пусть буква х обозначает одно изменяющееся измерение (например, длину прямоугольника), а буква у — другое изменяющееся измерение (ширину). Пусть х и у выражены в сантиметрах.
Так как произведение измерений прямоугольника равно его площади, то величины х и у при всех своих возможных изменениях будут давать в своем произведении число 100, т. е. произведение изменяющихся величин х и у будет оставаться неизменным.
Существенное отличие второго примера от первого заключается в том, что в нем произведение ху остается неизменным, в то время как в первом оно изменяется.
Определение:
Две величины х и у называются обратно пропорциональными, если при всех их возможных изменениях произведение ху остается равным одному и тому же числу.
Обозначая это число буквой k, получим
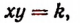
или
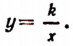
Следовательно, если величины х и у обратно пропорциональны, то величина у выражается через величину х по формуле следующего вида:
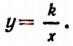
Число k называется коэффициентом обратной пропорциональности.
Длина прямоугольника и ширина прямоугольника при заранее заданной площади прямоугольника являются величинами обратно пропорциональными. Коэффициентом обратной пропорциональности служит как раз эта площадь.
Сторона основания прямоугольного параллелепипеда с квадратным основанием и высота параллелепипеда при заранее заданном объеме не являются величинами обратно пропорциональными.
Задача:
Зал освещается m лампами по а свечей каждая. Сколькими лампами в b свечей можно получить ту же освещенность зала?
Число ламп и число свечей каждой лампы при данной освещенности зала являются величинами обратно пропорциональными. Поэтому, обозначая число ламп в b свечей буквой x, получим

откуда
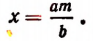
Пропорциональное деление
Задача:
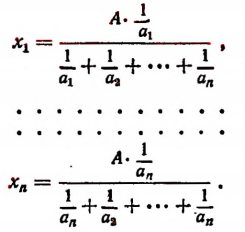
Число А разделить на n слагаемых прямо пропорционально числам
Обозначим искомые слагаемые буквами 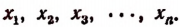
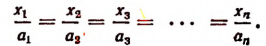
Пользуясь свойством ряда равных отношений, получим
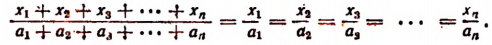
Но
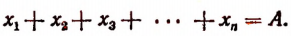
Поэтому
Задача:
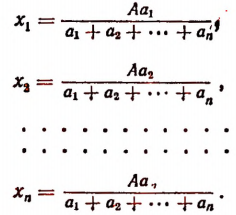
Число А разделить на n слагаемых обратно пропорционально числам
Обозначим искомые слагаемые буквами 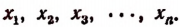
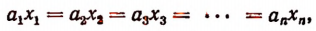
или
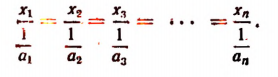
По свойству ряда равных отношений получим
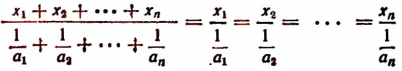
Но

Поэтому
Пропорции и пропорциональная зависимость
- Отношением числа а к числу b называется частное
, а называется предыдущим, b — последующим членом отношения.
- Пропорцией называется равенство, каждая часть которого является отношением двух чисел. В пропорции
члены а и d называются крайними, а b и с средними.
При изложении свойств пропорции будем считать, что ни один из членов пропорции не равен нулю.
Пример:
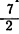
Пример:
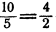
Главное свойство пропорции
Теорема:
Во всякой пропорции произведение крайних
членов равно произведению средних.
Доказательство:
Дана пропорция

Умножим обе части равенства (1) на bd, получим
Теорема доказана.
Теорема:
Если произведение двух чисел
равно произведению двух других чисел, то из этих четырех чисел можно составить пропорцию^ крайними членами которой являются сомножители одного из двух произведений, а средними—сомножители другого.
При этом предполагается, что ни один из сомножителей не равен нулю.
Доказательство:
Пусть
a, b, с, d все отличны от нуля. Разделим обе части равенства на bd, получим
Теорема доказана.
Пример:
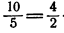
Пример:
8 • 9 = 3 • 24 — равенство двух произведений.
Разделим обе части этого равенства на 9 • 24, получим пропорцию
Определение неизвестного члена пропорции
Теорема:
Средний член пропорции равен произведению крайних, деленному на другой средний. Крайний член пропорции равен произведению средних, деленному на другой крайний.
Пусть

Покажем, что

На основании теоремы 1 имеем

Разделим обе части равенства (4) на с, получим равенство (2). Разделим обе части равенства (4) на d, получим равенство (3). Теорема доказана.
Пример:
Найти х, если
Решение:
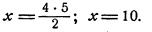
Пример:
Найти х, если 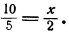
Решение:
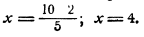
Перестановка членов пропорции
Теорема:
Во всякой пропорции можно переставить
средние члени, переставить крайние члени, переставить и средние члени и крайние, средние поставить на место крайних, а крайние на место средних.
Иными словами, если

то

(переставлены средние члены),

(в (1) переставлены крайние члены),

(в (1) переставлены и средние и крайние члены),

(средние поставлены на место крайних, крайние — на место средних).
Доказательство:
В пропорций (1)

Разделим обе части равенства (6) на cd, получим равенство (2). Точно так же, разделив обе части равенства (6) на аb, а затем на ас, получим равенства (3) и (4). Равенство (5) получается из равенства (4) посредством перестановки отношений. Теорема доказана.
Следствие:
Переставим отношения в равенствах (I), (2), (3), получим еще три пропорции
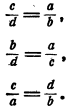
Таким образом, всякую пропорцию посредством перестановки ее членов можно представить в восьми различных видах.
Производные пропорции
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к последующему члену этого отношения, как сумма членов второго отношения относится к своему последующему.
2) Во всякой пропорции разность членов первого отношения так относится к последующему члену этого отношения, как разность членов второго отношения относится к своему последующему.
Иными словами, если

то

Доказательство:
Прибавим к каждой части равенства (1)
по 1, получим равенство (2). Вычтем из каждой части равенства (1) по 1, получим равенство (3). Теорема доказана.
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к предыдущему члену этого отношения, как сумма членов второго отношения относится к своему предыдущему.
2) Во всякой пропорции разность членов первого отношения так относится к предыдущему члену этого отношения, как разность членов второго отношения относится к своему предыдущему.
Иными словами, если
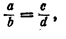
то

Доказательство:
Разделим равенство (2) почленно на
равенство (1), т. е., левую часть равенства (2) разделим на левую часть равенства (1), а правую часть равенства (2) на правую часть равенства (1). Получим равенство (4). Разделив равенство (3) почленно на равенство (1), получим равенство 5). Теорема доказана.
Теорема:
Во всякой пропорции сумма членов первого
отношения так относится к их разности, как сумма членов второго отношения относится к их разности, если только эти разности отличны от нуля.
Иными словами, если
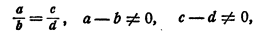
то

Доказательство:
Разделив почленно равенство (4) на
равенство (5), получим равенство (6).
Ряд равных отношений
Теорема:
Если даны несколько равных отношений* то
сумма всех предыдущих членов отношений относится к сумме всех последующих как любой из предыдущих к своему последующему.
Доказательство:
Пусть имеется несколько равных отношений
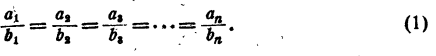
Обозначим результат деления 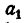
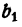
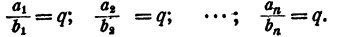
Отсюда
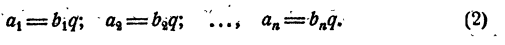
Сложив почленно все равенства (2), имеем
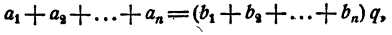
откуда
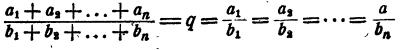
Теорема доказана.
Задача:
Дано, что
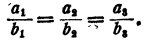
Доказать, что при любых 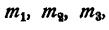
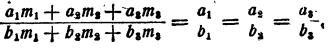
Решение:
Умножим каждый, член первого отношения на 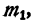
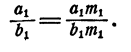
Точно так же
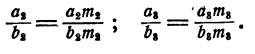
Значит,
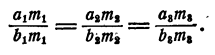
На основании теоремы 8 имеем
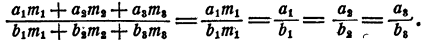
Задача:
Решить уравнение
Решение:
Пользуясь теоремой 7 § 5, имеем
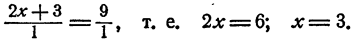
Пропорциональная зависимость
Мы много раз составляли уравнения, выражающие зависимость между величинами, и могли наблюдать, что. зависимости эти бывают весьма разнообразны.
При решении многих задач мы встречаемся с двумя величинами, зависимость между которыми такова, что при изменении этих величин их отношение остается неизменным. Такие величины называются прямо пропорциональными, а зависимость между ними — пропорциональной зависимостью.
Для примера приведем несколько задач, в которых мы встретимся с величинами, находящимися в пропорциональной зависимости.
Задача:
Скорость течения реки 3 км в час. Плот за t часов прошел вниз по реке S км. Составить уравнение, выражающее зависимость между S и t.
Ответ. S = 3t.
Задача:
С каждого гектара собрано 30 ц ржи и, таким образом, с k га собрано А ц. Составить уравнение, выражающее зависимость между А и k.
Ответ. А = 30k
Задача:
Основание прямоугольника 2 см, высота h см, площадь Q 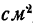
Ответ. Q = 2h.
Задача:
1 м материи стоит 20 руб. За m м этой материи
уплатили N pyб. Составить уравнение, выражающее зависимость между N и m.
Ответ. N=20m.
Мы рассмотрели четыре задачи, которые по своему содержанию относятся к различным областям практической деятельности. Нетрудно убедиться, что в каждой из этих задач мы действительно имеем дело с прямо пропорциональными величинами.
Так, в первой задаче отношение расстояния (в kм), пройденного плотом, к времени (в часах), в течение которого плот находился в пути, всегда одно и то же и равно 3. Поэтому расстояние, которое проходит плот вниз по реке, пропорционально времени, в течение которого плот находится в пути, при условии, что скорость течения реки повсюду одна и та же.
Точно так же во второй задаче количество ржи, собранной с нескольких гектаров, пропорционально количеству ржи, собранной с одного гектара, при условии, что с каждого гектара собрано по одному и тому же количеству ржи и т. д.
Заметим, что уравнения, к которым мы пришли в рассмотренных задачах, имеют один и тот же вид. В этих уравнениях одна, из величин равна произведению некоторого числового множителя на другую величину. Этот множитель называется коэффициентом пропорциональности. В первой задаче коэффициент
пропорциональности равен 3, во второй задаче он равен 30, в третьей задаче он равен 2, в четвертой задаче он равен 20.
Таким образом, пропорциональная зависимость между величинами всегда выражается уравнением y = kx, где k — коэффициент пропорциональности. Известно, что зависимость между двумя величинами может быть наглядно представлена таблицей, а затем и графиком.
Для примера представим таблицей зависимость, выражаемую уравнением S = 3/ (первая задача):
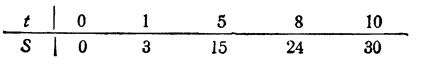
Построим график зависимости S = 3t (рис. 19). Обратим внимание на следующие обстоятельства:
- Отношение чисел, находящихся в одном столбце таблицы, повсюду одно и то же и равно коэффициенту пропорциональности:
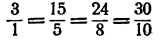
и т. д. (для первого столбца это отношение не имеет смысла; так как на нуль делить нельзя).
2, График представляет собой луч, выходящий из начала координат (при t= 0, S = 0). (Доказательство этого утверждения здесь провести нельзя, так как для этого требуются некоторые сведения из геометрии.)
То же самое можно наблюдать и при графическом представлении любой другой пропорциональной зависимости между двумя величинами.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат



































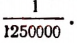
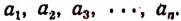
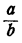 , а называется предыдущим, b — последующим членом отношения.
, а называется предыдущим, b — последующим членом отношения.