
µ=1/n – величина, обратная числу полуволн n синусоиды, по которой изогнется стержень. Постоянная µ называется коэффициентом приведения длины, а произведение µl – приведенной длиной стержня. Приведенная длина есть длина полуволны синусоиды, по которой изгибается этот стержень.
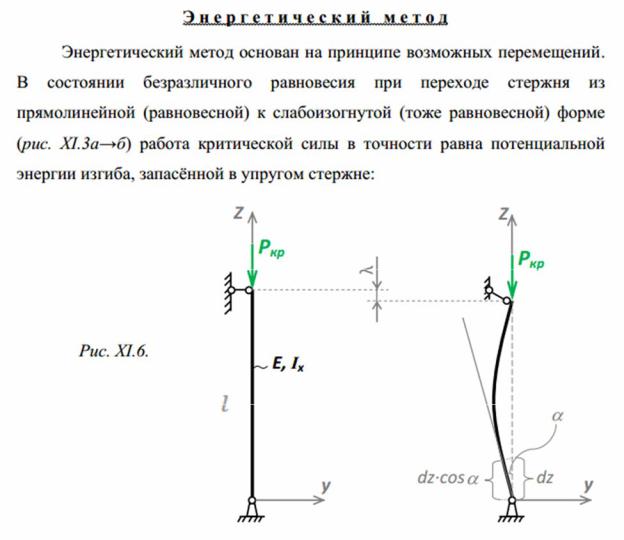
38. Устойчивость сжатых стержней. Вывод формулы вычисления критической нагрузки энергетическим методом. Выбор пробной функции прогиба для решения задачи нахождения критической силы энергетическим методом





39. Пределы применимости формулы Эйлера для вычисления критических нагрузок. Определение значения гибкости стержня, до которого справедлива формула Эйлера. График зависимости критических напряжений от гибкости. Определение критических напряжений при малой гибкости стержня.





Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рис.15.11
Рис.15.9 Рис.15.10 Рис.15.11
Отступление
Рассмотрим рис. 15.11. На этом рисунке пунктиром изображена в общем виде форма стойки после искривления, введены обозначения: v это перемещение по оси y, т.е функция прогибов, Q — угол поворота оси стойки, r — радиус кривизны оси стойки. Поскольку мы рассматриваем искривленное состояние стойки, бесконечно близкое к прямолинейной форме, то прогиб стойки v и угол поворота оси стойки Q бесконечно малы. При малых углах тангенс угла равен самому углу. С другой стороны тангенс угла касательной к кривой есть первая производная от функции, описывающей эту кривую. По этой причине можно принять, что
Q = tgQ = , т. е. первая производная от функции прогибов есть угол поворота оси стойки. Из математики известно, что кривизна
равна

Поскольку угол =
очень мал, то
и
Тогда, согласно формуле (2), можно принять, что
или кривизна оси стойки равна второй производной от функции прогибов v.
В разделе «Изгиб» для кривизны оси изогнутого бруса было получено выражение , откуда с подстановкой кривизны из выражения (3), получается
. (4)
Подставив в (1) вместо изгибающего момента его выражение через кривизну из формулы (4), получим уравнение равновесия в виде:
.
Упростим полученное выражение. Для этого разделим уравнение на изгибную жесткость E Jx и введем обозначение . Получим однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
. (5)
Решение этого уравнения известно
.
Коэффициенты С1 и С2 определим из граничных условий — на опорах прогиб стойки v равен нулю:
1) при z = 0, v = 0, т. е. 0 = C1×0+C2×1 = 0, откуда получается С2 = 0 и остается
v = C1 sin az;
2) при z = l, v = 0, т. е. 0 = C1 sin al.
Получили так называемое характеристическое уравнение. С1 ¹ 0, так как в этом случае v равно нулю при любых значениях a, т.е. силы F, так как . Это соответствует прямолинейной форме стойки, а мы рассматриваем криволинейную форму равновесия. Значит, равно нулю выражение sin al=0. Этому уравнению соответствуют следующие значения аргумента:
al = 0, p, 2p,…, np. Тогда a2 = n2 .
С другой стороны ранее было обозначено
, откуда следует
.
Поскольку критическая сила — это наименьшее значение нагрузки, при котором возможна криволинейная форма устойчивого равновесия, то из всех значений аргумента следует выбрать наименьшее: al = p или n =1. Мы рассматривали критическое состояние стойки, значит F = Fкр. Если стойка закреплена во всех направлениях одинаково, она будет выгибаться в плоскости наименьшей жесткости, поэтому следует принять Jx = Jmin. Получается
.
Это формула Эйлера для определения критической силы для шарнирно закрепленной сжатой стойки.
Лекция 16
Другие виды закрепления стойки
Рассмотрим стойку в виде консоли с заделкой, нагруженную на свободном конце сжимающей критической силой F (рис. 16.1а). Такая стойка находится в состоянии безразличного равновесия, когда равновозможны как прямолинейная, так и бесконечно близкая к ней криволинейная форма устойчивого равновесия. Рассмотрим криволинейную форму.


Рис.16.1
Изобразим стойку в отклоненном состоянии и поместим начало координат на отогнутом конце стойки (рис.16.1б). Применим метод сечений и рассмотрим равновесие отрезанной части стойки (рис.16.1в). Из суммы моментов относительно оси, проходящей через сечение и перпендикулярной к плоскости чертежа, получим
Mx + F v = 0 или
E Jx v» + Fv = 0.
Обозначив , получим дифференциальное уравнение
.
Решение этого уравнения
v = C1 sinaz + C2 cosaz.
Граничные условия для определения констант С1 и С2:
-
при z = 0, v = 0,
(в нашей системе координат прогиб на отогнутом конце равен нулю)
т. е. 0 = C1×0+C2×1, откуда получается C2 = 0 и остается
v = C1sin az , ;
-
при z = l,
Угол поворота оси стойки в заделке, в которую ось входит по касательной, равен нулю. Угол поворота оси это первая производная от функции прогибов v:
C1a cos al=0.
В полученном характеристическом уравнении C1 ¹ 0, так как в этом случае прогиб будет равен нулю при любом значении a. Это прямолинейная форма равновесия, а мы рассматриваем криволинейную форму. Также a ¹ 0, так как в этом случае получается . Это означает, что либо F = 0, т. е. стойка не нагружена, либо
, т. е. стойка абсолютно жесткая, а мы рассматриваем гибкую стойку, у которой
. Остается cos al = 0, что соответствует значениям аргумента al =
и т. д.
Поскольку критической является наименьшая сила, при которой возможна криволинейная форма устойчивого равновесия, выбираем меньшее значение аргумента al = , откуда получается
Ранее было обозначено
. Приравняв правые части этих двух выражений, получаем критическую сила для данной стойки
.
Коэффициент приведения длины стойки
Сравнивая полученные выше выражения для критической силы для сжатых стоек, отличающихся условиями закреплением, можно заметить, что различия в условиях закрепления проявляются только в виде коэффициента в знаменателе формулы. Поэтому можно записать формулу Эйлера в общем виде как
,
где m — коэффициент приведения длины стойки, m l — приведенная длина стойки, т. е это длина основной (шарнирно закрепленной) стойки, которая с точки зрения устойчивости эквивалентна данной стойке.
Определение коэффициента это отдельная задача. Для однопролетных стоек постоянной жесткости, нагруженных сжимающей осевой силой, приложенной на конце стойки, коэффициент приведения длины можно определять как величину, обратную числу полуволн:
, где n — число полуволн кривой, по которой выгнется стойка, теряя устойчивость (рис. 16.2).

Рис.16.2
Пределы применимости формулы Эйлера
При выводе формулы Эйлера была использована зависимость
(в виде E Jx v² = Mx), которая в свое время в разделе «Изгиб» была получена на основании закона Гука. Поэтому формула Эйлера применима только в пределах упругой зоны, там где справедлив закон Гука. Значит, критическое напряжение sкр не должно превышать предела пропорциональности sпц.
Чтобы получить выражение для критического напряжения, преобразуем формулу Эйлера, разделив критическую силу Fкр на площадь поперечного сечения стойки А
Ведем обозначения:
— это геометрическая характеристика сечения, называемая минимальным радиусом инерции;
— эта величина называется гибкостью стойки.
При этих обозначениях выражение для критического напряжения принимает вид
,
. (1)
Получили выражение критического напряжения через гибкость стойки l.
Определим предельную гибкость стойки lпц, при которой критическое напряжение равно пределу пропорциональности sпц. Из формулы (1) при sкр = sпц получается
Þ
.
Если гибкость стойки l больше предельного значения lпц, то формула Эйлера применима. Например, для стали, модуль упругости которой Е = 2×105 МПа, а предел пропорциональности sпц @ 200 МПа, предельная гибкость равна . Это означает, что для определения критической силы для стальной стойки формулой Эйлера можно воспользоваться в случае, если гибкость стойки l > 100. Стойки, имеющие гибкость более 200, считаются стойками большой гибкости. Расчет таких стоек производится по специальным формулам. Таким образом, формула Эйлера применима, если гибкость стойки находится в диапазоне
. Для стали этот диапазон равен 100
. Если гибкость стойки меньше предельной гибкости, то для определения критической силы используют формулы из справочника. Эти эмпирические формулы получены путем обработки результатов эксперимента. Реальные стойки, как правило, проектируются таким образом, чтобы их гибкость была меньше предельной гибкости lпц.
Пример.
Определить критическую силу для стойки, изображенной на рис. 16.3.
Дано: модуль упругости Е, предел пропорциональности sпц, длина стойки l, размер поперечного сечения B.
Решение
Для определения критической силы можно воспользоваться формулой Эйлера, которая применима в случае, если гибкость стойки l превышает предельное значение гибкости lпц. Поэтому сначала вычислим гибкость стойки и проверим условие l > lпц.


Рис.16.3
Ч

исло полуволн n, по которым выгнется стойка, теряя устойчивость, равно 2 (смотри рис. 16.3). Значит, коэффициент приведения длины для этой однопролетной стойки равен . Минимальный момент инерции площади поперечного сечения
.
Минимальный радиус инерции .
Гибкость стойки .
Предельная гибкость 
Если выполняется условие l > lпц, то формула Эйлера применима и критическая сила равна . Если гибкость стойки меньше предельного значения, т. е.
l < lпц, то для определения критической силы надо воспользоваться одной из эмпирических формул, приведенных в справочниках.
Лекция 17
Заключительное занятие
Продольный изгиб
При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.
Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.
Рассмотрим известные виды равновесия.
Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.
Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.
При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.
При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.
Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.
Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.
Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.
Критическая сила. Критическое напряжение
Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.
При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.
В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:
где Imin – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ — геометрическая длина стержня, μ – коэффициент приведенной длины или коэффициент приведения (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой закрепления стержней
Критическое напряжение вычисляется следующим образом
, где
гибкость стержня ,
а 
Введем понятие предельной гибкости.
Величина λпред зависит только от вида материала:
Если у стали 3 Е=2∙1011Па, а σпц=200МПа, то предельная гибкость
Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80
Таким образом, для стержней большой гибкости λ≥λпред критическая сила определяется по формуле Эйлера.
В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ0≤λ≤λпр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.
σк=а-bλ, или Fкр= A(a— bλ)
где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.
При значениях гибкости стержня 0≤λ≤λ0 (стержни малой гибкости) потеря устойчивости не наблюдается.
Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.
Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба
Условием устойчивости сжатого стержня является неравенство:
Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:
1) от длины стержня, от размеров и даже от формы поперечных сечений,
2) от способа закрепления концов стержня,
3) от материала стержня.
Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.
Поэтому
Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.
Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:
В этом случае 
где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).
Коэффициент φ<1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ] по прочности, или иначе коэффициентом продольного изгиба.
С учетом сказанного условие устойчивости сжатого стержня принимает вид:
Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня , где:
μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), ℓ — геометрическая длина стержня,
i – радиус инерции поперечного сечения 
Коэффициент φ изменяется в диапазоне 0≤φ≤1, зависит ,как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.
При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.
Значения коэффициента φ в зависимости от гибкости λ для материалов
На основании условия устойчивости решаются три вида задач:
- Проверка устойчивости.
- Подбор сечения.
- Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.
Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:
Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции 
, от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:
1 попытка: задаемся φ1 из средней зоны таблицы, находим 

, по таблице определяем
и сравниваем со значением φ1 . Если
, то:
2 попытка: принимаем 


, по таблице определяем
, и если
, то:
3 попытка: принимаем 


, по таблице определяем
, и т.д.
Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.










