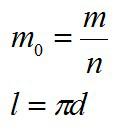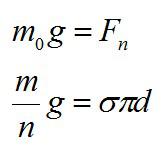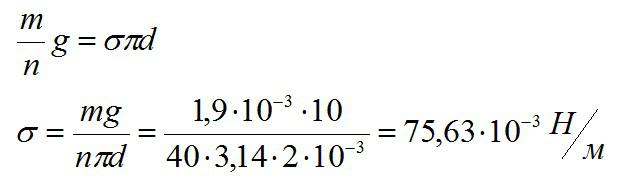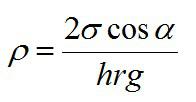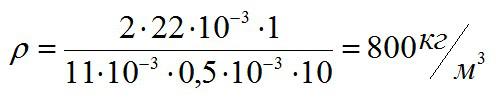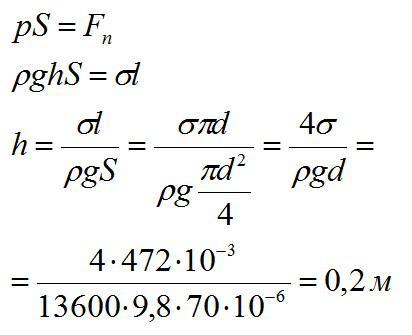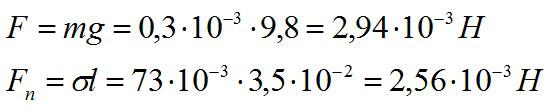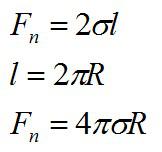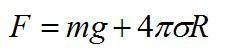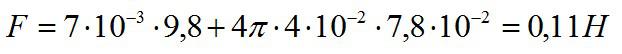Как найти коэффициент поверхностного натяжения мыльного раствора - Avtoru.top

Министерство образования Российской Федерации

МОАУ гимназия № 25

Исследовательская работа:

Всё или почти всё о мыльном пузыре

Работу выполнила ученица10 класса

Трофимова Ольга

Руководитель: учитель физики

Хабарова Ольга Николаевна

Благовещенск 2013 год.

Содержание

Введение

Цель

Задачи

Гипотеза

I Теоретическая часть

1.Коэффициент поверхностного натяжения стр.4

1.1 Поверхностное натяжение стр.4

1.2Коэффициент пропорциональности стр.4

1.3 Проявление поверхностного натяжения стр.4

1.4 Способы определения поверхностного натяжения стр.4

1.5 Использование в производстве стр.5

2. Все или почти все о мыльном пузыре.

2.1 Что являет собой мыльный пузырь стр.5

2.2 Почему мыльный пузырь имеет форму сферы? стр.6

2.3 Интерференция света в мыльной пленке стр.6

II Экспериментальная часть

Методика приготовления мыльных растворов стр.7

Методика определения коэффициента поверхностного натяжения стр.7

1 Опыт № 1Определение коэффициента поверхностного натяжения растворов моющих средств стр.8

2 Опыт № 2Зависимость коэффициента поверхностного натяжения от температуры стр.9

3 Опыт № 3Определение «времени жизни» и размера мыльных пузырей в зависимости от коэффициента поверхностного натяжения стр.12

4 Опыт № 4 Существование мыльного пузыря при низкой

температуре стр.12

III Заключение стр.13

IV Литература

Введение

Почему мы выбрали эту тему?

Тема мыльных пузырей раскрывает перед исследователем огромный спектр возможных работ и опытов с точки зрения физики. Изучение многих из свойств пузырей является наглядным пособием для описания таких явлений, как интерференция, поверхностное натяжение и многие другие.

Пусть тема и кажется на первый взгляд не актуальной и не имеющей применения в современной жизни, мы смело можем возразить на это, сказав,что, во-первых — саморазвитие никогда не потеряет своей актуальности в глазах юных исследователей, а во-вторых — данная тема является по истине интересной и увлекательной, тем самым упрощая для нашего понимания сложные законы физики.К тому же на сегодняшний день шоу мыльных пузырей являются востребованными среди людей из разных возрастных категорий.Эта забава известна с давних времён и привлекает как детей, так и взрослых. Например, при раскопках известного города Помпеи были найдены фрески с изображением детей, выдувающих мыльные пузыри.Раствор для мыльных пузырей можно купить в магазине или приготовить самостоятельно. Еще в детстве мы не раз пытались приготовить такой раствор, тратя кучу шампуней, порошков и других моющих средств, способных пениться. Но не всегда результат нас радовал: зачастую пузыри получались невзрачными, маленькими и совсем недолговечными.Собственно говоря, эти воспоминания и подтолкнули нас на то, чтоб сделать это темой исследовательской работы. Её целью стало исследование физических свойств жидкости и выявление оптимальной комбинации её составляющих для мыльных пузырей. По ходу исследования мы будем раскрывать ранее известные нам физические законы экспериментальным путем, фиксируя каждое новое открытие и постепенно приближаясь к ответу на главный ,интересующий нас и многих других детей и взрослых, вопрос.

Не только мы сочли данную тему интересной для рассмотрения.

Более ста лет тому назад Чарльз Бойс опубликовал фундаментальный труд «Мыльные пузыри», который по сей день остается настольным пособием для физиков-теоретиков и экспериментаторов. Поэтому целью нашей работы является:

«Исследование коэффициента поверхностного натяжения посредством рассмотрения свойств мыльных пузырей»

Для этого мы должны решить следующие задачи:

Изучить литературу по теме исследования
Экспериментальным путем определить коэффициент поверхностного натяжения для различных растворов моющих средств
Экспериментальным путем исследовать зависимость коэффициента поверхностного натяжения от температуры
Экспериментально определить «время жизни» и размер мыльных пузырей в зависимости от коэффициента поверхностного натяжения
Определить, может ли мыльный пузырь существовать при минусовой температуре

ГИПОТЕЗА:

Предположим, что размеры и «время жизни» мыльного пузыря зависят от коэффициента поверхностного натяжения мыльных растворов.

«Выдуйте мыльный пузырь и смотрите на него: вы можете заниматься всю жизнь его изучением, не переставая извлекать из него уроки физики.»

Л.Кельвин

I Теоретическая часть.

1Поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости. Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Иначе говоря, на границу, где свободная поверхность жидкости граничит с твердым телом (со стенкой сосуда, например) или другой жидкостью, действует сила поверхностного натяжения.Причина её возникновения та же, что и при возникновении поверхностной «пленки» жидкости — притяжение внутренних молекул.С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена ЛорандомЭтвёшом, так называемое правило Этвёша (англ.). В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правилоЭтвёша.[1]

1.2 Коэффициент пропорциональности — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.[1]

1.3 Проявление.Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ».

Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности: в невесомости капля принимает сферическую форму, струя воды «слипается» в цилиндр. Некоторые насекомые способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения. На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.[7]

1.4 Способы определения поверхностного натяжения делятся на статические и динамические.

Статические методы:

Метод поднятия в капилляре
Метод Вильгельми
Метод лежачей капли
Метод определения по форме висячей капли.
Метод вращающейся капли

Динамические методы:

Метод дюНуи (метод отрыва кольца).
Сталагмометрический, или метод счета капель.
Метод максимального давления пузырька.
Метод осциллирующей струи
Метод стоячих волн
Метод бегущих волн[2]
1.5 Использование в производстве.

Как извлечь из массы добытой горной породы рассеянные в ней мелкие зернышки «вкрапленной» руды? Это было труднейшей задачей горных техников, вставшей перед ними в конце прошлого века. Истощались богатые жильные залежи медных, свинцовых и цинковых руд. Все большее внимание привлекали к себе бедные «вкрапленные» руды. В них заключались огромные запасы металла. Некоторые же «редкие» металлы, как, например, ванадий, цирконий, ниобий и другие, вовсе не образовали крупных скоплений. Их можно добыть только из месторождений «вкрапленных» руд. Случай помог открыть замечательный способ механически извлекать из массы «пустой» горной породы мельчайшие зернышки руд. Рассказывают, будто шахтеры заметили, что при стирке их одежды с мыльной пеной выносилась рудная пыль. Песчинки же пустой руды осаждались на дно корыта. Это наблюдение и навело на мысль, как можно «обогащать» руду, то есть извлекать ее зернышки из рудоносной горной породы. Добытую горную породу дробят и размалывают в мелкий порошок. При этом рудные зернышки освобождаются из горной породы, превращающейся в песок. Смесь рудных зерен с песком разбалтывают в ящике с водой, к которой примешивают сосновое масло и другие вещества, называемые «реагентами». При взбалтывании воды лопастями, вращающимися в ящике флотационного аппарата, или вдувании под давлением воздуха образуется обильная пена, поднимающаяся на поверхность. Вместе с пеной увлекаются рудные зернышки и пылинки, а песок пустой породы опускается на дно ящика. Пену собирают, высушивают и получают рудный «концентрат» с большим процентным содержанием металла. Песок же уносится из ящика водой в реку. Для извлечения большей части рудных зерен нужна очень обильная пена из устойчивых пузырьков. Воздушные пузырьки в чистой воде не могли бы вынести рудные зернышки на ее поверхность, потому что они быстро лопаются. Чтобы получить устойчивую пену, и прибавляются в воду реагенты. Кроме того, эти вещества обволакивают рудные зерна, делая их поверхность несмачиваемой водой. Рудные зерна прилипают к пузырькам и поднимаются с ними, как воздухоплаватели на воздушных шарах за счет поверхностного натяжения.

Итак, изучив понятие «поверхностное натяжения» мы пришли к выводу, что наиболее подходящим объектом для наглядногорассмотрения его свойств является мыльный пузырь[7]}

Что являет собой мыльный пузырь?

2.1 Мыльный пузырь — тонкая плёнка мыльной воды, которая формирует сферу с переливчатой поверхностью. Мыльные пузыри обычно недолговечны, существуют лишь несколько секунд и лопаются при прикосновении или самопроизвольно.[1]

Почему мыльный пузырь имеет форму сферы?

За счет поверхностного натяжения.Поверхность любой жидкости имеет некоторое поверхностное натяжение. Именно оно делает поведение поверхности жидкости похожим на поведение эластичной (например, резиновой) плёнки. Иными словами, поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости. Сила поверхностного натяжения определяется по формуле:

F= 2σπR,

где σ — коэффициент поверхностного натяжения.

Однако, пузырь, сделанный только из воды, нестабилен и быстро лопается. Для того, чтобы стабилизировать его состояние, в воде растворяют какие-нибудь поверхностно-активные вещества, например, мыло. Оно уменьшает поверхностное натяжение чистой воды.

Следовательно, больший мыльный пузырь будет выдуваться из раствора, чей коэффициент поверхностного натяжения будет являться наименьшим.

Силы натяжения формируют сферу потому, что сфера имеет наименьшую площадь поверхности при данном объёме. Из-за того-же натяжения мыльный пузырь всегда стремится минимизировать свою площадь поверхности. Таким образом, оптимальная форма отдельного мыльного пузыря — это сфера.Эта форма может быть существенно искажена потоками воздуха и самим процессом надувания пузыря. Однако,если оставить пузырь плавать в воздухе, его форма очень скоро станет близкой к сферической.[4]

Интерференция света в мыльной пленке

Переливчатые «радужные» цвета мыльных пузырей получаются за счёт интерференции световых волн.Интерференция присуща волнам любой природы. В свою очередь интерференцией света называют сложение двух световых когерентных волн, вследствие которого можно наблюдать усиление или ослабление световых колебаний в различных точках пространства.В физике когерентностью называется согласованность нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.Когерентность волны означает, что в различных точках волны разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем.Данная тема изучается лишь в 11 классе, но мы решили углубиться в этот материал и включить его в свою работу, т.к. интерференция света является одним из важнейших свойств мыльной пленки.[2]

IIЭкспериментальная часть

Для того, чтобы провести экспериментальную часть нашей исследовательской работы, нам нужно было для начала приготовить разныемыльные растворы для исследования зависимости коэффициента поверхностного натяжения от состава растворов.

Методика приготовления мыльных растворов:

Для исследования используется три вида растворов:

1.С добавлением шампуня

2.С добавлением средства для мытья посуды

3.С добавлением хозяйственного мыла.

В состав раствора входят:

Дистиллированная вода (20 градусов по Цельсию) (600 мл)

Глицерин (100 мл)

Один из трех вышеуказанных компонентов (150 мл)

(Приложение № 1)

Методика определения коэффициента поверхностного натяжения:

К ёмкости с мыльным раствором мы прикрепили капельницу. Сделали мы это для того, чтоб получить необходимые данные для определения коэффициента поверхностного натяжения.

Метод счета капель считается самым простым способом измерения поверхностного. В основе расчетов лежит закон, согласно которому вес капли, отрывающейся от пипетки, пропорционален поверхностному натяжению жидкости ( σ ) и радиусу пипетки (R) , т.е.

m=2πRσ /g , где

g — ускорение свободного падения;

m — масса капли исследуемой жидкости.

Процесс измерений прост и состоит их двух этапов. На первом этапе определяется радиус пипетки (сталагмометра). Величина радиуса вычисляется по результатам измерения весакапли. Для измерения радиуса не используются какие-либо дополнительные измерительные инструменты, такие как микрометр, поскольку величина радиуса в формуле лишь приближенно отражает действительные размеры используемой пипетки.

Второй этап состоит в том, что из пипетки выдавливается несколько капель (в моем случае 40 капель) исследуемой жидкости в посуду для взвешивания. Первая капля не должна попасть в число взвешиваемых. Далее взвешиванием на весах определяется общий вес капель.

Важным является процесс формирования отдельной капли. Формировать каплю быстро недопустимо, так как результат последующего измерения будет недостоверен из-за того, что сила инерции поступающей жидкости оторвет каплю раньше времени. Медленно же формировать каплю не рационально. Обычно поступают следующим образом: каплю формируют быстро, но на последней стадии формирования (до ее отрыва от пипетки) замедляют процесс. Капля должна оторваться при очень медленном поступлении жидкости.[7]

Опыт 1

Определение коэффициента поверхностного натяжения растворов моющих средств.

Цель: Экспериментально доказать,что коэффициент поверхностного натяжения от состава раствора (метод сталагмометрический)

Оборудование: Растворы моющих средств(средство для мытья посуды,шампунь,хоз.мыло), приготовленные по специальной методике, химические стаканы по 50 мл, капельница, весы, разновесы, штангенциркуль, штатив.

Для того, чтобы начать эксперимент, необходимо приготовить мыльные растворы. Изучив статьи из сети «Интернет» и проанализировав комментарии, оставленные интернет-пользователями, мы разработали собственную методику, которую и применяли для всех экспериментальных работ далее.

Порядок выполнения опыта:

Приготовить растворы моющих средств по методике(при температуре 20 градусов по Цельсию);
Собрать установку,состоящую из ёмкости сраствором моющего средства и капельницы;
Отрегулировать капельницу;
Измерить массу химического стакана;
Определить массу 40 капель раствора;
Рассчитать массу одной капли по формуле:
Рассчитать коэффициент поверхностного натяжения по формуле F = g 2σπR = gσ = , где D = 2R – диаметр капельницы.
Результаты измерений занести в таблицу:
Фотоотчет по опыту (Приложение № 2)

Таблица № 1

№	Название раствора	Масса хим. стакана	Масса стакана с раствором	Диаметр капель ницы	Масса раствора	Масса одной капли	σ н/м
1	Pantine	30,3*	31,5*	2*	1,23*	0,0308*	49*
2	AOS	30,3*	31,66*	2*	1,36*	0,0339*	54*
3	Мыло	30,3*	31,4*	2*	1,108*	0,0276*	44*

Данные мы занесли в таблицу и по ранее упомянутой формуле вычислили коэффициент поверхностного натяжения для каждой из исследуемых жидкостей.

Вывод:У раствора № 2 коэффициент поверхностного натяжения наибольший, а у № 3 – наименьший. Это связанно с вязкостью растворов. Таким образом, мы выяснили, что у раствора из хозяйственного мыла наибольшая вязкость.

Опыт 2

Зависимость коэффициента поверхностного натяжения от температуры.

Цель:Убедиться в том,что коэффициент поверхностного натяжения растворов зависит от температуры.

Оборудование: термометр, растворы моющих средств, приготовленные по специальной методике, установка для счета капель, весы, разновесы, спиртовка.

Порядок выполнения работы:

Приготовить раствор моющих средств с использованием воды разной температуры (200 С , 400 С, 600 С);
Используя метод отрыва капель вычислить массу капель;
По ранее упомянутой схеме вычислить коэффициент поверхностного натяжения каждого раствора;
Результаты занести в таблицу:

Таблица № 2:

№	Растворс добавлением:		Масса 40 капель	Масса одной капли кг.	Диаметр м	σ н/м
1	Pantеne	20			2*
		40
		60
2	AOS	20		339*
		40
		60	1,29*
3	Мыло хозяйственное	20	1,105*
		40
		60

Используя метод отрыва капель, описанный в предыдущем опыте, мы рассчитали коэффициенты поверхностного натяжения все тех-же мыльных растворов, но на этот раз при разных температурах. Для нагревания растворов до нужной температуры мы использовали спиртовку.

Вывод: С увеличением температуры раствора коэффициент поверхностного натяжения уменьшается, так как изменяется вязкость растворов.

Опыт 3

Определение «времени жизни» и размера мыльных пузырей в зависимости от коэффициента поверхностного натяжения

Цель: Убедиться в том, что размеры мыльных пузырей зависят от состава раствора

Оборудование: химические стаканы, растворы, соломинки.

Порядок выполнения опыта:

Выдуть мыльный пузырь из растворов 1, 2, 3(Приложение № 3);
Сравнить размеры и время жизни мыльных пузырей;
Сопоставить результаты данного эксперимента с результатами экспериментов, проведенных ранее

Таблица № 3

Раствор с добавлением:	Диаметр мыльного пузыря (см)	«Время жизни» мыльного пузыря (с)
Pantene	7	32
AOS	10	38
Хозяйственное мыло	25	45

Вывод: Из раствора №3 выдуваются пузыри большего диаметра и «время жизни» пузырей из него наибольшее. Это связанно с вязкостью раствора.

Опыт 4

Существование мыльного пузыря при низкой температуре.

Цель: убедиться в том, что мыльный пузырь может существовать при низкой температуре.

Оборудование: раствор № 3(с добавлением хозяйственного мыла), трубка.

Заинтересовавшись поведением мыльного пузыря в условиях минусовой температуры, мы решили провести эксперимент. В предлагающейся с данной исследовательской работой презентациимы разместили видео с этимопытом.Для этого эксперимента мы использовали раствор под номером 3 (приготовлен из хозяйственного мыла), так как из ранее проведенных опытов выяснили, что он более остальных подходит для выдувания пузырей.

Зафиксировав температуру на улице ( —С ), мы выдули несколько пузырей и дождались начала и окончания процесса кристаллизации поверхности мыльного пузыря.Процесс этот довольно увлекателен, так как по мере замерзания на пузыре образуются красивейшие ледяные рисунки.Немного отступив от темы, уместным будет упомянуть следующий факт:когда облако образуется при очень низкой температуре, вместо дождевых капель пары воды сгущаются в крошечные иголочки льда; иголочки слипаются вместе, и на землю падает снег. Хлопья снега состоят из маленьких кристалликов, расположенных в форме звездочек удивительной правильности и разнообразия. Каждая звездочка делится на три, на шесть, на двенадцать частей, симметрично расположенных вокруг одной оси или точки. А для того, чтоб это пронаблюдать стоит лишь в сильный мороз выйти из дома и выдуть мыльный пузырь. Тотчас же в тонкой плёнке воды появятся ледяные иголочки; они будут на глазах собираться в чудесные снежные узоры.Сопоставив свои наблюдения с изученной литературой, мы выяснили:Если надуть пузырь при температуре −15 °C, то он замёрзнет при соприкосновении с поверхностью. Воздух, находящийся внутри пузыря, будет постепенно просачиваться наружу и в конце концов пузырь разрушится под действием собственного веса.При температуре −25 °C пузыри замерзают в воздухе и могут разбиться при ударе о землю. Если при такой температуре надуть пузырь тёплым воздухом, то он замёрзнет почти в идеальной сферической форме, но по мере того, как воздух будет охлаждаться и уменьшаться в объёме, пузырь может частично разрушиться, и его форма будет искажена. Пузыри, надутые при такой температуре, всегда будут небольшими, так как они будут быстро замерзать, и если продолжать их надувать — они лопнут.

Вывод: При низкой температуре мыльный пузырь покрывается тончайшей ледяной корочкой и разбивается, падая на землю.

Заключение

Изучив литературу и проделав опыты, мы убедились в том, что

Коэффициент поверхностного натяжения действительно зависит от состава раствора.

Размер и «время жизни» мыльного пузыря определяет коэффициент его поверхностного натяжения, который, в свою очередь, напрямую связан с температурой мыльного раствора.
Более вязкий раствор имеет меньший коэффициент поверхностного натяжения и мыльный пузырь, выдутый из этого раствора, имеет большее «время жизни» и больший диаметр.
Мыльный пузырь способен выдерживать низкие температуры, при этом он замерзает. На его поверхности начинается процесс кристаллизации, превращающий его в ледяную сферу.

Таким образом, мы подтвердили свою гипотезу о том, что размер и «время жизни» мыльного пузыря зависят от коэффициента поверхностного натяжения.

Изучив результаты данной исследовательской работы, каждый желающий может самостоятельно организовать шоу мыльных пузырей, которые в настоящее время пользуются большой популярностью. Так же это работой вполне могут воспользоваться преподаватели школ и других образовательных учреждений с целью наглядно показать и описать многие из физических свойств, так как физические законы, представленные напримере мыльных пузырей, по моему мнению, гораздо более доступны для восприятия, чем научные формулировки.

Литература

http://ru.wikipedia.org/wiki/%D0%9C%D1%8B%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BF%D1%83%D0%B7%D1%8B%D1%80%D1%8C
http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D0%BD%D0%BE%D0%B5_%D0%BD%D0%B0%D1%82%D1%8F%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5
http://bubble-show.ru/ru/milnie_puziri/
http://afizika.ru/svojstvazhidkostejgazov/103-milniepuziri
http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D1%80%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D1%8F
http://www.stroitelstvo-new.ru/tehnika/zagadka-flotacii.shtml
журнал «Квант»

Приложение № 1

Приложение № 2

Приложение № 3

Источник

Сегодня поверхностно рассматриваем тему поверхностного натяжения и решаем соответствующие задачи по физике.

Даже если вы не большой любитель жидкости, подписывайтесь на наш телеграм-канал, это интересно и полезно для всех.

Поверхностное натяжение, задачи

Задача №1. Поверхностное натяжение

Условие

Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия d=2 мм. Оказалось, что n=40 капель имеют массу m=1,9 г. Каким по этим данным получится коэффициент поверхностного натяжения «сигма»?

Решение

На каплю действует сила тяжести и сила поверхностного натяжения. Эти силы уравновешивают друг друга. Из условия задачи можно найти массу одной капли m0 и длину ее окружности l:

Далее запишем условие равновесия капли:

Отсюда находим коэффициент поверхностного натяжения:

Ответ: 75,63*10^-3 Н/м.

Задача №2. Капиллярные явления

Условие

В капиллярной трубке радиусом 0,5 мм жидкость поднялась на высоту 11 мм. Оценить плотность данной жидкости, если ее коэффициент поверхностного натяжения равен 22 мН/м.

Решение

Для капилляра существует формула:

Альфа в этой формуле – угол смачивания стенки капилляра жидкостью. Пример его равным 90 градусов.

Ответ: 800 килограмм на кубический метр.

Задача №3. Поверхностное натяжение

Условие

В дне сосуда со ртутью имеется круглое отверстие диаметром 70 мкм. При какой максимальной высоте слоя ртути H она не будет вытекать через отверстие?

Решение

Ртуть не будет вытекать до тех пор, пока сила ее давления не превысит силу поверхностного натяжения:

Значения коэффициента поверхностного натяжения разных жидкостей берутся в справочнике.

Ответ: 0,2 м.

Задача №4. Поверхностное натяжение

Условие

Швейная игла имеет длину 3,5 см и массу 0,3 г. Будет ли игла лежать на поверхности воды, если ее положить аккуратно?

Решение

Найдем силу тяжести, которая действует на иглу и сравним ее с силой поверхностного натяжения.

Ответ: Так как сила тяжести больше, игла утонет.

Задача №5. Поверхностное натяжение

Условие

Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г.

Решение

На кольцо действуют силы поверхностного натяжения, сила тяжести и внешняя сила, стремящаяся оторвать кольцо от поверхности. Найдем силу поверхностного натяжения:

Множитель «2» используется в формуле, так как кольцо взаимодействует с жидкостью двумя своими сторонами.

Теперь запишем условие отрыва кольца:

Значение поверхностного натяжения мыльного раствора при комнатной температуре возьмем из таблицы, подставим числа, и получим:

Ответ: 0,11 Н.

Вопросы на тему «Поверхностное натяжение и свойства жидкостей»

Вопрос 1. Что такое жидкость?

Ответ. Жидкость – физическое тело, которое не может самостоятельно сохранять свою форму. Агрегатное состояние вещества между твердым телом и газом.

Вопрос 2. Какие свойства жидкости вы знаете?

Ответ. Среди основных свойств жидкости можно выделить:

текучесть;
вязкость;
сохранение объема;
поверхностное натяжение.

Вопрос 3. Что такое поверхностное натяжение?

Ответ. Поверхностное натяжение – это явление, при котором жидкость стремиться приобрести форму с наименьшей возможной площадью поверхности.

Примеры поверхностного натяжения в природе:

Именно благодаря поверхностному натяжению в поле силы тяжести Земли жидкость приобретает форму капли.
В отсутствие силы тяжести жидкости капля примет шарообразную форму.
Водомерка удерживается на поверхности воды благодаря силе поверхностного натяжения.

Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью S при постоянной температуре.

Вопрос 4. Что такое капиллярные явления?

Ответ. Капиллярные явления – подъем или опускание жидкости в капиллярах (трубках малого диаметра).

Вопрос 5. Что называется смачиванием?

Ответ. Смачивание – это искривление поверхности жидкости вблизи твердого тела. Возникает из-за взаимодействия молекул жидкости с молекулами твердого тела.

Количественная характеристика этого явления – угол смачивания.

Нужна помощь в решении заданий по учебе? Профессиональный студенческий сервис всегда готов ее оказать! Оформляйте заявку в любое время суток и забудьте о наболевших вопросах.

Источник

ОБЛАСТНАЯ
НАУЧНАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ

Секция:
ФИЗИКА

Измерение
и исследование поверхностного натяжения

Автор: Морунов Никита

учащийся
11 класса

ГБОУ
СОШ №14

Научный
руководитель: Белоглазова Алёна Сергеевна

учитель
физики

Жигулёвск,
2012 г.

Содержание

Введение
3

Глава
1 Поверхностное натяжение 4

1.1        Определение
поверхностного натяжения                                                   4

1.2
Способы
определения
11

1.2.1Сталагмометрический
метод 12

1.2.2 Метод измерения
капиллярного поднятия жидкости 16

1.2.3
Метод вращающейся капли 18

1.2.4
Метод Дю Нуи (метод отрыва кольца) 18

1.2.5
Метод бегущих волн 18

1.3
Теоретическая формула поверхностного
натяжения 19

1.4 Объединение
пузырей 19

1.5
Интерференция и отражения 20

1.6
Изменение цвета пузыря со временем 21

1.7
Математические свойства 22

Глава
2 Экспериментальная
часть 23

Эксперимент №1 «Определение поверхностного натяжения жидкости» 23

Эксперимент №2 «Расчёт толщины плёнки мыльного пузыря и экспериментальная проверка
расчетов» 24

Эксперимент
№3 «Выяснение влияния мыла на поверхностное натяжение воды» 24

Эксперимент №4 «Лопание мыльных пузырей» 25

Заключение
27

Литература
28

Введение

Такие силы, как тяготение, упругость и трение,
бросаются в глаза; мы ощущаем их непосредственно каждый день. Но в окружающем
нас мире повседневных явлений действует еще одна сила, на которую мы обычно не
обращаем никакого внимания. Сила эта сравнительно невелика, ее действия никогда
не вызывают мощных эффектов. Тем не менее мы не можем налить воды в стакан,
вообще ничего не можем проделать с какой-либо жидкостью без того, чтобы не
привести в действие силы, о которых у нас сейчас пойдет речь. Это силы
поверхностного натяжения.

Сила поверхностного натяжения – это сила,
обусловленная взаимным притяжением молекул жидкости, направленная по
касательной к ее поверхности.

Действие сил поверхностного натяжения приводит к тому,
что жидкость в равновесии имеет минимально возможную площадь поверхности. При
контакте жидкости с другими телами жидкость имеет поверхность, соответствующую
минимуму ее поверхностной энергии.

Понятие «поверхностное натяжение» впервые ввел Я.
Сегнер (1752 год).

К вызываемым поверхностным натяжением эффектам мы
настолько привыкли, что не замечаем их, если не развлекаемся пусканием мыльных
пузырей. Однако в природе и нашей жизни они играют немалую роль.

Цель
работы: измерить и исследовать поверхностное
натяжение мыльных растворов.

Задачи:
1) разобрать и описать методику
измерения коэффициента поверхностного натяжения жидкостей, дав достаточно
подробное теоретическое обоснование методики измерения;

2)
провести достаточно подробную обработку результатов измерений с указанием
погрешностей;

3)
исследовать характер изменения толщины плёнки;

В
работе использовались следующие методы и приемы:
1) работа с источниками информации (Интернет-ресурсы,
литература);                                               2)
эксперимент;
3) сравнительный анализ полученных данных

ГЛАВА
1 Поверхностное натяжение

1.1 Определение
поверхностного натяжения

Поверхностное натяжение имеет двойной физический смысл —
энергетический (термодинамический) и силовой (механический). Оба эти понятия
может пояснить простой опыт (рис. 4.1). На проволочной рамке EDCF помещается подвижная перекладина АВ длиной l, легко скользящая по рамке.
Между перекладиной и верхней стороной рамки DC находится тонкая пленка
жидкости, например, мыльного раствора (мыло обеспечивает стабильность пленки).
Приложим к подвижной перекладине AB направленную вниз силу f, ее создает груз G. Под действием силы f перекладина АВ переместитcя на малое расстояние dx и займет положение А’В’. Сила
f произведет
при этом работу dW=fdx; если процесс происходит при постоянной температуре
(изотермически), то эта работа затрачивается только на увеличение поверхности
пленки. Прирост площади составит dΩ = 2/dx; коэффициент 2 учитывает, что пленка имеет две стороны. Таким
образом, на увеличение единицы площади пленки затрачивается работа (о, Дж/м²)

(1.1)

Из
уравнения (1.1) следует энергетическое (термодинамическое) определение:
поверхностное натяжение — это удельная работа увеличения поверхности
при ее растяжении при условии постоянства температуры.

При
выполнении этого условия работа а, затраченная на обрабатывание единицы новой
поверхности, полностью переходит в свободную энергию поверхности, также
рассчитанную на единицу поверхности. При условии постоянства объема пленки
новая поверхность создается благодаря переходу некоторой массы жидкости из ее
внутреннего объема на поверхность. Поэтому используют еще одно определение
поверхностного натяжения, как термодинамическою параметра поверхности жидкости:
поверхностное натяжение равно избыточной удельной свободной энергии (энергии
Гельмгольца) единицы площади поверхности жидкости при определенной температуре.
Термин «избыточность» подчеркивает, что энергия Гельмгольца молекул,
находящихся на поверхности жидкости больше, чем молекул в ее внутреннем объеме.
Это различие играет важнейшую роль в термодинамике поверхностных явлений.

Рассмотренный
выше опыт выявляет еще один физический смысл поверхностного натяжения.
Определим условия силового механического равновесия перекладины АВ при
приложении к ней силы f . Такое равновесие может обеспечить сила, направленная
в противоположную сторону. Обозначим эту силу (в расчете на единицу длины
перекладины АВ) σ [Н/м]. Равновесию отвечает условие

(1.2)

коэффициент
2 учитывает, что пленка мыльного раствора на рамке имеет две стороны.

Уравнение
(1.2) представляет силовое (механическое) определение: поверхностное натяжение
— это сила, действующая на единицу длины линии, которая ограничивает
поверхность жидкости.

Температура. Для всех индивидуальных (однокомпонентных) жидкостей
поверхностное натяжение на границе с газовой фазой уменьшается при повышении
температуры (Т), т.е. выполняется соотношение.

Для растворов (особенно растворов поверхностно-активных веществ)
температурная зависимость поверхностного натяжения носит более сложный
характер. Экстраполяция линейной зависимости σ =f(T) вплоть до σ = 0 определяет
(по Д. И. Менделееву) критическую температуру (Тс) данного вещества. При этой
температуре двухфазная система жидкость—пар перестает существовать и становится
однофазной, т.е. при Т > Тс поверхность раздела фаз исчезает.

При
линейном характере зависимости σ =f(T) производная a = dσ/dT для данного
вещества имеет постоянное значение, ее называют температурным коэффициентом
поверхностного натяжения жидкости.

Для
многих веществ температурные коэффициенты поверхностного натяжения составляют
примерно от -0,1 до -0,2 мДж/(м2- К).

Для
описания температурной зависимости поверхностного натяжения предложено
несколько эмпирических уравнений. Одно из них — уравнение Ван-дер-Ваальса:

где σ0 — поверхностное натяжение данной жидкости вблизи температуры плавления.

Асимметрия сил взаимодействия молекул переходного слоя
с окружающими их (в пределах объёма молекулярного действия) молекулами
приводит, как известно, к представлению о наличии тангенциальных и нормальных
относительно поверхности раздела фаз сил, действующих на молекулы переходного
слоя. Это – силы поверхностного межфазового натяжения и молекулярного давления.

Обе эти категории сил, действующих на молекулы,
которые находятся на различных расстояниях от поверхности раздела фаз, не
одинаковы по величине: они монотонно убывают в обоих направлениях по нормали к
нормали раздела фаз.

В этом легко разобраться, рассмотрев прохождение молекулы m
через поверхность раздела фаз MN(рис. 2.). Пусть, например, перемещение
молекулы происходит через границу раздела между жидкостью и её насыщенным паром
с расстояния r радиуса молекулярного действия внутри жидкой фазы на то же расстояние в
газообразной фазе.

Молекула переходного слоя, находящаяся на произвольном
расстоянии c от фазовой границы (рис. 1), взаимодействует со всеми молекулами,
находящимися в пределах шарового объёма её молекулярного действия.
Результирующая этого взаимодействия равна, однако, разности суммарных
взаимодействий молекулы m с молекулами, находящимися в шаровых сегментах EFG и
CHD, так как взаимодействия с молекулами в шаровых поясах ACDB и ABFE
уравновешиваются. Если пренебречь притяжением молекул газа, то
некомпенсированным остаётся лишь притяжение молекул, заполняющих сегмент EFG.
Величину этого притяжения следует считать пропорциональной числу молекул,
находящихся в объёме w сегмента, а при постоянной их плотности внутри сегмента –
объёму w.

При перемещении молекулы через фазовую границу на
расстоянии 2r объём w возрастает от нуля до , а затем вновь убывает
до нуля. Пропорционально этому объёму изменяется и величина силы, действующих
на молекулу m. Отсюда можно сделать заключение, что чем ближе молекула жидкости
находится к поверхности фазы, тем больше при тепловых соударениях вероятность
её выхода в газовую фазу (испарения), и чем ближе молекула пара к фазовой
границе, тем

больше вероятность её захвата жидкой
фазой (конденсации).

Таким образом, во время перехода молекулы через
фазовую границу равнодействующая молекулярных сил изменяется пропорционально
объёму шарового сегмента

, (2)

где h – высота сегмента. На рис. 3 приведена
зависимость w=j(h); геометрический смысл она имеет в пределах значений h от нуля до 2r. На рис. 6 представлено
изменение величины силы, действующей на молекулу при прохождении ею фазовой
границы; за начало отчётов принята плоскость ОВ (рис. 1), положение молекулы
определяется координатой z. Из рисунка видно, что кривая имеет максимум,
соответствующей нахождению молекулы на границе фаз. Зависимость f=y(z) в равной мере относится
как к поверхностному натяжению, так и к молекулярному давлению. Таким образом, s=y(z) и p_m=y(z).

До сих пор мы говорили об
элементарных силах, действующих на отдельные молекулы. Однако величину
поверхностного натяжения s, как известно, принято относить к единице длины
контура, а молекулярное давление – к единице площади на поверхности фазы. В
связи с наличием зависимости s=y(z), строго говоря, величину поверхностного натяжения
(численно равную работе образования элемента поверхности) следует относить к
элементарному моноатомному слою поверхностного слоя фазы, находящемуся на
определённом расстоянии z от поверхности отсчёта. Обычно поверхностное
натяжение относят к самому поверхностному слою фазы (z=r), где оно имеет максимальное
значение. Учитывая указанные соотношения, можно было бы говорить о «среднем»
значении поверхностного натяжения переходного слоя фазы, что соответствовало бы
понятию «линейного напряжения переходного слоя».

Что касается молекулярного давления, то ввиду наличия
зависимости p_m=y(z) его величину также следует представлять себе как
результат суммирования элементарных сил по толщине r от переходного слоя.

До последнего времени не было найдено метода измерения
молекулярного давления. Решение этой задачи встречает большие трудности,

так как молекулярное давление по его
происхождению связано с взаимодействиями молекул переходного слоя чрезвычайно
малой толщины (~10^{-7 см) по всей поверхности фазы. Молекулярное

давление доступно, однако, вычислению:}

, (3)

где p_BH – внешнее давление, I –
механический эквивалент, С_р и С_u — молярные теплоёмкости при
постоянном давлении и объёме, g — термический коэффициент объёма u. Величина p_m
может быть также вычислена на основании уравнения Ван-дер-Ваальса, если
известны его константы.

Изменение молекулярного давления для жидкостей и
твёрдых тел охватывает три порядка: 10^-3¸10^-5 атм.
Индивидуальные вариации величины p_m являются прямым следствием
индивидуальных различий атомных и молекулярных структур вещества. Поэтому
молекулярное давление может служить надёжным критерием интенсивности
молекулярного взаимодействия.

Если известна зависимость f=y(z), то можно подсчитать
работу выхода молекулы на поверхность фазы. Максимальная работа выхода:

. (4)

Таким образом, увеличение поверхности связано с
затратой работы; при сжатии поверхность сама совершает работу. Из этих
термодинамических предпосылок и вытекает представление о поверхностном
натяжении как тангенциальных силах, совершающих работу при изменении величины
поверхности. Для фазовых поверхностей, имеющих кривизну, ещё Лапласом было
введено представление о капиллярном дополнительном давлении р как
тангенциальных силах, действующих на поверхностный слой фазы таким образом, что
их результирующая направлена к центрам кривизны поверхности:

. (5)

1.2
Способы определения

Способы
определения поверхностного натяжения делятся на статические и динамические. В
статических методах поверхностное натяжение определяется у сформировавшейся
поверхности, находящейся в равновесии.

Динамические
методы связаны с разрушением поверхностного слоя. В случае измерения
поверхностного натяжения растворов (особенно полимеров или ПАВ) следует
пользоваться статическими методами. В ряде случаев

равновесие
на поверхности может наступать в течение нескольких часов (например, в случае
концентрированных растворов полимеров с высокой вязкостью). Динамические методы
могут быть применены для определения равновесного поверхностного натяжения и
динамического поверхностного натяжения. Например, для раствора мыла после перемешивания
поверхностное натяжение 58 мДж/м², а после отстаивания — 35 мДж/м² . То есть
поверхностное натяжение меняется. До установления равновесного оно будет
динамическое.

Статические
методы:

Метод
поднятия в капилляре

Метод
Вильгельми

Метод
лежачей капли

Метод
определения по форме висячей капли.

Метод
вращающейся капли

Динамические
методы:

Метод
дю Нуи (метод отрыва кольца).

Сталагмометрический,
или метод счета капель.

Метод
максимального давления пузырька.

Метод
осциллирующей струи

Метод
стоячих волн

Метод
бегущих волн

1.2.1Сталагмометрический метод

Сталагмометрический метод основан на измерении массы
капель Р, образующихся при вытекании жидкости
из вертикальной трубки с радиусом выходного отверстия r. Расчет проводят по
формуле

где f (r/a) – некоторая функция, определяемая из
таблиц Гаркинса и Брауна; а – капиллярная постоянная.

Если жидкости хорошо смачивают материал капилляра,
то, пренебрегая различием между углами смачивания,
можно проводить относительное измерение поверхностного
натяжения, используя стандартную жидкость.
В этом случае обычно принимают, что масса капли Р

в
момент отрыва пропорциональна поверхностному
натяжению на границе раздела
жидкость–пар, т.е.

Р = ks ,

где k – постоянная данного
прибора.

Массу одной капли определяют,
подсчитывая число капель (n), вытекающих из сталагмометра объемом V:

При калибровке сталагмометра стандартной жидкостью , поэтому

Рис.1.4.Схема автоматизированного сталагмометра

Таким образом, зная плотность жидкости и число вытекающих капель, можно найти поверхностное натяжение исследуемой жидкости.

В общем случае сталагмометр, предназначенный для
измерения поверхностного
натяжения жидкости на границе с газом (паром) состоит (рис. 1.4) из
толстостенной трубки 5 с калиброванным выходным отверстием; шарообразного сосуда с метками, ограничивающими объем жидкости, дозирующего устройства 1
позволяющего изменять и стабилизировать скорость истечения жидкости из капилляра; специального устройства,
фиксирующего моменты начала и конца истечения жидкости 2; устройства 3, устанавливающего или
регистрирующего промежутки времени между двумя последовательно образующимися
каплями. Устройство 4 может обрабатывать данные от блоков 2 и 3 и после
обработки выдавать результат измерения в виде значений поверхностного натяжения с учетом поправочных коэффициентов.

Рис. 1.5. Схема простейшего сталагмометра

На рис.
1.5 показана схема простейшего
сталагмометра, который представляет собой сферический пузырек В известного
объема V_k, ограниченный метками b и d и соединенный с двумя
калиброванными капиллярами, имеющими объем каждого деления v_е. Сталагмометр заполняют жидкостью, затем позволяют мениску очень медленно перемещаться по
капилляру, перекрывая частично доступ воздуха в капилляр А с помощью резиновой
трубки и зажима таким образом, чтобы каждая капля образовывалась за время не
менее 4 с. После падения первой капли проводится отсчет деления, соответствующего верхнему мениску a в капилляре А (n делений от метки a). Скорость последующего
образование капель также контролируют и устанавливают время образования капли
не менее 4–5 с. После достижения мениском метки, например e в нижнем капилляре C
(m делений от метки d), определяют объем одной
капли при числе подсчитанных вытекших из сталагмометра капель N :

Если использовать относительный метод определения поверхностного
натяжения водных растворов ПАВ с использованием в качестве
стандартной жидкости воды, то его расчет можно проводить по
формуле

К недостаткам сталагмометрического метода можно
отнести возможность испарения жидкости с поверхности капель при их длительном
образовании и необходимость введения поправочных коэффициентов для точного
определения поверхностного
натяжения.

При учете всех поправок погрешность
сталагмометрического метода не превышает 1%. Метод используется для измерения
полустатического поверхностного
натяжения при продолжительности
образования капли 2–10 с. На практике допускается быстрое увеличение объема
капли до V = 0,95 V_пр, где V_пр – предельный объем капли. Дальнейший
рост объема необходимо проводить медленно — в течении нескольких минут. Кроме
того, в процессе отрыва капли через определенный промежуток времени формируются
две капли, меньшая из которых, известная как «сфера Плато», образуется из шейки
первичной капли. Часто эта часть капли остается на конце капилляра. Поэтому на
конце капилляра может оставаться до 40% массы первоначально сформировавшейся
капли, а отрывается только часть капли, достигшая зоны нестабильности. Именно это
учитывается поправкой f (r/a).

Метод взвешивания или счета капель можно использовать и
для определения межфазного
натяжения на границе двух жидкостей при выдавливании по каплям одной жидкости в другую. В этом случае для расчета
используются те же уравнения с поправкой на массу жидкости, вытесненной при формировании
капли.

1.2.2 Метод измерения
капиллярного поднятия жидкости

Этот метод считают наиболее
точным, потому что для него разработана довольно точная теория, а
экспериментальные данные легко контролируются.

Метод измерения капиллярного
поднятия основан на определении разности уровней жидкости в капилляре радиуса r и в широком сосуде. Расчет проводится по формуле
Жюрена

, где h_m– предельная высота поднятия жидкости в капилляре, Q – краевой угол смачивания жидкостью материала капилляра, Dr —
разность плотностей жидкости и пара.

Жидкость поднимается или опускается по
капилляру до тех пор, пока высота мениска не достигнет высоты, при которой масса
столба жидкости не уравняет давление внутри и снаружи капилляра. Процесс
установления предельной высоты поднятия мениска жидкости в капилляре происходит достаточно
долго. Так, например, для чистой воды h = 0,995 h_m достигается за 1,5 мин. Метод
измерения капиллярного поднятия жидкости является
одним из более точных и простых по аппаратурному оформлению и применяется там,
где продолжительность формирования поверхности раздела фаз не ограничивается.

Устройства, принцип действия
которых основан на методе измерения капиллярного поднятия жидкости, состоят из основного
элемента — широкой трубки, верхний и нижний конец которой сообщаются с
калиброванным капилляром. Для точного определения поверхностного натяжения необходимо с максимальной точностью
измерить разность уровней жидкости в узком и широком капиллярах, что
составляет известную трудность. Поэтому как один из возможных вариантов может
быть использован метод уравнивания высоты столбов жидкости в капиллярах при помощи избыточного давления на мениск в узком капилляре. В данном случае
измеряется то давление, которое
необходимо, чтобы уровень жидкости в капилляре не превышал уровня жидкости в сосуде,
с которым капилляр сообщается. Расчет проводится по формуле

, где P- измеренное уравновешивающее давление.

К недостаткам всех вариантов
метода капиллярного поднятия жидкости следует отнести зависимость
измеренного поверхностного
натяжения от краевого угла смачивания жидкостью материала капилляра, что позволяет
определить поверхностное
натяжение при существовании
поверхности в течение не менее 10 с; отсутствие возможности обновления
поверхности в капилляре; высокую погрешность измерения динамического поверхностного натяжения. Кроме того,
формула Жюрена, основанная на уравнении
Лапласадля цилиндрического капилляра, не учитывает количества жидкости, находящейся в мениске (высотой x). Краевой угол смачивания капилляра жидкостью должен быть равен нулю и в каждом
опыте необходимы довольно большие объемы растворов.
Радиус большого капилляра должен быть не менее 5
см. Щелочность раствора не
должна приводить к растворению вещества капилляра. Для повышения точности
измерений поверхностного натяжения следует
вводить поправки, используя таблицы Сагдена.

1.2.3 Метод
вращающейся капли

Сущностью метода является
измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости. Этот
способ измерения годится для измерения низких или сверхнизких значений межфазного
натяжения. Он

широко применяется для микроэмульсий,
измерения эффективности ПАВ в нефтедобыче, а также для определения адсорбционных свойств.

1.2.4 Метод Дю Нуи (метод
отрыва кольца)

Метод является классическим. Сущность метода вытекает
из названия. Платиновое кольцо поднимают из жидкости, смачивающей его, усилие
отрыва и есть сила поверхностного натяжения и может быть пересчитано в
поверхностную энергию. Метод подходит для измерения ПАВ, трансформаторных масел
и т. д.

1.2.5 Метод
бегущих волн

При возмущении жидкости пластиной «лежащей» на её
поверхности, по ней начинает распространяться круг волн. Если просветить кювету
с жидкостью импульсным источником света с частотой равной частоте возмущения,
то на экран спроецируется «стоячая» волновая картина. Измеряя длину волны на
экране и геометрически перерассчитывая её (зная расстояние от источника света
до поверхности жидкости и расстояние от поверхности до экрана, а также про подобие треугольников) можно получить
величину поверхностного натяжения по формуле:

$sigma = frac{rho lambda^2}{4 pi^2}(2 pi nu^2 lambda - g)$ , где:

σ — поверхностное натяжение;

ρ — плотность жидкости;

λ — длина волны;

ν — вынуждающая частота;

g — ускорение свободного падения.

1.3 Теоретическая формула
поверхностного натяжения

Формулу для определения
коэффициента поверхностного натяжения жидкости σ можно записать через
удельную теплоту парообразования r как:

$sigma= left(r - frac{R_u T}{M} left(1-frac{rho_v}{rho} right) right)cdot frac{M^{1/3} rho^{2/3}}{6 N^{1/3}}$

или через внутреннюю энергию
U:

$sigma= U left(frac{M^{1/3}rho^{2/3}}{6 N^{1/3}}right)$

где r – теплота
парообразования, Дж/кг;
ρ – плотность жидкости, кг/ м³; ρ_v –
плотность пара, кг/ м³;
R_u – универсальная газовая постоянная, Дж/(кмоль * K);
T – температура, K;

U –
внутренняя энергия жидкости, Дж/кг;
M – молекулярная масса, кг/кмоль;
N – число Авогадро, кмоль^-1 ;

1.4 Объединение пузырей

Когда два пузыря соединяются, они
принимают форму с наименьшей возможной площадью поверхности. Их общая стенка
будет выпячиваться внутрь большего пузыря, так как меньший пузырь имеет
бо́льшую среднюю кривизну и большее внутреннее давление. Если пузыри
одинакового размера, их общая стенка будет плоской.

Соединение мыльных пузырей

Правила, которым подчиняются пузыри
при соединении, были экспериментально установлены в XIX веке бельгийским
физиком Жозефом Плато и доказаны математически в 1976 г.
Жаном Тейлором.

Мыльные плёнки представляют собой
кусочно-гладкие поверхности, средняя кривизна которых постоянна на каждом
гладком участке.

Если пузырей больше чем три, они
будут располагаться таким образом, что возле одного края могут соединяться
только три стенки, при этом углы между ними будут равны 120°, в силу равенства
поверхностного натяжения для каждой соприкасающейся поверхности.

Линии пересечения поверхностей
пересекаются в одной точке по четыре штуки, причём угол между любыми двумя
примерно равен 109,47°.

Пузыри, не подчиняющиеся этим
правилам, в принципе могут образовываться, однако будут сильно неустойчивыми и
быстро примут правильную форму либо разрушатся. Пчёлы, которые стремятся
уменьшить расход воска, соединяют соты в ульях также под углом 120°, формируя,
тем самым, правильные шестиугольники.

1.5 Интерференция и отражения

Отражение облаков в мыльном пузыре

Переливчатые «радужные» цвета мыльных пузырей
получаются за счёт интерференции световых волн и определяются толщиной мыльной
плёнки.

Когда свет проходит сквозь тонкую плёнку пузыря, часть
его отражается от внешней поверхности, в то время как другая часть проникает
внутрь плёнки и отражается от внутренней поверхности. Наблюдаемый в отражении
цвет излучения определяется интерференцией этих двух отражений. Поскольку
каждый проход света через плёнку создает сдвиг по фазе пропорциональный толщине
плёнки и обратно пропорциональный длине волны, результат интерференции зависит
от двух величин: толщины пленки и длины волны. Отражаясь, некоторые волны
складываются в фазе, а другие в противофазе, и в результате белый свет,
сталкивающийся с плёнкой, отражается с оттенком, зависящим от толщины плёнки.

1.6
Изменение цвета пузыря со временем

По мере того, как плёнка становится тоньше из-за
испарения воды, можно наблюдать изменение цвета пузыря. Более толстая плёнка
убирает из белого света красный компонент, делая тем самым оттенок отражённого
света сине-зелёным. Более тонкая плёнка убирает жёлтый (оставляя синий свет),
затем зелёный (оставляя пурпурный), и затем синий (оставляя золотисто-жёлтый).
В конце концов стенка пузыря становится тоньше, чем длина волны видимого света,
все отражающиеся волны видимого света складываются в противофазе и мы перестаем
видеть отражение совсем (на тёмном фоне эта часть пузыря выглядит «чёрным
пятном»). Когда это происходит, толщина стенки мыльного пузыря меньше 25 нм, и
пузырь, скорее всего, скоро лопнет. Такое явление называется ньютоновской
плёнкой.

Эффект интерференции также зависит от угла, с которым
луч света сталкивается с плёнкой пузыря. Таким образом, даже если бы толщина
стенки была везде одинаковой, мы бы всё равно наблюдали различные цвета из-за
движения пузыря. Но толщина пузыря постоянно меняется из-за гравитации, которая
стягивает жидкость в нижнюю часть так, что обычно мы можем наблюдать полосы
различного цвета, которые движутся сверху вниз.

1.7 Математические свойства

Мыльные пузыри образуют пену

Мыльные пузыри являются физической иллюстрацией
проблемы минимальной поверхности, сложной математической задачи. Например,
несмотря на то, что с 1884 года известно, что мыльный пузырь имеет минимальную
площадь поверхности при заданном объёме, только в 2000 году было доказано, что
два объединённых пузыря также имеют минимальную площадь поверхности при
заданном объединённом объёме. Эта задача была названа теоремой двойного пузыря.
Также, лишь с появлением геометрической теории меры удалось доказать, что оптимальная
поверхность будет кусочно-гладкой, а не бесконечно изломанной.

Плёнка мыльного пузыря всегда стремится минимизировать
свою площадь поверхности. Это связано с тем, что свободная энергия жидкой
плёнки пропорциональна площади её поверхности и стремится к достижению
минимума:

где σ (сигма) — поверхностное натяжение вещества,
а S — полная площадь поверхности плёнки. Оптимальная форма отдельного
пузыря — сфера, однако несколько пузырей, объединённых вместе, имеют
гораздо более сложную форму.

Глава
2 Экспериментальная часть

Эксперимент
№1 «Определение поверхностного натяжения жидкости»

Цель
эксперимента: Определить коэффициент поверхностного
натяжения мыльного
раствора.
Оборудование: установка(2.1),
горячая вода, глицерин, нашатырный спирт, порошкообразное моющее средство,
соломинки(трубочки)

Ход
эксперимента:
                                                  1.
На поверхность мыльного раствора ставят установку

2.
На установку накладывают соломинки, пока та не утонет.

3.
Подставляют число соломинок в формулу(2.2) и рассчитывают

коэффициент
поверхностного натяжения.

4.
Учитывают погрешности

Установка
состоит из основания и 2 креплений

рис. (2.1)

σ
= g(Π*R(ρпр—ρж)+(2*mк+mс)*n/L)/2 (2.2)

σ
– коэффициент поверхностного натяжения

ρпр – плотность
проволоки; ρ_ж– плотность жидкости,
R –
радиус сечения проволоки,
g – ускорение свободного
падения;
m – масса «соломинок» вместе с
верхним каркасом;
L – длина проволоки,
соприкасающейся с водой

mк – масса крепления

mс – масса соломинки

В
основном погрешности зависят от массы соломинок.

Но
также чем больше радиус основания (длина проволоки, соприкасающейся с
поверхностью жидкости) тем больше соломинок выдержит жидкость, а следовательно
понизятся погрешности.

Вывод: Вывел
формулу для экспериментального нахождения коэффициента поверхностного натяжения
и проверил её.

Эксперимент №2 «Выяснение
влияния мыла на поверхностное натяжение воды»

Цель эксперимента:
качественно оценить влияние мыла на величину поверхностного натяжения воды.
Оборудование:
канцелярская скрепка, стакан с водой, пипетка, пинцет, мыльный раствор.

Ход эксперимента:
                                                                                                                     1.
На поверхность воды, находящейся в стакане, пинцетом укладывают
скрепку.
                 2. В стакан с водой и лежащей на поверхности воды
скрепкой, капают каплю мыльного раствора.

Вывод: Скрепка
утонула, так как добавление мыла не
увеличивает, а уменьшает поверхностное натяжение примерно до трети от
поверхностного натяжения чистой воды. Это легко объяснить: молекулы мыла,
вклиниваясь между молекулами воды, снижают их взаимное притяжение.

Эксперимент №3 «Расчёт
толщины плёнки мыльного пузыря и экспериментальная проверка расчетов»

Цель эксперимента:
Рассчитать толщину плёнки мыльного пузыря,
проверить расчеты
экспериментом
Оборудование: горячая вода, глицерин, нашатырный спирт,
порошкообразное моющее средство, рамка для выдувания мыльного
пузыря                                                                         Ход
эксперимента:
1.Теоретический расчет

Рассчитаем предельный радиус пузыря R*, до которого не будет происходить
нарушения сплошной поверхности.   Пусть r – радиус капли мыльного пузыря, c –
концентрация мыла в капле раствора, a — среднее межмолекулярное расстояние в
жидкости, n_с
— количество молекул мыла, которые мы можем расположить на поверхности пузыря
предельного размера, тогда   n_с= (4/3πr³/a³)с. С другой стороны, для того чтобы и внешнюю, и внутреннюю поверхность мыльного
пузыря покрыть однослойной пленкой молекул мыла, необходимо иметь n_s = 2•4π (R*/а)²молекул.
                                                                                                                                                                                                                                                                                                                                                                                                                          Тогда R * находится из условия n_s = n_с, т.е.
R*=(сr³/6а)^1/2
.                                                                                                                                                                                                    Приравнивая объем начальной капли объему пленки
пузыря :4/3*πr³= 4π R*²h*можно найти толщину пленки предельного пузыря:h=2а/с
Вывод: толщина пленки оказалась не зависящей ни от радиуса начальной
капли, ни от радиуса предельного пузыря. Это означает, что пленка предельного
пузыря состоит из чистой, «обезмыленной» воды между двумя слоями молекул мыла. Чем больше было
растворено мыла в воде (больше с), тем меньше будет
«обезмыленной» воды (меньше h *)

Практическая
оценка: Сделаем некоторые количественные оценки.
Если r = 10^{-3 м, с ≈ 0,1}, а≈5 ∙10
—¹⁰м [1, с. 116],то оказывается, что R * ≈ 0,2
м, а h*≈
10^{-8 м}.
А вот если r
= 10~² м, то
R* ≈ 6
м. Такой
пузырь очень сложно выдуть по
«техническим причинам»: он лопнет раньше, чем созреет. Вывод:
Мы смогли выдуть пузыри диаметром не более 0,92 м

Эксперимент №4
«Лопание мыльных пузырей»

Цель эксперимента:
выяснить, как происходит лопание мыльных пузырей      Оборудование:
раствор для выдувания мыльных пузырей, фотокамера «Samsung»,
ноутбук «Lenovo» программа Light
Alloy — компактный мультимедийный плеер, с
функцией замедленного просмотра видео.
                       Ход
эксперимента:
1. Съёмка процесса лопания мыльного пузыря на
камеру                                                                      2.
Покадровый просмотр отснятого материала с помощью плеера Light
Alloy
3.Отбор скриншотов, на которых можно различить моменты лопания
пузыря                 Вывод:                                                                                                                                                 — Для того, чтобы заснять процесс лопания мыльного
пузыря необходима высокоскоростная видеокамера.                                                                                                        —
Процесс разрыва пузыря идет по путям
наименьшего сопротивления. Когда пузырь цел, можно видеть на нем дифракционные
переливы отраженного света. Это говорит о том, что отражающая мыльная пленка не
всюду имеет одинаковую толщину. Когда мыльная плёнка растягивается,
концентрация мыльных молекул на поверхности уменьшается, увеличивая при этом
поверхностное натяжение. Именно по этой причине, в момент разрыва пузыря, он
мгновенно минимизирует поверхность. А из-за инерционности капельки не успевают
разлететься в стороны

ЗАКЛЮЧЕНИЕ

В результате проделанной нами работы мы пришли к следующим выводам:

1)
Добавление мыла не увеличивает, а
уменьшает поверхностное натяжение;

2) Собрали установку и вывели к ней формулу для определения
поверхностного натяжения σ = g(Π*R(ρпр—ρж)+(2*mк+mс)*n/L)/2

3)
Улучшить качество мыльных пузырей можно заменив обычную воду дистиллированной, обычная
вода из-за минерального содержания будет причиной хрупких пузырей; 4)
Формула
для вычисления предельного радиуса мыльного пузыря R*=(сr³/6а)^1/2
, для вычисления толщины пленки предельного
пузыря: h=2а/с.Толщина пленки
оказалась не зависящей ни от радиуса начальной капли, ни от радиуса
предельного пузыря. Это означает, что пленка предельного пузыря состоит из
чистой, «обезмыленной» воды между двумя
слоями молекул мыла.

5) Мы смогли выдуть
пузыри диаметром не более 0,92 м

6)
Когда два пузыря соединяются, они принимают форму с
наименьшей возможной площадью поверхности. Их общая стенка будет
выпячиваться внутрь большего пузыря. Если пузыри одинакового размера, их общая
стенка будет плоской. Если пузырей больше чем три, они будут располагаться
таким образом, что возле одного края могут соединяться только три стенки, при
этом углы между ними будут равны 120°, в силу равенства поверхностного
натяжения для каждой соприкасающейся поверхности

ЛИТЕРАТУРА

1.
Гегузин Я.Е. «Пузыри» — М.: Наука, 1985.

2.
Физика 10. Под
редакцией Пинского А.А. Просвещение, Москва, 1995.

3.
Г.Я.Мякишев,
Б.Б.Буховцев. Физика 11. Просвещение, Москва, 1994.

4.
Физика 11. Под
редакцией Пинского А.А. Просвещение, Москва, 1995.

5. «XuMuK» xumuk.ru

6. «Википедия»
http://ru.wikipedia.org/wiki/

Источник

Поверхностное натяжение, задачи

Задача №1. Поверхностное натяжение

Задача №2. Капиллярные явления

Задача №3. Поверхностное натяжение

Задача №4. Поверхностное натяжение

Задача №5. Поверхностное натяжение

Вопросы на тему «Поверхностное натяжение и свойства жидкостей»

1.4 Объединение пузырей 19

1.4 Объединение пузырей

Не пропустите также:

1.4 Объединение
пузырей 19