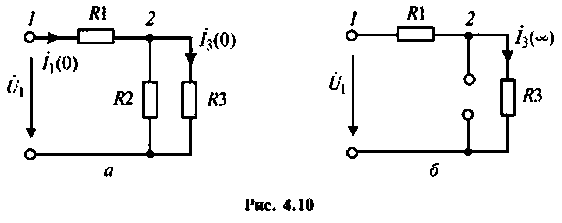
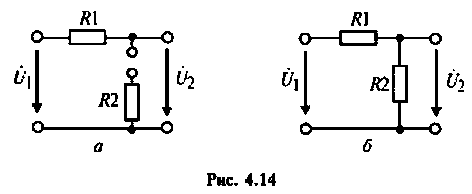
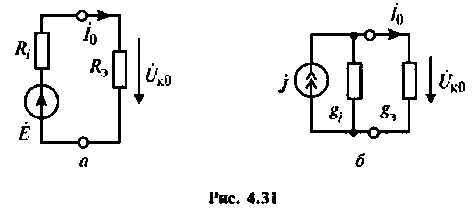
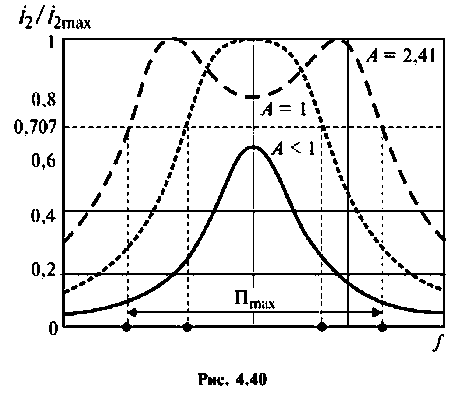
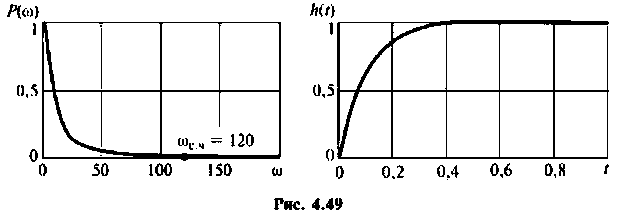
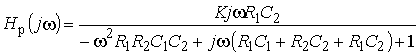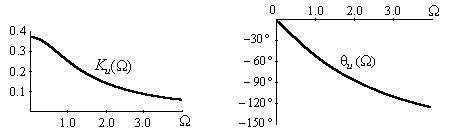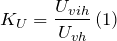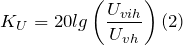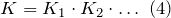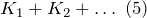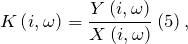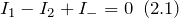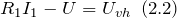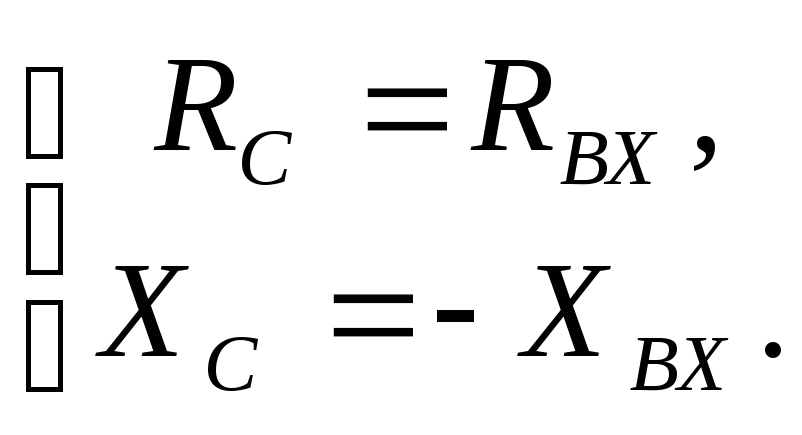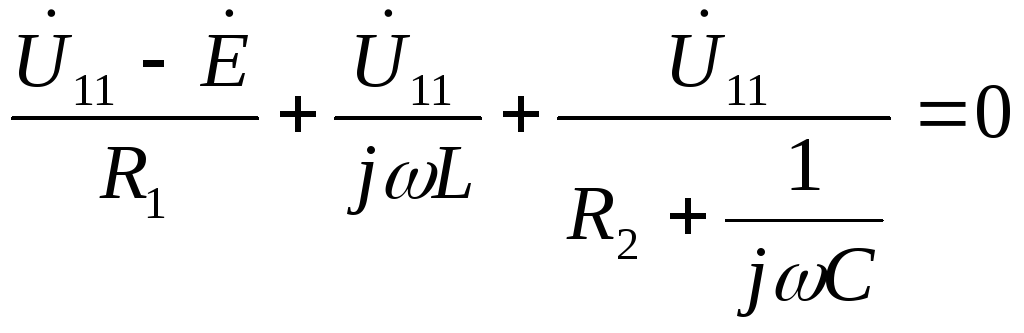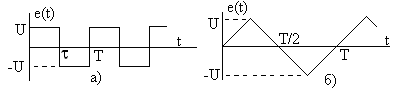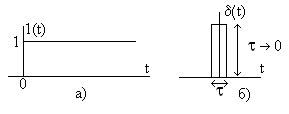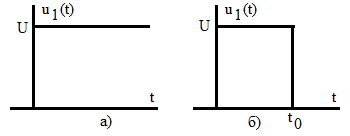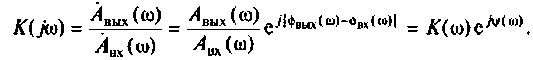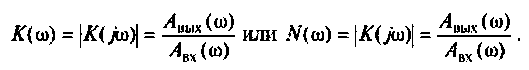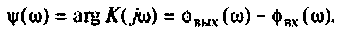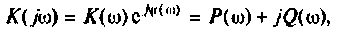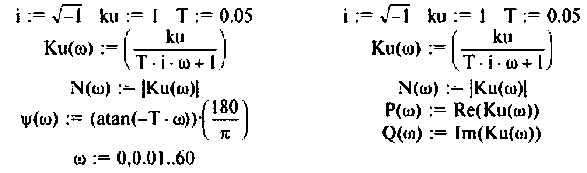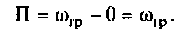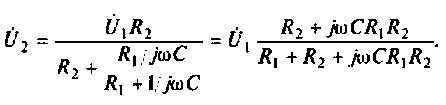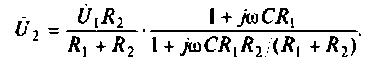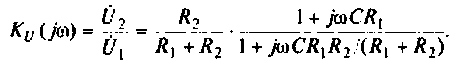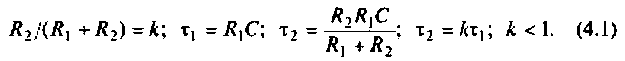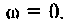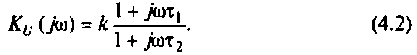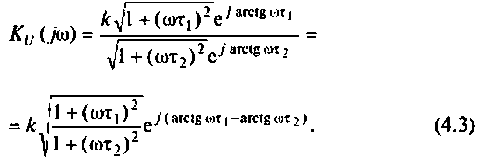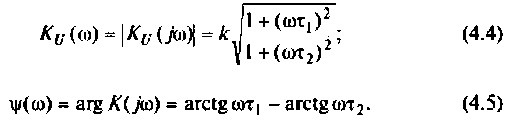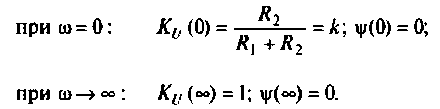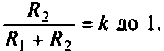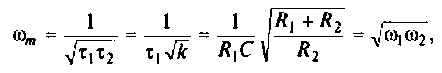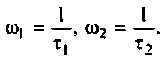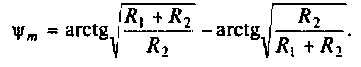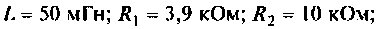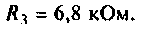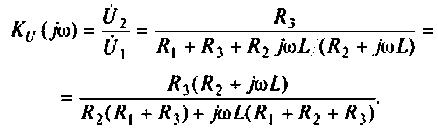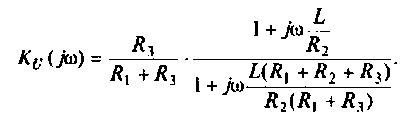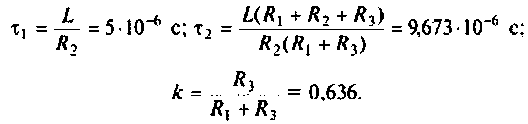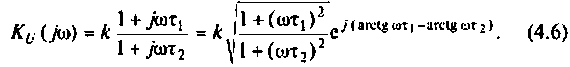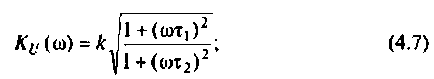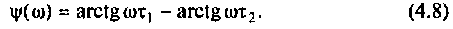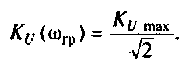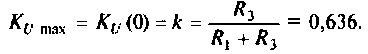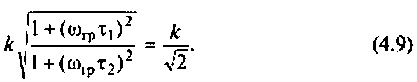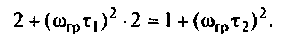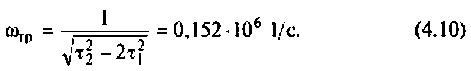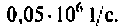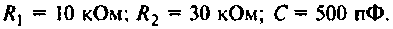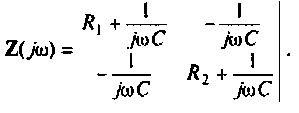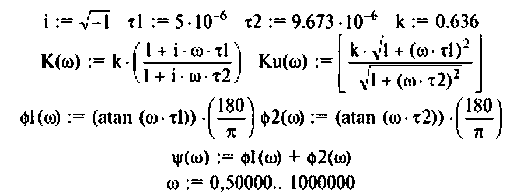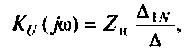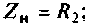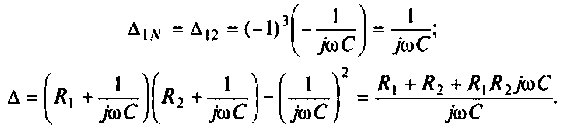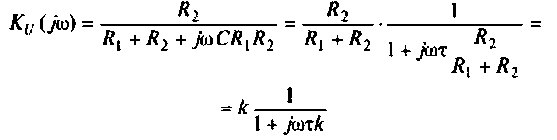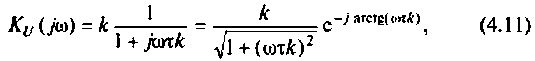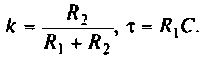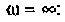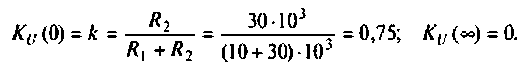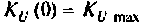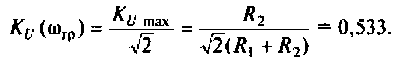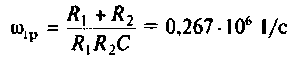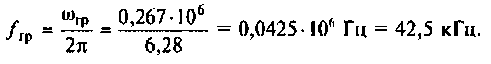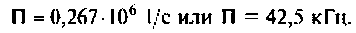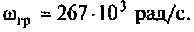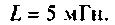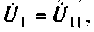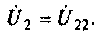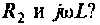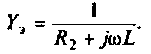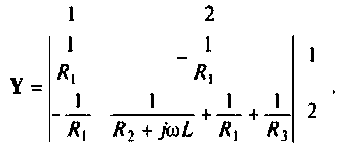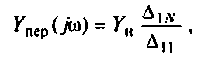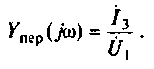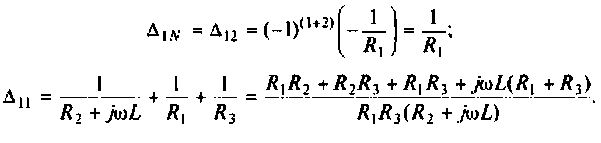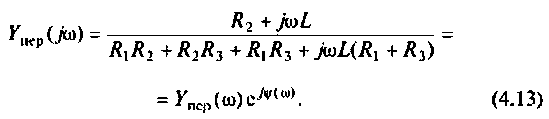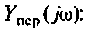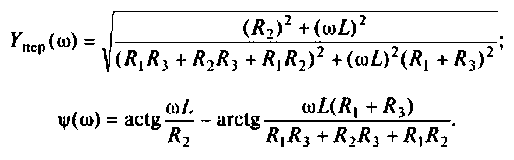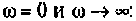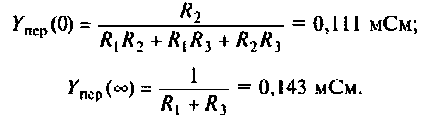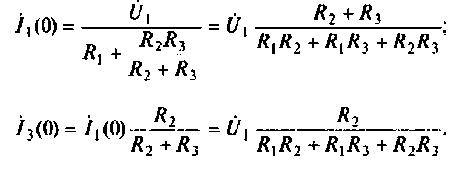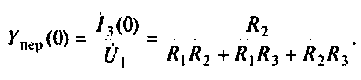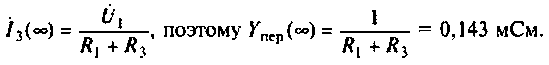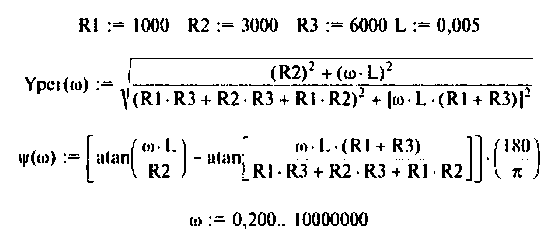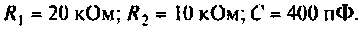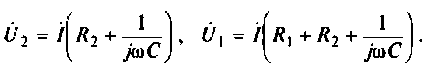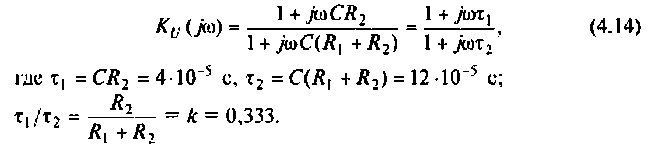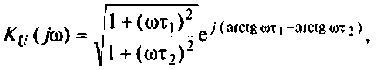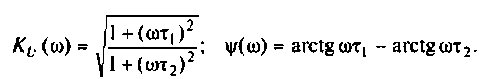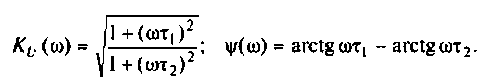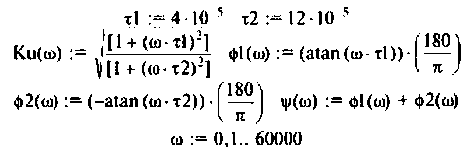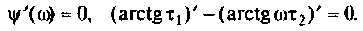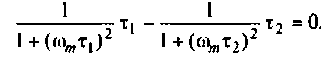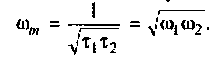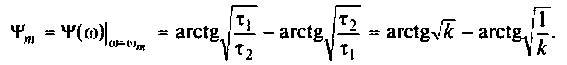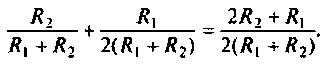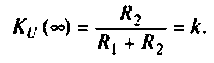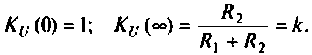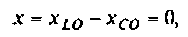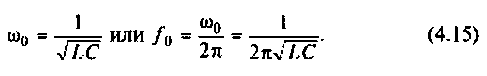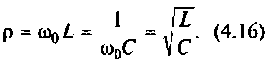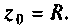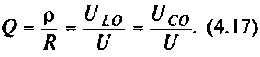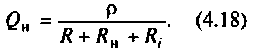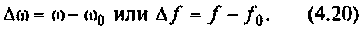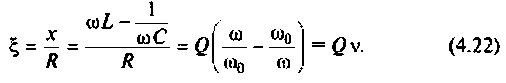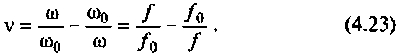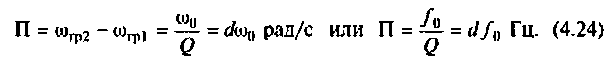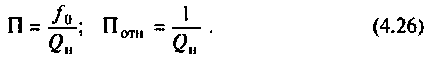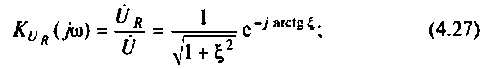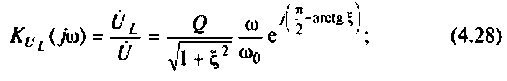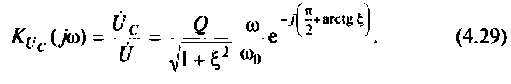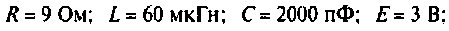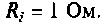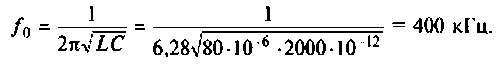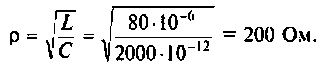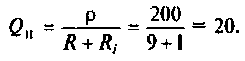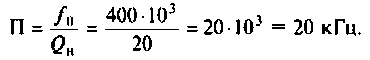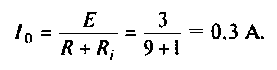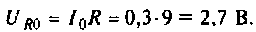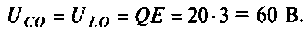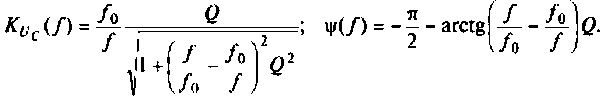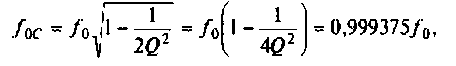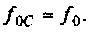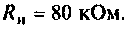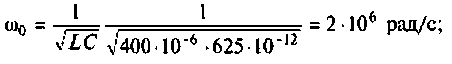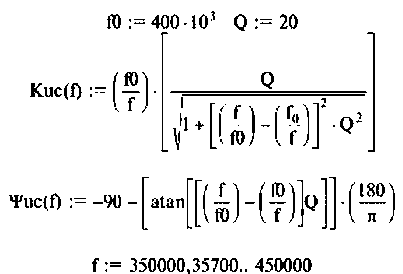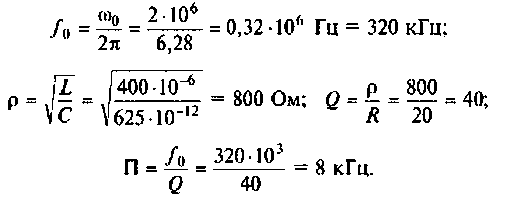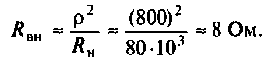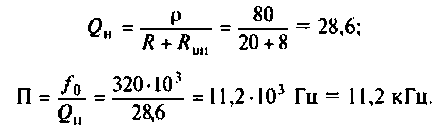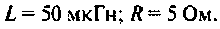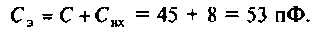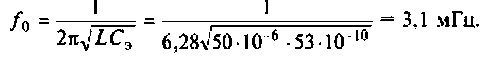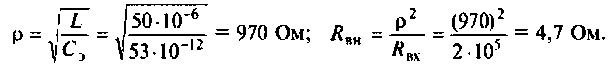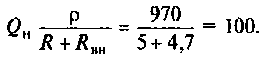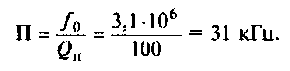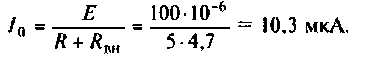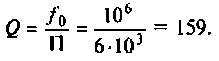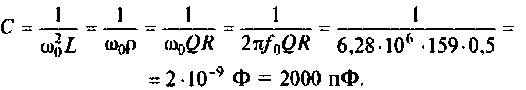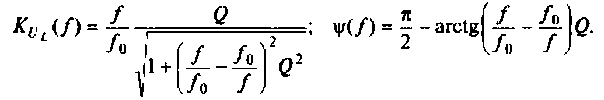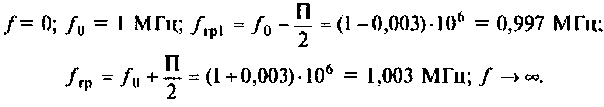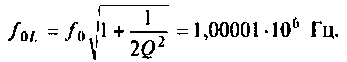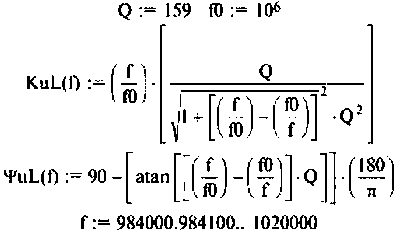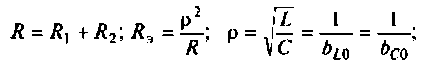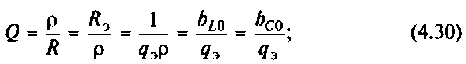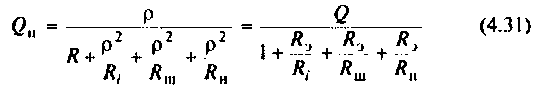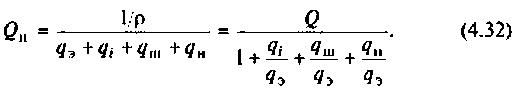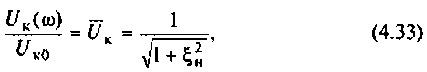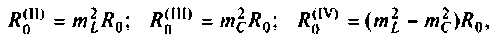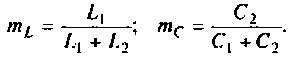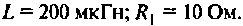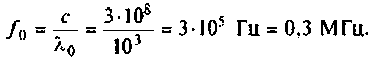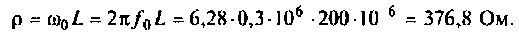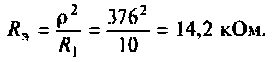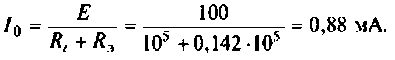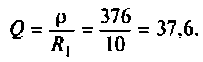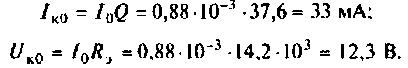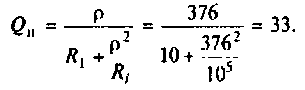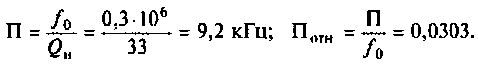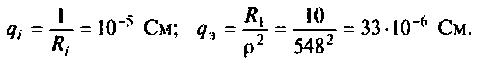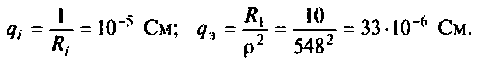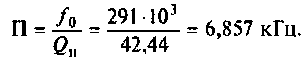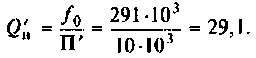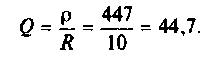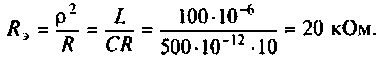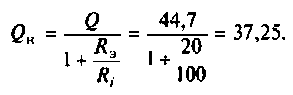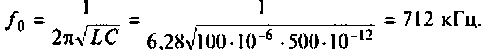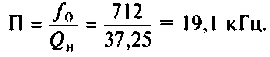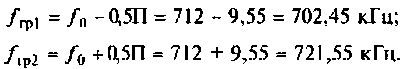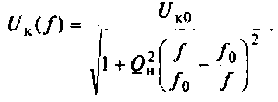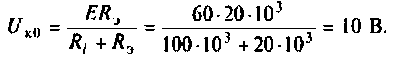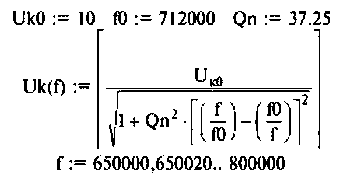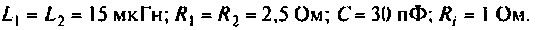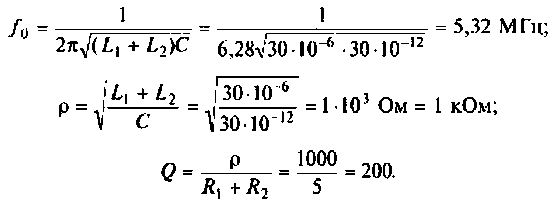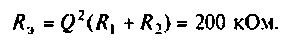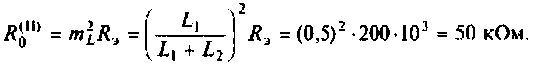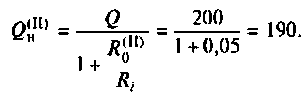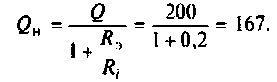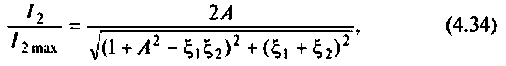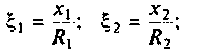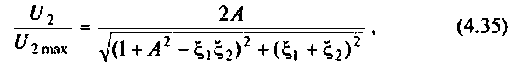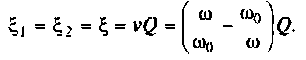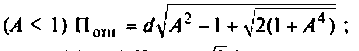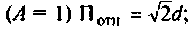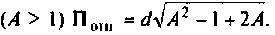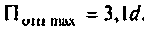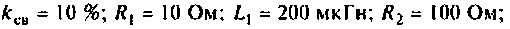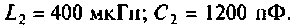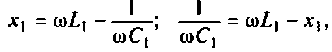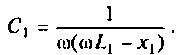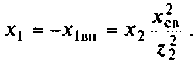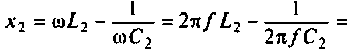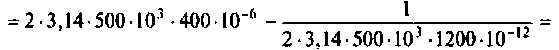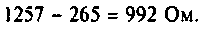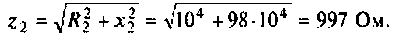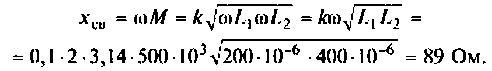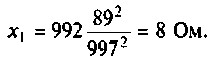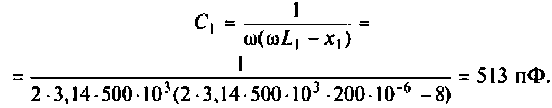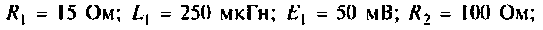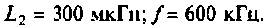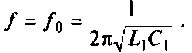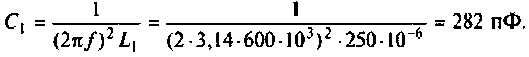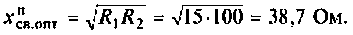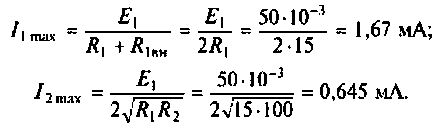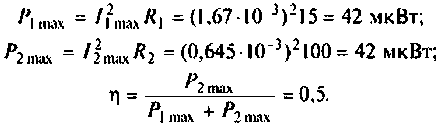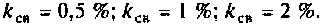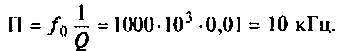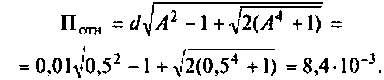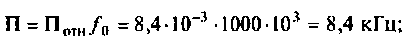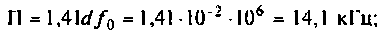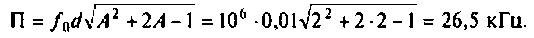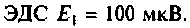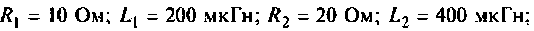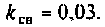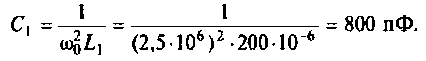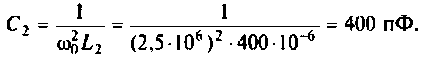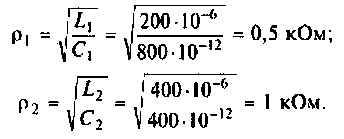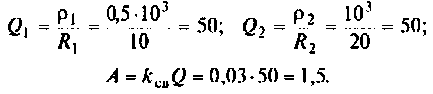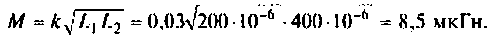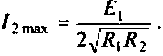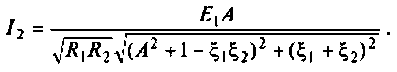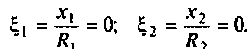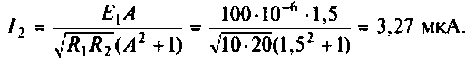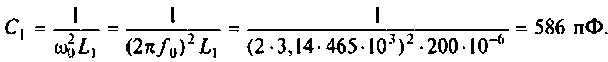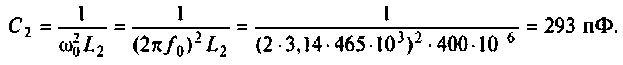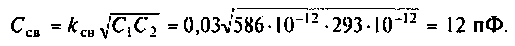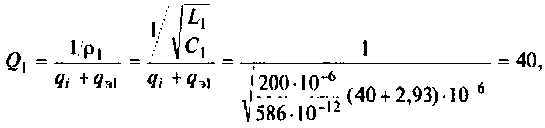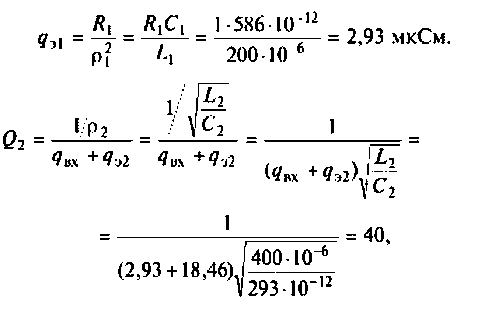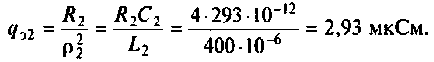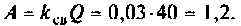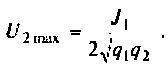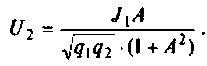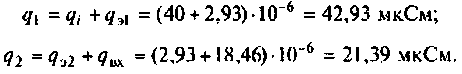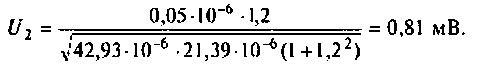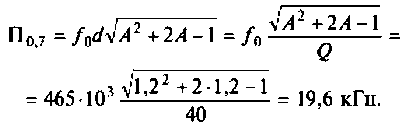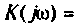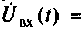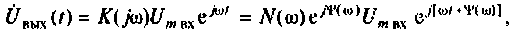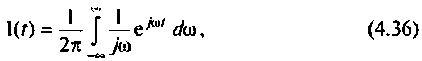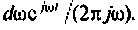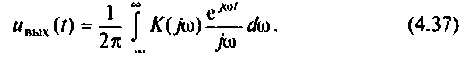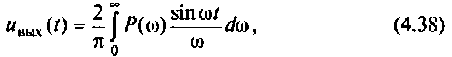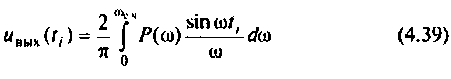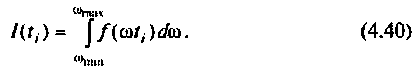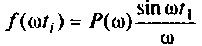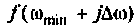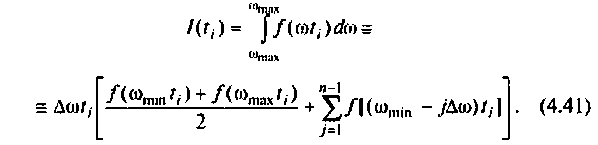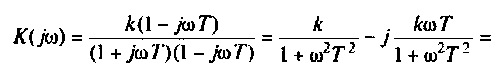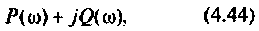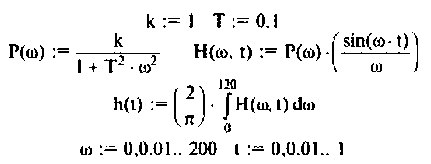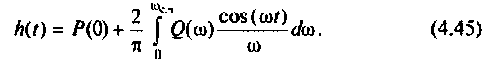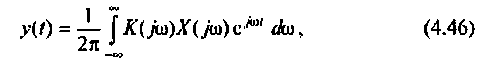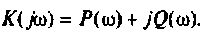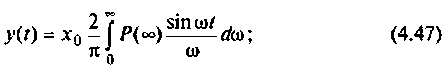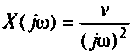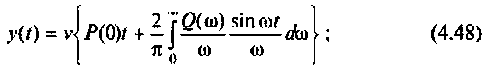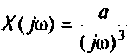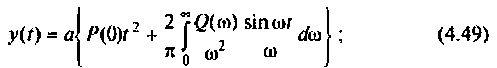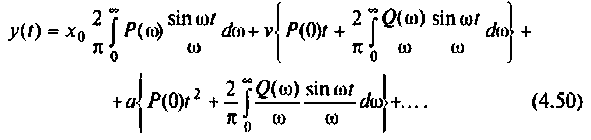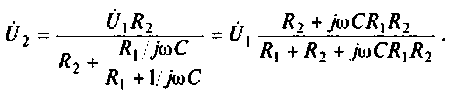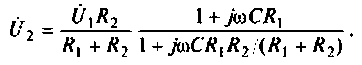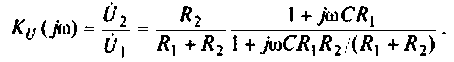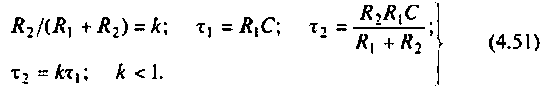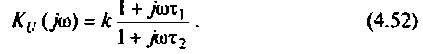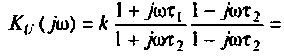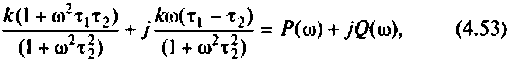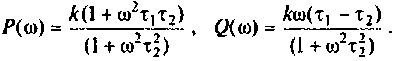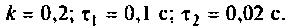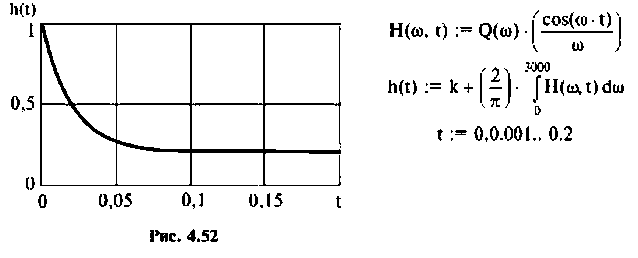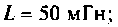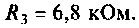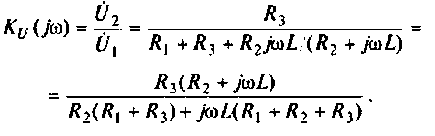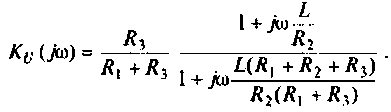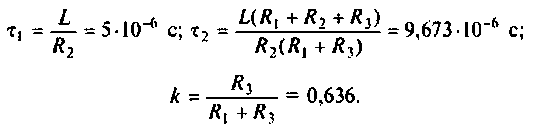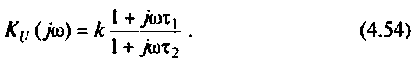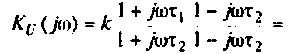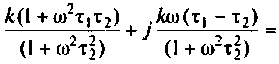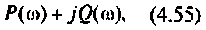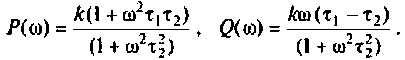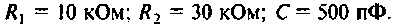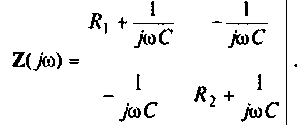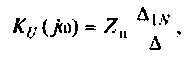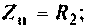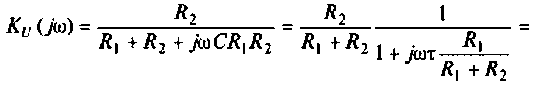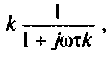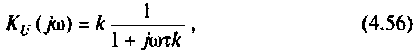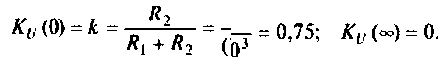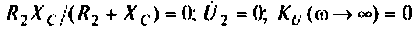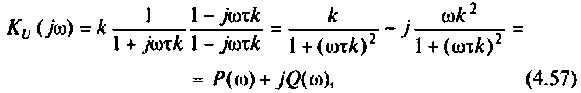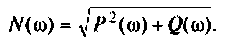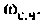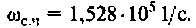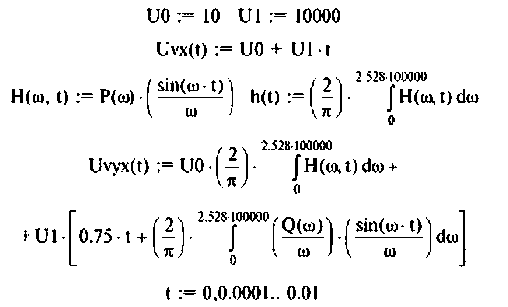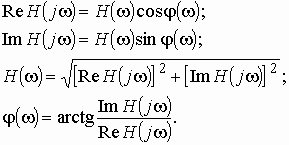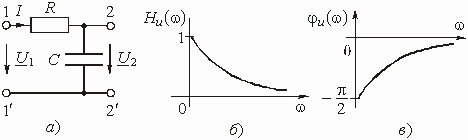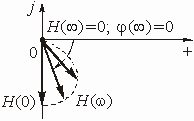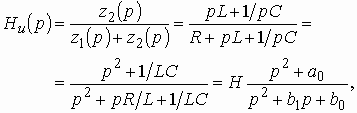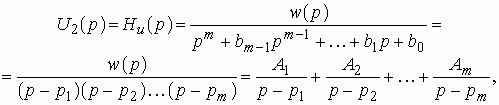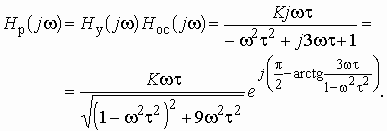Как найти коэффициент передачи по напряжению
1.5 Определение внешних частотных характеристик
четырехполюсников через A параметры
Частотные характеристики четырехполюсника определены выражениями (1.11) — (1.17) в самой общей форме. Однако если взять за основу уравнения четырехполюсника (1.20) и добавить к ним соотношение, связывающее ток и напряжение в нагрузке: 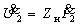
1. Входное сопротивление со стороны первичных зажимов:
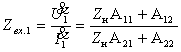
2. Входная проводимость со стороны первичных зажимов:
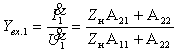
3. Коэффициент передачи по напряжению:
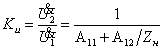
В частном случае, когда Zн = 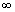
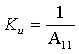
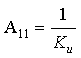
4. Коэффициент передачи по току:
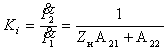
В частном случае, когда Zн = 0, т.е. имеет место режим короткого замыкания в нагрузке, получим
5. Передаточное сопротивление:
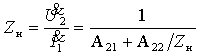
6. Передаточная проводимость:
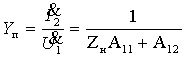
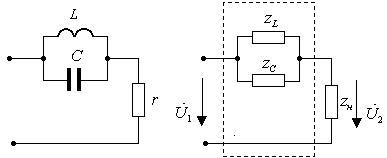
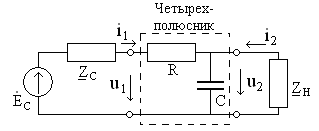
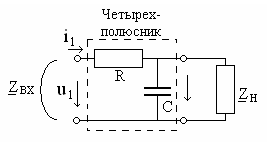
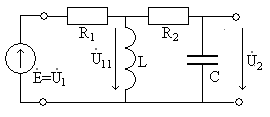
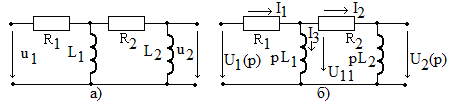
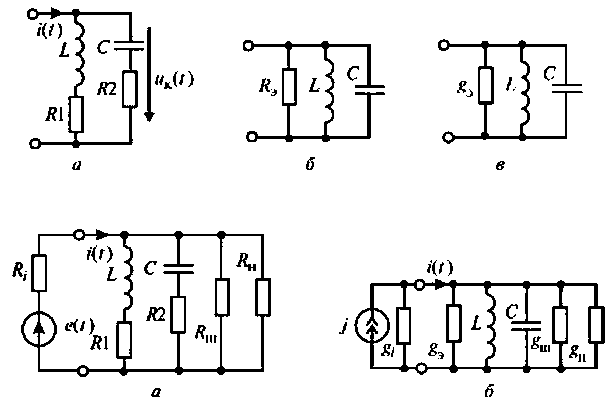
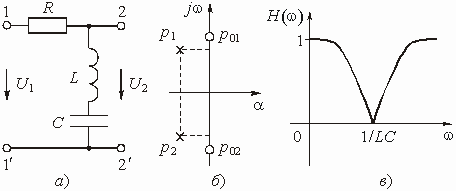
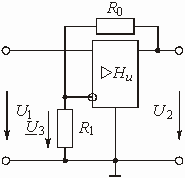
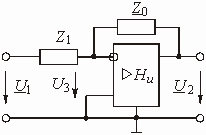
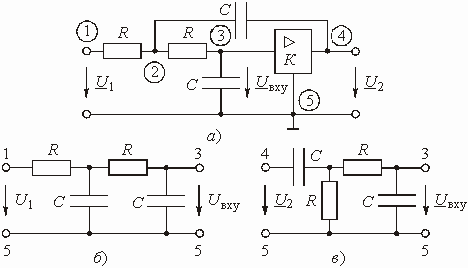
Пример 1.11. Найти коэффициент передачи по напряжению для цепи, представленной на рис. 1.16а.
Четырехполюсник представляет собой «продольное» звено (рис. 1.16(б)) с эквивалентным сопротивлением:
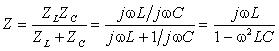
Используя результат ранее рассмотренного примера 1.7, получим набор А- параметров
Рис.1.16. Схема продольного реактивного звена, нагруженного на резистивное сопротивление: а)исходная цепь; б)комплексная схема
Тогда по формуле (1.27) с учетом равенства Z н = r найдем коэффициент передачи по напряжению
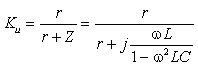
Запишем полученное выражение в показательной форме, выделяя АЧХ и ФЧХ искомой частотной характеристики
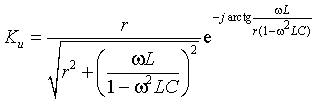
где 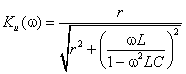
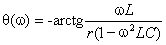
В цепях при наличии полного набора элементов r, L, C целесообразно также ввести в рассмотрение относительную частоту, определив ее в долях резонансной частоты колебательного контура. Для данного примера имеем:
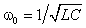
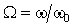
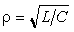
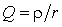
С учетом введенных обозначений выражения (1.31) и (1.32) принимают вид:
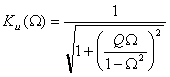
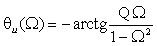
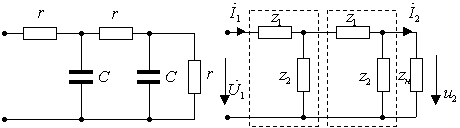
Пример1.12. Найти А — параметры цепочечной схемы RC фильтра нижних частот (рис. 1.17а). По найденным параметрам определить коэффициенты передачи 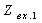
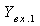
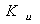
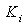
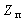
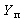
Рис. 1.17. Схема RC фильтра нижних частот:а)исходная цепь;
Решение задачи начинаем с изображения комплексной расчетной схемы замещения расчетной цепи (рис. 1.17б), где 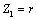
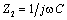
На основании (1.24) найдем А — параметры исследуемой схемы, перемножив две одинаковые матрицы. 
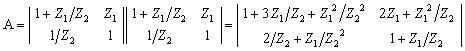
Для определения коэффициентов передачи воспользуемся полученными ранее выражениями (1.25) — (1.30), и после подстановки в них комплексных параметров 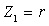
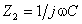
1. Входное сопротивление четырехполюсника:
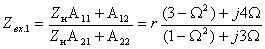
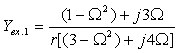
3. Коэффициент передачи по напряжению:
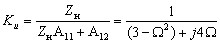
4. Коэффициент передачи по току:
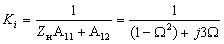
5. Передаточное сопротивление:
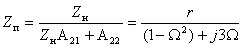
6. Передаточную проводимость:
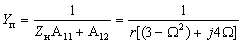
Каждое из полученных выражений следует записать в показательной форме, чтобы выделить АЧХ и ФЧХ. Например, для коэффициента 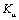
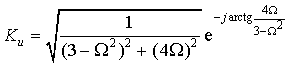
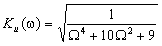
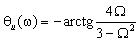
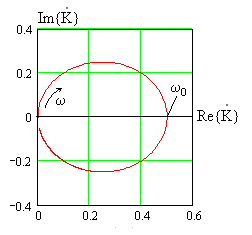
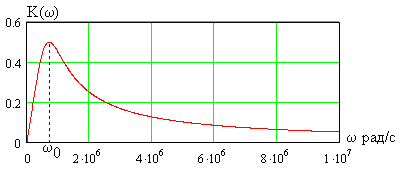
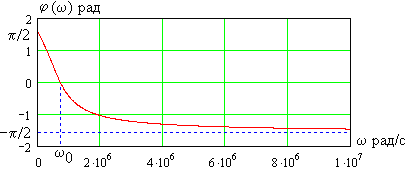
На рис. 1.18а,б показано поведение АЧХ и ФЧХ функции 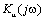
Рис. 1.18. Частотные зависимости коэффициента передачи напряжения К u
Анализ показывает, что RC фильтр нижних частот обеспечивает плавное уменьшение амплитуд гармонических сигналов с ростом частоты. При этом даже для очень низких частот, близких к нулю, имеет место трехкратное уменьшение сигнала на выходе. Фазовая характеристика указывает на увеличение модуля угла сдвига фаз с ростом частоты. Для частот Ω > 1.73 этот угол превосходит по величине 90˚.
Изучение материала первого раздела пособия рекомендуется завершить решением задач приложения 1. Вариант указывается преподавателем или выбирается самостоятельно.
Источник
Коэффициент передачи
Определение и формула коэффициента передачи
Форма представления коэффициента передачи зависит от формы математического представления сигналов входа и выхода. Это могут быть, например, операторы Лапласа или Фурье, тогда коэффициенты передачи называют операторными.
Коэффициент передачи и коэффициент усиления
В частности, если величины входного и выходного сигналов однородны, тогда коэффициент передачи называют коэффициентом усиления. Так, коэффициентом усиления по напряжению (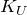
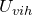
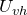
В выражении для коэффициента усиления можно использовать не только амплитуды, но и действующие значения напряжения.
Если коэффициенты усиления выражают в децибелах, то определением коэффициента преобразования (усиления) по напряжению будет выражение:
Коэффициенты усиления по току и мощности в децибелах выражают как:
Коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах:
Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
K(дб)=
Если в усилителе коэффициент передачи больше единицы для безразмерного коэффициента или больше нуля для коэффициента, представленного в децибелах, то коэффициент называют коэффициентом усиления.
Коэффициент передачи может быть представлен в комплексном виде. Он используется для анализа устройств, которые зависят от частоты сигналов.
Комплексный коэффициент передачи линейного звена находят как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:
где 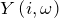
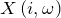

Единицы измерения
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.
Примеры решения задач
| Задание | Что такое частотный годограф? |
| Решение | Комплексный коэффициент передачи применяют для графического изображения свойств звена. С этой целью строят частотный годограф. Частотным годографом называют геометрическое место точек, которое создает конец вектора комплексного коэффициента передачи, если частота сигнала изменяется от 0 до  . Форма диаграммы сложная и только в простейших случаях это может быть окружность или прямая. Годограф строят как параметрическую кривую на комплексной плоскости, где параметром является частота. Данную характеристику можно построить в декартовой и полярной системах координат. Для построения годографа в декартовой системе координат комплексный коэффициент передачи представляют в алгебраической форме. При этом по оси абсцисс откладывают вещественную часть, по оси ординат мнимую. Для каждой частоты наносят точку на комплексной плоскости. Полученные точки соединяют плавной кривой. Около каждой точки выставляют соответствующие ей частоты. Фактически частотный годограф представляет собой кривую зависимости модуля комплексного коэффициента передачи от угловой частоты. Она показывает, как система преобразует сигналы разной частоты. . Форма диаграммы сложная и только в простейших случаях это может быть окружность или прямая. Годограф строят как параметрическую кривую на комплексной плоскости, где параметром является частота. Данную характеристику можно построить в декартовой и полярной системах координат. Для построения годографа в декартовой системе координат комплексный коэффициент передачи представляют в алгебраической форме. При этом по оси абсцисс откладывают вещественную часть, по оси ординат мнимую. Для каждой частоты наносят точку на комплексной плоскости. Полученные точки соединяют плавной кривой. Около каждой точки выставляют соответствующие ей частоты. Фактически частотный годограф представляет собой кривую зависимости модуля комплексного коэффициента передачи от угловой частоты. Она показывает, как система преобразует сигналы разной частоты. |
Для узла, к которому подключен инвертирующий выход, запишем закон Кирхгофа для токов:
Рассмотрим контур, который включает источник напряжения, вход усилителя, и сопротивление 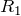
Рассмотрим контур, который включает вход усилителя, сопротивление 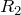
Выразим из (2.3) выходное напряжение и учтем, что: если усилитель работает в линейном режиме, то входные токи в рассматриваемый усилитель равны нулю (в нашем случае 
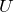
Источник
Коэффициент передачи
Коэффициент передачи (также коэффициент преобразования) — отношение напряжения на выходе той или иной системы, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, когда значения выходного и входного сигнала являются однородными, коэффициент передачи называют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи часто выражают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ.
Содержание
Коэффициент усиления и ослабления сигнала
- В усилительных устройствах коэффициент передачи больше единицы (больше нуля в логарифмическом масштабе) называют коэффициентом усиления (не путать с коэффициентом усиления антенны).
- При рассмотрении пассивных устройств, а также линий передачи, когда выходное напряжение меньше входного, употребляют понятие ослабление сигнала.
Комплексный коэффициент передачи
При анализе частотнозависимых устройств часто возникает необходимость в векторном представлении коэффициента передачи
- Комплексный коэффициент передачи K(jω) — отношение комплексной амплитуды (КА)Y выходной величины системы к комплексной амплитуде X входной величины синусоидальной формы при заданном значении её частоты ω.
Также ещё используется (в основном на практике в теории передачи сигналов по каналу связи) обратный комплексный коэффициент передачи (1/K(jω)). Так как ККП в этом случае меньше единицы и имеет дробный вид, что усложняет расчёты, комплексную амплитуду выходного сигнала Y можно вычислить умножением КА входного сигнала X на K(jω), если комплексный коэффициент передачи априори известен. Комплексный коэффициент передачи является комплексной величиной, а его компоненты зависят от частоты входного сигнала. Может быть представлен вектором на комплексной плоскости (построенная таким образом кривая называется годографом коэффициента передачи).
Измерения
- Прямое измерение — производится с помощью установок для измерения ослаблений или измерителей коэффициента передачи, в том числе панорамных.
- Совокупное измерение — производится с помощью измерения мощности или напряжения сигнала на выходе и на входе, и последующего расчета.
- Измерение методом сравнения — производится с помощью аттенюатора, являющегося мерой ослабления. В качестве меры коэффициента усиления, в принципе, можно применить откалиброванный измерительный усилитель, однако на практике это, как правило, не используется.
- Для измерения комплексных коэффициентов передачи применяются измерители импеданса и комплексных коэффициентов передачи, или, на сверхвысоких частотах, измерители комплексных коэффициентов и КСВ.
Литература
- Хлытчиев С. М. Основы автоматики и автоматизации производственных процессов. — 1985
- Словарь радиолюбителя — Л.: Энергия, 1979
- Гусев В. Г. Электроника. — 1991
Ссылки
- Добавить иллюстрации.
- Радиотехнические величины и параметры
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Коэффициент передачи» в других словарях:
коэффициент передачи — Отношение комплексной амплитуды сигнала на выходе системы (усилителя, фильтра и т.п) к комплексной амплитуде сигнала на ее входе. Часто используют модуль коэффициента передачи, являющийся действительной величиной. [Система неразрушающего контроля … Справочник технического переводчика
коэффициент передачи — perdavimo koeficientas statusas T sritis automatika atitikmenys: angl. transfer coefficient; transfer gain; transmission gain vok. Übertragungskoeffizient, m; Übertragungsmaß, n rus. коэффициент передачи, m pranc. coefficient de transfert, m;… … Automatikos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus elektrinės grandinės išėjimo ir įėjimo signalų įtampų, srovių arba galių dalmeniui. atitikmenys: angl. transfer coefficient; transfer factor;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis fizika atitikmenys: angl. transfer factor; transfer ratio vok. Übertragungsfaktor, m; Übertragungsverhältnis, n rus. коэффициент передачи, m pranc. facteur de transmission, m; rapport de transfert, m … Fizikos terminų žodynas
коэффициент передачи при виброизоляции — коэффициент передачи Ндп коэффициент амортизации Отношение амплитуды виброперемещения (виброскорости, виброускорения защищаемого объекта или действующей на него силы) к амплитуде той же величины источника возбуждения при гармонической вибрации.… … Справочник технического переводчика
коэффициент передачи между оптическими полюсами — коэффициент передачи между полюсами Отношение мощности оптического излучения на одном из оптических полюсов компонента ВОСП к мощности оптического излучения на другом из его оптических полюсов, выраженное в децибелах. [ГОСТ 26599 85] Тематики… … Справочник технического переводчика
коэффициент передачи интегральной микросхемы — коэффициент передачи Отношение абсолютного значения изменения выходного напряжения усилителя рассогласования интегральной микросхемы к абсолютному изменению входного напряжения. Обозначение KUP [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
коэффициент передачи модуля СВЧ — коэффициент передачи Кпер Отношение мощности на выходе модуля СВЧ к мощности на его входе при согласовании входа и выхода по заданному коэффициенту стоячей волны. [ГОСТ 23221 78] Тематики компоненты техники связи Обобщающие термины модули СВЧ,… … Справочник технического переводчика
коэффициент передачи мощности преобразовательного прибора СВЧ — коэффициент передачи мощности Кпер Отношение мощности преобразованного сигнала прибора СВЧ к мощности входного сигнала. [ГОСТ 23769 79] Тематики приборы и устройства защитные СВЧ Синонимы коэффициент передачи мощности … Справочник технического переводчика
коэффициент передачи по напряжению интегральной микросхемы — коэффициент передачи по напряжению Отношение напряжения на выходе интегральной микросхемы к заданному значению коммутируемого напряжения при включенном канале. Обозначение Кп KU [ГОСТ 19480 89] Тематики микросхемы Синонимы коэффициент передачи по … Справочник технического переводчика
Коэффициент передачи
Форма представления коэффициента передачи зависит от формы математического представления сигналов входа и выхода. Это могут быть, например, операторы Лапласа или Фурье, тогда коэффициенты передачи называют операторными.
Коэффициент передачи и коэффициент усиления
В частности, если величины входного и выходного сигналов однородны, тогда коэффициент передачи называют коэффициентом усиления. Так, коэффициентом усиления по напряжению () называют физическую величину, равную отношению амплитуды переменной компоненты выходного напряжения (
) к амплитуде входного напряжения (
):
В выражении для коэффициента усиления можно использовать не только амплитуды, но и действующие значения напряжения.
Если коэффициенты усиления выражают в децибелах, то определением коэффициента преобразования (усиления) по напряжению будет выражение:
Коэффициенты усиления по току и мощности в децибелах выражают как:
Коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах:
Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
K(дб)=
Если в усилителе коэффициент передачи больше единицы для безразмерного коэффициента или больше нуля для коэффициента, представленного в децибелах, то коэффициент называют коэффициентом усиления.
Коэффициент передачи может быть представлен в комплексном виде. Он используется для анализа устройств, которые зависят от частоты сигналов.
Комплексный коэффициент передачи линейного звена находят как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:
где — комплексная амплитуда выходного сигнала,
— комплексная амплитуда сигнала на входе,
— частота.
Единицы измерения
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.
Примеры решения задач
| Задание | Что такое частотный годограф? |
| Решение | Комплексный коэффициент передачи применяют для графического изображения свойств звена. С этой целью строят частотный годограф. Частотным годографом называют геометрическое место точек, которое создает конец вектора комплексного коэффициента передачи, если частота сигнала изменяется от 0 до |
Для узла, к которому подключен инвертирующий выход, запишем закон Кирхгофа для токов:
Рассмотрим контур, который включает источник напряжения, вход усилителя, и сопротивление , запишем второй закон Кирхгофа для этого контура:
Рассмотрим контур, который включает вход усилителя, сопротивление и выход схемы, получаем:
Выразим из (2.3) выходное напряжение и учтем, что: если усилитель работает в линейном режиме, то входные токи в рассматриваемый усилитель равны нулю (в нашем случае ); напряжение на входе в такой усилитель равно нулю
=0. Тогда:
Коэффициент передачи
- Коэффициент передачи (также коэффициент преобразования) — отношение мощности, напряжения или тока на выходе той или иной системы, предназначенной для передачи электрических сигналов, соответственно, к мощности, напряжению или току на входе системы. Например, выражение для коэффициента передачи по напряжению: KV = V2 / V1.
Коэффициент передачи часто выражают в децибелах (дБ, dB), в основе которых лежит десятичный логарифм отношения величин. Например: KV (дБ) = 20 lg (V2 / V1). В случае, когда значения рассматриваемых величин уже представлены в децибелах: KV (дБ) = V2 (дБ) − V1 (дБ). Коэффициент передачи, выраженный в децибелах, может иметь знак плюс или минус в зависимости от соотношения величин на выходе и на входе.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В статье описаны некоторые типовые применения операцио́нных усили́телей (ОУ) в аналоговой схемотехнике.
При включении биполярного транзистора по схеме с общим эмиттером (ОЭ) входной сигнал подаётся на базу относительно эмиттера, а выходной сигнал снимается с коллектора относительно эмиттера. При этом выходной сигнал инвертируется относительно входного (для гармонического сигнала фаза выходного сигнала отличается от входного на 180°). Данное включение транзистора позволяет получить наибольшее усиление по мощности, потому что усиливается и ток, и напряжение.
ЧЕТЫРЕХПОЛЮСНИКОВ
3.1.
Частотные характеристики четырехполюсников
Четырехполюсником
называют цепь с четырьмя полюсами
(выводами, контактами), разделенными на
пару входных и пару выходных полюсов,
как показано на рис. 3.1.
Свойства
электрической цепи с реактивными
элементами зависят от частоты сигнала.
Частотными
называют характеристики цепи, рассматри-
Рис.
3.1 ваемые в заданном
диапа-
зоне
частот. В инженерной
практике
рассматриваются различные частотные
характеристики. Чаще всего свойства
четырехполюсника анализируются при
гармонических воздействиях, которые
описываются комплексными
амплитудами.
В линейном четырехполюснике при
гармоническом воздействии все токи и
напряжения являются также гармоническими
с той же частотой.
3.2.
Входное и выходное сопротивления
четырехполюсника
В
качестве частотных характеристик
рассматриваются входное
и выходное
сопротивления как функция частоты
сигнала. По определению при заданном
сопротивлении нагрузки четырехполюсника,
подключенном к его выходу, равны
.
44
Выходное
сопротивление определяется при известном
внутреннем сопротивлении источника
входного сигнала,
.
Знание
этих характеристик необходимо при
анализе возможностей подключения к
четырехполюснику реального источника
сигнала и нагрузки.
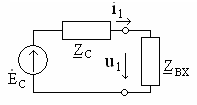
В
качестве примера рассмотрим цепь на
рис. 3.2, в состав которой входят источник
входного сигнала (реальный источник
гармонического напряжения с комплексной
амплитудой
и частотой
),RC
— четырехполюсник и нагрузка
.
Рис. 3.2
Схема
цепи для определения входного сопротивления
нагруженного четырехполюсника показана
на рис. 3.3. Величина
определяется выражением
Рис.
3.3
45
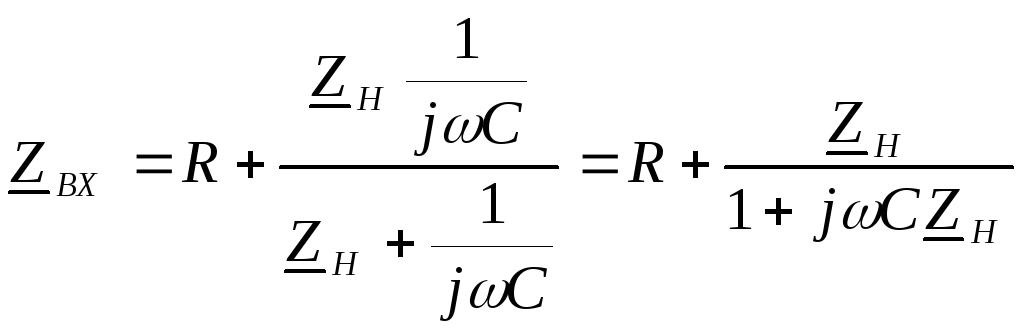
При
активной нагрузке
,
умножая числитель и знаменатель дроби
на комплексно-сопряженный множитель,
получим

модуль входного
сопротивления равен

а
активную
и реактивную
составляющие можно записать в виде
,

На
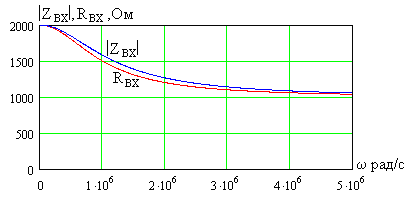
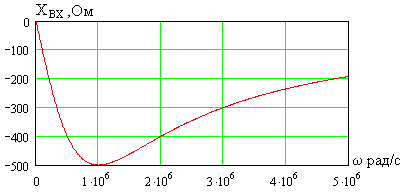
рис. 3.4 приведены зависимости от частоты
модуля
и активной составляющей
входного сопротивления четырехполюсника
прикОм
инФ.
На
рис. 3.5 показана зависимость от частоты
реактивной составляющей входного
сопротивления четырехполюсника.
46
Рис. 3.4
Рис. 3.5
Как
видно, входное сопротивление
четырехполюсника существенно изменяется
в выбранном диапазоне частот и имеет
емкостный характер. Модуль и активная
составляющая сопротивления уменьшаются
с ростом частоты от значения
при
до
на бесконечной частоте (на высоких
частотах емкость шунтирует нагрузку).
Знание
входного сопротивления четырехполюсника
необходимо при анализе возможностей
подключения к нему реального источника
напряжения, схема входной цепи показана
на рис. 3.6.
47
Если
необходимо обеспечить максимум амплитуды
входного напряжения
,
то по закону Ома получим
.
Представляя
и
,
можно записать
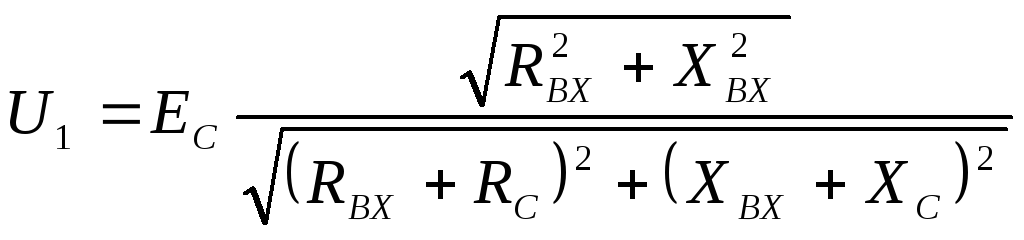
Анализ
полученного выражения известными
методами может быть задачей исследовательской
части курсовой работы (проекта).
Если
решается задача
Рис.
3.6 обеспечения максимума
мощно-
сти
,потребляемой
четырехполюсником от источника сигнала,
то из общего выражения
,
где
—
комплексно сопряженная амплитуда
входного тока, получим
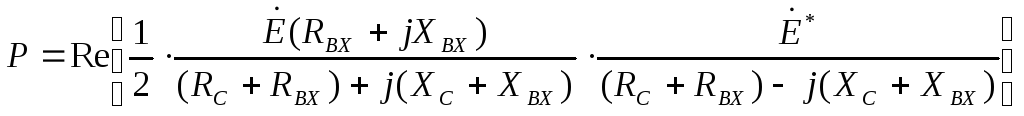
48
где
— комплексно-сопряженная ЭДС источника,
а— оператор вычисления реальной части
числа. С учетом того, что произведение
комплексно-сопряженных чисел равно
квадрату их модуля, можно записать
,
в результате
получим
.
Из
полученного выражения нетрудно получить
условие максимума потребляемой
четырехполюсником (рис. 3.6) мощности
(условие
согласования четырехполюсника с
источником сигнала),
Полученные
результаты можно использовать в
исследовательской части курсовой
работы.
Аналогичный
анализ можно провести и для выходной
цепи четырехполюсника, рассматривая
условия максимизации выходного напряжения
на нагрузке, или выделяемой в ней
мощности.
3.3.
Комплексный коэффициент передачи
Чаще
всего в качестве частотных характеристик
рассматривается его коэффициент
передачи. Комплексный коэф-
49
фициент
передачи по напряжению определяется
выражением
.
(3.1)
Аналогично
вводятся в рассмотрение комплексный
коэффициент передачи тока
(3.2)
и
коэффициент (не
комплексный)
передачи мощности
,
(3.3)
где
— мощность, потребляемая четырехполюсником,
а— мощность, передаваемая в нагрузку.
Для
расчета коэффициентов передачи необходимо
при заданном источнике входного сигнала
определить комплексные амплитуды
входного и выходного напряжений или
токов (а при необходимости и величины
мощностей).
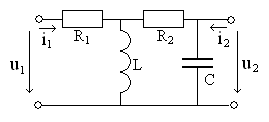
В
качестве примера рассмотрим четырехполюсник,
схема которого показана на рис. 3.7, и
определим его комплексный коэффициент
передачи напряжения вида (3.1).
Рис. 3.7
50
Расчет
целесообразно провести, подключив на
вход четырехполюсника идеальный источник
напряжения с ЭДС
,
как показано на рис. 3.8, методом узловых
напряжений. В цепи имеется два узла,
следовательно необходимо определить
единственное узловое напряжение.
Рис. 3.8
Выражая
через
токи ветвей, и используя первый закон
Кирхгофа, получим уравнение метода
узловых напряжений в виде
После
алгебраических преобразований получим
.
(3.4)
Тогда
по Закону Ома можно определить выходное
напряжение
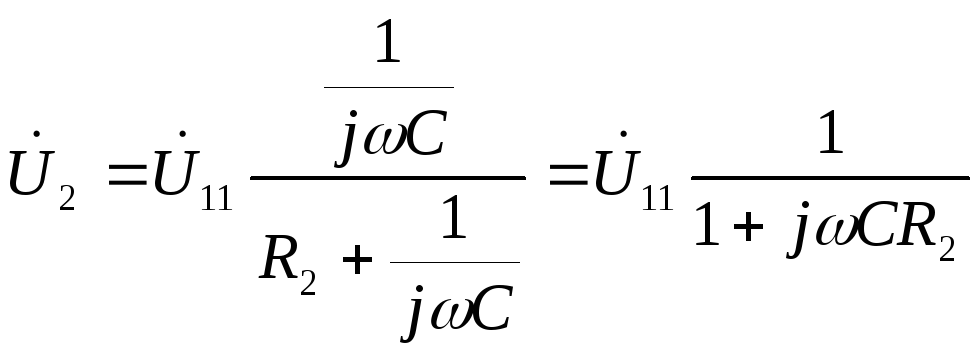
51
Подставляя
(3.4), с учетом
получим
.
Тогда
комплексный коэффициент передачи
четырехполюсника по напряжению равен
.
(3.5)
Как
видно,
— комплексная функция частоты сигнала,
ее называюткомплексной
частотной характеристикой (КЧХ).
Графически она отображается линией в
трехмерном пространстве, что неудобно
практически.
На
плоскости КЧХ изображается в виде
годографа.
Для его построения заданный интервал
частот разбивается с равномерным шагом,
для каждого значения частоты вычисляются
и отображаются на комплексной плоскости
по осям абсцисс и ординат соответственно
действительная
и
мнимаясоставляющие комплексного коэффициента
передачи.
Пример
годографа КЧХ цепи на рис. 3.8 при
кОм,
мГн
инФ
показан на рис. 3.9. Стрелка показывает
направление увеличения частоты
входного
Рис.
3.9 сигнала. На частоте
52
величина
действительна, а точка годографа
расположена на оси абсцисс.
3.4.
Амплитудно-частотная и фазочастотная
характеристики
четырехполюсника
Комплексный
коэффициент передачи четырехполюсника
можно представить в показательной форме
,
(3.6)
где
—
его модуль, а— аргумент.
Амплитудно-частотная
характеристика
(АЧХ)
представляет собой зависимостьмодуля
комплексного коэффициента передачи от
частоты.
Фазочастотная
характеристика
(ФЧХ)
– это зависимость от частотыаргумента
комплексного коэффициента передачи.
Обычно
выражение для
представляет собой дробь с комплексными
числителем и знаменателем, которую
необходимо представить в виде
.
(3.7)
Тогда
модуль
частного (дроби) равен частному модулей
числителя и знаменателя:
,
(3.8)
53
а
ее аргумент
– разности аргументов числителя и
знаменателя:
.
(3.9)
Аргумент
комплексного числа
определяется выражением
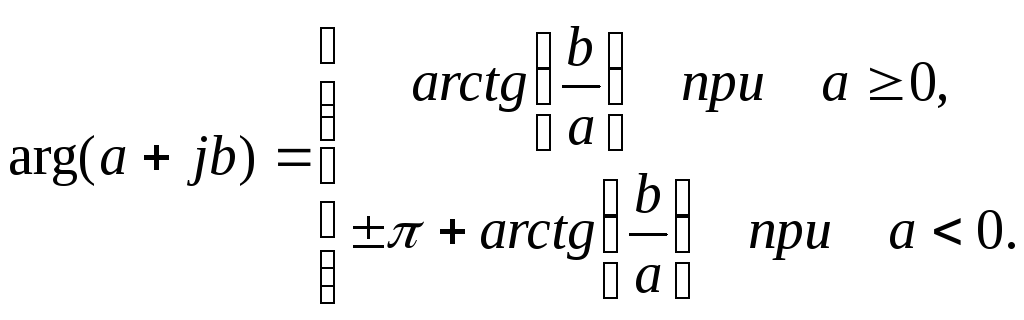
Определим
АЧХ и ФЧХ цепи, показанной на рис. 3.7. Ее
комплексный коэффициент передачи по
напряжению определяется выражением
(3.5). Тогда его модуль (АЧХ) и аргумент
(ФЧХ) соответственно равны
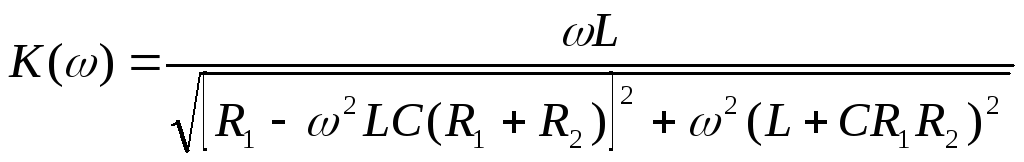
(3.11)
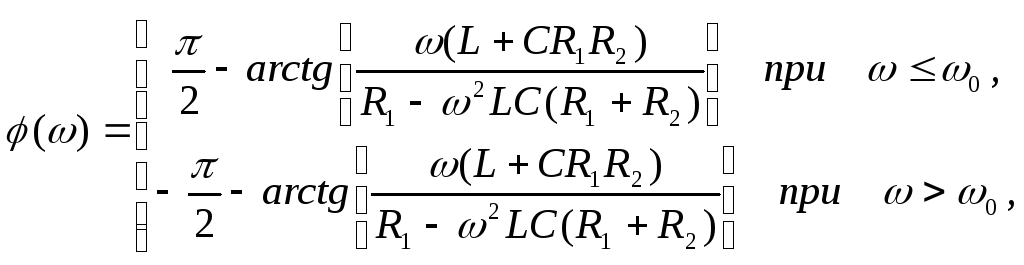
где
.
(3.13)
На
рис. 3.10 показан график АЧХ четырехполюсника,
54
показанного
на рис. 3.7 при
кОм,
мГн
инФ.
Как видно, он представляет собой полосовой
фильтр. Максимум АЧХ имеет место на
частотеиз (3.13), в чем нетрудно убедиться, взяв
производнуюи приравняв ее нулю. На рис. 3.11 приведен
график ФЧХ четырехполюсника.
Рис. 3.10
Рис. 3.11
На
частотах
ФЧХ
,
то есть выходное напряжение опережает
по фазе входное, а если,
то наоборот. На частотесдвиг фаз между этими напряжениями
равен нулю (они синфазны).
55
3.5. Характеристики
избирательности
Избирательность
характеризует способность четырехполюсника
со свойствами частотного фильтра хорошо
передавать на выход сигналы одних частот
и подавлять сигналы на других частотах.
Д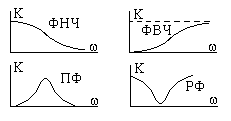
четырех основных типов фильтров: нижних
частот (ФНЧ), верхних частот (ФВЧ),
полосовых (ПФ) и режекторных (РФ), типовые
графики амплитудно-частотных характеристик
показаны на рис. 3.12.
Фильтры
нижних частот (ФНЧ) и полосовые
Рис.
3.12 фильтры (ПФ) характеризуют
всего полосой
пропускания
– диапазоном
частот, внутри которого АЧХ уменьшается
не более, чем в
раз или на 3 дБ (децибела) относительно
максимального значения.
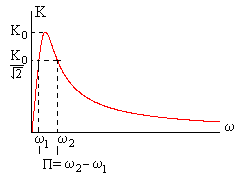
Это определение применительно к
полосовому фильтру иллюстрирует график
на рис. 3.13. Прежде всего определяется
максимум
АЧХ и величина АЧХ на границе полосы
пропускания, равная.
Затем по графику или из решения уравнения
вида
Рис.
3.13
56
(3.14)
находятся
частоты
и
,
соответствующие границам полосы
пропускания, которые называютчастотами
среза. Тогда
полоса пропускания
равна
.
(3.15)

фильтров верхних частот (ФВЧ) и режекторных
фильтров (РФ) полоса пропускания
бесконечна, и для их описания используетсяполоса
удержания
—диапазон
частот, внутри которого АЧХ уменьшается
более,
чем в
раз или на 3 дБ (децибела) относительно
максимального значения,
что иллюстрирует график, показанный на
рис. 3.14. Расчет проводится аналогично
предыдущему и
Рис.
3.14
,
(3.16)
а
частоты среза определяются из уравнения
(3.14).
Полоса
пропускания (удержания) характеризует
частотный диапазон, в котором фильтр
выполняет заданные функции передачи
(не прохождения) сигнала. Как видно из
приведенных рисунков, характер передачи
сигнала меняется достаточно плавно и
представляют интерес характеристики
избирательности, показывающие резкость
перехода от пропускания до удержания
сигнала при изменении частоты.
57
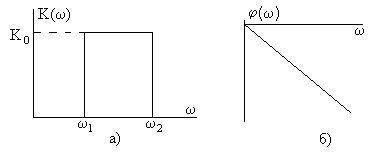
Наилучшей
избирательностью обладает идеальный
фильтр с прямоугольной АЧХ и прямолинейной
ФЧХ, как показано на рис. 3.15 для ПФ.
Рис.
3.15
Такой
идеальный фильтр физически
нереализуем,
но к его частотным характеристикам
можно приблизиться за счет усложнения
схемы реального фильтра.
Мерой
близости АЧХ реального фильтра к
показанной на рис. 3.15а является коэффициент
прямоугольности
.
Для ФНЧ и ПФ он равен отношению полосы
пропускания
на уровне
(-3 дБ) к аналогичной полосе пропускания
на уровне
(-20 дБ),
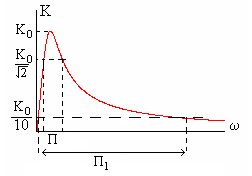
(3.17)
Расчет
иллюстрирует рис. 3.16. Полоса
вычисляется из уравнения
.
(3.18)
Рис.
3.16
58
Для
ФВЧ и РФ коэффициент прямоугольности
равен обратной величине
.
(3.19)
Для
реальных фильтров величина
всегдаменьше
единицы. Чем
ближе
к 1, тем выше избирательность частотного
фильтра.
Рассмотрим
пример цепи на рис. 3.7. Выражение для АЧХ
имеет вид (3.11). Максимум АЧХ имеет место
на частоте
(3.13) и равен
.
(3.20)
Тогда
согласно (3.14) уравнение для полосы
пропускания имеет вид
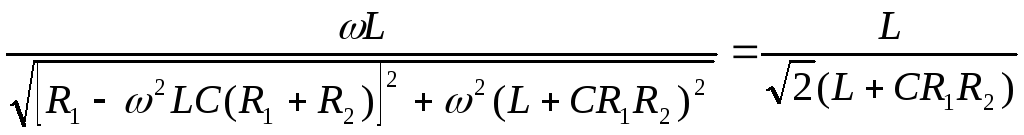
(3.21)
Возводя
обе части (3.21) в квадрат и проведя
алгебраические преобразования с учетом
(3.13), получим уравнение
(3.22)
где
константа
равна
.
(3.23)
59
Решение биквадратного
уравнения (3.21) имеет вид
.
(3.24)
Из (3.23) можно
записать, что
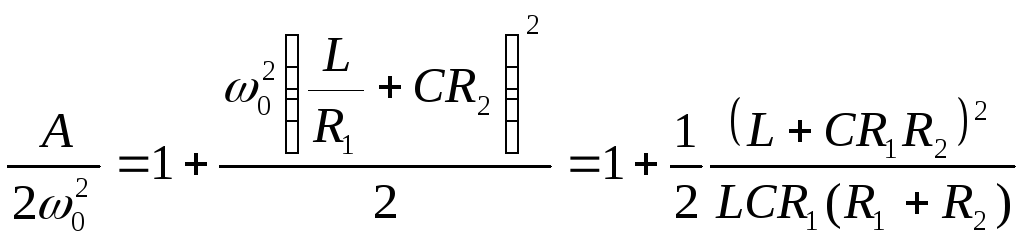
(3.25)
тогда
и подкоренные выражения в (3.24) всегда
положительны.
Если
представить выражение для
из (3.25) в виде
,
(3.26)
где
,
(3.27)
то
из (3.24) получим выражение для частот
среза
,
(3.28)
а
величина
из (3.27) безразмерна, положительна и
определяется параметрами четырехполюсника.
Полоса пропусканияравна разности верхней и нижней частот
среза
.
(3.29)
60
Если
возвести обе части выражения (3.29) в
квадрат, то можно записать
=
,
тогда получим
.
(3.30)
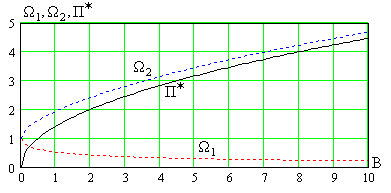
На
рис. 3.17 показаны зависимости от параметра
нормированных к
значений частот среза и полосы пропускания
,
,
.
Рис.
3.17
Как
видно, при
частоты
и
равны
,
полоса пропусканияравна нулю. Согласно (3.27), малые значения
обеспечиваются при
и
.
С ростомполоса пропускания расширяется,
практически стремясь к вели-
61
чине
.
ПрикОм,
мГн
инФ
получим,
рад/с,
рад/с,
при этом полоса пропускания равнарад/с или
кГц.
Вычислим
коэффициент
прямоугольности,
для этого определим полосу пропускания
на уровне 0,1 от максимума АЧХ
из уравнения вида
.
(3.31)
С
учетом выражения для АЧХ (3.11) можно
записать уравнение для граничных частот
полосы пропускания
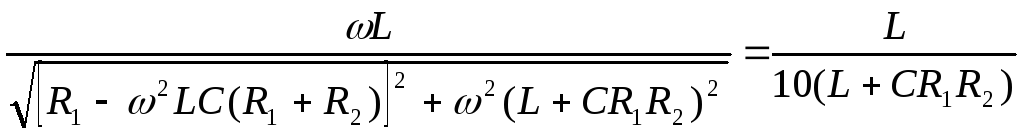
(3.32)
Как
и для (3.21), возводя обе части уравнения
(3.31) в квадрат и проведя алгебраические
преобразования с учетом (3.13), получим
уравнение
(3.33)
где
константа
равна
.
(3.34)
Как
видно, величина
отличается от полученной ранее константы
множителем перед вторым слагаемым.
Решение биквадратного уравнения (3.32)
имеет вид
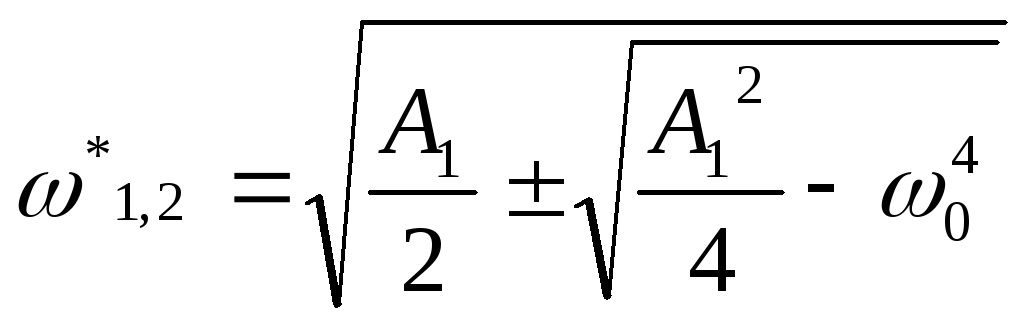
(3.35)
62
Представим
выражение для
из (3.33) в виде
,
(3.36)
где
,
(3.37)
тогда
из (3.34) получим аналогичное (3.28) выражение
для частот среза
.
(3.38)
Полоса
пропускания
равна разности верхней и нижней частот
среза
.
(3.39)
Аналогично (3.30)
нетрудно получить
.
(3.40)
Сравнивая
величины
(3.27) и
(3.37), получим
.
(3.41)
В
результате выражение для коэффициента
прямоугольности согласно (3.17) принимает
вид
.
(3.42)
63
Коэффициент
прямоугольности рассматриваемой цепи,
схема которой приведена на рис. 3.8, не
зависит от ее параметров и равен 0,1.
3.6.
Расчет реакции цепи на сложное входное
воздействие
В
качестве факультативного
задания при выполнении курсовой работы
можно провести расчет сигнала на выходе
заданной цепи при воздействии на ее
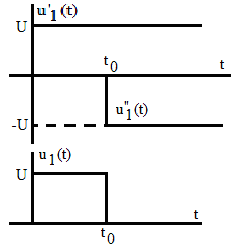
вход импульсной последовательности,
примеры которой показаны на рис. 3.18.
Рис.
3.18.
Известны
[1,2] методы расчета реакции цепи на
сложное входное воздействие (частотный,
операторный, временной). В данном случае
целесообразнее использовать временной
метод (метод интеграла Дюамеля), в рамках
которого выходное напряжение
четырехполюсника
равно
64
,
(3.43)
где
—
входное напряжение, равное нулю при,
— импульсная характеристики цепи.
Переходная
характеристика
безразмерна
и численно равна реакции (выходному
сигналу) четырехполюсника на входное
воздействие в виде единичной функции
(известной в математике функции Хевисайда)вида рис. 3.19а.
Импульсная
характеристика
имеет размерность
и численно равна реакции цепи на входное
воздействие в видедельта-функции
(функции Дирака)
,
показанной на рис. 3.19б.
Рис.
3.19.
Расчет
временных характеристик цепи
и
проводится с помощью операторного
коэффициента передачи,
который определяется через комплексный
коэффициент передачизаменой
.
Переходная
характеристика
является обратным преобразованием
Лапласа от,
,
(3.44)
65
где
— символ взаимно однозначного соответствия.
Импульсная
характеристика
является обратным преобразованием
операторного коэффициента передачи
.
(3.45)
Преобразование
Лапласа проводится по таблицам [1].
В
таблицах преобразования Лапласа
изображение
представляется в виде правильной дроби,
числитель и знаменатель которой является
произведением простейших сомножителей,
в каждом из которых коэффициент при
старшей степениравен
единице.
Рассмотрим
пример расчета временных характеристик
цепи, показанной на рис. 3.20а, ее операторная
эквивалентная операторная схема
приведена на рис. 3.20б (аналогичный
расчет можно провести в исследовательской
части курсовой работы).
Рис. 3.20
Определим
операторный коэффициент передачи
методом узловых напряжений. В цепи на
рис. 3.20б два узла и единственное узловое
напряжение обозначено как
,
тогда для токов ветвей получим
,
66
,
.
Подставив их в
уравнение первого закона Кирхгофа вида
,
для узлового напряжения получим уравнение
,
из которого
определим узловое напряжение
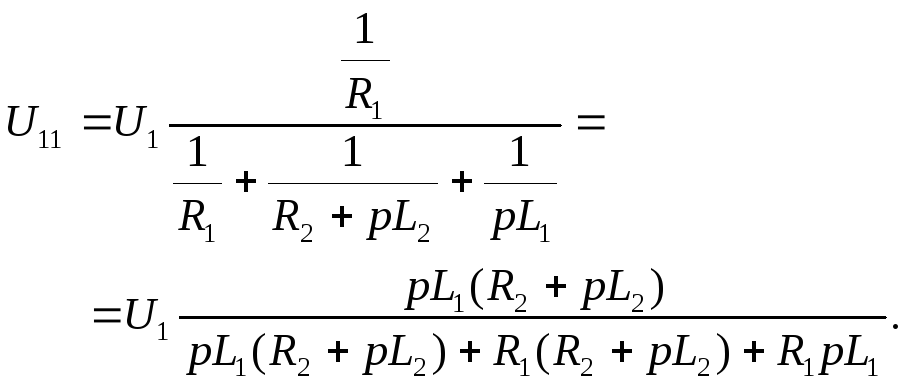
Выходное напряжение
четырехполюсника на рис. 3.20б связано с
узловым напряжением соотношением
,
тогда с учетом
(3.46) получим
(3.47)
67
Из
(3.47) определим операторный
коэффициент передачи
в виде (проведите преобразования
самостоятельно)
,
(3.48)
где
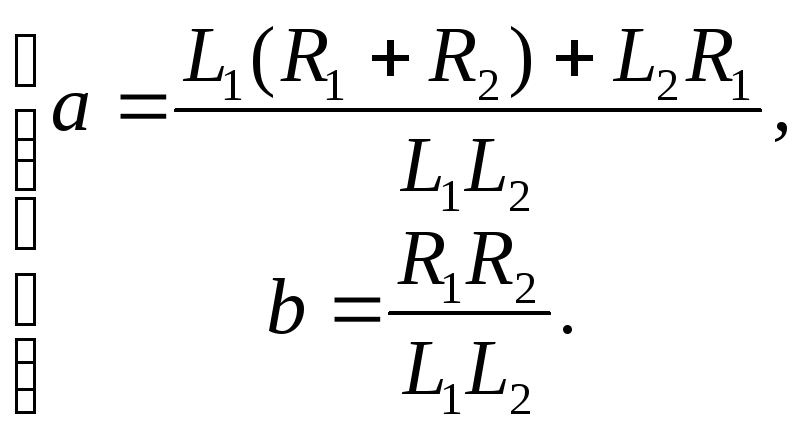
Для
простоты положим одинаковыми
одноименные параметры цепи,
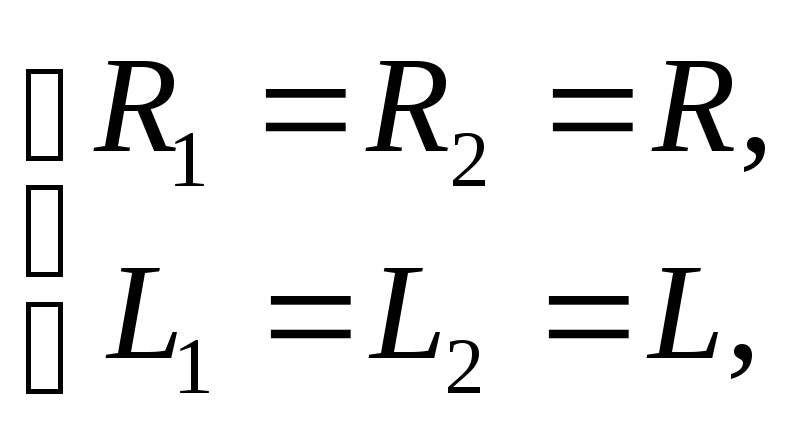
тогда
для параметров операторного коэффициента
передачи из (3.49) получим
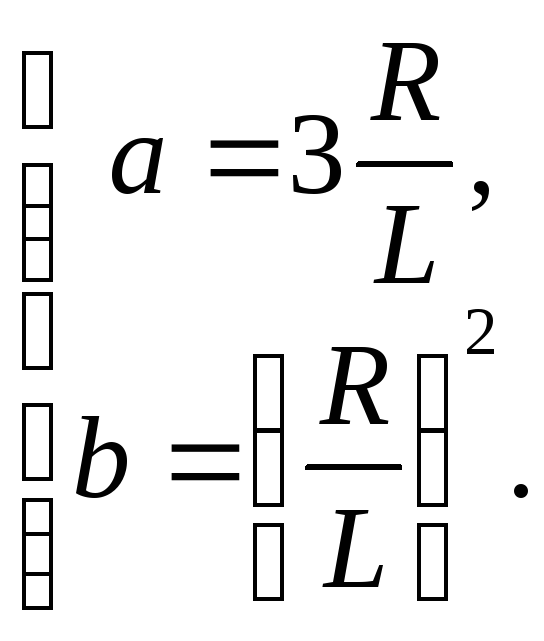
Выражение (3.48)
можно записать в виде
,
(3.52)
где
и
— полюсы
— корни полинома знаменателя,
68
.
(3.53)
С
учетом (3.51) можно записать
,
(3.54)
в результате
получим
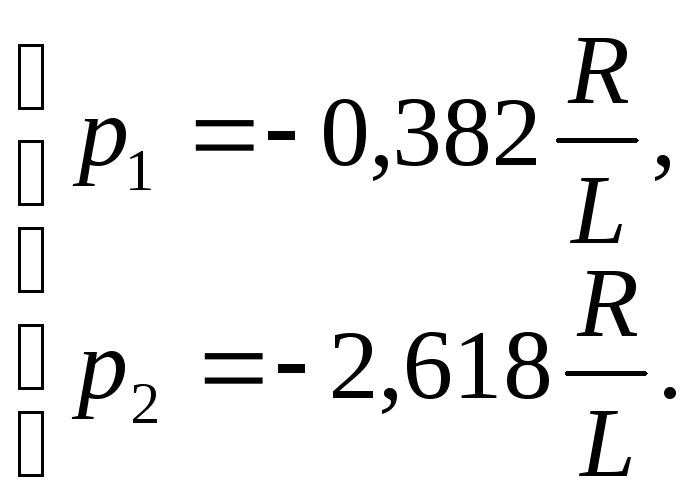
Выражение (3.52)
можно представить в виде
.
(3.56)
Константы
и
можно определить, сложив дроби в (3.56) и
уравняв коэффициенты с (3.52). Из (3.56)
(3.57)
тогда
(3.52) для
и
получим уравнения
(3.58)
из которых
69
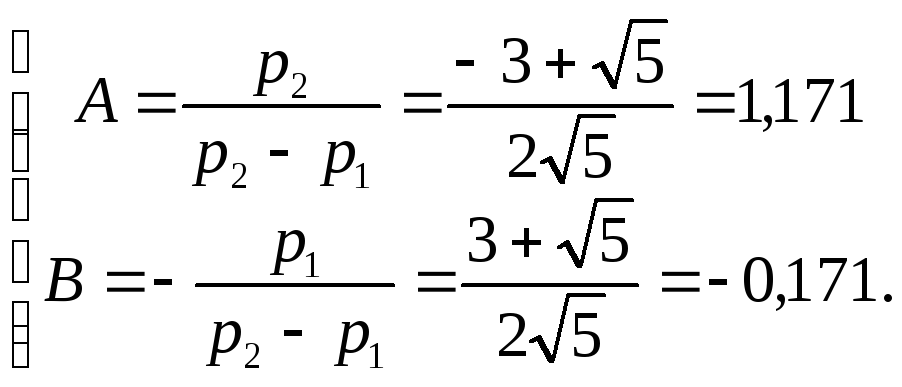
Из
(3.56) по таблицам преобразования Лапласа
определим переходную
характеристику
цепи
как оригинал
,
тогда
(3.60)
(проведите
расчет самостоятельно).
Для
расчета импульсной характеристики
преобразуем с учетом
операторный коэффициент передачи
(3.56) к виду
,
(3.61)
тогда
импульсная
характеристика
цепи
будет равна оригиналу
.
(3.62)
Как
видно, в состав
входит
-функция
(функция Дирака). Нетрудно убедиться,
что импульсная характеристикаявляется производной от переходной
характеристики(проверьте
это самостоятельно).
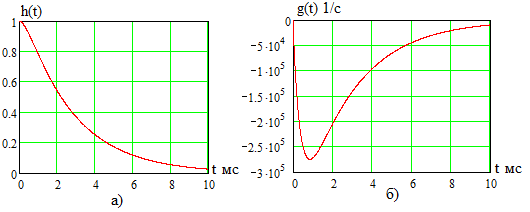
Графики
рассмотренных временных характеристик
и
(без
-функции)
цепи рис. 3.20а прикОм
имГн
показаны на рис. 3.21а и рис. 3.21б
соответственно.
70
Рис. 3.21
Определим
реакцию цепи рис. 3.20а на входное
воздействие
в виде скачка напряжения с амплитудой
,
показанного на рис. 3.22а.
Рис. 3.22
Входной сигнал
можно записать в виде
,
(3.63)
где
— функция Хевисайда.
Эту
задачу можно решить просто, вспомнив
определение переходной характеристики
цепи (это реакция цепи на входной
воздействие в виде единичного скачка
напряжения – функции Хевисайда с
амплитудой 1 В).
71
В
результате выходное напряжение линейной
цепи на рис.
3.20а будет равно
.
(3.64)
Определим
выходное напряжение методом интеграла
Дюамеля [3] (3.43),
.
(3.65)
Из
(3.60) с учетом (3.58)
,
тогда прии
.
(3.66)
В
соответствии с «фильтрующим свойством
-функции»
,
(3.67)
тогда
с учетом того, что переменная
является константой в интеграле по
,
получим
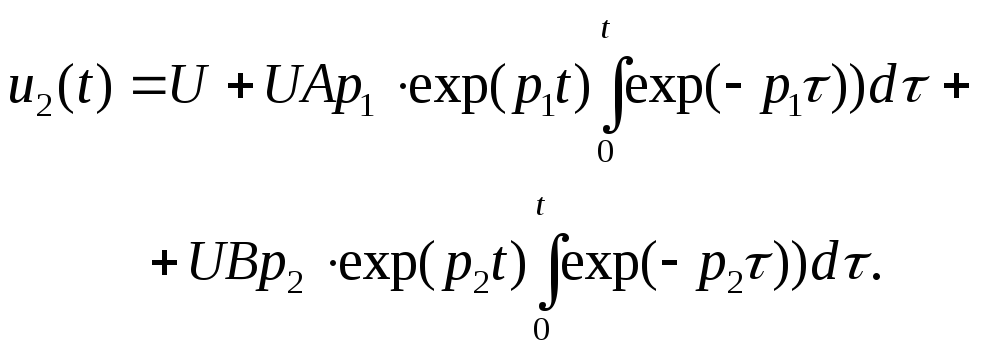
72
Вычислим интегралы,
тогда
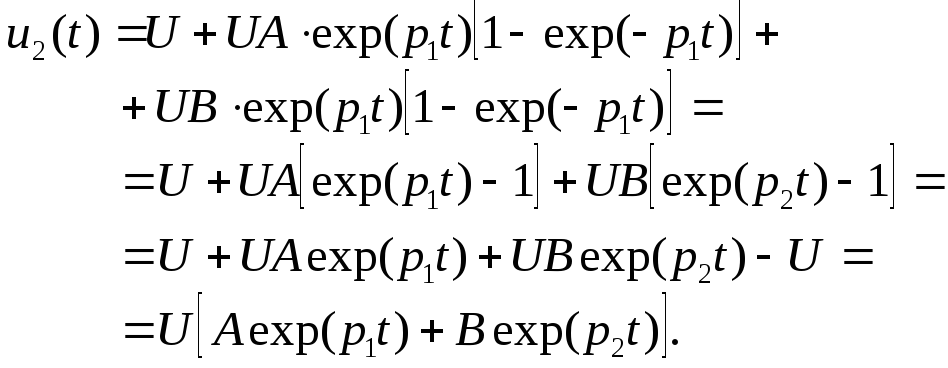
Как видно, полученный
результат совпадает с (3.64).
Проведем
расчет реакции цепи (рис. 3.20а) на входное
воздействие в виде одиночного
прямоугольного импульса, показанного
на рис. 3.22б. Для этого можно использовать
два подхода.
В
первом из них импульс
на рис. 3.22б можно представить суммой
двух скачков напряженияи
,
как показано на рис. 3.23.
Рис. 3.23
73
Реакция
цепи
на входной сигнал
пропорциональна переходной характеристике
(2.60) с коэффициентом
,
.
(3.70)
Аналогично
входное воздействие
(рис. 3.23) вызовет реакцию цепи
,
пропорциональную переходной характеристикес коэффициентом
,
в виде формулы
,
(3.71)
справедливой
только
при
.
В результате получим выражение для
выходного напряжения
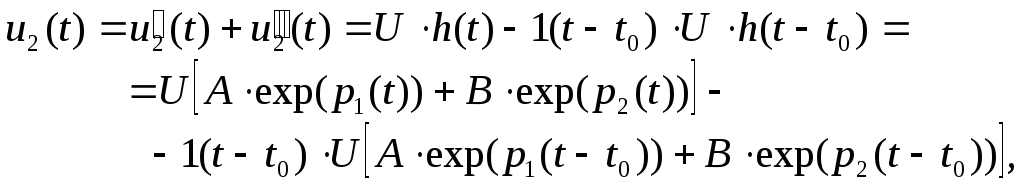
где
— функция Хевисайда,
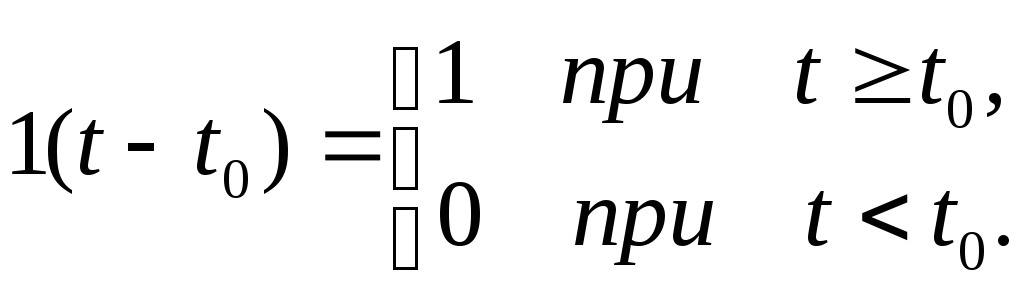
Зависимость
показана на рис. 3.24.
Второй
подход предполагает прямое применение
формулы интеграла Дюамеля (3.43). На
интервале времени
входной сигнал равен
(рис. 3.23), тогда с учетом
(рис. 3.21) и выражения для импульсной
характеристики (3.62) получим
74
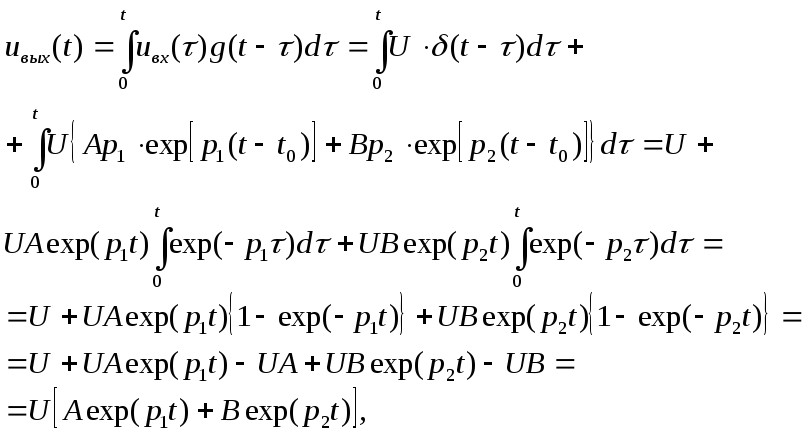
что
совпадает с (3.70) (проведите
преобразования самостоятельно).
Рис. 3.24
На
интервале времени
входной сигнал равен нулю и тогда для
интеграла Дюамеля получим
.
(3.75)
75
Тогда с учетом
(3.62)
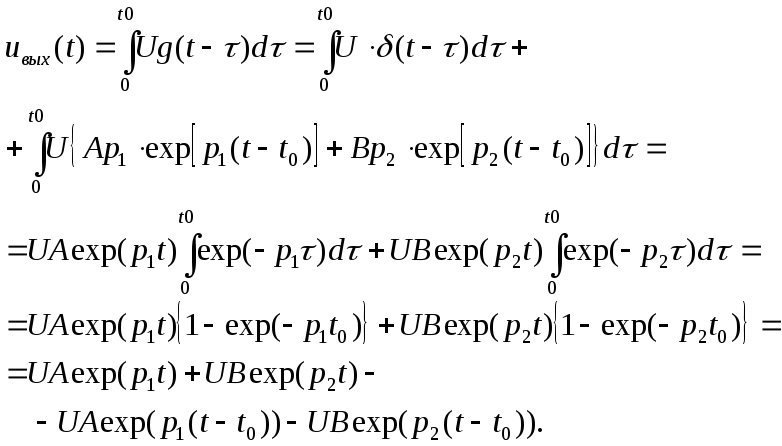
В (3.76) интеграл
так
как
и на интервале интегрирования
.Сравните
формулы (3.76) и (3.72) в области
и убедитесь в их совпадении.
Как
видно, имеется возможность аналитического
определения выходного сигнала.
Для
нахождения выходного сигнала можно
использовать методы численного
интегрирования с помощью систем объектно
ориентированного программирования
(например, Delphi) или пакета программ
MathCAD, пример которой в рассматриваемом
случае показан на рис. 3.25. Как видно,
полученная на рис. 3.25 временная диаграмма
выходного сигнала совпадает с показанной
на рис. 3.24.
Аналогичные
расчеты целесообразно провести в рамках
исследовательской части курсовой
работы.
76
Рис. 3.25
77
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
Амплитудно-частотная характеристика (АЧХ)
Фазочастотная характеристика (ФЧХ)
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
где 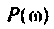
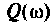
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
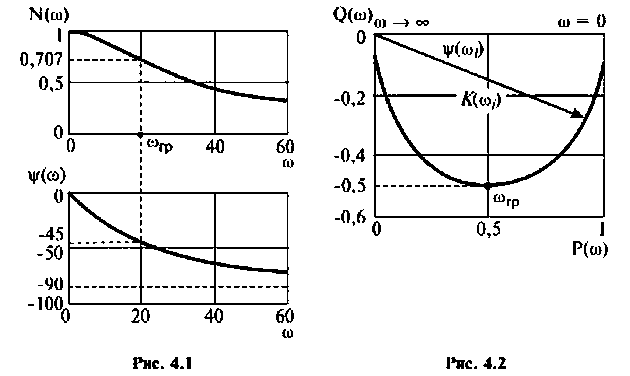
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 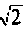
Полоса пропускания может измеряться в радианах в секунду 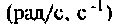
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
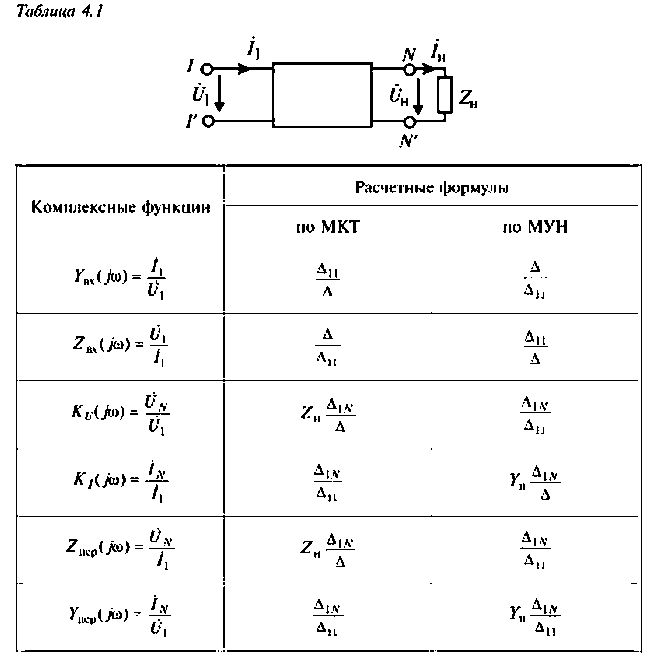
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
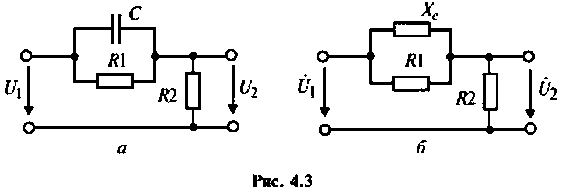
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 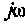
Следовательно.
Введем обозначения:
Величина 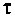
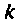
С учетом принятых обозначений
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
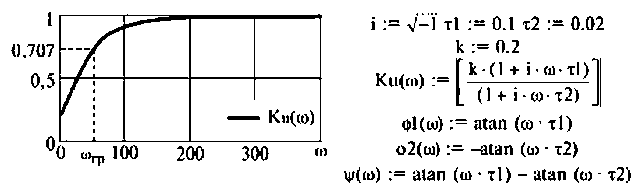
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 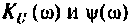
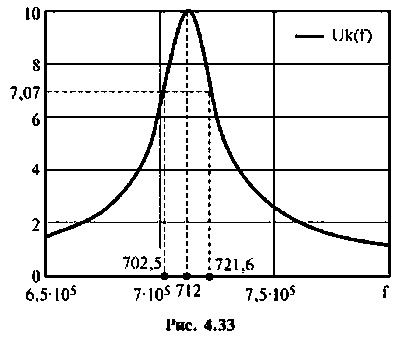
График АЧХ 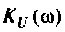
График функции ФЧХ 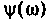
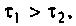
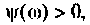
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
где
Подставляя 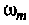
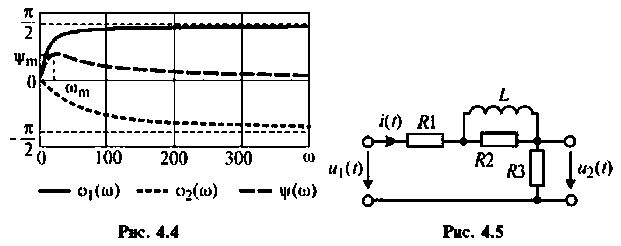
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
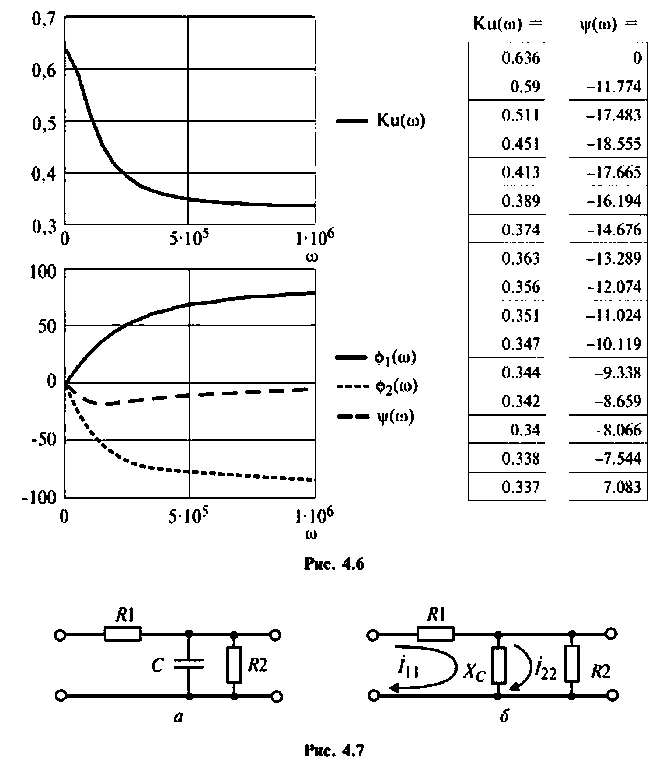
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 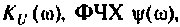
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Отсюда: АЧХ
ФЧХ
2. Рассчитаем граничную частоту. По определению
Из (4.7) найдем
Следовательно,
Из уравнения (4.9) получаем, что
Отсюда
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи:
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 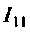
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки равно
Подставляя найденные выражения, получаем
или
где
4. Рассчитаем 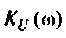
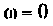
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 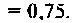
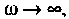
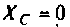
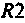
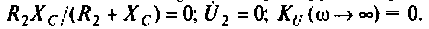
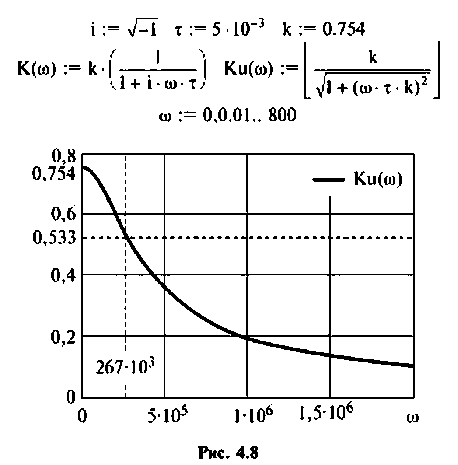
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
Поэтому из (4.11) имеем
После преобразований уравнения (4.12) получаем
откуда
или
Следовательно, цепь имеет полосу пропускания
На рис. 4.8 указана граничная частота
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 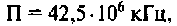

Пример 4.2.4.
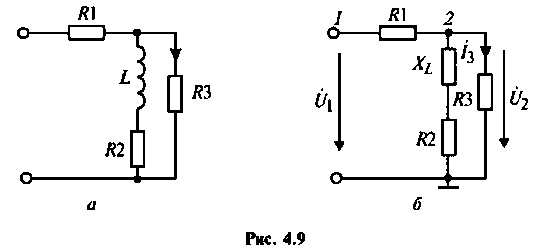
Найти комплексную передаточную проводимость 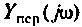
Параметры цепи: 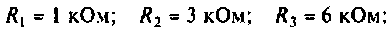
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 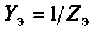
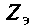
В начале рассчитывают комплексное сопротивление этой ветви, 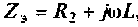
Составим матрицу проводимостей цепи 1 2
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 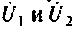
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
где 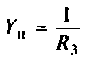
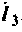
Найдем алгебраические дополнения:
После подстановки найденных значений получим
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента
4. Рассчитаем значения 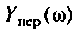
Примечание. Эти значения можно найти без вывода аналитического выражения для 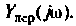
Учитывая, что 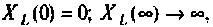
Для первой схемы:
Следовательно,
Аналогично для второй схемы получим
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
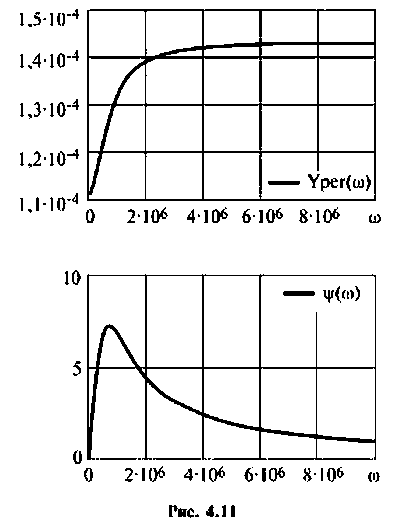
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
Пример 4.2.5.
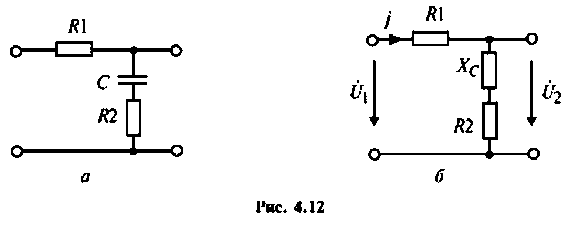
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 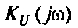
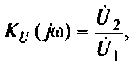
Следовательно.
3. Для нахождения АЧХ и ФЧХ комплексную функцию 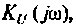
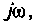
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 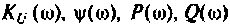
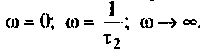
Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
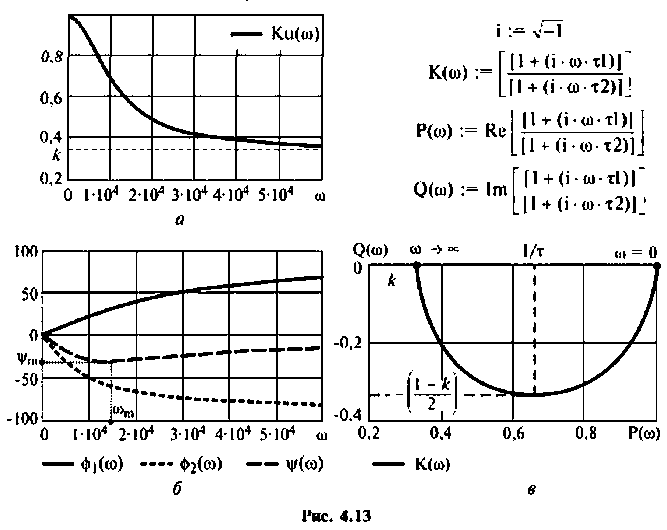
Графики характеристик приведены на рис. 4.13.
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте 
Взяв производную, получим
Решая полученное уравнение относительно 
Подставляя 
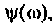
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 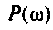
Радиус окружности нетрудно определить из соотношения:
МЧХ:
Отрицательное значение 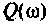
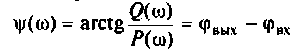
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 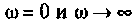
На частоте 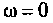
При 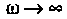
Подставляя эти значения частот в аналитическое выражение (4.14) для 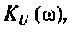
Следовательно, расчет АЧХ выполнен верно.
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
т. е. 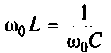
Резонансная частота
Волновое сопротивление контура
Сопротивление контура при резонансе
Собственная добротность контура
Добротность нагруженного контура
Затухание контура
Абсолютная расстройка
Относительная расстройка
Обобщенная расстройка
Фактор расстройки:
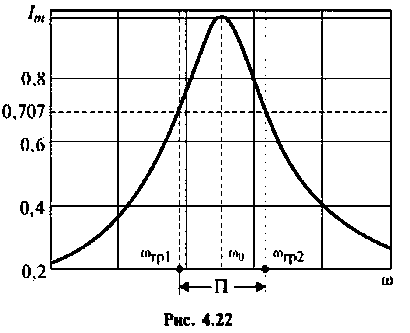
Абсолютная полоса пропускания (рис. 4.22)
Относительная полоса пропускания
Для нагруженного контура:
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
на индуктивности
на емкости
Примеры решения типовых задач:
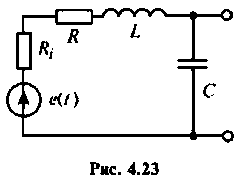
Пример 4.3.1.
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи:
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
1. Определяем резонансную частоту контура
2. Находим волновое сопротивление контура
3. Вычисляем добротность нагруженного контура
4. Определяем полосу пропускания
5. Рассчитываем ток и напряжения на элементах контура при резонансе
Напряжение на R равно
Напряжения на реактивных элементах
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
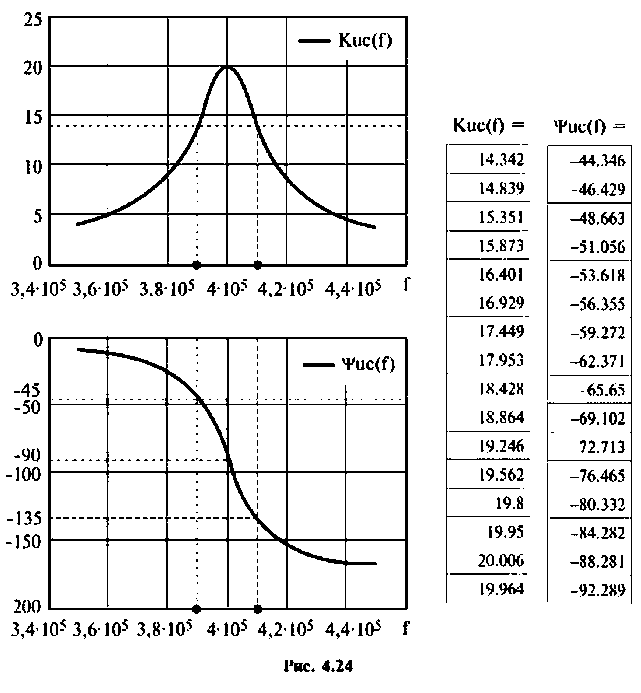
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
т.е. при 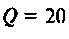
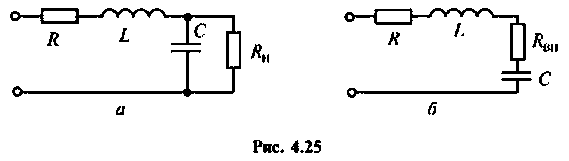
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 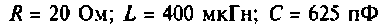
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 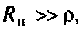
Для определения добротности рассчитаем сопротивление 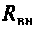
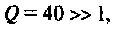
Следовательно,
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
Пример 4.3.3.
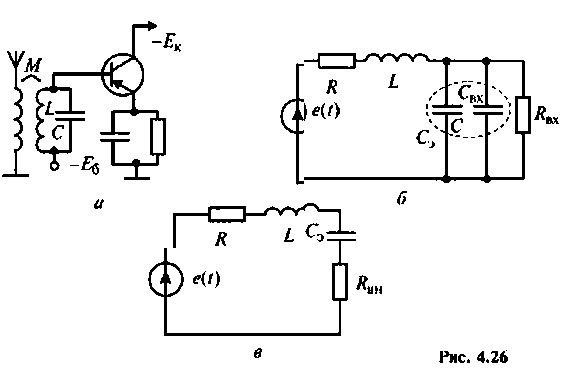
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ: 
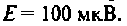
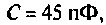
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
2. Рассчитываем резонансную частоту контура
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
4. Определяем добротность нагруженного контура
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
6. Находим ток в контуре
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 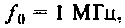
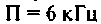
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
2. Рассчитаем емкость конденсатора. Из формулы 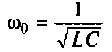
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
Вычислим значения функций на частотах:
Определим частоту, при которой АЧХ имеет максимум
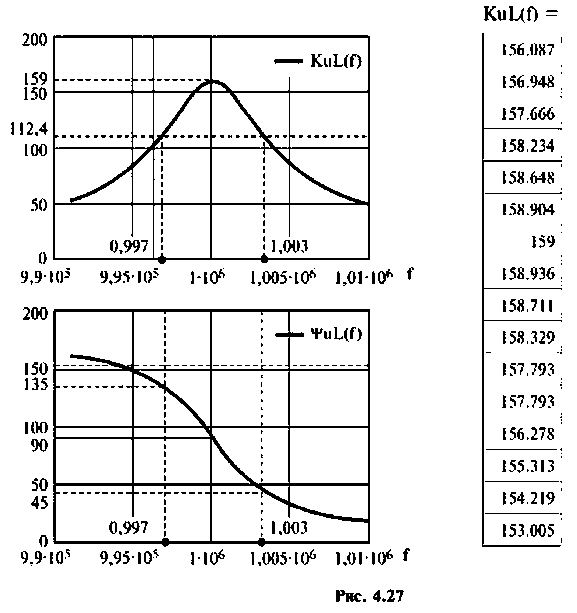
Смещением частоты 
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений
где резонансная частота колебаний
Для реального контура 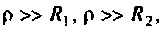
При резонансе сопротивление контура является активным, поэтому ток 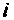
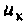
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
где
Добротность 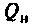
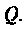
или через их проводимости
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
При этом напряжение на контуре максимально и равно
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
где 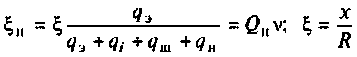
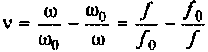
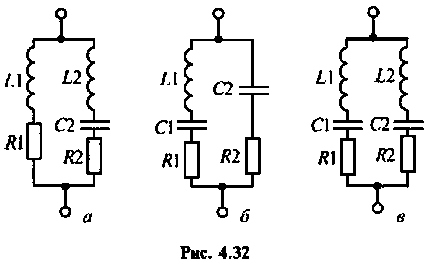
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
где 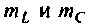
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 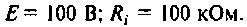
Параметры катушки индуктивности:
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
2. Рассчитаем волновое сопротивление
3. Определим сопротивление контура при резонансе
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
5. Определим соответственную добротность контура
6. Найдем ток в контуре и напряжение на нем:
7. Определим добротность нагруженного контура
8. Рассчитаем абсолютную и относительную полосы пропускания:
9. Определяем добавочное cопротивление 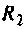
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано:
Определить сопротивление 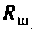
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
Тогда
3. Определим полосу пропускания
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
Тогда из (4.32) получаем
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 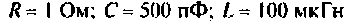
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
2. Рассчитаем собственную добротность контура
3. Найдем сопротивление контура при резонансе
4. Определим добротность нагруженного контура по формуле (4.31)
5. Рассчитаем резонансную частоту
6. Найдем полосу пропускания
7. Определим граничные частоты полосы пропускания:
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот: 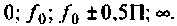
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано:
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
Сопротивление контура при резонансе
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
3. Найдем добротность нагруженного контура II вида
Сравним значения 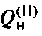
Вывод. За счет неполного включения индуктивности 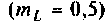
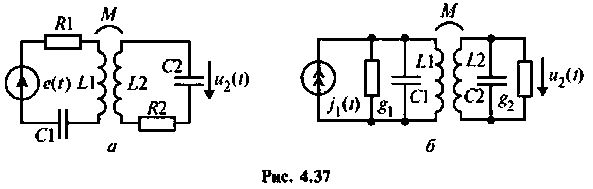
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
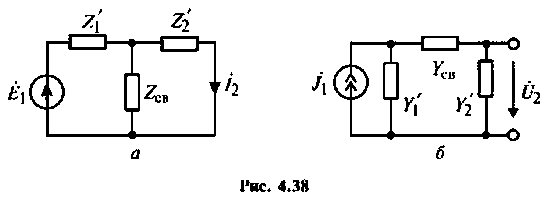
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 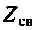
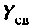
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;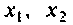
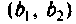
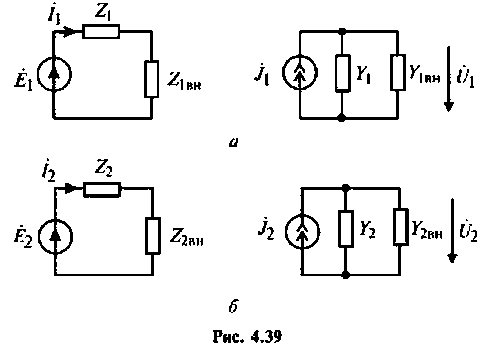
Для этого используют понятия вносимого сопротивления 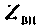
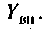
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.
Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
где
параллельного питания:
где 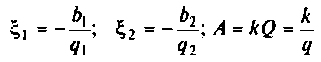
Если контуры идентичны, то обобщенная расстройка
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая
б) связь критическая
в) связь сильная
При 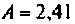
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
Определить емкость 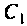
Решение
Емкость конденсатора 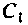
отсюда
Определим реактивное сопротивление 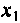
Peaктивное сопротивление второго контура
Рассчитаем полное сопротивление второго контура
Определим сопротивление связи контуров
Следовательно
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано:
Решение
1. Определим емкость конденсатора 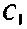
Отсюда
2. Сопротивление оптимальной связи при полном резонансе
3. Рассчитаем токи в первом и втором контурах при полном резонансе
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 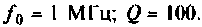
Решение
1. Определим полосу пропускания одиночного контура
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для
Таким образом при 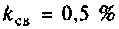
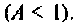
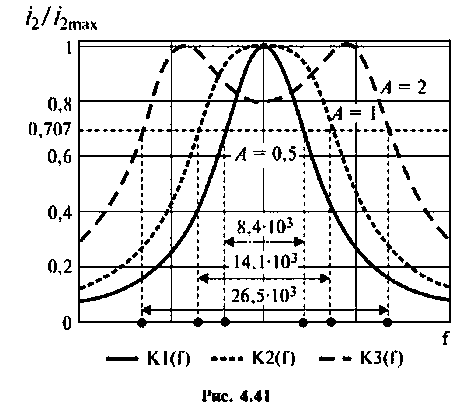
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
2) при 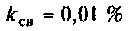
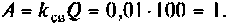
3) если 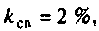
Рассчитаем полосу пропускания для этого случая.
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 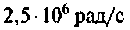
Дано:
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
Емкость конденсатора второго контура
2. Рассчитаем волновое сопротивление контуров:
3. Рассчитаем добротности контуров и параметр связи:
4. Определим взаимную индуктивность двух связанных контуров
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
С учетом этого рассчитаем ток во втором контуре
6. Найдем напряжение на конденсаторе вторичного контура
Пример 4.5.5.
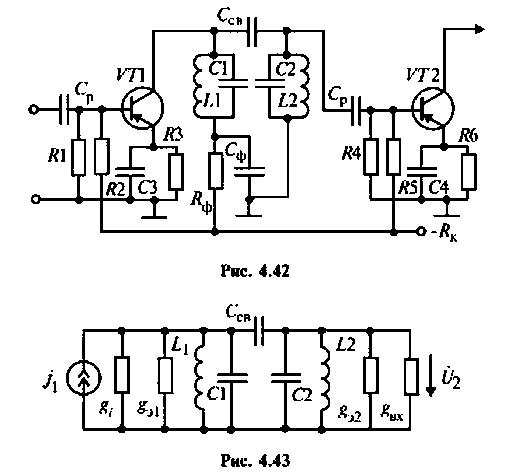
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 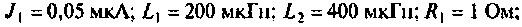
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 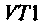
Емкость второго контура с учетом влияния входной емкости транзистора 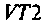
2. Определим емкость связи
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
где
где
4. Рассчитаем параметр связи
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс 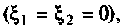
Найдем проводимость контуров
Тогда
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 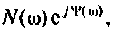
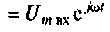
где 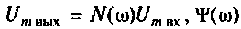
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 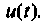
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида
Каждому из этих колебаний соответствует выходное колебание 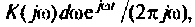
Представляя 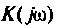
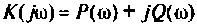
где 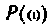
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 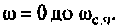

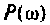
В результате интегрирования получают совокупность значений 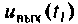
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
Вид подынтегральной функции, соответствующей выражению
при фиксированном времени 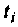
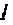
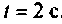
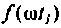
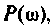
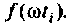
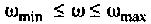
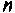
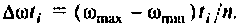
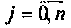

Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 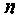
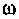
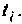
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
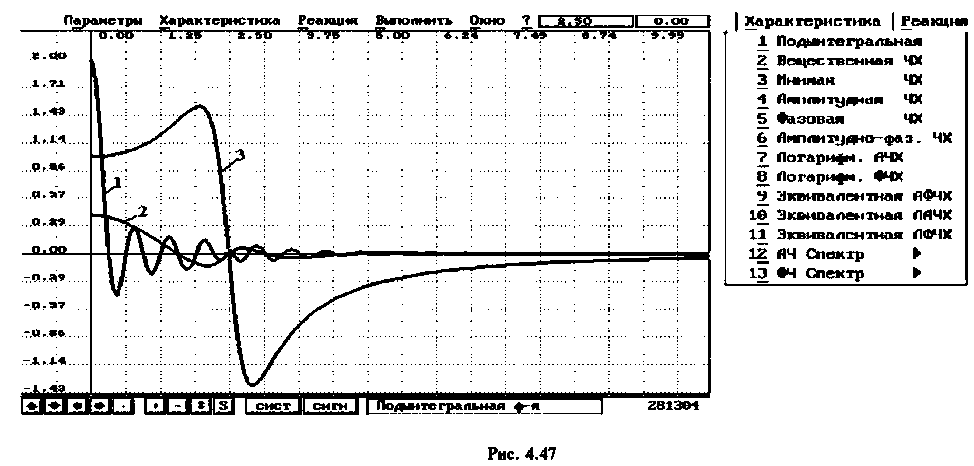
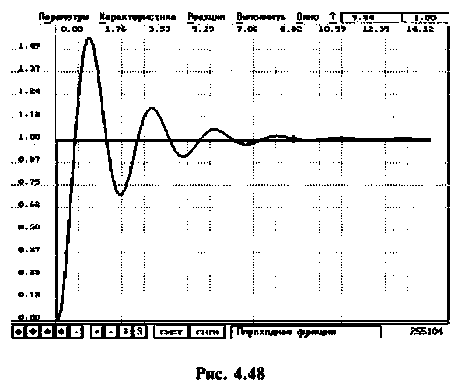
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 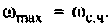
Алгебраическая форма КФ
где 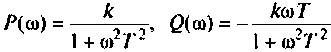
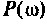
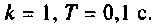
Из графика ВЧХ видно, что при 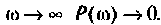
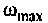
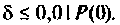
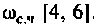
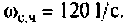
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 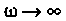
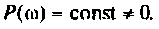
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
где
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 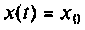
2) для линейной входной функции 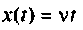
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 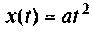
4) для полиномиального воздействия вида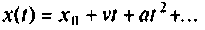
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
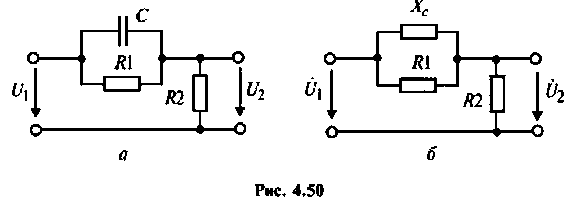
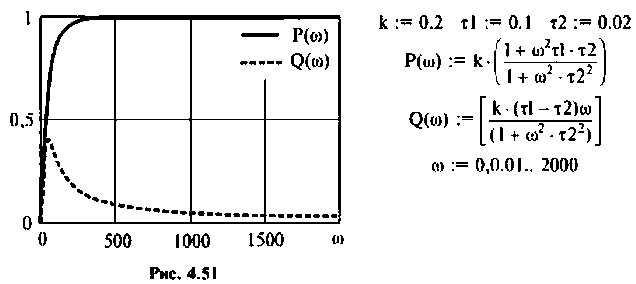
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 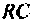
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 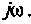
Следовательно
Введем обозначения:
Величина 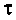
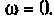
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Примем:
Для определения частоты 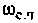
Из частотных характеристик КПФ принимаем 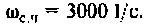
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
Пример 4.6.2.
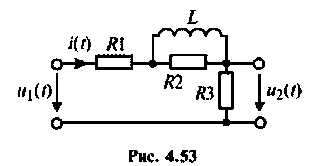
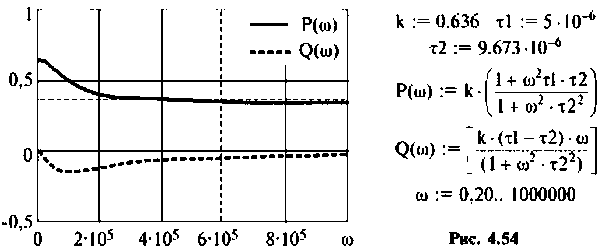
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 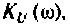
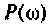
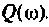
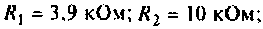
Решение
1. Найдем комплексную функцию 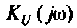
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Для определения частоты 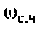
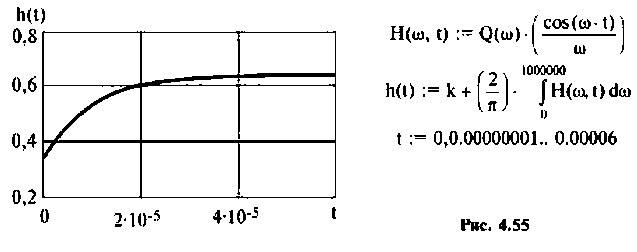
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 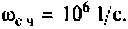
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
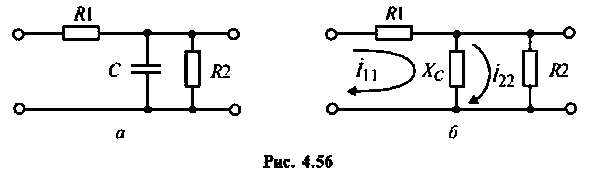
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 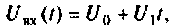
Параметры цепи:
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 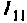
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки
Подставляя найденные выражения, получаем
т.е.
где
4. Рассчитаем 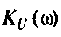
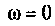
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 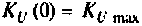
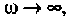
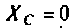
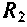
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
где 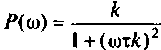
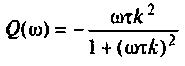
Амплитудно-частотную характеристику запишем в виде
6. В среде Mathcad построим частотные характеристики и определим
По ВЧХ на рис. 4.57 определяем, что существенная частота
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
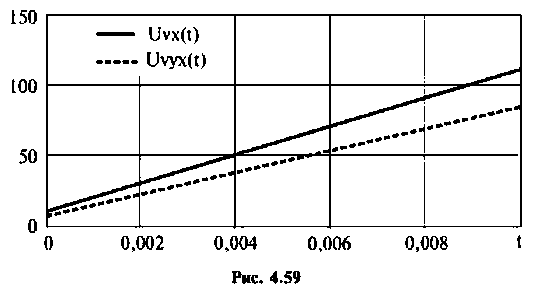
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
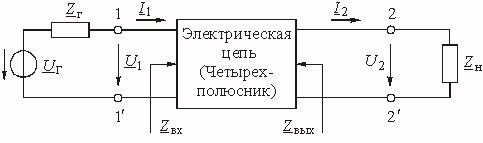
Электрическую цепь любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии, в технике связи называют четырехполюсником. Зажимы, к которым подключается источник, называются входными, а зажимы, к которым присоединяется приемник (нагрузка) – выходными зажимами (полюсами).
В общем виде четырехполюсник изображают, как показано на рис. 1.1. К входу четырехполюсника 1–1′ подключен источник электрической энергии с комплексным действующим значением напряжения и внутренним сопротивлением
. К выходным зажимам 2–2′ присоединена нагрузка с сопротивлением
. К входным зажимам приложено напряжение с комплексным действующим значением
, к выходным – с комплексным действующим значением
. Через входные зажимы протекает ток с комплексным действующим значением
, через выходные зажимы – с комплексным действующим значением
. Заметим, что в роли источника и приемника электрической энергии могут выступать другие четырехполюсники.
Рис. 1.1
На рис. 1.1 использованы символические обозначения напряжений и токов. Это означает, что анализ электрической цепи проводится для гармонического колебания определенной частоты. Для данного гармонического колебания можно определить передаточную функцию нагруженного четырехполюсника, которая будет представлять собой отношение комплексного действующего значения выходной электрической величины к комплексному действующему значению входной электрической величины.
Если входным воздействием считать напряжение генератора с комплексным действующим значением , а реакцией четырехполюсника на это воздействие – напряжение с комплексным действующим значением
или ток с комплексным действующим значением
, то получаются комплексные передаточные функции общего вида:
, (1.1)
. (1.2)
В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций:
– комплексный коэффициент передачи по напряжению (для активных четырехполюсников, например усилителей, он носит название коэффициента усиления по напряжению);
– комплексный коэффициент передачи по току (для активных цепей – коэффициент усиления по току);
– комплексное передаточное сопротивление;
– комплексная передаточная проводимость.
Часто в теории цепей используют нормированную или рабочую передаточную функцию четырехполюсника:
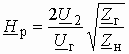
которая получается путем нормирования (1.1) множителем 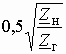
Как всякую комплексную величину Н можно представить в показательной форме:
, (1.4)
где – модуль комплексной передаточной функции, а j – ее аргумент.
Рассмотрим комплексную передаточную функцию по напряжению
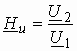
Подставляя в (1.5) запись комплексных действующих значений
,
получим
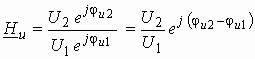
Из сравнения этого выражения с (1.4) видно, что
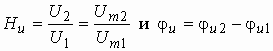
т. е. модуль комплексной передаточной функции по напряжению (или комплексного коэффициента усиления по напряжению) показывает во сколько раз изменяется действующее значение (амплитуда) гармонического колебания напряжения на выходе цепи по сравнению с аналогичным значением на входе цепи, а аргумент этой функции определяет сдвиг фаз между гармоническими колебаниями напряжения на входе и выходе.
Точно так же можно найти:
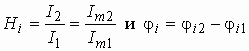
Все сказанное выше о коэффициенте передачи по напряжению справедливо и для коэффициента передачи по току.
Если мы будем изменять частоту гармонического колебания, то выражение (1.4) следует записать в виде:
. (1.6)
Функция частоты называется амплитудно-частотной характеристикой цепи (АЧХ). Она показывает какие изменения в амплитуды гармонических колебаний вносит цепь на каждой частоте.
Функция частоты называется фазо-частотной характеристикой цепи (ФЧХ). Соответственно эта характеристика показывает какой фазовый сдвиг приобретает гармоническое колебание каждой частоты при распространении по цепи.
Комплексную передаточную функцию можно представить также в алгебраической форме:
,
где Re и Im означают реальную и мнимую части комплексной величины.
Из теории комплексных величин известно, что
Пример 1.1
Определить коэффициент передачи по напряжению , АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а.
Согласно (1.5) запишем
.
Найдем комплексную функцию на выходе цепи:
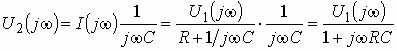
Подставив в формулу для
, получим комплексную передаточную функцию:
;
Рис. 1.2
АЧХ цепи
;
ФЧХ цепи
.
Изменяя частоту w от 0 до Ґ , можем изобразить графики АЧХ и ФЧХ цепи (рис. 1.2, б и в).
АЧХ и ФЧХ цепи можно представить единым графиком, если построить зависимость комплексной передаточной функции от частоты w на комплексной плоскости. При этом конец вектора
опишет некоторую кривую, которая называется годографом комплексной передаточной функции (рис. 1.3).
Рис. 1.3
Часто специалисты оперируют понятием логарифмической амплитудно-частотной характеристики (ЛАХ):
.
Значения величины К оцениваются в децибелах (дБ). В активных цепях, содержащих усилители, величину К называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления вводят понятие ослабления цепи:
, (1.7)
которое также оценивается в децибелах.
Пример 1.2
Известно, что модуль коэффициента передачи по напряжению цепи принимает следующие значения:
f = 0 кГц Н(f) = 1
f = 1 кГц Н(f) = 0,3
f = 2 кГц Н(f) = 0,01
f = 4 кГц Н(f) = 0,001
f = 8 кГц Н(f) = 0,0001
Рис. 1.4
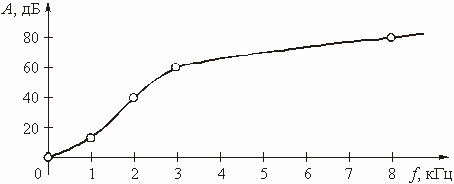
Изобразить график ослабления цепи.
Значения ослабления цепи, рассчитанные по (1.7), приведены в таблице:
|
f, кГц |
0 |
1 |
2 |
4 |
8 |
|
А(f), дБ |
0 |
12 |
40 |
60 |
80 |
График А(f) приведен на рис. 1.4.
Если вместо комплексных сопротивлений емкости и индуктивности
иметь дело с операторными сопротивлениями емкости
и индуктивность pL, то в выражении
нужно заменить
на р.
Операторная передаточная функция цепи может быть записана в общем виде как дробно-рациональная функция с вещественными коэффициентами:
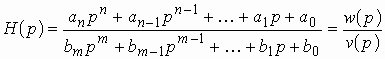
или в виде
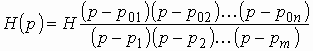
где – нули;
– полюсы передаточной функции;
.
Заменив в (1.8) оператор р на jw , вновь получим комплексную передаточную функцию цепи
,
где АЧХ цепи
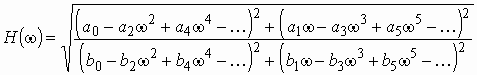
ФЧХ цепи
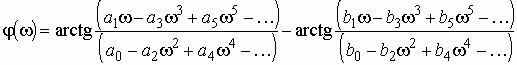
Учитывая, что является иррациональной функцией, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
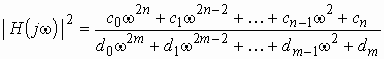
где коэффициенты получаются путем объединения коэффициентов при одинаковых степенях переменной w .
Пример 1.3
Найти коэффициент передачи по напряжению и квадрат АЧХ цепи, изображенной на рис. 1.5, а.
Коэффициент передачи по напряжению этой цепи равен
где Н = 1, ,
.
Корни числителя этой рациональной дроби, т. е. нули передаточной функции,
.
Корни знаменателя, или полюсы передаточной функции,
Рис. 1.5
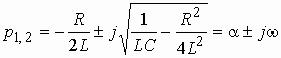
На рис. 1.5, б показано расположение нулей и полюсов функции при .
По теореме Виета
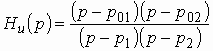
Амплитудно-частотная характеристика определяется из путем замены р на
и вычисления модуля полученной функции
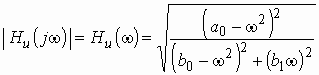
Квадрат АЧХ запишется в виде
где ;
;
;
.
АЧХ цепи изображена на рис. 1.5, в.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции . Выберем входное воздействие
или в операторной форме
. Изображение выходного напряжения
в этом случае численно равно
, т. е.
где – полином числителя передаточной функции;
– коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения к оригиналу
:
, (1.13)
где в общем случае .
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (1.13) вещественные части полюсов должны быть отрицательными
, т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. n Ф m. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при w > 0. Неотрицательность следует из свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных частотах объясняется так же, как и в свойстве 3.
В большинстве цепей с зависимыми источниками имеется по крайней мере два пути прохождения сигнала: прямой (от входа к выходу) и обратный (с выхода на вход). Обратный путь прохождения сигнала реализуется с помощью специальной цепи обратной связи (ОС). Таких путей, а значит и цепей ОС, может быть несколько. Наличие в цепях с зависимыми источниками ОС придает им новые ценные качества, которыми не обладают цепи без ОС. Например, с помощью цепей ОС можно осуществить температурную стабилизацию режима работы цепи, уменьшить нелинейные искажения, возникающие в цепях с нелинейными элементами и т. д.
Любую цепь с обратной связью можно представить состоящей из двух четырехполюсников (рис. 1.6).
Рис. 1.6
Активный линейный четырехполюсник с передаточной функцией по напряжению является усилителем. Его иногда называют основным элементом цепи и говорят, что он образует канал прямого усиления.
Пассивный четырехполюсник с передаточной функцией по напряжению называется цепью обратной связи. На входе цепи осуществляется суммирование входного напряжения
и напряжения обратной связи
.
Выведем формулу передаточной функции по напряжению цепи, изображенной на рис. 1.6. Пусть на вход подается напряжение . Его операторное изображения
. На выходе цепи возникает напряжение
. В соответствии с рис. 1.6 его операторное изображение
. (1.14)
Операторное изображение можно записать через передаточную функцию
цепи обратной связи
.
Тогда выражение (1.14) можно переписать в виде
или
. (1.15)
Операторная передаточная функция по напряжению цепи с ОС (см. рис. 1.6).
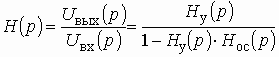
Пример 1.4
На рис. 1.7 изображена цепь на операционном усилителе (ОУ), предназначенная для масштабирования напряжения. Найти передаточную функцию этой цепи.
Получим передаточную функцию этой цепи как цепи с обратной связью, используя формулу (1.16).
Цепью обратной связи на схеме рис. 1.7 служит Г-образный делитель напряжения, составленный из резистивных сопротивлений и
. Выходное напряжение усилителя
поступает на вход цепи ОС; напряжение ОС
снимается с резистора
. Передаточная функция по напряжению цепи ОС
Рис. 1.7
.
Воспользуемся формулой (1.16) и учтем, что входное напряжение и напряжение обратной связи
не суммируются, а вычитаются. Тогда получим передаточную функцию масштабного усилителя:
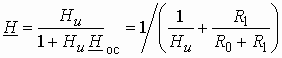
Учитывая, что в реальных ОУ значение >> 1, окончательно имеем:
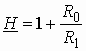
Пример 1.5
Звено на ОУ с частотно-зависимой ОС представлено на рис. 1.8. Найти передаточную функцию этого звена.
Рис. 1.8
Чтобы проанализировать прямой путь прохождения сигнала и путь прохождения сигнала ОС, необходимо воспользоваться методом наложения. Для этого следует поочередно исключать источники входного напряжения и напряжения обратной связи, заменяя их внутренним сопротивлением. В случае идеальных источников напряжения их внутреннее сопротивление равно нулю. Напряжение , приложенное к звену, ослабляется входной цепью, представляющей собой Г-образный делитель напряжения с сопротивлениями
и
в плечах. Передаточная функция по напряжению такого делителя равна
.
Цепь обратной связи также является Г-образным четырехполюсником с передаточной функцией.
Коэффициент усиления ОУ .
В соответствии с формулой (1.16) получаем передаточную функцию звена:
Учитывая, что >> 1, получаем:
.
Данное звено может выполнять различные функции в зависимости от вида сопротивлений и
. При
и
звено превращается в инвертирующий масштабный усилитель; при
и
– в интегратор; при
и
– в дифференциатор.
Пример 1.6
Звено второго порядка с регулируемым коэффициентом усиления представлено на рис. 1.9, а. Найти передаточную функцию этого звена.
Анализ прохождения входного сигнала и сигнала в цепи ОС показывает, что звено имеет входную цепь, изображенную на рис. 1.9, б и цепь ОС, показанную на рис. 1.9, в. Передаточные функции этих цепей можно получить матричным методом, например, рассматривая каждую цепь как каскадное соединение соответствующих Г-образных четырехполюсников.
Рис. 1.9
Для входной цепи
. (1.17)
Для цепи ОС
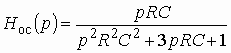
С учетом (1.16) получим передаточную функцию звена
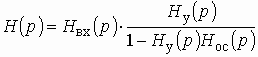
Коэффициент передачи усилителя . Тогда, подставляя (1.17) и (1.18) в (1.19), после преобразования имеем
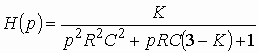
Переходя в (1.16) от оператора р к оператору , получаем комплексную передаточную функцию
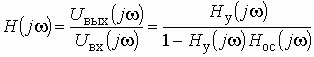
Произведение представляет собой комплексную передаточную функцию усилителя и цепи обратной связи при условии, что обратная связь разорвана (рис. 1.10). Функцию
называют передаточной функцией по петле ОС или петлевым усилением. Введем понятия положительной и отрицательной обратной связи. Эти понятия играют заметную роль в теории цепей с обратной связью.
Рис. 1.10
Предположим вначале, что передаточные функции ,
,
не зависят от частоты и являются вещественными числами. Такая ситуация возможна, когда в цепи отсутствуют LC-элементы. При этом
может быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз между входным и выходным напряжениями или, другими словами, сдвиг фаз по петле обратной связи равен нулю или
, k = 0, 1, 2, … Во втором случае, когда
, сдвиг фаз по этой петле равен
или
.
Если в цепи с обратной связью сдвиг фаз по петле равен нулю, то обратная связь называется положительной, если же сдвиг фаз равен , то такая обратная связь называется отрицательной.
Передаточную функцию можно изобразить в виде векторов и показать их на комплексной плоскости. При положительной обратной связи вектор
находится на положительной вещественной полуоси, а при отрицательной обратной связи – на отрицательной вещественной полуоси.
Кривая, которую описывает конец вектора при изменении частоты w (рис. 1.11), называется, как известно, годографом.
Рис. 1.11
Представление в виде годографа позволяет определить вид обратной связи в случае частотнозависимой обратной связи.
Обратная связь называется положительной, если годограф лежит в правой, и отрицательной – если в левой полуплоскости комплексной плоскости. Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления паразитных сигналов, коррекции частотных характеристик; положительная ОС может являться причиной неустойчивости цепи.
Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой, особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.
Рассмотрим цепь (см. рис. 1.6) и выведем ее характеристическое уравнение. Пусть и, значит,
. Тогда из (1.15) следует:
. (1.21)
Здесь (в противном случае цепь нельзя считать возбужденной) и поэтому равенство (1.21) выполняется при условии
. (1.22)
Если записать передаточную функцию основной цепи в виде , а цепи ОС –
, то уравнение (1.22) перепишется следующим образом:
.
Это равенство выполняется при
. (1.23)
Выражение в левой части этого равенства является полиномом, поэтому (1.23) можно записать в общем виде:
. (1.24)
Это и есть характеристическое уравнение цепи.
Корни уравнения (1.24) в общем случае являются комплексными величинами
где . Зная корни характеристического уравнения, можно записать выходное напряжение:
. (1.25)
Чтобы напряжение не возрастало безгранично, всем корням
характеристического уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны располагаться в левой полуплоскости комплексной переменной
. Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.
При исследовании цепей с обратной связью могут возникать две проблемы. Если проектируемая цепь должна быть устойчивой, то необходимо располагать критерием, который по виду функций и
позволял бы судить об отсутствии корней характеристического уравнения в правой полуплоскости р. Если обратная связь используется для создания неустойчивой автоколебательной цепи, то следует убедиться, что корни уравнения (1.24) расположены, наоборот, в правой полуплоскости. При этом необходимо иметь такое расположение корней, при котором самовозбуждение происходило бы на требуемой частоте.
Рассмотрим критерий устойчивости цепи, названный критерием Найквиста, и позволяющий судить об устойчивости цепи с обратной связью по свойствам разомкнутой цепи (рис. 1.10).
Передаточная функция разомкнутой цепи, или петлевое усиление, входит в характеристическое уравнение (1.22):
, (1.26)
Если найдется такая частота w , для которой конец вектора попадает в точку с координатами (1, j0), то это будет означать, что выполняется условие (1.26), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит, по годографу можно определить, устойчива цепь или нет. Для этого используется критерий Найквиста, который формулируется следующим образом: если годограф передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0), то при замкнутой цепи обратной связи цепь является устойчивой. В том случае, когда годограф
охватывает точку (1, j0), цепь неустойчива. На рис. 1.11 показаны годографы трех цепей с положительной обратной связью (цифра 1 соответствует годографу устойчивой цепи).
Пользуясь критерием Найквиста, легко получить условия самовозбуждения цепи с ОС. Запишем выражение для в виде
,
где ,
– модули передаточных функций;
,
– фазовые сдвиги соответственно в основном элементе и в цепи ОС.
Условия пересечения годографом оси абсцисс при
Х 1 можно записать в виде двух условий:
- условие (уравнение) баланса фаз
, где n = 0, 1, 2, …;
- амплитудное условие
Х 1, или
Х 1.
Выполнение неравенства соответствует режиму возникновения колебаний с нарастающей амплитудой, что характерно для начального этапа самовозбуждения. Выполнение равенства соответствует режиму генерации гармонического напряжения на частоте с постоянной амплитудой и носит название баланса амплитуд.
Как будет показано ниже, уравнение баланса фаз позволяет определить частоту, на которой происходит самовозбуждение цепи с ОС, а уравнение баланса амплитуд дает возможность определить величину амплитуды генерируемого колебания с частотой
в стационарной режиме.
Пример 1.7
Исследуем устойчивость цепи, изображенной на рис. 1.9, а. В ней можно выделить усилительный элемент с передаточной функцией и цепь обратной связи (рис. 1.9, в) с передаточной функцией (1.18)
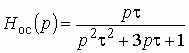
где .
Кроме того, напомним, что на усилитель сигнал поступает через входную цепь (рис. 1.9, б), передаточная функция которой (см. (1.17))
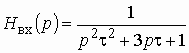
Получим характеристическое уравнение цепи:
или
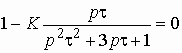
Откуда окончательно получаем
.
Корни этого характеристического уравнения
зависят от коэффициента усиления усилителя К. Расположение корней и
на плоскости комплексного переменного р для разных коэффициентов усиления и соответствующие этому графики свободных колебаний в цепи показаны на рис. 1.12.
Устойчивость данной цепи можно исследовать и с помощью критерия Найквиста. Комплексная передаточная функция разомкнутой цепи равна
Рис. 1.12
На рис. 1.11 приведены годографы устойчивой (К = 2, кривая 1) и неустойчивой (К = 3, кривая 2; К = 4, кривая 3) цепи.
Вопросы и задания для самопроверки
1. Что такое комплексная передаточная функция? Какие виды комплексных передаточных функций четырехполюсника известны?
2. Определить коэффициент передачи по напряжению , АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а, если выходным напряжением является напряжение на резисторе R. Построить графики АЧХ и ФЧХ.
Ответ: 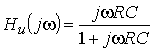
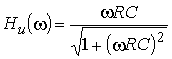
90° – arctg wRC.
3. Определить коэффициент передачи по напряжению при холостом ходе и коэффициент передачи по току при коротком замыкании для П-образного четырехполюсника в продольную ветвь которого включена индуктивность L, а в поперечные ветви – емкость С. Ответ: 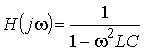
4. Определить ослабление, вносимое цепью рис. 1.2, а, при R = 31,8 кОм и = 10 кОм.
Ответ: 12 дБ.
5. Что такое операторная передаточная функция? Как она связана с комплексной передаточной функцией? Как определить нули и полюсы операторной передаточной функции?
6. Определить операторную передаточную функцию, комплексный коэффициент передачи по напряжению, АЧХ и квадрат АЧХ последовательного колебательного контура, изображенного на рис. 1.5, а, если выходным напряжением является напряжение на емкости С. Построить график АЧХ цепи.
Ответ: 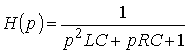
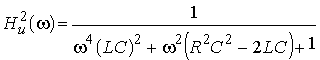
7. Перечислить основные свойства операторных передаточных функций пассивных цепей.
8. Как рассчитывается передаточная функция цепи с обратной связью?
9. Доказать, что операторная передаточная функция дифференциатора на операционном усилителе равна (–pRC). Построить график АЧХ такого дифференциатора.
10. Рассчитать передаточную функцию каскадного соединения цепей, изображенных на рис. 1.2, а и 1.7. Построить график АЧХ полученной цепи.
11. Определить передаточную функцию фильтра, изображенного на рис. 1.13.
Рис. 1.13
Ответ: 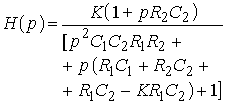
12. Что такое годограф петлевого усиления? Как по годографу определить тип обратной связи?
13. Как формулируется критерий устойчивости Найквиста? Для каких цепей он используется?
14. Определить комплексную передаточную функцию разомкнутой цепи, изображенной на рис. 1.13. Исследуйте зависимость устойчивости цепи от величины коэффициента усиления К.
Ответ: