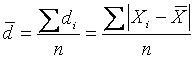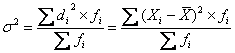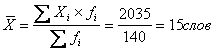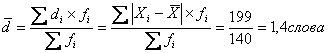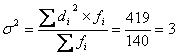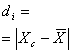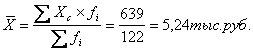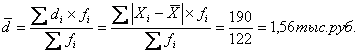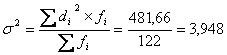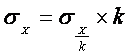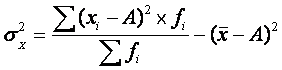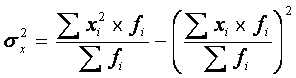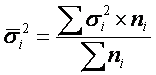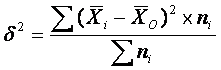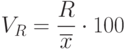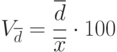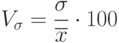VR
=
100%
В регионе 2 разница
межу крайними значениями на 14,3% превышает
среднее значение товарооборота на одно
предприятие:
VR2
=100%
= 114,3%
В то же время в
регионе 1 этот показатель составляет
VR1=
40/105*100%=38,1%
2. Относительно линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины
100%
В регионе 1 составило
5,3%, а в регионе 2 21,7%
V1=
5,6/105*100%=5,3%, V2=
22,8/105*100%=21,7%,
3. Коэффициент вариации – используется
для оценки типичности средних величин
Если V>33%, то это
говорит о большей колеблемости признака
в изучаемой совокупности
По величине
коэффициента вариации можно судить об
интенсивности вариации признака, а
следовательно, и об однородности состава
изучаемой совокупности (если V
<33%)
Чем больше значение
коэффициента вариации, тем больше
разброс значений признака вокруг
средней, те больше неоднородность
совокупности.
1=8/105*100%=7,6%,
2=27,5/105*100%=26%
в регионе 2
колеблемость товарооборота больше, чем
в регионе 1.
По величине
коэффициента вариации можно судить об
интенсивности вариации признака, а
следовательно, и об однородности состава
изучаемой совокупности. Чем больше
значение коэффициента вариации, тем
больше разброс значений признака вокруг
средней, те больше неоднородность
совокупности. При этом вопрос о степени
интенсивности вариации должен решаться
для каждого изучаемого признака
индивидуально исходя из сравнения
наблюдаемой вариации с некоторой её
обычной интенсивностью, принимаемой
за норму. Общепринятым является следующее
– совокупность считается однородной,
если коэффициент вариации не превышает
33%.
Регион 1
|
Группы п/п |
Число п/п fi |
|
Расчетные |
|||||
|
хi |
хifi |
|
|
|
|
|||
|
90-100 |
28 |
95 |
2660 |
-10 |
-280 |
100 |
2800 |
|
|
100-110 |
48 |
105 |
5040 |
0 |
0 |
0 |
0 |
|
|
110-120 |
20 |
115 |
2300 |
10 |
200 |
100 |
2000 |
|
|
120-130 |
4 |
125 |
500 |
20 |
80 |
400 |
1600 |
|
|
Итого |
100 |
105 |
10500 |
560 |
560 |
6400 |
Регион 2
|
Группы п/п |
Число п/п fi |
|
Расчетные |
|||||
|
хi |
хifi |
|
|
|
|
|||
|
60-80 |
21 |
70 |
1470 |
-35 |
-735 |
1225 |
25725 |
|
|
80-100 |
27 |
90 |
2430 |
-15 |
-405 |
225 |
6075 |
|
|
100-120 |
24 |
110 |
2640 |
50 |
120 |
2500 |
60000 |
|
|
120-140 |
16 |
130 |
2080 |
25 |
400 |
625 |
10000 |
|
|
140-160 |
8 |
150 |
1200 |
45 |
360 |
2025 |
16200 |
|
|
160-180 |
4 |
170 |
680 |
65 |
260 |
4225 |
16900 |
|
|
Итого |
100 |
105 |
10500 |
2280 |
10825 |
134900 |
Регион 1
|
Группы п/п |
Число п/п fi |
|
Расчетные |
|||||
|
хi |
хifi |
|
|
|
|
|||
|
90-100 |
28 |
95 |
2660 |
-10 |
-280 |
100 |
2800 |
|
|
100-110 |
48 |
105 |
5040 |
0 |
0 |
0 |
0 |
|
|
110-120 |
20 |
115 |
2300 |
10 |
200 |
100 |
2000 |
|
|
120-130 |
4 |
125 |
500 |
20 |
80 |
400 |
1600 |
|
|
Итого |
100 |
105 |
10500 |
560 |
560 |
6400 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике под вариацией понимают количественные
изменения величины исследуемого признака в пределах однородной совокупности,
обусловленные взаимодействием различных факторов. Причины, порождающие вариацию социально-экономических
явлений, очень сложны и многообразны. Они лежат в коренных особенностях
исследуемого явления, в его сущности, а также в методологии сбора исходной
информации. Социально-экономические явления, как правило, обладают большой
вариацией. Если исследуются результаты целенаправленной человеческой
деятельности, то вариация будет выражать вмешательство многочисленных факторов,
природу которых не всегда можно установить. Однако, в большинстве теоретических
исследований и практических применений статистики необходимы наряду со средней
показатели вариации, характеризующие группировку значений признака вокруг
средней, т. е. степень упорядоченности
статистической совокупности.
В соответствии с определением вариация измеряется
степенью колеблемости вариантов признака от уровня их
средней величины. Именно на этом и основано большинство показателей,
применяемых в статистике для измерения вариации значений признака в
совокупности. К показателям вариации относятся: размах вариации, среднее
линейное отклонение, дисперсия, среднее квадратическое
отклонение, коэффициент вариации.
Простейшим показателем вариации является размах вариации, определяемый как разность между максимальным и минимальным значениями
признака:
Размах вариации выражается в тех же единицах
измерений, что в варианты ряда. По величине его можно определить, например,
передовое и отстающее в достижении какой-либо цели. Величина вариации служит
также и для характеристики средней. Размах вариации имеет и самостоятельное
значение. Например, в промышленности для измерения точности изделий
устанавливают определенные пределы, соответствующие иногда величине размаха
вариации их признаков.
Однако показатель размаха вариации не может в полной
мере охарактеризовать колеблемость ряда, поскольку он
не учитывает промежуточных значений вариантов внутри этих пределов, а по этому
не отражает колеблемость ряда в целом, кроме того, он
полностью зависит от максимального и минимального значений, которые могут
оказаться не достаточно характерными.
Таким образом, размах вариации отражает иногда
случайную, а не типичную для данного ряда величину колеблемости.
По этому необходимы другие показатели вариации, основанные на всех значениях
признака в данной совокупности, а именно: среднее линейное отклонение,
дисперсия и среднее квадратическое отклонение.
Среднее линейное отклонение представляет среднюю
арифметическую из абсолютных значений отклонений отдельных вариантов от их
среднего значения.
Для данных, где частота каждого варианта равна
единице, среднее линейное отклонение определяется по формуле:
Для вариационных рядов
определяется с учетом частот по формуле:
Среднее линейное отклонение по сравнению с размахом
вариации дает более полную характеристику колеблемости
признака в совокупности.
Средний квадрат отклонений вариантов от их средней
величины называют дисперсией
.
Дисперсия рассчитывается по формуле:
Для негруппированных
данных, где частота каждого варианта равна единице, дисперсия рассчитывается по
формуле простой средней:
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
либо при равенстве весов:
Среднее квадратическое
отклонение является также обобщающим показателем колеблемости
признака и характеризует средний показатель отклонения вариантов ряда от их
общей средней. Выражается s в тех же именованных числах, в которых выражены
варианты совокупности и средняя величина.
Дисперсия и среднее квадратическое отклонение — наиболее широко применяемые
показатели вариации. Объясняется это тем, что они входят в большинство теорем
теории вероятностей, служащих фундаментом математической статистики. Кроме
того, дисперсия может быть разложена на составные элементы, позволяющие оценить
влияние различных факторов, обусловливающих вариацию признака. Порядок расчета
среднего квадратического отклонения следующий:
1) Определяется средняя
величина:
2) Рассчитывается
отклонения вариантов от средней:
3) Отклонение каждого
варианта от средней возводится в квадрат:
4) Квадрат отклонений
взвешивается по частотам:
5) Взвешенные по
частотам квадраты отклонений суммируются:
6) Полученная сумма
делится на сумму частот, и из нее извлекается квадратный корень.
Среднее квадратическое
отклонение можно вычислить, составив следующую расчетную таблицу:
| № п/п |
|
Линейные отклонения от средней
|
Квадрат линейных отклонений
|
Взвешенные квадраты
|
| … | … | … | … | … |
|
Итого |
Среднее квадратическое
отклонение можно вычислить на основании математических преобразований значений
варьирующего признака, применяя способ условных моментов:
где первый условный
момент:
второй условный момент:
Среднее квадратическое
отклонение по способу условных моментов определяется по формуле:
Система условных
моментов различных порядков, в частности, третьего
и
четвертого
используется при расчете различных
статистических характеристик (например, коэффициентов асимметрии и эксцесса).
Чем больше σ, тем разнообразнее состав
совокупности по величине изучаемого признака, и, наоборот, чем меньше σ, тем
состав совокупности по величине изучаемого признака более одинаков. Однако
оценка величины σ
как качественной характеристики ряда в конечном итоге определяется сущностью
изучаемых явлений. Среднее квадратическое отклонение
используется для сопоставления вариации по однородным совокупностям, а также
для одной совокупности за разные годы. Среднее квадратическое
отклонение является критерием надежности средней. Чем меньше оно, тем лучше
средняя арифметическая отражает всю представляемую совокупность.
Коэффициент осцилляции – процентное отношение размаха
вариации к средней
Линейный
коэффициент вариации (относительное линейное отклонение) измеряют через
соотношение среднего линейного отклонения и средней:
Коэффициент вариации представляет собой отношение
среднего квадратического отклонения к средней
арифметической:
Характеризуя степень колеблемости
признака, коэффициент вариации позволяет давать сравнительную характеристику
этой колеблемости одного и того же признака в
различных совокупностях.
Коэффициент вариации используется также, если
сравнивается степень вариации одного и того же признака в двух совокупностях,
имеющих разные по величине средние. Как относительные величины коэффициенты
вариации могут сопоставляться не только для одинаковых одноименных показателей,
но и для различных показателей, выраженных в разных единицах измерения. Таким
образом, коэффициент вариации в отличие от среднего квадратического
отклонения позволяет сопоставить глубину вариации неоднородных совокупностей.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5.
Расчёт показателей вариации.
Студент должен:
знать:
— область применения и методику расчёта
степенных средних величин;
уметь:
— исчислять
степенные средние
величины;
— формулировать вывод по полученным
результатам.
Методические указания
Наряду со средними
величинами в статистике исчисляются показатели вариации. Вариацией в статистике
называются различия индивидуальных значений изучаемого признака. Возникает
вариация в силу того, что отдельные значения признака статистической совокупности
формируются под воздействием разнообразных факторов. Значение изучения вариации
в том, что по колеблемости признаков можно судить о качественной однородности
совокупности. Совокупности могут иметь одинаковые значения средней величины, но
отличаться колеблемостью индивидуальных значений.
Например: По имеющимся данным о дневной выработке рабочих двух бригад определить
среднюю выработку рабочего за день в каждой бригаде, сделать вывод об
однородности рассматриваемых совокупностей и надёжности их средних.
Выработка в первой
бригаде: 31, 25, 30, 26, 28 деталей.
Выработка во второй
бригаде: 27, 20, 56, 19, 18 деталей.
Решение:
Исходные данные не
сгруппированы, поэтому для расчёта средней выработки применяем среднюю
арифметическую простую. Средняя дневная выработка рабочего:
в первой бригаде
во второй бригаде
Среднедневная выработка рабочего в
обеих бригадах одинакова, но индивидуальные
значения выработки во второй бригаде подвержены значительным колебаниям. Это
вызывает необходимость измерять вариацию.
К
абсолютным показателям вариации относятся
размах вариации, среднее линейное отклонение,
дисперсия и среднее квадратическое отклонение.
Элементарным
показателем колеблемости является размах вариации, который определяется
как разность между наибольшим и наименьшим значением признака: R=Хmax — Xmin
В нашем примере размах
вариации индивидуальной выработки:
в первой бригаде R1 =31-25=6 деталей
во второй бригаде R2 =56-18=38 деталей
Сравнение этих
показателей свидетельствует о том, что размах вариации индивидуальной выработки
во второй бригаде на 32 детали больше, чем в первой бригаде. Однако размах
вариации не улавливает колеблемости вариантов внутри изучаемой совокупности.
Для получения обобщающей характеристики колеблемости всех вариантов
совокупности исчисляются другие показатели вариации.
Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака
в совокупности относительно среднего уровня признака и рассчитывается как средняя арифметическая из индивидуальных
линейных отклонений по формуле:
—
для
невзвешенных данных
—
для
взвешенных данных 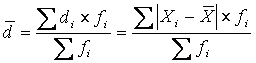
где — индивидуальное
линейное отклонение.
Показатель
среднего линейного отклонения нашел широкое применение на практике. С его
помощью анализируют состав работающих, ритмичность производства, равномерность
поставок материалов; разрабатывают системы материального стимулирования. Но
этот показатель усложняет расчёты вероятностного типа, затрудняет применение
методов математической статистики. Поэтому в статистических научных
исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
В
статистике дисперсия, центральный момент второго порядка, является оценкой
одноимённого показателя теории вероятностей и оценкой дисперсии в
математической статистике, что позволяет использовать теоретические положения
этих дисциплин для анализа социально – экономических процессов. На дисперсии
практически основаны все метод математической статистики. Большое значение
имеет правило сложения дисперсий. Дисперсия рассчитывается как средний квадрат отклонений индивидуальных значений
признака от среднего
значения признака по формуле:
—
для
невзвешенных данных
—
для
взвешенных данных
Среднее квадратическое отклонение является обобщающей характеристикой размеров вариации признака совокупности. Это — мера вариации, показатель надёжности средней. Чем меньше значение
среднего квадратического отклонения, тем лучше средняя величина представляет собой
рассматриваемую совокупность.Среднее квадратическое отклонение рассчитывается
по формуле:
Для
расчёта показателей вариации в нашем примере строим вспомогательную таблицу:
|
Первая бригада |
Вторая бригада |
||||
|
Выработка,деталей (Хi ) |
Индивидуальное линейное отклонение |
|
Выработка, деталей (Хi ) |
Индивидуальное линейное отклонение |
|
|
25 |
|-3| |
9 |
18 |
|-10| |
100 |
|
26 |
|-2| |
4 |
19 |
|-9| |
81 |
|
28 |
0 |
0 |
20 |
|-8| |
64 |
|
30 |
2 |
4 |
27 |
|-1| |
1 |
|
31 |
3 |
9 |
56 |
28 |
784 |
|
Итого: |
10 |
26 |
56 |
1030 |
Среднее
линейное отклонение:
в первой бригаде ; во второй
бригаде .
Дисперсия:
в первой бригаде ; во
второй бригаде .
Среднее квадратическое отклонение:
в первой бригаде ; во второй бригаде
Таким образом,
выполненные нами расчёты показывают, что колеблемость индивидуальных значений
выработки во второй бригаде намного выше, чем в первой бригаде.
Для
целей сравнения колеблемости различных признаков в одной и той же совокупности
или же при сравнении колеблемости одного и того же признака в нескольких
совокупностях исчисляют показатели
вариации в относительных величинах. Базой для сравнения должна служить
средняя арифметическая. Эти показатели вычисляются как отношение размаха
вариации, среднего линейного отклонения или среднего квадратического отклонения
к средней арифметической (реже к медиане). Чаще всего они выражаются в
процентах и определяют не только сравнительную оценку вариации, но и дают
характеристику однородности совокупности. Совокупность
считается однородной, если коэффициент вариации не превышает 33% (для
распределения близкого к нормальному). Различают следующие относительные
показатели вариации:
Коэффициент осцилляции (vR) рассчитывается по формуле:
и отражает относительную меру
колеблемости крайних значений признака вокруг средней.
Линейный коэффициент вариации (vd) рассчитывается
по формуле:
и отражает долю усреднённого значения
абсолютных отклонений от средней величины.
Коэффициент вариации (vσ ) как относительное квадратическое отклонение от средней величины
рассчитывается по формуле:
Рассчитаем относительные
показатели вариации для нашего примера.
Коэффициент осцилляции
Для первой бригады: Для
второй бригады:
Линейный коэффициент вариации
Для первой бригады: Для
второй бригады:
Коэффициент вариации
Для первой бригады: Для
второй бригады:
Величина рассчитанных
нами коэффициентов свидетельствует о том, что колеблемость индивидуальных
значений выработки во второй бригаде высокая. Первую совокупность можно считать
однородной, а её среднюю – надёжной. Вторую совокупность следует считать
неоднородной, а её среднюю – ненадёжной.
Рассмотрим
примеры расчёта показателей вариации для сгруппированных данных.
Пример
1. По имеющимся данным узла связи рассчитайте абсолютные и относительные
показатели вариации. Сделать вывод об однородности рассматриваемой совокупности
и надёжности её средней.
|
Количество |
Число |
|
12 13 14 15 16 17 18 |
18 22 34 26 20 13 7 |
|
Итого |
140 |
Решение:
Исходные
данные представлены в виде дискретного ряда распределения.
Для
исчисления среднего значения признака и показателей вариации строим и
рассчитываем вспомогательную таблицу:
|
Количество слов в телеграмме(Хi) |
Число телеграмм (fi) |
|
|
|
|
|
|
12 |
18 |
216 |
|
54 |
9 |
162 |
|
13 |
22 |
286 |
|
44 |
4 |
88 |
|
14 |
34 |
476 |
|
34 |
1 |
34 |
|
15 |
26 |
390 |
0 |
0 |
0 |
0 |
|
16 |
20 |
320 |
1 |
20 |
1 |
20 |
|
17 |
13 |
221 |
2 |
26 |
4 |
52 |
|
18 |
7 |
126 |
3 |
21 |
9 |
63 |
|
итого |
140 |
2035 |
199 |
419 |
1). Определяем среднее количество слов в телеграмме по
формуле средней арифметической взвешенной, так как исходные данные
сгруппированы:
2). Определяем абсолютные показатели
вариации:
Размах вариации R=Хmax — Xmin=18-12=6 слов
Среднее линейное отклонение по
формуле для взвешенных данных:
где — индивидуальное
линейное отклонение.
Дисперсию исчисляем по формуле для
взвешеных данных
Среднее квадратическое отклонение:
3). Определяем относительные
показатели вариации:
Коэффициент осцилляции: т.е. колеблемость крайних значений признака вокруг средней
составляет 40%.
Линейный коэффициент
вариации:
, т.е. доля усреднённого значения абсолютных отклонений от
средней величины составляет 9,3%.
Коэффициент вариации:
Вывод:
Величина рассчитанного нами коэффициента вариации свидетельствует о том, что
колеблемость индивидуальных значений слов в телеграмме невысокая, т.е. Vσ ≤ 33%.
Поэтому совокупность можно считать
однородной, а её среднюю – надёжной.
Пример 2. Имеются следующие данные о
распределении сотрудников организации по среднемесячной заработной плате.
Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об
однородности рассматриваемой совокупности и надёжности её средней.
|
Группы сотрудников по |
Количество сотрудников, чел. (fi) |
|
До 3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10 и свыше |
14 22 25 29 10 8 6 5 3 |
|
Итого: |
122 |
Решение:
Исходные данные представлены в виде
интервального ряда распределения.
Для исчисления среднего значения
признака и показателей вариации строим и рассчитываем вспомогательную таблицу:
|
Группы по ной |
Централь- ное (Хс) |
Коли- чество ников, |
|
|
|
|
|
|
До 3 |
2,5 |
14 |
35 |
|
38,36 |
7,51 |
105,14 |
|
3-4 |
3,5 |
22 |
77 |
|
38,28 |
3,03 |
66,61 |
|
4-5 |
4,5 |
25 |
112,5 |
|
18,5 |
0,55 |
13,69 |
|
5-6 |
5,5 |
29 |
159,5 |
0,26 |
7,54 |
0,07 |
1,96 |
|
6-7 |
6,5 |
10 |
65 |
1,26 |
12,6 |
1,59 |
15,90 |
|
7-8 |
7,5 |
8 |
60 |
2,26 |
18,08 |
5,11 |
40,86 |
|
8-9 |
8,5 |
6 |
51 |
3,26 |
19,56 |
10,63 |
63,76 |
|
9-10 |
9,5 |
5 |
47,5 |
4,26 |
21,3 |
18,15 |
90,74 |
|
10 и выше |
10,5 |
3 |
31,5 |
5,26 |
15,78 |
27,67 |
83,00 |
|
итого |
122 |
639 |
190 |
481,66 |
1). Определяем среднюю
заработную плату по формуле средней арифметической взвешенной для интервального
ряда распределения:
2). Определяем абсолютные показатели
вариации:
Размах вариации не рассчитываем, т.к.
нижняя граница первого интервала и верхняя граница последнего интервала не
указаны.
Среднее линейное отклонение по
формуле для взвешенных данных:
где — индивидуальное
линейное отклонение.
Дисперсию исчисляем по формуле для
взвешеных данных:
Среднее квадратическое отклонение:
3). Определяем относительные показатели вариации:
Коэффициент осцилляции (VR) не рассчитываем, т.к. не
рассчитывали размах вариации.
Линейный коэффициент вариации:
, т.е. доля усреднённого значения абсолютных отклонений от
средней величины составляет 29,8%.
Коэффициент вариации:
Вывод: Величина
рассчитанного нами коэффициента вариации свидетельствует о том, что
колеблемость индивидуальных значений заработной платы высокая, т.е. Vσ ≥ 33%. Поэтому совокупность считаем неоднородной, а
её среднюю – ненадёжной.
Свойства дисперсии
Свойство 1.
Дисперсия постоянной величины равна нулю.
Свойство 2.
Уменьшение всех значений признака на одну и ту же величину А не меняет величины
дисперсии:
Значит, средний квадрат отклонений можно вычислить не по заданным
значениям признака, а по отклонениям их от какого-то постоянного числа.
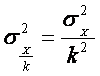
Свойство 3.
Уменьшение всех значений признака в раз уменьшает
дисперсию в раз, а среднее квадратическое
отклонение — в раз:
Значит, все значения признака можно разделить на какое-то постоянное
число (скажем, на величину интервала ряда), исчислить среднее квадратическое
отклонение, а затем умножить его на постоянное число:
Свойство 4.
Если исчислить средний квадрат отклонений от любой величины А, в той или иной
степени отличающейся от средней арифметической (), то он всегда будет больше среднего квадрата отклонений,
исчисленного от средней арифметической:
Средний квадрат отклонений при этом будет больше на вполне определенную
величину — на квадрат разности средней и этой условно взятой величины, т. е. на
:
или
Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от
любых других величин, т. е. она имеет свойство минимальности.
В случае когда А приравнивается к нулю и, следовательно, не вычисляются
отклонения, формула принимает такой вид:
или
Значит, средний квадрат отклонений равен среднему квадрату значений
признака минус квадрат среднего значения признака
Виды (показатели) дисперсий и правило
их сложения
В статистическом исследовании очень
часто бывает необходимо не только изучить вариации признака по всей
совокупности, но и проследить количественные изменения признака по однородным
группам совокупности, а также и между группами. Следовательно, помимо общей
средней для всей совокупности необходимо просчитывать и частные средние
величины по отдельным группам.
Различают три вида дисперсий:
—
общая;
—
средняя
внутригрупповая;
—
межгрупповая.
Общая дисперсия () характеризует вариацию признака всей совокупности под
влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина
определяется по формуле
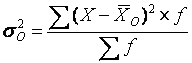
где — общая средняя
арифметическая всей исследуемой совокупности.
Средняя внутригрупповая
дисперсия () свидетельствует о случайной вариации, которая может
возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от
признака-фактора, положенного в основу группировки. Данная дисперсия
рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным
группам ():
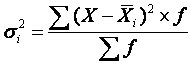
а затем — рассчитывается средняя внутригрупповая дисперсия :
где ni —
число единиц в группе
Межгрупповая дисперсия
() (дисперсия групповых средних) характеризует систематическую
вариацию, т.е. различия в величине исследуемого признака, возникающие под
влиянием признака-фактора, который положен в основу группировки. Эта дисперсия
рассчитывается по формуле:
где — средняя величина по отдельной группе.
Все три вида дисперсии связаны между собой: общая дисперсия
равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:
Данное соотношение отражает закон,
который называют правилом сложения дисперсий.
Согласно этому закону (правилу), общая дисперсия, которая возникает под
влиянием всех факторов, равна сумме дисперсий, которые появляются как под
влиянием признака-фактора, положенного в основу группировки, так и под влиянием
других факторов. Благодаря правилу сложения дисперсий можно определить, какая
часть общей дисперсии находится под влиянием признака-фактора, положенного в
основу группировки.
Правило сложения дисперсий широко
применяется при исчислении показателей тесноты связи, в дисперсионном анализе,
при оценке точности типической выборки и в ряде других случаев.
Аннотация: В процессе статистического анализа может сложиться ситуация, когда значения средних величин совпадают, а совокупности, на основе которых они рассчитаны, состоят из единиц, значения признака у которых достаточно резко различаются между собой. Возьмем, например, данные о количестве договоров, заключенных в двух филиалах страховой компании. Предположим, что в каждом из филиалов работает по два агента. В первом филиале один агент заключил 5 договоров, а второй — 25; во втором филиале каждый агент заключил по 15 договоров. Как видим, среднее число договоров, заключенных одним агентом в каждом филиале совпадает (15 договоров), в то же время очевидно, что первая и вторая совокупности качественно неоднородны, т.д. вариация значений признака внутри них различна.
Данная глава посвящена рассмотрению показателей, с помощью которых можно оценить и измерить вариацию признака.
7.1. Абсолютные и относительные показатели вариации
Рассмотрим две совокупности сотрудников рекламных агентств.
Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 4 000-6 000 | 5 000 | 10 | 50 000 |
| 6 000-8 000 | 7 000 | 6 | 42 000 |
| 8 000-10 000 | 9 000 | 19 | 171 000 |
| 10 000-12 000 | 11 000 | 26 | 286 000 |
| 14 000-16 000 | 15 000 | 10 | 150 000 |
| 16 000-18 000 | 17 000 | 5 | 85 000 |
| Сумма | — | 95 | 1 031 000 |
Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., fi | xi*fi |
|---|---|---|---|
| 1 500-4 500 | 3 000 | 9 | 27 000 |
| 4 500-7 500 | 6 000 | 26 | 156 000 |
| 7 500-10 500 | 9 000 | 24 | 216 000 |
| 10 500-13 500 | 12 000 | 18 | 216 000 |
| 13 500-16 500 | 15 000 | 14 | 210 000 |
| 16 500-19 500 | 18 000 | 10 | 180 000 |
| 19 500-22 500 | 21 000 | 9 | 189 000 |
| Сумма | — | 110 | 1 194 000 |
Рассчитаем средний уровень заработной платы:
- для первого агентства:
- для второго агентства:
Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.
Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.
К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака
 |
( 7.1) |
Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение
 |
( 7.2) |

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:
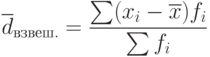 |
( 7.3) |

Дисперсией (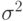
- для несгруппированных данных:
(
7.4) - для сгруппированных данных:
(
7.5)
Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):
- для несгруппированных данных:
(
7.6) - для сгруппированных данных:
(
7.7)
Абсолютные показатели вариации, за исключением дисперсии, имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Поэтому, если экономическая интерпретация, например, среднего линейного отклонения, проста и понятна физически, то в случае с дисперсией она затруднена. Однако дисперсия рассчитывается в статистическом анализе гораздо чаще, чем другие показатели вариации. Связано это с тем, что дисперсия широко используется в таких видах статистического анализа, как корреляционный, регрессионный, дисперсионный, при оценках результатов выборочного наблюдения. Кроме того, именно с помощью дисперсии можно оценить влияние случайных и систематических факторов на формирование значений случайной величины.
Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:
- коэффициент осцилляции:
(
7.8) - относительное линейное отклонение:
(
7.9) - коэффициент вариации:
(
7.9)
Принято считать, что если значение 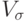
Рассчитаем показатели вариации для приведенных в табл. 7.1 и 7.2 вариационных рядов (табл. 7.3 и 7.4).
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., yj | (xi-x)*f | (xi-x)2*f |
|---|---|---|---|---|
| 4 000-6 000 | 5 000 | 10 | 58 530 | 342 576 090 |
| 6 000-8 000 | 7 000 | 6 | 23 118 | 89 073 654 |
| 8 000-10 000 | 9 000 | 19 | 35 207 | 65 238 571 |
| 10 000-12 000 | 11 000 | 26 | 3 822 | 561 834 |
| 12 000-14 000 | 13 000 | 19 | 40 753 | 87 582 571 |
| 14 000-16 000 | 15 000 | 10 | 41 470 | 171 976 090 |
| 16 000-18 000 | 17 000 | 5 | 30 735 | 188 928 045 |
| Сумма | — | 95 | 233 675 | 945 936 855 |
По первому агентству получим следующие данные.
Размах вариации:
R = xmax — xmin = 18 000 — 4000 = 14 000 (руб.).
Среднее линейное отклонение (так как ряд сгруппирован и частоты не равны между собой) рассчитываем как взвешенную величину:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент осцилляции:

Относительное линейное отклонение:
Коэффициент вариации:

Судя по коэффициенту вариации, совокупность по данному признаку можно считать однородной.
Проведем расчет аналогичных характеристик вариации по второму агентству (табл. 7.4).
| Размер месячной заработной платы, руб. | Середина интервала, xi | Число сотрудников, чел., yj | (xi — x)*f | (xi — x)2*f |
|---|---|---|---|---|
| 1 500-4 500 | 3 000 | 9 | 70 686 | 555 167 844 |
| 4 500-7 500 | 6 000 | 26 | 126 204 | 612 594 216 |
| 7 500-10 500 | 9 000 | 24 | 44 496 | 82 495 584 |
| 10 500-13 500 | 12 000 | 18 | 20 628 | 23 639 688 |
| 13 500-16 500 | 15 000 | 14 | 58 044 | 240 650 424 |
| 16 500-19 500 | 18 000 | 10 | 71 460 | 510 653 160 |
| 19 500-22 500 | 21 000 | 9 | 91 314 | 926 471 844 |
| Сумма | — | 110 | 482 832 | 2 951 672 760 |
Показатели вариации по второму агентству:
Размах вариации:
R = 22 500 — 1500 = 21 000 (руб.);
Среднее линейное отклонение:

Дисперсия:
Среднее квадратическое отклонение — 5180 (руб.).
Коэффициент осцилляции — 193%.
Относительное линейное отклонение — 40%.
Коэффициент вариации — 48%.
Таким образом, по данному признаку вторая совокупность сотрудников неоднородна.
Сравнение относительных показателей вариации по двум совокупностям говорит о том, что дифференциация по уровню заработной платы во втором агентстве гораздо выше, чем в первом, хотя их средние практически совпадают между собой.
Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
К показателям вариации относятся:
I группа — абсолютные показатели вариации
- размах вариации
- среднее линейное отклонение
- дисперсия
- среднее квадратическое отклонение
II группа — относительные показатели вариации
- коэффициент вариации
- коэффициент осцилляции
- относительное линейное отклонение
Самым элементарным показателем вариации признака является размах вариации R. Размах вариации показывает лишь крайние (min, max) отклонения признака от общей средней.
Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.
Среднее линейное отклонение — средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической:
- для несгруппированных данных (простое)
- для сгруппированных данных (взвешенное)
Дисперсия признака — средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:
- Простая дисперсия для несгруппированных данных
- Взвешенная дисперсия для вариационного ряда
Cвойства дисперсии:
- если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится;
- если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k2 раз.
Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
где i – величина интервала, X1 — новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.
- Момент второго порядка
- Квадрат момента первого порядка
Среднее квадратическое отклонение равно корню квадратному из дисперсии:
- для несгруппированных данных (простое)
- для вариационного ряда по сгруппированным данным (взвешенное)
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от их среднего значения.
Среднее значение альтернативного признака и его дисперсия:
- Среднее значение альтернативного признака
- Дисперсия альтернативного признака
Подставив в формулу дисперсии q = 1 – p, получим:
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком.
Среднее квадратическое отклонение альтернативного признака:
Показатели относительного рассеивания
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умноженное на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.
3. Коэффициент вариации – отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Пример расчета абсолютных и относительных показателей вариации:
Распределение КФХ области по урожайности зерновых культур
| Группы хозяйств по урожайности (ц/га) |
Середина интервала |
Число хозяйств |
Расчетные значения |
||||
|
Xi |
ƒi |
Xi ƒi |
|Хi-Хср| |
|Хi – Хср|*ƒi |
(Χi-Χср)2 |
(Χi-Χср)2 *ƒi |
|
| 9,1-15 |
12,1 |
2 |
24,20 |
12,44 |
24,87 |
154,641 |
309,28 |
| 15,1-21,1 |
18,1 |
31 |
561,1 |
6,44 |
199,50 |
41,415 |
1283,88 |
| 21,1-27,1 |
24,1 |
54 |
1301,40 |
0,44 |
23,52 |
0,190 |
10,24 |
| 27,1-33,1 |
30,1 |
30 |
903,00 |
5,56 |
166,94 |
30,964 |
928,92 |
| > 33,1 |
36,1 |
7 |
252,7 |
11,56 |
80,95 |
133,738 |
936,17 |
| Всего |
X |
124 |
3042,40 |
36,44 |
495,77 |
360,948 |
3468,48 |
| Средние |
X |
X |
24,54 |
X |
4,00 |
27,97 |
Смотри также: