Как найти коэффициент мощности катушки

Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.

Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.

В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I²

а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = I_msinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции e_L поэтому ток зависит от действия приложенного напряжения и эдс e_L. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых u_R равно падению напряжения в активном сопротивлении, а другое u_L уравновешивает эдс самоиндукции.

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — u_R совпадает по фазе с током, U_L опережает ток на 90°.

Поэтому:

u = R*I_msinωt  + ωLI_msin(ωt+π/2).

Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

U_mR = RI_m;       U_mL = ωLI_m ,

а действующие величины

U_R = RI; U_L = X_LI .

Вектор общего напряжения

U = U_R + U_L

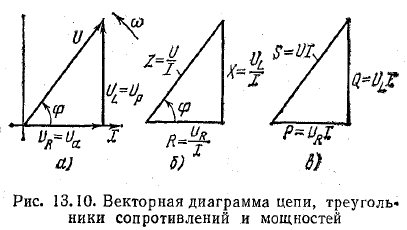
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор U_R по направлению совпадает с вектором тока I, а вектор U_L направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях U_R и U_L :

U_R = Ucosφ 

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается U_a. Для катушки по схеме рис. 13.9 при U_a = U_R

U = Usinφ                                                        (13.14)

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается U_p. Для катушки U_p = U_L

При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде

U = U_msin(ωt+φ)

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = U_R/I и индуктивное X_L = U_L/I, сопротивления, а гипотенузой величина Z = U/I.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:

Из треугольников сопротивления и напряжения определяются

cosφ = U_R/U = R/Z;    sinφ = U_L/U = X_L/Z;    tgφ = U_L/U_R = X_L/R. (13.18)

Мощность реальной катушки

Мгновенная мощность катушки

p = ui = U_msin(ωt+φ) * I_msinωt

Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).

Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).

Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.

Согласно выводам полученных в этих предыдущих  (первая, вторая) статьях — в активном сопротивлении P = U_RI   Q = 0;  а в индуктивном Р = 0; Q = U_LI. 

Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении X_L. Подставляя значения U_R = Ucosφ и U_L = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:

                   P = UIcosφ                                (13.19)

                    Q = UIsinφ                                (13.20)

Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;

                   S = UI = I²Z                                (13.21)

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

                        (13.22)                         

Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить

cosφ = P/S;       sinφ = Q/S;     tgφ = Q/P.             (13.23)

Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).

Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.

Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.

Схема замещения реальной катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной B_L проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

                                             I = I_G + I_L                                           (13.24)

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: I_G —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; I_L — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие I_G и I_L образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

I_G = Icosφ

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается I_а. Для катушки по схеме на рис. 13.12, б I_a = I_G.

Составляющая тока в реактивном элементе

I_L = Isinφ

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки I_р = I_L .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = I_G/U и индуктивная В_L = I_L/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

Коэффициент мощности (cos φ) это параметр, характеризующий искажения формы тока, потребляемого от электросети переменного тока. Важный показатель потребителя электроэнергии. Во многом он определяет требования к питающей сети. От него  зависят потери в проводах и на внутреннем сопротивлении сети.

В цепях постоянного тока мощность, впрочем, как и все остальные параметры, не меняет своего значения в течение определенного отрезка времени. Поэтому, при постоянном токе, существует единственное понятие электрической мощности как произведение значений тока и напряжения.

При переменном токе значения тока и напряжения постоянно меняются с течением времени. Мощность тоже меняется. Поэтому вводится понятие мгновенной мощности.

Мгновенная мощность.

Мгновенная мощность это произведение значения мгновенного напряжения цепи на значение мгновенного тока. На практике мощность связана с выделением тепла, механической работой и т.п. А эти явления имеют инерционный характер. Поэтому понятие мгновенной мощности не имеет практического значения, а используется для расчетов и понимания происходящих процессов.

Действующие значения тока и напряжения.

Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения.

Действующее значение переменного тока определяется как величина такого эквивалентного постоянного тока, который проходя через то же активное сопротивление, что и переменный ток, выделяет на нем за период то же количества тепла. Математически действующее значение определяется как среднеквадратичное за период.

Вольтметры и амперметры переменного тока показывают именно действующие значения. Все операции по тепловым расчетам происходят так же, как и на постоянном токе, только с использованием действующих значений. Но это не всегда правильно.

Полная мощность.

Полная мощность вычисляется как произведение действующих значений тока и напряжения цепи.

S = U * I

В случае синусоидальной формы тока и напряжения, а также отсутствия фазового сдвига, вся полная мощность выделяется на нагрузке. Расчеты для переменного тока соответствуют анализу цепей постоянного тока, только используются действующие значения тока и напряжения.

Полная мощность фактически показывает требования к электрической сети. Измеряется она в В ·А , не в Вт.

Реактивная мощность.

Как только в цепи переменного тока появляются реактивные элементы ( индуктивность и емкость) все меняется. Реактивные элементы обладают способностью накапливать энергию и отдавать ее в цепь обратно. Появляется реактивная мощность.

Реактивная мощность не выделяется на нагрузке, не создает полезной работы. Она накапливается на реактивных элементах нагрузки ( конденсаторах, катушках индуктивности), а затем возвращается обратно в питающую сеть. Понятно, что возвращается она с потерями на проводах, на внутреннем сопротивлении питающей сети и т.п. Поэтому в любой энергосистеме стремятся уменьшить реактивную мощность до минимума.

Реактивная мощность может быть как положительной (для индуктивных цепей), так и отрицательной (для емкостной составляющей).

Единица измерения – вольт-ампер реактивный (ВАР).

Активная мощность.

На нагрузке остается активная мощность. Она и совершает полезную работу. Активная мощность это среднее значение мгновенной мощности за период.

Основные соотношения между параметрами.

Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей.

S = √ ( P² + Q²)

Активная мощность вычисляется как:

P = I * U * cos φ

I и U это действующие значения тока и напряжения.

Или:

P = S * cos φ

Т.е. активная и полная мощности связаны через коэффициент — cos φ.

cos φ – это косинус угла сдвига между напряжением питающей сети и током, потребляемым нагрузкой.  Это соотношение верно только для синусоидальной формы тока и напряжения. При cos φ = 1  активная мощность на нагрузке равна полной. Вся энергия  питающей сети используется для полезной работы. Происходит это только на чисто активной нагрузке, без реактивной составляющей.

cos φ  и есть коэффициент мощности  (КМ) для переменных цепей с током и напряжением синусоидальной формы.

Но многие потребители энергии не только сдвигают фазу, но искажают форму тока. Примером может служить блок питания с бестрансформаторным входом. Это эквивалентная схема подключения его к питающей сети.

В подобных устройствах напряжение питающей сети выпрямляется и сглаживается на конденсаторе большой емкости. Полученное постоянное напряжение с малым уровнем пульсаций используется для дальнейшего преобразования.

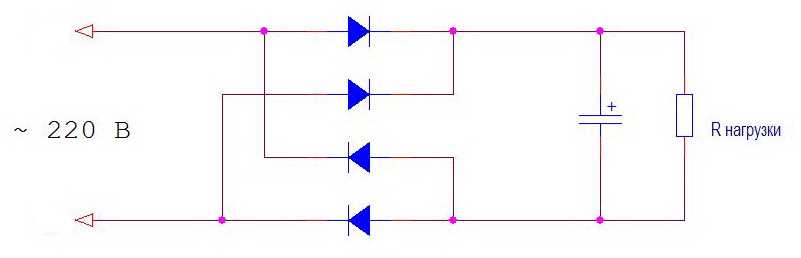
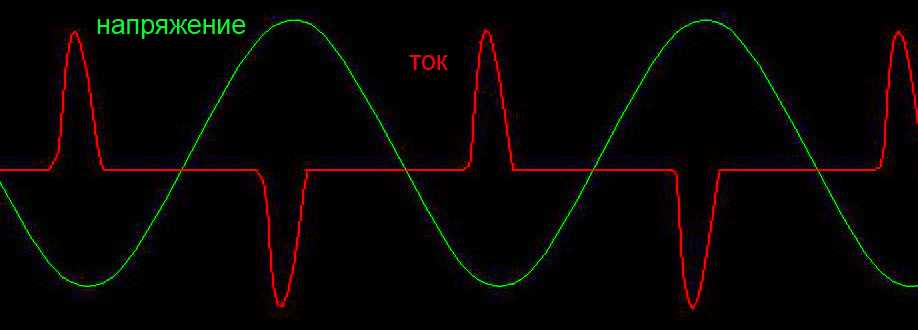
Для питающей сети эта схема представляет нагрузку  активно-емкостного характера. Но диоды выпрямительного моста имеют нелинейную характеристику. В начале и в конце периода они закрыты и нагрузка отключена. А в середине периода диоды открываются и кроме активной нагрузки подключают к сети значительную емкость сглаживающего фильтра. В результате ток имеет искаженную форму, показанную на рисунке.

Это один из самых неприятных типов нагрузки, но и самый распространенный. Вся бытовая техника (телевизоры, компьютеры …) представляют такой характер нагрузки.

Коэффициент мощности (КМ) в переменных цепях с искаженной формой тока определяется как отношение активной мощности к полной.

λ = P / S

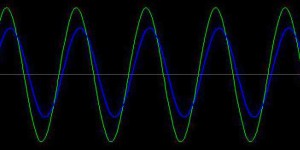
Следующие диаграммы иллюстрируют, как КМ влияет на работу потребителей электроэнергии.

На этом рисунке показаны осциллограммы чисто активной нагрузки. Фазового сдвига нет, cos φ = 1, вся энергия из сети переходит в активную мощность на нагрузке.

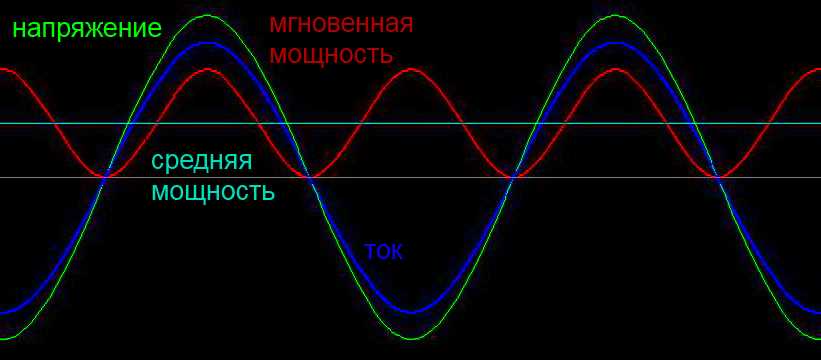
На втором рисунке крайний, самый плохой вариант.

Сдвиг фазы между током и напряжением 90°, cos φ  = 0. Видно, что диаграмма мгновенной мощности расположена симметрично относительно 0. Средняя активная мощность равна 0. Конечно, устройств с cos φ  = 0 на практике не бывает, но промежуточных вариантов сколько угодно. Например, бестрансформаторный блок питания, приведенный в качестве примера выше, имеет КМ 0,6 — 0,7.

Значимость КМ можно показать простейшими расчетами.

Два потребителя электроэнергии с одинаковой активной (полезной) мощностью. У первого cos φ  = 1, а у второго 0,5. Это означает, что второй потребитель потребляет от сети ток в два раза больше, чем первый. Т.к. зависимость потерь в проводах от тока имеет квадратичный характер (P = I² * R), то потери на активном сопротивлении проводов во втором случае будут в 4 раза больше. Потребуются провода большего сечения.

Для мощных нагрузок, длинных линий электропередач высокий КМ особенно важен.

Измерение коэффициента мощности.

Для измерения cos φ используются специальные приборы – фазометры. Они применяются в сетях с потребляемым током синусоидальной формы, без искажения.

Для измерения КМ у нагрузок, искажающих ток, обычно пользуются следующей методикой.

Схема измерения коэффициента мощности.

Необходимо вычислить полную мощность, как произведение  показаний вольтметра и амперметра.

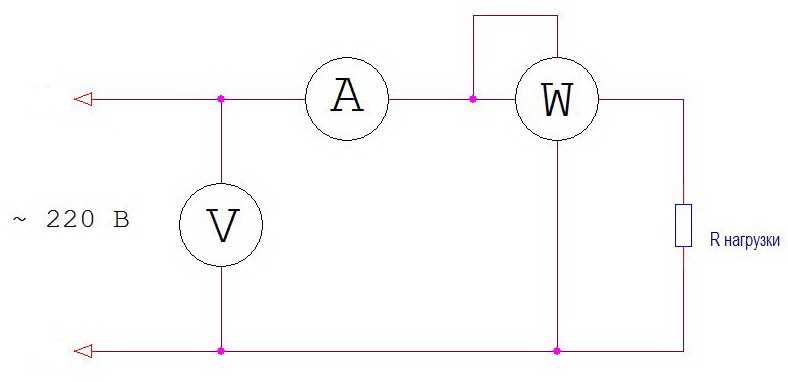
S = U * I

Теперь надо активную мощность (показания ваттметра) разделить на полную.

λ = P / S

При отсутствии ваттметра можно использовать счетчик электроэнергии.

Для этого необходимо замерить время 10 калибровочных импульсов (миганий светодиода на корпусе счетчика). Вычислить время периода одного импульса (разделить на 10). Зная коэффициент счетчика (обычно 3200 импульсов на кВт) можно посчитать активную мощность нагрузки. С учетом того, что счетчики электроэнергии имеют класс точности 1.0, измерение получится довольно точным.

Коррекция коэффициента  мощности.

Для увеличения КМ существуют специальные устройства – корректоры коэффициента мощности (ККМ). Они бываю пассивными и активными.

Для пассивной коррекции КМ в цепь питания последовательно включают дроссель. Такое решение часто применяется для трансформаторных станций катодной защиты. Но это от безвыходности. Других решений для трансформаторных станций не существует. Дроссель требуется громадных размеров, не меньше чем силовой трансформатор станции. Размеры, вес, цена станции увеличиваются практически в 2 раза, а коэффициент мощности удается поднять только до 0,85.

В инверторных станциях катодной защиты без корректора мощности (выпрямительно-емкостная нагрузка, пример был выше) КМ порядка 0,6 — 0,7. Для его увеличения используют специальные электронные модули – активные корректоры коэффициента мощности. Их схемы, построены по принципу повышающего импульсного преобразователя. Специальные управляющие микросхемы отслеживают форму тока потребления и так управляют ключом преобразователя, что она становится синусоидальной. На выходе активного ККМ формируется постоянное напряжение 380 – 400 В. Поэтому использовать их с трансформаторами невозможно.

Активные корректоры повышают КМ до 0,95 – 0,99.

Пример активного ККМ 2000 Вт для инверторной станции катодной защиты серии «ТИЭЛЛА».

Схемотехнике активных ККМ я посвящу отдельную статью.

Коэффициент мощности () приемников электрической энергии

Обычно
электрические приемники (двигатели,
трансформаторы) носят активно-индуктивный
характер и работают с углом сдвига фаз
.
Генератор, питающий такой приемник,
линия передачи к нему и сам приемник
рассчитываются на полную мощность
.
Средняя (или активная) мощность приемника,
соответствующая преобразованию
электрической энергии в тепло или
механическую работу, соответствует
равенству
.
Здесь

– коэффициент мощности приемника;
–
т.е. коэффициент мощности – это отношение
активной мощности к полной. Как правило,
,
т.е. расчетная (полная) мощность генератора
и линии передачи используются не с
полной эффективностью. Отсюда ясна
важность для народного хозяйства
повышения коэффициента мощности (в
предельном случае до
).

Ток,
потребляемый приемником от генератора,
также зависит от коэффициента мощности,
т.е.

.

Если
приемник работает при постоянной
мощности

и на­пряжении
,
соответствующих

номинальным
(паспортным) данным приемника, то ток

будет тем больше, чем ниже.
Увеличение тока

приводит к увеличению потерь энергии
в генераторах, линиях передачи и
приемниках. Таким образом, для полного
использования расчетной мощности
генераторов и уменьшения потерь энергии
необходимо повышать

приемников. С целью повышения коэффициента
мощности к приемнику подключают
параллельно батарею конденсаторов.

В
этом случае
,
где
–
емкостная мощность конденсаторов;

– индуктивная мощность приемника.

При
резонансе токов
,
,
.
Обычно коэффициент мощности приемников
повышают до значения
0,92-0,95,
так как дальнейший его рост требует
значительного увеличения емкости
батареи конденсаторов, а следовательно,
увеличения ее стоимости. Емкость
конденсатора, который необходимо
подключить параллельно приемнику для
повышения коэффициента мощности с
величины

до величин!
,
может быть определена по формуле

,

где

– активная мощность приемника;

– частота сети,
50
Гц;

– напряжение сети.

Программа
работы

1.
Исследовать работу схемы, включая
поочередно резистор, катушку и конденсатор.

2.
Исследовать работу параллельно включенных
резистора, катушки и конденсатора при
переменной емкости до резонанса токов,
при резонансе и после резонанса.

3.
Рассчитать величину емкости, необходимую
для повышения коэффициента мощности
приемника, состоящего из параллельно
включённых резистора и катушки
индуктивности, до наибольшего значения
1
и сравнить с данными опыта (строка 6 в
табл. 3)^*.

Порядок
выполнения работы

1.
Собирается схема (рис. 19). Автотрансформатором
AT устанавливается напряжение в пределах
90 … 120 В, которое поддерживается постоянным
при всех измерениях.

Рис.19

2.
Для выполнения первой части работы
поочередно включаются резистор, катушка
и конденсатор. В каждом случае показания
приборов записываются в таблицу
наблюдений.

3.
Вторая часть работы выполняется при
одновременном включении всех трех
приемников. Исследование ведется
следующим образом. Изменяя емкость
батареи конденсаторов, цепь настраивают
по фазометру ()
в резонансное состояние. Некоторая
доводка до резонансного состояния
возможна изменением положения сердечника
в катушке. После этого сердечник
заклинивают, чтобы
.
Далее, изменяя емкость от 0 до максимально
возможного значения, снимают показания
приборов двух опытов до резонанса токов
и двух – после резонанса. Результаты
опытов заносят в табл. 3.

Таблица
3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #