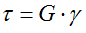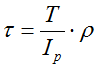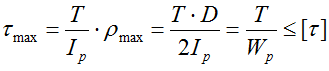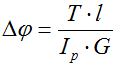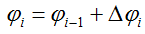Внутренний крутящий момент в сечении вала Мк (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.
где Мi – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.
Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:
где — это полярные моменты инерции для сплошного и кольцевого сечений соответственно, ρ – координата произвольной точки сечения, D, d – наружний и внутренний диаметры сечения.
Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρmax
Условие прочности по допускаемым напряжениям
где — это допускаемое касательное напряжение.
Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом
где G – модуль сдвига
Относительный угол закручивания (рад/м) для силового участка
Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде
где допускаемый относительный угол закручивания.
Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.
В характерных точках сечения
угол закручивания на силовом участке вала
где α, η, β – коэффициенты, зависящие от отношения a/b (или h/b — отношение большей стороны прямоугольника к меньшей)
Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.
Касательные напряжения в характерных точках сечения
Угол закручивания на силовом участке вала
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение пустотелых валов круглого сечения
Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.
Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ<1 берутся из той же таблицы, что и значения α и β.
1.1.
Общие сведения о деформации тел при
кручении и моменте сил упругих деформаций
нитей в установках типа крутильных
весов и крутильного маятника.
Крутильный
маятник по своему конструктивному
устройству аналогичен крутильным
весам. Различие, однако, в том, что весы
используются в статическом режиме
равновесия, а маятник применяется в
динамическом режиме. При этом детали
его конструкции вращаются, периодически
изменяя направление поворота.
Простейшая
конструкция крутильных весов (и
крутильного маятника) представляет
собой подвес на вертикальной нити, на
свободном конце которой закреплена
симметричная горизонтальная штанга
или иное приспособление (например, рамка
для установки изучаемых тел). С целью
лучшей стабилизации оси поворота часто
применяют растяжку, т.е. натянутые и
закреплённые на концах две нити. В
средней части располагается штанга
либо рамка с боковыми рычагами (см.
рис.1).
Рис.1
I
– нити, 2 — рамка с рычагами
Если
к рычагам рамки приложить горизонтальную
силу, тогда нить, закреплённая на другом
конце, начинает закручиваться. При
закрутке нити происходят деформации
сдвига её слоёв и возникает момент
упругих сил, препятствующий повороту
и стремящийся вернуть нить в исходное,
недеформированное состояние.
При
излишне большой закрутке деформация
нити становится неупругой (пластической),
т.е. после снятия внешней силы, приложенной
к рычагу, нить не возвращается в исходное
состояние.
Все измерения на крутильных весах (и
маятнике) требуется выполнять в условиях
упругой деформации при ограниченном
угле закрутки нити.
В этом случае по углу закрутки, т.е. по
углу поворота рычага (и рамки)
на крутильных весах можно определить
момент внешних силМвн,
приложенных к рычагам.
В
условиях равновесия имеем:
М
вн = Мкр
,
(1)
где
Мкр.
— момент сил упругой деформации закрученной
нити, равный:
;
(2)
(Единица
измерения «радиан»,
как дополнительная в системе
СИ,
размерности не имеет).
В
формуле (2) величина f
называется коэффициентом
кручения, который определяется для
каждой данной конструкции в зависимости
от материала, радиуса и длины нити
следующим выражением:
,
(3)
где
r
— радиус нити;
— длина нити;G
—
модуль
сдвига
материала нити. Размерность коэффициента
,
согласно формуле (2), равна=Н∙м/рад.=
Н∙м.
Выражение
(3) определяет коэффициент кручения для
подвеса на одной нити. В случае растяжки
на двух разных нитях действуют два
момента упругих сил, равные:
;
, (4)
где:
(5)
Суммарный
момент сил упругой деформации растяжки
на двух разных нитях равен:
Мкр
=
М1
+ М2
(5а)
или
(5б)
Если
нити растяжки изготовлены из одного
материала, имеют одинаковые радиусы,
но разную длину, тогда выражение (5б)
преобразуется к виду:
(6)
В
формулах (5б) и (6) коэффициент при угле
поворота
является коэффициентом кручения
для данной, конкретной установки и
обозначается аналогично формуле
(2). Для растяжки на двух нитях из
одинакового материала при равных
радиусах получаем:
(7)
ПРИМЕЧАНИЕ
I. Формулы (2), (4), (5б) и (6) определяют
величину (модуль) момента сил упругой
деформации кручения без учёта знака
проекции вектора момента этих сил.
ПРИМЕЧАНИЕ
2. Нити подвесов и растяжек для крутильных
весов и маятников изготавливают из
тонкого стального провода специальных
марок. Для особо точных приборов
применяются кварцевые нити.
ПРИМЕЧАНИЕ
3. Вывод формулы (3) для коэффициента
кручения изучается в курсе «Сопротивление
материалов». Модуль сдвига G
наряду с модулем
Юнга
Е
являются справочными данными как модули
упругости для каждого сорта материалов.
Сведения об этих модулях необходимы
для расчёта прочности и жёсткости любой
конструкции машин, двигателей,
строительных сооружений и т.д.
Модуль
Юнга определяется как отношение
плотности силы FN,
действующей по нормали к сечению, к
величине относительной деформации
растяжения материала
, т.е. равен E=FN/
; размерность [ Е
] = Н/м2
. Модуль сдвига G
определяется как отношение плотности
силы Fτ
, действующей по касательной к сечению,
к величине угла скоса
рёбер куба, основание которого
закреплено и остается неподвижным,
а противоположная грань, к которой
приложена касательная сила с плотностьюFτ,
сдвигается. Формула для величины G
имеет вид:
G
= Fτ
/;
размерность [G]
= Н/м2
•рад. = Н/м2.
Модули
Е
и G
для каждого материала определяются
опытным методом. Для измерения величины
Е
существуют специальные установки,
где материал подвергается испытаниям
на сжатие и растяжение. Измерение
величины G
выполняется обычно методом кручения,
т.е. для расчётов применяется формула
типа (3), где коэффициент кручения
измеряется независимо также на основе
опытных данных.
Понятие
о модулях как характеристиках упругих
свойств материалов при малых
деформациях было введено в конце XVIII-
начале XIX веков. В этот же период С.
Пуассоном было теоретически вычислено
соотношение между модулями Е
и G
, имеющее вид:
,
где
— коэффициент Пуассона, который равен
отношению относительного поперечного
сжатия образца материала к соответствующему
относительному продольному удлинению.
Например, для многих металлов коэффициент
0,3.
Устройства,
использующие подвесы (или растяжки) на
тонких нитях, были и остаются одними
из наиболее чувствительных приборов
для измерения сил. Применяя установку
типа крутильных весов, Ш. Кулон в 1785 г.
исследовал взаимодействие электрически
заряженных тел и установил закон,
определяющий силу электростатического
взаимодействия; Г. Кавендиш в 1798 г.
измерил силу гравитационного притяжения
двух небольших свинцовых шаров и впервые
определил величину гравитационной
постоянной в законе всемирного тяготения;
П.Н. Лебедев в 1899 г. экспериментально
доказал, что свет оказывает давление
на твёрдые тела.
Полезно
отметить, что наиболее точные измерения
коэффициентов кручения в особо
чувствительных крутильных весах
выполняются методом крутильных
колебаний, т.е. с использованием той же
установки в динамическом режиме
крутильного маятника.
1.2.
Вывод уравнения крутильных колебаний
и методика определения коэффициента
кручения.
Показанная
на рис.1 рамка на растяжке из двух нитей
может находиться в состоянии покоя
сколь угодно большое время. Однако,
если рамку вывести из состояния покоя,
например, повернуть на некоторый угол
в пределах упругой деформации нитей
и затем отпустить, тогда рамка начнёт
периодически поворачиваться то в одну,
то в другую стороны, вращаясь вокруг
оси, проходящей через нити. Такая система
называется крутильным маятником.Получим
уравнение движения этой системы и
покажем, что оно имеет вид известного
в теории уравнения свободных
гармонических колебаний, которые в
данной установке называются крутильными
колебаниями.
Пренебрегая
сопротивлением воздуха, считаем, что
вращение рамки происходит только
под действием момента сил упругой
деформации закручиваемых нитей.
Обозначим момент инерции рамки
относительно оси вращения J0
и запишем уравнение вращательного
движения рамки под действием момента
сил Мкр
:
J0
∙ ε
= Мкр
(8)
Здесь
ε
и Мкр
—
проекции векторов углового ускорения
рамки и момента сил упругой деформации
на ось координат, проходящую через ось
вращения.
С
учётом направлений соответствующих
векторов и выражений для ε
и Мкр
запишем (8) в виде дифференциального
уравнения:
(9)
Здесь:
— вторая производная по времени от угла
поворота рамки, определяющая её угловое
ускорение
— коэффициент кручения, определяемый
формулой (7) для растяжки на двух нитях
разной длины, изготовленных из стали
одной марки с одинаковыми радиусами
(такие нити используются в установке
настоящей лабораторной работы). В
установках, применяемых в качестве
крутильного маятника, коэффициентиногда называют коэффициентом
жёсткости.
Уравнение
(9) преобразуется к более наглядной
канонической форме, позволяющей сразу
найти его решение, т.е. функцию
,
определяющую зависимость угла поворота
от времени. Для этого надо перенести
все члены (9) в левую часть, разделить
на коэффициент при второй производной
по времени иввести
обозначение:
.
Полученное таким способом уравнение
имеет вид:
+
(10)
Уравнение
типа (10) называется уравнением свободных
гармонических колебаний, т.к. решение
этого уравнения
(11)
показывает,
что угол поворота периодически изменяется
с течением времени. Значение
определяет максимальный угол поворота
(амплитуду);называется собственной циклической
частотой колебаний и определяет число
одинаковых состояний системы за время
2сек;
— начальная фаза колебаний;
— время.
Примечание.
Колебаниями
называются
периодические изменения состояния
системы при условии, что данная система
обладает собственной циклической
частотой и состоянием с минимальной
потенциальной энергией.
Период
колебаний Т0,
т.е. интервал времени между двумя
ближайшими одинаковыми состояниями
системы, определяется формулой:
(12)
Отметим,
что при исследовании крутильного
маятника уравнение (10) называется
уравнением крутильных колебаний, т.к.
период колебаний определяется формулой:
,
(13)
где
— коэффициент кручения, зависящий
только от параметров нитей исследуемой
установки.
Рассмотрим
теперь методику определения коэффициента
кручения с помощью крутильных колебаний.
Согласно формуле (13) период колебаний
зависит от момента инерции, если
коэффициент кручения
постоянный.
Обычно
момент инерции рамки
нельзя вычислить теоретически
с
достаточной точностью, т.к. её детали
имеют разную конструктивную
форму и
массу. Следовательно, если выполнить
измерение периода колебаний с одной
рамкой и рассматривать формулу (13) в
качестве уравнения для определения
величины,
то в этом уравнении будут две неизвестные:и
.
Однако это уравнение можно дополнить
вторым уравнением, измеряя период
колебаний рамки с дополнительным
грузом, момент инерции которого известен
(обычно такой груз имеет форму однородного
цилиндра с известными массой и радиусом,
при этом цилиндр устанавливается строго
на оси вращения маятника).
Обозначая
известный момент инерции добавочного
груза
,
период колебаний рамки с грузом,
имеем:
(14)
Возводя
в квадрат выражения (13) и (14) и затем
вычитая первое из второго, получим:
(15)
Из
(15) находим коэффициент кручения:
(16)
Периоды
колебаний Т0
и Т1
измеряются в опыте. Описанный здесь
метод применялся для определения
коэффициентов
в установках, на которых выполнялись
отмеченные выше классические эксперименты.
1.3.
Определение моментов инерции тел
относительно главных и параллельных
осей.
Моменты
инерции являются одной из важнейших
характеристик твёрдых тел, т.к.
определяют инертные свойства тел при
поворотах (вращениях) в пространстве.
Повороты (вращения) могут происходить
относительно различных осей и
соответствующие этим осям моменты
инерции тел обычно имеют разные значения.
Теорией
и опытом доказано, что все твёрдые тела
(любой формы) обладают тремя особыми
взаимно-перпендикулярными осями,
пересекающимися в центре масс. Эти
оси называются главными
осями
тела ввиду их примечательных свойств,
описанных в литературе (см. Приложение).
Моменты
инерции тел относительно главных осей
принято называть главными
моментами инерции, для
однородных симметричных тел главные
моменты инерции легко вычисляются
способом интегрирования. Такие
моменты инерции тел простейших
геометрических форм приводятся в
справочной литературе (см.
Приложение).
При известных главных моментах инерции
можно рассчитать моменты инерции тел
относительно любых других осей. Наиболее
просто такие расчёты выполняются для
осей, параллельных главным осям (с
применением теоремы Штейнера).
На
практике, однако, часто применяются
вращающиеся неоднородные тела
сложной формы (например, гребные винты
судов, роторы турбин, роторы
электродвигателей и т.п.). Моменты
инерции таких тел относительно заданных
осей определяют опытным методом с
помощью различных экспериментальных
установок, где исследуемые тела
совершают вращательное движение.
Наиболее
точные измерения моментов инерции
выполняются на установках типа
физического и крутильного маятников.
Для
измерений моментов инерции относительно
осей, проходящих через центр масс тела,
исследуемое тело устанавливают на
платформе крутильного маятника
(закреплённой, например, в рамке,
показанной на рис.1). Заданную ось тела
совмещают с осью вращения маятника и
затем измеряют период колебаний Т.
Обозначая
момент инерции рамки
, (который можно найти в предварительном
опыте при известном коэффициенте
кручения),
запишем формулу для периодаколебаний:
(17)
Здесь
— неизвестный момент инерции исследуемого
тела.
Возводя
(17) в квадрат, получаем:
(18)
В
данной лабораторной работе формула
(18) применяется для определения
главных моментов инерции тел разной
формы. Для однородных симметричных тел
результаты измерений можно сравнить
с результатами расчётов моментов
инерции по формулам, данным в Приложении.
Измерения
моментов инерции относительно
параллельной оси
на крутильном маятнике следует выполнять
с использованием двух одинаковых
тел. Исследуемые тела необходимо
установить на платформе внутри рамки
симметрично, на одинаковых расстояниях
заданных осей тел от оси вращения
маятника (см. рис.2).
Рис.
2.
По
теореме Штейнера момент инерции тела
JN
относительно некоторой оси N
,
не проходящей через центр масс тела,
равен сумме момента инерции тела Jc
относительно оси, проходящей через
центр масс тела параллельно заданной
оси N
, и произведения
,
где— масса тела,
— расстояние между параллельными осями.
(19)
В
крутильном маятнике осью N
является ось вращения маятника,
проходящая через нити растяжки (показана
на рис.2). Параллельные оси, проходящие
через центры масс тел на расстоянии
от оси N
,
также показаны на рис.2.
Суммарный
момент инерции конструкции (рис.2) равен
,
где— момент инерции рамки. Период колебаний
маятника:
(20)
Возводя
(20) в квадрат, получаем:
(21)
Выражение
(21) позволяет определить момент инерции
для тела любой формы. Если момент инерции
известен (для однородного симметричного
тела), можно сравнить результаты
измерения и расчёта с помощью формул
(19) и (21).
Соседние файлы в папке ЛР №5
- #
- #
27.04.20153.66 Кб10Содержание OneNote.onetoc2
Подборка формул для расчета валов и брусьев на кручение и решения задач сопротивления материалов по расчету внутренних моментов, касательных напряжений, деформаций и углов закручивания при кручении.
Обозначения:
τ — касательные напряжения,
T – внутренний крутящий момент,
Ip – полярный момент инерции сечения вала,
Wp – полярный момент сопротивления сечения,
[τ] – допустимое напряжение,
G – модуль упругости II рода (модуль сдвига),
ρ — расстояние от центра сечения до рассматриваемой точки,
D – внешний диаметр вала,
d – внутренний диаметр вала кольцевого сечения.
Закон Гука при кручении (чистом сдвиге)
Расчет касательных напряжений в произвольной точке сечения вала
Условие прочности при кручении (проверочный расчет)
Формулы полярных моментов инерции и сопротивления
Формулы для подбора диаметра вала по условию прочности
Абсолютные деформации (угол закручивания участков вала)
Перемещение (угол поворота) сечений.
Здесь: φi — угол поворота рассматриваемого сечения,
φi-1 — перемещение предыдущего сечения,
Δφi — деформация участка между указанными сечениями.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
Коэффициент концентрации напряжений в галтели при кручении [c.276]
Эффективный коэффициент концентрации напряжений в галтели при кручении [c.277]
Прочность деталей машин, работающих при большом числе перемен нагрузок, в значительной степени зависит от состояния поверхностных слоев. Усталостная трещина возникает на поверхности детали, где действуют наибольшие напряжения при изгибе, кручении. Дефекты поверхности в виде рисок от прохождения режущей кромки при обработке, неравномерности структуры, остаточных напряжений и неравномерности физико-меха-нических свойств подповерхностного слоя способствуют возникновению очагов концентрации напряжений, что приводит при некоторых методах обработки к резкому снижению предела выносливости (рис. 133). На рис. 133 по оси ординат отложены значения коэффициента р, характеризующего влияние метода обработки (качества поверхности) на предел выносливости в зависимости от предела прочности [c.402]
Сопоставление концентрации напряжений при растяжении, изгибе и кручении приведено на рис. 2.8, на котором показано, что в плоском образце при растяжении концентрация напряжений больше (коэффициент концентрации Ск = 2,65), чем при изгибе (ок = 2,01). Причина этого заключается в том, что исходная неравномерность напряженного состояния при изгибе существует и у гладкого образца и потому относительное влияние надреза при изгибе слабее. [c.99]
Коэффициент концентрации касательных напряжений в галтели при кручении вычисляется по формуле [c.258]
Указание. Сечение шпонки выбрать самостоятельно. Припять, что нормальные напряжения изгиба изменяются по симметричному циклу, а касательные напряжения кручения — по пульсирующему. При определении коэффициента запаса прочности для сечения под серединой подшипника, учесть концентрацию напряжений от напрессовки. [c.208]
Коэффициент концентрации напряжений при кручении для валов из етали, имеющей в Мн/м- [c.320]
Коэффициент концентрации напряжении при кручении Ат для валов из стали, имеющей в Мн /м [c.321]
П42. Эффективные коэффициенты концентрации напряжения при изгибе и кручении для валов и осей [c.322]
Для нешлифованных поверхностей вводятся коэффициенты концентрации напряжений, вызываемой н ровностями поверхности кап и kxn, принимаемые одинаковыми при изгибе и кручении (табл. 3.9). [c.57]
Эффективный коэффициент концентрации напряжений при кручении / .j=2,2 (см. рис. 1.7). [c.19]
Влияние концентрации напряжений на прочность деталей машин, испытывающих деформацию растяжения (сжатия), изгиба или кручения, проявляется примерно одинаково. Опыты показывают, что для пластичных материалов концентрация напряжений при статических нагрузках не представляет опасности, поскольку за счет текучести в зоне концентрации происходит перераспределение (выравнивание) напряжений. Величина эффективного коэффициента концентрации в этом случае близка к единице. [c.219]
Величина наибольшего напряжения при кручении в зоне концентрации (пик напряжения) выражается как произведение номинального напряжения т на коэффициент концентрации а- [c.236]
Такое высокое значение коэффициентов концентрации при кручении валов с отверстием (часто такие отверстия делают для смазки) обязывает особенно осторожно подходить к выбору размеров валов, изготавливаемых из хрупких материалов. Для снижения концентрации напряжений в машиностроительной практике приходится прибегать к различным технологическим мерам сглаживанию резких переходов, закруглению кромок (у отверстий) и т. п. [c.240]
Заметим, что степень влияния концентрации напряжений на пределы выносливости зависит от вида напряженного состояния. При циклическом кручении, например, эффективные коэффициенты концентрации оказываются обычно более низкими, чем при изгибе для одних и тех же конструктивных форм (рис. 567 и 568). Соотношение между коэффициентами при изгибе и кручении, представленными [c.606]
Определим коэффициенты концентрации при кручении. Теоретический коэффициент концентрации примем = 3 коэффициент чувствительности к концентрации напряжений примем тот же, что и при изгибе, т. е. = q = 0,65. Тогда эффективный коэффициент концентрации при кручении [c.617]
На рис. V. 18 дан график для определения значения теоретического коэффициента концентрации напряжений при кручении вала с сопряжением частей по круговой галтели радиуса г. Как видим, при резких переходах, т. е. при малых значениях r/d, сильно возрастает. [c.128]
Эффективные коэффициенты концентрации напряжений при изгибе Ка и кручении Кх в зависимости от наличия в сечении концентраторов напряжений определяют из табл. 27.1. [c.315]
Величину теоретического коэффициента концентрации напряжений при кручении вала с галтелью находим по таблице 37 курса. Интерполируя между [c.326]
Рис. 5. график эффективного коэффициента концентрации напряжений для валов с поперечным отверстием при кручении [c.455]
Концентрация напряжений возникает также и при других видах деформаций— кручении, изгибе и т. д. Например, при чистом изгибе полосы, ослабленной двумя симметричными выточками (рис. 2.22), коэффициент концентрации можно определить по формуле [c.51]
D d г d Коэффициент концентрации напряжений при изгибе для деталей из стали, имеющей Oj,, кГ/мм Коэффициент концентрации напряжений при кручении ftj для деталей из стали, имеющей ад, кГ мм [c.607]
Для испытаний были приняты круглые тонкостенные образцы (см. рис. 25), рабочая часть которых оставалась неизменной при кручении и растяжении — сжатии. Выбор таких образцов позволил обеспечить практически однородное напряженное состояние при кручении и получить полностью сопоставимые результаты при кручении и растяжении — сжатии. Концентратор наносился на образец в виде сверления на рабочей части диаметром 1,3 мм. Как известно, такой концентратор соответствует теоретическому коэффициенту концентрации напряжений а = 4 (при кручении) и а = 3 (при растяжении — сжатии). Зарождение и распространение магистральных трещин на ранних стадиях исследовалось на сталях 45, I2XH3A и 40Х [16П. Состояние и механические свойства исследованных сталей приведены в табл. 4, [c.46]
Большой практический интерес при кручении круглых валов представляет концентрация напряжений у продольных пазов, предназначенных для помещения шпонок. Если шпоночный паз имеет прямоугольное сечение (рис. 150, а), то в выступающих углах т касательные напряжения равны нулю, а во входящих углах п напряжения теоретически бесконечно велики (практически же их величина ограничена пределом текучести ). Как показали исследования, коэффициент концентрации напряжений для паза при заданных глубине его и размерах вала зависит главным образом от кривизны поверхности по дну паза. Поэтому углы п необходимо скруглять, причем с увеличением радиуса скругления концентрация напряжений будет уменьшаться. Так, с увеличением р1адиуса от 0,1 до 0,5 глубины паза коэффициент к снижается более чем в. 2 раза. [c.218]
Определить наибольшую допускаемую величину крутящего момента. Коэффициенты концентрации напряжений принять равными при изгибе ос д=1,8, а при кручении aJJд = l,56 масштабный коэффициент считать равным двум, а основной коэффициент запаса прочности Ад =1,7., [c.408]
В формулах (1.7)…(1.12) t j и т , — пределы выносливости при симметричном цикле напряжений соответственно при растяжении, сжатии, изгибе и кручении и К, — эффективные коэффициенты концентрации напряжений K — коэффициент влияния абсолютных размеров поперечного сечения (масштабный фактор) — коэффициент влияния поверхностного упрочнения 1/ и ]/, — коэффициенты чувствительности асимметрии цикла напряжений. [c.14]
Если одновременно имеются концентрг горы напряжений, определяемые формой вала, которые учитывак тся коэффициентами ка н то общий коэффициент концентрации 1апряжений при изгибе будет ко + кап — К а при кручении—А 4-— I- При поверх- [c.57]
Учитывая сделанные в начале параграфа оговорки о малости концентратора, позволившей заменить задачу кручения задачей об антиплоской деформации, мы можем определить коэффициент концентрации иначе это множитель, показывающий во сколько раз увеличивается напряжение при лаличии концентратора по сравнению с тем, которое было бы в этом же месте при кручении стержня без концентратора. [c.307]
Коэффициент концентрации напряжений при кручении для деталей из стали, имеющей KrjMM [c.608]
Эффективный коэффициент концентрации напряжений у поперечного сверления аэфф = 3. Предел текучести материала при изгибе От = 4300 кПсм -, предел текучести при кручении х- = 2200 кПсм , предел усталости на изгиб a i = 2700 кГ/см -, предел усталости на кручение t i=1500 кГ1см ,