Как найти кинетическую энергию зная потенциал

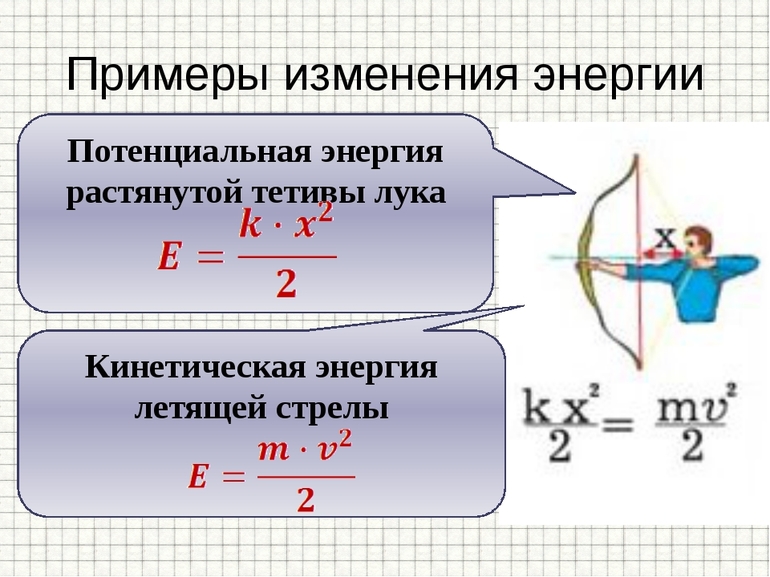
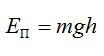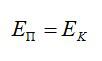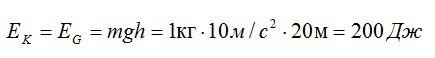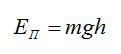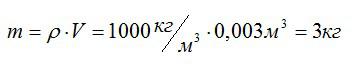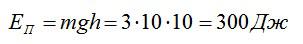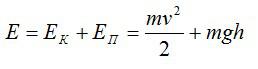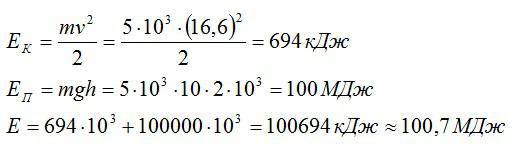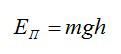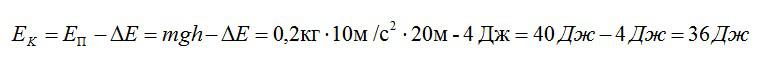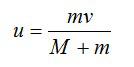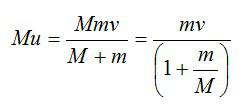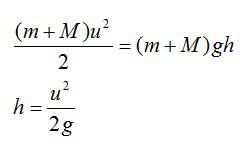Энергия является важнейшим понятием в механике. Данный термин определяет способность тела совершать работу. Универсальная количественная мера в физике характеризует движение и взаимодействие объектов. Она может быть двух типов: потенциальной и кинетической.

Потенциальная и кинетическая энергия

Потенциальной энергией называют энергию взаимодействия тел.

Определить потенциальную энергию тела можно, зная его массу, ускорение свободного падения и положение относительно земли. Формула для расчета имеет следующий вид:

E = m * g * h

В международной системе СИ потенциальная энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В вышеуказанной формуле m является массой тела, h представляет собой высоту, а g – ускорением свободного падения, которое приблизительно равно 9,8 м/с2.

Величина потенциальной энергии определяется выбранной системой отсчета. Это связано с тем, что отсчет высоты можно выполнять не только относительно земной поверхности, но и от какой-то точки или определенного уровня.

Кинетической энергией называют энергию, которой обладает тело во время движения.

Кинетическая энергия служит для определения запаса энергии тела, обладающего определенной скоростью. Определить кинетическую энергию можно с помощью формулы:

(E=frac{mv^{2}}{2})

В международной системе СИ кинетическая энергия обозначается буквой Е и измеряется в Дж (Джоуль).

В уравнении m является массой тела, а v представляет собой его скорость.

Скорость тела определяется выбранной системой отсчета. Поэтому кинетическая энергия также зависит от того, каким образом рассчитывают характеристики системы, в которой движется тело.

Представленное уравнение для расчета кинетической энергии справедливо в том случае, когда рассматривают скорости, намного меньшие, чем скорость света в вакуумной среде в 300 тысяч километров в секунду. Если скорость близка к световой, то расчеты необходимо производить с учетом теории относительности, созданной Эйнштейном.

Каким законам подчиняется, формулы

Потенциальная энергия характерна не только для тела, находящегося на определенной высоте. Несколько иначе выполняют расчет потенциальной энергии упруго деформированного тела. При деформации изменяется его форма и объем, при этом объекту передается определенный запас энергии. К примеру, если растянуть пружину или, напротив, сжать ее, то такие действия меняют расстояние, на которое удалены атомы и молекулы друг от друга. Таким образом, создается потенциальная энергия.

Расчет потенциальной энергии деформированного объекта выполняют с помощью уравнения:

(E=frac{k(Delta x)^{2}}{2})

k является жесткостью пружины, (Delta x) — это изменение длины пружины.

Следует отметить, что значение потенциальной энергии пружины будет всегда положительным, так как формула содержит ее изменение в квадрате. Даже в случае, когда изменение будет иметь знак «-», потенциальная энергия в любом случае останется положительной.

Говоря об энергии, следует учитывать, что объект обладает несколькими типами энергии одновременно. К примеру, летящий на большой высоте самолет имеет запас потенциальной энергии, так как удален от поверхности земли, и кинетической энергии из-за своей скорости движения.

Ели принять земную поверхность за уровень нулевой энергии, то данное утверждение будет справедливо. В случае, когда рассматривают объект в других системах отсчета, его энергия будет отличаться.

Рассматривая качели, можно сказать, что они обладают запасом и кинетической, и потенциальной энергии. Когда конструкция максимально отклоняется от равновесного положения, энергия будет рассчитываться таким образом:

Е_п = макс

Е_к = 0, так как скорость имеет нулевое значение.

В момент, когда качели пересекают точку равновесного положения, энергия будет распределена следующим образом:

Е_к = макс

скорость качелей в этой точке будет максимальна;

Е_п = мин

высота, на которой тело находится над землей, будет минимальной.

При сложении двух видов энергии получают полную механическую энергию тела. Она включает потенциальную и кинетическую энергии.

Задачи по теме с подробными решениями

Задача 1

Самолет, масса которого составляет 50 тонн, пролетает на высоте 10 километров. Скорость транспортного средства равна 900 км/ч. Требуется рассчитать, какова полная механическая энергия самолета.

Решение

Первым шагом является перевод искомых данных, согласно системе СИ. В таком случае масса самолета составит 50 000 кг, скорость – 250 м/с, а высота – 10 000 м.

Самолет обладает запасом полной энергии, которая включает и потенциальную, и кинетическую.

E = E_п + Е_к

E_п = m * g * h

Е_к = m * v² / 2

Таким образом, полная энергия составит:

(E=mtimes gtimes htimes frac{mv^{2}}{2})

Если подставить в полученную формулу числовые значения величин из условия задачи, то получим полную энергию:

(E=6.5625times 10^{9}) Дж

Если записать ответ сокращенно, то он примет такой вид:

(Е = 6,5625) Гдж.

Ответ: в рассмотренной системе отсчета значение полной механической энергии самолета составит 6.5625 Гдж.

Однако, данную задачу можно решить, принимая за нулевой уровень отметку в 10 километров. Тогда транспортное средство будет характеризоваться лишь запасом кинетической энергии, а значение потенциальной энергии будет равно нулю.

Задача 2

Пружину закрепили к стене и поместили на гладкую поверхность. На конце пружины зафиксировали тело. Растяжение пружины, которая обладает жесткостью в 400 Н/м, происходит при воздействии силы в 80 Н. Требуется рассчитать запас энергии в пружине.

Решение

Согласно условию задачи, поверхность обладает гладкостью, что позволяет сделать вывод о нулевом значении силы трения. Таким образом, потери энергии исключены. Воздействуя на пружину, можно наблюдать ее деформацию. Весь запас энергии будет сосредоточен в ней. Найти данную величину можно по формуле:

(E=frac{k(Delta x)^{2}}{2})

Сила упругости равна произведению жесткости на изменение длины пружины:

(ktimes Delta x=F)

Деформацию пружины можно рассчитать таким образом:

(Delta x=frac{F}{k})

Используя последнее равенство, можно преобразовать формулу для расчета энергии:

(E=frac{k(frac{F}{k})^{2}}{2}=frac{kF^{2}}{2k^{2}}=frac{F^{2}}{2k})

Далее следует подставить числовые значения в полученное выражение:

(E=frac{80^{2}}{2times 400}=8) Дж

Ответ: запас энергии в пружине составляет 8 Дж.

Задача 3

Масса пули составляет 9 грамм. Ее выпустили из оружия вертикально в верхнем направлении. Скорость пули при этом составила 700 м/с. Требуется рассчитать ее кинетическую энергию.

Решение

Условия задачи удобно представить в виде рисунка.

Расчет нужно выполнить по формуле:

(E=frac{mv^{2}}{2})

Перед тем, как подставить в уравнение числовые значения, требуется перевести их в систему СИ. Тогда масса пули составит 0,009 кг. Выражение будет записано следующим образом:

(E=frac{0.009times 49times 10^{4}}{2}=2200) Дж

Ответ: запас кинетической энергии пули равен 2200 Дж.

Задача 4

Масса ракеты составляет 0,2 кг. Ее выпустили из орудия вертикально вверх. После этого ракета достигла высоты в 60 метров. Требуется рассчитать значение потенциальной энергии ракеты, характерной для этой отметки.

Решение

Условие задачи можно представить с помощью рисунка.

Для того чтобы рассчитать потенциальную энергию, требуется воспользоваться формулой:

E = m * g * h

Далее необходимо подставить в выражение числовые значения:

Е = 0,2 * 9,8 * 60 = 118 Дж

Ответ: потенциальная энергия ракеты на заданной высоте составит 118 Дж.

Задача 5

Пружину растянули на 5 мм. Коэффициент ее жесткости составляет 10000 Н/м. Требуется вычислить, какова энергия пружины.

Решение

Следует представить условия задачи на рисунке.

Уравнение, с помощью которого можно рассчитать энергию пружины, имеет такой вид:

(E=frac{k(Delta x)^{2}}{2})

Далее необходимо привести к системе СИ расстояние, на которое растянули пружину. Оно составит 0,005 м.

После преобразований можно подставить числовые значения в искомую формулу:

(E=frac{10^{4}times 25times 10^{-6}}{2}=0.125) Дж

Ответ: энергия пружины составляет 0,125 Дж.

Знание основных формул для расчета кинетической, потенциальной и полной энергии тела позволит решить задачи любой сложности. Наиболее простым способом является выполнение последовательных действий, включая запись условий задачи, графическое изображение системы, представление формул для вычисления энергии, решение уравнения с помощью подстановки числовых значений. Важно отметить, что механическая энергия представляет собой сумму потенциальной и кинетической энергии.

Если в процессе поиска решений уравнений возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.

Концепция и классификация

Ещё в древности энергию определяли как свойство или способность, которые тела и вещества должны производить вокруг себя и которые во время преобразований обмениваются через два механизма: в форме работы или тепла. Правда, тогда еще не знали, что таким образом выполняется закон сохранения энергии. Но кроме физических изменений, проявляющихся, например, в подъёме объекта, его транспортировке, деформации или нагревании, энергия также присутствует в химических изменениях, таких как сжигание куска дерева или разложение воды электрическим током.

Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм:

• тепловой;
• механической;
• химической;
• электрической;
• ядерной.

В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp.

Энергия движения

Кинетическая энергия тела — это та, которой тело обладает благодаря своему движению. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости. Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины.

Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Для того чтобы найти её количество можно использовать онлайн-калькулятор.

История и определение

Прилагательное «кинетический» в названии произошло от древнегреческого слова кίνησις kinēsis, что означает «движение».

Идею связи классической механики и кинематической энергии впервые выдвинули Готфрид Вильгельм Лейбниц и Даниэль Бернулли. Учёный Грейвсанд из Нидерландов предоставил экспериментальное подтверждение этой связи.

Но первые теоретические выкладки этих идей приписаны Гаспар-Гюстав Кориолису, который в 1829 году опубликовал статью, где была изложена математика этого процесса. Сам термин появился в 1849 году благодаря Уильяму Томсону, более известному как лорд Кельвин.

Теорема о кинетической энергии гласит: изменение кинетической силы тела равно работе равнодействующей всех сил, действующих на тело. Эта теорема справедлива независимо от того, какие силы действуют на тело.

Часто различают кинетическую силу поступательного и вращательного движения. Как и любая физическая величина, которая является функцией скорости, она не только зависит от внутренней природы этого объекта, но также зависит от отношений между объектом и наблюдателем (в физике наблюдатель формально определяется классом определённая система координат, называемая инерциальной системой отсчёта).

Эта энергия деградирует и сохраняется в каждой трансформации, теряя способность совершать новые трансформации, но она не может быть создана или разрушена, только трансформирована, поэтому её сумма во вселенной всегда постоянна.

Кинематика системы частиц

Для частицы или для твёрдого тела, которое не вращается, кинетическая энергия падает до нуля, когда тело останавливается. Однако для систем, которые содержат много частиц с независимыми движениями, это не совсем верно.

Для твёрдого тела, которое вращается, полная кинетическая сила может быть разбита на две суммы: энергия перемещения, связанная со смещением центра масс тела в пространстве, и вращения (с вращательным движением с определённой угловой скоростью).

Потенциальная энергия

Этот термин был введён в XIX веке учёным Уильямом Ренкином и связан с механической энергией, которая зависит от расположения тела в силовом поле (гравитационное, электростатическое и т. д. ) или с наличием силового поля внутри тела.

Теорема о потенциальной энергии утверждает, что она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Независимо от силы, её порождающей, потенциальная энергия, которой обладает физическая система, хранится благодаря своему положению и / или конфигурации, в чём и заключается её различие с кинетической энергией.

Значение потенциала всегда зависит от нахождения или конфигурации, выбранной для её измерения, поэтому иногда говорят, что физически имеет значение только его изменение отношений между двумя конфигурациями.

Потенциальная энергия присутствует не только в классической физике, но также в релятивистской и квантовой физике. Эта концепция также была распространена на физику элементарных частиц.

Смысл потенциальной силы связан с работой, выполняемой силами физической системы для перемещения её из одного состояния в другое. А её функция будет существенно зависеть от типа силового поля или взаимодействия, действующего на систему.

Это относится, например, к атомной физике при получении электронных состояний атома или к молекулярной физике для получения таких состояний молекулы, как:

• электронных;
• вибрационных;
• вибрационно-вращательных;
• вращательных.

В других более общих формулировках физики потенциальная функция также играет важную роль. Среди них лагранжева и гамильтонова формулировки механики.

Гравитационная сила

Потенциальной гравитацией обладают тела в силу того, что они имеют массу и находятся на определённом взаимном расстоянии. Среди огромных масс действуют силы притяжения. Применительно, например, к планетарному движению, основная масса солнечной системы состоит из массы Солнца, которая создаёт гравитационное силовое поле, воздействующее на малые массы планет. В свою очередь, каждая планета создаёт такое же поле, которое воздействует на второстепенные тела, находящиеся на её поверхности. Зависимость силы тяжести от высоты можно изобразить на графике. При увеличении массы тела линейно увеличивается и она.

Энергия упругой деформации

Эластичность — это свойство определённых материалов, благодаря которому, будучи деформированными, растянутыми или отделёнными от своего исходного положения, они могут восстановить своё первоначальное состояние или равновесие. Восстановительными силами, ответственными за восстановление, являются силы упругости, как в случае пружин, резиновых полос или струн музыкальных инструментов.

Многие древние военные машины использовали эти силы для запуска объектов на расстоянии, таких как дуга, которая стреляет стрелой, арбалет или катапульта. Вибрации или колебания материальных объектов, вызванные упругими силами, являются источником звуковых волн. Силы восстановления, когда объект восстанавливает свою первоначальную форму практически без какого-либо демпфирования или деформации, являются консервативными, и может быть получена упругая сила.

Пружина является примером упругого объекта, который точно восстанавливает первоначальную форму: при растяжении он создаёт упругую силу, стремящуюся вернуть его к первоначальной длине. Экспериментально подтверждено, что эта восстановительная сила пропорциональна растянутой длине пружины. Способ выразить эту пропорциональность между силой и растянутой суммой — через закон Гука.

Коэффициент пропорциональности при этой деформации зависит от типа материала и рассматриваемой геометрической формы. Для твёрдых тел сила упругости обычно описывается в терминах величины деформации, вызванной растягивающей силой, возникающей в результате этого растяжения, называемого упругостью или модулем Юнга. Для жидкостей и газов это выражается изменением давления, способного вызвать изменение объёма, и называется модулем сжимаемости.

Одним из свойств упругости твёрдого тела или жидкости при растяжении или деформации является то, что растяжение или деформация пропорциональны приложенному усилию. То есть для создания двойного растяжения потребуется двойная сила. Эта линейная зависимость смещения от приложенной силы известна как закон Гука.

Прикладное значение

Потенциальная электростатическая энергия может храниться с помощью конденсаторов. Конденсатор — это устройство, которое накапливает её внутри. Чтобы сохранить электрический заряд, он использует две проводящие поверхности, как правило, в форме листов или пластин, разделённых диэлектрическим материалом (изолятором). Эти платы являются электрически заряженными при подключении к источнику питания.

Две пластины имеют одинаковую величину, но с разными знаками, причём величина нагрузки пропорциональна приложенной разности потенциалов. Константа пропорциональности между зарядом, приобретённым конденсатором, и разностью потенциалов, достигнутой между двумя пластинами, называется ёмкостью конденсатора:

Области применения конденсаторов многочисленны в области электроники, и, следовательно, они также предназначены для бытовых приборов. В современных технологических приложениях их используют:

• в компьютерах;
• в средствах связи;
• в видео, аудиоплеерах и т. д.

В этих применениях современной технологии конденсаторы способны накапливать электростатическую энергию в течение коротких периодов времени и с не слишком высокими значениями.

Читайте также:

• Эксперимент Милгрэма

Энергия – скалярная величина. Любую энергию в системе СИ измеряют в Джоулях.

В механике рассматривают два вида энергии тел – кинетическую энергию и потенциальную энергию.

Сумма кинетической и потенциальной энергии называется полной механической энергией

Кинетическая энергия

Кинетическая энергия – это энергия движения. Любое тело, находящееся в движении, обладает кинетической энергией.

В русском языке есть глагол «кинуть». Бросим (кинем) камень – он будет находиться в движении, то есть, будет обладать кинетической энергией.

Когда тело изменяет свою скорость, изменяется его кинетическая энергия.
Скорость увеличивается – кинетическая энергия тоже растет, скорость падает – кинетическая энергия уменьшается.
Если тело покоится, кинетической энергии нет. Математики в таком случае запишут: (E_{k}=0 ).

Рассмотрим тело, движущееся по поверхности с какой-либо скоростью (рис 1а).

Зная массу и скорость тела, можно рассчитать его кинетическую энергию с помощью формулы:

[ large boxed{ E_{k} = m cdot frac{v^{2}}{2}}]

( E_{k} left( text{Дж}right) ) – кинетическая энергия;

( m left( text{кг}right) ) – масса тела;

( v left( frac{text{м}}{c}right) ) – cскорость, с которой тело движется.

Потенциальная энергия

Любое тело, поднятое над поверхностью, обладает потенциальной возможностью упасть и совершить работу. Например, потенциальная энергия поднятого над гвоздем молотка переходит в работу по забиванию гвоздя в доску.

Физики говорят: поднятое на высоту тело обладает потенциальной энергией.

Примечание: Потенциальная энергия возникает у тела из-за притяжения Земли.

Вообще, потенциальная энергия – это энергия взаимодействия (притяжения, или отталкивания). В нашем примере – энергия притяжения тела и Земли.

Если тело изменит высоту, на которой оно находится, будет изменяться его потенциальная энергия.
Тело опускается вниз – потенциальная энергия уменьшается.
Тело поднимается выше – потенциальная энергия растет.
Когда тело находится на поверхности земли, потенциальной энергии у него нет (E_{p}=0).

Рассмотрим тело, находящееся на какой-либо высоте над поверхностью земли (рис 1б).

Можно рассчитать потенциальную энергию тела, зная его массу и высоту тела над поверхностью земли, с помощью формулы:

[ large boxed{ E_{p} = m cdot g cdot  h}]

( E_{p} left( text{Дж}right) ) – потенциальная энергия;

( m left( text{кг}right) ) – масса тела;

( h left( text{м}right) ) – высота, на которую тело подняли над поверхностью земли.

Полная механическая энергия тела

Если сложить кинетическую энергию тела с его потенциальной энергией в какой-либо момент времени, мы получим полную механическую энергию, которой тело обладало в этот момент времени.

Летящий в небе самолет (рис. 3) одновременно будет обладать и кинетической энергией – он движется, и потенциальной энергией – он находится на высоте.

Любая энергия – это скаляр (просто число).  Значит, энергия направления не имеет и ее можно складывать алгебраически.

[ large boxed{ E_{k} + E_{p} = E_{text{полн. мех}} }]

( E_{p} left( text{Дж}right) ) – потенциальная энергия тела;

( E_{k} left( text{Дж}right) ) – кинетическая энергия, которой обладает тело;

( E_{text{полн. мех}} left( text{Дж}right) ) – полная механическая энергия этого тела;

Советую далее прочитать о законе сохранения энергии

Сегодня мы отбросим лишние научные абстракции и попробуем придать энергии численное значение. Что важнее, мы разберемся в двух крайне важных концепциях механической энергии — в том, что такое потенциальная энергия и что такое кинетическая энергия. Мы узнаем, как выглядит формула потенциальной энергии и формула кинетической энергии. А на закуску ответим на вопрос: «Как найти высоту потенциальной энергии?»

Всеми любимые американские горки, которые можно встретить в любом парке аттракционов. Не исключено, что вы хотя бы раз сами имели удовольствие сидеть в связке цветастых вагонеток. Вы поднимаетесь цепью на завораживающую высоту и… Красота.

Возможность рассмотреть городскую панораму, адреналин, ощущение свободного падения, истошные крики соседей по «вагону». Конечно, самые длинные очереди собираются именно около кассы с билетами на американские горки.

Устройство горок на удивление прозаично. Имеется группа вагончиков на жесткой сцепке, рельсы и цепной привод. Привод единожды тянет конструкцию высоко наверх.

Все — никаких двигателей внутри вагончиков или дополнительных механизмов, дающих разгон, по траектории движения. А вагончики, идеально останавливаясь в точке старта, успевают пройти на большой скорости кластер крутых виражей. Включая мертвые петли!

Как же это работает?

Механическая энергия

Вспомним, что по одному из определений:

Энергия — это способность тела производить работу.

Мы также помним, что энергия проявляет себя в самых различных формах и системах. Что бы мы ни взяли (магнит, атом или чашку чая), каждый объект Вселенной обладает энергией.

Однако не будем закапываться в кварки, кванты, электрические импульсы и прочее. Лучше остановиться на проявлении энергии в обычных механических системах (совокупности материальных точек). Здесь очевидно следующее:

Любой объект механической системы либо находится в состоянии покоя, либо в движении.

Что-то либо стоит, лежит, сидит… либо двигается. Третьего не дано. Следовательно, механическая энергия делится на две категории: энергию «лежания» и энергию «движения».

Хорошо-хорошо, ваши аргументы «против» принимаются. Но что насчет, например, яблока, которое, созрев, падает с дерева? Если бы яблоко не обладало энергией «лежания», в нашем случае — энергией «висения», оно бы никак не смогло прийти в движение.

Тело и механическая энергия, которой оно обладает

Энергия не может взяться из ниоткуда, как по мановению волшебной палочки. Так что если мы не будем учитывать энергию «лежания», будет сложно говорить об энергии «движения». Ведь не будет стартовой точки.

Не зря определение энергии включает в себя условность в виде слова «способность». Уже сама способность производить работу говорит о том, что тело обладает энергией. Энергия «лежания» лишь дает понимание, насколько на практике велика эта способность. Так что в определение, выходит, вшито и «лежание», и «движение» — два варианта развития событий.

Ну, единственное, нам бы термины научнее.

Потенциальная энергия механической системы

Этим как раз в XIX веке и озаботился Уильям Ренкин, шотландский механик. С его легкой руки выше нами описанные умозаключения приобрели физическую строгость. В виде термина «потенциальная энергия».

Какую энергию называют потенциальной?

Потенциальная энергия — способность материального тела совершать работу за счет своего нахождения в поле сил. Является частью общей механической энергии системы.

Другими словами, тело находится в поле действия силы и от этого имеет способность совершить работу. Конечно, фактически работу выполняет сила, действующая на тело. Если говорить о механических системах, указанное в определении поле сил включает в себя две возможности:

• Сила тяжести. Яблоко, падающее на землю, совершает работу за счет нахождения в поле действия силы гравитационного притяжения. Как только точка опоры пропадает, Земля притягивает яблоко к себе. Лежи яблоко само по себе на земле, упасть никуда оно бы не смогло. Таким образом, потенциальная энергия тела выражает потенциал работы с некоторой высоты от тела до земли. 
• Сила упругости. На упругое тело в сжатом или разжатом состоянии действует сила упругости. Она стремится вернуть его в положение равновесия. Например, пружина, легко поддающаяся деформации. Если видоизменить пружину сжатием или разжатием, вы сообщаете ей потенциальную энергию — определенный потенциал работы от точки деформации до положения равновесия.  

Выходит, что внутри механических систем потенциальная энергия определяет потенциал движения тела. Так, сколько работы совершается телом, если сила, действующая на тело, превысит по значению равнодействующую силу. Потенциальную энергию в этом плане можно рассматривать как «резерв» или «запас» работы.

Формула потенциальной энергии

О потенциальной энергии деформированной механической системы мы обязательно поговорим. Но как-нибудь далее в курсе физики. Для начала нужен ряд определений для механики деформации. Так что пока остановимся на потенциальной энергии под действием знакомой нам силы — силы тяжести.

Если взять за ноль потенциальную энергию точки, находящейся на земле, то потенциальная энергия точки, находящейся на некотором расстоянии от земли, определяется работой, которая выполнится гравитационной силой при падении.

Договоримся обозначать такую потенциальную энергию как $E_П$. Далее вспомним важное условие:

Работа равна изменению энергии тела.

Следовательно $A=Delta{E_п}$. Помним, что работа равна произведению значения силы на пройденный путь, $A=Fcdot s$. Теперь формула потенциальной энергии в шаге от готовности, если вспомнить, что $F=ma$. Под силой сейчас понимается конкретная сила — сила тяжести $mg$. Тогда заметим, что:

$A=mgcdot s$.

Но это еще не конечный вариант того, как выглядит формула потенциальной энергии. Пройденный путь $s$ имеет немного другое прочтение, когда речь идет о гравитационном притяжении. Раз мы говорим прежде всего о падении, путь такой работы — высота, на которую было поднято тело.

Получается, что формула потенциальной энергии, с учетом всех моментов, выглядит так:

$$A=Delta{E_п}=mgh,$$

где $m$ — масса тела, $h$ — высота подъема, $g$ — ускорение свободного падения.

Как найти высоту потенциальной энергии

«Высота подъема» — формулировка условная. Еще ее часто определяют в справочной литературе как «высота от центра тяжести до Земли». Дадим этому разъяснение.

Для примера рассмотрим следующую конструкцию. Пусть есть стол, на котором лежит коробка, на верху которой, в свою очередь, расположен предмет — кастрюля. Итого, как найти высоту потенциальной энергии кастрюли?

Высота потенциальной энергии может быть определена относительно стола. Или относительно пола. Может быть, уровня земли, если стол расположен внутри здания. Относительно подвала? Иными словами, подъем тела рассчитывается относительно чего угодно. Выходит, нужно всегда заранее условиться, относительно какого уровня производится замер.

Однако помните, что именно «условиться» — выбрать точку отсчета можно произвольно. Чтобы она была максимально удобная для расчетов. Намного важнее — величина изменения потенциальной энергии, а совсем не то, как найти высоту потенциальной энергии. Очевидно, вне зависимости от выбранной точки отсчета, изменение потенциальной энергии будет одним и тем же.

Еще немаловажен фактор центра тяжести. Если тело маленькое и располагается на поверхности «земли», говорят, что его потенциальная энергия равна нулю. Расстоянием от центра тяжести до нулевого уровня можно пренебречь. Другое дело, когда тело габаритное.

Обратите внимание на изображение. Несмотря на то, что крупный предмет находится на нулевом уровне, его потенциальная энергия больше нуля. В общей сложности, важнее не вопрос «как найти высоту потенциальной энергии», ибо он не конкретен. Важнее вопрос — какую точку отсчета выбрать?

Высота потенциальной энергии: задача на расчет

Условие. Альпинист покоряет гору высотой $6000~м$. На предпоследний день он решает разбить перевалочный лагерь на высоте $5100~м$, чтобы утром следующего дня выдвинуться на вершину. Какую работу совершит альпинист при подъеме на вершину горы от станции перевалочного лагеря? Масса альпиниста — $80~кг$.

С учетом, что формула потенциальной энергии $E_п=mgh$:

$$A=Delta{E_п}=mgh_2-mgh_1,$$

где $h_2$ — высота подъема тела в конце работы, $h_1$ — высота подъема тела в начале работы. 

Также помним, что при расчете потенциальной энергии в первую очередь выбирается точка отсчета. У нас два варианта:

• принять за ноль уровень моря;
• принять за ноль высоту, на которой расположен перевалочный лагерь.

Не забываем, точка отсчета — условность, и хорошо выбирать ее так, чтобы математические вычисления проводились проще. Ростом альпиниста и соответствующими вычислениями центра тяжести можем пренебречь, поскольку дистанции рассматриваются километражные.

Вернемся к точкам отсчета. Если остановиться на варианте с уровнем моря, нам придется рассчитывать потенциальную энергию $mgh_1$, с учетом, что $h_1=5100~м$, а после рассчитывать потенциальную энергию $mgh_2$, с учетом, что $h_2=6000~м$. Числовые значения выйдут громоздкими, поэтому примем для удобства за нулевой уровень расположение перевалочного лагеря:
$Delta{h}=h_2-h_1=6000-5100=900~м$.

Альпинист суммарно поднялся вверх на $900~м$. В нашем случае формула потенциальной энергии — $A=mgDelta{h}$. Определим по ней совершенную работу альпинистом при подъеме на эту высоту:

$A=mgDelta{h}=80~кгcdot 9,8~м/сcdot 900~м=705600~Дж=705,6~кДж$.

Кинетическая энергия механической системы

«Запасом» работы обладают не только лишь те тела, которые находятся в поле действия определенных сил. Так что, естественно, второе органичное проявление энергии связано, наконец, с движением.

Вспомним американские горки, о которых мы говорили в самом начале. За счет подъема на высоту, вагончики запасаются потенциальной энергией $mgh$. При этом чем выше поднять вагончики, тем больший запас энергии сообщается механической системе. И тем дальше вагончики смогут проехать вперед по рельсам.

Как только конструкция начинает движение вниз, потенциальная энергия начинает поступательное превращение в энергию движения. Так, вагончики без толчка самостоятельно въезжают на крутой уклон или проходят петли. Все потому, что они обладают скоростью.

Видим взаимосвязь: скорость — энергия — работа.

Таким образом, мы можем сделать вывод, что тело, имеющее скорость отличную от нуля, всегда обладает энергией. И способностью, как следствие, совершать работу благодаря движению.

О таком теле говорят, что оно обладает кинетической энергией. Это и есть ранее нами не очень научный термин об «энергии движения».

Теперь, когда все термины и их смысл окончательно сформированы, мы готовы дать определение:

Кинетическая энергия — мера способности движущегося материального тела совершать работу.

Лирическое отступление — На тропу войны

«Бог создал людей сильными и слабыми. Сэмюэл Кольт сделал их равными», — гласит старое американское присловье конца XIX века.  

Сэмюэл Кольт.
Инженер, оружейник и очень талантливый изобретатель. Именно он первым запатентовал культовое короткоствольное оружие с вращающимся барабаном, которое мы знаем под названием «револьвер», произошедшее от английского глагола ‘revolve’, в переводе — «вращаться». Кольт создал бренд, сотворил империю, возвел целую стрелковую эпоху…

Философски заметить — вообще-то стал причиной гибели огромного количества людей. А все потому, что кинетическая энергия по своей природе ну никак не безобидна.

Еще задолго до револьвера Кольта и подъема оружейной промышленности, человек понял, что движущиеся предметы обладают разрушительной способностью. Например, копье, летящее с расстояния в плиоценского мамонта, вонзается в тело животного из-за того, что человек сообщает инструменту кинетическую энергию. И древний человек хорошо понимал эту взаимосвязь, кидая на дистанции камни, палки с заостренными концами и прочие колюще-режущие-убивающие предметы.

Вечно тело в движении находиться не может. Либо его остановит по пути потеря энергии на преодоление трения — кинетическая энергия преобразуется как следствие в тепловую, — либо это тело остановит что-то, как бы принимая удар, вбирая в себя энергию. Вот так, фундаментальная сила природы стала основанием для учинения хаоса на планете, ведь любое стрелковое оружие — это предмет, сообщающий кинетическую энергию некоему предмету, находящемуся внутри. Пуле ли, снаряду, или ядру.

Формула кинетической энергии

Раз тело движущееся и энергией обладает именно за счет движения, можно выдвинуть кое-какое предположение. Логично, что при формула кинетической энергии «завязана» со значением скорости.

Во-вторых, неглупо предположить, что масса также связана с количеством энергии в системе. Если кинуть в соседа бумажный самолетик, это будет называться шалостью — величина кинетической энергии несущественная. А вот если кинуть в соседа кирпич… Не шалость. Целое покушение!

Понятие о том, что совершенная работа равна изменению энергии, остается неизменным. Просто на этот раз будем иметь в виду энергию кинетическую. Условимся обозначать ее как $E_к$. Заранее обозначим связь работы и кинетической энергии:
$A=Delta{E_к}$.

Продолжим выяснять, как выглядит формула кинетической энергии. Для этого предположим, что на тело с массой $m$ действует постоянная сила $F$. В результате тело проходит некоторое расстояние $s$. По второму закону Ньютона значение силы равно произведению массы на ускорение:
$F=ma$.

Перемещение при равноускоренном движении, при условии, что тело начинает движение из состояния покоя, равно:
$s=frac{upsilon^2}{2a}$.

Связывая две обозначенных формулы с формулой работы, находим:
$A=Fcdot s=Fcdot frac{upsilon^2}{2a}=frac{macdot upsilon^2}{2a}=frac{mv^2}{2}$.

Полученное в результате подстановок полупроизведение массы на квадрат скорости — это и есть формула кинетической энергии $E_к$.

Экспериментально формула кинетической энергии была подкреплена нидерландским ученым Вильгельмом Гравезандом в XVIII веке. Он обнаружил, что мячик, брошенный в стену с удвоенной скоростью, оставляет в четыре раза большее углубление. Следовательно энергия пропорциональна квадрату скорости. Это мы непосредственно и наблюдаем в формуле, выведенной от работы и перемещения.  

Формула кинетической энергии: задача на расчет

Условие. Автомобиль массой $1~т$ тянет буксир с постоянной силой. Определите кинетическую энергию автомобиля в момент времени $4~с$ на основе предложенного графика зависимости скорости от времени.

Решение. Формула кинетической энергии:
$E_к=frac{m upsilon^2}{2}$.

Опираясь на график, находим, что в момент времени $4~с$ скорость автомобиля составляла $8~м/с$. Масса автомобиля указана в тоннах, переведем ее в СИ: $m=1~т=1000~кг$. Подставим значения с формулу и посчитаем кинетическую энергию.

Получается:
$E_к=frac{1000~кг cdot (8frac{м}{с})^2}{2}=32000~Дж=32~кДж$.

Если бы мы каким-нибудь образом придумали устройство, которое бы позволяло переводить кинетическую энергию нашего автомобиля из задачи в электроэнергию, мы бы здорово удивились. $32~кДж$ хватило бы максимум на час работы двух энергосберегающих лампочек мощностью $20~Вт$.

Потенциальная энергия: в заключение

И вот мы закономерно, изучив понятия о механической энергии и ее видах, приходим к логичному выводу, что кинетическая энергия имеет прямую связь с потенциальной энергией.

Вот, вагонетка поднимается цепным приводом наверх, а после летит с огромной скоростью вниз, вновь забираясь на горку, но уже без помощи цепи. Созревшее яблоко с дерева падает к земле. Толчок пороховых газов придает пуле ускорение, выбрасывая ее из ствола. Сжатая пружина получает возможность свободного хода и толчками совершает возвратно-поступательные движения. Все рассмотренные нами случаи и примеры показывают, как один вид энергии преобразуется в другой. Кинетическая энергия в потенциальную. И наоборот.

Об этой потрясающей связи, а также о глубокомысленном «ничто ниоткуда не берется и в никуда не исчезает» вы узнаете уже на следующем уроке.

Упражнения

Дано:
$m = 100 space кг$
$h = 10 space м$
$g = 9.8 frac{Н}{кг}$

$E_п — ?$

Посмотреть решение и ответ

Скрыть

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

$E_к — ?$

Посмотреть решение и ответ

Скрыть

А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.

А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.

Задачи на кинетическую и потенциальную энергию

Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.

Задача №1 на кинетическую энергию

Условие

Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.

Решение

Потенциальная энергия тела над поверхностью Земли составляет:

Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:

Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:

Ответ: 200 Дж.

Задача №2 на потенциальную энергию

Условие

Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?

Решение

По определению, потенциальная энергия равна в поле силы тяжести равна:

Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:

Осталось вычислить потенциальную энергию:

Ответ: 300 Дж.

При решении задач не забывайте переводить все размерности величин в систему СИ.

Задача №3 на полную механическую энергию

Условие

Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?

Решение

Полная механическая энергия состоит из кинетической и потенциальной энергий:

Вычислим:

Ответ: 100,7 МДж.

Задача №4 на кинетическую и потенциальную энергию

Условие

Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.

Решение

Перед началом падения потенциальная энергия шарика составляет:

По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:

Ответ: 36 Дж.

Задача №5 кинетическую и потенциальную энергию

Условие

Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?

Решение

Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна

Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.

Найдем импульс, переданный шарику при попадании пули:

Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.

Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:

Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.

Ответ: см решение выше.

Вопросы на потенциальную и кинетическую энергию

Вопрос 1. Что такое энергия? Что такое механическая энергия?

Ответ. Для энергии существует множество определений. В наиболее общем смысле:

Энергия – мера способности тела совершать работу.

Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.

Вопрос 2. Сформулируйте закон сохранения энергии

Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.

Вопрос 3. Какие силы называются консервативными?

Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.

Вопрос 4. Какую энергию называют кинетической?

Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.

Вопрос 5. Какую энергию называют потенциальной?

Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.

Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.