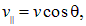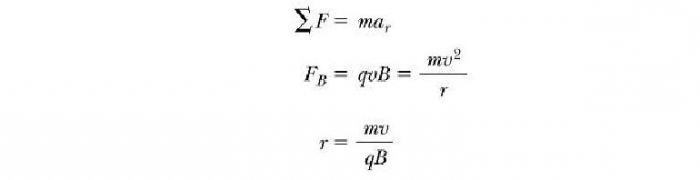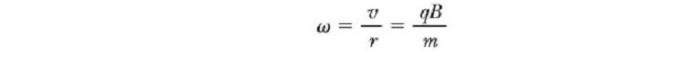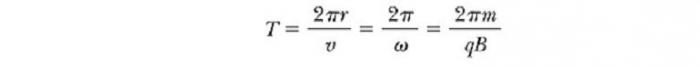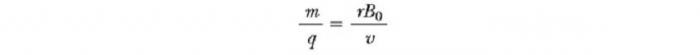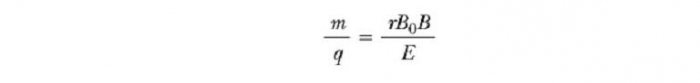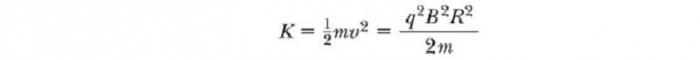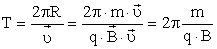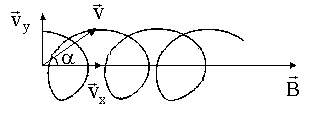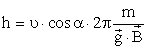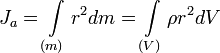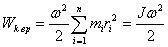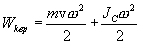Мы уже ввели релятивистскую частицу и эффекты, связанные с релятивистским движением. Напомним, что прилагательное «релятивистское» обозначает движение тел с близкими к световой скоростями. Большинство соотношений в данной теме вывести достаточно сложно, поэтому просто верим.
Итак, введённый нами импульс () при условии релятивистской массы (
) может быть записан как:
(1)
- где
Немного о — массе неподвижного в данной системе тела, называемой массой покоя.
Великим Эйнштейном было получено уникальное соотношение, характеризующее полную энергию движущейся частицы:
(2)
- где
Логично предположить, что наименьшей энергией обладает тело, которое покоится в данной системе, назовём эту энергию энергией покоя:
(3)
- где
Тогда кинетическая энергия движущегося тела может быть найдена как разность между полной энергией и энергией покоя:
(4)
- где
Или:
(5)
При условии 
(скорость тела очень мала по сравнению со скоростью света) получим 
(отношение скорости тела к скорости света стремиться к нулю), и соотношение (5) принимает вид — т.е. вид кинетической энергии в классической механике.
Вывод: в случае релятивистской механики (скорость частицы велика) достаточно помнить, что энергетические характеристики тела выражаются через более сложные соотношения (1) — (5). С точки зрения энергии, главное понять по задаче, какую энергию нам необходимо найти — покоя, полную или кинетическую.
Кинетическая энергия вещества
4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
Любое физическое тело представляет собой набор веществ (одного или нескольких), которые состоят из молекул и атомов. Если тело как целое находится в состоянии покоя, то это не значит, что молекулы вещества “замерли” и не двигаются. Такая ситуация возможна только, если температура тела станет равна абсолютному нулю, то есть Tтела = 00К, а при любой температуре, больше нуля, частицы вещества непрерывно, хаотически двигаются с различными скоростями, поэтому полная кинетическая энергия вещества равна сумме кинетических энергий всех частиц.
Чему равна энергия движущейся частицы
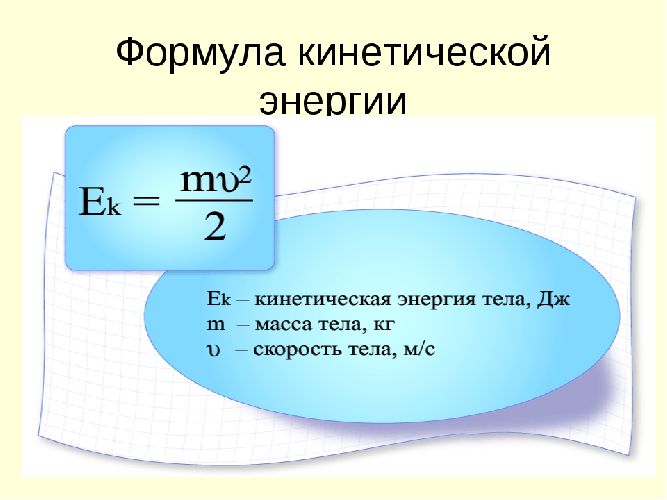
В разделе механики была получена формула для кинетической энергии Ек движущегося со скоростью v тела массой m. Эта формула универсальна и справедлива не только для тел макроскопических размеров, но и для микрочастиц (молекул, атомов, электронов и т.п.):
$ Ек = {m * v^2over 2} $ (1),
Для того чтобы узнать полную кинетическую энергию вещества Епк, необходимо сложить энергии всех частиц:
$ Е^п_к = Е_1+ Е_2 + Е_3 +…. Е_N $ (2),
где N — полное число частиц в веществе.
Понятно, что для вычисления кинетической энергии всего вещества по формуле (2) необходимо знать скорости всех частиц, их массы и общее количество. Но это в принципе нереально хотя бы потому, что в одном моле вещества находится гигантское количество молекул — 6,023*1023 !
Эксперименты показывали, что чем сильнее нагрето вещество, тем быстрее (“энергичнее”) двигаются частицы. Например, исследователи могли это видеть, наблюдая броуновское движение в микроскоп. После изобретения итальянским ученым Галилео Галилеем (1564-1642 г.г.) термометра у физиков появилась возможность проводить измерения величины, названной температурой, которая показывала степень теплового состояния вещества.
Общая кинетическая энергия непрерывного хаотического движения всех частиц входит в состав внутренней энергии вещества, которая кроме кинетической включает в себя:
- Потенциальную энергию частиц, вызванную силами межмолекулярного взаимодействия;
- Энергию электронов в атомах;
- Ядерную энергию.
Что же такое температура?
В молекулярно-кинетической теории теплота рассматривается как одна из форм энергии, а именно — кинетическая энергия атомов и молекул. Чем “горячее” тело, тем с большей скоростью двигаются молекулы вещества и, значит, больше становится их кинетическая энергия. Эта величина, будучи усредненной по всему числу беспорядочно движущихся частиц, и есть температура тела (вещества).
Вместо того, чтобы пытаться вычислить энергию по формуле (2), физиками были получены математические формулы, связавшие кинетическую энергию Епк вещества и температуру T. Использование понятия температуры, которое распространяется на все вещества — газообразные, жидкие и твердые, позволило решить задачу по определению энергии Епк.
Как перейти от температуры к энергии
Для измерения энергии в Международной системе СИ используется единица измерения джоуль (Дж), а температура, как известно, измеряется в градусах. Как количественно связаны эти величины? На примере одноатомного идеального газа попробуем получить формулу, связывающую эти величины.
Напомним, что температура в системе СИ измеряется в градусах Кельвина. Связь температуры в градусах Кельвина и температуры в единицах энергии (Дж) выражается формулой:
$ θ = k * T $ (3),
где: k =1,38*10-23 Дж/К — постоянная Больцмана.
Для идеального газа справедлив закон Клапейрона-Менделеева, выражаемый в виде уравнения состояния:
$ p * V = {mover μ} * R * T $ (4),
где:
p, m и V — давление, масса и объем газа, μ — молярная масса газа,T — температура в градусах по шкале Кельвина, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
В то же время газовая постоянная R равна:
$ R = k * N_a $ (5),
где: k — постоянная Больцмана, Na = 6,023*1023 — число Авогадро, количество молекул в одном моле вещества. Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
$ {mover μ} * {Naover V } = n $ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$ p = n * k * T $ (6).
Для давления одноатомного идеального газа воспользуемся выражением:
$ p = {1over 3} * n * m * v^2_c $ (7),
где: v2c — средний квадрат скорости по всем группам молекул. Напомним, что молекулы в газе двигаются с разными скорости. Распределение по скоростям, то есть количество молекул с определенной скоростью, имеет колоколообразный вид, и впервые было получено английским физиком Максвеллом.
Из формул (6), (7) и выражения (1) для кинетической энергии Ек, получим:
$ Ек = { 3 over 2} * k * T $ (8).
Уравнение (8) устанавливает однозначную связь между средней кинетической энергией вещества и его абсолютной температурой.
Если газ будет не одноатомный, то часть энергии уйдет на колебания атомов внутри молекул и на вращение самих молекул. Колебания и вращения тоже обусловлены движением частицы, но выражения для этих составляющих энергии будут несколько иные. Формулы (1) и (7) получены в предположении, что одноатомные частицы двигаются только поступательно.
Что мы узнали?
Итак, мы узнали что кинетическая энергия веществ, представляет собой сумму кинетических энергий всех частиц вещества. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. Приведена формула, связывающая среднюю кинетическую энергию вещества с температурой.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
А какая ваша оценка?
Кинетическая энергия движения частицы по окружности
2017-05-20
Кинетическая энергия частицы, движущейся по окружности радиуса $R$, зависит от пройденного пути $s$ по закону $T = as^<2>$, где $a$ — постоянная. Найти силу, действующую на частицу, в зависимости от $s$.
Дифференцируя уравнение (1) по времени
Следовательно, искомое ускорение частицы
Следовательно, искомая сила $F = mw = 2as sqrt<1 + (s/R)^<2>>$
Кинетическая энергия движения частицы по окружности
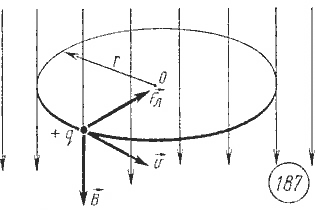
Протоны в однородном магнитном поле между полюсами магнита движутся по окружностям радиусом R под действием силы Лоренца. После замены магнита по окружностям тем же радиусом между полюсами стали двигаться α-частицы, обладающие такой же кинетической энергией, как и протоны. Как изменились индукция магнитного поля и скорость движения α-частиц по сравнению со скоростью протонов?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Индукция
магнитного поля |
Скорость α-частиц |
При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями
Индукция магнитного поля равна
Кинетическая энергия частицы выражается как Масса альфа-частицы в четыре раза больше массы протона, следовательно, при сохранении кинетической энергии, скорость альфа-частиц меньше скорости протонов в два раза. Заряд альфа-частицы в два раза больше заряда протона, тогда из формулы для индукции магнитного поля получаем, что индукция магнитного поля не изменилась.
Движение заряженных частиц по окружности
5.3. Движение заряда в однородном магнитном поле
Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)
Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле
Сила Лоренца FL, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем
следовательно, можем записать уравнение
из которого легко получить выражение для угловой скорости частицы
Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период
тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты
Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).
Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками
Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.
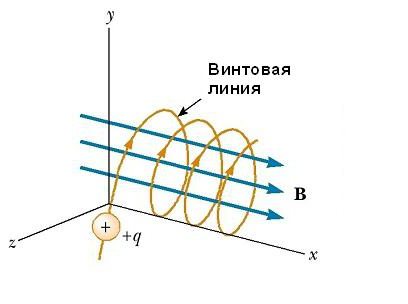
Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых
направлена вдоль поля, а вторая
перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью 
и вращения по окружности с угловой скоростью 
. Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):
Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле
Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?
Решение. Из уравнений (5.11) находим угол между скоростью протона и полем
Кинетическая энергия протона будет
Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.
Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов
Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).
Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В
Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).
Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле
Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы FB, которую поле оказывает на частицу при ее движении в нем со скоростью v.
Общие свойства магнитной силы
Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:
- Величина FB магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
- Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
- Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, FB перпендикулярна плоскости, образованной v и B (см.рис. ниже).
- Величина и направление FB зависит от скорости частицы и от величины и направления магнитного поля B.
- Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
- Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.
Сила Лоренца
Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде FB = qv х B.
Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца FB при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.
Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно FЛ = qE + qv х В. Его принято называть так: полная сила Лоренца.
Движение заряженных частиц в однородном магнитном поле
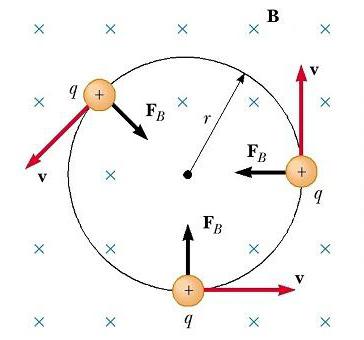
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила FB направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и FB изменяются непрерывно, как показано на рисунке. Так как FB всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.
Динамика кругового движения частицы
Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем FB центробежной силе, требуемой для сохранения круговой траектории движения:
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.
Движение частицы под углом к вектору магнитного поля
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы FB в этом направлении. В результате составляющая ускорения ax= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила FB = qv х В вызывает изменение во времени компонентов скорости vy и vz. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν⊥ = √(νу 2 + νz 2 ).
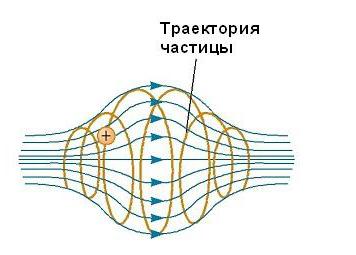
Неоднородное магнитное поле: как в нем движутся частицы
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.
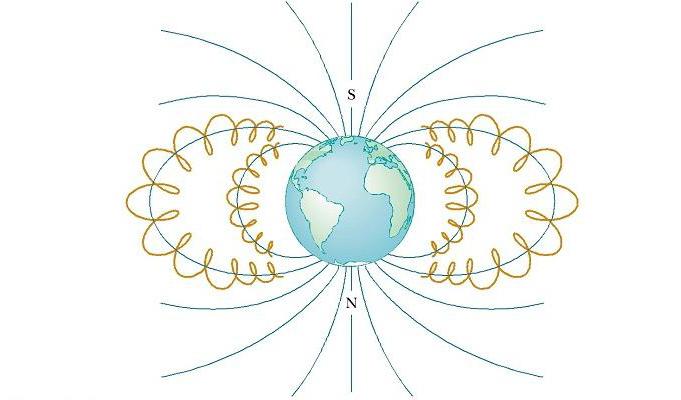
Как Земля влияет на движение космических частиц
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.
Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.
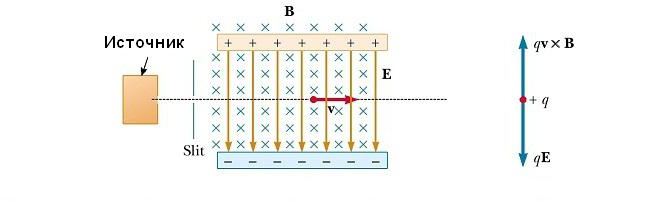
Селектор скоростей
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).
Масс-спектрометр
Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B0, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q
и затем, используя уравнение v=E/B, мы находим, что
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B0, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/mе для электронов.
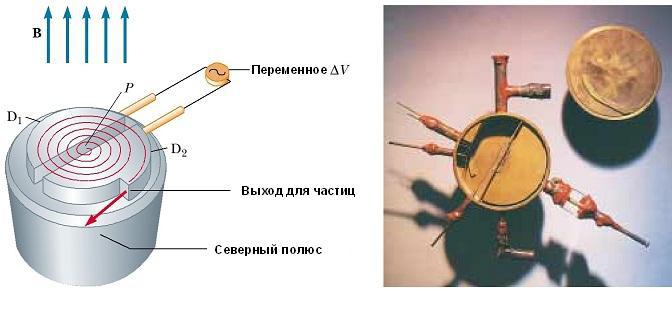
Циклотрон
Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).
Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.
Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D2 получает более низкий электрический потенциал, чем D1 на величину qΔV, то ион ускоряется в зазоре перед входом в D2, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D2 по полукруглой траектории большего радиуса (потому что его скорость увеличилась).
Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.
Эффект Холла
Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.
Движение заряженной частицы в магнитном поле.
Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:
а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю
б) Если заряженная частица движется в магнитном поле со скоростью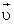 
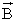
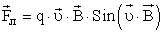
, перпендикулярно к вектору 
, то сила Лоренца, равная 
постоянна по модулю и перпендикулярна к траектории частицы.
Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:
, 
, 
,
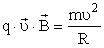
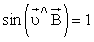
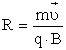
период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,
в) Если скорость заряженной частицы направлена под углом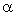 
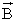
к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).
В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору 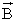. Шаг винтовой линии:
Направление, в котором закручивается частица, зависит от знака её заряда.
Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией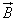 
.
Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью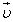 
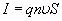
их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:
,(1)
где q — заряд отдельной частицы.
.
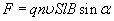
Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l
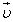
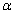
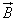
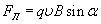
то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом 
к вектору индукции, равна
.(2)
Эту силу называют силой Лоренца.
Направление вектора силы Лоренца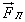 
определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.
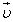
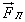
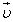
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).
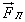
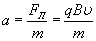
В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение
(3)
и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия
, 
.(4)
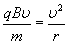
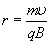
Период обращения частицы в однородном магнитном поле равен
.(5)
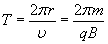
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости 
и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.
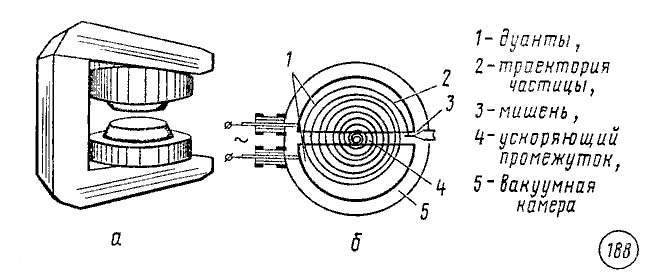
Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).
Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом.
Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.
топлива по сравнению с обычной тепловой электростанцией.
В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:
http://phys-ege.sdamgia.ru/problem?id=17662
http://b4.cooksy.ru/articles/dvizhenie-zaryazhennyh-chastits-po-okruzhnosti
Полная и кинетическая энергии частицы. Энергия покоя
Эйнштейн установил формулу связи между энергией частицы, движущейся со скоростью 
, и её массой:
Полная энергия тела или системы тел равна релятивистской массе, умноженной на квадрат скорости света.
Кинетическая энергия релятивистской частицы определяется выражением:
Согласно формуле (4.5) тело обладает энергией и при скорости, равной нулю. Это энергия покоя:
Любое тело уже только благодаря факту своего существования обладает энергией, которая пропорциональна массе покоя т.
Уравнение (4.6) — это формула Эйнштейна, первая из двух великих формул физики (вторая — это формула Планка).
При превращениях элементарных частиц, обладающих массой покоя, в частицы, у которых т = 0, энергия покоя целиком превращается в кинетическую энергию вновь образовавшихся частиц. Это является наиболее очевидным экспериментальным доказательством существования энергии покоя.
При скоростях движения, много меньших скорости света, справедливы классические представления о пространстве и времени и законы механики Ньютона. Это — проявление общего принципа соответствия физических теорий.
Эта лекция взята со страницы лекций по всем темам предмета физика:
Предмет физика
Возможно эти страницы вам будут полезны:
Кинети́ческая
эне́ргия — энергия механической системы,
зависящая от скоростей движения её
точек. Часто выделяют кинетическую
энергию поступательного и вращательного
движения.
Более
строго, кинетическая энергия есть
разность между полной энергией системы
и её энергией покоя; таким образом,
кинетическая энергия — часть полной
энергии, обусловленная движением.
и/или
Механическая
энергия бывает двух видов: кинетическая
и потенциальная. Кинетическая энергия
(или энергия движения) определяется
массами и скоростями рассматриваемых
тел. Потенциальная энергия (или энергия
положения) зависит от взаимного
расположения (от конфигурации)
взаимодействующих друг с другом тел.
Работа
определяется как скалярное произведение
векторов силы и перемещения. Скалярным
произведением двух векторов называется
скаляр равный произведению модулей
этих векторов и косинус угла между ними.
Понятия
энергии и работы тесно связаны друг с
другом.
Кинетическая
энергия частицы
доп.
работа
результирующей всех сил, действующих
на частицу, идет на приращение кинетической
энергии частицы.
№10
Момент
импульса тела, вращающегося вокруг
неподвижной оси.
Момент
импульса материальной точки относительно
точки O определяется векторным
произведением
,
где 
—
радиус-вектор, проведенный из точки
O, 
—
импульс материальной точки.
Момент
импульса материальной точки относительно
неподвижной оси 
равен проекции на эту ось вектора момента
импульса, определенного относительно
произвольной точки O данной оси. Значение
момента импульса
не зависит от положения точки O на оси z.
Момент
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц, из которых состоит
тело относительно оси. Учитывая, что 
,
получим
.
Если
сумма моментов сил, действующих на тело,
вращающееся вокруг неподвижной оси,
равна нулю, то момент импульса сохраняется
(закон
сохранения момента импульса):
.
Производная
момента импульса твердого тела по
времени равна сумме моментов всех сил,
действующих на тело:
.
№11
Момент импульса системы. Закон
сохранения момента импульса.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц:
Используя
формулу vi =
ωri,
получим
т.
е. 
2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени:
т.
е.
Эта
формула — еще одна форма уравнения
динамики вращательного движения твердого
тела относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси равна моменту сил относительно той
же оси.
Можно
показать, что имеет место векторное
равенство
(3)
В
замкнутой системе момент внешних
сил 
и 
откуда
(4)
Выражение
(4) представляет собой закон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т. е. не изменяется с течением
времени.
Закон
сохранения момента импульса также как
и закон сохранения энергии является
фундаментальным законом природы. Он
связан со свойством симметрии пространства
— его изотропностью,
т. е. с инвариантностью физических
законов относительно выбора направления
осей координат системы отсчета
(относительно поворота замкнутой системы
в пространстве на любой угол).
№12
Момент импульса и момент
силы относительно точки и оси. Уравнение
моментов.
Моментом
импульса (количества движения) материальной
точки А относительно неподвижной точки
О называется
физическая величина, определяемая
векторным произведением:
где r —
радиус-вектор, проведенный из точки О
в точку A, p=mv —
импульс материальной точки (рис. 1); L —
псевдовектор, направление которого
совпадает с направлением поступательного
движения правого винта при его вращении
от r к р.
Рис.1
Модуль
вектора момента импульса
где
α — угол между векторами r и р, l —
плечо вектора р относительно
точки О.
Моментом
импульса относительно неподвижной оси
z называется
скалярная величина Lz,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки О
данной оси. Момент импульса Lz не
зависит от положения точки О на оси
z.
При
вращении абсолютно твердого тела вокруг
неподвижной оси z каждая точка тела
движется по окружности постоянного
радиуса riсо
скоростью vi .
Скорость vi и
импульс mivi перпендикулярны
этому радиусу, т. е. радиус является
плечом вектора mivi .
Значит, мы можем записать, что момент
импульса отдельной частицы равен
(1)
и
направлен по оси в сторону, определяемую
правилом правого винта.
Монет
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц:
Используя
формулу vi =
ωri,
получим
т.
е.
2)
Таким
образом, момент импульса твердого тела
относительно оси равен моменту инерции
тела относительно той же оси, умноженному
на угловую скорость. Продифференцируем
уравнение (2) по времени:
т.
е.
Эта
формула — еще одна форма уравнения
динамики вращательного движения твердого
тела относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси равна моменту сил относительно той
же оси.
Момент
силы. Момент
силы относительно точки 
.
Момент
силы относительно неподвижной оси равен
проекции вектора 
на
эту ось.
Проекция вектора
на
ось не зависит от положения точки,
относительно которой определяется
радиус-вектор силы
.
Если
вектор 
лежит
в плоскости перпендикулярной оси
вращения, то проекция момента силы на
ось равна произведению величины силы
на плечо. Плечо силы — это длина
перпендикуляра, опущенного на прямую,
вдоль которой направлена сила.
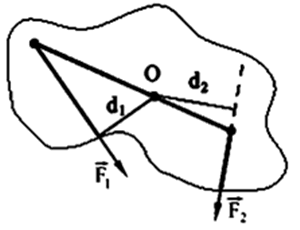
Определение
моментов сил: 
, 
.
№13
Момент инерции твердого тела.
Момент
инерции — скалярная физическая
величина, мера инертности
во вращательном
движении вокруг оси, подобно
тому, как масса тела является мерой его
инертности в поступательном
движении. Характеризуется
распределением масс в теле: момент
инерции равен сумме произведений
элементарных масс на квадрат их расстояний
до базового множества (точки, прямой
или плоскости).
Единица
измерения СИ: кг·м².
Обозначение: I или J.
Различают
несколько моментов инерции — в
зависимости от многообразия, от которого
отсчитывается расстояние точек.
Моментом
инерции механической
системы относительно неподвижной
оси («осевой момент инерции») называется
величина Ja, равная сумме
произведений масс всех n материальных
точек системы на квадраты их
расстояний до оси:
,
где:
-
mi —
масса i-й точки, -
ri —
расстояние от i-й точки до оси.
Осевой момент
инерции тела Ja является
мерой инертности тела вовращательном
движении вокруг оси подобно тому,
как масса тела
является мерой его инертности
в поступательном
движении.
,
где:
-
—
масса
малого элемента объёма тела
, -
—
плотность, -
—
расстояние
от элемента
до
оси a.
Если
тело однородно, то есть его плотность всюду
одинакова, то
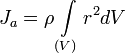
№14
Уравнение
динамики твердого тела, вращающегося
вокруг неподвижной оси.
Момент
силы. Момент
силы относительно точки
.
Момент
силы относительно неподвижной оси равен
проекции вектора
на
эту ось.
Проекция вектора
на
ось не зависит от положения точки,
относительно которой определяется
радиус-вектор силы
.
Если
вектор
лежит
в плоскости перпендикулярной оси
вращения, то проекция момента силы на
ось равна произведению величины силы
на плечо. Плечо силы — это длина
перпендикуляра, опущенного на прямую,
вдоль которой направлена сила.
Определение
моментов сил:
,
.
Уравнение
динамики твердого тела,
вращающегося вокруг неподвижной
оси:
суммарный момент сил, действующих
на тело, равен произведению момента
инерции тела на угловое ускорение:
.
Учитывая,
что момент импульса твердого тела 
,
уравнение динамики твердого тела можно
представить в виде
.
№15
Момент инерции. Теорема Штейнера.
Момент
инерции. Твердое
тело можно представить в виде системы
жестко связанных между собой материальных
точек.
Момент инерции системы
материальных точек относительно оси
вращения равен сумме произведений масс
материальных точек системы на квадраты
их расстояний до оси вращения:
.
где:
-
mi —
масса i-й точки, -
ri —
расстояние от i-й точки до оси.
Для
расчета момента инерции используют
интегрирование:
.
Единица
измерения СИ: кг·м².
Теорема
Гюйгенса-Штейнера
Момент
инерции твёрдого тела относительно
какой-либо оси зависит не только от массы,
формы и размеров тела, но также от
положения тела по отношению к этой оси.
Согласно теореме
Штейнера (теореме Гюйгенса-Штейнера), момент
инерции тела Jотносительно
произвольной оси равен сумме момента
инерции этого тела Jc относительно
оси, проходящей через центр
масс тела параллельно рассматриваемой
оси, и произведения массы тела m на
квадрат расстояния d между
осями:
где 
—
полная масса тела.
№16
Кинетическая энергия вращающегося
твердого тела (ось вращения неподвижна).
Кинетическая
энергия тела, движущегося произвольным
образом, равна сумме кинетических
энергий всех n материальных точек па
которые это тело можно разбить:
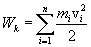
Если
тело вращается вокруг неподвижной оси
с угловой скоростью 
, то
линейная скорость i-ой точки равна 
,
где 
,
— расстояние от этой точки до оси вращения.
Следовательно.
где 
—
момент инерции тела относительно оси
вращения.
В
общем случае движение твердого тела
можно представить в виде суммы двух
движений — поступательного со скоростью,
равной скорости 
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
где 
—
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
№17
Работа, совершаемая при вращении твердого
тела.
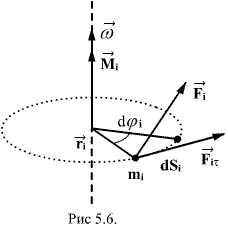
Рассмотрим
действие внешней силы 
,
приложенной к точке массой 
.
За время 
элементарная
масса
проходит
путь 
Работа
силы
на
этом пути определяется проекцией силы
на направление перемещения, которая
очевидно, равна тангенциальной
составляющей 
силы.
Но
равна
модулю момента 
силы
относительно
оси вращения. Работа 
,
и будет положительна, если
имеет
такое же направление, как и 
отрицательное,
если направление векторов
и
противоположны.
С
учетом, что 
Работа
всех сил, приложенных к телу
Полная
работа
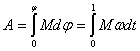
№18
Уравнение гармонических колебаний
математического маятника.
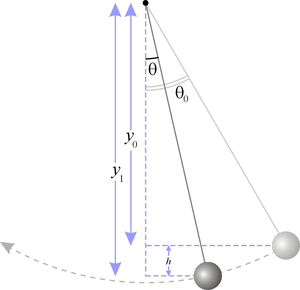
Математи́ческий
ма́ятник — осциллятор,
представляющий собоймеханическую
систему, состоящую из материальной
точки, находящейся на невесомой нерастяжимой нити
или на невесомом стержне в
однородном поле сил тяготения. Период малых
собственных колебаний
математического маятника длины L неподвижно
подвешенного в однородном поле тяжести
с ускорением
свободного падения g равен
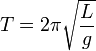
и
не зависит от амплитуды и массы маятника.
Гармонические
колебания
Маятник,
совершающий малые колебания, движется
по синусоиде. Поскольку уравнение
движения является обыкновенным ДУ
второго порядка, для определения закона
движения маятника необходимо задать
два начальных условия — координату
и скорость, из которых определяются две
независимых константы:
где 
— амплитуда колебаний
маятника, 
—
начальная фаза колебаний, 
— циклическая
частота, которая определяется из
уравнения движения. Движение, совершаемое
маятником, называется гармоническими
колебаниями
№19
Уравнение гармонических колебаний для
физического маятника.
Физический
маятник —
это твердое тело, которое совершает
колебания под действием силы тяжести
вокруг неподвижной горизонтальной оси,
которая проходит через точку О, не
совпадающую с центром масс С тела (рис.
1).
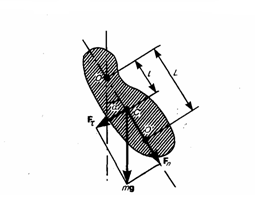
Рис.1
Если
маятник из положения равновесия отклонили
на некоторый угол α, то, используя
уравнение динамики вращательного
движения твердого тела, момент M
возвращающей силы
где
J — момент инерции маятника относительно
оси, которая проходит через точку подвеса
О, l – расстояние между осью и центром
масс маятника, Fτ ≈
–mgsinα ≈ –mgα — возвращающая сила (знак
минус указывает на то, что направления
Fτ и
α всегда противоположны; sinα ≈ α поскольку
колебания маятника считаются малыми,
т.е. маятника из положения равновесия
отклоняется на малые углы). Уравнение
запишем как
или 
Принимая
получим уравнение
Из
формулы вытекает, что при малых колебаниях
физический маятник совершает гармонические
колебания с циклической частотой ω0 и
периодом
где
введена величина L=J/(ml)
— приведенная
длина физического маятника.
№20
Закон равного распределения
энергии по степеням свободы в термодинамике.
Большинство
химических веществ состоит из многоатомных
молекул. Если рассматривать газообразное
состояние вещества, то при столкновениях
молекул тепловая энергия газа случайным
образом расходуется на изменение
кинетических энергий поступательного
и вращательного движений молекул, а
также на возбуждение колебаний атомов
в молекуле. Естественно предположить,
что указанные движения в молекуле могут
происходить одновременно.
Средняя
энергия приходящаяся на одну степень
свободы:
У
одноатомной молекулы i =
3, тогда для одноатомных молекул
для
двухатомных молекул
для
трёхатомных молекул
Таким
образом, на среднюю кинетическую
энергию молекулы, имеющей i-степеней
свободы, приходится
|
|
Это
и есть закон
Больцмана о равномерном распределении
средней кинетической энергии по степеням
свободы.
Если
система находится в состоянии
термодинамического равновесия, при
температуре Т,
то средняя кинетическая энергия
равномерно распределена между всеми
степенями свободы. На каждую
поступательную iп и
вращательную iвр степени
свободы приходится энергия 1/2
kT.
Для колебательной iкол,
степени свободы она равна kT.
Таким образом число степеней свободы i
= iп +
iвр +
2iкол
Закон о равномерном распределении
энергии по степеням свободы перестает
быть справедливым при квантовом описании
системы частиц, когда каждому квантовому
состоянию системы с i-степенями
свободы соответствует ячейка объемом hi в
фазовом пространстве “координаты –
импульсы” тождественных (неразличимых
между собой) частиц, где h –
постоянная Планка (М. Планк (1858-1947) –
немецкий физик–теоретик).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #