Утверждение
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Дано:
∆ ABC,
∠C=90º,
∠A=30º.
Доказать:
![[BC = frac{1}{2}AB]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-079c3a0516262be534ab9a83be60f2cf_l3.png "Rendered by QuickLaTeX.com")
Доказательство:
I способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Проведем из вершины прямого угла медиану CF.
Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то
![[CF = frac{1}{2}AB,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a9a779ae05f7196b9a70c2cbc9c021cb_l3.png "Rendered by QuickLaTeX.com")
то есть, CF=AF=BF.
Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.
Следовательно, у него углы при основании равны:
∠B=∠BCF=60º.
Так как сумма углов треугольника равна 180º, то в треугольнике BFC
∠BFC =180º -(∠B+∠BCF)=60º.
Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.
Значит, все его стороны равны и
![[BC = CF = BF = frac{1}{2}AB]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-af056013a524dd68afc73d72fcdc266a_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
II способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Построим треугольник ADC, равный треугольнику ABC.
В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).
Отсюда, ∠BAD=∠CAD+∠CAB=60º.
Следовательно, в треугольнике ABD все углы равны:
∠BAD=∠D=∠B=60º.
Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.
BC=DC (по построению), поэтому
![[BC = frac{1}{2}BD = frac{1}{2}AB.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-690c38cc0c5d2e691b99af535a7fc517_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Преподаватель который помогает студентам и школьникам в учёбе.
Свойство катета прямоугольного треугольника, лежащего против угла в 30°:
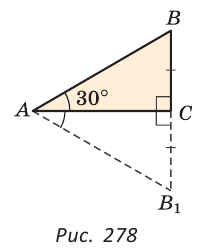
Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Дано: 
Доказать: ВС =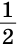 
АВ.
Доказательство:
На луче ВС отложим отрезок СВ1 равный отрезку ВС. Так как АВ1С =АВС по двум катетам (катет АС — общий), то 
B1AC =
BAC = 30°,
BAB1 = 60°. Но В = В1 = 60°. Известно, что если у треугольника все углы равны, то он равносторонний. Отсюда АВВ1 — равносторонний, АВ = ВВ1, ВС = 
ВВ1 =
АВ. Теорема доказана.
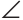
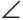
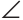
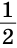
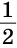
Верно и утверждение, обратное данному. Докажем его.
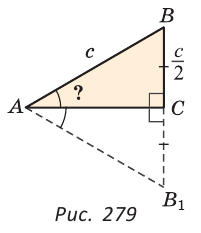
Теорема. Если в прямоугольном треугольнике катет равен половине гипотенузы, то этот катет лежит против угла в 30°.
Доказательство:
Пусть в треугольнике ABC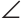 
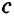
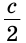
C = 90°, АВ = 
, ВС=
(рис. 279).
Докажем, что 
BAC = 30°. Продлим катет ВС на его длину: СВ1 = ВС. Из равенства прямоугольных треугольников АСВ1 и АСВ (по двум катетам) следует, что АВ1 = АВ = ВВ1 = . Значит, 
АВВ1 — равносторонний, все его углы равны по 60°, а его высота АС является биссектрисой. Поэтому BAC = 30°. Что и требовалось доказать.
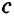
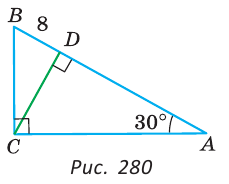
Пример:
В прямоугольном треугольнике ABC, у которого C = 90°, A=30°, проведена высота CD. Найти отрезок AD, если BD = 8 см.
Решение:
Так как угол А и угол BCD дополняют угол В до 90°, то BCD=A=30° (рис. 280).
В прямоугольном треугольнике CDB катет BD лежит против угла в 30°. Поэтому СВ = 2BD = 16 см.
В треугольнике ABC катет ВС лежит против угла в 30°. Поэтому АВ = 2ВС = 32 см.
Отсюда AD=AB-BD = 32 — 8 = 24 (см).
Ответ: 24 см.
Замечание. Мы доказали, что BC = 2BD, AB = 2BC = 4BD, AD = АВ — BD = 3BD, то есть в прямоугольном треугольнике с углом 30° высота делит гипотенузу в отношении 1 : 3.
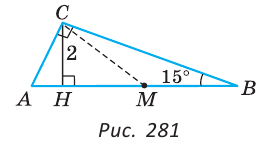
Пример:
Дан прямоугольный треугольник с углом 15°. Высота, проведенная к гипотенузе, равна 2 см. Найти гипотенузу.
Решение:
Пусть в треугольнике ABC 
ACB = 90°, 
B = 15°, СН = 2 см — высота (рис. 281).
Нужно найти АВ. Проведем медиану СМ треугольника ABC. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то СМ = MB. Треугольник СМВ — равнобедренный, MCB = CBM = 15°, AMC — его внешний угол.
По свойству внешнего угла AMC =MCB +MBC = 15° + 15° = 30°.
В прямоугольном треугольнике СНМ катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы СМ. Отсюда СМ = 2СН = 4 см, АВ = 2СМ = 8 см.
Ответ: 8 см.
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
- Площадь параллелограмма
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Найти сторону треугольника, лежащую против угла в 30 градусов?
Геометрия | 5 — 9 классы
Найти сторону треугольника, лежащую против угла в 30 градусов.
Дано предоставленно во вложениях, ниже :
1) Опустим высоту ВД (Д лежит на АС).
Рассм тр АВД (уг Д = 90 * ) ВД = 1 / 2 * 1 = 0, 5 дм (по св — ву катета, лежащего напротив угла в 30 * ) ; уг АВД = 60 * ( по т о сумме углов треугольника : 180 * — 30 * — 90 * )
2) Рассм тр СДВ (уг Д = 90 * ) уг СВД = 45 * ( 105 * — 60 * = 45 * ), уг ВСД = 45 * ( по т о сумме углов треугольника : 180 * — 90 * — 45 * ) След тр СДВ — р / б ( по признаку р / б треуг — ка : уг В = уг С = 45 * )
Следовательно, ВД = СД = 0, 5 дм
3) по т Пифагора к тр СВД ( уг Д = 90 * ) получаем : ВС ^ 2 = 1 / 4 + 1 / 4 = 1 / 2, BC = корень из (1 / 2) дм = 1 / корень из (2) дм
Ответ : Г) 1 / корень из 2.
Две стороны треугольника равны 12 и 9 см, угол между ними 30 градусов, найти площадь треугольника — провести высоту и найти её как катет лежащий против угла 30 градусов?
Две стороны треугольника равны 12 и 9 см, угол между ними 30 градусов, найти площадь треугольника — провести высоту и найти её как катет лежащий против угла 30 градусов.
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 6 и 10 см?
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 6 и 10 см?
Гипотенуза прямоугольного треугольника равна 10 см, а один из углов – 30 градусов?
Гипотенуза прямоугольного треугольника равна 10 см, а один из углов – 30 градусов.
Найдите катет, лежащий против данного угла.
Помогите пожалуйста?
1)Построить треугольник по двум сторонам и углу, лежащему против большей из них.
2)Построить треугольник по двум сторонам и углу, лежащему против меньшей из них.
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 5 и 3?
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 5 и 3.
Найти сторону треугольника, лежащую против его угла в 45°, если против второго угла этого треугольника градусной меры 60° расположена сторона длиной 3 см?
Найти сторону треугольника, лежащую против его угла в 45°, если против второго угла этого треугольника градусной меры 60° расположена сторона длиной 3 см.
Помогите?
Дан треугольник, один из углов которого равен 30 градусам.
Сторона треугольника, лежащая против угла в 30 градусов равна √13, а длины двух других сторон находятся в отношении 2 : 3√13.
Найдите длину наименьшей стороны треугольника.
Может ли наименьшая сторона треугольника лежать против угла 63°?
Может ли наименьшая сторона треугольника лежать против угла 63°?
Найдите сторону треугольника, лежащую против его угла в 45 градусов, если против второго угла этого треугольника градусной меры 60 градусов расположена сторона длиной : а)3см, б) , в)?
Найдите сторону треугольника, лежащую против его угла в 45 градусов, если против второго угла этого треугольника градусной меры 60 градусов расположена сторона длиной : а)3см, б) , в).
Найдите сторону треугольника лежащую против угла 45 градусов?
Найдите сторону треугольника лежащую против угла 45 градусов.
Вы перешли к вопросу Найти сторону треугольника, лежащую против угла в 30 градусов?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Треугольники АВС и А1В1С1 подобны, все их углы попарно равны. Если градусные меры относятся как 1 : 2 : 3, всего 6 частей, и сумма углов 180, то одна часть 180 / 6 = 30 градусов, а максимальный угол — это три части, 30 * 3 = 90 градусов. Если подоб..
11 см так как любые 2 стороны должны быть больше 1.
AB — средняя линия трапеции, она равна полсумме оснований ⇒ — PO — FE ОТВЕТ : PO = 18, FE = 12.
Из неравенств треугольников 5 + AB>18 , AB + 5>18, 23>AB следует что 13.
Надеюсь, все понятно Если что спрашивай.
Проще всего найти угол, для которого указан внешний. Он равен 180 — 110 = 70 градусов. Сумма всех углов равна 180. X + x + 14 + 70 = 180 2x = 96 x = 48, это меньший угол 48 + 14 = 62 и это последний угол.
Катет АС лежит против угла B угол B = 180 — 90 — 60 = 30 градусов. По опредению : катет лежещий против угла 30 градусов равен половине гипотенузы, находим этот катет : 16 / 2 = 8 дм. Ответ : катет АС = 8 дм.
Тут угол AMB = углуMAD = 34 BAM = AMB = 34 = > ABM = 112 В паралелограмме противоположные углы равны = > ABM = ADC = 112. Т. к. Сумма углов в 4ех угольнике равна 360 градусов = > С = (360 — 112×2) / 2 = = 68 градусов.
5 узлов делят веревку на 6 частей чтобы получить 7 частей нужно завязать 6 узлов.
Средняя линия — это полусумма оснований, если одно а второе b, то (a + b) / 2 = 6 Если в трапеции нарисовать диагональ, получить два треугольника, один с онованием a, второй с основанием b, и высотой для каждого из треугольников h = 17 то площади тре..
Треугольник. Свойство прямоугольного треугольника с углом в 30°.
Катет прямоугольного треугольника, противолежащий углу в 30°, будет равняться половине гипотенузы.
Изобразим прямоугольный треугольник АСВ с углом В = 30°. В этом случае второй его острый угол будет 60°.
Обоснуем, что катет АС равняется половине гипотенузы АВ то есть АС = 1/2АВ.
Продлим катет АС за вершину прямого угла С и начертим отрезок СМ, причем части равные СМ=АС. Прочертим ВМ, соединив таким образом точки В и М. Сформированные прямоугольные треугольники ВСМ и АСВ эквиваленты (равны по двум катетам). Наглядно видно, что всякий угол треугольника АМВ по 60°, значит можно сделать вывод, что образовавшийся треугольник — равносторонний.
Сторона АС = 1/2 АМ, а поскольку АМ = АВ, а значит и катет АС будет равен 1/2 гипотенузы АВ.
http://geometria.my-dict.ru/q/2607032_najti-storonu-treugolnika-lezasuu-protiv-ugla/
http://www.calc.ru/Treugolnik-Svoystvo-Pryamougolnogo-Treugolnika-S-Uglom-V-30.html
Это смотря какие данные нам даны для решения.
Например есть теорема Пифагора:
по ней, если катеты a и b, а гипотенуза c, то:
a²+b²=c²
Отсюда можно найти катет, зная длину гипотенузы и второго катета:
a²=c²-b²
a=√(c²-b²)
Также находим и b:
b=√(c²-a²)
Ещё можно найти катет через тригонометрические функции, то есть зная угол через синусы, косинусы, тангенсы, котангенсы и т.д.
Если представить треугольник как вписанный в круг, то зная угол и размер гипотенузы можно найти катеты.
В рассматриваемом треугольнике, вписанном в круг, гипотенуза будет радиусом круга и приравнивается к 1 (к единице). А катеты — это синус и косинус, они меньше единицы.
Допустим зная угол α можно вычислить sin(α) и cos(α).
Синус соответствует вертикальному катету, а косинус горизонтальному.
Теперь, чтобы найти длины этих катетов, нужно перевести их из коэффициентов, которые меньше единицы, в реальные длины. Для этого их нужно домножить на длину гипотенузы:
Если:
Y — вертикальный катет, а X — горизонтальный катет (см. картинку) a Z — гипотенуза, то:
Y=Z*sin(α)
X=Z*cos(α)
Можно найти катет и зная лишь длину второго катета, а также угол.
Допустим знаем Y и угол α.
Тогда запросто находим гипотенузу, выражая её из предыдущей формулы:
Z=sin(α)/Y
А затем уже находим второй катет: X=Z*cos(α)
Если же наоборот знаем только X катет (горизонтальный, относительно приведённого рисунка), то находим гипотенузу так:
Z=X/cos(α)
А затем уже находим катет Y: Y=Z*sin(α)
