Как найти какой график изображен на рисунке

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола

Графиком функции y = a x 2 + b x + c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a < 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y.
Коэффициент b помогает найти x в – координату вершины параболы.

x в = − b 2 a

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D < 0 – нет точек пересечения.

Гипербола

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Квадратный корень

Функция y = x имеет следующий график:

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Скачать домашнее задание к уроку 5.

Источник

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Линейная функция

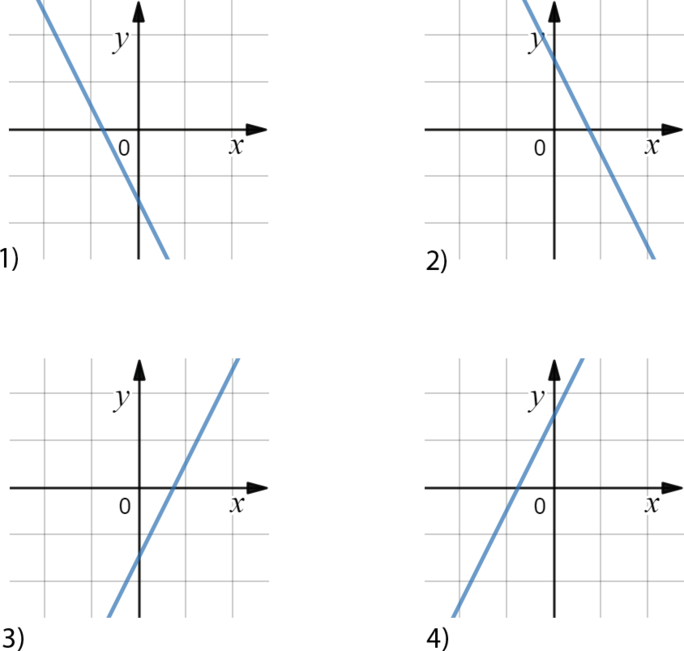
Дана функция (y=kx+b). Известно, что (b>0, k>0). На каком рисунке изображен график этой функции?

Общее уравнение прямой имеет вид (y=kx+b), где (k) — коэффициент (тангенс угла) наклона прямой, (b) — точка пересечения с осью (y).

Если (b>0), то график пересекает ось (y) выше 0. Если (k>0), то прямая образует острый угол с положительным направлением оси (x) (“наклонен вправо”). Подходит вариант 4).

Ответ: 4

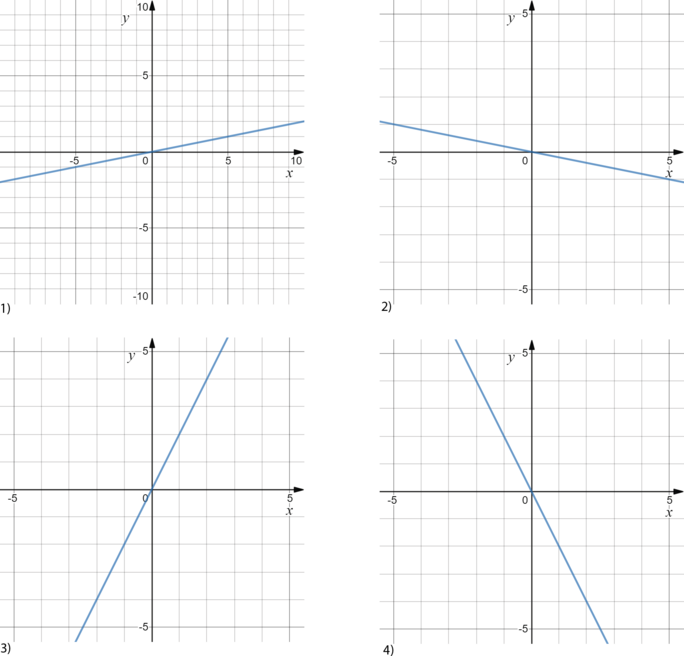
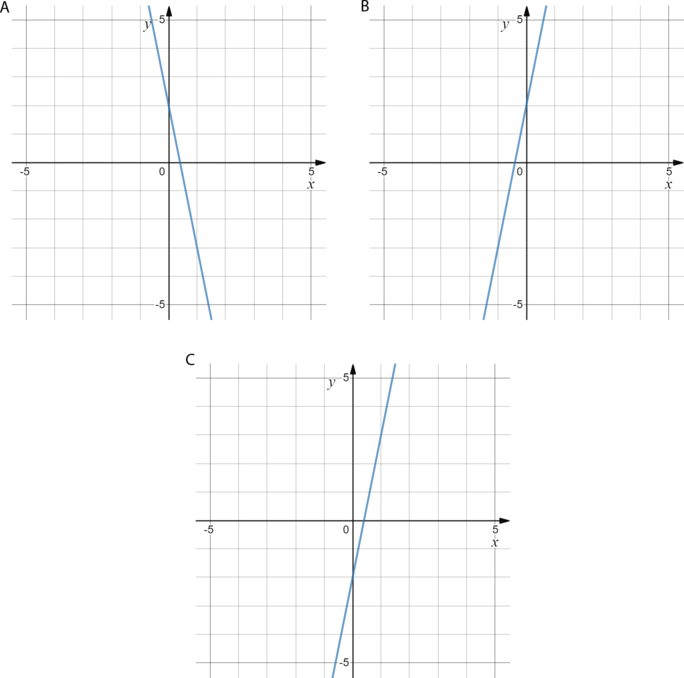
На каком рисунке изображен график функции (y=-frac{1}{5}x)?

У данной прямой (k<0), то есть ее график должен составлять тупой угол с положительным направлением оси (x) (“наклонен влево”). Значит, графики 1) и 3) точно не подходят.

Возьмем точку, принадлежащую графику 2) и подставим ее координаты в данное уравнение прямой. Если получим верное равенство, то нужный график будет найден. Пусть (x=-5,y=1). Тогда (-5 cdot (-frac{1}{5})=1) — верно. Значит, подходит ответ 2).

Ответ: 2

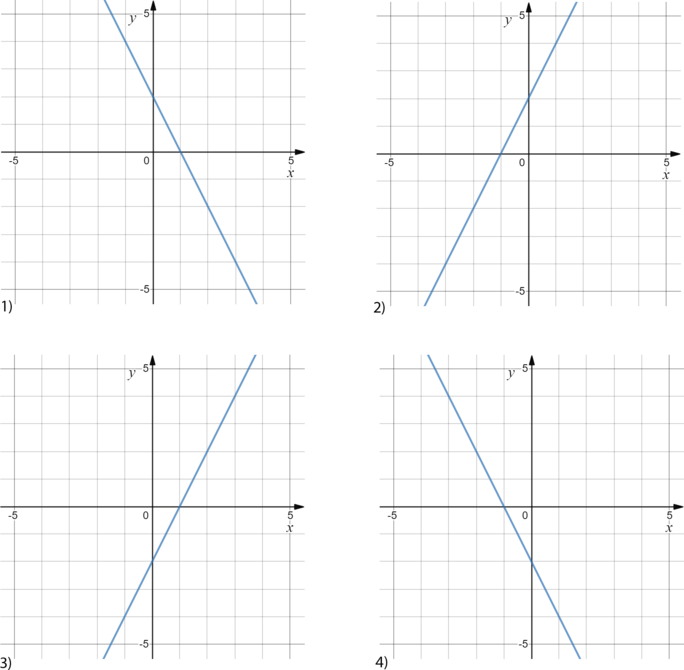
На каком рисунке изображен график функции (y=-2x + 2)?

У данной прямой (k<0), то есть ее график должен составлять тупой угол с положительным направлением оси (x) (“наклонен влево”). Значит, графики 2) и 3) точно не подходят.

Рассмотрим коэффициент (b). В данном случае (b=2), значит, график функции пересекает ось (y) выше 0. Подходит вариант 1).

Ответ: 1

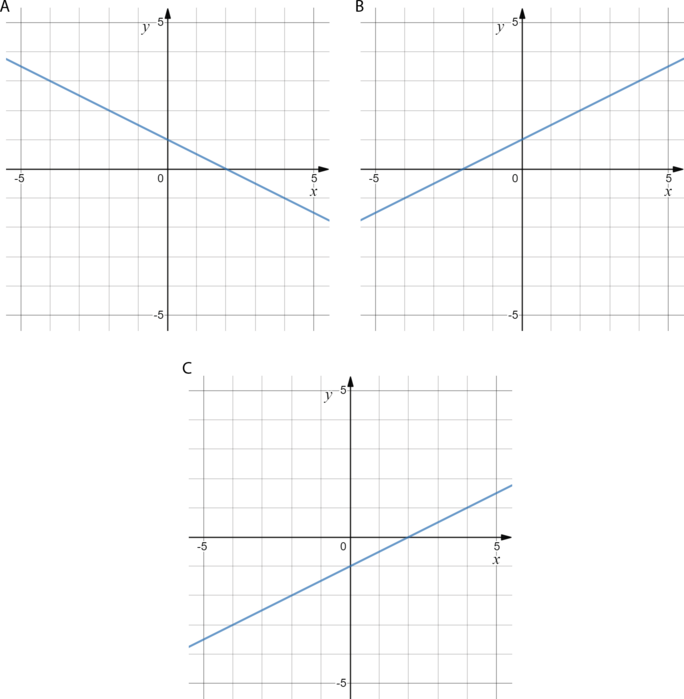
Установите соответствие между графиками функций и формулами, которые их задают.

Формулы:

1) (y=5x+2) (;;;) 2)(y=5x-2) (;;;) 3)(y=-5x+2)

В таблице под каждой буквой укажите соответствующий номер.

Только график A составляет тупой угол с положительным направлением оси (x) (“наклонен влево”). Значит, только ему соответствует отрицательный коэффициент (k). График A задан формулой 3).

Рассмотрим графики B и C. Первый из них пересекает ость (у) выше нуля, значит, ему соответствует формула с (b>0), то есть 1).

Графику C соответствует формула 2).

Ответ: 312

Установите соответствие между графиками функций и формулами, которые их задают.

Формулы:

1) (y=1+0,5x) (;;;) 2)(y=1-0,5x) (;;;) 3)(y=-1+0,5x)

В таблице под каждой буквой укажите соответствующий номер.

Графику C соответствует формула 3).

Ответ: 213

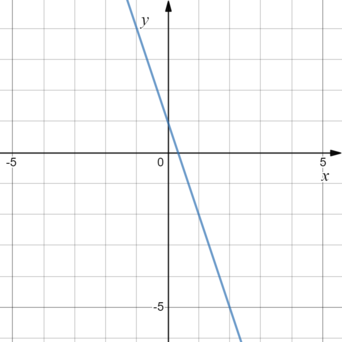
Дана функция (y=kx+b). Известно, что (b<0, k<0). На каком рисунке изображен график этой функции?

Если (b<0), то график пересекает ось (y) ниже 0. Если (k<0), то прямая образует тупой угол с положительным направлением оси (x) (“наклонен влево”). Подходит вариант 1).

Ответ: 1

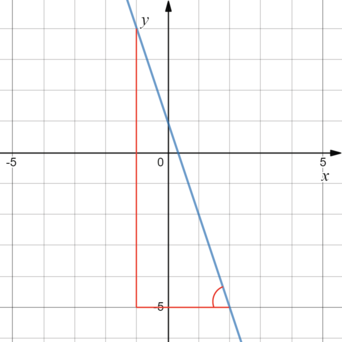
Определите значение коэффициента (k) функции (y=kx+b) по графику.

Коэффициент (k) равен тангенсу угла между графиком функции (y=kx+b) и положительным направлением оси (x). Так как в данном случае этот угол тупой, то найдем тангенс смежного острого угла, а затем поменяем его знак на противоположный.

Отметим на графике прямоугольный треугольник так, чтобы его катеты содержали целое число клеток.

Тангенс отмеченного угла равен (frac{9}{3}=3).

Коэффициент (k=-3).

Ответ: -3

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Основные теоретические сведения
- Координаты и базовые понятия о функциях
- График линейной функции
- График квадратичной функции (Парабола)
- Графики других функций
- Графики периодических (тригонометрических) функций

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

График квадратичной функции (Парабола)

К оглавлению…

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

Графики периодических (тригонометрических) функций

К оглавлению…

Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

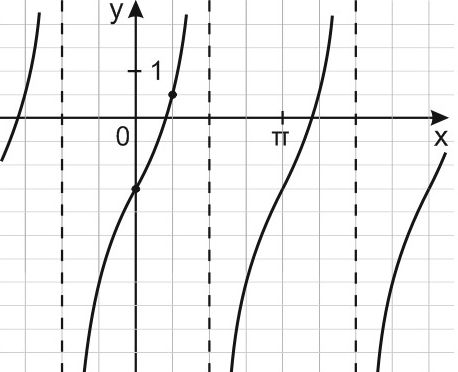
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.