Как найти изоморфный граф

Время на прочтение
13 мин

Количество просмотров 28K

Всем привет.

Есть такая задача – проверить, являются ли два графа изоморфными друг другу. Т.е., говоря по-простому, узнать, являются ли оба эти графа «одним и тем же» графом, но с разной нумерацией вершин и, в случае задания графов графически, с разным их пространственным расположением. Решение этой задачи не является таким уж очевидным, как может кому-то показаться на первый взгляд: даже для небольших графов взгляд на их графическое представление не всегда даст однозначный ответ. См., например, рисунок в той же Вики: ru.wikipedia.org/wiki/Изоморфизм_графов#Пример.

Ну как, очевидно?

А есть и более сложная задача: поиск в некотором «большом» графе всех подграфов, изоморфных некоторому другому графу «поменьше». Это еще более «темный лес». То есть, конечно, не совсем темный, но задача, согласитесь, не самая простая.

Итак, что же мы имеем?

1. Зачем вообще все это надо

И хотя задача про изоморфные (под)графы, как мы уже упомянули, сложная, она довольно нужная и полезная. А зачем? А затем, например, чтобы искать в базе данных химические соединения, подобные некоторой заданной молекуле по ее структурной формуле. Ведь ее можно представить себе в виде графа, не так ли? Этим занимается хемоинформатика – есть такая наука. А ведь есть еще задачи сопоставления с образцом, различные биоинформатические задачи, да много всего интересного.

2. Как решают эту задачу?

Классический подход к решению данной задачи был заложен Дж. Ульманом в 1976 году [3], впоследствии он существенно доработал свой алгоритм [4]. Также данный подход получил дальнейшее развитие в работах многих других авторов, например, Корделлы и соавторов [2] (алгоритм VF2), Бонници и соавторов [1] (алгоритм RI), и др.

Если кратко, то суть этого подхода заключается в «умном переборе» возможных соответствий вершин графа-образца B и графа A, в котором идет его поиск. «Умным» этот перебор делает ввод различных условий и ограничений, которые позволяют как можно раньше отсечь неподходящие варианты. Также для этих целей может проводиться различная предварительная обработка исходных данных.

Не будем здесь заниматься пересказом данных работ, а предложим читателю познакомиться с ними самостоятельно. Однако «показ лучше наказа», и, нужно отметить, что в Сети есть и неплохие графические примеры и объяснения этих алгоритмов. См., например, следующие:
coderoad.ru/17480142/Есть-ли-простой-пример-для-объяснения-алгоритма-Ульмана – очень хорошее и понятное объяснение с примером,
issue.life/questions/8176298 – шаги алгоритма VF2 с примером.

Однако возникает вопрос – возможны ли также еще какие-либо иные пути и подходы для решения этой задачи, пусть и для каких-то частных случаев? И вот с одним из возможных ответов на этот вопрос и хотелось бы Вас познакомить.

3. Изоморфизм графов и NB-пути

Давайте сразу договоримся: под NB-путями (и не из англомании, а просто потому, что так – короче) мы будем называть maximal non-branching paths, т.е. максимально протяженные неразветвляющиеся пути некоторого графа.

Итак, если у нас если два графа изоморфны друг другу, то для любого представления первого графа в виде последовательности максимально протяженных неразветвляющихся путей (т.е. этих наших NB-путей) всегда существует соответствующее ему такое же представление второго графа, и при этом:

• для ориентированных графов соответствующие друг другу пути будут сонаправлены,
• степени соответствующих друг другу вершин для неориентированных графов (а для ориентированных – количества входящих и исходящих ребер соответственно) будут равны,
• при «совмещении» таких представлений в результате мы будем иметь соответствие вершин первого и второго графов.

Пример. Граф A = {1->2, 1->6, 4->5, 5->1, 3->3}. Граф B = {3->4, 3->5, 1->2, 2->3, 6->6}
PathsA (maximal non-branching paths of A): 1->2, 1->6, 4->5->1, 3->3
PathsB (maximal non-branching paths of B): 3->4, 3->5, 1->2->3, 6->6
Соответствие вершин: 1(A):3(B), 2(A):4(B), 6(A):5(B), 4(A):1(B), 5(A):2(B), 3(A):6(B).

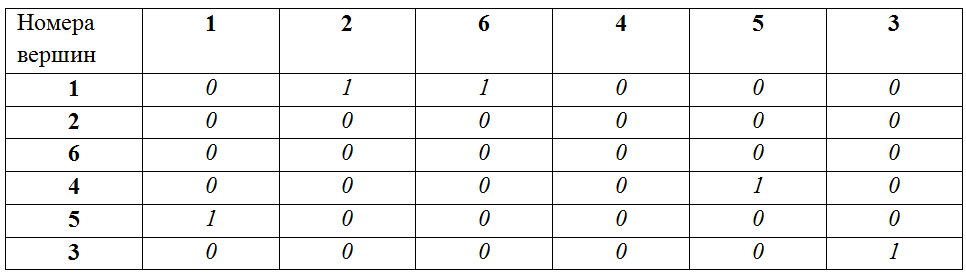
Таким образом, задачу проверки изоморфизма двух графов можно решить нахождением таких соответствующих друг другу путей и, затем, проверкой равенства друг другу матриц смежности, построенных исходя их сохранения порядка вершин в полученных последовательностях путей (при этом каждая вершина добавляется в порядок следования единожды, при ее первом «упоминании»). В нашем примере для построения матриц смежности будут использоваться следующие порядки вершин:

A: 1, 2, 6, 4, 5, 3
B: 3, 4, 5, 1, 2, 6

Матрица смежности для A для заданного порядка вершин:

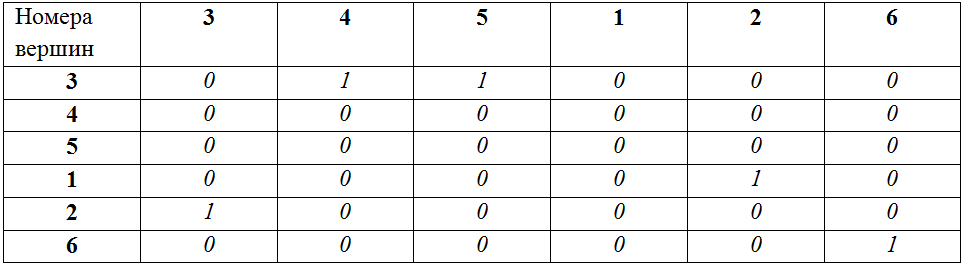
Матрица смежности для B для заданного порядка вершин:

Матрицы равны, следовательно, графы A и B – изоморфны.

При этом данный подход (1) применим как для ориентированных, так и неориентированных графов, (2) применим для графов, содержащих более одной компоненты связности/ сильной связности, (3) применим для графов, содержащих кратные (множественные) ребра и петли, однако (4) не учитывает вершины, для которых отсутствуют инцидентные им ребра.

4. Ну хорошо, проверили изоморфизм графов. А что же с поиском подграфов?

А тут, честно признаюсь, все значительно сложнее. Тут у нас будет следующее ограничение: исходя из самой сути метода можно находить не любые, но лишь

«вписанные» подграфы

. А

«вписанным» подграфом

графа A мы будем называть такой его подграф, который может быть «приклеен» к другим частям графа A только за счет ребер, инцидентных лишь граничным вершинам его (подграфа) неразветвляющихся путей максимальной длины (при этом граф A может содержать и иные компоненты связности). Не волнуйтесь, ниже будет пример, и все будет понятней. Прим. С 12.2020 все же удалось доработать данный метод для поиска всех (а не только «вписанных») подграфов, изоморфных данному. Но об этом в самом конце (см. Раздел 8. Вместо послесловия – Продолжение).

Кроме того, при решении данной задачи, помимо поиска соответствий NB-путей графов A и B по длине (как это было в рассмотренном выше примере с проверкой изоморфизма), также необходимо отдельно искать и следующие возможные соответствия между ними:

• Соответствия NB-путей – простых цепей из графа B NB-путям – простым цепям/ простым из циклам графа A. При этом изначально такие пути в графе A могут быть длиннее – в этом случае берутся их отрезки, равные по длине искомому пути из B.
• Соответствия NB-«концевых» путей графа B каким-либо NB-путям графа A (при этом пути из графа A также могут быть длиннее – в этом случае берутся их отрезки, равные по длине искомому пути из графа B).

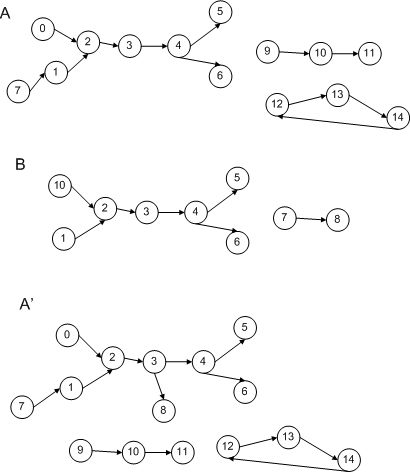
Разберемся на примере:

При поиске «вписанного» изоморфного подграфа графа B в графе A (см. рис. выше) будут обнаружены следующие соответствия:

• внутренний путь 2->3->4 графа B: внутренний путь 2->3->4 графа A,
• концевые пути 1->2 и 10->2 графа B: концевой путь 0->2 графа A и фрагмент концевого пути 7->1->2 графа A, а именно 1->2,
• простая цепь 7->8 графа B: отрезки простой цепи 9->10->11 графа A, а именно 9->10 и 10->11, а также отрезки простого цикла 12->13->14->12 графа A, а именно 12->13, 13->14, и 14->12.

Таким образом, в качестве «изоморфных графу B «вписанных» подграфов графа A могут быть найдены следующие 5 вариантов:

A1 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 9->10}
A2 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 10->11}
A3 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 12->13}
A4 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 13->14}
A5 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 14->12}

Однако, если мы добавим к графу A дополнительное ребро 3->8, у нас получится граф A’ (ниже на том же рисунке). И в A’ уже будет не найти «вписанных» подграфов, изоморфных графу B. Действительно: ребро 3->8 «разбивает» путь 2->3->4 графа A на два и, значит, путей-кандидатов для внутреннего пути 2->3->4 графа B обнаружено не будет.

5. Теперь сам алгоритм

Теперь мы можем перейти к более детальному рассмотрению алгоритма поиска «вписанных» в граф А подграфов, изоморфных некоторому графу B.

Итак, алгоритм будет состоять из 4-х этапов:

• Препроцессинг,
• Сопоставление,
• Прореживание,
• Заключение.

На данном этапе мы находим все NB-пути по каждому из графов, а также оцениваем факторы, ограничивающие пространство выбора при переборе. Т.е. мы делаем следующее:

1. Находим все NB-пути в графе A и заносим их в динамический массив (в С++ – в вектор) PathsA
2. Находим все NB-пути в графе B и заносим их в динамический массив (вектор) PathsB
3. Вычисляем и запоминаем кратность всех ребер графов A и B. Дальнейшие действия по этапам II-IV проводятся исходя из допущения, что кратности всех ребер равны 1. Однако на финальной стадии производится сравнение кратности ребер подграфа графа A-кандидата на изоморорфизм с графом B и кратности ребер самого графа B: все ребра подходящего графа-кандидата должны иметь кратность не меньшую, чем сопоставляемое им ребро графа B.
4. Подсчитываем степени всех вершин графов A и B (для ориентированных графов степени по входящим и исходящим ребрам учитываются отдельно).
5. Вычисляем матрицы кратчайших путей между каждой парой вершин в A и в B: назовем их DA и DB соответственно.
6. Формируем матрицу смежности – назовем ее B0 – для графа B таким же образом, как мы это делали выше, когда проверяли изоморфизм двух графов.

Итак, у нас есть NB-пути по обоим графам и параметры-ограничители из п.п. 3-5.

На данном этапе мы будем подбирать NB-пути-кандидаты (далее – просто «пути-кандидаты») из графа A для каждого из NB-путей графа B. Отметка о каждом пути-кандидате из PathsA для каждого i-го пути PathsB[i] будет записываться в двумерный динамический массив (в C++ – в вектор векторов) NPaths – соответственно в i-й вектор (i-ю строку) – в виде упорядоченного триплета чисел: номер соответствующего пути в PathsA – номер стартовой позиции в нем – длина пути.

Например, PathsB[2] = {1, 0, 3, 3, 1, 3} означает, что пути PathsB[2] сопоставлено 2 пути-кандидата из A: из PathsA[1] – 3 первых элемента пути начиная с нулевого (начального), и из PathsA[3] – также 3 элемента начиная с первого (следующего за начальным).

При этом поиск (подбор) путей-кандидатов мы будем производить по 4-м направлениям:

1. Поиск путей-кандидатов для всех внутренних NB-путей графа B из PathsB, т.е. тех, обе граничных вершины которых соединены в графе B как минимум с 2-мя другими вершинами (независимо от направления такой связи) и при этом такой путь не является простым циклом (ориентированным – для ориентированных графов).
2. Поиск путей-кандидатов для концевых NB-путей из PathsB.
3. Поиск путей-кандидатов для NB-путей – простых циклов из PathsB.
4. Поиск путей-кандидатов для NB-путей – простых цепей из PathsB.

При отборе путей-кандидатов для каждого i-го пути из PathsB сравниваются (вот тут-то нам и начинают пригождаться некоторые из вычисленных ранее параметров-ограничителей):

• его длина и длина пути-кандидата (должны быть равны для случаев 1 и 3, а для случаев 2 и 4 путь-кандидат из PathsA также может быть длиннее),
• степени его граничных вершин и соответствующих им вершин пути-кандидата (у вершин из пути-кандидата данные значения должны быть не менее чем у пути из PathsB),
• кратность ребра пути-кандидата должна быть не менее, чем у пути из PathsB,
• другие возможные ограничения (например, совпадения меток вершин, если мы говорим о тех же химических соединениях, когда вершины можно маркировать соответствующими атомами, и т.д.)

Если по результатам этапа II для какого-либо из путей в PathsB не найдено ни одного пути-кандидата из PathsA, то считается, что A не содержит «вписанных» подграфов, изоморфных графу B.

Теперь давайте попробуем «ужать» граф A. Оставим в нем лишь те ребра, которые вошли в найденные нами пути-кандидаты. Если при этом граф A потерял хоть бы одно ребро по сравнению с его изначальным состоянием – возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.

Целью настоящего этапа является дальнейшее максимально возможное исключение неподходящих путей кандидатов. Для этого осуществим следующие действия.

1. Исключение заведомо неподходящих путей-кандидатов исходя из минимальных расстояний между вершинами в графе B. Исключению подлежит тот путь-кандидат по каждому PathsB[i], для которого хотя бы по одному PathsB[j] не нашлось ни одного такого пути-кандидата, чтобы кратчайшие расстояния между их граничными вершинами в графе A было меньше или равно кратчайшему расстоянию между соответствующими им граничными вершинами путей PathsB[i] и PathsB[j] из графа B.
2. Исключение для всех циклов из PathsB сопоставленных им нециклических путей-кандидатов и наоборот.
3. Аналогичное п. 1 исключение путей-кандидатов, но не по критерию кратчайшего расстояния между граничными вершинами, а их (граничных вершин) взаимному равенству либо неравенству.

Например, если:

• начальный элемент пути PathsB[i] не равен начальному элементу пути PathsB[j], и
• конечный элемент пути PathsB[i] не равен конечному элементу пути PathsB[j], и
• начальный элемент пути PathsB[i] равен конечному элементу пути PathsB[j], и
• начальный элемент пути PathsB[j] не равен конечному элементу пути PathsB[i],

то исключению подлежит тот путь-кандидат по пути PathsB[i], для которого хотя бы по одному PathsB[j] не нашлось ни одного пути-кандидата, удовлетворяющего приведенному выше условию относительно равенства/ неравенства соответственно их (путей-кандидатов) начальных и конечных вершин.

Т.е., грубо говоря, мы выкидываем те пути-кандидаты, которые заведомо не войдут в искомые подграфы – исходя из расстояния до всех прочих путей-кандидатов (страшно далеки эти пути от всех прочих), исходя из их цикличности/ нецикличности, а также исходя из должного равенства/ неравенства их граничных вершин с граничными вершинами других путей-кандидатов.

Если по результатам этапа III хотя бы 1 путь-кандидат был удален из PathsA, то – опять же – обновляется граф А – в нем остаются только те ребра, которые вошли в оставшиеся пути-кандидаты. И, опять же, если при этом граф A «похудел» хотя бы на одно ребро – снова возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.

Каждое возможное сочетания всех оставшихся путей-кандидатов задает подграф графа A. Для каждого такого подграфа строится матрица смежности с учетом порядка следования путей кандидатов таким же образом, как была построена матрица смежности B0 для графа B, а затем эти матрицы смежности сравниваются между собой.

Если они равны, то сравниваются кратности ребер (см. п. 3 Этапа I Препроцессинг). Если все эти условия выполнены – найденный подграф считается изоморфным графу B и добавляется в множество найденных результатов.

При проведении этапа IV “Заключение” возможно применение различных дополнительных проверок, ускоряющих выявление и отбрасывание неподходящего подграфа.

6. Как все запутано… Рассмотрим пример работы алгоритма

Не знаю как Вам, а мне без примера было бы непонятно. Давайте рассмотрим все на примере.

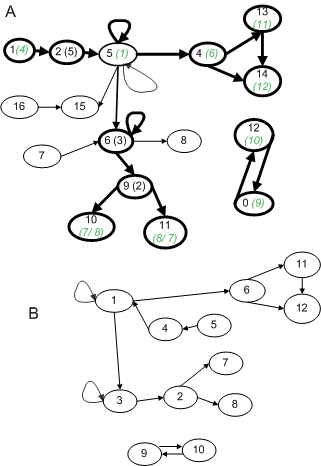
На рис. ниже приведены графы A = {1->2, 2->5, 5->15, 16->15, 5->5, 5->5, 5->4, 5->6, 7->6, 6->8, 6->6, 6->9, 9->10, 9->11, 12->0, 0->12, 4->13, 13->14, 14->4} и B = {1->1, 4->5, 5->1, 1->3, 3->3, 3->2, 2->7, 2->8, 9->10, 10->9, 1->6, 6->11, 11->12, 12->6}. Нашей задачей является нахождение в графе A всех «вписанных» подграфов, изоморфных графу B. Результат также отражен на рисунке: найденные вершины и ребра графа A выделены толстой линией, а номера соответствующих вершин графа B указаны в скобках (если вариантов несколько – они указываются через дробь).

При решении задачи поиска в графе A «вписанных» подграфов, изоморфных графу B, имеем следующие результаты работы алгоритма.

Этап I: Выполнены все действия и расчеты по п.п. 1-5 данного этапа, ниже приводятся полученные PathsA и PathsB.

PathsA:

1->2->5
4->13->14 4
5->4
5->5
5->6
5->15
6->6
6->8
6->9
7->6
9->10
9->11
16->15
0->12->0

PathsB:

1->1
1->3
1->6
2->7
2->8
3->2
3->3
4->5->1
6->11->12->6
9->10->9

Этапы II-III. Сопоставление показало, что для каждого пути из PathsA находится как минимум один путь-кандидат из PathsB, а по результатам предварительного прореживания PathsA был сокращен. На этапе основного прореживания (III) дальнейшего сокращения PathsA не произошло. В результате PathsA и PathsB приняли вид:

PathsA:

1->2->5
4->13->14->4
5->4
5->5
5->6
6->6
6->9
9->10
9->11
0->12->0

PathsB:

1->1
1->3
1->6
2->7
2->8
3->2
3->3
4->5->1
6->11->12->6
9->10->9

Итоговое сопоставление NPaths имеет вид:
NPaths:

i=0: 3 0 2
i=1: 4 0 2
i=2: 2 0 2
i=3: 7 0 2 8 0 2
i=4: 7 0 2 8 0 2
i=5: 6 0 2
i=6: 5 0 2
i=7: 0 0 3
i=8: 1 0 4
i=9: 9 0 3

Здесь самое время вспомнить, что каждый упорядоченный триплет чисел в NPaths[i] задает соответствующий PathsB[i] путь-кандидат из A в формате: номер соответствующего пути из PathsA – стартовая позиция отрезка из данного пути – длина отрезка. Таким образом, нетрудно убедиться, что пути PathsB[0] = {1->1} (i=0: 3 0 2) соответствует единственный путь из A, а именно: отрезок из пути PathsA[3], начинающийся с его самого начала и имеющий длину 2.

Этап IV. В результате в графе A был найден единственный подграф A1, изоморфный графу B. A1 = {0->12, 1->2, 2->5, 4->13, 5->4, 5->5, 5->6, 6->6, 6->9, 9->10, 9->11, 12->0, 13->14, 14->4}.

7. Что же дальше?

А, дальше, в принципе, и все. Хотя не совсем: автор должен признаться, что алгоритм может еще дорабатываться и дорабатываться. Что тут нужно добавить?

1. При введении дополнительных признаков вершин графов A и B (например, при задании графами химических соединений каждой вершине может быть сопоставлен числовой код, соответствующий одному и только одному атому (изотопу)) процесс поиска может быть ускорен за счет большей точности сопоставлений по Этапу II: дополнительным условием отбора путей-кандидатов будет соответствие меток вершин.
2. Скорость работы представленного алгоритма очень сильно зависит от структур исходных графов и их взаимного соответствия. Алгоритм будет работать тем быстрее, чем более «уникальную», «нестандартную» и несимметричную структуру имеет граф-образец B.
3. Исходя из этого, одним из возможных путей использования представленного алгоритма может являться, в том числе, «скриннинговый» поиск решения по любому из направлений:
   (1) поиск именно «вписанных» подграфов, изоморфных данному,
   (2) проверка изоморфности двух различных графов.
   «Скрининг» здесь подразумевает «предварительный экспресс-поиск решения», для чего необходимо задать некоторое предельное время его работы, по истечении которого при отсутствии результата можно считать, что данная задача подлежит решению другим алгоритмом.
4. Возможно, для кого-то представленный алгоритм может оказаться полезным как при решении различных практических задач, так и при разработке новых алгоритмов решения задачи об изоморфном подграфе.

8. Вместо послесловия – Продолжение

В декабре 2020 случилось то, что должно было случиться: удалось как адаптировать данный подход для поиска всех (а не только «вписанных») подграфов в графе по образцу, так и воплотить это на практике. Решение, в принципе, лежало на поверхности: вместо non-branching paths (нет короткого аналога термина по-русски) были взяты сами ребра графов. И с января 2021 также на практике была реализована функция, позволяющая искать изоморфные подграфы с учетом меток вершин, причем произвольного типа (в т.ч. — строкового, что позволяет использовать «многогранные» метки; возможно, это может оказаться полезным для различных задач, в том числе, в области химии).

Литература

Общее по проблематике:
1. Bonnici, V., Giugno, R., Pulvirenti, A. et al. A subgraph isomorphism algorithm and its application to biochemical data. BMC Bioinformatics 14, S13 (2013). doi.org/10.1186/1471-2105-14-S7-S13.
2. Cordella L, Foggia P, Sansone C, Vento M: A (Sub)Graph Isomorphism Algorithm for Matching Large Graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004, 26 (10): 1367-1372. 10.1109/TPAMI.2004.75.
3. Ullmann Julian R.: An algorithm for Subgraph Isomorphism. Journal of the Association for Computing Machinery. 1976, 23: 31-42. 10.1145/321921.321925.
4. Ullmann Julian R.: Bit-vector algorithms for binary constraint satisfaction and subgraph isomorphism. J Exp Algorithmics. 2011, 15 (1.6): 1.1-1.6. 1.64

Написанный более официальным языком препринт автора про это самый «алгоритм на основе анализа NB-Paths», содержащий также инфу о предпринятой попытке его реализации на C++:
5. Черноухов С.А. 2020. Preprints.RU. Проверка изоморфности двух графов и поиск изоморфных подграфов: подход, основанный на анализе максимально протяженных неразветвляющихся путей / Maximal non-branching paths approach to solve (sub)graph isomorphism problem. DOI: dx.doi.org/10.24108/preprints-3111977

Полезные интернет-источники по теме:
6. coderoad.ru/17480142/Есть-ли-простой-пример-для-объяснения-алгоритма-Ульмана
7. issue.life/questions/8176298.
8. github.com/chernouhov/CBioInfCpp-0- — репозиторий свободной библиотеки функций для работы со строками и графами на C++, алгоритм реализован с помощью функции SubGraphsInscribed.

Как мы увидели на примере выше, изоморфность доказать не всегда легко. С другой стороны, доказать неизоморфность двух графов обычно проще — нужно найти свойство, которое эти два графа не разделяют.

Например, два графа могут отличаться такими свойствами:

Чтобы лучше понять эти свойства, рассмотрим такой пример:

В этом примере графы имеют такие свойства:

Таким образом, первые три свойства не помогают. Однако нам на помощь приходит четвертое свойство: в первом графе нет треугольника-подграфа, а во втором — он есть.

Существует множество других возможностей доказать неизоморфность. Иногда для этого требуется немного творчества.

Например, вот эти графы неизоморфны:

Обратите внимание, что у них одинаковое количество вершин и ребер, степени почти всех вершин тоже одинаковы. Определим, в чем разница между ними. Второй граф содержит вершину степени

, смежную с двумя вершинами степени

— в первом графе это не так.

К этому же примеру можно подойти по-другому:

From Wikipedia, the free encyclopedia

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.

The problem is not known to be solvable in polynomial time nor to be NP-complete, and therefore may be in the computational complexity class NP-intermediate. It is known that the graph isomorphism problem is in the low hierarchy of class NP, which implies that it is not NP-complete unless the polynomial time hierarchy collapses to its second level.^[1] At the same time, isomorphism for many special classes of graphs can be solved in polynomial time, and in practice graph isomorphism can often be solved efficiently.^[2][3]

This problem is a special case of the subgraph isomorphism problem,^[4] which asks whether a given graph G contains a subgraph that is isomorphic to another given graph H; this problem is known to be NP-complete. It is also known to be a special case of the non-abelian hidden subgroup problem over the symmetric group.^[5]

In the area of image recognition it is known as the exact graph matching.^[6]

State of the art[edit]

In November 2015, László Babai announced a quasipolynomial time algorithm for all graphs, that is, one with running time for some fixed .^{[7][8][9][10]} On January 4, 2017, Babai retracted the quasi-polynomial claim and stated a sub-exponential time bound instead after Harald Helfgott discovered a flaw in the proof. On January 9, 2017, Babai announced a correction (published in full on January 19) and restored the quasi-polynomial claim, with Helfgott confirming the fix.^[11][12] Helfgott further claims that one can take c = 3, so the running time is 2^{O((log n)3)}.^[13][14]

Prior to this, the best currently accepted theoretical algorithm was due to Babai & Luks (1983), and is based on the earlier work by Luks (1982) combined with a subfactorial algorithm of V. N. Zemlyachenko (Zemlyachenko, Korneenko & Tyshkevich 1985). The algorithm has run time 2^{O(√n log n)} for graphs with n vertices and relies on the classification of finite simple groups. Without this classification theorem, a slightly weaker bound
2^{O(√n log2 n)} was obtained first for strongly regular graphs by László Babai (1980), and then extended to general graphs by Babai & Luks (1983). Improvement of the exponent √n is a major open problem; for strongly regular graphs this was done by Spielman (1996). For hypergraphs of bounded rank, a subexponential upper bound matching the case of graphs was obtained by Babai & Codenotti (2008).

There are several competing practical algorithms for graph isomorphism, such as those due to McKay (1981), Schmidt & Druffel (1976), Ullman (1976), and Stoichev (2019). While they seem to perform well on random graphs, a major drawback of these algorithms is their exponential time performance in the worst case.^[15]

The graph isomorphism problem is computationally equivalent to the problem of computing the automorphism group of a graph,^[16][17] and is weaker than the permutation group isomorphism problem and the permutation group intersection problem. For the latter two problems, Babai, Kantor & Luks (1983) obtained complexity bounds similar to that for graph isomorphism.

Solved special cases[edit]

A number of important special cases of the graph isomorphism problem have efficient, polynomial-time solutions:

• Trees^[18][19]
• Planar graphs^[20] (In fact, planar graph isomorphism is in log space,^[21] a class contained in P)
• Interval graphs^[22]
• Permutation graphs^[23]
• Circulant graphs^[24]
• Bounded-parameter graphs
  • Graphs of bounded treewidth^[25]
  • Graphs of bounded genus^[26] (Planar graphs are graphs of genus 0.)
  • Graphs of bounded degree^[27]
  • Graphs with bounded eigenvalue multiplicity^[28]
  • k-Contractible graphs (a generalization of bounded degree and bounded genus)^[29]
  • Color-preserving isomorphism of colored graphs with bounded color multiplicity (i.e., at most k vertices have the same color for a fixed k) is in class NC, which is a subclass of P^[30]

Complexity class GI[edit]

Since the graph isomorphism problem is neither known to be NP-complete nor known to be tractable, researchers have sought to gain insight into the problem by defining a new class GI, the set of problems with a polynomial-time Turing reduction to the graph isomorphism problem.^[31] If in fact the graph isomorphism problem is solvable in polynomial time, GI would equal P. On the other hand, if the problem is NP-complete, GI would equal NP and all problems in NP would be solvable in quasi-polynomial time.

As is common for complexity classes within the polynomial time hierarchy, a problem is called GI-hard if there is a polynomial-time Turing reduction from any problem in GI to that problem, i.e., a polynomial-time solution to a GI-hard problem would yield a polynomial-time solution to the graph isomorphism problem (and so all problems in GI). A problem is called complete for GI, or GI-complete, if it is both GI-hard and a polynomial-time solution to the GI problem would yield a polynomial-time solution to .

The graph isomorphism problem is contained in both NP and co-AM. GI is contained in and low for Parity P, as well as contained in the potentially much smaller class SPP.^[32] That it lies in Parity P means that the graph isomorphism problem is no harder than determining whether a polynomial-time nondeterministic Turing machine has an even or odd number of accepting paths. GI is also contained in and low for ZPP^NP.^[33] This essentially means that an efficient Las Vegas algorithm with access to an NP oracle can solve graph isomorphism so easily that it gains no power from being given the ability to do so in constant time.

GI-complete and GI-hard problems[edit]

Isomorphism of other objects[edit]

There are a number of classes of mathematical objects for which the problem of isomorphism is a GI-complete problem. A number of them are graphs endowed with additional properties or restrictions:^[34]

• digraphs^[34]
• labelled graphs, with the proviso that an isomorphism is not required to preserve the labels,^[34] but only the equivalence relation consisting of pairs of vertices with the same label
• «polarized graphs» (made of a complete graph K_m and an empty graph K_n plus some edges connecting the two; their isomorphism must preserve the partition)^[34]
• 2-colored graphs^[34]
• explicitly given finite structures^[34]
• multigraphs^[34]
• hypergraphs^[34]
• finite automata^[34]
• Markov Decision Processes^[35]
• commutative class 3 nilpotent (i.e., xyz = 0 for every elements x, y, z) semigroups^[34]
• finite rank associative algebras over a fixed algebraically closed field with zero squared radical and commutative factor over the radical.^[34][36]
• context-free grammars^[34]
• balanced incomplete block designs^[34]
• Recognizing combinatorial isomorphism of convex polytopes represented by vertex-facet incidences.^[37]

GI-complete classes of graphs[edit]

A class of graphs is called GI-complete if recognition of isomorphism for graphs from this subclass is a GI-complete problem. The following classes are GI-complete:^[34]

• connected graphs^[34]
• graphs of diameter 2 and radius 1^[34]
• directed acyclic graphs^[34]
• regular graphs^[34]
• bipartite graphs without non-trivial strongly regular subgraphs^[34]
• bipartite Eulerian graphs^[34]
• bipartite regular graphs^[34]
• line graphs^[34]
• split graphs^[38]
• chordal graphs^[34]
• regular self-complementary graphs^[34]
• polytopal graphs of general, simple, and simplicial convex polytopes in arbitrary dimensions.^[39]

Many classes of digraphs are also GI-complete.

Other GI-complete problems[edit]

There are other nontrivial GI-complete problems in addition to isomorphism problems.

• The recognition of self-complementarity of a graph or digraph.^[40]
• A clique problem for a class of so-called M-graphs. It is shown that finding an isomorphism for n-vertex graphs is equivalent to finding an n-clique in an M-graph of size n². This fact is interesting because the problem of finding a clique of order (1 − ε)n in a M-graph of size n² is NP-complete for arbitrarily small positive ε.^[41]
• The problem of homeomorphism of 2-complexes.^[42]

GI-hard problems[edit]

• The problem of counting the number of isomorphisms between two graphs is polynomial-time equivalent to the problem of telling whether even one exists.^[43]
• The problem of deciding whether two convex polytopes given by either the V-description or H-description are projectively or affinely isomorphic. The latter means existence of a projective or affine map between the spaces that contain the two polytopes (not necessarily of the same dimension) which induces a bijection between the polytopes.^[39]

Program checking[edit]

Manuel Blum and Sampath Kannan (1995) have shown a probabilistic checker for programs for graph isomorphism. Suppose P is a claimed polynomial-time procedure that checks if two graphs are isomorphic, but it is not trusted. To check if graphs G and H are isomorphic:

• Ask P whether G and H are isomorphic.
  • If the answer is «yes»:
    • Attempt to construct an isomorphism using P as subroutine. Mark a vertex u in G and v in H, and modify the graphs to make them distinctive (with a small local change). Ask P if the modified graphs are isomorphic. If no, change v to a different vertex. Continue searching.
    • Either the isomorphism will be found (and can be verified), or P will contradict itself.
  • If the answer is «no»:
    • Perform the following 100 times. Choose randomly G or H, and randomly permute its vertices. Ask P if the graph is isomorphic to G and H. (As in AM protocol for graph nonisomorphism).
    • If any of the tests are failed, judge P as invalid program. Otherwise, answer «no».

This procedure is polynomial-time and gives the correct answer if P is a correct program for graph isomorphism. If P is not a correct program, but answers correctly on G and H, the checker will either give the correct answer, or detect invalid behaviour of P.
If P is not a correct program, and answers incorrectly on G and H, the checker will detect invalid behaviour of P with high probability, or answer wrong with probability 2⁻¹⁰⁰.

Notably, P is used only as a blackbox.

Applications[edit]

Graphs are commonly used to encode structural information in many fields, including computer vision and pattern recognition, and graph matching, i.e., identification of similarities between graphs, is an important tools in these areas. In these areas graph isomorphism problem is known as the exact graph matching.^[44]

In cheminformatics and in mathematical chemistry, graph isomorphism testing is used to identify a chemical compound within a chemical database.^[45] Also, in organic mathematical chemistry graph isomorphism testing is useful for generation of molecular graphs and for computer synthesis.

Chemical database search is an example of graphical data mining, where the graph canonization approach is often used.^[46] In particular, a number of identifiers for chemical substances, such as SMILES and InChI, designed to provide a standard and human-readable way to encode molecular information and to facilitate the search for such information in databases and on the web, use canonization step in their computation, which is essentially the canonization of the graph which represents the molecule.

In electronic design automation graph isomorphism is the basis of the Layout Versus Schematic (LVS) circuit design step, which is a verification whether the electric circuits represented by a circuit schematic and an integrated circuit layout are the same.^[47]

See also[edit]

• Graph automorphism problem
• Graph canonization

Notes[edit]

References[edit]

ПРАКТИЧЕСКАЯ РАБОТА №4

ОПРЕДЕЛЕНИЕ ИЗОМОРФНОСТИ ГРАФОВ

1. ОБЩИЕ СВЕДЕНИЯ

Отображение графов — это отображение
множеств вершин, которое сохраняет
отношение смежности и, таким образом,
индуцирует вполне определенное
отображение на множестве ребер.

Графы G1=(V1,E1) и G2=(V2,E2) называются изоморфными
(обозначение G1~G2), если между графами
существует взаимнооднозначное отображение
j: G1~G2 (V1~V2, E1~E2), которое сохраняет
соответствие между ребрами (дугами)
графов, т.е. для любого ребра (дуги)
e=(v,u) верно:

e’=j(v,u)=(j(v),j(u))
(e~E1, e’~E2) (1)

Отображение j называется изоморфным
отображением.

Дадим другое определение изоморфности:
два графа G1 и G2
называются изоморфными, если между их
вершинами установлено взаимнооднозначное
соответствие, такое, что любые две
вершины графа G1 соединены
так же, как и соответствующие вершины
графа G2

Рассмотрим графы 1 и 2

Рисунок 1 Изоморфные
графы

На рисунке 1 видно, что между графами
существует взаимнооднозначное
соответствие, то есть, например, ребро
(2,6) первого графа подобно ребру
(2,6) второго графа. Это можно наблюдать
для всех вершин и ребер.

    Иными словами, изоморфные
графы различаются только обозначением
вершин.

Условимся называть
(0,1)-матрицу булевой,
если с её элементами
мы намерены обращаться по правилам
булевой алгебры.

Изоморфизм графов можно
определить в матричных терминах.
Предварительно введём понятие
перестановочного подобия матриц.
Оно формулируется одинаково для булевых
матриц и матриц над полем.

Квадратная (0,1)-матрица P называется
перестановочной, если она имеет в
каждой строке и каждом столбце ровно
одну единицу. Легко проверить, что тогда

Матрицы A и B называются перестановочно
подобными, если

для некоторой перестановочной матрицы
P. Содержательный смысл этого определения
заключается в том, что A получается из
B одинаковыми перестановками строк и
столбцов.

Пусть графы с n вершинами, заданные
матрицами смежности A и B, изоморфны, то
есть существует такая биекция
(перестановка) σ на множестве {1,2, … , n},
что для любых ij

(2)

Сопоставим перестановке перестановочную
матрицу P = (p) порядка n, где

(3)

Прямыми вычислениями проверяется, что

(4)

Итак, если графы изоморфны, то их матрицы
смежности перестановочно подобны.
Наоборот, если матрицы смежности
перестановочно подобны, то графы
изоморфны, причем изоморфизм σ определяется
по матрице подобия P из равенств (3).

Вывод: графы изоморфны тогда и только
тогда, когда их матрицы смежности
перестановочно подобны.

В
соответствии с определением изоморфизма
графов у нас появляются варианты для
организации проверки изоморфизма
графов: либо мы для каждой пары графов
ищем свое взаимнооднозначное соответствие,
сохраняющее смежность; либо мы каждому
графу взаимнооднозначно сопоставляем
элемент некоторого одного и того же
множества, сохраняющий информацию о
смежности вершин графа, а затем ищем
взаимнооднозначное соответствие между
элементами этого множества. Понятно,
что в последнем случае нас также
интересует взаимнооднозначное
соответствие, которое сохраняло бы
информацию о смежности. В силу того, что
взаимнооднозначное соответствие,
сохраняющее смежность, рефлексивно,
симметрично и транзитивно, т.е. является
отношением эквивалентности, эти два
варианта организации проверки изоморфизма
графов равнозначны относительно
результата.

В
качестве упоминаемого выше множества,
элементам которого взаимнооднозначно
сопоставляются графы, можно взять
множество матриц смежности, поскольку
каждая матрица смежности несет в себе
информацию о смежности вершин графа.
Тогда в качестве соответствующего
взаимнооднозначного соответствия между
парами матриц смежности будет отношение
перестановочного подобия.

Для последующего рассмотрения алгоритма
определения изоморфности двух графов
дадим определение связных вершин и
подграфа.

Вершины в графе связаны,
если существует соединяющая их (простая)
цепь,
где цепь в графе — маршрут,
все рёбра которого различны. Если все
вершины
(а тем самым и рёбра) различны, то такая
цепь называется простой (элементарной).

Граф называется связным,
если любые две его
вер­шины связаны. Если граф не связен,
то он представляет собой объ­единение
нескольких связных подграфов.

Граф

называется подграфом
графа (V,E),
если
.
Например, цепь в графе
можно рассматривать как подграф. Говорят,
что подграф порождён
подмножеством вершин
если

состоит из рёбер,
соединяющих вершины из
.
Говорят, что подграф
порождён подмножеством
рёбер

если

состоит из концов рёбер из

.

Легко убедиться, что бинарное
отношение связанности на мно­жестве
вершин графа рефлексивно, симметрично
и транзитивно, то есть, связанность
вершин является отношением эквивалентности.

Замечание. Многие
практические задачи приводят к
необходимости распознавания изоморфизма
и изоморфного вложения сложных структур,
заданных в виде графов. С содержательной
точки зрения изоморфизм графов структур
означает тождественность функционирования
самих структур, что допускает в некоторых
случаях замену одной структуры другой,
ей изоморфной. Однако для того чтобы
выяснить, изоморфны ли два графа имеющие
 вершин,
в общем случае требуется выполнить
 попарных
сравнений, а для распознавания изоморфного
вложения графа
,
имеющего
 вершин,
в граф
,
у которого
 вершин,
необходимо провести
 сравнений.
Поэтому даже при относительно небольшом
количестве элементов в графах (порядка
100) решение задачи об изоморфизме методом
полного перебора практически не реально,
необходимо использовать для этой цели
специальные методы.

2. ЦЕЛЬ И ПОРЯДОК РАБОТЫ

Цель работы — научится определять
изоморфность двух графов.

Порядок работы:

• изучить описание работы;

• согласно своему варианту, решить
  заданные примеры без использования
  ЭВМ;

• написать и отладить программу в
  соответствии с заданием;

• оформить отчет.

3. ЗАДАНИЯ

3.1 Задания для ручного просчета:

Для данных графов выяснить, являются
ли они изоморфными. Если да, то установить
изоморфизм, в противном случае доказать,
почему графы неизоморфны.

Пример.

Даны два графа. Выяснить, являются ли
они изоморфными.

Покажем, что данные графы изоморфны.

Действительно,
отображение a e, b f, c g, d h, являющееся
изоморфизмом легко представить как
модификацию первого графа, передвигающую
вершину d в центр рисунка.

Составим матрицу смежности для первого
графа:

Составим матрицу смежности для второго
графа:

Так как соответствующие матрицы смежности
одинаковы, то графы 1 и 2 изоморфны.

Решите задание вашего варианта.

Вариант
1

Вариант 2

Вариант
3

Вариант 4

Вариант
5

Вариант
6

Вариант 7

Вариант
8

Вариант
9

Вариант 10

3.2 Задания для вычисления с помощью
программы:

Для заданных пользователем графов
определить изоморфность (результатом
программы является вывод «да-нет» в
зависимости от заданных графов)

4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Для проверки изоморфности графов можно
использовать следующий модуль (C#):

//проверка изоморфности подграфов

//int[, ,] X — матрица смежности подграфа

//int f1, int f2 — счетчики

//int k — кол-во вершин подграфа

//f1,f2 — номера
подграфов

bool izomorf(int[, ,] X, int f1, int f2, int k)

{

int i, j, f;

bool b;

int n = 1;

for (i = 1; i <= k; i++) n = n * i;

int[,] M = new int[n, k]; //массив перстановок
вершин,

perestan(M, k); //построение массива
перестановок вершин

//сравнение подграфов с перестановкой
строк и столбцов

for (f = 1; f < n; f++)

{

b = true;

for (i = 0; i < k; i++)

{

for (j = 0; j < k; j++)

if (X[f1, i, j] != X[f2, M[f, i], M[f, j]])

{

b = false; break;

}

if (!b) break;

}

if (b) return true;

}

return false;

}//izomorf

5. СОДЕРЖАНИЕ ОТЧЕТА

• наименование работы, постановку задачи;

• выбранный вариант задания;

• результаты решения задач без применения
  ЭВМ;

• программу решения задачи (представляется
  в электронном виде);

• результаты работы программы и их анализ.

6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие графы называются изоморфными?

2. Докажите, что графы на рис. 1 изоморфны
   (выпишите все соответствующие
   вершины и ребра).

3. Дайте определение булевой матрицы.

4. Объясните понятие перестановочного
   подобия матриц.

5. Известно, что если графы изоморфны, то
   их матрицы смежности перестановочно
   подобны. Верно ли это утверждение
   наоборот?

6. В каком случае вершины u
   и v связны?

7. Какой граф называется подграфом?

8. Среди данных графов выберете изоморфные
   и неизоморфные графы.

7. ОСНОВНАЯ ЛИТЕРАТУРА

1. Ф. А. Новиков, Дискретная математика
   для программистов: Учеб. пособие для
   ВУЗов по направлениям: «Информатика и
   вычислительная техника»/Ф. А. Новиков
   – 2-е изж. – М. Спб.: Питер, 2007 – 363 с.

2. А. И. Белоусов Дискретная математика:
   Учеб. пособие для втузов/Белоусов А.
   И., Ткачев С. Б., Под ред. Зарубина В. С.,
   Ирищенко А. П. – 3-е изд., стер. – М.: Изд-во
   МГТУ им. Баумана, 2004. – 743 с.

3. Оре, Ойстин Теория графов/ Пер. с
   англ. И. Н. Врублевской. Под редакцией
   Н. Н. Воробьева –2-е изд. Стереотипное.
   М.: Наука, 1980.-336с

4. Горбатов В. А. Дискретная математика:
   Учеб. для втузов В. А. Горбатов. – М.АСТ;
   Астель, 2003 – 447с (Высшая школа)

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. О.
П. Кузнецов «Дискретная математика
для инженера».
Издательство:
Лань,
2007 г., 400 стр.

2.Н.
И. Костюкова Графы и их применение.
Комбинаторные алгоритмы для программистов.

Издательства:
Интернет-университет
информационных технологий, Бином.
Лаборатория знаний, 2007 , 312 стр.

3. В.
Ф. Пономарев «Дискретная
математика для инженеров»
Издательство:
Горячая
Линия — Телеком, 2009 г. Мягкая
обложка, 320 стр.

4. Род
Хаггарти «Дискретная
математика для программистов. Discrete
Mathematics for
Computing».
Издательство:
Техносфера,
2005 г. Твердый переплет, 400 стр.

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #