Пример
1.
Найти
изображение единичной функции Хевисайда,
которая обозначается и определяется в
соответствии с равенством:
Решение.
Пользуясь определением изображения по
Лапласу, находим
.
Пример
2.
Найти изображение функции
Решение.
Имеем
.
Заметим,
что указанную функцию можно записать
короче, если использовать в качестве
множителя единичную функцию (t),
а именно:
.
Роль множителя
(t)
состоит в том, что он «гасит» (обращает
в нуль) функцию при t
< 0.
В дальнейшем, говоря о функциях-оригиналах,
будем считать, что все они снабжены
множителем (t),
хотя сам этот множитель в написании
часто будем опускать. Так, например, мы
будем писать tn,
eat,
sint
и т. д., подразумевая при этом соответственно
и т. д.
Единичная
функция играет важную роль в операционном
исчислении. Зная ее изображение и
используя правила операционного
исчисления, можно найти изображения
различных оригиналов. Например, используя
теорему смещения, можно записать: из
того, что
,
следует, что
,
и
не пользоваться определением преобразования
Лапласа, связанного с вычислением
несобственного интеграла.
Пример
3.
Найти изображения функций
и
.
Решение.
Воспользуемся формулами Эйлера:
;
.
Согласно
свойству линейности преобразования
Лапласа имеем
.
Следовательно,
.
Точно также
,
то есть
.
Применяя
к полученным соотношениям свойство
смещения, находим
,
.
Точно также для
гиперболических функций получаем
соответствия:
;
.
Пример
4.
Найти изображение функции
tn.
Решение.
Используем теорему дифференцирования
к изображению функции (t)
. Получим
;
.
.
Итак,
.
Пример
5.
Найти изображение функции
.
Решение.
На основании формулы
заменим
произведение
на
.
Тогда
.
Чтобы
найти изображение исходной функции,
воспользуемся тем, что операции умножения
на
в области оригиналов соответствует
операция смещения на 3 в области
изображений. Окончательно получим
.
Пример
6.
Найти изображение функции
.
Решение.
Воспользуемся соотношением
.
Далее,
согласно правилу (8), операции деления
на t
в области оригиналов соответствует
операция интегрирования в области
изображений.
Поэтому
.
Итак,
.
Пример
7.
Найти изображение функции
.
Решение.
Предварительно найдем изображение
функции
,
преобразовав ее по формуле
.
Имеем
.
Затем,
используя тот факт, что операции
интегрирования в области оригиналов
соответствует операция деления на р
в области изображений, окончательно
получим
.
Пример
8.
Найти изображение функции
Решение.
Воспользуемся равенством
.
Согласно теореме запаздывания имеем
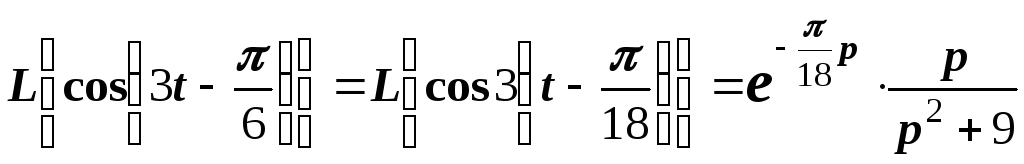
В
данном примере существенно равенство
нулю функции при
,
т.е. возможность представления функции
f(t)
в виде
,
а
соответственно, и возможность использования
теоремы запаздывания.
Иначе
поступаем, если функция задана следующим
соотношением:
В
этом случае осуществлен сдвиг вправо
на
графика функции
,
но не произведено «погашение» его нулем
на участке
.
Поэтому запаздывания оригинала по
времени не происходит, а функция
представима в виде
.
Для нахождения ее
изображения воспользуемся равенством
.
Применив теоремы
подобия и линейности, получим
.
Из
этого примера следует, что при записи
оригиналов, являющихся функциями
запаздывающего аргумента
,
опускать множитель
не рекомендуется во избежание
недоразумений. Так, например, для
обозначения оригиналов степенной
и
показательной
функций запаздывающего аргумента с
запаздыванием
следует пользоваться записью
,
,
а не записью
и
.
Последнюю
легко спутать с записью оригинала
незапаздывающего аргумента:
и
.
Пример
9.
Найти изображение функции
.
Решение.
Для того, чтобы применить теорему
запаздывания, предварительно преобразуем
оригинал как функцию аргумента
:
.
.
Заметим,
что изображение этого оригинала можно
найти согласно его определения:
.
Вычислив
интеграл, мы получим тот же результат.
Теорема
запаздывания является удобным способом
для нахождения изображений
кусочно-непрерывных функций.
Пример
10.
Найти изображение функции
Решение.
Пользуясь обобщенной единичной функцией,
оригинал f(t)
можно записать формулой
.
В
этом равенстве отражен тот факт, что
«сигнал» f1(t)=(t—a)
был «включен» в момент t=a
и
«выключен» в момент t=b.
После этого включен сигнал f2(t)=b—a.
Оригинал представим
в виде
.
При нахождении
его изображения исходим из соотношения
.
Используя теорему
запаздывания оригинала, получим
Пример
11.
Найти изображение функции
.
Решение.
Функция
есть свертка функций
и
.
Согласно теореме умножения свертке
двух функций соответствует произведение
их изображений. Если учесть, что
,
а
,
то
указанной свертке оригиналов будет
соответствовать изображение
.
Изображения
элементарных функций получаются путем
вычисления соответствующих несобственных
интегралов, иногда довольно сложных и
громоздких. Однако нет необходимости
проделывать все вычисления каждый раз
заново: достаточно составить таблицу
изображений и пользоваться ею подобно
тому, как мы пользуемся таблицей
производных или неопределенных
интегралов.
Приведем
таблицу изображений наиболее часто
встречающихся элементарных функций
(табл. 2).
Таблица
2 – Оригинал – изображение
|
№ |
Оригинал |
Изображение |
|
1 |
1 |
|
|
2 |
t |
|
|
3 |
tп |
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегральное преобразование Лапласа онлайн, калькулятор изображения функций.
Теория функций комплексного переменного.
: x^a
модуль x: abs(x)
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x]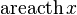 : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в
некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = int_0^infty f(t) e^{-pt}dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Полезная страница? Сохрани или расскажи друзьям
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
$$f(t)=frac{e^{2t}-e^{-3t}}{t}.$$
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^{-3tau}dtau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^{-px}dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
$$F(p)=frac{2p-1}{(p^2-4p+13)^2}.$$
Задача 6. Найти оригинал изображения
$$F(p)=frac{15p^2+3p+34}{(p^2+4p+8)(p^2-6p+5)}.$$
Задача 7. Найти оригинал для функции с помощью вычетов
$$F^*(p)=frac{1}{e^{4p}-625}.$$
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
$$x’+x=4e^t, x(0)=2.$$
Задача 9. Найти решение задачи Коши методами операционного исчисления
$$x»+2x’+2x=te^{-t}, quad x(0)=0, x'(0)=0.$$
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
$$x’=x-y,\
y’=x+y,\
x(0)=2, y(0)=1.$$
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
$$x»’+x»-2x’-5x=5e^t, quad x(0)=0, x'(0)=1, x»(0)=2.$$
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
$$frac{dx}{dt}=x-2y,\
frac{dy}{dt}=x+3y,\
x(0)=0, y(0)=1. $$
Задача 13. C помощью формулы Дюамеля найти решение уравнения
$$x»’+x’=tg t, quad x(0)=x'(0)=x»(0)=0.$$
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
$$
x’=-y+z,\
y’=z, quad x(0)=1, \
z’=-x+z;\
y(0)=z(0)=1/2.
$$
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$
Задача 16. Решить интегральное уравнение
$$ int_0^t ch (tau) x(t-tau)d tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Подробнее о решении заданий с преобразованием Лапласа
Дополнительная информация
- Онлайн-помощь по математическому анализу
- Дифференциальные уравнения — задачи с решениями
- Как решать ДУ с помощью операционного исчисления
Преобразование Лапласа и его свойства
Основные определения
1. Оригинал — это комплекснозначная функция действительного аргумента
, которая удовлетворяет следующим условиям:
а) при
;
б) на любом конечном отрезке функция
имеет не более чем конечное число точек разрыва первого рода;
в) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные
и
, что
при
.
Замечания 5.1
1. Величина называется показателем роста функции
. Для любой ограниченной функции, являющейся оригиналом, можно принять
.
2. Обозначим , если пределы существуют и конечны.
3. Совокупность всех оригиналов называется пространством оригиналов.
4. В точке разрыва первого рода функция имеет конечные односторонние пределы:
.
Пример 5.1
2. Изображение функции — функция
комплексного переменного
, определяемая равенством
(5.1)
Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции . Имеет место следующее утверждение.
Утверждение 5.1. Если функция , является оригиналом, то интеграл Лапласа сходится абсолютно в области
(рис. 5.1) , где
— показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве
, интеграл сходится равномерно и определяет аналитическую функцию
.
Замечания 5.2
1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.
2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.
3. Совокупность всех изображений называется пространством изображений.
4. Переход, определяющий изображение по оригиналу
, называется преобразованием Лапласа:
(5.2)
Запись означает, что оригиналу
соответствует изображение
.
5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения
(5.3)
где путь интегрирования — любая прямая , параллельная мнимой оси и лежащая правее прямой
(рис. 5.1).
Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.
Замечания 5.3
1. Для преобразования Лапласа используются различные обозначения, на пример и
, что означает: оригиналу
соответствует изображение
и изображению
соответствует оригинал
. В некоторых учебниках вместо аргумента
применяется
, то есть
и
.
2. Для компактной записи оригиналов используется единичная ступенчатая функция
(5.4)
где — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент
имеет смысл текущего времени, то
также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция
рассматривается как типовой входной сигнал.
При функция
является функцией Хевисайда:
(5.5)
Тогда, если функция удовлетворяет условиям «б», «в» в определении оригинала (п. 1), но не удовлетворяет условию «а», то функция
будет оригиналом, так как
Далее под заданной с помощью аналитической формулы функцией , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель
опускать.
3. Функции , являющиеся изображениями, удовлетворяют необходимому условию: если
есть изображение, то
при
. Поэтому функции
не являются изображениями. Однако в практических задачах функции типа
и другие встречаются. Это требует расширения понятий оригинала и изображения.
Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости . К числу таких обобщенных оригиналов относятся степенная функция
при
и некоторые другие.
4. Во всякой точке , являющейся точкой разрыва функции
, правая часть формулы (5.3) равна
.
Примеры 5.2-5.3
Пример 5.2. Найти изображение единичной функции Хевисайда .
Решение. Так как функция ограничена, то в качестве показателя роста можно положить
. По формуле (5.2) имеем
так как из равенства следует, что
при
.
Пример 5.3. Найти изображение функции , где
— действительное число.
Решение. Показателем роста можно считать . По формуле (5.2)
так как из равенства следует, что
при
.
Свойства преобразования Лапласа
Будем предполагать, что рассматриваемые далее функции являются оригиналами. Соответствующие им изображения (при
) обозначим
.
1. Линейность. Если — оригиналы, то для любых комплексных чисел
, функция
также является оригиналом и справедливо равенство
(5.6)
Заметим, что для функции существенно, что все слагаемыс являются оригиналами, так как, например, функция
является оригиналом, а слагаемые
и
не являются.
Справедливо и обратное утверждение: если — изображения, то
Здесь также важно, что слагаемые функции являются изображениями, поскольку из того, что
— изображение, не следует, что
— изображения. Например, функция
является изображением, а слагаемые
и
не являются.
Примеры 5.4-5.5
Пример 5.4. Найти изображение функции .
Решение. Из примера 5.2 имеем , а из примера 5.3 при
имеем
. Тогда согласно свойству линейности для оригинала
получаем
.
Пример 5.5. Найти изображение функции .
Решение. Используя формулу Эйлера (2.11), получаем .
Из примера 5.3 при и
следует:
. Тогда по свойству линейности
2. Подобие (теорема подобия). Для любого из
следует
(5.7)
и обратно: .
Пример 5.6
Найти изображение функции .
Решение. Из примера 5.5 следует, что . Тогда по теореме подобия
3. Смещение (теорема смещения). При любом комплексном из
следует
(5.8)
то есть умножению оригинала на соответствует смещение изображения на
.
Пример 5.7
Найти изображение функции .
Решение. Из примера 5.6 следует . Тогда по теореме смещения
.
Запаздывание оригинала
4. Запаздывание (теорема запаздывания). Для любого из
следует
(5.9)
где (рис. 5.3), т.е. запаздыванию оригинала на
соответствует умножение изображения на
.
Примеры 5.8-5.10
Пример 5.8. Найти изображение функции .
Решение. В примере 5.5 получено . По теореме запаздывания при
имеем
.
Пример 5.9. Найти оригиналы по изображениям: a) ; б)
.
а) Из примера 5.7 следует, что при изображению
соответствует оригинал
. Тогда по теореме запаздывания при
имеем
б) По формуле 3 из табл. 5.1 .По теореме запаздывания при
получаем
. Заметим, что для похожего, но отличного от полученного, оригинала
(его можно записать в виде
) изображение имеет вид
.
Пример 5.10. Найти изображение функции , график которой представлен на рис. 5.4.
С учетом (5.4) представим функцию в виде
.
Из примера 5.2 имеем . Применяя свойства линейности и запаздывания, получаем
Заметим, что, находя предел при в последнем выражении, можно получить изображение δ-функции
Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.
Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением
(5.10)
Дифференцирование оригинала
5. Если функции являются оригиналами и
, то
(5.11)
где .
Примеры 5.11-5.12
Пример 5.11. Найти изображение , если
.
Решение. Из примера 5.7 следует, что при имеем
.
Найдем . Согласно (5.11)
.
Пример 5.12. Найти изображение выражения с начальными условиями
.
Решение. Пусть , тогда
. В примере 5.2 получено
. Используя свойство линейности, имеем
Интегрирование оригинала
Если функция является оригиналом и
, то
(5.12)
т.е. интегрированию оригинала соответствует деление изображения на .
Пример 5.13
Найти изображение интеграла от функции
.
Решение. Из примера 5.6 следует, что . Тогда
, то есть
.
Дифференцирование изображения
Если функция является оригиналом и
. то
(5.13)
Примеры 5.14-5.15
Интегрирование изображения
Если функция является оригиналом, то из
следует
(5.14)
Пример 5.16
Найти изображение функции .
Решение. Функция является оригиналом, так как
(условие «в») и точка
является точкой разрыва первого рода (условие «б»). Из примера 5.13 следует
.
Отсюда .
Умножение изображений (теорема Бореля)
Из и
следует
(5.15)
т.е. свертке оригиналов соответствует произведение изображений. Функция определяется формулой
(5.16)
и называется сверткой оригиналов и
.
Пример 5.17
Найти оригинал, соответствующий изображению .
Решение. Представим в виде произведения изображений:
.
Из примеров 5.6 и 5.13 следует .
Согласно (5.15),(5.16) получаем искомый оригинал:
Дифференцирование свертки (интеграл Дюамеля)
10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:
С другой стороны,
или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем
Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид
Объединяя полученные результаты, можно записать:
(5.17)
Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.
Пример 5.18
Найти оригиналы, соответствующие изображениям: a) ; б)
.
Решение. а) Заметим, что здесь нельзя непосредственно воспользоваться теоре мой Бореля, так как в произведении множитель
не является изображением (не выполняется необходимое условие).
Представим изображение в виде произведения . Из примера 5.3 вытекает
Тогда по формуле (5.17) имеем
Можно решить этот пример с помощью теоремы Бореля, представив изображение в виде
Тогда, используя свойство линейности и теорему Бореля, получаем
б) Представим изображение в виде произведения:
Из примера 5.6 при и
следует
Тогда по формуле (5.17) получаем
Теорема о связи «начальных» и «конечных» значений оригинала и изображения
Начальное значение оригинала находится по формуле
(5.18)
Если существует конечный предел , то
(5.19)
Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.
Пример 5.19
Найти начальное и конечное значения оригинала, которому соответствует изображение .
Решение. Согласно (5.18) и (5.19) имеем
С другой стороны, из примера 5.7 следует, что
поэтому легко убедиться в правильности полученного результата.
Полученные решения примеров 5.2–5.17 позволяют сформировать таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц, используемых далее при решении примеров и задач.
Нахождение изображения по оригиналу
Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.
Таблица 5.1. Таблица основных преобразований Лапласа
Посмотреть
Пример 5.21
Найти изображения функций:
a) ; б)
;
в) ; г)
;
д) ; е)
;
ж) ; з)
.
Решение
а) Согласно формуле 12 из табл. 5.1 . По свойству дифференцирования изображения (формула (5.13) при
):
или
.
Поэтому .
Можно решать иначе, используя формулу 10 из табл. 5.1 при а = 3 и свойство смещения при
и
.
б) Применим свойства линейности и интегрирования изображения. Так как в силу формул 1 и 9 из табл. 5.1 , то согласно (5.14)
в) По формуле 9 из табл. 5.1 . Функцию fit) можно записать, используя единичную ступенчатую функцию:
. Поэтому для нахождения изображения следует применить теорему запаздывания (5.9) к оригиналу
при
г) Согласно теореме смещения (5.8) и с учетом результата п. «в» имеем
, так как
.
д) По теореме запаздывания (5.9) при и по формуле 7 из табл. 5.1 при
получаем
е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл. 5.1, получаем
ж) По формуле 19 из табл. 5.1 находим . По свойству интегрирования изображения (формула (5.14)):
По свойству интегрирования оригинала (5.12): .
з) Используем формулу косинуса разности и запишем оригинал в виде суммы:
По свойству линейности получаем:
Заметим, что здесь и результаты пп. «в» и «з» различны так как оригиналами являются разные функции.
Нахождение изображений функций, заданных графиком
При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.
Пример 5.22
Найти изображения функций, заданных графиками на рис. 5.5.
Решение.
а) Представим функцию в виде .
По формуле 3 из табл.5.1 и теореме запаздывания (формула (5.9) при )
б) Запишем функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
в) Запишем изображенную функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
г) Представим функцию в виде
По формулам 3 из табл. 5.1 и (5.6), (5.9) имеем .
д) Запишем функцию в форме
По формулам З из табл. 5.1 и (5.6), (5.9) .
е) Представим изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) .
ж) Запишем функцию в форме .
По формуле 8 из табл. 5.1 и по теореме запаздывания .
з) Представим функцию в виде .
По формуле 6 из табл. 5.1 при и (5.9) при
имеем
и) Представим функцию в виде .
Используя формулы 2 из табл. 5.1 и (5.6), (5.9), получаем .
Нахождение изображений периодических функций
Во многих приложениях используются оригиналы, являющиеся периодическими функциями.
Пусть — оригинал с периодом
(рис. 5.6,в), образованный повторением функции
(рис. 5.6,б):
Для нахождения изображения периодической функции
следует:
1. Найти изображение функции .
2. Найти изображение по формуле
(5.20)
Пример 5.23.
Найти изображения функций, представленных на рис. 5.7.
Решение
а) По графику (рис. 5.7,в) получаем
Поэтому .
Поскольку , по формуле (5.20) находим
б) По графику (рис. 5.7,б) имеем , тогда
. По формуле (5.20) при
имеем
в) Функция, изображенная на рис. 5.7,в , имеет период . Запишем аналитическое выражение для
и соответствующее изображение
По формуле (5.20) получаем .
г) Для функции, изображенной на рис. 5.7,г, изображением для является
(см. пример 5.22 п.»ж»). Тогда по формуле (5.20) при
получаем
.
Нахождение оригинала по изображению
Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.
Применение теорем разложения
Теорема 5.1 (первая теорема разложения). Если функция аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням
имеет вид
, то функция (5.21) является оригиналом, соответствующим изображению
.
(5.21)
Теорема 5.2 (вторая теорема разложения). Если изображение является однозначной функцией и имеет лишь конечное число особых точек
лежащих в конечной части плоскости, то
(5.22)
Замечания 5.5
1. Формула (5.21) может быть записана в виде . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.
2. Формула (5.22) принимает наиболее простой вид в случае — рационального изображения, т.е.
, где
— многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы
функции
простые, то по формуле (4.24) получаем
, а формула (5.22) принимает вид
(5.23)
3. Если при выполнении условий п.2 коэффициенты многочлена — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке
, используя свойства сопряженных чисел, можно записать следующим образом:
Это означает, что вычет в точке есть число, сопряженное вычету в точке
, а сумма таких чисел равна их удвоенной действительной части:
Пример 5.24
Найти оригиналы для функций:
a) ;
б) .
Решение. В случае «а» для решения задачи используем теорему 5.1, а в случае «б» — теорему 5.2.
а) Используем типовые разложения
Для заданных изображений получаем:
Согласно первой теореме разложения
б) Представим в виде
где — простые полюсы функции
. По второй теореме разложения
Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:
Функция имеет четыре простых полюса:
.
Так как вычет в простом полюсе находится по формуле , то по второй теореме разложения
Функция имеет два полюса: простой
и полюс второго порядка
.
По второй теореме разложения . Находим вычеты
получаем окончательный ответ .
Применение таблицы и свойств преобразования Лапласа
Приведем ряд известных приемов нахождения оригинала.
1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.
Пример 5.25
2. Изображение, заданное в виде дроби , разлагается на сумму дробей.
Пример 5.26
Найти оригинал для функций: а) ; б)
; в)
.
Решение. Представим дроби в виде суммы двух слагаемых, а затем воспользуемся свойством линейности и формулами из табл. 5.1:
а) ;
б) .
в) представим в виде
. По формулам 4,6 из табл. 5.1 находим
.
3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: . При этом числитель дроби представляется в виде многочлена от
.
Пример 5.27
Найти оригиналы для функций: a) ; б)
.
Решение. а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл. 5.1 (по формуле 12 из табл. 5.1 при ):
б) Используем представление
По формулам 19,20 из табл. 5.1 и по теореме смещения (формула (5.8))
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.
Примеры 5.28-5.29
Пример 5.28. Найти оригиналы для функций:
а) ; б)
; в)
; г)
.
Решение. а) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда следует равенство .
Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений для нахождения неопределенных коэффициентов:
Решая ее, получаем
и
По формулам 1,12,13 из табл. 5.1 .
б) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда .
Подставляя последовательно , получаем
и поэтому
По формулам 6,7 из табл. 5.1 находим .
в) Представим изображение в виде . Отсюда
При получаем
, поэтому
По свойству линейности и по формуле 6 из табл. 5.1 получаем
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
г) Представим в виде
, где
— неопределенные коэффициенты.
Из равенства при
получаем
, поэтому
.
По формуле 6 из табл. 5.1 имеем .
Можно также решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24 и п. «в» данного примера):
Пример 5.29. Найти оригиналы для функций: a) ; б)
.
Решение. а) Решим пример различными способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формулам 2,3,6,7 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения, учитывая, что и
— полюсы второго порядка функции
Третий способ. Обозначим . Тогда
. Рассмотрим функцию
. По свойству интегрирования оригинала (формула (5.12)) получаем
Заметим, что . Применяя еще раз свойство интегрирования оригинала, имеем
Четвертый способ. Представим изображение в виде произведения
, где
.
По формулам 3 и 7 из табл. 5.1 . Далее по теореме Бореля (формула (5.15))
б) Решим пример также несколькими способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формуле 9 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 замечаний 5.5:
Третий способ. Представим изображение в виде произведения:
Отсюда . По теореме Бореля
Четвертый способ. Используем формулу 37 из табл. 5.1. При получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
По этой ссылке вы найдёте полный курс лекций по математике:
рассмотрели интегральное преобразование Фурье с ядром K(t, О = е Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t, Преобразование Лапласа позволяет освободиться от этого ограничения. Определение 1. Функцией-оригиналом будем называтьвсякую комплекснозначную функцию f(t) действитсл ьного аргумента t, удовлетворя юшую следующим условиям:
1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем накаждом конечном интервалеоси *такихточек можетбыть лишь конечное число; 2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при 3. при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и s такие, что для всех t Ясно, что если неравенство (1) выполняется при некотором s = aj, то оно будет ВЫПОЛНЯТЬСЯ и при ВСЯКОМ 82 > 8].
Точная нижняя грань s0 всех чисел з, «о = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t). Замечание. В общем случае неравенство не имеет места, но справедлива оценка где е > 0 — любое. Так, функция имеет показатель роста в0 = Для нее неравенство t ^ М V* ^ 0 не выполняется, но верно неравенство |f| ^ Меи. Условие (1) гораздо менее ограничительное, чем условие (*). Пример 1. функция не удовлетворяет условию (»), но условие (1) выполнено при любом s ^ I и А/ ^ I; показатель роста 5о = • •
Так что является функцией-оригиналом. С другой стороны, функция не является функцией-оригиналом: она имеет бесконечный порядок роста, «о = +оо. Простейшей функцией-оригиналом является так называемая единичная функция Если некоторая функция удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение уже является функцией-оригиналом.
Для простоты записи мы будем, как правило, множитель rj(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t), например, о sin ty cos t, el и т. д., то всегда подразумеваются следующие функции (рис. 2): п=п(0 Рис. 1 Определение 2. Пусть f{t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного , определяемая формулой ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения
Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции /(/); ядро преобразования K(t} р) = e~pt. Тот факт, что функция имеет своим изображением F(p), будем записывать Пример 2. Найти изображение единичной функции r)(t).
Возможно вам будут полезны данные страницы:
Функция является функцией-оригиналом с показателем роста в0 — 0. В силу формулы (2) изображением функции rj(t) будет функция Если то при интеграл в правой части последнего равенства будет сходящимся, и мы получим так что изображением функции rj(t) будет функция £. Как мы условились, будем писать, что rj(t) = 1, и тогда полученный результат запишется так: Теорема 1. Лгя всякой функции-оригинала f(t) с показателем роста з0 изображение F(p) определено в полуплоскости R ер = s > s0 и является в этой полуплоскости аналитической функцией (рис. 3).
Пусть Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при a > Используя (3), получаем что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Дифференцируя выражение (2) формально под знаком интеграла по р, находим Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).
Применяя для F'(p) интегрирование по частям, получаем оценку откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое ,0.,— при t +оо имеет предел, равный нулю). В любой полуплоскости Rep ^ sj > «о интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо. Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Rep = 5 > 5о является аналитической функцией. Из неравенства (4) вытекает Следствие.
Если тонка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то Пример 3. Найдем еще изображение функции любое комплексное число. Показатель росга «о функции /(() равен а. 4 Считая Rep = я > а, получим Таким образом, При а = 0 вновь получаем формулу Обратим внимание на то, что изображение функции eat является аналитической функцией ар1умента р не только в полуплоскости Rep > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс.
В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Rep > «о функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Rep = so, или на самой этой прямой. Замечай не. В операционном исчислении иногда пользуются изображением функции /(f) по Хевисайду, определяемым равенством и отличающимся от мображения по Лапласу множителем р. §2.
Свойства преобразования Лапласа В дальнейшем через будем обозначать функции-оригиналы, а через — их изображения по Лапласу, Из определения изображения следует, что если Теорема 2 (единстве* мости ). £biw dee непрерывные функции ) имеют одно и тоже изображение , то они тождественно равны. Teopewa 3 (п«иейиост* преобраэдоияя Лапласа). Если функции-оригиналы, то для любых комплексных постоянных аир Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение: , — показатели роста функций соответственно).
На основании этогосвойства получаем Аналогично находим, что и, далее, Теорема 4 (подобия). Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > О Полагая at = т, имеем Пользуясь этой теоремой, из формул (5) и (6) получаем Теорема 5 (о дифференцировании оригинала). Пусть является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, а где — показатель роста функции Тогда и вообще Здесь под понимается правое предельное значение Пусть .
Найдем изображение Имеем Интегрируя по частям, получаем Внеинтегральное слагаемое в правой части (10) обращается в нуль при к. при Rc р = s > з имеем подстановка t = Одает -/(0). Второе слагаемое справа в (10) равно pF{p). Таким образом, соотношение (10) принимает вид и формула (8) доказана. В частности, если Для отыскания изображения f(nt) запишем откуда, интегрируя п раз по частям, получи м Пример 4. Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin2 t.
Пусть Следовательно, Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р. Формула включения. Если являются функциями-оригиналами, то В самом деле, В силу следствия из теоремы 1, всякое изображение стремится к нулю при . Значит, , откуда вытекает формула включения ( Теорема 6 (о дифференцировании изображения).
Дифференцирование изображения сводится к умножению на оригинала, Так как функция F(p) в полуплоскости so является аналитической, то ее можно дифференцировать по р. Имеем Последнее как раз и означает, что Пример 5. Пользуясь теоремой 6, найти изображение функции 4 Как известно, Отсюда ( Вновь применяя теорему 6, найдем , вообще Теорема 7 (интегрирование оригинала). Интегрирование оригинала сводится к делению изображения на Положим Нетрудно проверить, что если есть функция-оригинал, то и будет функцией-оригиналом, причем .
Пусть . В силу так что С другой стороны, , откуда F= Последнее равносильно доказываемому соотношению (13). Пример 6. Найти изображение функции M В данном случае , так что . Поэтому Теорема 8 (интегрирование изображения). Если и интеграл сходится, то он служит изображением функции ^:
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений Действительно, Предполагая, что путь интегрирования лежите полуплоскости so, мы можем изменить порядок интегрирования Последнее равенство означает, что является изображением функции Пример 7. Найти изображение функции М Как известно, .
Поэтому Так как Положим получаем £ = 0, при. Поэтому соотношение (16) принимает вид Примере. Найти изображение функции f(t), заданной графически (рис.5). Запишем выражение для функции f(t) в следующем виде: Это выражение можно получить так. Рассмотрим функцию и вычтем из нее функцию Разность будет равна единице для . К полученной разности прибавим функцию В результате получим функцию f(t) (рис. 6 в), так что Отсюда, пользуясь теоремой запаздывания, найдем Теорема 10 (смещения). то для любого комплексного числа ро.
В самом деле, Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию , например, 2.1.
Свертка функций. Теорема умножения Пусть функции /(£) и определены и непрерывны для всех t. Сверткой этих функций называется новая функция от t, определяемая равенством (если этот интеграл существует). Для функций-оригиналов операция свертим всегда выполнима, причем (17) 4 В самом деле, произведение функций-оригиналов как функция от т, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка .
Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу Нетрудно проверить, что операциясвертки коммутативна, Теорема 11 (умножения). Если , то свертка t) имеет изображение Нетрудно проверить, что свертка ( функций-оригиналов есть функция-оригинал с показателем роста » где , — показатели роста функций соответственно. Найдем изображение свертки, Воспользовавшись тем, что будем иметь Меняя порядок интегрирования в интеграле справа ( такая операция законна) и применяя теорему запаздывания, получим.
Таким образом, из (18) и (19) находим — умножению изображений отвечает свертывание оригиналов, Пртер 9. Найти изображение функции А функция V(0 ость свортка функций . В силу теоремы умножения Задача. Пусть функция /(£), пориодическая с периодом Т, есгъ функция-оригинал. Показать, что ее изображение по Лапласу F(p) дается формулой 3. Отыскание оригинала по изображению Задача ставится так: дана функция F(p), надо найти функцию /(<)> изображением которой является F(p). Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.
Теорема 12. Если аналитическая в полуплоскости so функция F(p) 1) стремится к нулю при в любой полуплоскости R s0 равномерно относительно arg р; 2) интеграл сходится абсолютно, то F(p) является изображением некоторой функции-оригинала Задача. Может ли функция F(p) = служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению. 3.1. Отыскание оригинала с помощью таблиц изображений Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду.
Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа. Пример 1. Найти оригинал для Запишем функцию F{p) в виде Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем Пример 2. Найти оригинал для функции 4 Запишем F(p) в виде Отсюда 3.2.
Использование теоремы обращения и следствий из нее Теорема 13 (обращения). Если функция fit) есть функция-оригинал с показателем роста s0 и F(p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение где интеграл берется вдоль любой прямой и понимается в смысле главного значения, т. е. как Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина.
В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а) функция-оригинал-с показателем роста s0. Рассмотрим функцию любое. Функция удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье, Подставляя в (3) выражение найдем где F(p) — преобразование Лапласа функции f(t) при р = 8 + Формулу (2) можно переписать в виде откуда получаем формулу обращения преобразования Лапласа Как следствие из теоремы обращения получаем теорему единственности.
Теорема 14. Две непрерывные функции , имеющие одно и то же изображение F(p), тождественны. Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p). Теорема 15. Пусть изображение F(p) — дробно-рациональная функция с пмюсами Рп-
Тогда оригиналом для F(p) будет функция , где Пусть изображение F(p) — дробно-рациональная функция, многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т.к. для всякого изображения должно выполняться предельное соотношение Пусть корни знаменателя В(р), являющиеся полюсами изображения а их кратности равны тп соответственно.
Если число 5, фигурирующее в формуле (1), взять большим всех то по формуле обращения, которая в этих условиях применима, получим Рассмотрим замкнутый контур Гд (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = з), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри Гл. По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь Второе слагаемое слева в равенстве (5) стремится к нулю при R оо.
Это следует из леммы Жордана
если в ней заменить р на iz и учесть, что F(p) 0 при Rep +оо. Переходя в равенстве (5) к пределу при R-* оо, мы получим слева а справа,— сумму вычетов по всем полюсам функции F(p) ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений Замечание.
Воспользовавшись формулой для вычисления вычетов, найдем, что Если все полюсы р, рз,…, рп — просгые, то и формула (6) принимает вид Пример 3. Найти оригинал для функции Теорема 16. Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = оо, причем ее раз,южение в окрестности > R бесконечно удаленной точки имеет вид Тогда оригиначом для F{p) будет функция , где § 4. Приложения преобразования Лапласа (операционного исчисления) 4.1.
Решение линейных дифференциальных уравнений с постоянными коэффициентами Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами действительные числа) и требуется найти решение x(t) уравнения (1) для t > 0, удовлетворяющее начальным условиям Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть По теореме о дифференцировании оригинала имеем ,.
Перейдем в уравнении (1) от оригиналов к изображениям. Имеем Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) — Оригинал для Х(р) будет искомым решением x(t) задачи (1)-(2). Обший случай линейного дифференциального уравнения n-го порядка (n ^ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.
Приведем общую схему решения задачи Коши Х(р) = Задача Коши в пространстве оригиналов IV I Решение задачи Коши Т-Г’ Операторное уравнение в пространстве изображений Решение операторного уравнения III II Здесь Л означает применение к 1 преобразование Лапласа, JT1 — применение к III обратного преобразования Лапласа. Пример 1. Решить задачу Коши I. Операторное уравнение откуда По теореме о дифференцировании изображения Поэтому Формула Дюамеля В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.
Пусть — функции-оригиналы, причем функция f(t) непрерывна на непрерывно дифференцируема на Тогда если ,то потеоремеумножения получаем, что Нетрудно проверить, что функция ip(t) непрерывно дифференцируема на причем Отсюда, в силу правила дифференцирования оригиналов, учитывая, что , получаем формулу Дюамеля (4) Покажем применение этой формулы. Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ^ 1) с постоянными коэффициентами при нулевых начальных условиях (последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).
Если известно решение Х (t) дифференциального уравнения с той же левой частью и правой частью, равной единице, при нулевых начальных условиях то формула Дюамеля (4) позволяет сразу получить решение исходной задачи В самом деле, операторные уравнения, отвечающие задачам ), имеют соответственно вид и где F(p) — изображение функции ) легко находим Отсюда по формуле Дюамеля t или, поскольку Пример 2.
Решить задачу Коши Рассмотрим вспомогательную задачу Применяя операционный метод, находим По формуле (П) получаем решение x(t) исходной задачи: ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений 4.2.
Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы.
Оригинал для него будет решением исходной системы дифференциальных уравнений. Пример 3. Найти решение линейной системы удовлетворяющее начальным условиям 4 Пусть Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе Решение исходной задачи Коши 4.3. Решение интегральных уравнений Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла.
Мы рассмотрим лишь уравнение вида (12) называемое линейным интегральным уравнением Вольтерра второго рода с ядром зависящим от разности аргументов (уравнение типа свертки). Здесь — искомая фуннция, — заданные функции. Пусть f(t) и K(t) есть функции-оригиналы, . Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим Решая последнюю относительно, получаем Оригинал для Ф(р) будет решением интегрального уравнения (12).
Пример 4. Решить интегральное уравнение 4 Применяя преобразование Лапласа к обеим частям (14), получим Функция является решением уравнения (14) (подстановка уравнение (14) обращает поело дне© в тождество Замечание. Преобразование Лапласа может быть использовано также при решении некоторьж задач для уравнений математической физики. Функция-оригинал Преобразование Лапласа Упражнения Установите, каше из указанных функций являются функциями-оригиналами:
Пользуясь свойствами преобразования Лапласа, найдите изображения следующих функций: Найдите изображение следующих функций, заданных графически: Найдите оригиналы по заданному изображению: Решите задачу Коши для следующих дифференциальных уравнений: Решите задачу Коши доя следующих систем дифференциальных уравнений: Решите интегральные уравнения:

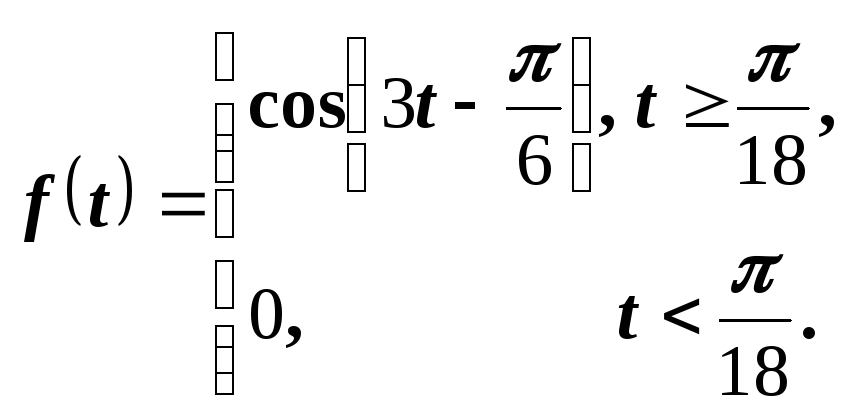
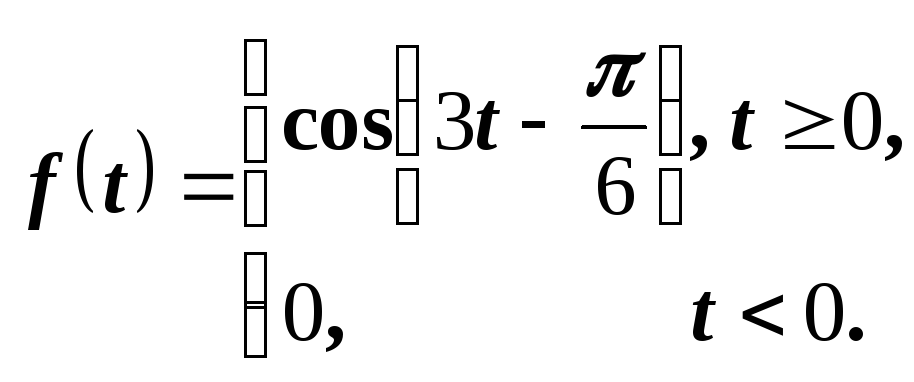
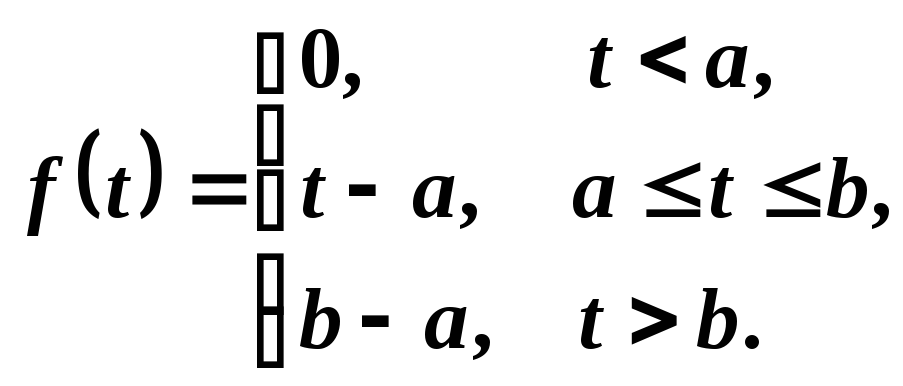
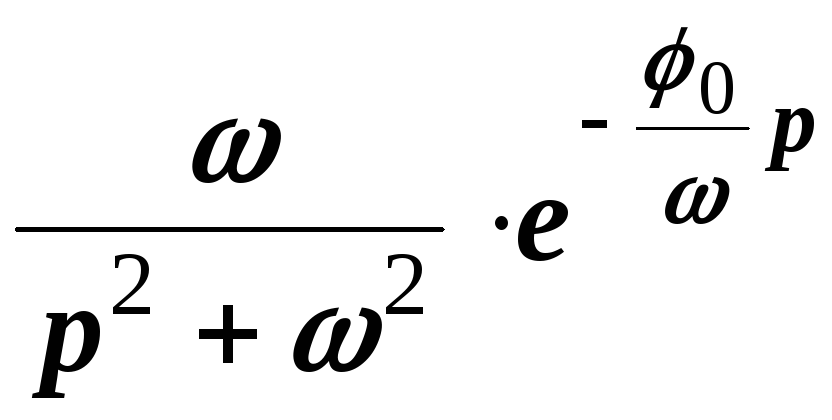
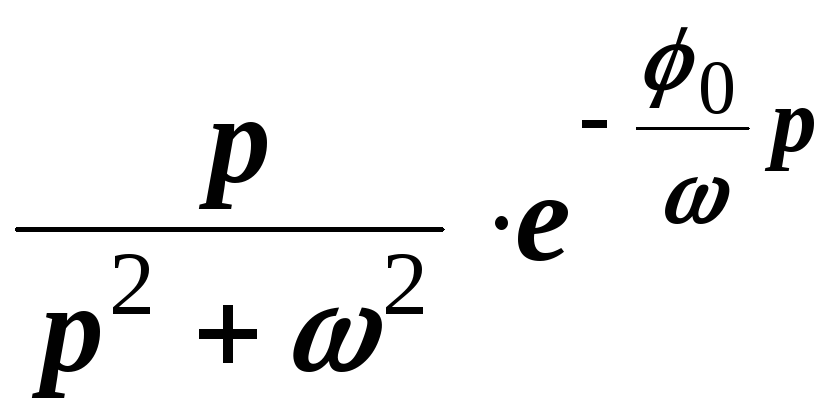
 : x^a
: x^a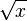 : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x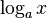 : Log[a, x]
: Log[a, x]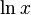 : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]




















