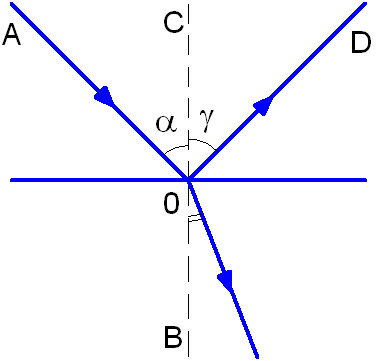
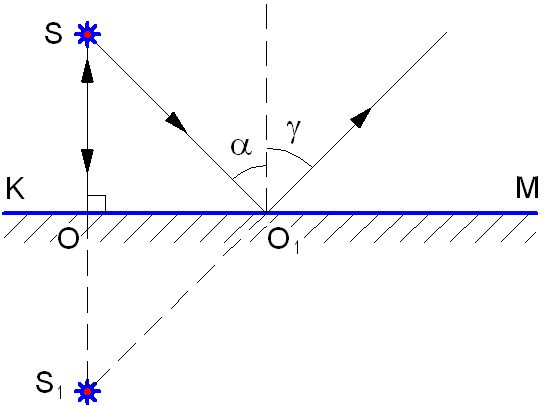
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.
Рис. 1.3. Отражение и преломление света.
Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.
Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.
Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.
Законы отражения света
| 1 | Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. |
| 2 | Угол отражения γ равен углу падения α:
γ = α |
Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.
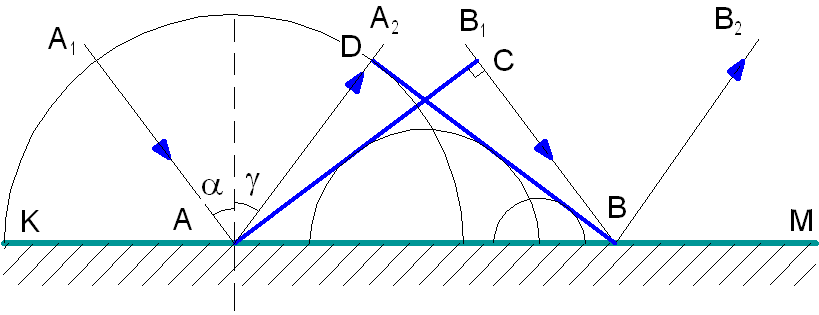
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.
Рис. 1.4. Построение Гюйгенса.
А1А и В1В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).
Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.
Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА2 и ВВ2.
Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.
Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ.
Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.
Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.
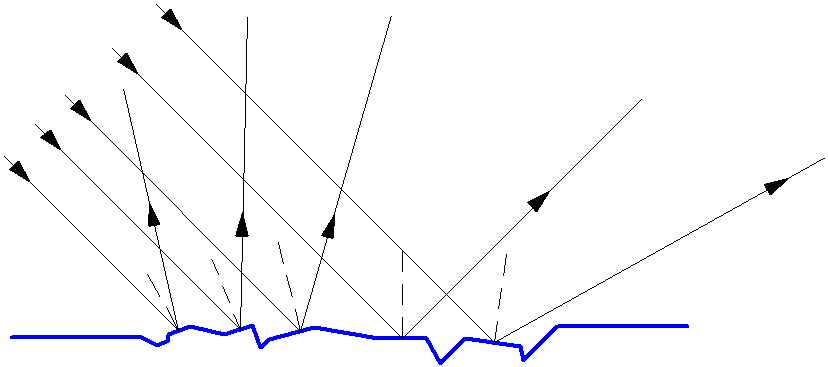
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.
Рис. 1.5. Диффузное отражение света.
Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.
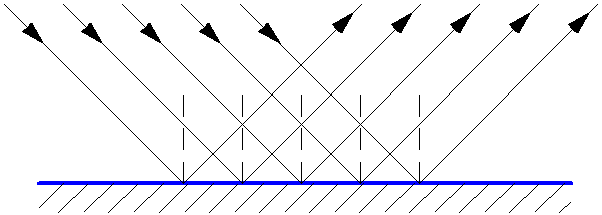
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.
Рис. 1.6. Зеркальное отражение света.
Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.
Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.
Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.
Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO1.
Луч SO1 падает на зеркало под углом α и отражается под углом γ (α = γ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S1, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S1, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S1расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.
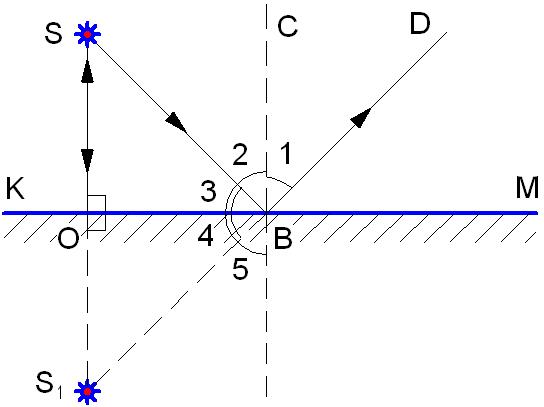
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.
Рис. 1.8. Отражение от плоского зеркала.
Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.
Прямоугольные треугольники ΔSOB и ΔS1OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS1, то есть точка S1 расположена симметрично точке S относительно зеркала.
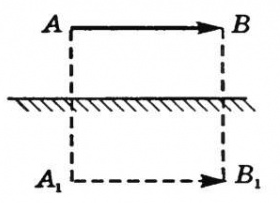
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.
Рис. 1.9. Изображение предмета в плоском зеркале.
В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
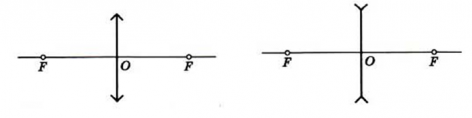
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
Построение изображения в собирающей линзе
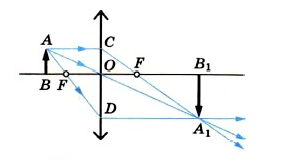
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
 |
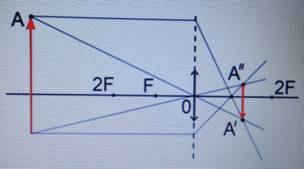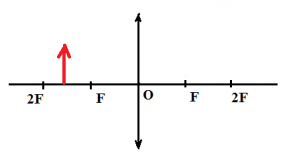
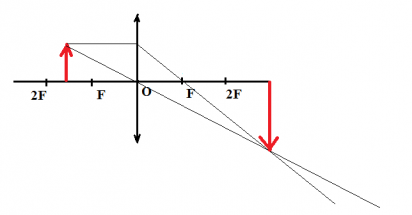
Предмет располагается за двойным фокусом.
Изображение:
|
 |
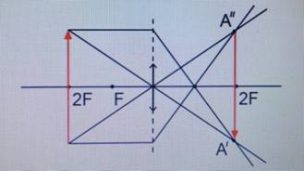Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
 |
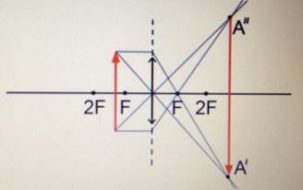Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
 |
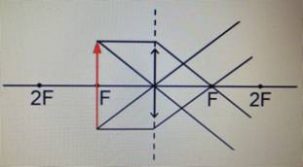Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
 |
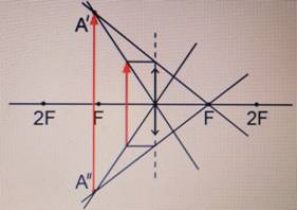Предмет располагается между линзой и фокусом.
Изображение:
|
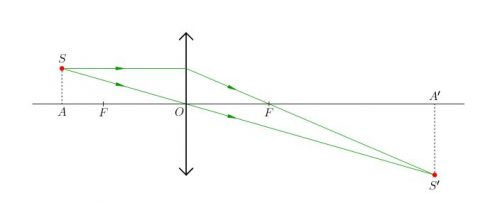
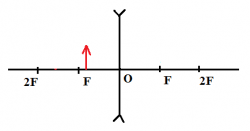
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
Частный случай — построение изображения точки
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
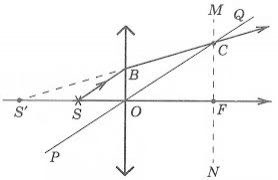
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
Построение изображения в рассеивающей линзе
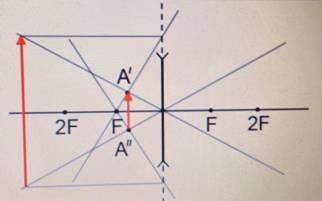
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
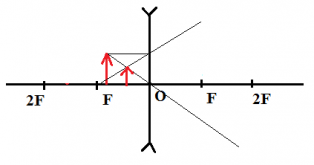
Пример №3. Построить изображение предмета в рассеивающей линзе.
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
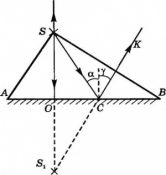
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
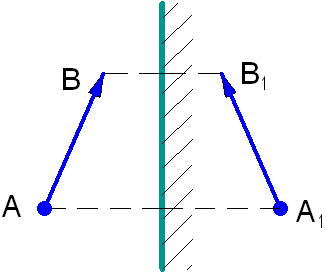
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Изображение и сам предмет всегда симметричны относительно зеркала.
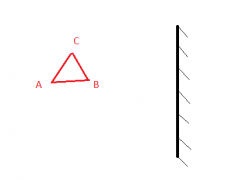
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
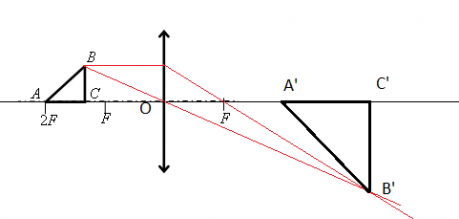
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
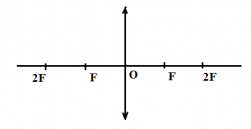
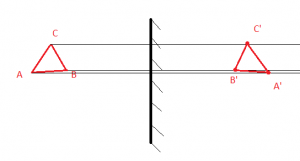
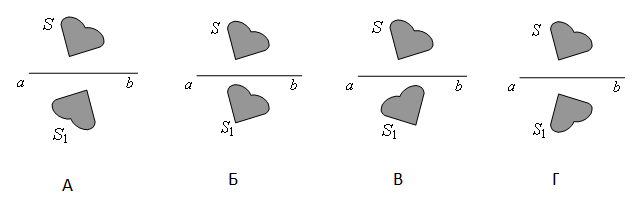
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18876
Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?
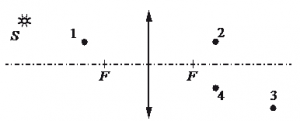
Алгоритм решения
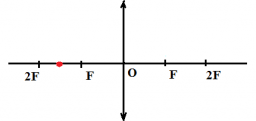
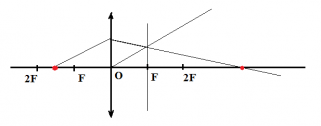
1.Построить изображение точки.
Решение
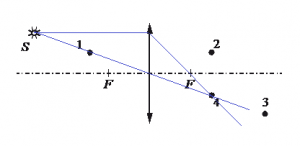
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 32.5k
В уроках «Изображение светящейся точки, даваемое линзой» и «Изображение предмета, даваемое линзой», мы уже рассматривали построение различных изображений. Также в этих уроках находятся памятки для построения изображения точки или предмета, которые могут вам пригодиться.
В данном уроке представлены дополнительные интересные задачи на построение изображений. И, конечно, вы можете ознакомиться с их решением, разбором построения и итоговым чертежом.
Задача №1
На рисунке 1 показан ход светового луча, падающего на рассеивающую линзу. Выполнив необходимые построения, найдите положения фокусов линзы и положение изображения светящейся точки $S$.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Если луч падает параллельно оптической оси на рассеивающую линзу и преломляется, то продолжение этого преломленного луча пересечет оптическую ось в мнимом фокусе рассеивающей линзы.
Поэтому мы продолжим преломленный луч (отмечен синим цветом) до пересечения с оптической осью. Точка пересечения — это мнимый фокус $F$. Отметим его на чертеже (рисунок 2, а).
С другой стороны от линзы отмерим точно такое же фокусное расстояние и отметим второй фокус линзы.
Теперь нужно построить изображение светящейся точки (рисунок 2, б). Один преломленный луч у нас на чертеже уже есть (использовать мы будем его продолжение). Значит, нужно провести второй луч.
Выберем и проведем на чертеже луч, проходящий через оптический центр линзы $O$. После прохождения через линзу он не изменит направления своего распространения. Поэтому его продолжение совпадет с падающим лучом $SO$.
В итоге, на пересечении двух продолжений преломленных лучей мы получаем мнимое изображение светящейся точки $S_1$.
Задача №2
На рисунке 3 изображены положения главной оптической оси линзы, источника света $S$ и его изображения $S_1$. С помощью этих данных постройте оптический центр, отметьте на чертеже саму линзу и ее фокусы.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
В этой задаче у нас уже есть изображение светящейся точки. Обычно, когда мы занимаемся его построением, мы используем два световых луча. Один из них — это луч, проходящий через оптический центр $O$, который лежит на оптической оси линзы. После прохождения через линзу (ее оптический центр) он не изменяет своего направления.
А изображение $S_1$ лежит на пересечении этого луча с другим. Значит, мы можем соединить точки $S$ и $S_1$ друг с другом (рисунок 4, а).
Полученная прямая $SS_1$ пересекает оптическую ось в точке — это и есть оптический центр $O$. Отметим его на рисунке.
Зная положение оптического центра, мы можем отметить на чертеже и саму линзу. Какая это будет линза: собирающая или рассеивающая? Изображение $S_1$ является действительным, так как оно находится по другую сторону от линзы и явно будет на пересечении двух преломленных лучей. Действительное изображение мы можем получить только с помощью собирающей линзы (рисунок 4, б).
Теперь у нас на чертеже есть: оптическая линза, оптическая ось, оптический центр $O$, точка $S$, ее изображение $S_1$, падающий луч $SO$ и преломленный луч $OS_1$. Построим ход второго луча.
Луч $SC$ падает на линзу параллельно ее оптической оси. По определению, после преломления он должен пройти через фокус линзы и пересечься с другим преломленным лучом.
Этот преломленный луч будет выходить из точки $C$ и пересекаться с другим преломленным лучом в точке $S_1$. Отметим на чертеже этот луч $CS_1$ (рисунок 4, в).
Он пересек оптическую ось в точке — это и есть фокус линзы $F$. Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №3
Постройте оптический центр, отметьте линзу и ее фокусы на чертеже, используя данные рисунка 5.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
По аналогии с построением в предыдущей задаче соединим прямой точку $S$ и ее изображение $S_1$. Но в этом случае прямая $SS_1$ не пересекла оптическую ось. Продолжим ее до пересечения, чтобы получить положение оптического центра $O$ (рисунок 6, а).
Мы видим, что точка и ее изображение находятся по одну сторону от линзы (ее оптического центра). Значит, изображение $S_1$ — мнимое. В точке $S_1$ должны пересечься продолжения преломленных лучей. Это возможно, если мы будем использовать рассеивающую линзу. Отметим ее на чертеже (рисунок 6, б).
Луч $SO$ после прохождения сквозь линзу не изменит своего направления. Продолжение преломленного луча совпадает с самим падающим лучом $SO$.
Проведем второй луч, идущий параллельно оптическое оси — луч $SС$. После прохождения сквозь линзу продолжение преломленного луча пересекается с продолжением другого преломленного луча $SO$ в точке $S_1$. Продолжим его до пересечения с оптической осью.
Так мы получили положение мнимого фокуса $F$ (рисунок 6, в). Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №4
Постройте изображение предмета, расположение которого показано на рисунке 7. Охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
На исходном рисунке 7 изображена выпуклая линза — собирающая. Отметим саму линзу и ее оптический центр $O$ на чертеже. Обозначим крайние точки предмета точками $A$ и $B$ (рисунок 8, а).
Начнем построение изображения предмета. Так как обе его точки не лежат на оптической оси, то и изображение нужно будет строить сначала для одной точки, а потом — для второй.
Займемся построением изображения точки $A$ (рисунок 8, б). Проведем два падающих луча $AC$ и $AO$. Луч $AO$ после преломления не изменит своего направления, а луч $AC$ преломится в линзе и после пройдет через фокус $F$.
Продолжим эти два преломленных луча до пересечения друг с другом. Получим изображение $A_1$.
Теперь построим изображение точки $B$ (рисунок 8, в). На линзу падают лучи $BO$ и $BD$. После преломления они пересекутся в точке $B_1$.
Соединим точки $A_1$ и $B_1$. Так мы получили изображение предмета $A_1B_1$. Охарактеризуем его.
Полученное изображение предмета:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 2F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №5
Постройте изображение предмета, находящегося в фокусе собирающей и рассеивающей линз (рисунок 9). Сравните полученные изображения.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Начнем с построения изображения предмета, даваемого собирающей линзой (рисунок 10, а). Из точки выходят два луча $AC$ и $AO$. Как видно из чертежа после прохождения сквозь линзу преломленные лучи параллельны друг другу — они никогда не пересекутся. Значит, изображения мы не получим.
Теперь построим изображение предмета в рассеивающей линзе (рисунок 10, б). Из крайней точки $A$ выходят два луча $AC$ и $AO$. Так как линза рассеивающая, изображение точки $A_1$ мы получим на пересечении продолжений преломленных лучей. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим полученные точки друг с другом — получим изображение предмета $A_1B_1$.
Если предмет находится в фокусе собирающей линзы, то мы не получим его изображения.
Если предмет находится в фокусе рассеивающей линзы, то изображение предмета:
1. Мнимое
2. Уменьшенное
3. Прямое
4. $f < F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №6
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $3F$ (рисунок 11).
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Из точка $A$ на линзу падают лучи $AC$ и $AO$ (рисунок 12). После прохождения сквозь линзу они преломляются и пересекаются друг с другом в точке $A_1$ — изображении точки $A$.
Опустим перпендикуляр на оптическую ось и получим точку $B_1$ — изображение точки $B$. Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 3F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Задача №7
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $4F$ (рисунок 13). Сравните его с изображением предмета, полученным в задаче №6.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Построим изображение точки $A$ (рисунок 14). Из нее выходят два луча: $AC$ и $AO$. После преломления они пересекаются в точке $A_1$. Опустим перпендикуляр на оптическую ось, чтобы получить изображение точки $B$ — $B_1$.
Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 4F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Сравнивая полученное изображение предмета с изображением, полученным в предыдущей задаче, мы уже можем сделать определенные выводы. Для полной картины используем полученное изображение в задаче, рассмотренной в уроке «Изображение предмета, даваемое линзой». Там предмет находился в двойном фокусе линзы, а его полученное изображение было действительным, перевернутым, равным по размеру предмету и находилось в двойном фокусе с другой стороны линзы.
Тогда мы можем сделать вывод:
по мере отдаления предмета от линзы на двойное фокусное расстояние и дальше, действительное и перевернутое изображение предмета уменьшается и приближается к фокусу линзы, но никогда не окажется в нем.
Постройте изображение предмета, расположение которого показано на рисунке 15, и охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Хоть одна из крайних точек предмета и находится на оптической оси, сам предмет расположен под углом к ней. Поэтому, при построении изображения необходимо будет отдельно строить изображения крайних точек $A$ и $B$.
Начнем с более сложного построения. Построим изображение точки, лежащей на оптической оси линзы — точки $B$ (рисунок 16).
Луч $BO$ проходит через оптический центр и после преломления не изменит своего направления. Эти лучи лежат оптической оси линзы.
Произвольный луч $BC$ падает на линзу. Теперь нам нужно построить ход этого луча после преломления в линзе. Для этого проведем побочную оптическую ось $MN$, параллельную этому лучу.
Далее отметим на чертеже фокальную плоскость, перпендикулярную оптической оси и проходящую через фокус $F$ (обозначена на рисунке пунктирной линией-перпендикуляром, опущенным в точку $F$).
Побочная оптическая ось $MN$ пересечет фокальную плоскость в точке $F’$ — побочном фокусе.
Преломленный луч будет проходить через этот побочный фокус. Соединим точки $C$ и $F’$ — получим преломленный луч $CF’$. Продолжим его до пересечения с первым преломленным лучом (который совпадает с оптической осью). На этом пересечении мы получаем точку $B_1$ — изображение точки $B$.
Теперь привычным для нас способом построим изображение точки $A$ (рисунок 17).
Лучи $AD$ и $AO$ после преломления в линзе пересекаются в точке $A_1$. Соединим точки $A_1$ и $B_1$ и получим изображение предмета $A_1B_1$.
Полученное изображение предмета, находящегося от линзы на расстоянии $2F > d >F$:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 3F$
Содержание:
- Линзы и получение изображений с помощью линз
- Собирающие и рассеивающие линзы. Оптические оси. Оптический центр линзы
- Главные фокусы и фокальные плоскости линзы
- Оптическая сила линзы
- Построение изображения светящейся точки, расположенной на главной оптической оси линзы
- Вывод формулы для сопряженных точек тонкой линзы
- Построение изображения светящейся точки, расположенной на побочной оптической оси линзы
- Построение изображений предмета, создаваемых линзой
- Линейное увеличение, полученное с помощью линзы
- Недостатки линз
Линза – это прозрачное тело, имеющая. 2. сферические поверхности. Она, является тонкой, если ее толщина меньше радиусов кривизны сферических поверхностей. Линза — это составляющая часть почти каждого оптического прибора.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Линзы и получение изображений с помощью линз
При помощи рассеивающей линзы невозможно получить действительное изображение. Изображение, даваемое рассеивающей линзой, является мнимым, прямым и уменьшенным, и не зависит от взаиморасположения линзы и предмета. При всех построениях лучей, проходящих через тонкую линзу, нужно лишь знать расположение оптического центра и главных фокусов.
Собирающие и рассеивающие линзы. Оптические оси. Оптический центр линзы
Для получения изображений различного вида в оптических приборах очень часто используют линзы.
Линза представляет собой прозрачное тело, ограниченное двумя гладкими выпуклыми или вогнутыми поверхностями (одна из них может быть плоской). Чаще всего поверхности линзы делают сферическими, а саму линзу изготовляют из специальных сортов стекла, например флинтгласа, или других веществ с подходящим показателем преломления. Линзы подразделяются на выпуклые (рис. 30.1, а —в), которые толще к середине, и вогнутые (рис. 30.1, г—в), которые к середине тоньше.
Рис. 30.1.
Прямую, которая проходит через сферические центры кривизны поверхностей линзы С1 и С2 или через сферический центр С перпендикулярно к плоской поверхности линзы, называют главной оптической осью линзы. Световой луч, направленный вдоль оптической оси, проходит линзу не преломляясь. (Почему?)
Изменения в ходе лучей, создаваемые линзой, легко выяснить на модели из призм (рис. 30.2). Призмы можно подобрать так, что параллельные лучи, пройдя их, соберутся почти все в одной точке Ф (рис. 30.2, а). Если эти призмы сложить вплотную, то они образуют тело, по форме близкое к выпуклой линзе. Оказывается, выпуклая линза обладает свойством собирать параллельные лучи в одной точке. Поэтому выпуклые линзы называют собирающими.
Рис. 30.2.
Модель действия вогнутой линзы изображена на рис. 30.2, б. (Объясните, почему вогнутые линзы называют рассеивающими.)
Внутри каждой линзы на главной оптической оси имеется точка О (рис. 30.3), которая замечательна тем, что проходящий через нее луч идет после выхода из линзы в том же направлении, что и до линзы. Точку О называют оптическим центром линзы.
Рис. 30.3.
Плоскости, проведенные через точки А и В, параллельны. Следовательно, луч, проходящий через точку О, идет в линзе так же, как и в плоскопараллельной пластинке, т. е. смещается параллельно самому себе, не изменяя своего направления. Поскольку это смещение луча тем меньше, чем тоньше пластинка, то в достаточно тонких линзах этим смещением луча можно пренебречь, особенно если луч составляет малый угол в главной оптической осью линзы. В дальнейшем будем! рассматривать только тонкие линзы небольших размеров, в которые попадают лишь лучи, составляющие маленький угол с главной оптической осью линзы. Условные изображения тонких линз показаны на рис. 30.4 (а — собирающая, б — рассеивающая линза). Можно считать, что в тонких линзах луч, который проходит через оптический центр линзы, не преломляется. Всякую прямую, которая проходит через оптический центр линзы О (кроме главной оптической оси), называют побочной оптической осью (КМ, К’М’ на рис. 30.5).
Рис. 30.4.
Рис. 30.5.
Главные фокусы и фокальные плоскости линзы
Если на собирающую линзу направить пучок лучей, параллельных ее главной оптической оси, то они соберутся в точке Ф с другой стороны линзы (рис. 30.6, а). У рассеивающей линзы такие лучи после линзы идут расходящимся пучком (рис. 30.6, б), но таким образом, что их продолжения сходятся в одной точке Ф.
Рис. 30.6.
Точку Ф на главной оптической оси линзы, в которой сходятся лучи, идущие до преломления в линзе параллельно ее главной оптической оси, называют главным фокусом линзы. Из сказанного выше следует, что у собирающих линз главный фокус действительный, а у рассеивающих — мнимый. У каждой линзы имеется два главных фокуса, расположенных симметрично относительно ее оптического центра О. Расстояние F между главным фокусом линзы и ее оптическим центром называют главным фокусным расстоянием. Если главный фокус действительный, то F считают положительным, а если мнимый — отрицательным.
Когда лучи падают на линзу параллельно ее побочной оси, например АО (рис. 30.7), то после преломления в линзе они собираются на этой же оси в одной точке В, которую называют фокусом линзы. Очевидно, различных фокусов у линзы имеется множество, но, как показывает опыт, все они расположены в фокальной плоскости КМ. Фокальной называют плоскость, которая перпендикулярна главной оптической оси линзы и проходит через ее главный фокус. Каждая линза имеет две фокальные плоскости.
Итак, лучи, которые параллельны любой оптической оси линзы, собираются после преломления в точке пересечения этой оси с фокальной плоскостью линзы (рис. 30.7, а). У собирающей линзы фокальные плоскости действительные, а у рассеивающей — мнимые (рис. 30.7, б).
Рис. 30.7.
Оптическая сила линзы
Положение главного фокуса оказывает существенное влияние на размеры и вид изображений, полученных с помощью линзы.
Величину D, которая характеризует оптические свойства линзы, определяемые положением ее главного фокуса на оптической оси, называют оптической силой линзы. Оптическая сила линзы измеряется числом, обратным главному фокусному расстоянию этой линзы F:
(30.1)
Единица оптической силы из (30.1):
В СИ за единицу оптической силы принимается диоптрия (дптр) — оптическая сила такой линзы, главное фокусное расстояние которой равно одному метру. Оптическую силу собирающих линз (как и фокусное расстояние F) условились считать положительной, а рассеивающих — отрицательной.
Оптическая сила линзы определяется кривизной ее поверхностей, а также показателем преломления ее вещества относительно окружающей среды и может быть вычислена по формуле
(30.2)
где R1 и R2 — радиусы сферических поверхностей линзы, a n — показатель преломления вещества линзы относительно среды, в которой находится эта линза. При вычислениях числовое значение R для выпуклой поверхности линзы следует считать положительным, а для вогнутой — отрицательным. Заметим, что при n<1, т. е. когда вещество линзы является средой оптически менее плотной, чем окружающая ее среда, выпуклые линзы будут рассеивающими, а вогнутые — собирающими.
Построение изображения светящейся точки, расположенной на главной оптической оси линзы
С помощью линзы можно собрать в одну точку не только параллельные лучи. Опыт показывает, что лучи, попадающие на собирающую линзу из одной точки S, после линзы снова собираются в одной точке S1 (рис. 30.8, а), т. е. линза создает действительное изображение светящейся точки S в точке S1. Это изображение может быть и мнимым. На рис. 30.8, б показан ход лучей, падающих из точки S на рассеивающую линзу. После линзы они идут расходящимся пучком, но так, что их продолжения в обратную сторону сходятся в S1. Выясним, как строится создаваемое линзой изображение светящейся точки, расположенной на главной оптической оси линзы, в трех случаях.
Рис. 30.8.
1. Точка S находится за главным фокусом линзы Ф (рис. 30.9). Так как в точке S, сходятся все лучи после преломления в линзе, то для определения положения точки S, достаточно установить, где пересекутся два таких луча.
Рис. 30.9.
Пусть прямая ФО является главной оптической осью собирающей линзы, а КМ — фокальная плоскость этой линзы. Луч, идущий из точки S вдоль главной оптической оси, проходит линзу не преломляясь, поэтому изображение точки S будет находиться на главной оптической оси ФО. Чтобы узнать, где именно будет изображение точки S, найдем ход произвольного луча SA после линзы. Для этого из точки О проведем побочную оптическую ось, параллельную лучу SA. Она пересечет фокальную плоскость КМ в некоторой точке A1. Прямая, проведенная через точки А и A1 устанавливает ход луча SA после преломления в линзе. Продолжив прямую AA1 до пересечения с главной оптической осью, получим точку S1, которая и определяет положение изображения точки S, создаваемого линзой. Ясно, что любой другой луч SB после преломления в линзе тоже пройдет через точку S1 (рис. 30.9); побочная оптическая ось OB1 параллельна лучу SB.
2. Точка S находится между главным фокусом и оптическим центром линзы (рис. 30.10). Как и в первом случае, изображение точки S будет находиться где-то на главной оптической оси. Чтобы установить, где именно, выделим произвольный луч SA, попадающий на линзу. Проведем побочную оптическую ось OA1, параллельную SA, и затем — прямую AA1 до пересечения с главной оптической осью в точке S1. Последняя и определяет положение мнимого изображения точки S для рассматриваемого случая.
Рис. 30.10.
3. Светящаяся точка находится на главной оптической оси рассеивающей линзы (рис. 30.11). При построении изображения в этом случае фокальную плоскость надо брать с той же стороны линзы, с которой находится точка S. Изображение светящейся точки S и в этом случае должно быть на главной оптической оси линзы. Выделим произвольный луч SA и проведем параллельную ему побочную ось OA1. Точка пересечения прямой AA1 с главной оптической осью и определит положение мнимого изображения S1. Заметим, что изображение действительного точечного источника света в рассеивающей линзе всегда получается мнимое.
Рис. 30.11.
Вывод формулы для сопряженных точек тонкой линзы
В предыдущем параграфе было показано, что положение изображения S1 однозначно определяется положением самой светящейся точки S относительно линзы. Поэтому точки S и S1 называют сопряженными точками линзы. Выведем формулу сопряженных точек линзы, позволяющую находить положение изображения S1 с помощью вычислений.
Пусть на главной оптической оси собирающей линзы с оптическим центром О и фокусами Ф1 и Ф2 находится светящаяся точка S (рис. 30.12), изображение которой получилось в точке S1. Напомним, что КМ — фокальная плоскость линзы, a 
Обозначим расстояние от светящейся точки S до оптического центра О через 
расстояние от изображения S1 до оптического центра О — через 
и главное фокусное расстояние — через 
Из подобия треугольников 
и 
имеем
или 
Рис. 30.12.
Из подобия треугольников 
и 
можно написать
или 
Поскольку правые части найденных пропорций равны, получаем
откуда 
После деления обеих частей этого равенства на 
получим формулу cопряженных точек линзы:
(30.3)
Так как справа стоит оптическая сила линзы, имеем
(30.4)
Из (30.3) видно, что от перемены местами значений d и f формула не изменяется. Это означает, что светящаяся точка и ее изображение в линзе переместимы, т. е. если светящуюся точку поместить туда, где было ее изображение, то изображение получится там, где была светящаяся точка. Именно поэтому точки S и S1 называют сопряженными.
Следует запомнить, что соотношения (30.3) и (30.4) применимы как к собирающим, так и к рассеивающим линзам. При расчетах числовые значения действительных величин всегда представляются со знаком плюс, а мнимых — со знаком минус. Например, для рассеивающей линзы на место F или D ставится число со знаком минус. Отрицательный ответ, полученный в результате вычислений, показывает, что соответствующая ему величина мнимая.
Напомним, что светящаяся точка S тоже может быть мнимой. На рис. 30.13, а показаны мнимый источник света S и его действительное изображение в собирающей линзе S1, а на рис. 30.13, б— мнимый источник света S и его действительное изображение в рассеивающей линзе.
Рис. 30.13.
Построение изображения светящейся точки, расположенной на побочной оптической оси линзы
Когда светящаяся точка S находится на побочной оптической оси линзы, то линза создает ее изображение на той же оси. Выясним, как строится это изображение.
1. Точка S находится за фокальной плоскостью собирающей линзы (рис. 30.14). Для определения положения изображения S1 можно воспользоваться любыми двумя из трех лучей, показанных на рис. 30.14. Луч 1 из точки S проводится параллельно главной оптической оси. После преломления в линзе он идет через главный фокус. Луч 2 проводится вдоль побочной оси, т. е. через оптический центр линзы. Этот луч проходит линзу, не преломляясь. Луч 3 проводится через главный фокус Ф. После преломления в линзе он идет параллельно главной оптической оси. Точка пересечения этих лучей после преломления в линзе S1 и определяет положение действительного изображения точки S для этого случая.
Рис. 30.14.
2. Точка S расположена между фокальной плоскостью собирающей линзы и самой линзой (рис. 30.15). В этом случае из точки S можно провести три таких же луча, как и в первом случае. Точка пересечения двух любых из них S1 определяет положение мнимого изображения точки S.
Рис. 30.15.
3. Точка S находится на побочной оси рассеивающей линзы (рис. 30.16). И в этом случае можно провести из точки S три таких же луча (как и в первом случае), но нужно помнить, что после преломления в линзе продолжение луча 1 должно проходить через фокус, который находится с той стороны линзы, где точка S. Луч 3 нужно проводить так, чтобы его продолжение проходило через фокус с другой стороны линзы, тогда после преломления в линзе луч пойдет параллельно главной оптической оси. Заметим, что изображение действительной светящейся точки S, создаваемое рассеивающей линзой, всегда мнимое.
Рис. 30.16.
Построение изображений предмета, создаваемых линзой
Пусть перед линзой расположен предмет, который мы в дальнейшем будем условно изображать стрелкой, перпендикулярной главной оптической оси линзы. Изображение этого предмета, создаваемое линзой, является совокупностью изображений отдельных его точек, поэтому для построения изображения предмета достаточно найти, где будут находиться изображения его крайних точек.
Различные типичные случаи построения изображений предмета АВ, создаваемых собирающей линзой, показаны на рис. 30.17. Само построение выполняют следующим образом. Сначала строят изображение точки А, затем — точки В. Полученные таким способом точки A1 и B1 соединяют прямой А1В1 которая и является изображением предмета АВ. Рассмотрим эти случаи.
Рис. 30.17.
1. Расстояние от предмета до линзы d больше 2F (рис. 30.17, а). В этом случае предмет и его изображение находятся по разные стороны линзы, а расстояние от линзы до изображения f оказывается больше F, но меньше 2F. Само изображение получается действительным, перевернутым и уменьшенным. В частности, когда светящийся предмет находится на бесконечно большом расстоянии от линзы 
его изображение получается в виде светящейся точки в главном фокусе линзы (рис. 30.17, б).
2. Расстояние от предмета до линзы d равно 2F (рис. 30.17, б). В этом случае предмет и его изображение находятся по разные стороны линзы, а расстояние от линзы до изображения F=d=2f. Само изображение получается действительным, перевернутым и в натуральную величину.
3. Расстояние от предмета до линзы d больше F, но меньше 2F (рис. 30.17, г). В этом случае предмет и его изображение находятся по разные стороны линзы, а расстояние от линзы до изображения f больше 2F. Само изображение получается действительным, перевернутым и увеличенным.
4. Предмет находится в главном фокусе линзы, т. е. расстояние от предмета до линзы d=F (рис. 30.17, д). В этом случае лучи от каждой точки предмета после преломления в линзе идут параллельным пучком. Это означает, что изображение должно получиться бесконечно большим и на бесконечно большом расстоянии от линзы, что практически равносильно отсутствию изображения.
5. Расстояние от предмета до линзы d меньше главного фокусного расстояния F (рис. 30.17, e). В этом случае предмет и его изображение находятся по одну сторону линзы, а расстояние от линзы до изображения f больше d. Само изображение получается мнимым, прямым и увеличенным.
Проследим, как изменяется изображение предмета и его расположение при перемещении предмета из бесконечности к линзе.
При перемещении предмета из бесконечности до расстояния 2F от линзы его перевернутое и действительное изображение, двигаясь от линзы, проходит расстояние от F до 2F и постепенно увеличивается, оставаясь меньше самого предмета. Когда предмет оказывается на расстоянии 2F от линзы, его перевернутое изображение в натуральную величину тоже оказывается на расстоянии 2F от линзы. При дальнейшем перемещении предмета к линзе до расстояния F от нее изображение предмета, которое уже больше самого предмета, постепенно возрастая, уходит в бесконечность.
Наконец, когда предмет движется от главного фокуса до линзы, его мнимое увеличенное изображение, которое находится сзади предмета, постепенно уменьшается и движется к линзе. Когда предмет приходит в соприкосновение с линзой, его мнимое изображение имеет натуральную величину и совпадает с предметом. Заметим, что переход изображения с одной стороны линзы на другую происходит в момент перемещения предмета через фокальную плоскость линзы. Таким образом, предмет и его изображение всегда движутся в одном направлении.
Построение изображения предмета, создаваемого рассеивающей линзой, показано на рис. 30.18. Рассеивающая линза всегда дает мнимое, уменьшенное и прямое изображение предмета, которое находится между главным фокусом и линзой. Расстояние от этого изображения до линзы f всегда меньше расстояния от предмета до линзы d. В этом случае предмет и его изображение тоже всегда движутся в одном направлении, а когда предмет соприкасается с линзой, его изображение совпадает с ними и имеет натуральную величину.
Рис. 30.18.
Линейное увеличение, полученное с помощью линзы
В предыдущем параграфе было установлено, что с помощью линзы можно получать увеличенные изображения предметов. На практике линзы часто используют для получения именно таких изображений.
Линейным увеличением 
называют отношение высоты (ширины) изображения предмета к истинной высоте (ширине) самого предмета. Если высоту предмета обозначить через h, а высоту изображения через H, то
(30.5)
Выясним, как связано увеличение 
с расстояниями от линзы до предмета d и до его изображения f. На рис. 30.19 показаны положения предмета AВ и его изображения A1B1 относительно линзы. Из подобия 
и 
следует, что 
Поскольку 
получаем формулу для вычисления линейного увеличения, создаваемого линзой:
или 
(30.6)
Рис. 30.19.
Из этих соотношений видно, что собирающая линза дает увеличение только в тех случаях, когда изображение оказывается дальше от линзы, чем предмет. (Подумайте, может ли рассеивающая линза дать увеличение, большее единицы).
Недостатки линз
Выясним, какие существенные недостатки встречаются у линз.
Первый недостаток заключается в том, что лучи, выходящие из одной точки S1, которая лежит на главной оптической оси, сходятся не в одной, а в различных точках (рис. 30.20). Чем дальше от оптического центра О лучи из точки S1 попадают на линзу, тем ближе к линзе находится их точка пересечения S2. Такое явление называют сферической аберрацией (от латинского «аберрацио» — отклонение). Этот недостаток частично можно исправить с помощью диафрагмы, которая ограничивает пучок лучей, попадающих на линзу. Диафрагма устраивается таким образам, что она может изменять входное отверстие, через которое свет попадает на линзу. Сферическую аберрацию часто также устраняют с помощью соединения двух специально подобранных линз, сложенных вплотную. Сложную линзу или систему, у которой устранена сферическая аберрация, называют апланатом.
Рис. 30.20.
Второй недостаток относится к изображению светящейся точки S1, расположенной на побочной оптической оси (рис. 30.21). Оказывается, что в этом случае возникают два изображения в виде отрезков прямых линий, расположенных перпендикулярно друг к другу в плоскостях I и II. Изображение точки S1 можно получить лишь в виде расплывчатого светлого кружка S2 между плоскостями I и II. Это явление называют астигматизмом. Линзу или систему линз, в которой устранен этот недостаток, называют анастигматом.
Рис. 30.21.
В § 29.7 говорилось, что показатель преломления зависит от частоты колебаний, т. е. от цвета лучей. Из-за этого фокус Фф для фиолетовых лучей находится ближе к линзе, чем фокус Фк для красных лучей (рис. 30.22). Поэтому изображение точечного источника белого света получается расплывчатым и окрашенным по краям. Это явление называют хроматической аберрацией. Линзы и оптические системы, у которых этот недостаток устранен для двух цветов, называют ахроматическими, а в случае совпадения изображений, для трех цветов систему называют апохроматом.
Рис. 30.22.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно — кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
В Genshin Impact Память Сэйрая является секретным заданием мира Инадзумы, в рамках которого вам нужно будет найти подходящие места для фотографирования. В этом руководстве мы расскажем, как начать данный квест, а также укажем, где нужно делать фото.
Как начать квест «Память Сэйрая»
Для этого вам нужно вначале попасть на архипелаг, пройдя сюжетное задание «Неизменный бог и вечная утопия». Затем направляйтесь на остров Сэйрай и отыщите святилище, расположенное к западу от Форта Хирауми. На скриншотах ниже показано его точное расположение.
Справа от святыни появится опция «Копать». Нажмите на нее, чтобы отыскать «Изображение острова Сэйрай». После этого сразу же стартует соответствующее задание. Рекомендуем вам перед его выполнением пройти квестовую цепочку «Охотники за грозами Сэйрая», чтобы вам было легче исследовать данный регион.
Расспросите искателей приключений
Телепортируйтесь в город Инадзума и отыщите там персонажа по имени Фуруя Нобору. Он будет стоять возле моста. Поговорите с ним. Затем направляйтесь к Оде Таро, который находится неподалеку. Пообщайтесь с ним. Вы получите от него еще 3 изображения. Он попросит вас сделать фотографии данных мест.
Где нужно сделать фотографии на Сэйрае
Искать подходящие места придется самостоятельно, ориентируясь по ранее полученным картинкам. Просматривать их можно в инвентаре в разделе «Задания». Если же вам лень отыскивать эти пейзажи, то просто посмотрите скриншоты ниже.
Первое место для фото
Оно находится недалеко от того места, где вы отыскали первое изображение и начали квест. Просто поднимитесь на холм и сфотографируйте скалу, расположенную впереди. Для этого воспользуйтесь фотоаппаратом из меню Паймон. Обязательно дождитесь появления надписи «Выбрано подходящее положение»
, прежде чем делать снимок.
Второе место для фото
Переместитесь в деревню Косэки и направляйтесь на юго-запад к побережью. Доберитесь до обрыва, а затем сфотографируйте небольшой островок впереди.
Третье место для фото
Оно находится к западу от корабля «Сэйраймару» на небольшом островке с фазовыми вратами. Разберитесь с врагами, а затем повернитесь в сторону мачты и сфотографируйте ее.
Четвертое место для фото
Искать нужно возле пика Амакумо, на дне воронки, заполненной водой и окруженной скалами. Встаньте в указанное место и сделайте снимок.
Получив фотографии, вернитесь к Оде Таро и передайте ему снимки. После разговора с ним квест завершится. В награду вы получите 200 очков приключений, 2 опыта героя, 30 камней истока и 15 000 моры. Плюс, вы разблокируете трофей «По ту сторону ностальгии».