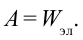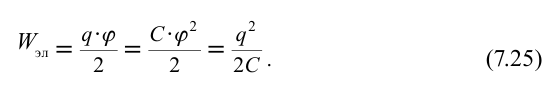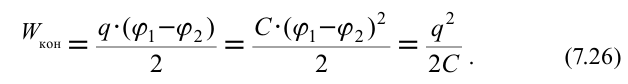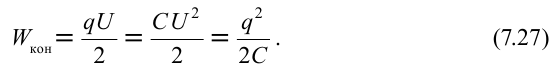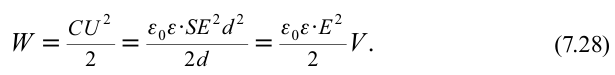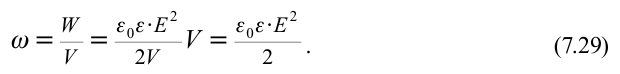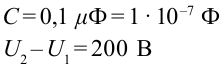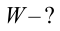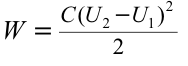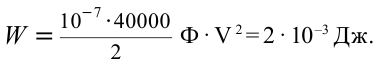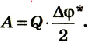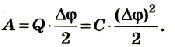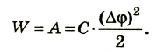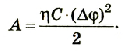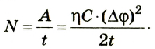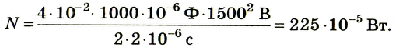Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е.
Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.
Поставляя значении 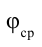
Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 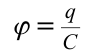
Согласно соотношению 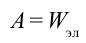
Если заряженное тело является конденсатором, то при расчете энергии (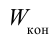
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 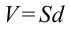
Учитывая емкость заряженного плоского конденсатора 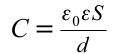
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 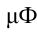
Дано:
Найти:
Формула:
Решение:
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: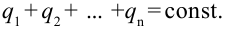 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 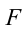 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 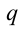 : :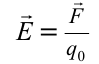 |
| Напряженность поля, создаваемого точечным зарядом 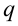 на расстоянии на расстоянии 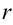 . . |
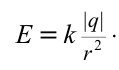 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 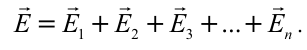 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
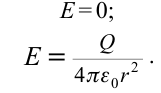 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
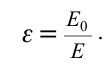 |
| Напряженность поля в точке на расстоянии 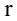 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
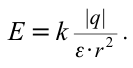 |
Потенциальная энергия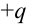 заряда, находящегося заряда, находящегосяна расстоянии 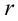 от неподвижного положительного от неподвижного положительногозаряда 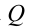 |
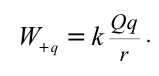 |
| Потенциал точечного заряда 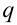 . . |
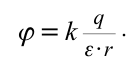 |
| Электрическое напряжение. |
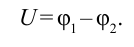 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
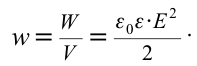 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
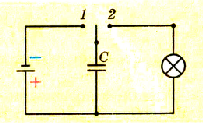
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
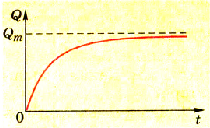
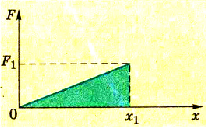
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
Если учесть, что 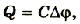
Таким образом, энергия электрического поля в конденсаторе равна:
Приняв во внимание, что 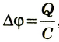
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N — ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
Подставив значения физических величин, получим:
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.
Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.
Pиc. 1.48 Электрический скат
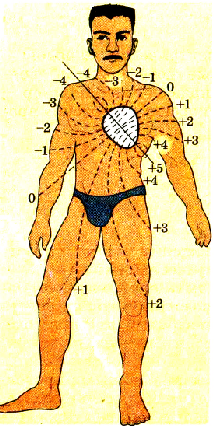
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики — несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
Конденсатор. Энергия электрического поля
-
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
-
Ёмкость уединённого проводника
-
Ёмкость плоского конденсатора
-
Энергия заряженного конденсатора
-
Энергия электрического поля
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
к оглавлению ▴
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать
, так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара,
— его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в
раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим
из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
к оглавлению ▴
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
— заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки,
— напряженность поля отрицательной обкладки,
— поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов
между обкладками равна произведению
на
(вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
к оглавлению ▴
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок
.
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды
второй обкладки. При этом суммировании постоянный множитель
вынесется за скобку, а в скобке просуммируются все
и дадут
. В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины
. Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины
, то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины
. Это как раз и означает, что
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в
раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина
войдёт в ёмкость
, и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
к оглавлению ▴
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме
.
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание книги
Предыдующая страница
§16. Превращение энергии в электрических и магнитных явлениях
16.7 Изменение энергии конденсатора при изменении его емкости.
Энергия конденсатора зависит от его емкости. Емкость конденсатора можно изменять, когда он заряжен — при этом будет изменяться его энергия. При рассмотрении этих процессов можно выделить два принципиально различных случая: первый — изменение емкости происходит при неизменных зарядах на обкладках; второй – емкость конденсатора изменяется при постоянном напряжении между обкладками (в этом случае конденсатор подключен к источнику постоянной ЭДС).
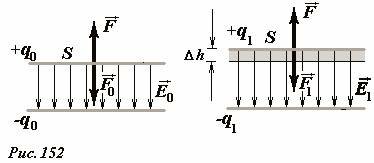
Рассмотрим теперь превращения энергии при изменении емкости плоского конденсатора, образованного двумя параллельными одинаковыми платинами площади S. Размеры пластин будем считать значительно превышающими расстояние между ними, что позволяет пренебречь краевыми эффектами, то есть считать электрическое поле (~vec E) однородным (Рис. 152). Пусть конденсатор заряжен, так что заряды каждой пластины одинаковы по модулю и равны q и противоположны по знаку, поверхностная плотность заряда на каждой пластине равна (~sigma = frac{q}{S}). Напряженность поля между пластинами в этом случае равна
(~E = frac{sigma}{varepsilon_0} = frac{q}{varepsilon_0 S}) , (1)
причем заряды каждой пластины создают поле, напряженность которого в два раза меньше напряженности суммарного поля (1); разность потенциалов между пластинами равна
(~Delta varphi = U = Eh = frac{qh}{varepsilon_0 S}) . (2)
Так заряды пластин разноименные, то пластины будут притягиваться друг к другу с некоторой силой F. Сила, действующая на одну пластину, равна произведению ее заряда на напряженность поля, создаваемого зарядом второй пластины,
(~F = q frac{E}{2} = frac{q^2}{2 varepsilon_0 S}) . (3)
Этой формуле можно придать иной вид, если выразить силу через напряженность электрического поля с помощью формулы (1)
(~F = frac{q^2}{2 varepsilon_0 S} = frac{varepsilon_0 E^2}{2} S) . (4)
Важно отметить, что давление электрического поля на проводящую платину в точности равно объемной плотности энергии поля
(~p = frac{F}{S} = frac{varepsilon_0 E^2}{2} = w) . (5)
Чтобы изменить (для определенности увеличить см. Рис. 152) расстояние между пластинами, к ним необходимо приложить внешнюю силу F0, превышающую по модулю силе электрического притяжения. При перемещении пластины (увеличении расстояния) на величину Δh эта внешняя сила совершит положительную работу.
Если пластины конденсатора изолированы, то электрический заряд и, как следствие, напряженность поля и сила притяжения не зависят от расстояния между пластинами. Поэтому работа внешней силы по перемещению пластины на расстояние Δh будет минимальна, когда эта сила равна силе притяжения между пластинами, при этом
(~A = F_0 Delta h = frac{varepsilon_0 E^2}{2} S Delta h) . (6)
Благодаря этой работе возрастает энергия электрического поля – при неизменной напряженности и плотности энергии возрастает объем, занятый полем ((Delta V = S Delta h)), что выражается формулой
(~A = Delta W = w Delta V) . (7)
При увеличении расстояния между пластинами емкость конденсатора изменяется (уменьшается). Изменение энергии конденсатора можно также рассчитать, с помощью формулы для его энергии, причем следует выразить энергию через не изменяющийся в данном случае заряд конденсатора, то есть
(~Delta W = W_1 — W_0 = frac{q^2}{2 C_1} — frac{q^2}{2 C_0} = frac{q^2}{2} left(frac{h_1}{varepsilon_0 S} — frac{h_0}{varepsilon_0 S}right) = frac{q^2 Delta h}{2 varepsilon_0 S}) . (8)
Эта формула равносильна полученным выше выражениям для изменения энергии. Таким образом, в рассмотренном процессе превращения энергии понятны: работа внешней силы увеличивает энергию электрического поля конденсатора.
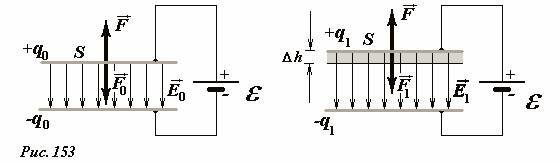
Рассмотрим теперь этот же процесс при условии, что обкладки конденсатора подключены к источнику постоянной ЭДС (Рис. 153). В этом случае при изменении расстояния между пластинами, остается неизменным напряжение U = ε между ними.
В этом случае разноименно заряженные пластины также притягиваются, поэтому для увеличения расстояния между ними внешняя сила также совершает положительную работу, однако при этом энергия конденсатора уменьшается, а не растет! Действительно, при постоянном напряжении между пластинами, изменение энергии конденсатора рассчитывается по формуле
(~Delta W_C = W_1 — W_0 = frac{C_1 U^2}{2} — frac{C_0 U^2}{2} = frac{U^2}{2} left(frac{varepsilon_0 S}{h_1} — frac{varepsilon_0 S}{h_0}right) = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_1} — frac{1}{h_0}right)) . (9)
Так как h1 > h0 , то C1 < C0 и ΔWC < 0.
Но и в этом случае нарушения закона сохранения энергии нет, переданная системе энергия (равная совершенной работе) не «теряется» — конденсатор не является замкнутой системой, он же подключен к источнику ЭДС. При увеличении расстояния между пластинами емкость конденсатора уменьшается, поэтому уменьшается заряд на пластинах, которому некуда деться, кроме как вернуться назад, в источник. Их возращению препятствуют сторонние силы (вспомните – сторонние силы источника стремятся «вытолкнуть заряды из источника), поэтому при возвращении зарядов энергия источника повышается. Таким образом, при раздвигании пластин конденсатора происходит подзарядка источника, а энергия, переданная посредством совершенной работы, переходит в энергию источника. Кроме того, энергия поля в конденсаторе также уменьшается, поэтому эта «потеря» энергии также переходит в источник. Иными словами, при перемещении пластины внешняя сила не только совершает работу по подзарядке источника, но и «заставляет» электрическое поле вернуть часть своей энергии. Схематически потоки энергии в этом процессе показаны на Рис. 154.
Подтвердим проведенные рассуждения расчетами энергетического баланса и покажем, что он точно выполняется. Силу притяжения между пластинами (4) выразим через постоянное напряжение между пластинами
(~F = frac{varepsilon_0 E^2}{2} S = frac{varepsilon_0}{2} left(frac{U}{h}right)^2 S = frac{varepsilon_0 U^2 S}{2 h^2}) . (10)
В данном случае эта сила зависит от расстояния между пластинами. Поэтому для расчета работы необходимо разбить процесс движения пластины на малые участки и затем просуммировать работы на этих участках. Чтобы избежать этой громоздкой математической процедуры, будем считать, что смещение Δh мало настолько, что можно пренебречь изменением силы притяжения. В этом приближении работа внешней силы будет равна
(~delta A_0 = F Delta h = frac{varepsilon_0 U^2 S}{2 h^2_0} Delta h) . (11)
Преобразуем также выражение для изменения энергии конденсатора с учетом малости смещения. Запишем (h_1 = h_0 + Delta h) и подставим в формулу (9)
(~Delta W_C = W_1 — W_0 = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_0 + Delta h} — frac{1}{h_0}right) = -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h_0(h_0 + Delta h)} approx -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h^2_0}) . (12)
Наконец, найдем работу по зарядке источника, которая равна произведению «вернувшегося» заряда на ЭДС источника (которая равна напряжению конденсатора):
(~Delta W_{ist} = U(q_0 — q_1) = U(C_0 U — C_1 U) = U^2 left(frac{varepsilon_0 S}{h_0} — frac{varepsilon_0 S}{h_0 + Delta h}right) = varepsilon_0 S U^2 left(frac{1}{h_0} — frac{1}{h_0 + Delta h}right) approx frac{varepsilon_0 S U^2 Delta h}{h^2_0}) .
Итак, проведенный расчет полностью подтверждает сделанные ранее заключения: увеличение энергии источника (что равносильно — работа по его подзарядке) равно сумме работы внешней силы и уменьшения энергии поля конденсатора
(~Delta W_{ist} = delta A_0 + (-Delta W_C)) .
Задание для самостоятельной работы.
- Докажите, что в рассмотренном процессе энергетический баланс выполняется при любом (не малом) смещении пластины.
Признавая, что «аналогии ничего не доказывают, но много объясняют», рассмотрим гидростатическую аналогию преобразования энергии при изменении «емкости» сосуда. Как мы указывали, аналогом электрического заряда может служить объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости, тогда аналогом электроемкости вертикального сосуда служит площадь его дна. Таким образом, изменению емкости должно соответствовать изменение площади поперечного сечения сосуда. Представим себе сосуд в форме параллелепипеда (аквариума), одна из стенок которого может двигаться – при ее смещении изменяется площадь сосуда, то есть изменяется его «емкость». При уменьшении площади сосуда уменьшается «емкость». В рассмотренных электростатических примерах – уменьшению емкости конденсатора соответствует увеличению расстояния между его пластинами.
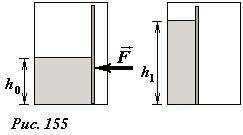
Пусть теперь в нашем сосуде находится некоторый объем жидкости, уровень которой равен h0 (Рис. 155 ). Чтобы сместить подвижную стенку, к ней необходимо приложить некоторую внешнюю силу F. Если объем жидкости в сосуде сохраняется, то при смещении стенки ее уровень повышается, следовательно, увеличивается ее энергия. Понятно, что увеличение потенциальной энергии жидкости равно работе внешней силы.
Сравните: при неизменном объеме жидкости (электрическом заряде) уменьшение площади сосуда (емкости конденсатора) под действием внешней силы приводит к возрастанию уровня жидкости (разности потенциалов) и гидростатической энергии жидкости (электростатической энергии поля).
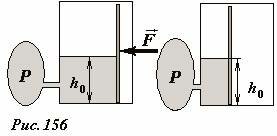
Если конденсатор подключен к источнику постоянной ЭДС, то его напряжение поддерживается постоянным. В гидростатической аналогии необходимо в этом случае говорить о постоянной высоте уровня жидкости в сосуде. В качестве устройства, поддерживающего постоянный уровень можно предложить, например, резиновый сосуд («грушу»), жидкость в которой поддерживается при постоянном давлении. Если теперь наш сосуд «переменной емкости» подключить к источнику постоянного давления (резиновой груше), то получим аналог конденсатора, подключенного к источнику постоянной ЭДС (Рис.156) При смещении подвижной стенки в этом случае внешняя сила также совершает положительную работу, но потенциальная энергия жидкости в сосуде уменьшается, так как уменьшается ее объем при неизменной высоте уровня. Под действием этой внешней силы часть жидкости из сосуда заталкивается в резиновую грушу, при этом энергия последней возрастает. Увеличение ее энергии равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде.
Сравниваем: при постоянном уровне жидкости в сосуде (напряжении конденсатора) уменьшение площади дна (емкости конденсатора) под действием внешней силы приводит к возвращению части жидкости (электрического заряда) в резиновый сосуд, поддерживаемый при постоянном давлении (источник постоянной ЭДС). При этом увеличение энергии жидкости в резиновом сосуде постоянного давления (источника ЭДС) равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде (энергии конденсатора).
Задание для самостоятельной работы.
- Докажите, что в рассмотренных гидростатических аналогиях энергетический баланс выполняется точно.
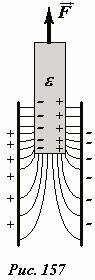
Электроемкость конденсатора зависит также от диэлектрической проницаемости вещества, находящегося между обкладками. Поэтому емкость конденсатора можно изменять, меняя вещество, находящееся между обкладками. Пусть, например, между обкладками плоского конденсатора находится диэлектрическая пластинка. Если конденсатор заряжен, то для извлечения пластинки необходимо приложить к ней внешнюю силу и совершить положительную работу. Механизм возникновения силы, действующей на пластинку со стороны электрического поля, проиллюстрирован на Рис. 157. При ее смещении изначально однородное распределение зарядов на обкладках конденсатора и поляризационных зарядов на пластинке искажается. Как следствие этого перераспределения зарядов искажается и электрическое поле, поэтому возникаю силы, стремящиеся втянуть пластинку внутрь конденсатора.
Расчет этих сил сложен, но энергетические характеристики происходящих процессов могут быть найдены без особого труда. С формальной точки зрения, не важно чем вызваны изменения емкости конденсатора, поэтому можно воспользоваться всеми рассуждениями и выводами предыдущего раздела, как для случая изолированного конденсатора (при сохранении заряда), так для конденсатора подключенного к источнику постоянной ЭДС.
Чрезвычайно интересными и практически важными являются энергетические характеристики процессов поляризации диэлектриков, однако их расчет представляет собой весьма сложную задачу. Для решения возникающих здесь проблем требует привлечения сведения о строении вещества. Некоторые из этих вопросов мы рассмотрим в следующем году после ознакомления с основами теории строения вещества.
Следующая страница
Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.
Потенциальные и непотенциальные силы в электродинамике
Все силы можно разделить на потенциальные и непотенциальные.
Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.
Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))
Энергия системы заряженных тел
Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.
Изменение потенциальной энергии заряда в однородном электрическом поле
Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).
Рис. (1). Перемещение заряда в однородном поле
Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.
Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б — vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б — vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:
(A=-E_Б). ((5))
Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))
Энергия взаимодействия точечных зарядов
Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.
Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).
Рис. (2). Перемещение заряда в поле точечного заряда
Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.
В таком случае работа электрического поля на дуге (СБ) будет нулевой:
(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))
поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:
(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)
(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))
Энергия системы (n) точечных зарядов
Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.
Свойство линий напряжённости электрического поля
Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).
Рис. (3). Замкнутая линия электрического поля
Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).
Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.
Источники:
Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.
Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.
Рис. 3. Замкнутая линия электрического поля. © ЯКласс.
Сообщение от Rj_Traum
Пластины плоского конденсатора подключены к источнику с э.д.с 2 В. Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2. Граница между диэлектриком и воздухом расположена перпендикулярно пластинам. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см2.
—
Ёмкость плоского конденсатора определяется выражением
S — площадь пластин
d — расстояние между пластинами
ε — диэлекстрическая проницаемость диэлектрика между пластинами
см Электрическая ёмкость — Википедия
Полагая что вначале между пластинами конденсатора воздух ε = 1 его ёмкость равна
Энергия поля вначале
Добавлено через 8 минут
Конденсатор с половинным заполнением пространства между пластинами диэлектриком ε = 2, можно рассмотреть как параллельное соединение двух конденсаторов, с расстоянием между пластинами d/2. Пространство между пластинами 1-го из них заполнено воздухом ε = 1, второго диэлектриком ε = 2.
Результирующаяя ёмкость последовательно соединенных конденсаторов C1 и С2 определяется выражением
Обозначаяя ёмкость половинки с воздухом между пластинами как С1 и с диєлектриком как С2 получим
С2 = ε*С1
Ёмкость после заполнения половины пространства диэлектриком составит
Добавлено через 5 минут
Энергия после заполнения половины пространства диэлектриком составит
Добавлено через 5 минут
Чтобы ответить на этот вопрос
Сообщение от Rj_Traum
Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2.
Найдём отношение
Добавлено через 3 минуты
Подставив числовые значения получим
раза
Ответ: энергия поля после заполнения половины пространства между пластинами диэлектриком с ε = 2 увеличится в 4/3 раза