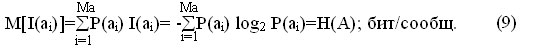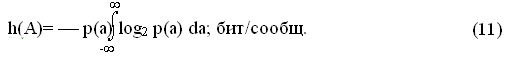Как найти избыточность источника информации

Как было показано,
энтропия максимальна при равновероятном
выборе элементов сооб­щений и отсутствии
корреляционных связей. При неравномерном
распределении вероятностей и при наличии
кор­реляционных связей между буквами
энтропия уменьшается.

Чем ближе энтропия
источника к максимальной, тем рациональнее
работает источник. Чтобы судить о том,
насколько хорошо использует источник
свой алфавит, вводят понятие избыточности.
Избыточность, с которой мы имеем дело
в теории информации, не зависит от
содержания сообщения и обычно заранее
известна из статистических данных.

Информационная
избыточность
показывает относительную
недогруженность на символ алфавита и
является безразмерной величиной:

где
—
коэффициент
сжатия (относительная энтропия).
и
берутся относительно одного и того же
алфавита.

Наличие избыточности
приводит к загрузке канала связи
передачей лишних букв сообщений, которые
не несут информации (их можно угадать
и не передавая).

Однако, преднамеренная
избыточность в сообщениях иногда
используется для повышения досто­верности
передачи информации — например, при
помехоустойчивом кодировании в системах
передачи информации с исправлением
ошибок. Большую избыточность имеет
любой разговорный язык. Например,
избыточность русского языка (как и
других) 
около 50%. Благо­даря избыточности
облегчается понимание речи при наличии
дефектов в произношении или при искажениях
речевых сигналов в каналах связи.

Если энтропия
источника сообщений не равна максимальной
энтропии для алфавита с данным количеством
качественных при­знаков (имеются в
виду качественные признаки алфавита,
при помо­щи которых составляются
сообщения), то это прежде всего означает,
что сообщения данного источника могли
бы нести большее количество информации.

Абсолютная
недогруженность
на символ сообщений такого источника

Избыточность еще
называют мерой относительного
«расточительства» в использовании
символов при передаче данного сообщения.
Избыточность отсутствует (D=0),
когда
=H,
т.е когда символы выбраны «хорошо»
(равновероятно), и избыточность стремится
к 100% (D=1),
когда полезный выход, т.е. эффективность
способа передачи, характеризуемая
частотным словарем (частотами появления
слов), и, следовательно, эффективность
используемого языка, являются
незначительными.

Таким образом, мы
имеем дело с «коэффициентом эффективности»
языка, используемого в канале передачи
сообщений.

Кроме общего
понятия избыточности существуют частные
виды избыточности.

Избыточность,
обусловленная не равновероятным
распределением символов в сообщении,

Избыточность,
вызванная статистической связью между
симво­лами сообщения,

Полная информационная
избыточность

Пример
3.35. А лфавит
источника состоит из трех букв x₁
, x₂
и
x₃
.

Определить
энтропию на 1 букву текста Х⁽¹⁾,
Х⁽²⁾
для следующих
случаев:

а)
буквы неравновероятны: p(x₁)=0,5,
p(x₂)=
p(x₃)=0,25,
а символы в последовательности на выходе
источника статистически зависимы.
Условные вероятности переходов
p(x_j⁽²⁾/x_i⁽¹⁾)
заданы таблицей

б)
вероятности букв те же, что и в п. а), но
символы независимы; в) символы в
последовательности независимы, а
вероятности букв одинаковы.

Вычислить
избыточность источника для случаев а)
и б).

Решение.
а) В случае
неравновероятных и зависимых сообщений
энтропия текста

где

а условная энтропия

Энтропия на один
символ

б)
При неравновероятных, но независимых
сообщениях энтропия

Избыточность,
обусловленная статистической зависимостью

D₁=
1 – H₁(X)/
H(X)=1-1,36/1,5=1-0,9=0,1.

в)
В случае равновероятных и независимых
сообщениях энтропия по формуле

H_max(X)=log₂m
= log₂3=1,585
бит.

Избыточность,
обусловленная неоптимальностью
распределения

D₂=
1 – H(X)/
H_max(X)=1-1,5/1,585=1-0,95=0,05.

Полная избыточность
(за счет неоптимальности распределения
и наличия статистических зависимостей)

D=
1 – H₁(X)/
H_max(X)=1-1,36/1,585=1-0,86=0,14.

Пример
3.36. Источник
сообщений вырабатывает ансамбль символов

Символы в
последовательности статистически
независимы. Вычислить энтропию источника
и определить избыточность.

Решение.
Энтропия
источника для случая неравномерных и
независимых сообщений определяется

Избыточность за
счет неоптимальности (неравновероятности)
распределения сообщений в источнике
определяется формулой

D = 1 —
H/ H_max,.
где
H_max=log₂m

Отсюда

D
= 1 — H/
H_max=1-2,27/
log₂6=1-0,87=0,13.

Количественная мера информации

Поскольку любая система связи предназначена для передачи информации, то возникает задача в оценке количества информации в передаваемом сообщении. Оценить количество информации с точки зрения ее ценности для получателя невозможно, т. к. одно и тоже сообщения для различных получателей несет различную ценность, так, например, информация получаемая при изучении данного материала для специалиста имеет весьма большую ценность.

Поэтому для определения количества информации используют вероятностные характеристики сообщения, которые не связаны с конкретным содержанием сообщения, а отражают степень их неопределенности (неожиданности). Поскольку информация это новые сведения, то и сообщения менее вероятные несут больше информации, нежели сообщения более вероятные. Таким образом, имеет место обратно пропорциональная зависимость между количеством информации в сообщении и вероятностью его появления.

Также для определения количества информации используются две зависимости:

• линейная выражающая зависимость количества информации в сообщении от его длины,   т. е. например, книга несет больше информации, чем одна ее страница;
• экспоненциальная выражающая зависимость количества информации в сообщении от возможных перестановок одних и тех же элементов этого сообщения, так, например, если источник сообщения имеет словарный запас в 1000 слов и формирует сообщение длинной 50 слов, то количество возможных сообщений будет равно 50¹⁰⁰⁰.

Чтобы учесть обе этих зависимости принимается логарифмическая шкала  для оценки количества информации. Исходя из выше сказанного количество информации в сообщении будет определятся:

I(a_i) = log_b 1/P(a_i) = -log_b P(a_i);

где I(a_i) — количество информации в сообщении a_i;

P(a_i) — вероятность появления сообщения a_i.

Выбор основания логарифма определяет единицу измерения количества информации. Для удобства в качестве основания в системах с двоичными кодами используется основание b=2 и тогда информация измеряется в битах — бинарных или двоичных единицах (от английских слов binary digit). Таким образом, количество информации определяется как:

I(a_i) = -log₂ P(a_i); бит                                                                 (8)

Из данного выражения следует, что один бит информации это:

P(a_i) = 0,5I(a_i)= -log₂ 0,5=1 бит.

т. е. 1 бит ? это количество информации, которое несет сообщение с вероятностью P(a_i)=0,5.

Термин бит используется в вычислительной и импульсной технике, поскольку там используются сообщения формируемые двумя равновероятными символами 1 и 0.

Как следует из выражения, количество информации не может быть отрицательным.

 Энтропия источника

Большинство реальных источников формирует сообщения с различным количеством информации, однако, при решении практических задач необходимо знать среднее количество информации приходящееся на одно сообщение. Среднее количество информации определяется как математическое ожидание количества информации в сообщении.

где Ма — количество возможных сообщений источника.

Величина Н(А) называется энтропией источника и характеризует среднее количество информации приходящейся на одно сообщение.

Приведенное выражение используется для определения энтропии источников дискретных сообщений. Для непрерывных сообщений а(t) энтропия теоретически стремится к бесконечности, т. к. сообщение может принимать бесконечное число значений, следовательно P(a_i)®0, а  I(a_i)®?. Однако если сообщение подвергнуть дискретизации и представить его конечным числом квантованных значений по уровню L, то можно определить среднее количество информации в одном отсчете (энтропию отсчета):

где p_i — вероятность появления в квантованном сообщении i-го уровня.

Lкв — количество уровней квантования.

Если осуществить предельный переход устремив L к бесконечности, то получится величина, называемая дифференциальной энтропией.

Энтропия является объективной информационной характеристикой источника сообщений. Она всегда положительна.

Свойства энтропии.

1⁰ Энтропия равна нулю, если одно сообщение достоверно (P(a_i)=1), а другие не возможны.

2⁰ Энтропия максимальна, когда все сообщения равновероятны, и растет с увеличением равновероятных сообщений.

3⁰ Энтропия обладает свойством аддитивности, т. е. энтропии различных источников можно складывать.

 Избыточность источника

Под избыточностью понимают наличие в сообщении «лишних» элементов, т. е. элементов не несущих смысловой нагрузки (например, союзы, предлоги). Данные элементы могут быть восстановлены за счет статистических взаимосвязей между другими элементами сообщения. Например, союзы, предлоги и знаки препинания можно восстановить, зная правила построения предложений. Таким образом:

избыточность — это мера сокращения сообщения без потери информации, за счет статистических взаимосвязей между элементами сообщения.

Количественной мерой информации является коэффициент избыточности:

c_и= [Hmax(A) ? H(A)]/Hmax(A)                                               (12)

где Н(А) — энтропия, вычисленная на основе учета статистических характеристик сообщений;

Hmax(A) — максимальная энтропия источника, которая согласно второму свойству равна:

Hmax(A)= log₂ Ma; бит/сообщ.                                                 (13)

Наличие избыточности при передаче сообщений имеет свои положительные и отрицательные стороны. Сообщение, обладающее избыточности требует большего времени передачи и, соответственно большего времени занятия канала. Однако повышение избыточности приводит к увеличению помехоустойчивости сообщения. Она способствует обнаружению и исправлению ошибок в принятых сообщениях. Это связано с тем, что для формирования сообщения используются не все возможные комбинации символов, а лишь определенные (разрешенные), которые заносятся в специальные справочники (словари). При приеме сообщения с элементами (словами) которых нет в справочниках говорит о наличии ошибки и ошибочный элемент может быть заменен похожим по написанию или подходящим по смыслу. Все языки обладают избыточностью равной c_и»0,5.

 Производительность источника

Производительность источника — это среднее количество информации создаваемое источником в единицу времени.

Производительность источника дискретных сообщений определяется как:

H’д.с.(А)=Н(А)/tср; бит/с                                                          (14)

где tср — средняя длительность сообщения:

tср=tн/n; с                                                                                   (15)

где tн — время, в течении которого было сформировано n сообщений.

Производительность источника непрерывных сообщений определяется как:

H’н.с.(А)=fд Hотсч(А); бит/с                                                    (16)

где fд — частота дискретизации (2Fmax).

Если сообщение квантуется равновероятными уровнями, т. е. p_i=1/L, то производительность источника может быть определена как:

H’н.с.(А)=fд log₂ L; бит/с                                                          (17)

Категория: Основы теории информации

Привет, Вы узнаете про избыточность информации, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
избыточность информации, коэффициент стохастичности , настоятельно рекомендую прочитать все из категории Синергетика.

Избыточность — термин из теории информации, означающий превышение количества информации, используемой для передачи или хранения сообщения, над его информационной энтропией. Для уменьшения избыточности применяется сжатие данных без потерь, в то же время контрольная сумма применяется для внесения дополнительной избыточности в поток, что позволяет производить исправление ошибок при передаче информации по каналам, вносящим искажения (спутниковая трансляция, беспроводная передача и т. д.).

избыточность информации Информация может быть избыточной. Например, сообщение, переданное на естественном языке, может быть избыточным на 70% (или даже на 80%). Информация может быть избыточной. Например, сообщение, переданное на естественном языке, может быть избыточным на 70% (или даже на 80%). Русский язык является более избыточным, чем, например, Английский. Русский язык является более избыточным, чем, например, Английский. Избыточной может быть и формализованная информация. Избыточной может быть и формализованная информация.

Количественное определение

Информационное содержание одного сообщения в потоке, в наиболее общем случае, определяется как:

Обозначим как R логарифм числа символов в алфавите сообщений:

Абсолютная избыточность может быть определена как разность этих двух величин:

Соотношение называется относительной избыточностью и дает математическую оценку максимальной степени сжатия, на которую может быть уменьшен размер файла.

Другие определения избыточности

Мера избыточности между двумя случайными величинами — взаимная информация.

Сжатие и избыточность

• Сжатие информации возможно при наличии избыточности.
• Информация, закодированная последовательностью нулей и единиц, также может содержать некоторую степень избыточности.
• На практике используются различные методы сжатия информации.

Виды избыточности информации

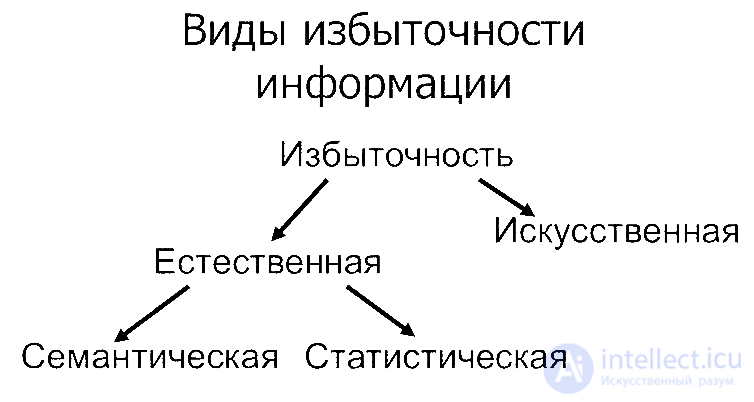
Примеры

1) Задание: найти производную: y=x2

Решение: y'(x)= 2x

Можно было записать и так: y’= 2x

т.е. указание аргумента в скобках является избыточным. т.е. указание аргумента в скобках является избыточным

2) 3*3*3*3 = 3 * 4

Здесь избыточность информации левой части перекодируется в более компактную запись в правой части

3) Избыточность информации в информационных технологиях

• Многие форматы данных при хранении на дисках в виде последовательности нулей и единиц являются избыточными.
• Например, файлы баз данных.
• Текстовые файлы.
• Файлы изображений типа *.bmp
• Звук в аудио CD формате.

4) Искусственно созданная избыточность

• Для повышения надежности связи идут по пути создания резервных каналов, либо по пути многократного повтора сообщения.
• Для ввода очень критичной к ошибкам информации применяют труд сразу нескольких операторов, вводящих одну и ту же информацию.

5)Запишем последовательные значения информационной энтропии при учете все более протяженной корреляции для русского языка

Вернемся к текстам, представленным в табл . Об этом говорит сайт https://intellect.icu . 1. предыдущего параграфа

С помощью функции можно подсчитать, что при переходе от фразы 1 к фразе 4 энтропия текста уменьшилась примерно в 5 раз. Во фразе 2 неопределенность появления каждой буквы составляет примерно 4 бита на букву. Во фразе 4 неопределенность составляет 1 бит на букву. Это вызвано тем, что в структуре реального текста содержится информация обо всех грамматических и фонетических правилах русского языка. Разница между энтропией реального текста = 1 бит/буква и максимальной энтропией фразы I_max = 5 бит/буква и есть количество информации, содержащейся в правилах.

Язык характеризуется избыточностью информации, которую можно определить по формуле

, (1)

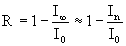
где I_n — значение информационной энтропии при данном уровне n корреляций.

Для русского языка избыточность для корреляций n = 0, 1, 2, 3 составляет

Однако на избыточность информации можно посмотреть по-иному, а именно: исследование сообщений текстов телеграмм, кодов и т. д. показало, что все они обладают избыточной информацией, которую можно и не передавать по каналам связи. Но то, что избыточно для каналов связи, вовсе не лишнее для самого языка. Именно избыточная информация, накапливаемая в совокупности всех грамматических и фонетических правил и сделала язык языком. Функция отразила в себе весь процесс упорядочивания как постепенный переход от равенства всех вероятностей к их существенному различию, когда вероятность буквы «О» возрастает до 0,09, а буквы «Ф» — падает до 0,0002.

Избыточность текста имеет очень широкое применение на практике. Широко известные среди пользователей ЭВМ программы-упаковщики (архиваторы) сжимают файлы как раз за счет избыточности информации.

Если процесс упорядочивания текста будет и дальше продолжаться, то можно предсказать, что же в конце концов получится. Бессмысленная фраза 1 получила подобие знакомых нам текстов, когда разные буквы стали иметь разные вероятности. Но чем больше вероятности одних букв, тем меньше вероятности остальных в силу условия : преимущество одних букв оплачивается бесправием других.

Продолжим этот процесс далее, и тогда одна какая-нибудь буква, например А, заберет все права, т. е. W_А = 1, а вероятности появления остальных букв W_i = 0. Итак, доведенное до конца упорядочивание, приводит к странному тексту типа АААА…, т. е. происходит вырождение.

Однако в некоторых случаях и такой текст может оказаться полезным: он может служить сигналом какого-нибудь события. Например, сообщение о том, что прибыл груз, человек и т. д. Пока вероятности букв одинаковы, текст бессмысленно хаотичен; вероятности появления букв различны — в тексте появляется некоторый порядок; продолжаем этот процесс дальше и текст превращается в повторение одной буквы. Избегнув хаоса, текст устремляется к упрощению, не несущему информации. Но так это кажется на первый взгляд, дело гораздо сложнее: в мире есть и такие явления, которые похожи на текст из одной буквы, но, тем не менее, такая информация полезна. Например, на некоторые воздействия внешней среды организм отвечает стереотипно: почувствовали при ожоге боль — отдернули рефлекторно руку. По одной и той же команде осуществляется одно и то же движение, независимо от того нагрет ли предмет до 70, 100 или 500 градусов. Пока есть различные вероятности, ответы разнообразны; когда все свелось к одной букве, на любые запросы система дает один и тот же ответ. Это жестко детерминированные системы. Примером может служить Солнечная система, где движения планет предопределены на бесконечно долгое время. Но ведь эта система была когда-то энтропийной и непредсказуемой, хаосом движущихся в пространстве частиц.

Из хаоса возникла жестко детерминированная система, т. к. условия существования системы тоже жестко определены. Можно ожидать, что в отдаленном будущем, исчерпав энергию, погаснет Солнце, или произойдет какое-либо космическое столкновение, и Солнечная система опять превратится в хаос частиц.

В значительной степени детерминированной системой можно считать сердце, задача которого ритмично сжиматься, разжиматься и гнать кровь. При изменении внешних условий ритмичность работы сердца может нарушиться, и здесь для регулировки процесса создана нервная система и другие органы (гормональная система). Без них сердце при изменении условий не сможет выполнить своих функций и станет непригодным как текст из одной буквы А, когда даже не ясно, куда посылать эту примитивную команду.

Для выявления закономерностей взаимодействия информации с энтропией удобной системой оказался письменный текст, который отражает в себе более сложную систему — человеческий язык. Отметим, что исследование различных языков показало, что все они обладают близкими статистическими характеристиками.

Наш язык — это гибкая, подвижная, легко адаптирующаяся в различных условиях система. В языке существует определенная доля непредсказуемости, доля «энтропии». Рассмотрим этот вопрос подробнее.

Обозначим через избыточную предсказуемую информацию, которая позволяет прочитать текст при нехватке букв.

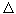
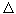
Величина I_n равна разности между энтропией реального текста = 1 бит на букву и максимальной энтропией, например, фразы 1 (табл. 1) I₀ = 5 бит на букву, т. е.

I = I₀ — = 5 — 1 = 4 бита на букву.

Это и есть количество информации, содержащейся в грамматических и фонетических правилах, которым подчиняются реальные тексты. Этого количества информации 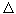I = 4 бита/буква оказывается достаточно, чтобы превратить абракадабру (фраза 1) в осмысленный текст.

Обозначим через G
коэффициент стохастичности , равный

. (2)

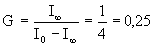
Сопоставляя формулы (1) и (2) найдем связь между избыточностью информации R и коэффициентом стохастичности G

.

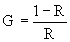
Итак, для обычного текста G = 0,25; текст из одних «А» обладает нулевой энтропией, т. е. = 0, поэтому G = 0. Текст с максимальной энтропией I = I₀ — = 0 не подчиняется правилам и G = . В официальных документах существует более жесткая детерминированность, чем в литературных текстах, и G < 0,25.

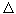
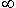
При G = 0 ничего нового сообщить нельзя, при G = 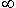невозможно ничего понять, т. к. обрушивается поток слов, оптимальное соотношение непредсказуемости (энтропийности) и детерминации (правил) G = 0,25. Это результат длительной эволюции языка.

Исследования на энтропийность сочетания звуков в музыкальных произведениях выявили оптимальное соотношение детерминированности и стохастичности, и оно также G ~ 0,25.

В картинах также соблюдается правило золотой середины. Если картина несет в себе строгие классические законы, то их G близко к нулю. Напротив, в творениях без оглядки G возрастает, в подобных произведениях не всегда возможно уловить смысл.

В заключение заметим, что для реальных случаев коэффициент G определить очень сложно, здесь можно рассуждать только о тенденциях (тяготению к G = 0 или G = 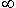), окончательный суд могут вынести на интуитивном уровне эксперты.

Рассуждения о коэффициенте стохастичности применимы ко многим явлениям социальной жизни — к архитектуре городов, феномену моды, к психике человека и т. д. Психический комфорт, ощущение счастья, по-видимому, определяется тем, насколько условия жизни индивидуума соответствуют потребностям его психики. Последняя как заложена в нем от природы, так и сформирована его воспитанием и может также характеризоваться критерием G. Натуре человека противопоказаны как чрезмерное бравирование спонтанностью (оригинальничанье), так и излишняя детерминированность, подчиненная требованиям выгоды и удобства. Высокая психическая спонтанность приводит к нравственной неустойчивости, беспокойству, лишает способности к сосредоточенной работе. Чрезмерно детерминированная психика убивает творческое начало, лишает артистизма. Задача психиатрии заключается в создании обстановки, способной детерминировать слишком спонтанную психику или напротив, с помощью эмоций «расшевелить» спонтанность. Природа предоставляет человеку свободу выбора, позволяющую внезапно найденным удачным решением найти неожиданный поворот.

Наверное, должен сформироваться в любой ситуации оптимальный коэффициент стохастичности G_опт на всех уровнях организации — в косной, живой и социальной природе.

Цель человека на земле только и заключается в одной беспрерывности процесса достижения, иначе сказать, в самой жизни, а не собственно в цели, которая есть формула «дважды два четыре». А ведь «дважды два четыре» есть уже не жизнь, а начало смерти.

Вау!! 😲 Ты еще не читал? Это зря!

• Обнаружение и исправление ошибок
• Алгоритмическая теория информации
• Колмогоровская сложность
• Кодирование с минимальной избыточностью
  • Кодирование Хаффмана
• Сжатие данных
• Функция Хартли
• Негэнтропия
• Теорема исходного кода
• Неполнота

На этом все! Теперь вы знаете все про избыточность информации, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое избыточность информации, коэффициент стохастичности
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Синергетика