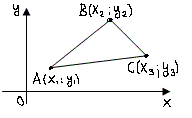Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
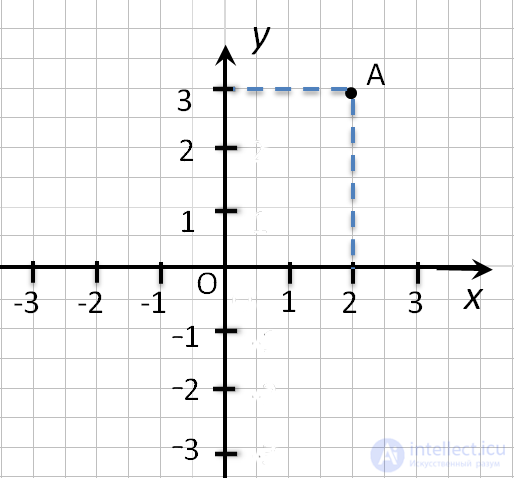
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
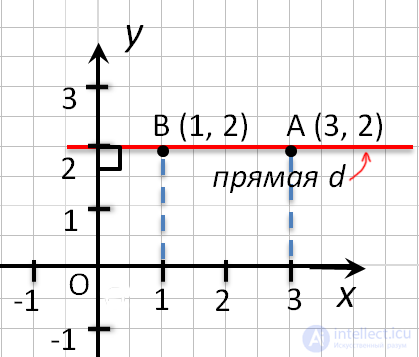
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
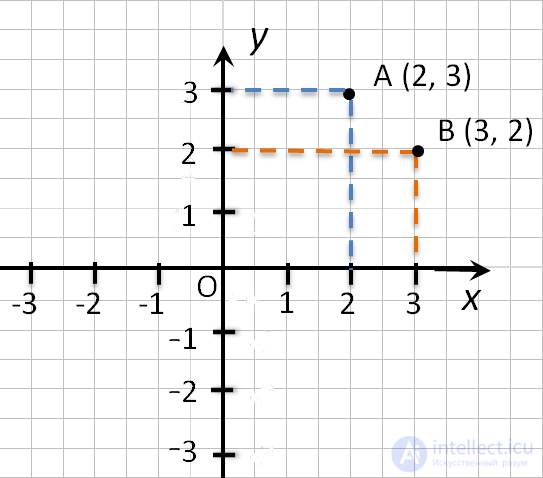
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
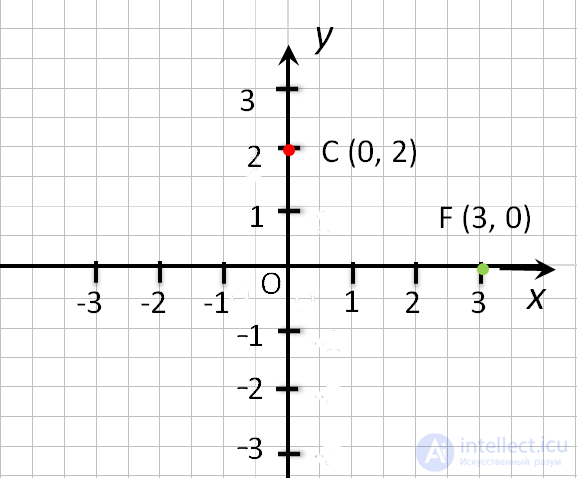
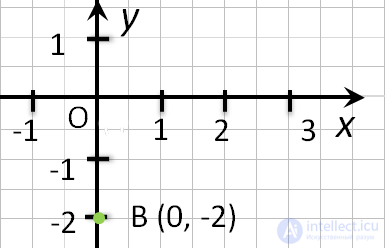
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
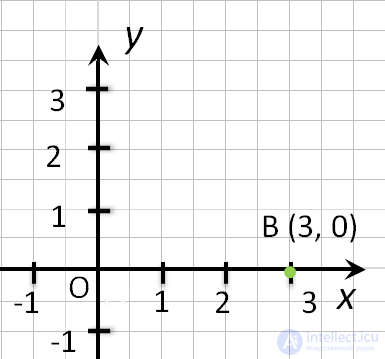
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
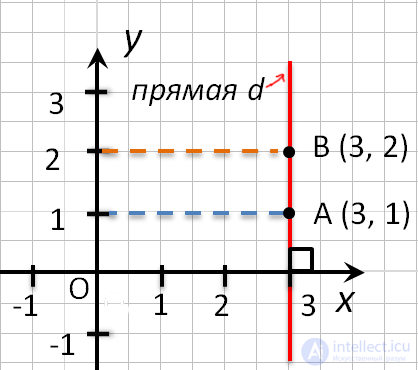
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
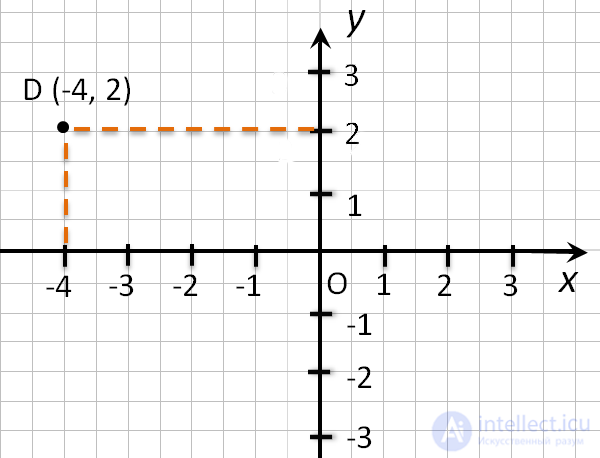
Чтобы определить положение точки по её координатам,
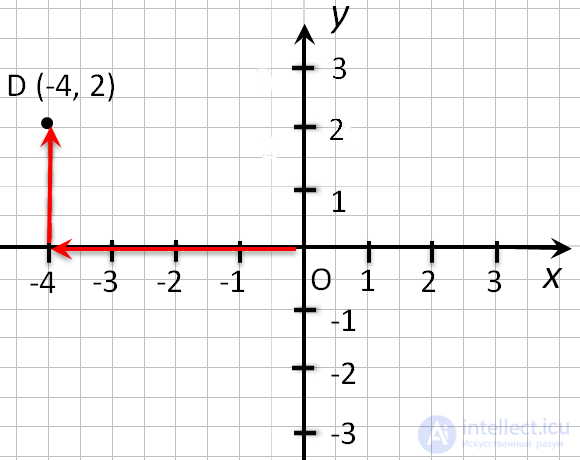
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
«Координаты точки и координаты вектора. Как найти координаты вектора» 👇
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ — единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$
Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$
$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$
Следовательно
$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а
$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$
Значит
$koverline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.
Решение.
$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Привет, мой друг, тебе интересно узнать все про координаты точки, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
координаты точки , настоятельно рекомендую прочитать все из категории Арифметика.
каждой точке координатной плоскости соответствуют две координаты.
координаты точки на плоскости — это пара чисел, в которой на первомместе стоит абсцисса,
а на втором — ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.
Точка пересечения с осью x называется абсциссой точки А, а с осью y называется ординатой точки А.
Обозначают координаты точки, как указано выше (•) A (2; 3).
Пример (•) A (2; 3) и (•) B (3; 2).
На первом месте записывают абсциссу (координату по оси x), а на втором — ординату (координату по оси y) точки.
Особые случаи расположения точек
- Если точка лежит на оси Oy, то ее абсцисса равна 0 . Об этом говорит сайт https://intellect.icu . Например, точка С (0, 2).
- Если точка лежит на оси Ox, то ее ордината равна 0. Например, точка F (3, 0).
- Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по ее координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по ее координатам, например, точки D (-4 , 2), надо:
- Отметить на оси Ox, точку с координатой (-4), и провести через нее прямую перпендикулярную оси 0x.
- Отметить на оси Oy, точку с координатой (2), и провести через нее прямую перпендикулярную оси 0y.
- Точка пересечения перпендикуляров (•) D — искомая точка. У нее абсцисса равна (-4), а ордината равна (2).
Второй способ
Чтобы найти точку D (-4 , 2) надо:
- Сместиться по оси x влево на 4 единицы, так как у нас перед 4 стоит «-».
- Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.
Как ты считаеешь, будет ли теория про координаты точки улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое координаты точки
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Из статьи мы узнали кратко, но емко про координаты точки
Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.
Оси координат (Ox), (Oy) и (Oz) называются соответственно: (Ox) — ось абсцисс, (Oy) — ось ординат, (Oz) — ось аппликат.
Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: ((Oxy)), ((Oyz)) и ((Oxz)).
Положение точки (A) в пространстве определяется тремя координатами: (x), (y) и (z).
Координата (x) называется абсциссой точки (A), координата (y) — ординатой точки (A), координата (z) — аппликатой точки (A).
Записываются так: (A(x; y; z)).
Если точка находится на оси (Ox), то её координаты (X(x; 0; 0)).
Если точка находится на оси (Oy), то её координаты (Y(0; y; 0)).
Если точка находится на оси (Oz), то её координаты (Z(0; 0; z)).
Если точка находится в плоскости (Oxy), то её координаты
A1x;y;0
.
Если точка находится в плоскости (Oyz), то её координаты
A20;y;z
.
Если точка находится в плоскости (Oxz), то её координаты
A3x;0;z
.
Если в системе координат от начальной точки отложить единичные векторы
i→
,
j→
и
k→
, то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде
OA→=x⋅i→+y⋅j→+z⋅k→
.
Коэффициенты (x), (y) и (z) определяются одним-единственным образом и называются координатами вектора.
Записываются так:
OA→x;y;z
.
Рассмотрим правила о том, как с помощью координат записать:
— координаты суммы векторов, если даны координаты векторов:
,
b→x2;y2;z2
,
a→+b→x1+x2;y1+y2;z1+z2
;
— координаты разности векторов, если даны координаты векторов:
a→−b→x1−x2;y1−y2;z1−z2
;
— координаты произведения вектора на число, если даны координаты вектора:
— длину вектора:
— координаты вектора, если даны координаты начальной и конечной точек вектора:
,
BxB;yB;zB
,
AB→xB−xA;yB−yA;zB−zA
;
— расстояние между двумя точками, если даны координаты точек:
;
— координаты серединной точки отрезка, если даны координаты начальной и конечной точек отрезка:
.
Простейшие задачи аналитической геометрии на плоскости
1. Расстояние между двумя точками.
Теорема
1.
Для любых двух точек




(1.1)
Например,
если
даны точки
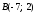
то расстояние между ними:

2. Площадь треугольника.
Теорема
2.
Для любых точек

не лежащих на одной прямой, площадь
треугольника


(1.2)
Например,
найдем площадь треугольника, образованного
точками




Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.
3. Деление отрезка в заданном отношении.
Пусть
на плоскости дан произвольный отрезок
и
пусть

точка этого отрезка, отличная от точек
концов. Число

определенное равенством
называетсяотношением,
в
котором точка

.
Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
и данным координатам точек
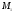


Теорема
3.
Если
точка
делит отрезок
в
отношении
то
координаты этой точки определяются
формулами:





Следствие:
Если
– середина отрезка

где

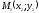
то

Например.
Даны точки
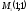

Найти координаты точки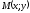
которая в два раза ближе к
чем к
Решение:
Искомая точка
делит
отрезок
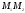
отношении

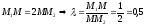
тогда
,
получили

Полярные координаты
Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
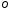
называемойполюсом,
и исходящего из нее луча

оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть

–
расстояние от точки
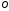
точки
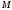

полярную ось для совмещения с лучом
Полярными
координатами точки

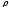

При этом число
радиусом,
число

углом.
Обозначается

Полярный радиус может иметь любое
неотрицательное значение:
Обычно считают, что полярный угол
изменяется в следующих пределах:
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.
Связь между полярными координатами точки и ее прямоугольными координатами.
Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.
Пусть


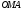

Тогда(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.
С
другой стороны, по теореме Пифагора

(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.
Заметим,
что формула


так как
Из этих двух значений угла
равенства
Например,
найдем полярные координаты точки




т.к.
четверти
Пример
1:
Найти точку, симметричную точке
относительно
биссектрисы первого координатного
угла.
Решение:
Проведем
через точку А
прямую l1,
перпендикулярную биссектрисе l
первого координатного угла. Пусть

На прямой
l1
отложим отрезок
СА1,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А1СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA1|.
Треугольники
ADO
и
ОЕА1
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA1|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А1(4;-2).
Отметим,
что имеет место общее утверждение: точка
A1,
симметричная точке
относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
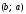
то есть
Пример
2:
Найти точку, в которой прямая, проходящая
через точки

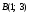
пересечет ось
Ох.
Решение:
Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где
–
координаты точки А,
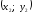
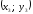
Получаем

т.е.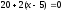


Следовательно, точка
С
имеет координаты


т.е.
Пример
3: В
полярной системе координат заданы точки


Найти:
а)
расстояние между точками
и

б)
площадь треугольника
ОМ1М2
(О
– полюс).
Решение:
а)
Воспользуемся формулами (1.1) и (1.5):

то
есть,
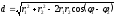
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом


находим площадь треугольника
ОМ1М2.