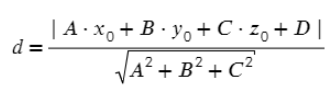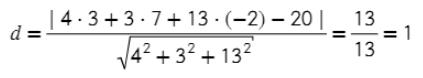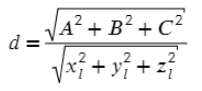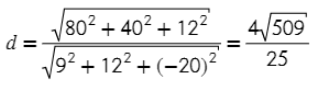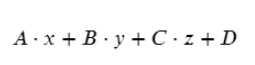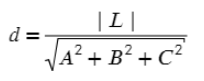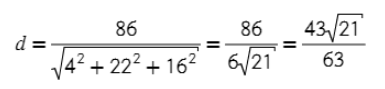Интервал и уклон прямой.
Длина проекции
отрезка прямой называется его заложением
и обозначается буквой L
(рис. 99),
разность расстояний концов отрезка до
плоскости П0
называется
превышением и обозначается буквой Н.
Наклон прямой
может быть выражен не только величиной
угла α, но
также уклоном. Уклон — i
— равен
тангенсу угла наклона прямой к плоскости
П0:
i
=H
/ L =
tg α.
Если превышение равно единице (Н=1),
то заложение,
ему соответствующее, называется
интервалом и обозначается буквой l.
Уклон в этом случае равен i=1
/ l.
Откуда следует, что уклон и интервал
прямой — величины, обратные друг другу.
Следствие:
прямую линию в проекциях с числовыми
отметками можно задать направлением
ее проекции с проекциями одной точки и
интервалом или уклоном (рис. 100).
Проградуировать
прямую — это значит, определить точки,
отметки которых выражены целыми числами.
Существует несколько способов
градуирования прямой.
1 способ (рис. 101) —
проведем через произвольные, но равные
интервалы, параллельно отрезку АВ серию
параллельных прямых; обозначим их как
горизонтали с целыми отметками.
На перпендикулярах,
восстановленных к проекции прямой АВ
из точек
А5,8
и В3,5,
отметим положение точек А1В1.
Точки пересечения ее с построенными
горизонталями дают положение искомых
точек.
2 способ (рис. 101)
— вариант решения задачи делением отрезка
в заданном отношении по теореме Фалеса.
3 способ — аналитический
— с помощью формул уклона и интервала
прямой. Зная длину проекции прямой —
заложение L
(рис. 101) легко определить величину
интервала из отношения: l
= L/H,
где Н
— превышение точки В
над точкой
А.
14.3. Взаимное положение двух прямых
Параллельные
прямые (рис. 102а).
Две прямые
параллельны между собой, если их проекции
также параллельны, интервалы и уклоны
равны и числовые отметки возрастают в
одну и ту же сторону.
ℓAB=ℓCD;
ίAB=ίCD
Пересекающиеся
прямые (рис. 102б).
Точка пересечения
пересекающихся прямых имеет одинаковые
отметки на первой и второй прямой. Это
легко проверить, если прямые проградуированы:
прямые, соединяющие точки с одинаковыми
отметками, параллельны между собой.
Скрещивающиеся
прямые (рис. 102в).
Если признаки
параллельности и пересечения прямых
отсутствуют, прямые скрещиваются.
Отметки прямых в точке пересечения их
проекций разные для каждой прямой.
14.4. Проекции плоскости.
Плоскость в
проекциях с числовыми отметками может
быть задана всеми известными в
начертательной геометрии способами.
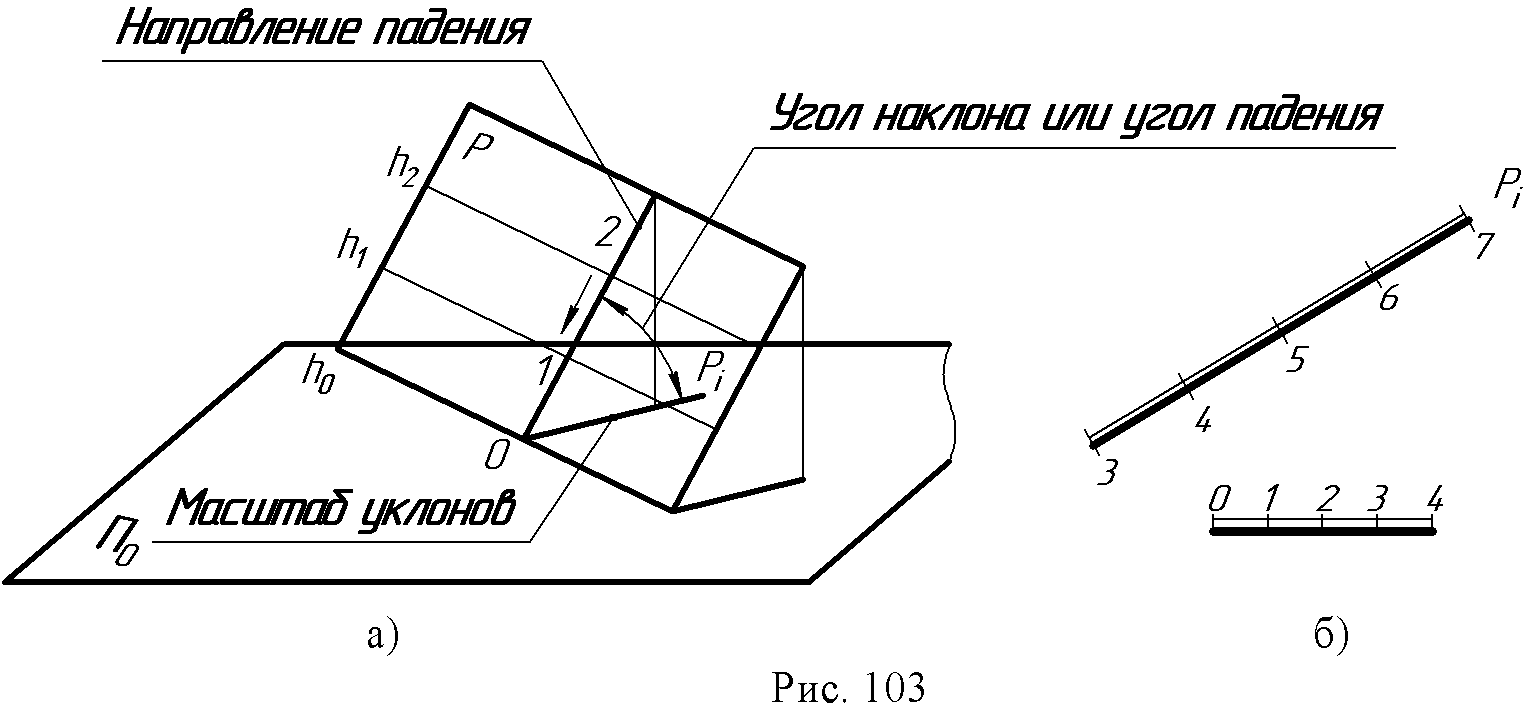
Но часто плоскость задается масштабом
уклонов (рис. 103 а, б). Такое задание
является наиболее наглядным и удобным
при решении инженерных задач.
Проекции горизонталей
плоскости и масштаб уклонов пересекаются
под прямым углом. Интервал плоскости
равен интервалу ее линии ската. Линия
ската плоскости иначе называется линией
падения. Она определяет угол наклона
или угол падения плоскости (рис. 103а).
Масштабом уклонов
называют проградуированную проекцию
линии ската плоскости. Масштаб уклонов
изображается на плане двумя параллельными
прямыми: толстой и тонкой с нанесенными
на ней отметками горизонталей плоскости
(рис. 103б).
Направление и угол
простирания. При проведении проектно
– изыскательских и геологических работ
возникает необходимость определять
положение плоскости относительно сторон
света. Это положение определяется такими
понятиями как направление простирания
и угол простирания. За направление
простирания плоскости принимается
направление вправо по горизонталям,
если смотреть на масштаб уклона плоскости
в сторону возрастания отметок (рис. 103
а, в).
Углом простирания
плоскости называется угол между северным
концом меридиана и направлением
простирания против хода часовой стрелки
(рис. 103в).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Очень часто на практике необходимо найти расстояние между точкой и некой прямой линией или между двумя прямыми линиями в пространстве, например, иногда определять расстояние между двумя линиями приходится и в реальной жизни. Хорошая иллюстрация такого примера — это знак, который вешают на мосты для грузовиков, указывающий максимальную высоту грузовика, которая может проехать под данным мостом.
Расстояние от верхней грани грузовика и нижней грани в данном случае определяют как расстояние между двумя прямыми.
Расстояние между 2 прямыми в пространстве — это отрезок, соединяющий две прямые линии по наикратчайшему расстоянию между ними, то есть перпендикулярный к обеим прямым.
Определение 1
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной заданной прямой и плоскостью, в которой лежит вторая прямая.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Чтобы было чуть проще понять, что это такое, давайте повторим определение скрещивающихся прямых:
Определение 2
Скрещивающиеся прямые — это две прямые, которые не лежат в одной плоскости и не имеют каких-либо совместных друг для друга точек.
Соответственно, для того чтобы найти расстояние между скрещивающимися прямыми в пространстве, необходимо от одной из прямых опустить перпендикуляр на плоскость, в которой лежит другая прямая.
Расстояние же между двумя параллельными прямыми в пространстве является одинаковым на протяжении всей длины параллельных прямых, то есть перпендикуляр, опущенный из одной параллельной прямой на другую, всегда будет одной и той же длины вне зависимости от того, из какой именно точки его опустили.
Метод координат для определения расстояния между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми в пространстве можно найти используя метод координат, для этого необходимо:
«Расстояние между 2 прямыми в пространстве» 👇
- Найти координаты точек $M_1$ и $M_2$, лежащих на прямых $a$ и $b$ соответственно.
- Вычислить икс, игрек и зет направляющих векторов для прямых $a$ и $b$.
- С помощью векторного произведения векторов $overline{a}$ и $overline{b}$ нужно найти вектор-нормаль для плоскости, в которой лежит прямая $b$. Затем необходимо записать общее уравнение плоскости: $A (x – x_0) + B(y – y_0) + C(z – z_0) = 0$, и от него перейти к нормированному виду уравнения плоскости следующего вида: $ x cdot cos α + y cdot cos β + z cdot cos{γ} – p = 0$, где $cos α, cos β$ и $cos γ$ — координаты единичного нормального вектора плоскости, а $p$ — свободный член, это число равно расстоянию от точки начала координат до плоскости.
- Для вычисления расстояния от точки $M$ до искомой плоскости, нужно воспользоваться следующим уравнением:
$M_1H_1 = |x_1 cdot cos α + y_1 cdot cos β + z_1 cdot cos{γ} – p|$, где $x_1, y_1, z_1$ – координаты точки $M_1$, лежащей на прямой $a$, а $H_1$ — точка, лежащая на искомой плоскости.
Пример 1
Найти расстояние между двумя скрещивающимися прямыми, заданными уравнениями:
$d_1$:
$frac {x-2}{2} = frac {y + 1}{-3} = frac{z}{-1}$
и $d_2$: $begin{cases} frac{x + 1}{1} = frac{y}{-2} \ z – 1 = 0 end{cases}$
Рисунок 1. Расстояние между двумя скрещивающимися прямыми в пространстве
Для этого воспользуемся следующей формулой:
$ ρ(d_1d_2) = frac{| overline{p_1} cdot overline{p_2} cdot overline{M_1M_2}|}{[overline{p_1} × overline{p_2}]}$
Сначала найдём смешанное произведение векторов. Для этого найдём точки, лежащие на данных прямых, и их направляющие вектора:
$d_1$: $frac {x-2}{2} = frac {y + 1}{-3} = frac{z}{-1}$, точка, лежащая на прямой — $M_1$ с координатами $(2;-1;0)$, а направляющий вектор — $overline{p_1}$ с координатами $(2; -3; -1)$
$d_2$: $begin{cases} frac{x + 1}{1} = frac{y}{-2} \ z – 1 = 0 end{cases}$, точка, лежающая на прямой — $M_2$ с координатами $(-1; 0; 1)$,
а её направляющий вектор — $overline{p_2}$ с координатами $(1; -2; 0)$
Теперь найдём вектор $overline{M_1M_2}$:
$overline{M_1M_2} = (-1-2;0-(-1);1-0) = (-3; 1; 1)$
Найдём смешанное произведение векторов:
$overline{p_1} cdot overline{p_2} cdot overline{M_1M_2} = begin{array}{|ccc|} 2& 1 & -3 \ -3& -2 & 1 \ -1 & 0 & 1 \ end{array} = — begin{array}{|cc|} 1 & -3 \ -2 & 1 \ end{array} + begin{array}{|cc|} 2 & 1 \ -3 & -2 \ end{array} = -(1 — 6) + (4 + 3) = 4$
Теперь найдём векторное произведение векторов:
$[|overline{p_1} × overline{p_2}|] = begin{array}{|ccc|} i& j & k \ 2 & -3 & -1 \ 1 & -2 & 0 end{array} = begin{array}{|cc|} -3 & -1 \ -2 & 0 end{array} cdot overline{i} — begin{array}{|cc|} 2 & -1 \ 1 & 0 end{array} cdot overline{j} + begin{array}{|cc|} 2 & -3 \ 1 & -2 end{array} cdot overline{k}$
$[|overline{p_1} × overline{p_2} |]= -2 overline{i} — overline{j} — overline{k}$
Длина этого векторного произведения составит:
$overline{p_1} × overline{p_2} = sqrt{(-2)^2 + (-1)^2 + (-1)^2} = sqrt{6}$
Соответственно, длина между скрещивающимися прямыми составит:
$ ρ(d_1d_2) = frac{|4|}{sqrt{6}} ≈ 1,63$
Пример 2
Даны две параллельные несовпадающие прямые $g$ и $m$, ниже приведены уравнения для них. Определить расстояние между ними.
$g$: $frac{x-1}{4} = frac{y + 1}{6}= frac{z+3}{8}$
$m$: $frac{x+1}{2} = frac{y — 1}{3}= frac{z — 3}{4}$
Расстояние в этом случае для них вычисляется по следующей формуле:
$ρ(m;g) =frac{|[overline{r_2} — overline{r_1} × overline{s_1}]|}{|overline{s_1}|}$, где
$overline{r_2}, overline{r_1}$ — радиус-векторы для каждой прямой, а $s_1$ — направляющий вектор.
Радиус-вектор для первой прямой будет $r_1={1; -1; -3}$, а направляющий вектор $s_1 = {4; 6; 8}$.
Радиус-вектор для второй прямой будет $r_2={-1; 1; 3}$, а направляющий вектор $s_2 = {2; 3; 4}$.
Найдём векторную разность радиус-векторов:
$overline{r_2} — overline{r_1} = {-1; 1; 3} — {1; -1; -3} = {-2;0;0}$
Теперь найдём её произведение с направляющим вектором для первой прямой:
$[overline{r_2} — overline{r_1} × overline{s_1}] = begin{array}{|ccc|} i & j & k \ -2 & 0 & 0 \ 4 & 6 & 8 \ end{array} = — 16j – 12k = {0;-16;-12}$
$|[overline{r_2} — overline{r_1} × overline{s_1}]| = sqrt{(-16)^2 + (-12)^2} = 20$
$|overline{s_1}| = sqrt{4^2 + 6^2 +8^2} = 2sqrt{29}$
$ρ(m;g) = frac{20}{2sqrt{29}} = frac{10}{sqrt{29}} ≈ 1.85$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Нахождение кратчайшего расстояния между прямыми в пространстве
Содержание:
- Что такое расстояние между прямыми в пространстве
- Метод координат для определения расстояния
-
Примеры задач с решением
- Задача 1
- Задача 2
Что такое расстояние между прямыми в пространстве
Для начала дадим определение этому понятию.
Определение
Расстояние между прямыми в пространстве — это отрезок, который соединяет две прямые линии по самому короткому пути. Иными словами, он перпендикулярен обеим этим прямым.
Но не всегда две линии могут быть параллельны друг другу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, чтобы найти расстояние между этими скрещивающимися прямыми, нужно от одной из прямых провести перпендикуляр на плоскость, в которой лежит другая прямая.
Между параллельными прямыми расстояние одинаково на протяжении всей их длины: перпендикуляр, опущенный из любой точки одной из этих линий, всегда будет одной и той же величины.
Метод координат для определения расстояния
Разберем пошагово способ определения расстояния между двумя скрещивающимися прямыми с помощью метода координат.
- Определить координаты точек (М_1) и (М_2), лежащих соответственно на прямых a и b.
- Найти x, y и z направляющих векторов для прямых a и b.
- Найти вектор-нормаль для плоскости, в которой лежит прямая b с помощью векторного произведения (overrightarrow a) и (overrightarrow b).
- Записать общее уравнение плоскости: (A(x-x_0)+B(y-y_0)+C(z-z_0)=0) и потом записать к нормированному виду уравнения плоскости, которое выглядит так: (xtimescosleft(alpharight)+ytimescosleft(betaright)+ztimescosleft(gammaright)-p=0), где p — свободный член (число, которое равно расстоянию точки начала координат до плоскости), а (cosleft(alpharight),;cosleft(betaright)) и (cosleft(gammaright)) — координаты единичного нормального вектора плоскости.
- Далее, для определения расстояния от точки M до искомой плоскости, воспользуемся следующим уравнением: (M_1H_1=left|x_1timescosleft(alpharight)+y_1timescosleft(betaright)+z_1cosleft(gammaright)-pright|), где (x_1), (y_1) и (z_1) — координаты точки (M_1), лежащей на прямой a, а (H_1) — точка, лежащая на искомой плоскости.
Примеры задач с решением
Задача 1
Дан куб (ABCDA_1B_1C_1D_1) с ребром равным (sqrt{32}) см. Найти расстояние между прямыми (DB_1) и (CC_1).
Решение
Расстояние между скрещивающимися прямыми будем искать в качестве расстояния между прямой (CC_1) и плоскостью, проходящей через (DB_1) параллельно (CC_1). Так как (DD_1parallel CC_1), плоскость ((B_1D_1D)) параллельна (СС_1).
Сначала нужно доказать, что (CO) — перпендикуляр, проведенный к этой плоскости. (COperp BD) (как диагонали квадрата) и (COperp DD_1) (так как ребро (DD_1) перпендикулярно всей плоскости ((ABC))). Получается, (CO) перпендикулярен двум пересекающимся прямым из плоскости. Значит, (COperp(B_1D_1D)).
(AC) — диагонально квадрата — равна (ABsqrt2), то есть (AC=sqrt{32}timessqrt2=sqrt{64}=8) см. Следовательно, (CO=frac12times AC=4) см.
Ответ: 4 см.
Задача 2
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве:
(left{begin{array}{l}x=-2\y=1+2timeslambda\z=4-3timeslambdaend{array}right.)
А прямую b канонические уравнения прямой в пространстве:
(frac x1=frac{y-1}{-2}=frac{z+4}6).
Вычислить расстояние между заданными прямыми.
Решение
Прямая a проходит через точку (M_1(-2, 1, 4)) и имеет направляющий вектор (overrightarrow a=(0, 2, -3)). Прямая b проходит через точку (M_2 (0, 1, -4)), а ее направляющий вектором является вектор (overrightarrow b=(1, -2, 6)).
Найдем векторное произведение векторов( overrightarrow a=(0, 2, -3)) и (overrightarrow b=(1, -2, 6): left[overrightarrow atimesoverrightarrow bright]=begin{vmatrix}overrightarrow i&overrightarrow j&overrightarrow k\0&2&-3\1&-2&6end{vmatrix}=6timesoverrightarrow i-3timesoverrightarrow j-2timesoverrightarrow k).
Так, (overrightarrow n=left[overrightarrow atimesoverrightarrow bright]) плоскости X, проходящей через прямую b параллельно прямой a, имеет координаты (6, -3, -2).
Таким образом, уравнение плоскости X есть уравнение плоскости, проходящей через точку (M_2(0, 1, -4)) и имеющей нормальный вектор (overrightarrow n=(6, -3, -2)):
(6times(x-0)-3times(y-1)-2times(z-(-4))=0;leftrightarrow6x-3y-2z-5=0)
Нормирующий множитель для общего уравнения плоскости (6x-3y-2z-5=0) равен (frac1{sqrt{6^2+{(-3)}^2+{(-2)}^2}}=frac17). Значит, нормальное уравнение этой плоскости выглядит как (frac67x-frac37y-frac27z-frac57=0).
Воспользуемся формулой для вычисления расстояния от точки (M_1(-2, 1, 4)) до плоскости (frac67x-frac37y-frac27z-frac57=0: left|M_1H_1right|=left|frac67times(-2)-frac37times1-frac27times4-frac57right|=left|frac{-28}7right|=4) см.
Ответ: 4 см.
ИНТЕРВА́Л И ОТРЕ́ЗОК, простейшие множества точек на прямой. Интервалом (открытым промежутком) называется множество точек на прямой, заключённых между точками $a$ и $b$, причём сами точки $a$ и $b$ в интервал не включаются. Отрезком (сегментом, замкнутым промежутком) называется множество точек на прямой, заключённых между точками $a$ и $b$, $a⩽b$, причём сами точки $a$ и $b$ включаются в отрезок. Термины «интервал» и «отрезок» используются также для соответствующих множеств действит. чисел: интервал состоит из чисел $x$, удовлетворяющих неравенствам $a<{x}<{b}$ сегмент – из чисел $x$, удовлетворяющих неравенствам $a⩽x⩽b$. Интервал обозначается $(a,, b)$, иногда $]a,, b[$, отрезок обозначается $[a,, b]$.
Термин «интервал» (чаще «промежуток») употребляют и в более широком смысле для обозначения произвольного связного множества на прямой. В этих случаях имеются в виду собственно интервал $(a,, b)$, бесконечные (несобственные) интервалы $(-∞,, a),, (a,, +∞),, (-∞,, +∞)$, отрезок $[a,, b]$ и полуинтервалы (полуотрезки) $[a,, b),, (a,, b],, (-∞,, a],, [a,, +∞)$. При этом круглая скобка означает, что соответствующий конец интервала не принадлежит, а квадратная, что он принадлежит к рассматриваемому множеству. Напр., $(a,, b]$ обозначает множество чисел $x$, удовлетворяющих неравенствам $a<{x}⩽{b}$.
Обозначение $(a,, b)$ ввёл нем. математик Г. Ковалевский (1909), $[a,< b]$ – нем. математик Х. Хан (1921).
Метод координат (расстояние между точкой и плоскостью, между прямыми)
Расстояние между точкой и плоскостью.
Расстояние между точкой и прямой.
Расстояние между двумя прямыми.
Первое, что полезно знать, это как найти расстояние от точки до плоскости:
Значения A, B, C, D — коэффициенты плоскости
x, y, z — координаты точки
Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z — 20 = 0.
Все дано, можно сразу подставить значения в уравнение:
Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).
- Находим вектор прямой.
- Вычисляем вектор, проходящий через искомую точку и любую точку на прямой.
- Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
- Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).
1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)
2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.
TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)
3) Получится матрица без коэффициента D (здесь он не нужен для решения):
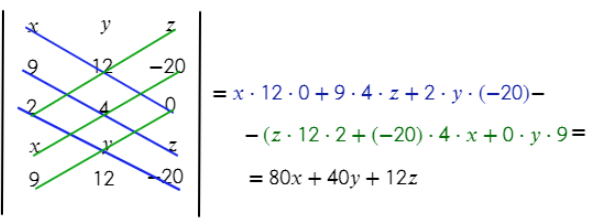
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,
x, y, z — координаты вектора прямой, в данном случае — вектор TV имеет координаты (9; 12; −20)
Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).
- Задаем векторы обеих прямых.
- Находим вектор, взяв по одной точке с каждой прямой.
- Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
- Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
- Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4.
Перейдем к цифрам:
1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)
ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4)
2) Найдем вектор EM (можно было так же найти EL или GM, или GL).
EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)
3) Составляем матрицу из трех выше найденных векторов и находим определитель.
4) Составляем матрицу из первых двух выше найденных векторов и находим определитель
без коэффициента D (здесь он не нужен для решения).
Вспомним, что уравнение плоскости задается так:
В нашем случае А = 4, В = 22, С = 16, D = 0.
5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)
Будь в курсе новых статеек, видео и легкого математического юмора.