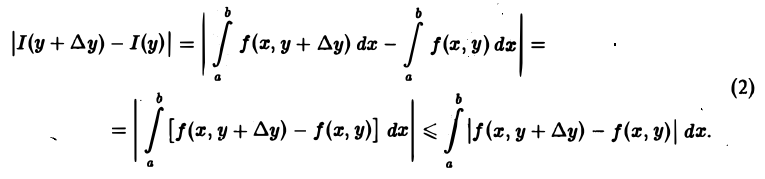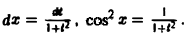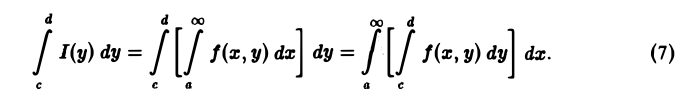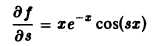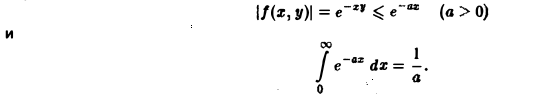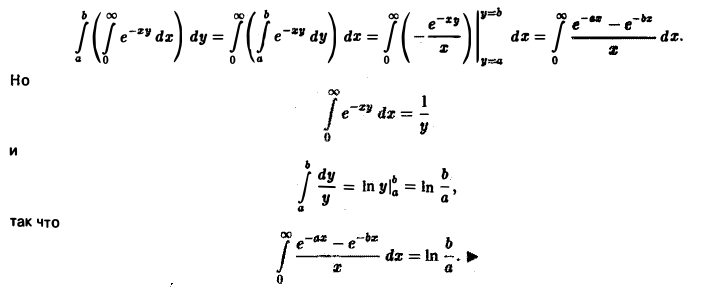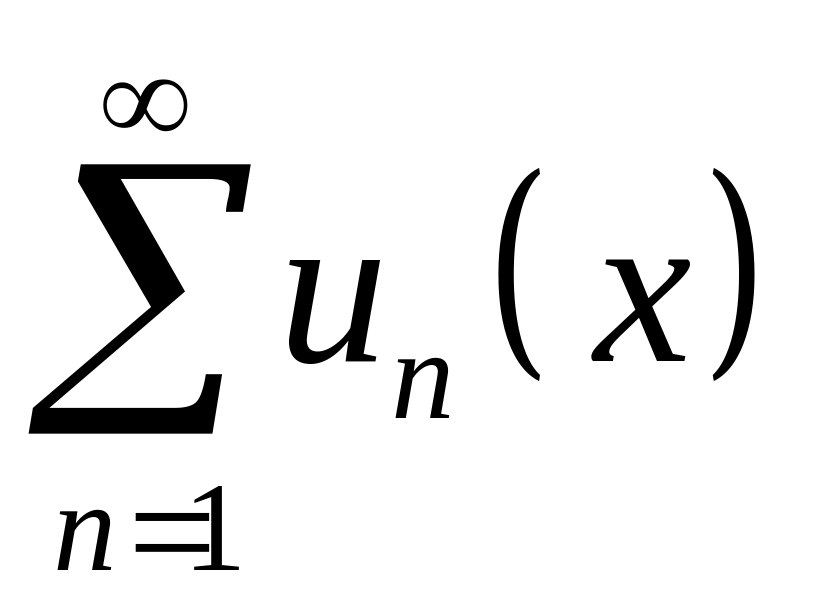Как найти интеграл зависящий от параметра

Понятие интеграла, зависящего от параметра, и его непрерывность:

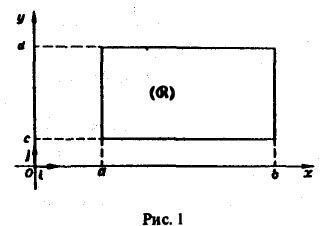
Пусть в прямоугольнике

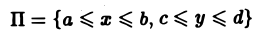
определена функция двух переменных f(x,y) (рис. 1).

Предположим, что при любом фиксированном значении у ∈ [с, d] существует интеграл

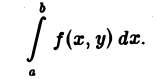
Ясно, что этот интеграл является функцией переменного у,

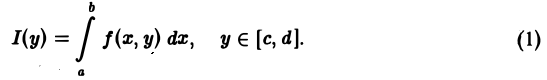
Интеграл (1) называется интегралом, зависящим от параметра у.

Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.

Теорема:

Если функция f(x, у) непрерывна в прямоугольнике П, то функция I(у), определенная соотношением (1), непрерывна на отрезке [с, d].

Из формулы (1) вытекает, что приращение ∆I = I(у + ∆у) — I(у) функции I(у), соответствующее приращению аргумента ∆у, можно оценить так:

По условию теоремы функция f(x, у) непрерывна в замкнутом прямоугольнике П, а значит, f(x,y) равномерно непрерывна в этом прямоугольнике. Следовательно, для любого ε > 0 можно указать такое δ > 0, что при всех х из [а, b] и всех у и у + ∆у из [с, d] таких, что | ∆у| < δ, будет выполняться неравенство

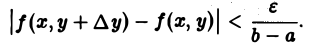
Отсюда и из оценки (2) получаем, что

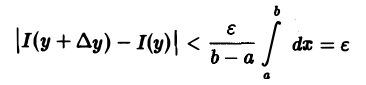
при |∆у| < δ.

Это означает, что функция I(у) непрерывна в каждой точке отрезка [c, d].

Следствие (переход к пределу под знаком интеграла). Если функция f(x, у) непрерывна в прямоугольнике П, то

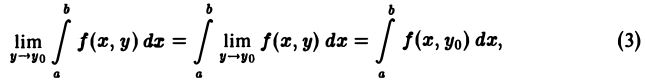
где уо — любое фиксированное число, принадлежащее отрезку [с, d],

Так как функция I(у) непрерывна на [с, d], то имеют место равенства

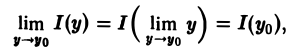
равносильные равенствам (3).

Пример:

Вычислить предeл

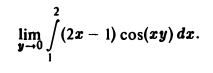
Функция

f(x, у) = (2x — 1) cos(xy)

непрерывна в любом прямоугольнике

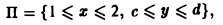
где с < 0 < d. Отсюда по формуле (3) получаем

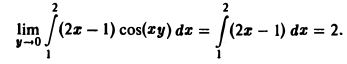
Дифференцирование интеграла no параметру

Теорема:

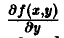
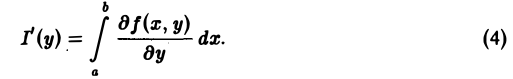
Если функция f(x, у) и ее частная производная непрерывны в прямоугольнике П = {а ≤ х ≤ b, с ≤ у ≤ d}, то для любого у ∈ [с, d] справедлива формула Лейбница дифференцирования по параметру под знаком интеграла

Предполагая, что у + ∆у ∈ [с, d], составим разностное отношение

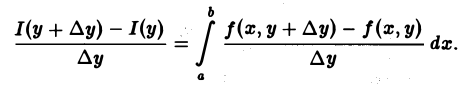
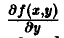
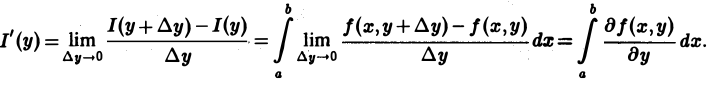
Переходя в этом равенстве к пределу при ∆у —> 0 и пользуясь непрерывностью частной производной и формулой (3), получим

Замечание:

Пусть пределы интегрирования зависят от параметра у. Тогда

где а(у) ≤ х ≤ b(у) и функции а(у) и b(у) дифференцируемы на отрезке с ≤ у ≤ d. При условии, что функции f(x, у) и f`y(x, у) непрерывны в области D = {а(у) ≤ х ≤ b(у), c ≤ y ≤ d} (рис. 2), получаем, что функция F(y) дифференцируема на [с, d], причем
(6)

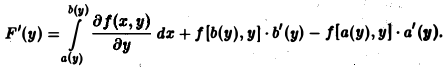
Формула (6) доказывается с помощью дифференцирования сложной функции.

Так как F(у) = F(у, а(у), b(у)), то полная производная

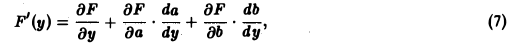
где

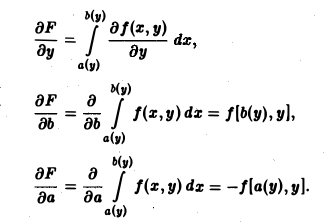
Подставляя выражения для производных и в формулу (7), получим требуемую формулу (6).

Пример:

Применяя дифференцирование по параметру, вычислить интеграл

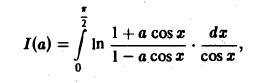
где |a| < 1.

Функция

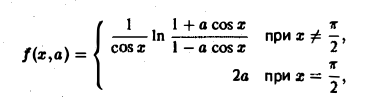
а также ее производная по параметру

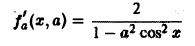
непрерывны в прямоугольнике

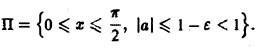
Поэтому применима теорема 2 о дифференцировании интеграла по параметру при |а| ≤ 1 — ε < 1. Имеем

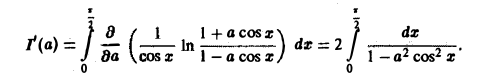
Положим tg x = t, тогда

Интегрируя no t от 0 до + ∞, получим

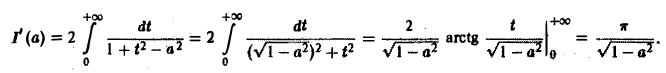
Отсюда I(a) = π arcsin a + С. Устремляя a к нулю и замечая, что I(0) = 0, имеем С = 0. Следовательно, I(a) = π arcsin а.

Пример:

Найти производную F'(y) для функции

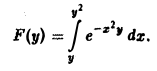
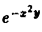
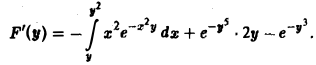
Здесь f(x,у) =, а(у) = у, b(у) = у². Применяя формулу (6), получим:

Интегрирование интеграла по параметру

Теорема:

Если функция f(x, у) непрерывна в прямоугольнике П = {а ≤ x ≤ b, с ≤ у ≤ d}, то функция

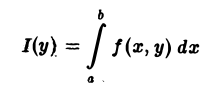
интегрируема на отрезке [с, d], причем справедливы равенства

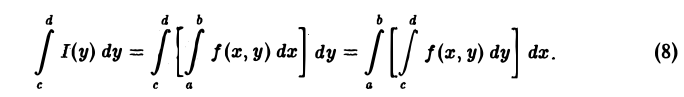
Другими словами, если f(x, у) непрерывна в П, то интеграл, зависящий от параметра, можно интегрировать по параметру под знаком интеграла.

Согласно теореме 1, функция I(у) непрерывна на отрезке [с, d] и поэтому интегрируема на нем. Справедливость формулы (8) следует из равенства повторных интегралов,

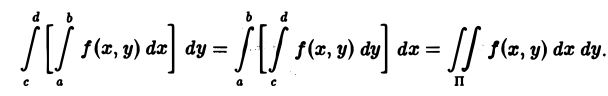
Пример:

Проинтегрировать по параметру у интеграл

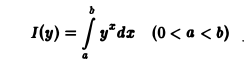
в пределах от 0 до 1.
Так как функция f(х, у) = у^x непрерывна в прямоугольнике

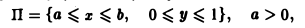
то применима теорема 3 об интегрировании интеграла по параметру. Имеем

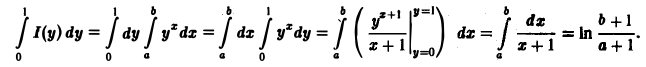
Несобственные интегралы, зависящие от параметра

Понятие несобственного интеграла первого рода, зависящего от параметра:

Пусть функция двух переменных f(х, у) определена в полуполосе

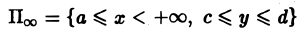
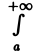
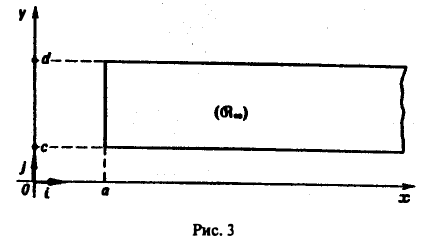
(рис.3) и при каждом фиксированном у ∈ [с, d] существует несобственный интеграл f(x,y)dx, являющийся функцией от у.

Тогда функция

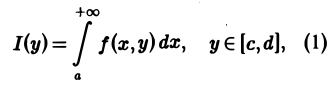
называется несобственным интегралом первого рода, зависящим от параметра у. Интервал (с, d) может быть и бесконечным.

Определение:

Несобственный интеграл (1) называется сходящимся в точке у ∈ [с, d], если существует конечный предел

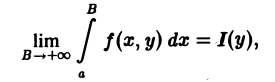
т.е. если для любого ε > 0 существует число Во такое, что для всех В ≥ Вo выполняется неравенство

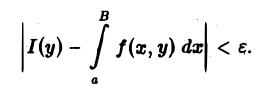
Если несобственный интеграл (1) сходится в каждой точке у отрезка [с, d], то он называется сходящимся на этом отрезке. Интеграл (1) называется абсолютно сходящимся на отрезке [с, d], если сходится интеграл

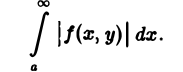
Равномерная сходимость несобственного интеграла. Критерий Коши

Определение:

Несобственный интеграл (1) называется равномерно сходящимся по параметру у на отрезке (с, d), если он сходится на этом отрезке и для любого ε > 0 можно указать такое А ≥ а, зависящее только от ε, что для всех В > А и для всех у из отрезка [с, d] выполняется неравенство

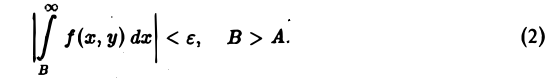
Имеет место следующий критерий Коши равномерной сходимости несобственных интегралов, зависящих от параметра.

Теорема:

Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d], необходимо и достаточно, чтобы для любого ε > 0 можно было указать число А ≥ а, зависящее только от ε и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство

Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости.

Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра.

Теорема:

Признак Вейерштрасса. Пусть функция f(x,y) определена в полуполосе и для каждого у ∈ [с, d] интегрируема по х на любо мот резке [а, А]. Пусть, кроме того, для всех точек полуполосы выполняется неравенство

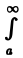
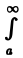
Тогда из сходимости интеграла g(x) dx вытекает равномерная сходимость по у на отрезке [с, d] несобственного интеграла I(y) =f(x, у) dx.

В силу критерия Коши сходимости интеграла от функции g(х), для любого ε > О можно указать число А ≥ а такое, что при всех С > В ≥ А выполняется неравенство

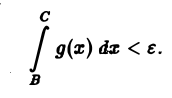
Используя неравенство (4), отсюда получим, что

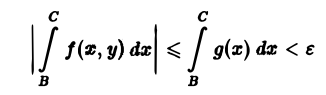
для всех у из отрезка [с, d). Тем самым, критерий Коши равномерной сходимости интеграла

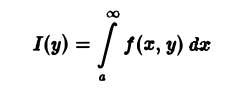
выполнен.

Пример:

Исследовать на равномерную сходимость несобственный интеграл

Так как при любом s ∈ [а, β], где а и β — произвольные вещественные числа, выполняется неравенство

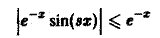
и интеграл

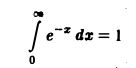
сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех s ∈ [а, β].

Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра

Свойство:

Непрерывность несобственного интеграла по параметру. Если функция f(х, у) непрерывна в области и интеграл

сходится равномерно по у на отрезке [с,d], то функция I(у) непрерывна на [с, d].

Свойство:

Интегрируемость несобственного интеграла по параметру. Если функция f(x, у) непрерывна в области и интеграл (6) сходится равномерно по у на [с, d], то

Свойство:

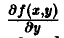
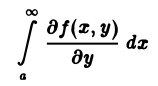
Дифференцируемого несобственного интеграла по параметру. Пусть функция f(x,y) и ее частная производная непрерывны в области несобственный интеграл (6) сходится, а интеграл

сходится равномерно по у на [с, d]. Тогда

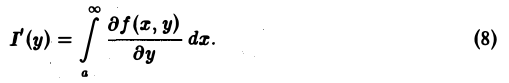
Пример:

Вычислить интеграл, зависящий от параметра s,

В примере 1 мы доказали равномерную сходимость интеграла

по параметру s на любом отрезке [a, β]. Покажем, что интеграл (9) также равномерно сходится по параметру s на любом отрезке [а, β]. В самом деле,

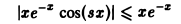
при любом s, и

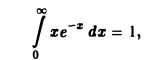
откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через f(x, s),

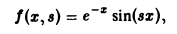
замечаем, что

— подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемости несобственного интеграла по параметру, получим

K(s)=I'(s).

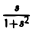
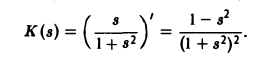
Так как I(s) = этом легко убедиться путем интегрирования по частям), то

Отсюда

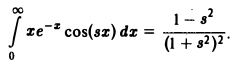
Пример:

Интегрируя равенство

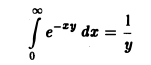
по у, у > 0, найти интеграл

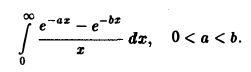
Покажем сначала, что несобственный интеграл

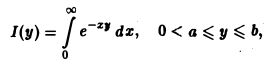
зависящий от параметра у, сходится равномерно на отрезке [a, b]. Это вытекает из признака Вейер-штрасса, так как

Проинтегрируем

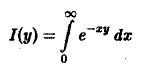
по параметру у в пределах от а до b. Имеем

Замечание:

До сих пор мы рассматривали несобственные интегралы вида

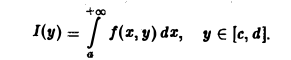
Эго несобственные интегралы первого рода, зависящие от параметра у. Несобственным интегралам второго рода, зависящим от параметра у, называется интеграл вида

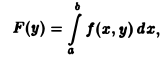
Теория несобственных интегралов второго рода, зависящих от параметра, аналогична рассмотренной нами теории для несобственных интегралов первого рода, зависящих от параметра.

Интегралы Эйлера. Гамма-функция и ее свойства

Гамма-функцией называется интеграл
(1)

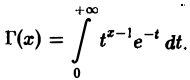
Область определения гамма-функции Г(х)

В интеграле (1) имеются особенности двух типов: ^интегрированиепо полупрямой 0 ≤ t < + ∞;

2) в точке 4 = 0 подынтегральная функция обращается в бесконечность (при х< 1).

Чтобы разделить эти особенности, представим функцию Г(х) в виде суммы двух интегралов

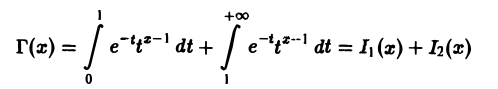
и рассмотрим каждый из них отдельно.

Так как 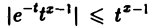при t > 0, то интеграл I1(x) сходится при х > 0 (по признаку сравнения).

Интеграл I2(x) сходится при любом х. В самом деле, взяв произвольное λ > 1, получим, что при любом х

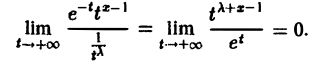
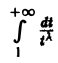
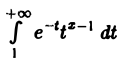
При λ > 1 интеграл сходится, следовательно, интеграл сходится при любом х.

Тем самым, 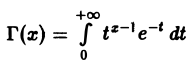сходится при х > 0, и мы доказали, что областью определения гамма-функции Г(x) является полупрямая х > 0

Покажем, что интеграл (1) сходится равномерно по х на любом отрезке [с, d], где 0 < с < d < + ∞. Пусть с ≤ х ≤ d. Тогда при 0 ≤ t ≤ 1 имеем

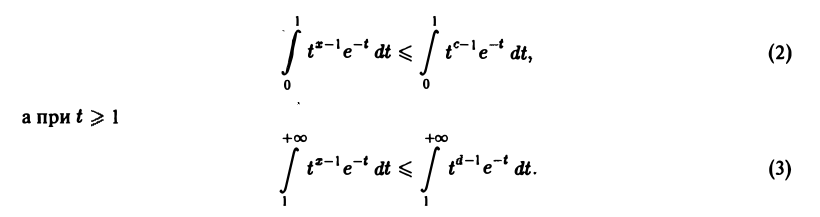
Интегралы в правых частях формул (2) и (3) сходятся, а по признаку Вейерштрасса равномерно сходятся интегралы, стоящие в левых частях неравенств (2) и (3). Следовательно, в силу равенства

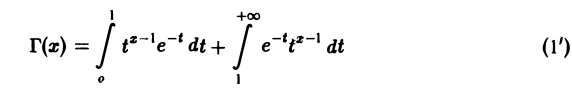
получаем равномерную сходимость Г(x) на любом отрезке [с, d], где 0 < с < d < + ∞. Из равномерной сходимости Г(х) вытекает непрерывность этой функции при х > 0.

Некоторые свойства гамма-функции

1, Г(х) > 0 при х > О (гамма-функция при х > 0 не имеет нулей).

2. При любом х > 0 имеет место формула приведения для гамма-функции

Г(х + 1) = хГ(x). (4)

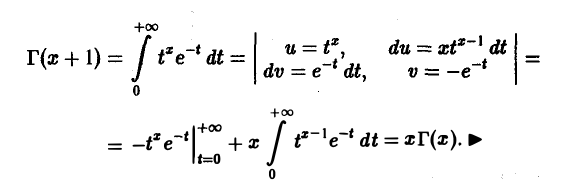
3. При x = n имеет место формула

Г(n + 1) = n! (5)

При х = 1 имеем

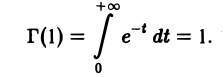
Пользуясь формулой (4), получим

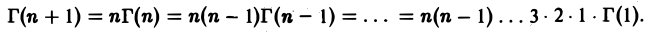
Применяя формулу (4) п раз, при х > 0 получаем

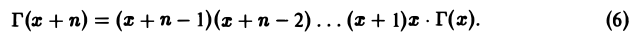
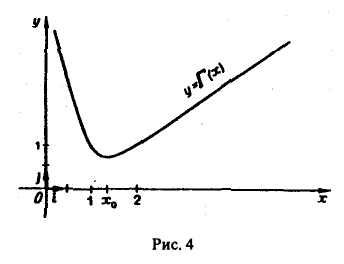
4. Кривая у = Г(х) выпукла вниз. В самом деле,

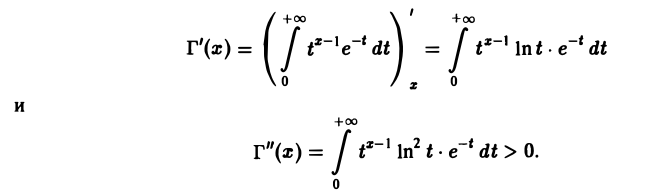
Отсюда следует, что производная Г'(х) на полупрямой (0, + ∞) может иметь только один нуль. А так как Г(1) = Г(2) = 1, то по теореме Ролля этот нуль х0 производной Г'(х) существует и лежит в интервале (1,2). Поскольку Г»(х) > 0, то в точке х0 функция Г(х) имеет минимум.

Можно показать, что на (0, + ∞) функция Г(х) дифференцируема любое число раз.

5. Из формулы Г(х + 1) = хГ(х) следует, что

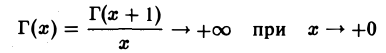
(ибо Г(х) непрерывна и Г(х+1) → Г(1) = 1 при х → +0).

6. Формула дополнения.

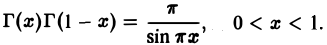
График гамма-функции имеет вид, изображенный на рис. 4.

Бета-функция и ее свойства

Бета-функцией называется интеграл
(7)

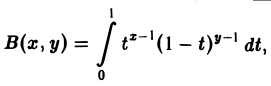
зависящий от параметров х и у.

Область определения бета-функции В (x)

Подынтегральная функция при х < 1 и у < 1 имеет две особые точки t = 0 и t = 1.

Для отыскания области определения В(х, у) представим интеграл (7) в виде суммы двух интегралов

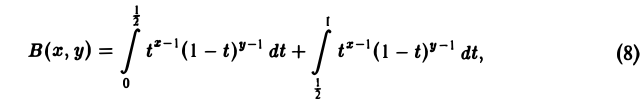
первый из которых (при х < 1) имеет особую точку t = 0, а второй (при у < 1) — особую точку t = 1. Интеграл

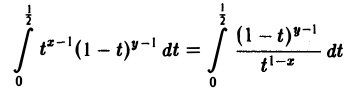
— несобственный интеграл 2-го рода. Он сходится при условии, что 1-х < 1, т. е. при х > 0, а интеграл

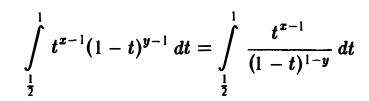
сходится при у > 0. Тем самым, бета-функция В(х, у) определена для всех положительных значений х и у.

Можно доказать, что интеграл (7) равномерно сходится в каждой области x≥ а > 0, у ≥ b > 0, так что бета-функция непрерывна при х > 0, у > 0.

Некоторые свойства бета-функции

1, При х > 0 и у > 0 справедлива формула
(9)

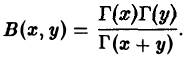
2. Бета-функция является симметричной относительно х и у, т. е.

В(х, у) = В(у, х).

Это следует из формулы (9).

Применение интегралов Эйлера в вычислении определенных интегралов

Рассмотрим несколько примеров.

Пример:

Вычислить интеграл

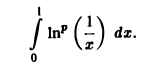
Введем замену

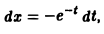
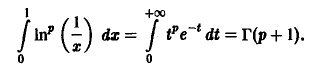
Тогда при х1 =0 имеем t1 = + ∞, а при x2 = 1 получаем t2 = 0. Поэтому

Пример 2. Вычислить интеграл

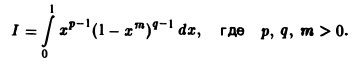
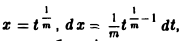
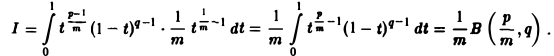
Положим х^m = t, тогда пределы интегрирования остаются прежними, так что заданный интеграл сводится к бета-функции:

Пример:

Исходя из равенства

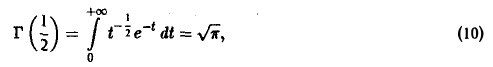
вычислить интеграл

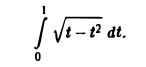
Имеем

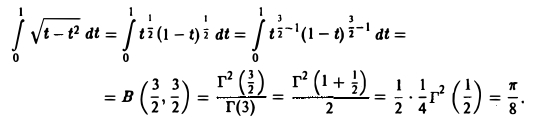
Здесь мы воспользовались определением бета-функции и формулами (9), (4), (5) и (10).

Определение интегралов, зависящих от параметра; их непрерывность и интегрируемость по параметру

Смотрите также:

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Квадратный трехчлен
38. Производная
39. Применение производной к исследованию функций
40. Приложения производной
41. Дифференциал функции
42. Дифференцирование в математике
43. Формулы и правила дифференцирования
44. Дифференциальное исчисление
45. Дифференциальные уравнения
46. Дифференциальные уравнения первого порядка
47. Дифференциальные уравнения высших порядков
48. Дифференциальные уравнения в частных производных
49. Тригонометрические функции
50. Тригонометрические уравнения и неравенства
51. Показательная функция
52. Показательные уравнения
53. Обобщенная степень
54. Взаимно обратные функции
55. Логарифмическая функция
56. Уравнения и неравенства
57. Положительные и отрицательные числа
58. Алгебраические выражения
59. Иррациональные алгебраические выражения
60. Преобразование алгебраических выражений
61. Преобразование дробных алгебраических выражений
62. Разложение многочленов на множители
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат