Любая задача машинного обучения — это задача оптимизации, а задачи оптимизации удобнее всего решать градиентными методами (если это возможно, конечно). Поэтому важно уметь находить производные всего, что попадается под руку. Казалось бы, в чём проблема: ведь дифференцирование — простая и понятная штука (чего не скажешь, например, об интегрировании). Зачем же как-то специально учиться дифференцировать матрицы?
Да в принципе-то никаких проблем: в этой главе вы не узнаете никаких секретных приёмов или впечатляющих теорем. Но, согласитесь, если исходная функция от вектора $x$ имела вид $f(x) = vertvert Ax — bvertvert^2$ (где $A$ — константная матрица, а $b$ — постоянный вектор), то хотелось бы уметь и производную выражать красиво и цельно через буквы $A$, $x$ и $b$, не привлекая отдельные координаты $A_{ij}$, $x_k$ и $b_s$. Это не только эстетически приятно, но и благотворно сказывается на производительности наших вычислений: ведь матричные операции обычно очень эффективно оптимизированы в библиотеках, чего не скажешь о самописных циклах по $i, j, k, s$. И всё, что будет происходить дальше, преследует очень простую цель: научиться вычислять производные в удобном, векторно-матричном виде. А чтобы сделать это и не сойти с ума, мы должны ввести ясную систему обозначений, составляющую ядро техники матричного дифференцирования.
Основные обозначения
Вспомним определение производной для функции $f:mathbb{R}^mrightarrowmathbb{R}^n$. Функция $f(x)$ дифференцируема в точке $x_0$, если
$$f(x_0 + h) = f(x_0) + color{#348FEA}{left[D_{x_0} f right]} (h) + bar{bar{o}} left(left| left| hright|right|right),$$
где $color{#348FEA}{big[D_{x_0} fbig]}$ — дифференциал функции $f$: линейное отображение из мира $x$-ов в мир значений $f$. Грубо говоря, он превращает «малое приращение $h=Delta x$» в «малое приращение $Delta f$» («малые» в том смысле, что на о-малое можно плюнуть):
$$f(x_0 + h) — f(x_0)approxcolor{#348FEA}{left[D_{x_0} f right]} (h)$$
Отметим, что дифференциал зависит от точки $x_0$, в которой он берётся: $color{#348FEA}{left[D_{color{red}{x_0}} f right]} (h)$. Под $vertvert hvertvert$ подразумевается норма вектора $h$, например корень из суммы квадратов координат (обычная евклидова длина).
Давайте рассмотрим несколько примеров и заодно разберёмся, какой вид может принимать выражение $color{#348FEA}{big[D_{x_0} fbig]} (h)$ в зависимости от формы $x$. Начнём со случаев, когда $f$ — скалярная функция.
Примеры конкретных форм $big[D_{x_0} fbig] (h)$, когда $f$ — скалярная функция
-
$f(x)$ — скалярная функция, $x$ — скаляр. Тогда
$$f(x_0 + h) — f (x_0) approx f'(x_0) (h)$$
$$color{#348FEA}{left[D_{x_0} fright] (h)} = f'(x_0) h = h cdot f'(x_0)$$
Здесь $h$ и $f'(x_0)$ — просто числа. В данном случае $color{#348FEA}{left[D_{x_0} fright]}$ — это обычная линейная функция.
-
$f(x)$ — скалярная функция, $x$ — вектор. Тогда
$$f(x_0 + h) — f(x_0) approx sumlimits_i left.frac{partial f}{partial x_i} right|_{x=x_0} h_i,$$
то есть
$$
color{#348FEA}{left[D_{x_0} fright]}(h) = left(color{#FFC100}{nabla_{x_0} f}right)^T h = langlecolor{#FFC100}{nabla_{x_0} f}, h rangle,
$$где $langlebullet, bulletrangle$ — операция скалярного произведения, а $color{#FFC100}{nabla_{x_0} f} = left(frac{partial f}{partial x_1}, ldots, frac{partial f}{partial x_n}right)$ — градиент функции $f$.
-
$f(x)$ — скалярная функция, $X$ — матрица. Дифференциал скалярной функции по матричному аргументу определяется следующим образом:
$$
f(X_0 + H) — f(X_0) approx sumlimits_{i,j} left.frac{partial f}{partial X_{ij}} right|_{X=X_0} H_{ij}
$$Можно заметить, что это стандартное определение дифференциала функции многих переменных для случая, когда переменные — элементы матрицы $X$. Заметим также один интересный факт:
$$
sum_{ij} A_{ij} B_{ij} = text{tr}, A^T B,
$$где $A$ и $B$ — произвольные матрицы одинакового размера. Объединяя оба приведённых выше факта, получаем:
$$
color{#348FEA}{left[D_{X_0} f right]} (H)
= sum limits_{ij}
left.
frac{partial f}{partial X_{ij}}
right|_{X = X_0}
left(
X — X_0
right)_{ij}
= text{tr},
left( left[left. frac{partial f}{partial X_{ij}}right|_{X=X_0}right]^T Hright).
$$Можно заметить, что здесь, по аналогии с примерами, где $x$ — скаляр и где $x$ — вектор (и $f(x)$ — скалярная функция), получилось на самом деле скалярное произведение градиента функции $f$ по переменным $X_{ij}$ и приращения. Этот градиент мы записали для удобства в виде матрицы с теми же размерами, что матрица $X$.
В примерах выше нам дважды пришлось столкнуться с давним знакомцем из матанализа: градиентом скалярной функции (у нескалярных функций градиента не бывает). Напомним, что градиент $color{#FFC100}{nabla_{x_0} f}$ функции в точке $x_0$ состоит из частных производных этой функции по всем координатам аргумента. При этом его обычно упаковывают в ту же форму, что и сам аргумент: если $x$ — вектор-строка, то и градиент записывается вектор-строкой, а если $x$ — матрица, то и градиент тоже будет матрицей того же размера. Это важно, потому что для осуществления градиентного спуска мы должны уметь прибавлять градиент к точке, в которой он посчитан.
Как мы уже имели возможность убедиться, для градиента скалярной функции $f$ выполнено равенство
$$
left[D_{x_0} f right] (x-x_0) = langlecolor{#FFC100}{nabla_{x_0} f}, x-x_0rangle,
$$
где скалярное произведение — это сумма попарных произведений соответствующих координат (да-да, самое обыкновенное).
Посмотрим теперь, как выглядит дифференцирование для функций, которые на выходе выдают не скаляр, а что-то более сложное.
Примеры конкретных форм $big[D_{x_0} fbig] (h)$, где $f$ — это вектор или матрица
-
$f(x) = begin{pmatrix} f(x_1) vdots f(x_m) end{pmatrix}$, $x$ — вектор. Тогда
$$
f(x_0 + h) — f(x_0) =
begin{pmatrix}
f(x_{01} + h_1) — f(x_{01})
vdots
f(x_{0m} + h_m) — f(x_{0m})
end{pmatrix}
approx
begin{pmatrix}
f'(x_{01}) h_1
vdots
f'(x_{0m}) h_m
end{pmatrix}
=
begin{pmatrix}
f'(x_{01})
vdots
f'(x_{0m})
end{pmatrix}
odot
h.
$$В последнем выражении происходит покомпонентное умножение:
$$color{#348FEA}{big[D_{x_0} fbig]} (h) = f'(x_0) odot h = h odot f'(x_0)$$
-
$f(X) = XW$, где $X$ и $W$ — матрицы. Тогда
$$f(X_0 + H) — f(X_0) = (X_0 + H) W — X_0 W = H W,$$
то есть
$$color{#348FEA}{big[D_{X_0} fbig]} (H) = H W$$
-
$f(W) = XW$, где $X$ и $W$ — матрицы. Тогда
$$f(W_0 + H) — f(W_0) = X(W_0 + H) — XW_0 = X H,$$
то есть
$$color{#348FEA}{big[D_{W_0} fbig]} (H) = X H$$
-
$f(x) = (f_1(x),ldots,f_K(x))$ — вектор-строка, $x = (x_1,ldots,x_D)$ — вектор-строка. Тогда
$$
color{#348FEA}{big[D_{x_0} fbig]}(h)
= left(sum_j
left.
frac{partial f_1}{partial y_j}
right|_{y=x_0}h_j, ldots, sum_j left. frac{partial f_K}{partial y_j} right|_{y=x_0}h_j right) = \
= h cdot
begin{pmatrix}
left.
frac{partial f_1}{partial y_1}
right|_{y=x_0} & ldots &
left.
frac{partial f_k}{partial y_1}
right|_{y=x_0} \
vdots & & vdots \
left.
frac{partial f_1}{partial y_D}
right|_{y=x_0} & ldots &
left.
frac{partial f_k}{partial y_D}
right|_{y=x_0}\
end{pmatrix}
= h cdot
left.
frac{partial f}{partial y}right|_{y = x_0}
$$Матрица, выписанная в предпоследней выкладке, — это знакомая вам из курса матанализа матрица Якоби.
Простые примеры и свойства матричного дифференцирования
-
Производная константы. Пусть $f(x) = a$. Тогда
$$f(x_0 + h) — f(x_0) = 0,$$
то есть $color{#348FEA}{big[D_{x_0} fbig]}$ — это нулевое отображение. А если $f$ — скалярная функция, то и $color{#FFC100}{nabla_{x_0} f} = 0.$
-
Производная линейного отображения. Пусть $f(x)$ — линейное отображение. Тогда
$$f(x_0 + h) — f(x_0) = f(x_0) + f(h) — f(x_0) = f(h)$$
Поскольку справа линейное отображение, то по определению оно и является дифференциалом $color{#348FEA}{big[D_{x_0} fbig]}$. Мы уже видели примеры таких ситуаций выше, когда рассматривали отображения умножения на матрицу слева или справа. Если $f$ — (скалярная) линейная функция, то она представляется в виде $langle a, vrangle$ для некоторого вектора $a$ — он и будет градиентом $f$.
-
Линейность производной. Пусть $f(x) = lambda u(x) + mu v(x)$, где $lambda, mu$ — скаляры, а $u, v$ — некоторые отображения, тогда
$$color{#348FEA}{big[D_{x_0} fbig]} = lambda color{#348FEA}{big[D_{x_0} ubig]} + mu color{#348FEA}{big[D_{x_0} vbig]}$$
Попробуйте доказать сами, прежде чем смотреть доказательство.
$$f(x_0 + h) — f(x_0) = (lambda u(x_0 + h) + mu v(x_0 + h)) — (lambda u(x_0) + mu v(x_0)) =$$
$$ = lambda(u(x_0 + h) — u(x_0)) + mu(v(x_0 + h) — v(x_0)) approx $$
$$approx lambda color{#348FEA}{big[D_{x_0} ubig]}(h) + mu color{#348FEA}{big[D_{x_0} vbig]}(h)$$
-
Производная произведения. Пусть $f(x) = u(x) v(x)$, где $u, v$ — некоторые отображения, тогда
$$color{#348FEA}{big[D_{x_0} fbig]} = color{#348FEA}{big[D_{x_0} ubig]} cdot v(x_0) + u(x_0) cdot color{#348FEA}{big[D_{x_0} vbig]}$$
Попробуйте доказать сами, прежде чем смотреть доказательство.
Обозначим для краткости $x = x_0 + h$. Тогда
$$u(x)v(x) — u(x_0)v(x_0) = u(x)v(x) — u(x_0)v(x) + u(x_0)v(x) — u(x_0)v(x_0) =$$
$$ (u(x) — u(x_0))v(x) + u(x_0)(v(x) — v(x_0))approx $$
$$approx color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x) + u(x_0)cdot color{#348FEA}{big[D_{x_0} vbig]}(h)$$
И всё бы хорошо, да в первом слагаемом $v(x)$ вместо $v(x_0)$. Придётся разложить ещё разок:
$$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x) approx $$
$$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot left(v(x_0) + color{#348FEA}{big[D_{x_0} vbig]}(h) + o(vertvert hvertvert)right) =$$
$$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x_0) + bar{bar{o}}left(vertvert hvertvertright)$$
Это же правило сработает и для скалярного произведения:
$$color{#348FEA}{big[D_{x_0} langle u, vranglebig]} = langlecolor{#348FEA}{big[D_{x_0} ubig]}, vrangle + langle u, color{#348FEA}{big[D_{x_0} vbig]}rangle$$
В этом нетрудно убедиться, повторив доказательство или заметив, что в доказательстве мы пользовались лишь дистрибутивностью (= билинейностью) умножения.
-
Производная сложной функции. Пусть $f(x) = u(v(x))$. Тогда
$$f(x_0 + h) — f(x_0) = u(v(x_0 + h)) — u(v(x_0)) approx $$
$$approxleft[D_{v(x_0)} u right] (v(x_0 + h) — v(x_0)) approx left[D_{v(x_0)} u right] left( left[D_{x_0} vright] (h)right)$$
Здесь $D_{v(x_0)} u$ — дифференциал $u$ в точке $v(x_0)$, а $left[D_{v(x_0)} u right]left(ldotsright)$ — это применение отображения $left[D_{v(x_0)} u right]$ к тому, что в скобках. Итого получаем:
$$left[D_{x_0} color{#5002A7}{u} circ color{#4CB9C0}{v} right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
-
Важный частный случай: дифференцирование перестановочно с линейным отображением. Пусть $f(x) = L(v(x))$, где $L$ — линейное отображение. Тогда $left[D_{v(x_0)} L right]$ совпадает с самим $L$ и формула упрощается:
$$left[D_{x_0} color{#5002A7}{L} circ color{#4CB9C0}{v} right](h) = color{#5002A7}{L} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Простые примеры вычисления производной
-
Вычислим дифференциал и градиент функции $f(x) = langle a, xrangle$, где $x$ — вектор-столбец, $a$ — постоянный вектор.
Попробуйте вычислить сами, прежде чем смотреть решение.
Вычислить производную можно непосредственно:
$$f(x_0 + h) — f(x_0) = langle a, x_0 + hrangle — langle a, x_0rangle = langle a, hrangle$$
Но можно и воспользоваться формулой дифференциала произведения:
$$color{#348FEA}{big[D_{x_0} langle a, xranglebig]} (h) = $$
$$ =langlecolor{#348FEA}{big[D_{x_0} abig]}(h), xrangle + langle a, color{#348FEA}{big[D_{x_0} xbig]}(h)rangle$$
$$= langle 0, xrangle + langle a, hrangle = langle a, hrangle$$
Сразу видно, что градиент функции равен $a$.
-
Вычислим производную и градиент $f(x) = langle Ax, xrangle$, где $x$ — вектор-столбец, $A$ — постоянная матрица.
Попробуйте вычислить сами, прежде чем смотреть решение.
Снова воспользуемся формулой дифференциала произведения:
$$color{#348FEA}{big[D_{x_0} langle Ax, xranglebig]}(h) = $$
$$ = langlecolor{#348FEA}{big[D_{x_0} Axbig]}(h), x_0rangle + langle Ax_0, color{#348FEA}{big[D_{x_0} xbig]}(h)rangle$$
$$= langle Ah, x_0rangle + langle Ax_0, hrangle$$
Чтобы найти градиент, нам надо это выражение представить в виде $langle ?, hrangle$. Для этого поменяем местами множители первого произведения и перенесём $A$ в другую сторону ($A$ перенесётся с транспонированием):
$$langle A^Tx_0, hrangle + langle Ax_0, hrangle = $$
$$= langle (A^T + A)x_0, hrangle$$
Получается, что градиент в точке $x_0$ равен $(A^T + A)x_0$.
-
Вычислим производную обратной матрицы: $f(X) = X^{-1}$, где $X$ — квадратная матрица.
Попробуйте вычислить сами, прежде чем смотреть решение.
Рассмотрим равенство $I = Xcdot X^{-1} = I$ и продифференцируем его:
$$0 = color{#348FEA}{big[D_{X_0} left( Xcdot X^{-1}right)big]}(H) = $$
$$ = color{#348FEA}{big[D_{X_0} Xbig]}(H)cdot X_0^{-1} + X_0cdot color{#348FEA}{big[D_{X_0} X^{-1}big]}(H)$$
Отсюда уже легко выражается
$$color{#348FEA}{big[D_{X_0} X^{-1}big]}(H) = -X_0^{-1}cdotcolor{#348FEA}{big[D_{X_0} Xbig]}(H)cdot X_0^{-1}$$
Осталось подставить $color{#348FEA}{big[D_{X_0} Xbig]}(H) = H$, но запомните и предыдущую формулу, она нам пригодится.
-
Вычислим градиент определителя: $f(X) = text{det}(X)$, где $X$ — квадратная матрица.
Попробуйте вычислить сами, прежде чем смотреть решение.
В предыдущих примерах мы изо всех сил старались не писать матричных элементов, но сейчас, увы, придётся. Градиент функции состоит из её частных производных: $color{#FFC100}{nabla_{x_0} f} = left(frac{partial f}{partial{x_{ij}}}right)_{i,j}$. Попробуем вычислить $frac{partial f}{partial{x_{ij}}}$. Для этого разложим определитель по $i$-й строке:
$$text{det}(X) = sum_{k}x_{ik}cdot(-1)^{i + k}M_{ik},$$
где $M_{ik}$ — это определитель подматрицы, полученной из исходной выбрасыванием $i$-й строки и $k$-го столбца. Теперь мы видим, что определитель линеен по переменной $x_{ij}$, причём коэффициент при ней равен $cdot(-1)^{i + k}M_{ik}$. Таким образом,
$$frac{partial f}{partial{x_{ij}}} = (-1)^{i + k}M_{ik}$$
Чтобы записать матрицу, составленную из таких определителей, покороче, вспомним, что
$$X^{-1} = frac1{text{det}(X)}left((-1)^{i+j}M_{color{red}{ji}}right)_{i,j}$$
Обратите внимание на переставленные индексы $i$ и $j$ (отмечены красным). Но всё равно похоже! Получается, что
$$color{#FFC100}{nabla_{x_0} f} = text{det}(X)cdot X^{-T},$$
где $X^{-T}$ — это более короткая запись для $(X^{-1})^T$.
-
Вычислим градиент функции $f(x) = vertvert Ax — bvertvert^2$. С этой функцией мы ещё встретимся, когда будем обсуждать задачу линейной регрессии.
Попробуйте вычислить сами, прежде чем смотреть решение.
Распишем квадрат модуля в виде скалярного произведения:
$$vertvert Ax — bvertvert^2 = langle Ax — b, Ax — brangle$$
Применим формулу дифференциала произведения и воспользуемся симметричностью скалярного произведения:
$$color{#348FEA}{big[D_{x_0} langle Ax — b, Ax — branglebig]}(h) = $$
$$ langle color{#348FEA}{big[D_{x_0} (Ax — b)big]}(h), Ax_0 — brangle + langle Ax_0 — b, color{#348FEA}{big[D_{x_0} (Ax — b)big]}(h)rangle$$
$$ = 2langle Ax_0 — b, color{#348FEA}{big[D_{x_0} (Ax — b)big]}(h)rangle =$$
$$ = 2langle Ax_0 — b, Ahrangle = langle 2A^T(Ax_0 — b), hrangle$$
Получаем, что
$$color{#FFC100}{nabla_{x_0} f} = 2A^T(Ax_0 — b)$$
Примеры вычисления производных сложных функций
-
Вычислим градиент функции $f(X) = text{log}(text{det}(X))$.
Попробуйте вычислить сами, прежде чем смотреть решение.
Вспомним формулу производной сложной функции:
$$left[D_{X_0} u circ v right](H) = left[D_{v(X_0)} u right] left( left[D_{X_0} vright] (H)right)$$
и посмотрим, как её тут можно применить. В роли функции $u$ у нас логарифм:
$$u(y) = text{log}(u),quad left[D_{y_0} uright](s) = frac1y_0cdot s,$$
а в роли $v$ — определитель:
$$v(X) = text{det}(X),quad left[D_{y_0} vright](H) = langle text{det}(X_0)cdot X_0^{-T}, Hrangle,$$
где под скалярным произведением двух матриц понимается, как обычно,
$$langle A, Brangle = sum_{i,j}a_{ij}b_{ij} = text{tr}(A^TB)$$
Подставим это всё в формулу произведения сложной функции:
$$left[D_{X_0} u circ v right](H) = frac1{text{det}(X)}cdotlangle text{det}(X)cdot X^{-T}, Hrangle =$$
$$= langle frac1{text{det}(X)}cdottext{det}(X)cdot X^{-T}, Hrangle =
langle X_0^{-T}, Hrangle$$Отсюда сразу видим, что
$$color{#FFC100}{nabla_{X_0} f} = X_0^{-T}$$
-
Вычислим градиент функции $f(X) = text{tr}(AX^TX)$.
Попробуйте вычислить сами, прежде чем смотреть решение.
Воспользуемся тем, что след — это линейное отображение (и значит, перестановочно с дифференцированием), а также правилом дифференцирования сложной функции:
$$left[D_{X_0} f right](H) = text{tr}left(left[D_{X_0} AX^TX right](H)right) =$$
$$=text{tr}left(Acdotleft[D_{X_0} X^T right](H)cdot X_0 + AX_0^Tleft[D_{X_0} X right](H)right) =$$
$$=text{tr}left(AH^TX_0 + AX_0^THright)$$
Чтобы найти градиент, мы должны представить это выражение в виде $langle ?, Hrangle$, что в случае матриц переписывается, как мы уже хорошо знаем, в виде $text{tr}(?^Tcdot H) = text{tr}(?cdot H^T)$. Воспользуемся тем, что под знаком следа можно транспонировать и переставлять множители по циклу:
$$ldots=text{tr}left(AH^TX_0right) + text{tr}left(AX_0^THright) =$$
$$=text{tr}left(X_0AH^Tright) + text{tr}left(H^TX_0A^Tright) =$$
$$=text{tr}left(X_0AH^Tright) + text{tr}left(X_0A^TH^Tright) =$$
$$=text{tr}left((X_0A + X_0A^T)H^Tright)$$
Стало быть,
$$color{#FFC100}{nabla_{X_0} f} = X_0A + X_0A^T$$
-
Вычислим градиент функции $f(X) = text{det}left(AX^{-1}Bright)$.
Подумайте, кстати, почему мы не можем расписать определитель в виде произведения определителей и тем самым сильно упростить себе жизнь
Расписать у нас может не получиться из-за того, что $A$ и $B$ могут быть не квадратными, и тогда у них нет определителей и представить исходный определитель в виде произведения невозможно.
Воспользуемся правилом дифференцирования сложной функции для $u(Y) = text{det}(Y)$, $v(X) = AX^{-1}B$. А для этого сначала вспомним, какие дифференциалы у них самих. С функцией $u$ всё просто:
$$left[D_{Y_0} uright](S) = langle text{det}(Y_0)Y_0^{-T}, Srangle =$$
$$= text{tr}left(text{det}(Y_0)Y_0^{-1}Sright)$$
Функция $v$ сама является сложной, но, к счастью, множители $A$ и $B$ выносятся из-под знака дифференциала, а дифференцировать обратную матрицу мы уже умеем:
$$left[D_{X_0} vright](H) = — AX_0^{-1}HX_0^{-1} B$$
С учётом этого получаем:
$$left[D_{X_0} f right](H) = left[D_{v(X_0)} u right] left( left[D_{X_0} vright] (H)right) =$$
$$=text{tr}left(text{det}(AX_0^{-1}B)(AX_0^{-1}B)^{-1}left(- AX_0^{-1}HX_0^{-1} Bright)right)$$
$$=text{tr}left(-text{det}(AX_0^{-1}B)(AX_0^{-1}B)^{-1}AX_0^{-1}HX_0^{-1} Bright)$$
Чтобы найти градиент, мы должны, как обычно, представить это выражение в виде $text{tr}(?^Tcdot H)$.
$$ldots=text{tr}left(-text{det}(AX_0^{-1}B)X_0^{-1} B(AX_0^{-1}B)^{-1}AX_0^{-1}Hright)$$
Стало быть,
$${nabla_{X_0} f} = left(-text{det}(AX_0^{-1}B)X_0^{-1} B(AX_0^{-1}B)^{-1}AX_0^{-1}right)^T =$$
$$=-text{det}(AX_0^{-1}B)X_0^{-T} A^T(AX_0^{-1}B)^{-T}B^TX_0^{-T}$$
Вторая производная
Рассмотрим теперь не первые два, а первые три члена ряда Тейлора:
$$f(x_0 + h) = f(x_0) + color{#348FEA}{left[D_{x_0} f right]} (h) + frac12color{#4CB9C0}{left[D_{x_0}^2 f right]} (h, h) + bar{bar{o}} left(left|left| hright|right|^2right),$$
где $color{#4CB9C0}{left[D_{x_0}^2 f right]} (h, h)$ — второй дифференциал, квадратичная форма, в которую мы объединили все члены второй степени.
Вопрос на подумать. Докажите, что второй дифференциал является дифференциалом первого, то есть
$$left[D_{x_0} color{#348FEA}{left[D_{x_0} f right]} (h_1) right] (h_2) = left[D_{x_0}^2 f right] (h_1, h_2)$$
Зависит ли выражение справа от порядка $h_1$ и $h_2$?
Этот факт позволяет вычислять второй дифференциал не с помощью приращений, а повторным дифференцированием производной.
Вторая производная может оказаться полезной при реализации методов второго порядка или же для проверки того, является ли критическая точка (то есть точка, в которой градиент обращается в ноль) точкой минимума или точкой максимума. Напомним, что квадратичная форма $q(h)$ называется положительно определённой (соответственно, отрицательно определённой), если $q(h) geqslant 0$ (соответственно, $q(h) leqslant 0$) для всех $h$, причём $q(h) = 0$ только при $h = 0$.
Теорема. Пусть функция $f:mathbb{R}^mrightarrowmathbb{R}$ имеет непрерывные частные производные второго порядка $frac{partial^2 f}{partial x_ipartial x_j}$ в окрестности точки $x_0$, причём $color{#FFC100}{nabla_{x_0} f} = 0$. Тогда точка $x_0$ является точкой минимума функции, если квадратичная форма $color{#348FEA}{D_{x_0}^2 f} $ положительно определена, и точкой максимума, если она отрицательно определена.
Если мы смогли записать матрицу квадратичной формы второго дифференциала, то мы можем проверить её на положительную или отрицательную определённость с помощью критерия Сильвестра.
Примеры вычисления и использования второй производной
-
Рассмотрим задачу минимизации $f(x) = vertvert Ax — bvertvert^2$ по переменной $x$, где $A$ — матрица с линейно независимыми столбцами. Выше мы уже нашли градиент этой функции; он был равен $color{#FFC100}{nabla_{x_0} f} = 2A^T(Ax — b)$. Мы можем заподозрить, что минимум достигается в точке, где градиент обращается в ноль: $x_* = (A^TA)^{-1}A^Tb$. Отметим, что обратная матрица существует, так как $text{rk}(A^TA) = text{rk}{A}$, а столбцы $A$ по условию линейно независимы и, следовательно, $text{rk}(A^TA)$ равен размеру этой матрицы. Но действительно ли эта точка является точкой минимума? Давайте оставим в стороне другие соображения (например, геометрические, о которых мы упомянем в главе про линейные модели) и проверим аналитически. Для этого мы должны вычислить второй дифференциал функции $f(x) = vertvert Ax — bvertvert^2$.
Попробуйте вычислить сами, прежде чем смотреть решение.
Вспомним, что
$$color{#348FEA}{big[D_{x_0} vertvert Ax — bvertvert^2big]}(h_1) = langle 2A^T(Ax_0 — b), h_1rangle$$
Продифференцируем снова. Скалярное произведение — это линейная функция, поэтому можно занести дифференцирование внутрь:
$$color{#348FEA}{big[D_{x_0} langle 2A^T(Ax — b), h_1ranglebig]}(h_2) =
langle color{#348FEA}{big[D_{x_0} (2A^TAx — 2A^Tb)big]}(h_2), h_1rangle =$$$$=langle 2A^TAh_2, h_1rangle = 2h_2^T A^TA h_1$$
Мы нашли квадратичную форму второго дифференциала; она, оказывается, не зависит от точки (впрочем, логично: исходная функция была второй степени по $x$, так что вторая производная должна быть константой). Чтобы показать, что $x_*$ действительно является точкой минимума, достаточно проверить, что эта квадратичная форма положительно определена.
Попробуйте сделать это сами, прежде чем смотреть решение.
Хорошо знакомый с линейной алгеброй читатель сразу скажет, что матрица $A^TA$ положительно определена для матрицы $A$ с линейно независимыми столбцами. Но всё же давайте докажем это явно. Имеем $h^TA^TAh = (Ah)^TAh = vertvert Ahvertvert^2 geqslant 0$. Это выражение равно нулю тогда и только тогда, когда $Ah = 0$. Последнее является однородной системой уравнений на $h$, ранг которой равен числу переменных, так что она имеет лишь нулевое решение $h = 0$.
-
Докажем, что функция $f(X) = log{text{det}(X)}$ является выпуклой вверх на множестве симметричных, положительно определённых матриц. Для этого мы должны проверить, что в любой точке квадратичная форма её дифференциала отрицательно определена. Для начала вычислим эту квадратичную форму.
Попробуйте сделать это сами, прежде чем смотреть решение.
Выше мы уже нашли дифференциал этой функции:
$$color{#348FEA}{big[D_{X_0} log{text{det}(X)}big]}(H_1) = langle X_0^{-T}, H_1rangle$$
Продифференцируем снова:
$$color{#348FEA}{big[D_{X_0} langle X^{-T}, H_1ranglebig]}(H_2) =
langle color{#348FEA}{big[D_{x_0} X^{-T}big]}(H_2), h_1rangle =$$$$=langle -X_0^{-1}H_2X_0^{-1}, H_1rangle$$
Чтобы доказать требуемое в условии, мы должны проверить следующее: что для любой симметричной матрицы $X_0$ и для любого симметричного (чтобы не выйти из пространства симметричных матриц) приращения $Hne 0$ имеем
$$color{#348FEA}{big[D^2_{X_0} log{text{det}(X)}big]}(H, H) < 0$$
Покажем это явно. Так как $X_0$ — симметричная, положительно определённая матрица, у неё есть симметричный и положительно определённый квадратный корень: $X_0 = X_0^{1/2}cdot X_0^{1/2} = X_0^{1/2}cdot left(X_0^{1/2}right)^T.$ Тогда
$$langle -X_0^{-1}HX_0^{-1}, Hrangle = -text{tr}left(X_0^{1/2} left(X_0^{1/2}right)^THX_0^{1/2} left(X_0^{1/2}right)^TH^Tright) =$$
$$-text{tr}left(left(X_0^{1/2}right)^THX_0^{1/2} left(X_0^{1/2}right)^TH^TX_0^{1/2}right) = $$
$$=-text{tr}left( left(X_0^{1/2}right)^THX_0^{1/2} left[left(X_0^{1/2}right)^THX_0^{1/2}right]^Tright) =$$
$$=-vertvertleft(X_0^{1/2}right)^THX_0^{1/2}vertvert^2,$$
что, конечно, меньше нуля для любой ненулевой $H$.
Дифференцирование матриц и векторов
2.3. МАТРИЧНОЕ ДИФФЕРЕНЦИРОВАНИЕ
Аппарат векторно-матричного исчисления не приспособлен для манипуляций, целью которых является нахождение интегралов и производных от функций матричного аргумента. Недостаток аксиоматики в этом направлении известен, памятная табличка формул матричного дифференцирования нет-нет, да встречается в работах – в приложении или в первой главе. При внимательном отношении табличкам свойственно разрастаться в таблицы. Чтобы от них избавиться, надо предложить систему формального дифференцирования, позволяющую находить результат, желательно, по простым правилам.
Попытаемся привести некоторые лежащие на поверхности соображения на этот счет. Начнем с формального определения.
Понятие производной скалярной функции по матрице уже устоялось. Это матрица, элементами которой являются частные производные функции по каждому элементу. Таков, например, градиент. Производная матрицы по скалярному аргументу образуется матрицей производных каждого ее элемента по одному и тому же аргументу. Расширяя эти толкования, придем к определению, согласно которому производная матрицы по матричному аргументу представляет собой блочную матрицу, в которой каждый блок включает производную дифференцируемой матричной функции по скалярному аргументу – элементу матричного аргумента.
Для того, чтобы лаконично записывать результаты формальных матричных действий, придется ввести пару относительно новых обозначений. Первое касается векторизации A ↑ матрицы, когда ее элементы строчка за строчкой последовательно слагаются в столбец. Второе обозначение для блочно-диагональной структуризации существует , но есть желание иногда писать его короче, просто . Количество повторений блоков A на диагонали, как и многое другое в матричной алгебре, остается за бортом, что не всегда правильно. Можно предложить другой эквивалент обозначения этой операции, например, такой: n>.
Указанные операции обладают рядом почти очевидных свойств, например, (x T ) ↑ =x и .
Отметим попутно у матричного дифференцирования коммутирующее знак транспонирования качество, оказывается что
Любопытно и просто выглядят производные векторных функций по векторному аргументу, существует несколько вариантов, в частности, такие
Производная произведения двух матриц по матричному же аргументу размера nxm трансформируется к виду
В случае скалярного аргумента формула становится тривиальной. Для часто встречаемого векторного аргумента первая диагонализация отмирает, поскольку m = 1. Символ n можно подразумевать.
В качестве демонстрации силы разделаемся с квадратичной формой, которую при ином подходе приходится дифференцировать поэлементно, а потом собирать ответ, как картинку из кубиков, итак
Метод наименьших квадратов связан с поиском сложной производной от матрицы, имеем
Так, в одну строчку, выводятся формулы, под которые бронируется место в приложениях. Идее нужно выдержать испытание временем, пусть пока эстетическая сторона дела доставит удовольствие.
В теоретической механике и теории поля есть свой набор дифференциальных операторов, например, ротор и дивергенция.
Вспоминая правило буравчика, незаменимое в исследовании электромагнитных явлений, отметим, что оно описывает поворот на 90 градусов. Механики для этой цели придумали векторное произведение y = ω⊗x, пасынка матричного исчисления: ортогональные матрицы закрывают потребности в обеспечении поворотов. Среди них есть конструкции кососимметрические, отвечающие за прямой угол. Поворот с дополнительным растяжением не меняет вида матрицы, так что для векторного произведения нетрудно подыскать матричный аналог y = Wx, где
Смешанное произведение векторов z(ω⊗x) выливается в привычную запись билинейной формы z T Wx.
Попробуем найти матричную интерпретацию дифференциальных операторов. Понять их содержание неспециалисту нелегко, между тем, они используются в уравнениях Максвелла, играющих фундаментальную роль в науке. Эти уравнения дали жизнь теории относительности и навели Шредингера на объяснение дискретной природы процессов микромира. Матричная аналогия способна внести некоторое более ясное видение сложных вещей. Физическое пространство, в котором распространяется электромагнитная волна, трехмерно. Изменения полей в нем оцениваются частными производными напряженности вдоль трех пространственных направлений.
Оператором Гамильтона ∇ называют собрание операций взятия частных производных по трем направлениям физического мира. Применительно к скалярной функции трех координат этот оператор порождает градиент. Что касается векторной функции θ(x), наделенной в каждой точке x пространства величиной и направлением, то количество частных производных расширяется до девяти, собираемых в матрицу dθ T /dx. Дивергенция представляет собой след этой матрицы, т.е. сумму трех обусловленных индексами координатных осей производных div θ(x) = trace dθ T /dx.
Дивергенция носит все признаки скалярного произведения векторов ∇ и θ(x). Ротор, напротив, формально определяется как векторное произведение, т.е. rot θ(x) = ∇⊗θ(x). Такого сорта дефиниции дают скудную пищу воображению. Недаром с уравнениями Максвелла пришлось поработать нескольким математикам, только чтобы их разъяснить [6].
Фарадей находил силовые лини магнитного поля, насыпая металлические опилки на лист бумаги и поднося его к полюсу магнита.
Попробуем воспользоваться его методом. Лучи силовых линий в чем-то подобны градиенту квадратичной функции f(x)=0.5x T Ax.
Фазовые портреты линейных динамических систем, описывающих движения вдоль градиента , являются удобным руководством для постижения топологических особенностей векторных полей. Дивергенция вектора градиента представляет собой сумму вторых частных производных (это действие приписывают оператору Лапласа Δ) квадратичной функции, в данном случае она равна сумме диагональных элементов матрицы A. Не менее просто определить у такого поля ротор. Он составлен из разностей внедиагональных элементов A. Полям с нулевым ротором отвечают диагональные матрицы простыми собственными значениями.
Полям с нулевой дивергенцией отвечаю матрицы с чисто мнимыми собственными значениями. Среди матриц c нулевой диагональю отметим кососимметрические. Квадратичную форму с их помощью не построишь, градиент не способен на такие фокусы, как замыкание. Но динамическая система ẋ=Ax существует. В отсутствии монополей силовые линии электрического и магнитного полей замкнуты, не имеют ни начала, ни конца. Такие траектории прочерчивают частицы несжимаемой жидкости, подкрученной в ванне без слива. Задание нулевых дивергенций электрического и магнитного полей сродни заданию начальных условий, определяющих пространственные характеристики силовых линий.
Электромагнитное поле распространяется благодаря самоиндукции. Для ее описания и потребовался ротор или вихрь – завиток (curl), как поэтично назвал его склонный к стихотворным опусам Джеймс Клерк Максвелл, имевший, к тому же, привычку подписываться формулой dp/dt=JCM. В безвихревом гравитационном поле книга падает на пол прямо, не совершая утиные движения сорванного осенью с ветки листка. Уравнение электростатического поля констатирует, что ротор его напряженности равен нулю. Такое поле развернуто и скручивается в пространстве, если происходят изменения во времени поля магнитного. И наоборот, магнитное поле скручивается под влиянием изменения во времени поля электрического.
Максвелл крест накрест приравнял (с точностью до коэффициентов) временные и вихревые пространственные производные напряженностей электрического и магнитного полей. Теорию ждало открытие. Коэффициенты уравнений можно установить из опыта с диэлектриками. Отсюда вычисляется скорость распространения электромагнитного излучения. Она оказалась равной скорости света, измеренной астрономами.
Векторное дифференцирование
В дальнейшем в различных главах будет использовано векторное дифференцирование, которое позволяет использовать более компактную и наглядную запись. Поэтому в этом параграфе кратко рассмотрим определения и свойства векторного дифференцирования (символ *= f обозначает равенство по определению).
1) Производная вектора х = (х Х2 . хп) Т по скаляру t:
2) Производная скалярной функции 5 = s (х) по вектору х = = (х Х2 . хп) Т :
3) Производная векторной функции f (х) (f = (Д . /п) т ) по вектору х = (si Х2 . хп) Т :
Используя приведенные определения и обычные правила дифференцирования, можно получить следующие правила векторного дифференцирования.
1°. Производная скалярного произведения по скаляру t:
Если у = х, то имеем
2°. Производная произведения матрицы и вектора по скаляру t:
А — (т х п)-матрица, зависящая от t.
3°. Производная скалярного произведения по вектору х =
Если у = z, то имеем
4°. Производная квадратичной формы по вектору х = = (Xj Х2 • • • &п) •
Q — симметрическг^я (тг х п)-матрица, не зависящей от х.
5°. Производная сложной векторной функции по скаляру t:
Дифференцирование матриц
Пусть A(t) – матрица (m x n), элементы которой aij есть дифференцируемые функции скалярной переменной t. Производная от матрицы A(t) по переменной t есть матрица, элементами которой являются :
.
Производная от суммыдвух матриц равна сумме производных от этих матриц:
.
Производная от произведенияматриц:
.
При этом должен сохраняться первоначальный порядок следования сомножителей произведения.
.
Интегрирование матриц
Интеграл от матрицы определяется как матрица, образованная из интегралов от элементов исходной матрицы. Следовательно,
Для обозначения интеграла от матрицы обычно используется символ Q=∫ ( )dt. Если оператор Q снабжен индексами (сверху t, а снизу t0), то они указывают нижний и верхний пределы интегрирования:
Пример 4. Найти
Определители
Определители существуют только для квадратных матриц.
В общем случае используется разложение Лапласа определителя n порядка по элементам строки (столбца) на сумму n определителей (n–1) порядка.
Например, для n = 3:
Свойства определителей
1. Определитель равен единице, если матрица А– единичная.
2. Определитель равен нулю, либо если все элементы матрицы равны нулю, либо все элементы строки (или столбца) равны нулю, или равны между собой или пропорциональны элементы произвольных двух строк (или двух столбцов).
3. Величина определителя остается неизменной по модулю при перестановке местами его строк (или столбцов).
4. Знак определителя изменяется на противоположный при замени местами его двух строк (или столбцов).
5. Значение определителя умножается на постоянную k, если все элементы какой-либо его строки (столбца) умножаются на k.
6. Значение определителя не изменяется, если к какой-либо его строке (или столбцу) прибавить умноженные на k соответствующие элементы другой строки (или столбца).
http://studme.org/270187/tehnika/vektornoe_differentsirovanie
http://helpiks.org/6-78299.html
Обновление: 8 января 2020
Обновление: 16 февраля 2020
Но наибольший успех достигается с помощью такого приема: из готовой рукописи вы вырываете две страницы выкладок, а вместо них вставляете слово «следовательно» и двоеточие. Гарантирую, что читатель добрых два дня будет гадать, откуда взялось это «следствие». Еще лучше написать «очевидно» вместо «следовательно», поскольку не существует читателя, который отважился бы спросить у кого-нибудь объяснение очевидной вещи. Этим вы не только сбиваете читателя с толку, но и прививаете ему комплекс неполноценности, а это одна из главных целей.
— Н.Вансерг «Математизация».
Вместо введения
С момента прошлой заметки по данной теме прошло много времени, но интерес к изложенному в ней не утихал. Разобравшись с основной проблемой (как, собственно, реализовать дифференцирование) читатели стали задавать вопросы о двух приведённых в тексте формулах. На этих формулах построен весь вывод, но сами они не выводятся, а сопровождены комментарием о простоте их получения при должной внимательности. Настало время.
Замечание о качестве
Мне никогда не попадался вывод этих формул. Обычно, если у вас проблемы с матрицей, то надо обращаться либо к Нео, либо к Гантмахеру [?]
Ф.Р. Гантмахер «ТЕОРИЯ МАТРИЦ»
. Но в этот раз — мне никто не помог. Так что, не обессудьте: вывел как умею.
Технология
Подобные формулы («Нагромождение из матриц» — «знак равенства» — «некоторая функция от матриц») выводятся стандартно: вы опускаетесь на уровень ниже — до компонент объектов (разбирая что там «под капотом» происходит), аккуратно (я бы даже сказал «осторожно») проделываете все преобразования с позиции компонент, получаете некий, более-менее конечный, результат и поднимаетесь на уровень выше (пытаясь интерпретировать формулы из компонент с позиции исходных объектов).
Первая формула
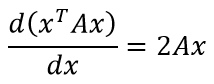
Отмечу, что это частный случай для симметричной матрицы A. В более же общем случае, формула имеет вид:
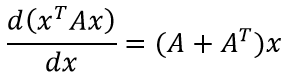
Для того, чтобы выражение в скобках можно было вычислить, необходимо, чтобы объекты имели следующие размеры:
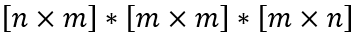
Так как x — вектор, то min(m,n) = 1.
Зададимся конкретикой: пусть x — вектор-столбец, тогда n=1.
Объекты, таким образом, будут иметь вид:

Теперь, наконец-то, можно приступить к выводу. Здесь главное ничего не потерять, поэтому сперва аккуратно проделаем умножение xTA, а затем домножим результат на x.

Ожидаемо, мы получаем скаляр, зависящий от вектора. Возьмём производную скалярной функции от векторного аргумента:
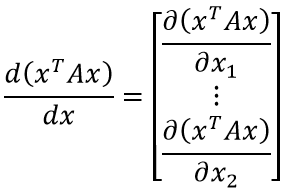
Чтобы получить данное выражение, необходимо найти общий вид производной по k-ой компоненте вектора. Попробуем сгруппировать слагаемые дифференцируемого выражения по компонентам вектора, опираясь на выражение для xTAx, полученное ранее:
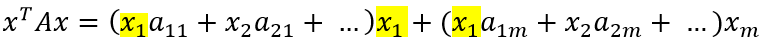
Очевидно, что раскрытие первых скобок даст нам x1 в квадрате с множителем a11 плюс сумму произведений x1 со всеми остальными слагаемыми внутри первых скобок. Также, x1 входит в остальные скобки по одному разу, что образует ещё слагаемые вида x1*a…*x….
Таким образом:
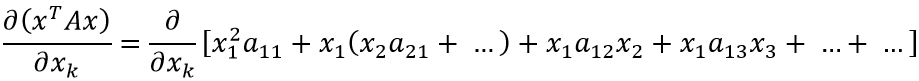
Если присмотреться, можно заметить закономерность (приведены множители xk: оставшаяся часть выражения скрыта за многоточием):
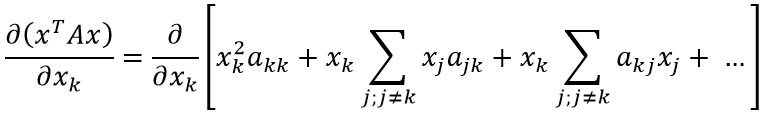
Теперь найти производную не составит труда:
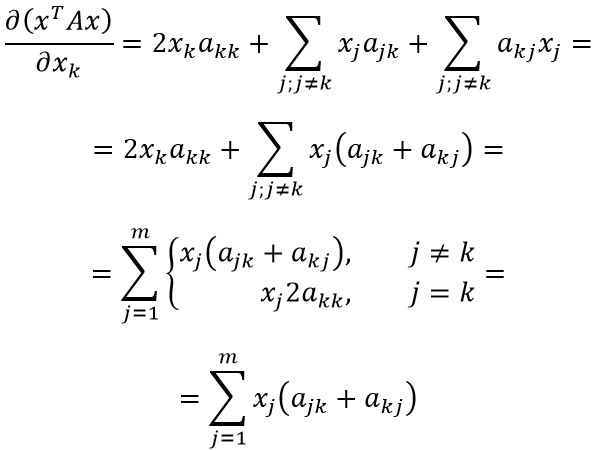
В преобразованиях выше мы сначала объединили две сумму в одну (т.к. индексы, по которым идёт суммирование совпадают), затем первое слагаемое внесли как частный случай суммы под знак суммирования (в соответствии с индексом при x). Последняя операция изменяет условия суммирования: теперь сумма определена для всех возможных значений индекса j.
Наконец, можно заметить, что (ajk+akj) при выполнении j=k соответствует (akk+akk) = 2akk. Таким образом, выражение для первого условия покрывает и выражение для второго условия — сумму можно переписать без ветвления. Для всех компонент вектора x формула коэффициента оказалась одинакова.
Теперь несложно продолжить дифференцирование:
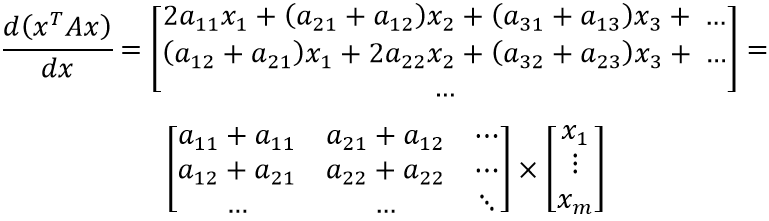
Осталось заметить, что левый множитель представляет собой специфическое суммирование элементов матрицы. Несложно догадаться, что компонент jk складывается с kj при сложении матрицы с её транспонированным вариантом:
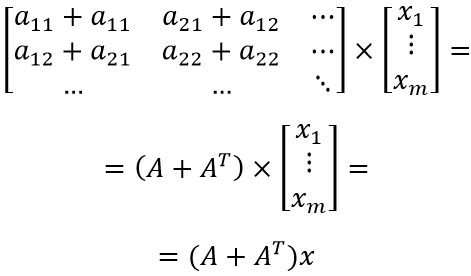
Оставляя начальное и конечное выражения, получаем:
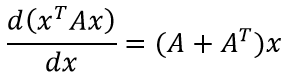
ЧТД
Вторая формула
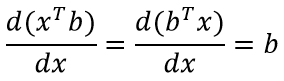
Формула (особенно, по сравнению с предыдущей) достаточна проста для восприятия и объясняется «на пальцах». xTb и bTx — это просто сумма попарного произведения компонент двух векторов (первый вектор приходится транспонировать для существования соответствующего матричного произведения). Ну и, не менее очевидное — скорость изменения от x каждой компоненты результирующего вектора определяется соответствующей компонентой вектора b.
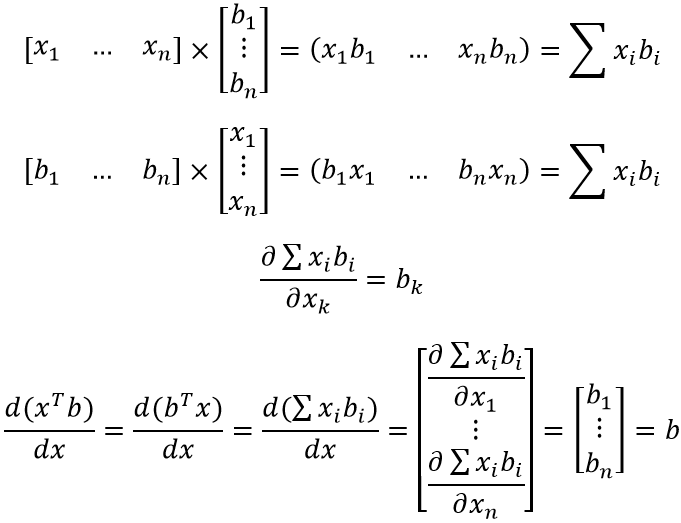
ЧТД
Вместо выводов
Профессор, стоя у доски, был погружен в длиннейший вывод. В каком-то месте он произнес стандартную фразу «отсюда с очевидностью вытекает следующее» и написал длинное и сложное выражение, абсолютно не похожее ни на что из написанного ранее. Затем он заколебался, на его лице появилось озадаченное выражение, он что-то пробормотал и прошел из аудитории в свой кабинет. Появившись оттуда через полчаса, он с довольным видом объяснил аудитории: «Я был прав. Это, действительно, совершенно очевидно».
— Дуайт Е.Грэй «Отчеты, которые я читал… и, возможно, писал».
План:
-
Основные понятия……………………………………………………ст.2
-
Определители…………………………………………………………ст.4
-
Векторы и линейное векторное
пространство……………………..ст.6 -
Характеристические числа и
характеристические векторы……….ст.8 -
Матричные преобразования…………………………………………ст.9
-
Билинейная и квадратичная
формы…………………………………ст.9 -
Матричные многочлены. Бесконечные ряды
и функции матриц…ст.10 -
Функциональное пространство………………………………………ст.12
-
Список литературы……………………………………………………ст.14
Система линейных уравнений
а11х1
+а12х2
+а13х3
+…+а1nхn
=у1
а21х1
+а22х2
+а23х3
+…+а2nхn
=у2
…………………………………………………………
аm1х1
+аm2х2
+аm3х3
+…+аmnхn
=уm
будет некоторое множество связей между
переменными х1,х2,…,хnиу1,у2,…,уm.
Эти связи, или линейное преобразование
переменныххв переменныеу,
полностью характеризуются упорядоченным
набором коэффициентовaij.
Если это множество коэффициентов
обозначить через А и записать в виде

то, как будет показано, посредством
введения определения «произведение
Ах» систему линейных уравнений можно
записать в виде: Ах = у. Несомненно,
приведенное выражение по виду значительно
проще, чем соответствующая система
линейных уравнений. Это одна из
соответствующих причин использования
матриц.
Столбцы матриц называются
векторами-столбцами, а строки матрицы
—векторами-строками. Матрица,
содержащаяmстрок иnстолбцов, называется (m×n)
матрицей. Квадратная матрица (m
=n),
является матрицаn-го
порядка.
1.1. Основные типы матриц.
-
Матрица типа (m×1)
называетсяматрицей-столбцомиливектором-столбцом, т.к. она состоит
из одного столбца иmстрок.

-
Матрица типа (1×n),
содержащая одну строку элементов,
называетсяматрицей строкой.
.
-
Диагональной матрицейназывается
квадратная матрица, элементы которой,
не лежащие на главной диагонали, равны
нулю.

-
Единичной матрицейназывается
диагональная матрица, диагональные
элементы которой равны единице.

-
Транспонирование матрицы А–
операция, при которой ее строки и столбцы
меняются местами (Ат). -
Матрица, все элементы которой тождественно
равны нулю, называется нулевой
матрицей.
1.2. Специальные типы матриц.
-
Квадратная матрица с действительными
элементами называется симметрической,
если А = Ат. -
Действительная квадратная матрица
называется кососимметрической,
если А = -Ат(нулевые элементы по
главной диагонали). -
Если элементы матрицы А комплексные
(aij= aij
+ ibij),
то комплексно сопряженная матрица В
содержит элементы
bij= aij
— ibij(B=A*). -
Матрица называется сопряженной,
если (А*)Т. -
Если А = А*, то матрица являетсядействительной.
-
Если А = -А*, то матрица А –мнимая.
-
Если А = (А*)Т, то матрица А
–эрмитова матрица. -
Если А = -(А*)Т, то матрица А
–косоэрмитоваматрица.
1.3. Простейшие операции.
-
Сложение матриц.
Если матрицы А и В одного порядка (m×n),
то суммой служит матрица С = А + В, элемент
которой определяется какcij=aij+bij,;
.
Свойства: А + В = В + А (коммутативность);
А + (В + С) = (А + В) + С (ассоциативность).
-
Вычитание матриц.
Разность матриц одного порядка (m×n)
равна матрицеD= А – В,
элементы которой определяются как:
dij=aij-bij,;
.
-
Матрицы А и В одинакового порядка равны,
если равны их соответствующие элементы:
a
= b. -
Произведение матриц.
Произведение матриц А и В может
рассматриваться как матрица С, где С =
АВ, или [Сik] = [aijbjk].
В общем случае: С = АВ = [aikbjk].
Если число столбцов матрицы А равно
числу строк матрицы В, то матрицы А и В
согласованы по форме, а если матрицы А
и В равны (А = В), т.е. АВ = ВА, то говорят,
что эти матрицы коммутативны.
-
Умножение матриц на скалярную величину.
При левом или правом умножении матрицы
на скалярную величину R,
каждый элемент данной матрицы умножается
на этот скалярR.
Произвольный элемент произведенияRAравенRaij.
-
Умножение транспонированных матриц.
ВтАт= (АВ)т.
В общем случае: Ст= (АВ)т=
ВтАт.
-
Умножение на диагональную матрицу.
Иногда удобно сконструировать матрицу
из элементов, являющихся матрицами.

Матрица В представляется аналогично.
Тогда произведение матриц:

Число выделенных в матрице А столбцов
должно равняться числу выделенных в
матрице В строк.
-
Дифференцирование матриц.
Производная от А(t) по
переменнойtопределяется
как:
=

Производная от суммы двух матриц: [A(t)
+B(t)] =(t)
+(t).
Производная от произведения двух
матриц: [A(t)B(t)]
=(t)B(t)
+A(t)(t).
-
Интегрирование матриц.
Подобно определению производной от
матрицы, интеграл от матрицы определяется
как матрица, образованная из интеграла
от элементов исходной матрицы.
dt.
Соседние файлы в папке лекции МОТС
- #
- #
- #
- #
- #
- #
- #
0 / 0 / 0
Регистрация: 27.12.2013
Сообщений: 9
1
Интерграл от матрицы
29.11.2015, 17:50. Показов 1398. Ответов 1

Нужно построить функцию:
где t изменяется от 0 до 0.5 с шагом 0.01
C,S,J,B — матрицы.
Исходные значения:
| Matlab M | ||
|
Для этого нужно найти предварительно матрицу:
Получается, нужно найти интеграл от матрицы expm(J*(t-tau)), т.е. найти интеграл от каждого элемента этой матрицы. А как это сделать, я не понимаю.
Я считала так:
| Matlab M | ||
|
Как я нашла в справочнике MatLab, так находится интеграл в виде массива… Но мне нужно найти интеграл от элементов матрицы, т.е. в итоге должна получится матрица. Поэтому данная программа выдает мне ошибку: Q=NaN+NaNi.
Помогите построить эту функцию) Быть может есть какой-нибудь другой способ, нежели считать интеграл матрицы…
Добавлено через 22 часа 31 минуту
Нашла другой способ решения этого задания (преобразовала функцию).
А встроенной функции MatLab, находящей интеграл от матрицы, я не нашла. Если только вручную брать интеграл от каждого элемента матрицы, а потом из них составлять саму матрицу.
В моем случае код следующий:
| Matlab M | ||
|
0

