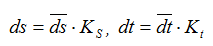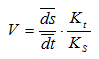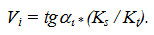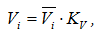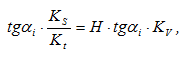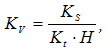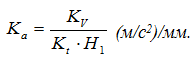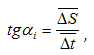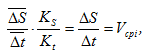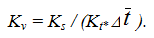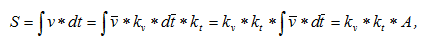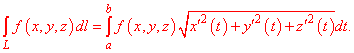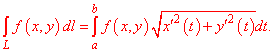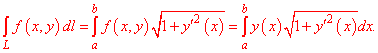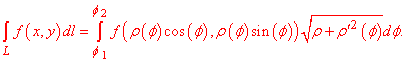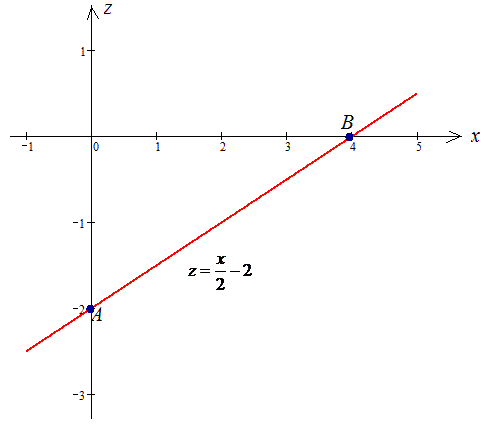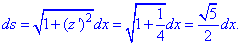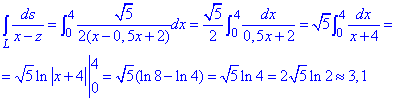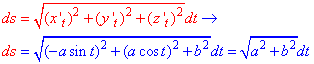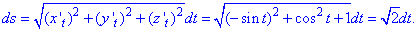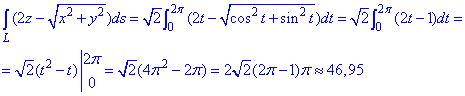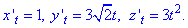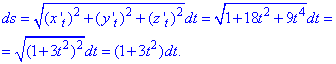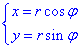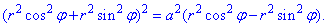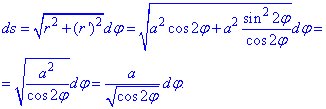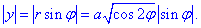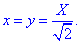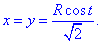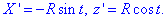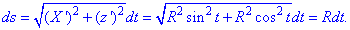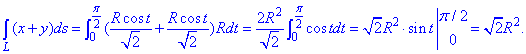Как найти интеграл графически

     Графическое интегрирование.

     Пусть нам известен график функции (y=f(x)). Поставим задачу: геометрическими средствами, не прибегая к вычислениям, найти приближенное значение интеграла $$I=int_{a}^{b}{f(x)dx}.$$

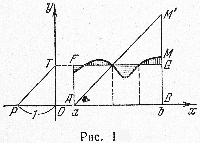
     Будем предполагать, что масштаб по оси (Ox) равен масштабу по оси (Oy) и что полюс графика (P) находится на расстоянии единицы масштаба от начала координат: (OP=1) (рис.1). Проведем прямую (FG), параллельную оси (Ox) и пересекающую линию (y=f(x)) так, чтобы площадь полученного прямоугольника как можно меньше отличалась от площади нашей криволинейной трапеции. Для этого нужно, чтобы площадь, заключенная между линией и прямой (FG) и лежащая над прямой, по возможности точно равнялась площади, заключенной между линией и прямой и лежащей под прямой. продолжим прямую (FG) до пересечения с осью (Oy) в точке (T) и соединим эту точку с полюсом графика. Наконец, из точки (A) проведем прямую, параллельную (PT), до пересечения с прямой (x=b) в точке (M’).

     Легко убедиться в том, что отрезок (M’B) изобраает искомую площадь, т.е. отрезок (M’B) содержит столько линейных масштабных единиц, сколько квадратных единиц содержит площадь криволинейной трапеции. В самом деле, из подобия треугольников (POT) и (ABM’) находим

но (OP=1), а (ABcdot OT) измеряет площадь трапеции.

     Если интервал ([a,b]) недостаточно мал, то проведение прямой (FG) на глаз может привести к ощутимой ошибке. Для того чтобы уточнить построение, разобьем интервал интегрирования на частичные интервалы (не обязательно равные между собой) и всю трапецию — на ряд трапеций, опирающихся на эти частичные интервалы. Точки деления выберем таким образом, чтобы каждый частичный интервал был интервалом монотонности подынтегральной функции и чтобы в числе точек деления находились все точки пересечения линии (y=f(x)) с осью (Ox). Если в каждом интервале линия незначительно отличается от прямой, то в качестве средних линий частичных трапеций можно брать просто ординаты в средних точках частичных интервалов. Тогда отпадает необходимость проводить на глаз вспомогательные линии. Практически обычно так и поступают.

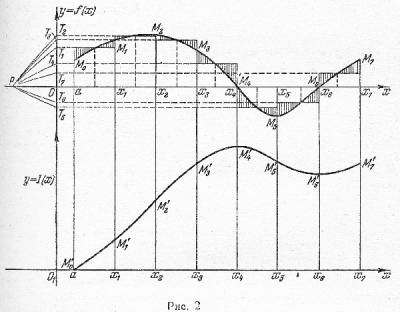
     Последовательно для каждой из частичных криволинейных трапеций построим указанным выше путем отрезок, изображающий ее площадь. В целях ясности чертежа удобно откладывать этот отрезок не от данной оси (Ox), а от другой оси (O_{1}x), параллельной первой (рис.2). В точке (x=a) площадь трапеции, отсчитываемая от прямой (x=a), очевидно, равна нулю. Отметим на оси (O_{1}x) точку (M’_{0}(a,0)), она соответствует точке (M_{0}) линии (y=f(x)). До прямой (x=x_{1}) площадь трапеции равна площади первой частичной трапеции; она изобразится отрезком (M_{1}x_{1}), которой мы получим, если из точки (M’_{0}) проведем прямую, параллельную (PT_{1}), до пересечения с прямой (x=x_{1}) в точке (M’_{1}). Эта точка соответствует точке (M_{1}) на линии. Площадь трапеции до прямой (x=x_{2}) (т.е. значение интеграла, взятого от (a) до (x_{2})) равна сумме (в алгебраическом смысле) площадей первой и второй частичных трапеций. Она изобразится отрезком (M’_{2}x_{2}), который получится, если из точки (M’_{1}) провести прямую, параллельную (PT_{2}), до пересечения с прямой (x=x_{2}) в точке (M’_{2}). Эта точка соответствует точке (M’_{2}) на линии. Продолжая так же дальше, построим последовательно точки (M’_{3}, M’_{4}, … ,) соответствующие точкам (M_{3}, M_{4}, … ) линии. Ордината точки (M’_{n}), соответствующей точке (M’_{n}[b,f(b)]) линии, и даст нам искомое значение интеграла (I). Ясно, что чем больше точек деления, тем точнее получится построение.

     Соединим полученные точки (M’_{0},M’_{1},M’_{2},…, M’_{n}) плавной линией. Ординаты этой линии, очевидно, приближенно изображают значения интеграла, взятого от (x=a) до соответствующих точек основания трапеции. Другими словами, эта линия является графиком функции, определяемой нашим интегралом с переменным верхним пределом: $$I(x)=int_{a}^{x}{f(x)dx}.$$

     Линия (y=I(x)) называется интегральной кривой функции (y=f(x)). Рассмотренное геометрическое построение интегральной кривой по графику подынтегральной функции называется графическим интегрированием.

     Так же как и в случае графического дифференцирования, графическое интегрирование бывает наиболее удобным тогда, когда подынтегральная функция задается графически, а аналитическое ее выражение неизвестно. Это нередко встречается в практике, например, когда функция определяется графиком, записываемым самопишущим прибором.

2012-11-08 • Просмотров [ 12497 ]

Рассмотрим известные методы графического дифференцирования и интегрирования:

Методы графического дифференцирования

Существует три метода графического дифференцирования: метод касательных, метод хорд и метод приращений.

Метод касательных

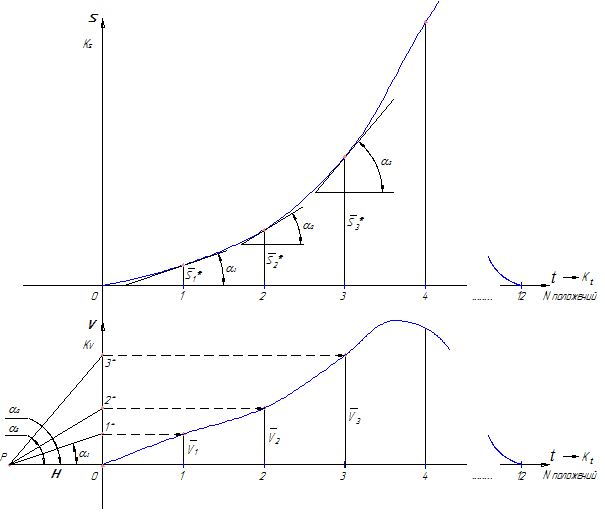
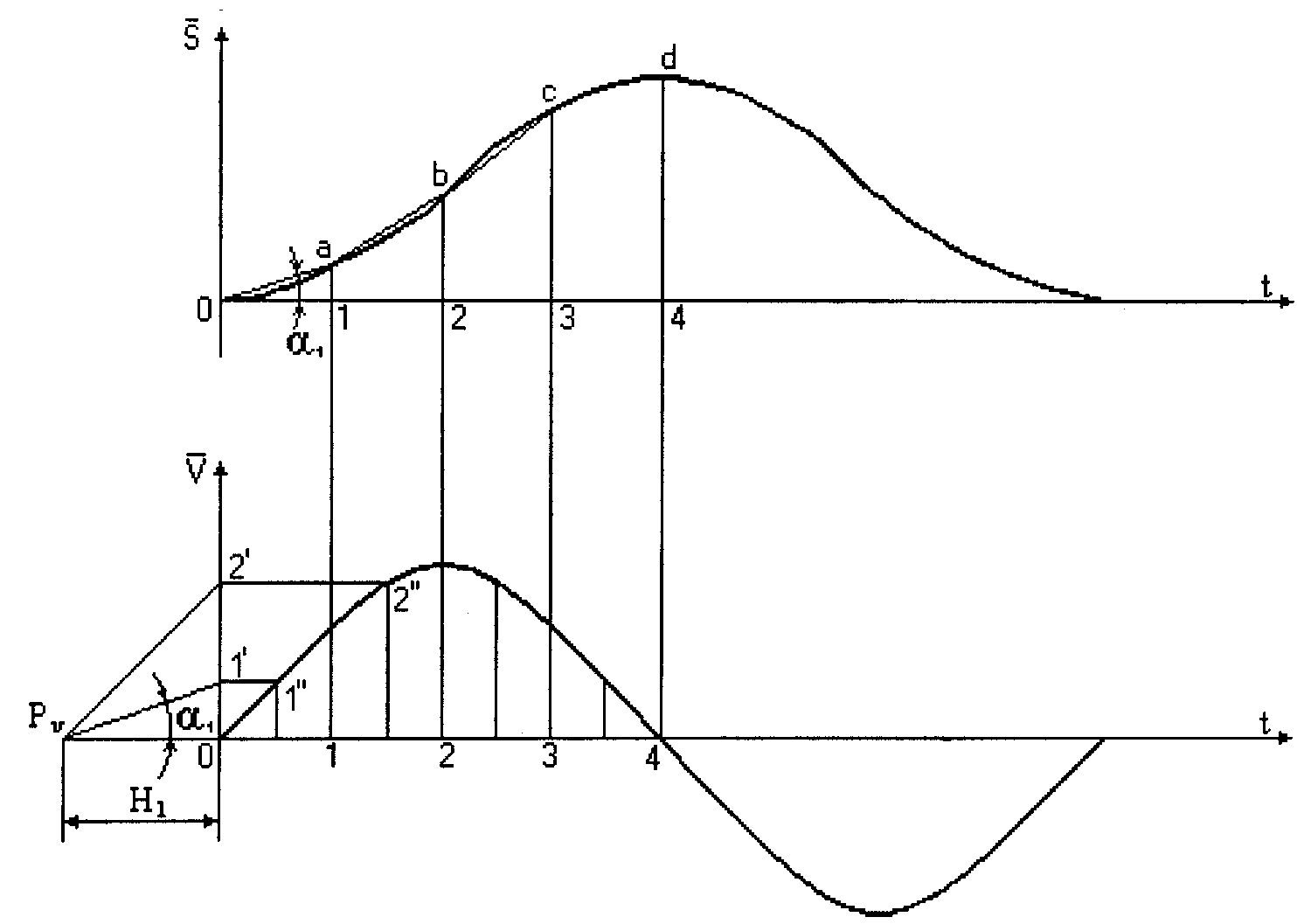
Метод касательных основан на геометрической интерпретации производной. При использовании метода кинематических диаграмм вначале дифференцируется диаграмма перемещений для получения графика (диаграммы) скоростей. Рассмотрим графическое дифференцирование на этом примере.

V = ds/dt, но т.к. аналитическое выражение для перемещений в данном случае отсутствует, то представляем значения перемещений и времени через отрезки на диаграмме перемещений:

тогда

Но отношение бесконечно малого приращения функции к бесконечно малому приращению аргумента на графике представляет собой тангенс угла наклона касательной к данной кривой в рассматриваемой точке, т.е.

Используя данное обстоятельство, диаграмму скоростей строят в следующем порядке (рисунок 11):

• проводят касательные к диаграмме перемещений в намеченных положениях;
• слева от начала координат на оси абсцисс будущей диаграммы скоростей отмечают полюс P на некотором расстоянии H (которое называется полюсным расстоянием);
• из полюса проводят лучи, параллельные проведенным касательным на диаграмме перемещений. Эти лучи отсекают на оси ординат будущей диаграммы скоростей отрезки

oi^*=H∙tg
α_i

Таким образом, и скорость в i-том положении и отрезки oi* пропорциональны tgα_i, а значит отрезки oi* пропорциональны V_i (скорости исследуемого звена в соответствующем положении механизма), т.е. они представляют собой изображение скорости в виде отрезка в некотором масштабе – V_i.

или

т.е.

где K_v – масштаб диаграммы скоростей по оси ординат в (м/с)/мм.

Далее отрезки oi* переносят в соответствующие положения, отмеченные на оси абсцисс, и, соединив концы отрезков плавной кривой, получают диаграмму скоростей исследуемого звена. Аналогично строится диаграмма ускорений. При этом масштаб ускорений

Рисунок 11

Теоретически метод касательных самый точный из графических методов дифференцирования, т.к. дает значение мгновенной скорости (ускорения) именно в том положении, в котором проведена касательная.

Однако из-за трудности точного проведения касательных (и сама дифференцируемая кривая, построенная по точкам, имеет отклонения от ее теоретической функции), практическая точность этого метода весьма низкая, поэтому он используется редко (обычно когда надо проанализировать характер движения звена без получения конкретных численных результатов).

Метод хорд

При графическом дифференцировании методом хорд последовательность действий точно такая же, что и при методе касательных, но вместо касательных к дифференцируемому графику в конкретных положениях проводят хорды на выделенных участках. В этом случае

но

т.е. тангенс угла наклона хорды пропорционален средней скорости на выделенном участке, поэтому отрезки 0i* с оси ординат надо переносить на середины соответствующих участков (считая, что средняя скорость примерно совпадает с мгновенной скоростью посередине выделенного участка). По полученным точкам строят диаграмму скоростей (см. рисунок 12).

Аналогично, дифференцируя диаграмму скоростей, получают диаграмму ускорений. Масштабы всех диаграмм определяют точно так же, как и при использовании метода касательных.

Рисунок 12 – Графическое дифференцирование методом хорд

Изначально в методе хорд имеется неточность, связанная с тем, что на самом деле средняя скорость на участке не обязательно совпадает с мгновенной скоростью на его середине. Однако практическая точность его значительно выше, чем при использовании метода касательных, т.к. хорду по двум точкам провести легко с достаточно высокой степенью точности.

Метод тем точнее, чем ближе хорда к дифференцируемой кривой, поэтому делением кривой на более мелкие участки, можно добиться достаточной для практики точности. Поэтому метод хорд применяется значительно чаще, чем метод касательных.

Метод приращений

Метод приращений является частным случаем метода хорд, когда полюсное расстояние принимается равным выделенным участкам на оси абсцисс (при этом все участки должны иметь одинаковую величину H=Δt). В этом случае приращение перемещений на выделенном участке представляет собой среднюю скорость на данном участке в некотором масштабе

Аналогично дифференцируется диаграмма скоростей для получения диаграммы ускорений. Метод удобен тем, что не надо проводить никаких вспомогательных линий, дифференцирование осуществляется очень быстро. Однако при повторном дифференцировании (дифференцировании диаграммы скоростей для получения диаграммы ускорений) приращения уменьшаются и точность результатов резко снижается (получается большая относительная погрешность).

Методы графического интегрирования

При анализе и, особенно, при синтезе механизмов может быть графически задана функция изменения скорости звена, а необходимо иметь функцию перемещения (или необходимо определить функцию изменения скорости при заданной графически функции ускорения). В этом случае можно воспользоваться методами графического интегрирования.

Применяется два метода графического интегрирования – метод площадей и метод хорд.

Графическое интегрирование методом площадей

Этот метод основан на геометрической интерпретации (физическом смысле) интеграла. Рассмотрим данный метод на примере интегрирования диаграммы скоростей. В результате интегрирования необходимо построить диаграмму перемещений.

где А – площадь под кривой скорости на выделенном участке (что соответствует физическому смыслу интеграла).

Для интегрирования методом площадей выделяют на оси абсцисс N положений (в пределах одного цикла). Определяют площадь А₁ (в мм²) под графиком скорости на участке 0-1, площадь А₂ – на участке 1-2, площадь А₃ – на участке 2-3 и т.д.

Умножив эти площади на масштаб скоростей и масштаб времени диаграммы скоростей, получают истинные перемещения на выделенных участках, по которым определяют общие перемещения в каждом положении исследуемого звена в расчете от нулевого положения:

S_0-1 = K_v ∙ K_t ∙ A₁;
S_1-2 = K_v ∙ K_t ∙ A₂;
S_2-3 = K_v ∙ K_t ∙ A₃; и т.д.

S₁ = S_0-1;
S₂ = S₁ + S_1-2;
S₃ = S₂ + S_2-3; и т.д.

После определения всех перемещений задают масштаб K_s, в котором строят диаграмму перемещений.

Графическое интегрирование методом хорд

Данный метод основан на том, что интегрирование есть процесс обратный дифференцированию. Поэтому при этом методе производятся все те же действия, что и при дифференцировании методом хорд, только в обратном порядке:

В результате, после построения всех хорд, формируется ломаная кривая, по вершинам которой надо провести плавную кривую.

При интегрировании диаграммы скоростей полученная кривая будет представлять собой диаграмму перемещений (соответственно, при интегрировании диаграммы ускорений, получается диаграмма скоростей). Масштабы полученных диаграмм определяются из зависимостей, выведенных для графического дифференцирования:

K_s = K_v ∙ K_t ∙ H

K_v = K_at ∙ H₁

Графический метод как алгоритм решения на ЭВМ >
Курсовой проект по ТММ >

Вычисление
интеграла, выведенного в аналитическом
виде — операторы eval
или evalf
(см. п. 5).
Для примера п. 14:

>
phi:=rho*r^2*sin(alpha); int(int(int((phi), beta=0..2*Pi),
alpha=0..Pi), r=0..R): M:=evalf(subs([rho=2, R=5], %));

Когда
промежуточная формула не интересует
нас, можно вставить команды evalf(subs(…))
сразу в предыдущую команду (как внешние)
и получим численное значение М.

>
M:=evalf(subs([rho=2,R=5],int(int(int((phi),beta=0..2*Pi),alpha=0..Pi),
r=0..R)));

Другие примеры:

> V:=evalf(4*Pi*int(r^2,
r=0..1), 7);

(объём шара
единичного радиуса);

>
int(x^2*exp(-x),x=0..infinity); evalf(int(x^2*exp(-x),x=0..1));

Последние
примеры показывают вычисление
интеграла без его предста-вления
формулой.
Это можно применять, когда интеграл не
имеет анали- тического выражения («не
берётся»). Тогда программа вычисляет
его численным
методом
с достаточной точностью.

В тех
же случаях можно и представить
интеграл графически:

>
plot(int(x^2*exp(-x), x=0..z), z=0..10);

График 15.1. Асимптотическое приближение
интеграла к вышенайденному значению 2

>

16. Ряды, разложение функций в ряды.

Ряд
представляется последовательностью с
бесконечным числом членов. которую
невозможно ни ввести в команду, ни
вывести на экран. При выводе Maple выводит
несколько первых членов ряда (по умолчанию
— 6), а остаточный член, пренебрежимый в
данном приближении, имеет специальное
обозначение O
= Omicron
(см. 11.2),
причём в скобках указана его главная
зависимость от аргумента. Задаётся
общий член ряда u[k].

16.1. Суммирование рядов.

Оператор
суммы — sum
(см. п. 6);
формат команды: sum(u[k],
k=m..n); k
— индекс суммирования, номер общего
члена ряда. Для нахождения полной суммы
ряда следует положить m=0
(или m=1,
если u[0]=
или не определено) и n=
(infinity). Конечное
значение суммы существует только для
сходящихся рядов!
Иногда сумма имеет аналитическое
выражение в виде комбинации чисел и
математических констант. В других
случаях она выражается трансцендентными
функциями параметра. Возможно вычисление
суммы ряда без вывода её аналитического
выражения.

Примеры
(иногда надо вводить условия на параметры
общего члена ряда).

> sum(‘1/k’,
‘k’=1..infinity);

(Расходящийся
гармонический ряд).

>
sum(‘1/k!’, ‘k’=0..infinity); evalf(%);

Сумма
есть число
Непера
— основание натурального логарифма.

Сумма
геометрического ряда (обобщение
геометрической прогрессии на нецелые
степени q
(q<1!))

> sum(‘q^(k/2)’,
‘k’=0..infinity); evalf(subs(q=1/2,%));

>
sum(‘1/(k!)^2’, ‘k’=0..infinity); evalf(%);

Результат
представлен функцией
Бесселя.

16.1.1. Справка по функциям Бесселя.

BesselI, BesselJ — The Bessel functions of the first kind

Calling Sequence

BesselI(v, x);
BesselJ(v, x).

Parameters

v — algebraic expression (the order or
index), x — algebraic expression (the argument)

Description

BesselI and BesselK are the modified Bessel
functions of the first and second kinds, respectively. They satisfy
the modified Bessel equation: x^2*y» + x*y’^2 — (x^2 + v^2 ) y = 0

Более подробно о фунциях
Бесселя см. п. 17.

> assume(n>1);
sum(‘1/k^n’, ‘k’=1..infinity);

Результат
представлен дзета-функцией
Римана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определенные интегралы в случаях когда интегрирование проводится не вдоль отрезка, а некоторой кривой (на плоскости или в пространстве) называются криволинейными. Различают криволинейные интегралы І и ІІ рода.

Формулы криволинейного интегралу первого рода

Пусть в пространстве (на плоскости) задано параметрическое уравнение гладкой кривой f (x, y, z)
x=x(t), y=y(t), z=z(t).
tє[a, b].
Каждая из функций непрерывна на промежутке интегрирования.
Функция f(x, y, z)=0 описывает кривую в пространстве.
В таком случае криволинейный интеграл первого рода равен интегралу за параметром от функции умноженной на корень квадратный из суммы квадратов производных координат за параметром

Для случая кривой на плоскости формула неопределенного интегралу I роду упрощается

Когда кривая интегрирования задана явно y=y(x), формула перехода к определенному интегралу имеет вид

Пусть функция задана полярными координатами rho=rho(phi), phi₁<phi<phi₂. Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле

На этом все формулы, что Вам нужны для вычисления интегралов, однако без готовых ответов трудно представить их приложение, поєтому перейдем к практической части.

Примеры подобрано из учебной программы для студентов ЛНУ им. И. Франко. Они охватывают широкий класс заданий, которые непременно встретите на контрольной работе и экзаменах. Поэтому внимательно разберите ответы к примерам и выучите приведенные наверху формулы вічисления криволинейных интегралов.

Пример 1.7 Вычислить криволинейный интеграл 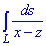вдоль дуги L — отрезок прямой z=x/2-2, что соединяет точки A(0;- 2) и B(4;0) в плоскости xOz.
Решение: Построим графически прямую и нанесем на нее точки ограничивающие дугу

За видом видим, что необходимо вычислить криволинейный интеграл I рода.
z=x/2-2, z’=1/2.
Подынтегральная функция примет значение
1/(x-z)=1/(x -(x/2-2))=1/(0,5x+2).
Найдем дифференциал дуги заданной кривой по формуле

Подставляем и находим криволинейный интеграл

Неопределенный интеграл сводится к логарифму, который не имеет особенностей (гладкая функция) на промежутке интегрирования.

Пример 1.10 Вычислить криволинейный интеграл вдоль дуги L:
, где L — дуга кривой x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
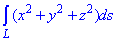
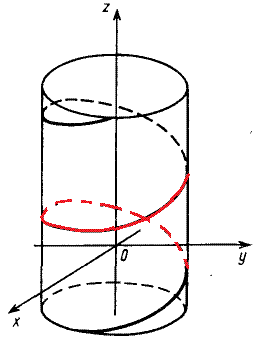
Решение: Параметрическая кривая x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi] описывает часть винтовой линии.
Ее график на цилиндрической поверхности имеет вид.

Часть винтовой линии, которая отвечает промежутку [0;2pi] изображена красным цветом.
Подынтегральная функция равна x²+y²+z².
Нужно вычислить криволинейный интеграл I рода.
Находим производные координат по параметру
x’_t=a*sin(t), y’_t=a*sin(t), z’_t=b.
Дальше вычисляем дифференциал дуги параметрически заданной кривой согласно формуле:

Формулы дифференциалу дуги в декартовой, полярной и пространственной системах координат приведены в теоретическом материале и поэтому здесь на них задерживаться не будем.
Интегрированием вычисляем криволинейный интеграл

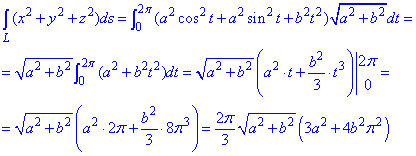
Интеграл не сложен в плане расчетов.

Пример 1.12 Вычислить криволинейный интеграл 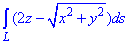вдоль дуги L, где L — дуга кривой x=cos(t), y=sin(t), z=t [0;2pi].
Решение: Имеем идентичное уравнение x=cos(t), y=sin(t), z=t — винтовой линии.

Для вычисления криволинейного интеграла I рода находим производные координат
x’_t=-sin(t), y’_t=cos(t), z’_t=1.
Подставляем их в дифференциал дуги винтовой линии:

Превращаем подінтегральную функцию и находим криволинейный интеграл

Пример 1.14 Вычислить криволинейный интеграл int(x+y, dS)
вдоль дуги L — дуга кривой x=t, , z=t^₃, [0;1].
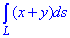
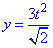
Решение: Прежде чем вычислить криволинейный интеграл I рода находим производные за параметром.

Подставляем их в формулу дифференциала дуги:

Определенный интеграл вычисляем в указанных пределах

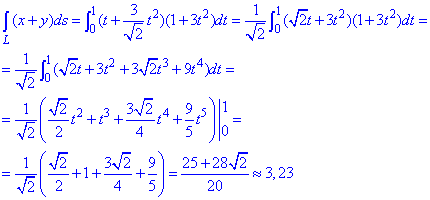
Под интегралом раскрыли скобки и применили простые формулы интегрирования.

Пример 1.18 Вычислить криволинейный интеграл int (1/x²+y²+z²,ds)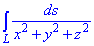
вдоль дуги кривой L:
x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
Решение: Интегрировать опять придется вдоль винтовой линии.

Производные за параметром имеют вид
x’_t=-a*sin(t), y’_t=a*sin(t), z’_t=b.
Вычисляем дифференциал дуги кривой:

Дальше превращаем криволинейный интеграл к определенному и находим его значение

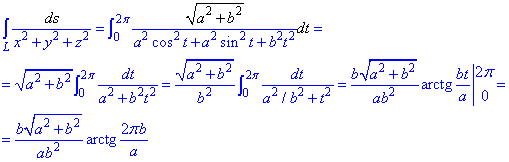
При интегрировании будем иметь арктангенс.
В результате вычислений получили компактную формулу через параметры формы цилиндра.

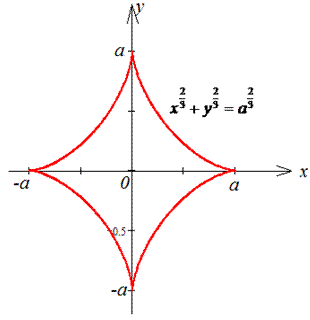
Пример 1.20 Вычислить криволинейный интеграл int(x^4/3+y^4/3,ds) вдоль дуги L:
дуга астроиды x^2/3+y^2/3=a^2/3.
Решение: Запишем параметрическое уравнение астроиды:
x=a*cos³(t), y=a*sin³(t), где t[0;2pi].
График астроиды в декартовой системе координат имеет вид

Для вычисления криволинейного интеграла I рода вычисляем производные за параметром
x’_t=-3a*cos²(t)*sin(t), y’_t=3a*cos(t)*sin²(t).
и подставляем в дифференциал дуги астроиды:

Криволинейный интеграл 1 рода находим методом замены переменной

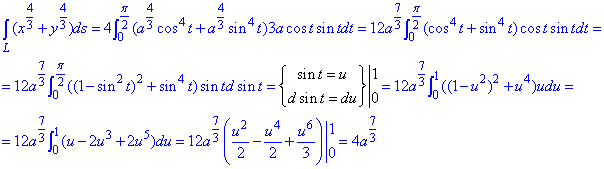
Это позволяет перейти к простому понятному виду подынтегральной функции.

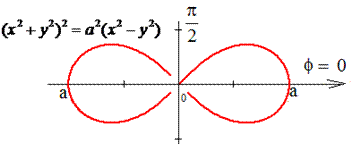
Пример 1.21 Вычислить криволинейный интеграл 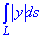вдоль дуги лемнискаты (x²+y²)²=a²(x²-y²).
Решение: Для лемнискаты раньше рассматривали интегралы на нахождение площади.

Запишем уравнение лемнискаты в полярной системе координат, используя превращение координат:

Тогда из уравнения дуги

выражаем радиус-вектор и вычисляем производную за углом

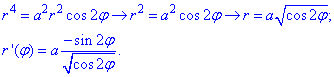
Найдем дифференциал дуги по формуле:

Запишем подынтегральную функцию:

Вычисляем криволинейный интеграл первого роду как 4 интеграла по 1 четверти

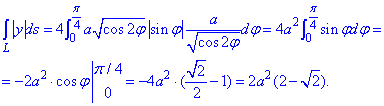
Синус в первой четверти положителен, поэтому модуль опускаем.

Пример 1.25 Вычислить криволинейный интеграл вдоль дуги L:
, где L — четверть круга x²+y²+z²=R², y=x что лежит в первом октанте.
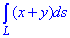
Решение: Имеем сферу x²+y²+z²=R² и плоскость y=x, которая ее пересекает.
График дуги в пространстве имеет вид как на рисунку

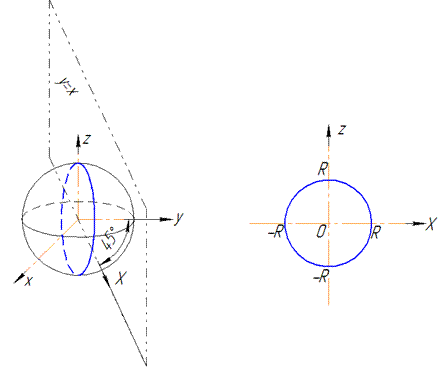
В сечении получим круг, который проектируется на плоскость y=x уравнением X²+z²=R², где
Такие манипуляции необходимы, чтобы параметризовать круг
Параметрическое уравнение круга:
x=R*cos(t), z=R*sin(t) и t[0;Pi/2] (I октант).
Тогда переменные выражаются зависимостью

Вычисляем производные

затем находим дифференциал дуги:

Подставляем все в интеграл и выполняем вычисление

Как Вы могли убедиться, ничего сложного в нахождении криволинейных интегралов первого рода нет. В теории известны формулы как переходить от криволинейных к определенным интегралам, ими и воспользовались. Сами же интегралы не сложны, да и кривые на практике подбираются таким образом, чтобы Вы с ними долго не возились на практических занятиях.
Все сводится к умению интегрировать, что в свою очередь требует знания таблицы основных интегралов.

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.