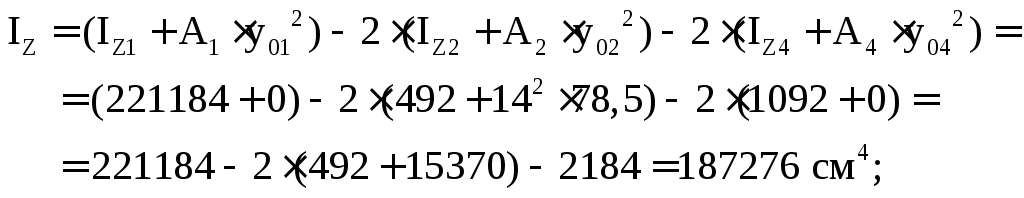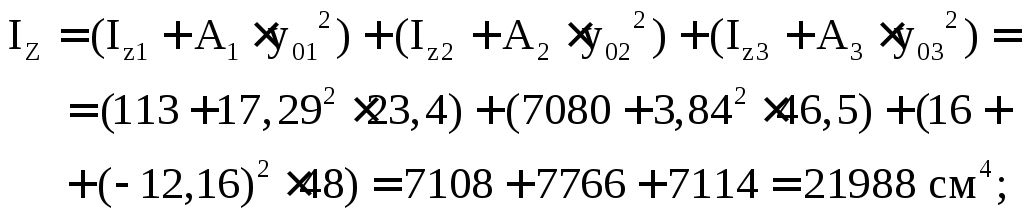Как найти инерции сечения относительно центральных осей

Нижеприведенные формулы для определения
моментов инерции простых сечений
относительно их центральных осей
получены из интегральных выражений для
моментов инерции (5.4), (5.5), (5.6):

1.
Прямоугольник

(5.10)

(5.11)

так как оси Z иY– оси
симметрии.

2. Круг

(5.12)

(5.13)

Здесь
–
полярный момент инерции сечения.

3. Полукруг

(5.14)

(5.15)

Рис. 5.5

4. Равнобедренный треугольник

(5.16)

(5.17)

5. Прямоугольный треугольник

(5.18)

(5.19)

(5.20)

Полезно запомнить, что в формулах
(5.10), (5.11) и (5.16)–(5.19) возводится в куб
размер стороны фигуры, перпендикулярной
рассматриваемой оси.

В формуле (5.20) при определении центробежного
момента инерции знак «минус»
ставится тогда, когда острые углы
треугольника находятся в отрицательных
четвертях (т.е. 2-й и 4-й). В тех случаях,
когда эти углы находятся в положительных
четвертях (т.е. 1-й и 3-й), в формуле (5.20)
ставится знак «плюс».

5.3. Главные центральные моменты инерции сложных симметричных сечений

Положение главных центральных осей и
величины главных центральных моментов
инерции для симметричных сечений
определяются в следующем порядке:

1. Сложное сечение разбивается на
простые фигуры (круг, прямоугольник,
двутавр, уголок и т.п.) и проводятся их
центральные оси Z_i
и Y_i
(как правило – горизонтально и
вертикально).

2. Определяется по формулам (5.3) положение
центра тяжести всего сечения и через
эту точку проводятся его центральные
оси Z и Y. При наличии двух осей симметрии
центр тяжести всего сечения находится
в точке их пересечения.

Если сечение обладает только одной осью
симметрии, то по формулам (5.3) определяется
только одна координата центра тяжести.
Поясним это для фигуры, показанной на
рис. 5.8:

а) оси Z’ и Y’ выбираем так, чтобы ось Y’
совпала с осью симметрии фигуры, а ось
Z’ – чтобы было удобно определить
расстояние до этой оси от центральных
осей простых фигур;

б) определяем статический момент
площади сечения относительно произвольной
оси Z’ по формуле:

= А₁у₁+ А₂у₂,

где А_i– площади
сечений простых фигур; у_i– расстояния от произвольной осиZ’
до центральных осей простых фигурZ_i.
Расстояния у_iнеобходимо брать с учетом знаков;

в) определяем координату
у_Cцентра тяжести
по формуле (5.3):

=

г) на расстоянии у_Cот осиZпроводим вторую центральную осьZ.
Первой центральной осью является ось
симметрии Y.

3. Моменты инерции
относительно главных центральных осейZиY(рис. 5.8)
определяем по формулам (5.9), которые в
развернутом виде запишутся так:

так как одна из рассматриваемых осей

(ось Y) является осью симметрии.

В этих формулах:

– осевые моменты инерции простых фигур
относительно своих центральных осей
(собственные моменты инерции), которые
определяются по формулам (5.10)–(5.19) или
по таблицам сортаментов для прокатных
элементов;

– расстояния от общих центральных осей
сеченияZиYдо центральных осей простых фигур. В
рассматриваемом примереипоказаны на рис. 5.8;

A_i–
площади простых фигур. Если простой
фигурой является фигура, вырезанная от
общей, т.е. «пустая» фигура, то в
соответствующие формулы площади таких
фигурAи их собственные моменты инерцииподставляются со знаком «минус».

ПРИМЕР 5.1

Требуется определить главные центральные
моменты инерции сечения, изображенного
на рис. 5.9.

РЕШЕНИЕ:

1. Разбиваем сечение на простые фигуры
и проводим их горизонтальные и вертикальные
центральные оси Z_iиY_i

2. Проводим центральные оси для всей
фигуры, т.е. оси симметрии ZиY.

3. Определяем расстояния от общих
центральных осей ZиYдо центральных осей простых фигур и
площади этих фигур:

4. Вычисляем собственные центральные
моменты фигур по формулам (5.10)–(5.17):

5. Определяем осевые моменты инерции
всего сечения относительно центральных
осей ZиY:

Центробежный момент инерции
так какZиY– оси симметрии. Поэтому вычисленные
намиI_ZиI_Y
поэтому являются главными центральными
осями:

ПРИМЕР 5.2

Требуетсяопределить главные
центральные моменты инерции сечения
показанного на (рис. 5.10).

РЕШЕНИЕ

1. Разбиваем сечение на простые фигуры
и проводим их центральные оси
иY_i.

2. Проводим ось симметрии
Y. Она является главной центральной осью
заданного сечения.

3. Для определения положения 2-й главной
центральной оси выбираем произвольную
ось Z,
перпендикулярную оси симметрии. Пусть
эта ось совпадает с осьюZ₃.

4. По формуле (5.3) определяем ординату у_сцентра тяжести поперечного сечения по
оси Y:

Откладываем размер у_Cвверх от осиZ’ и проводим
2-ю главную центральную осьZ.

5. Определяем осевые моменты инерции
простых фигур относи­тельно собственных
центральных осей (см. формулы (5.10)–(5.17)):

6. Вычисляем расстояния от центральных
осей всего сечения ZиYдо центральных осей отдельных фигур
(рис. 5.10):

так как оси Y₁,Y₂,Y₃совпадают с осью
симметрииY.

7. Вычисляем осевые моменты инерции
всего сечения относи­тельно центральных
осей ZиYпо формулам (5.9):

Центробежный момент инерции I_ZYвсего сечения равен нулю, так как ось Y
является осью симметрии, т.е. осиZиYявляются главными
центральными осями инерции сечения, а
вычисленные осевые моменты инерции
являются главными центральными моментами
инерции:

ПРИМЕР 5.3

Требуетсяопределить главные
центральные моменты инерции составного
сечения, показанного на (рис. 5.11).

РЕШЕНИЕ

Порядок решения подробно рассмотрен в
примере 5.2.

1. Разбиваем сечение на отдельные фигуры,
геометрические характеристики которых
приводятся в таблице сортаментов
(двутавр и швеллер) или легко вычисляются
по формулам (5.10)–(5.20) (в данном примере
прямоугольник) и проводим их центральные
оси.

2. Проводим ось симметрии Y. Центр тяжести
всего сечения лежит на этой оси.

3. Выбираем произвольную ось Z.
Пусть в данном примере эта ось совпадает
с осьюZ₃.

4. Расстояние у_Cопределяем от произвольной осиZдо центра тяжести всего сечения:

Расстояния от произвольно выбранной
оси Z’ до центральных осей
каждой фигуры (у₁, у₂, у₃)
показаны на рис. 5.11.

Площади сечений швеллера А₁и
двутавра А₂выписываем из
соответствующих таблиц сортамента, а
площадь прямоугольника А₃вычисляем:

А₁= 23,4 см², А₂= 46,5
см², А₃= 242 = 48
см².

Отложим величину у_Cвверх от осиZ’ (так как
у_C > 0)
и на этом расстоянии проведем главную
центральную осьZ.

5. Геометрические
характеристики прокатных профилей
выписываем из таблицы сортаментов,
учитывая различие в ориентации осей в
таблице сортаментов и на рис. 5.12а, в.

1. Швеллер № 20

ГОСТ 8240-89

(рис. 5.12а) ;

Двутавр № 30

ГОСТ 8239-89

(рис. 5.12б) h= 30 см.

Буква «с» в индексе осевых моментов
инерции I означает ссылку на обозначение
осей в сортаменте.

Моменты инерции прямоугольника
(рис. 5.12в) вычисляем отдельно по
формулам (5.10) и (5.11):

6. Определяем расстояния от общих
центральных осей Y и Z до центральных
осей отдельных фигур (они показаны на
рис. 5.11):

так как оси Y₁,Y₂,Y₃ совпадают с осью
симметрии всего сеченияY.

7. Определяем осевые моменты инерции
сложной фигуры относительно центральных
осей ZиYпо формулам (5.9):

Центробежный момент инерции
так как ось Y является осью симметрии.
Поэтому оси Z и Y являются главными
центральными осями.