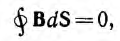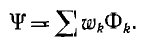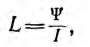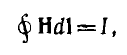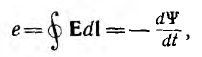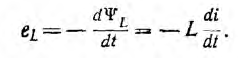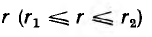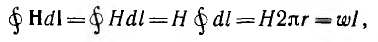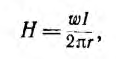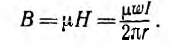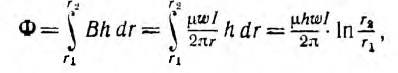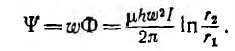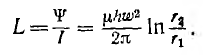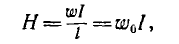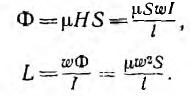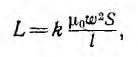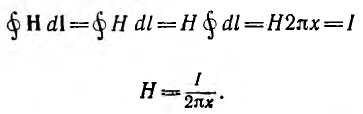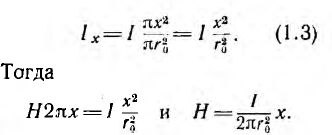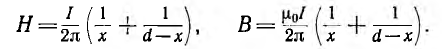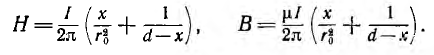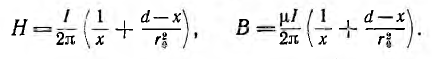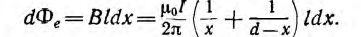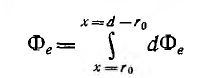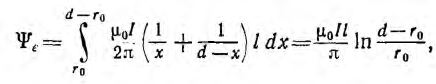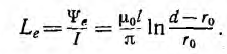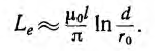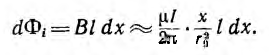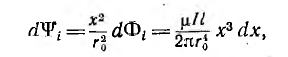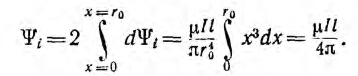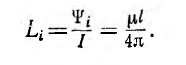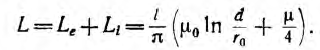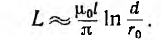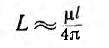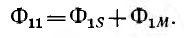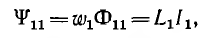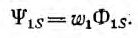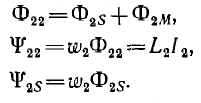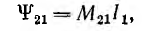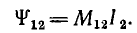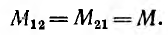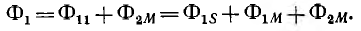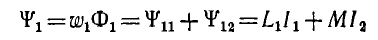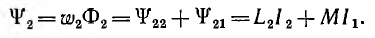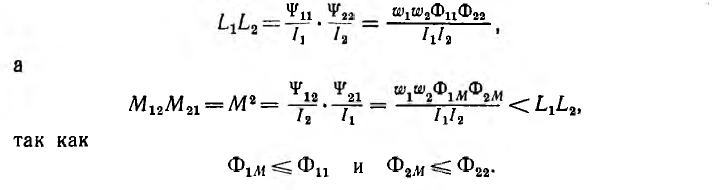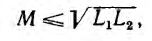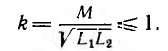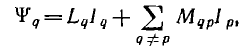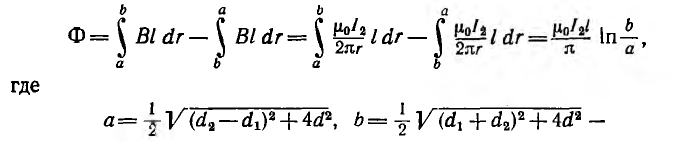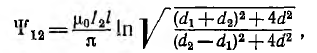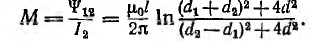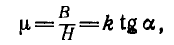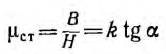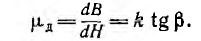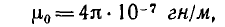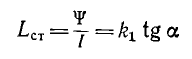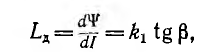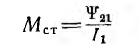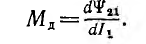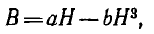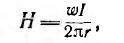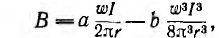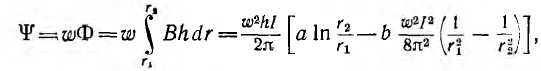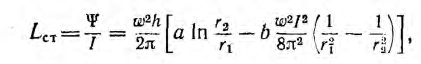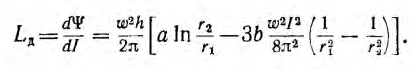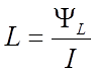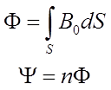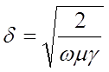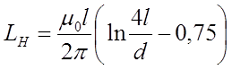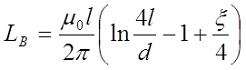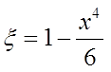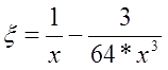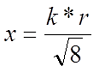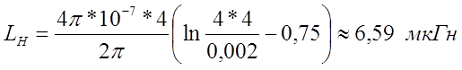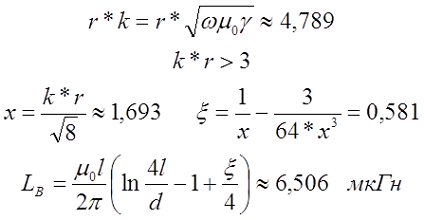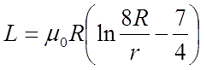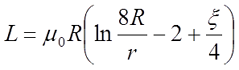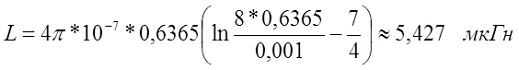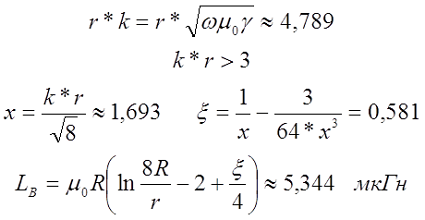- Информация о материале
-
Опубликовано: 24 августа 2011
-
Обновлено: 21 декабря 2022
-
Просмотров: 40047
Простые формулы расчета индуктивностей катушек
Радиотехника в целом и электродинамика в частности являются довольно сложными науками. Электродинамика, как наука изучающая переменное электромагнитное поле, основана на фундаментальных уравнениях в интегральной форме, которые оперируют векторными или комплексными величинами. Решения таких комплексных уравнений для нахождения величины индуктивности в виде простых аналитических формул чаще всего просто невозможны и используются численные методы решения задачи. Любые простые справочные эмпирические формулы являются обычно существенным упрощением таких численных методов, по этой причине они имеют ограничения в области и точности расчета. Основные положения электромагнетизма, в том числе определение понятия индуктивность — здесь.
Формулы и численные методы расчета катушек индуктивности, которые использует Coil64, вы можете посмотреть в справочном разделе сайта.
Здесь приведены простые эмпирические формулы расчета индуктивностей, которые Coil64 не использует, но которые могут быть полезны и радиолюбителям и студентам.
| Индуктивность | Формула | |
|---|---|---|
| Прямой провод |  |
 |
| Параллельные провода (ток в одном направлении) r≪w |
 |
 |
| Параллельные провода (ток в противоположных направлениях) r≪w |
 |
 |
| Полосковая линия |  |
 |
| Коаксиальная линия |  |
 |
| Однослойная катушка (l > 0.8 R) (онлайн калькулятор) |
 |
 |
| Многослойная катушка (l ≈ w) (онлайн калькулятор) |
 |
 |
| Плоская катушка (онлайн калькулятор) |
 |
 |
| Коническая катушка (онлайн калькулятор) |
 |

LH-индуктивность эквивалентной цилиндрической катушки |
Во всех расчетных формулах таблицы все размеры в метрах, индуктивность в Генри.
Теория индуктивностей
Характеристики магнитного поля
Магнитное поле создается постоянными магнитами и проводниками, по которым протекает электрический ток. Для характеристики магнитного поля вводятся такие величины:
Напряженность магнитного поля, характеризующая интенсивностъ магнитного поля в данной точке пространства. Напряженность магнитного поля, создаваемого током, определяется его величиной и формой проводника. Напряженность магнитного поля, в а/м внутри катушки. у которой длина намного больше диаметра, может быть определена по формуле
где I — ток (в а); w— число витков, l — длина катушки (в м).
Магнитный поток — общее количество магнитных силовых линий, пронизывающих контур. Для вакуума и практически для воздуха магнитный поток в веберах – вб, определяется по формуле
где S — площадь контура в квадратных метрах.
Магнитная индукция — интенсивность результирующего магнитного поля в данном веществе измеряется в веберах на метр квадратный (вб/м2)
Магнитная проницаемость — величина, показывающая, во сколько раз магнитная индукция в данном веществе больше или меньше на пряжеиности внешнего магнитного поля (ом*сек)/м
Магнитная проницаемость вакуума (магнитная постоянная) равна единице. Для воздуха μ приблизительно равна 1. У парамагнитных веществ (алюминий, платина) μ > 1, у диамагнитных (медь, висмут и др.) μ < 1, а у ферро магнитных (железо, никель, кобальт и некоторые сплавы) μ >>> 1. В соответствии с приведенными выше формулами для любого вещества можем написать:
Кроме практической системы единиц, пользуются абсолютной электромагнитной системой единиц. Соотношение между единицами этих систем следующее:
1 = 12,56*10-3 Э (эрстед);
1 вб = 108 мкс (максвелл);
1 вб/м2 = 104 гс (гаусс).
Индуктивность и взаимоиндуктивность
Индуктивность (коэффициент самоиндукции) численно равна э. д. с. самоиндукции (eL), возникающей в проводнике (контуре) при равномерном изменении тока в нем на 1 а в 1 сек.
Индуктивность, измеряется в следующих единицах:
1 гн = 1000 мгн;
1 мгн = 1000 мкгн;
1 мкгн = 1000 см.
Рис. 1 Схема взаимосвязанных индуктивностей.
Коэффициент взаимоиндукции М численно равен э. д. с. взаимоиндукции, возникающей в одном контуре при равномерном изменении тока на 1 а в 1 сек. в другом контуре (рис. 1).
Коэффициент взаимоиндукции измеряется в тех же единицах, что и индуктивность. Связь через общий магнитный поток двух катушек индуктивностью L1 и L2 называется индуктивной связью, характеризуемой коэффициентом связи
Зная коэффициент связи, можно определить коэффициент рассеяния
Если катушки находятся на общем замкнутом ферромагнитном сердечнике достаточно большого сечения, то k приблизительно равно 1, а ϭ приблизительно равна 0.
Соединение индуктивностей
Общая индуктивность L нескольких последовательно или параллельно соединенных индуктивностей при отсутствии, а также при наличии индуктивной связи между ними определяется по формулам, приведенным в таблице №1.
Таблица № 1
| Схема соединения | Общая индуктивность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В формулах отмеченных значком * верхний знак алгебраического сложения, используется при согласованном включении индуктивностей, а нижний знак алгебраического сложения, используется при встречном включении индуктивностей.
Катушки с малой индуктивностью
Однослойные катушки
применяются на частотах выше 1500 кГц. Намотка может быть сплошная и с принудительным шагом. Однослойные катушки с принудительным шагом отличаются высокой добротностью (Q = 150 — 400) и стабильностью. Они применяются в основном в контурах КВ и УКВ. Высокостабильные катушки, применяемые в контурах гетеродинов на КВ и УКВ, наматываются при незначительном натяжении проводом, нагретым до 80—120°.
Для катушек с индуктивностью выше 15 — 20 мкГн применяется сплошная однослойная намотка. Целесообразность перехода на сплошную намотку определяется диаметром катушки. В таблице № 2, приведены ориентировочные значения индуктивности, при которых целесообразен переход на сплошную намотку:
Таблица № 2
| Диаметр каркаса (в мм.) |
6 |
10 |
15 |
20 |
25 |
|
Предельная индуктивность (в мкГн) |
1,8 |
4 |
10 |
20 |
30 |
Катушки со сплошной намоткой также отличаются высокой добротностью и широко используются в контурах на коротких, промежуточных и средних волнах, если требуется индуктивность не выше 200—500 мкГн. Целесообразность перехода на многослойную намотку определяется диаметром катушки. В таблице № 3, приведены ориентировочные значения индуктивности при заданных диаметрах, при которых целесообразен переход на многослойную намотку:
Таблица № 3
| Диаметр каркаса (в мм.) |
10 |
15 |
20 |
25 |
30 |
|
Предельная индуктивность (в мкГн) |
30 |
50 |
100 |
200 |
500 |
Индуктивность простой однослойной катушки может быть рассчитана по формуле (1):
где L — индуктивность (в мкГн), D — диаметр катушки (в см), I — длина намотки (в см), w — число витков.
При намотке однослойной катушки индуктивности с принудительным шагом, общая индуктивность (в мкГн), рассчитывается по формуле (2):
где L — индуктивность катушки, найденная по формуле (1) т. е. без поправки на шаг намотки;
А и В — поправочные коэффициенты, определяемые по графикам рис. 2а и 2б;
D — диаметр (в см);
w — число витков катушки.

Рис. 2 Графики поправочных коэффициентов для расчета индуктивности однослойных катушек с принудительным шагом намотки
d — диаметр провода;
t – шаг намотки;
Многослойные катушки могут быть разделены на простые и сложные. Примерами простых намоток являются рядовая многослойная намотка и намотка внавал.
Несекцнонированные многослойные катушки с простыми намотками отличаются пониженной добротностью и стабильностью, большой собственной емкостью, требуют применения каркасов со щечками.
Широкое применение имеют сложные универсальные намотки. В радиолюбительской практике находит применение также сотовая намотка. Индуктивность многослойной катушки может быть рассчитана по формуле:
где L — индуктивность катушки (в мкГн), D — средний диаметр намотки (в см), l — длина намотки (в см), t — толщина катушки (в см), w — число витков.
Если задана индуктивность и нужно рассчитать число витков, то следует задаться величинами D, l и t и подсчитать необходимое число витков. После этого следует произвести проверку толщины катушки по формуле:
где t — толщина катушки (в см), l — длина намотки (в мм), w — число витков. d0 — диаметр провода с изоляцией (в мм), α — коэффициент неплотности намотки. Значения коэффициента неплотности α, для многослойной намотки, могут быть взяты из таблицы 4.
Таблица 4
|
Диаметр провода без изоляции в (мм) |
Коэффициент неплотности α |
|
0,08 — 0,11 |
1,3 |
|
0,15 — 0,25 |
1,25 |
|
0,35 — 0,41 |
1,2 |
|
0,51 — 0,93 |
1,1 |
|
Более 1,0 |
1,05 |
Для намотки «внавал» α надо увеличить на 10% — 15%. Если фактическая толщина катушки отличается от принятой в начале расчета более чем на 10%, то следует задаться другими размерами катушки и повторить расчет.
Секционированные катушки индуктивности — рисунок 3, характеризуются достаточно высокой добротностью, пониженной собственной емкостью, меньшим наружным диаметром и допускают в небольших пределах регулировку индуктивности путем смещения секций.
Рис. 3 Секционированная катушка индуктивности.
Они применяются как в качестве контурных в контурах длинных и средних волн, так и в качестве дросселей высокой частоты.
Каждая секция представляет собой обычную многослойную катушку с небольшим числом витков. Число секций n может быть от двух до восьми, иногда даже больше. Расчет секционированных катушек сводится к расчету индуктивности одной секции. Индуктивность секционированной катушки, состоящей из n секций,
где Lc — индуктивность секции, k — коэффициент связи между смежными секциями.
Коэффициент связи зависит от размеров секций и расстояния между ними. Эта зависимость изображена на графике — рисунок 4.
Рис. 4 График зависимости коэффициента связи от размеров секций и расстояния между ними.
Отношение b/Dср выбирается так, чтобы величина коэффициента связи была в пределах 0,25 — 0,4. Это получается при расстояниях b = 2l. Расчет каждой секции производится обычным способом.
Корзиночная катушка, изображена на рисунке 5. Это плоскоспиральная намотка на основание в виде круга с нечетным числом радиальных прорезей. Через каждый разрез провод переходит с одной стороны круглого основания на другую.
Рис. 5 Корзиночная катушка индуктивности.
Индуктивность такой катушки в мкГн определяется по формуле:
где w — число витков, D2 — внешний диаметр намотки (в см), D1 — внутренний диаметр намотки (в см), k — поправочный коэффициент для корзиночных катушек, определяемый из таблицы 5.
Таблица 5. Поправочный коэффициент k для корзиночных катушек.
|
|
k |
|
1,2 |
3,3 |
|
1,5 |
3,0 |
|
1,8 |
2,7 |
|
2,0 |
2,6 |
|
3,0 |
2,1 |
|
5,0 |
1,6 |
|
8,0 |
1,2 |
|
10,0 |
1,0 |
Наилучшим соотношением для корзиночных катушек является D2 = 2D1
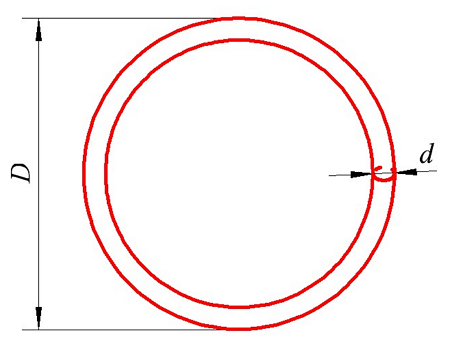
Торроидальные катушки индуктивности на немагнитном сердечнике — выполняются сплошной намоткой на кольцевом немагнитном сердечнике, со средним диаметром D, как правило, поперечное сечение кольца имеет форму окружности с диаметром d. Эскиз торроидальной катушки индуктивности на немагнитном сердечнике изображен на рисунке 6.
Рис. 6 Торроидальная катушка индуктивности на немагнитном сердечнике.
Индуктивность такой катушки в мкГн определяется по следующей формуле:
где D — средний диаметр торроидального сердечника (в см.), w — количество витков катушки, d — диаметр витка (в см.)
Собственная емкость катушек индуктивности
Собственная емкость изменяет параметры катушки, понижает добротность и стабильность настройки контуров. В диапазонных контурах эта емкость уменьшает коэффициент перекрытия диапазона.
Величина собственной емкости определяется типом намотки и размерами катушки. Наименьшая собственная емкость (несколько пф) у однослойных катушек, намотанных с принудительным шагом. Многослойные катушки обладают большей емкостью, величина которой зависит от способа намотки. Так, емкость катушек с универсальной намоткой составляет 5—25 пф, а с рядовой многослойной намоткой может быть выше 50 пф.
Катушки с большой индуктивностью
В катушках с большой индуктивностью применяются сердечники из ферромагнитных материалов. Индуктивность катушки с замкнутым стальным сердечником, измеряется в генри (гн) и рассчитывается по формуле:
Где μ – магнитная проницаемость материала, Sc – сечение сердечника в квадратных сантиметрах см2, ω – число витков катушки, lc– средняя длина магнитного пути в см. Схематическое изображение Ш – образного магнитного сердечника, приведено на рисунке 7.
Рис. 7 Ш – образный магнитный сердечник
Следует помнить, что магнитная проницаемость материала зависит от переменной составляющей индукции в сердечнике и от величины постоянного подмагничивания, а также от частоты. Ниже приводится методика расчета катушек индуктивности, работающих при малых значениях переменной составляющей индукции, например, дросселей сглаживающих фильтров для выпрямителей. Для катушек индуктивности, работающих без постоянного подмагничивания, число витков определяется по формуле:
Где L – индуктивность катушки в гн, lc — средняя длина магнитного пути в см, μн – начальная проницаемость магнитного материала, Sc – сечение сердечника в квадратных сантиметрах см2.
Для катушек индуктивности с постоянным подмагничиванием предварительно определяем ориентировочное значение действующей магнитной проницаемости, с учетом подмагничивания, по графикам для разных электротехнических сталей, приведенным на рис. 8, где I0 — ток подмагничивания, L — индуктивность.
Рис. 8 Графики для ориентировочного определения
действующей магнитной проницаемости при
постоянном подмагничивании
Ориентировочное число витков для катушек индуктивности с постоянным подмагничиванием определяем по формуле (*) :
Где μд – истинное значение магнитной проницаемости материала ферромагнитного сердечника. Истинное значение действующей магнитной проницаемости μд определяется по кривым рисунка 9.
Рис. 9 Графики для определения истинного значения
действующей магнитной проницаемости при
постоянном подмагничивании
Постоянное подмагничивание awo на 1 см длины магнитного пути для работы с графиками рисунка 4, можно определить по формуле:
где Io — ток подмагничивания в ма, lс — длина магнитного пути в см.
Далее определяется точное число витков катушки по приведенной выше формуле (*). Диаметр провода катушки в мм :
Где Io — ток подмагничивания в а.
Величина немагнитного зазора в сердечнике, изображенного на рисунке 1 высчитывается по формуле:
причем Z% определяется по кривым рисунка 10. Толщина немагнитной прокладки выбирается равной 0,5δз. Прокладки можно делать из любого листового изоляционного материала.
Рис. 10 Кривые для определения величины z%
Содержание:
Индуктивность и ее расчет:
Основным соотношением для магнитного поля является принцип непрерывности магнитного потока:
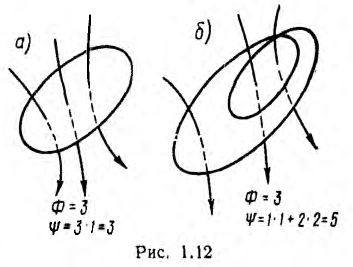
На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.
Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:
пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:
устанавливающему связь между напряженностью магнитного поля 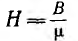
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:
где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.
Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψL созданное этим током, и в контуре наводится э. д. с. самоиндукции
Индуктивность тороида и соленоида
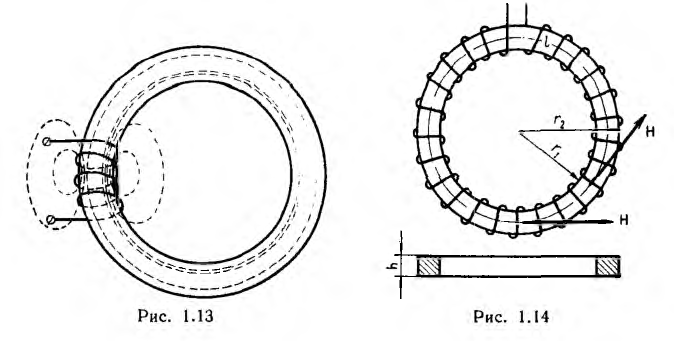
Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ0, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.
Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.
Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г1 и г2, магнитная проницаемость материала µ.
По закону полного тока для окружности с радиусом
откуда
т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции
Поток в сердечнике тороида
а потокосцепление
Отсюда индуктивность тороида
Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность
где w0 — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,
Обычно в реальных тороидах отношение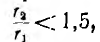
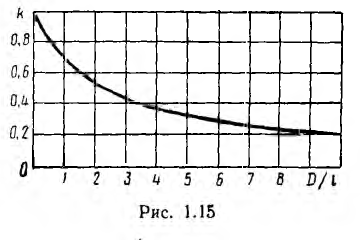
где k < 1 — коэффициент, учитывающий, что в таком соленоиде не весь поток пронизывает все витки.
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При 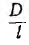
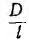
Индуктивность двухпроводной линии
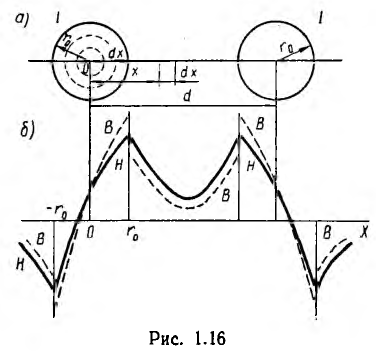
Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г0, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ0. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.
Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса 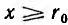
При интегрировании по окружности, лежащей внутри отдельного провода 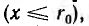
В воздухе между проводами на линии, соединяющей центры их сечений 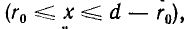
Эти же формулы справедливы и для 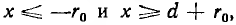
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:
Внутри правого провода 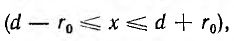
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ0. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.
На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,
Весь поток между проводами — внешний поток
одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому
а соответствующая ему внешняя индуктивность
Для большинства линий расстояние d между проводами значительно превышает радиус r0 проводов. В этом случае
Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r0 поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода
Так как поток dФi охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление
Весь поток между проводами — внешний поток
Соответственно, внутренняя индуктивность
Суммарная индуктивность линии
При медных или алюминиевых проводах (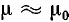
Для стальных проводов (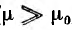
внутренний поток и индуктивность
практически не будет зависеть от расстояния между проводами.
Взаимоиндуктивность и ее расчет
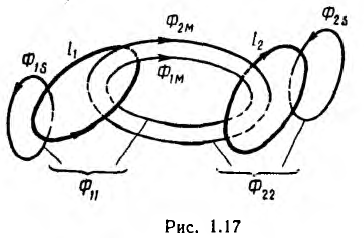
Для двух контуров, имеющих w1 и w2 витков с токами I1 и I2 (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф1l—может быть разложен на поток рассеяния Ф1s, пронизывающий только этот контур, и поток взаимоиндукции Ф1m, пронизывающий также и второй контур:
Потокосцепление, соответствующее потоку Ф11 (при условии, что этот поток пронизывает все витки первого контура, равно
а потокосцепление рассеяния
Аналогично для второго контура
Потокосцепление второго контура, определяемое током первого,
а потокосцепление первого контура, определяемое током второго,
Можно показать, что
Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,
Суммарное потокосцепление первого контура
и соответственно для второго контура
В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф1м и Ф2м (см. рис. 1.17).
Из изложенного видно, что
Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству
а используемый в технических расчетах коэффициент связи двух контуров
Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:
где Lq — индуктивность q-то контура, Мqp = Мрq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.
Взаимоиндуктивность двух параллельных двухпроводных линий
Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г0 внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I2 второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,
расстояния от провода линии 1 до проводов линии 2 .
Магнитный поток Ф одновременно является потокосцеплением 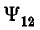
а взаимоиндуктивность
Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 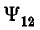
Линейные и нелинейные катушки индуктивности
У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 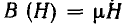
где k — масштабный коэффициент.
К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика 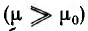
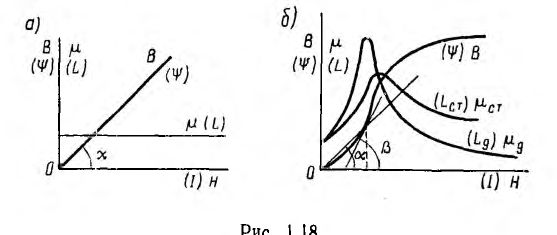
Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость
и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость
На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную
магнитной проницаемости вакуума.
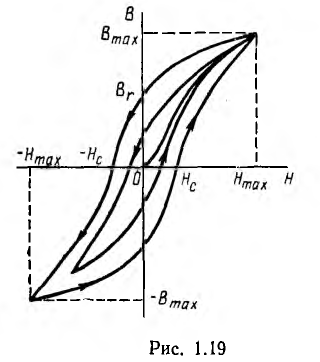
В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.
Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.
Для расчета индуктивности основной является зависимость потокосцепления ψ от тока I, называемая веберамперной характеристикой.
В зависимости от материала сердечника тороиды по виду своей веберамперной характеристики будут также линейными или нелинейными. В качестве примера рассматривается нелинейный тороид.
Для тороида 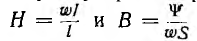
Для нелинейных тороидов вводятся понятия статической индуктивности
и дифференциальной, а также динамической индуктивности
являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.
Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность
и дифференциальная, взаимоиндуктивность, а также динамическая
Индуктивность нелинейного тороида
Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.
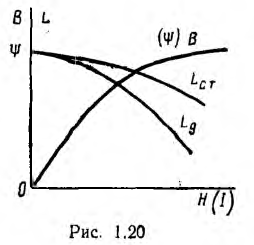
Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет
где а и b — постоянные.
Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой
то индукция будет равна
а потокосцепление
откуда статическая индуктивность
а дифференциальная индуктивность
Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
- Электрическая ёмкость и ее расчет
- Линейные н нелинейные диэлектрики и конденсаторы
- Сопротивление и его расчет
- Линейные и нелинейные резисторы
Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Методы расчёта индуктивностей
Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается ΨL) и электрическим током, который возбуждает данное потокосцепление.
В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B0 (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления ΨL
где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;
n – количество контуров с током, которые пронизывает магнитный поток.
Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению
где δ – глубина проникновения переменного тока или толщина скин-слоя;
μ – магнитная проницаемость вещества;
γ – удельная электрическая проводимость материала проводника;
ω – круговая частота переменного тока, ω = 2πf.
Поэтому непосредственный способ вычисления индуктивности практически не применяется.
На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.
Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:
индуктивные элементы без сердечников;
индуктивные элементы с замкнутыми сердечниками;
индуктивные элементы с сердечниками, имеющие воздушный зазор.
Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.
Индуктивность прямолинейного провода круглого сечения
При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.
Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.
В случае постоянного тока или тока низкой частоты индуктивность составит
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
l – длина провода, м;
d – диаметр провода, м.
Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где
d = 2r – диаметр поперечного сечения провода, м.
где ω – угловая частота переменного тока, ω = 2πf;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
γ – удельная проводимость вещества проводника.
Тогда если k*r < 3, то
если k*r > 3, то
где
Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.
На постоянном токе
На частоте 50 кГц
Online калькулятор индуктивности прямолинейного проводника
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
На частоте 50 кГц
Online калькулятор индуктивности кольца кругового сечения
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:
Ф (1)
- где
Рис. 1. Соленоид
В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:
(1)
- где
Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда
. Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда
и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.
Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:
- при параллельном подключении:
(2)
- где
В случае двух элементов, соединённых параллельно:
(3)
- при последовательном подключении:
(4)
- где