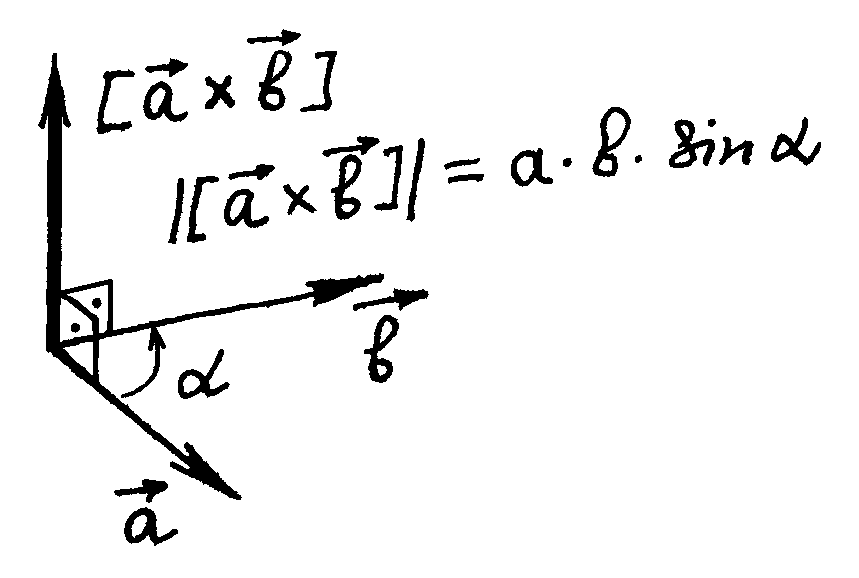Индуктивность контура — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
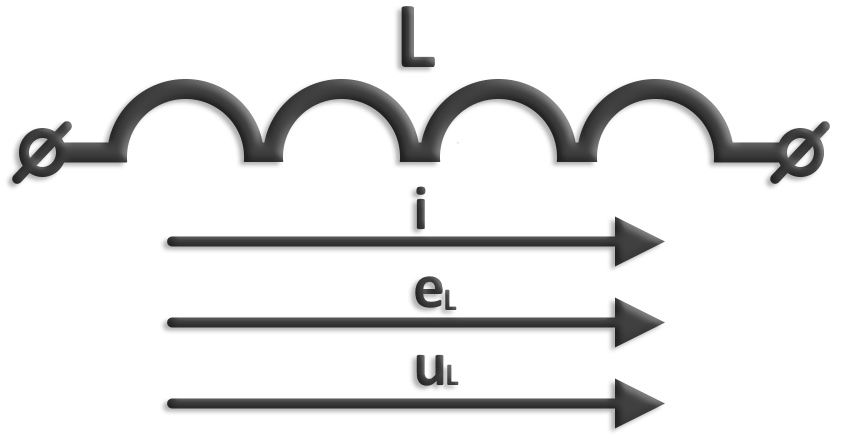
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Электрическая цепь и индуктивность контура
Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.
Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
-
- Индукционный ток возникает только при изменении линий магнитной индукции.
-
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Самоиндукция и измерение индуктивности
Индуктивность проводника
При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.
Напряжение ЭДС определяется формулой расчета индукции:
Ꜫ=-L∙di/dt.
То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».
Как найти индуктивность контура
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
- L= µ0n2V,
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
- L = µ0N2S : l,
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
- Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
“Катушка ниток”
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от “витков в квадрате”.
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
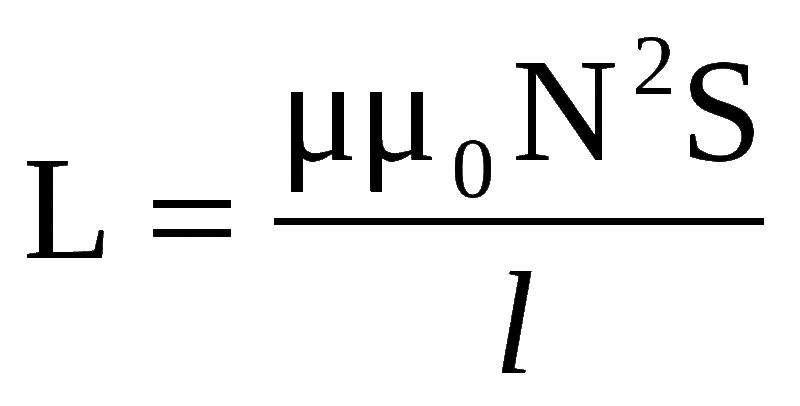
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
-
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр); - N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.

Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
-
l — длина проводника в метрах; - r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
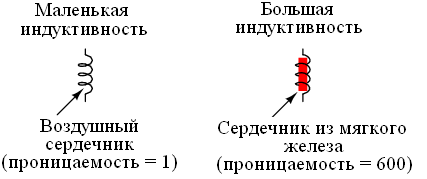
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Индукти́вность— коэффициент
пропорциональности междумагнитным
потоком(создаваемымтокомкакого-либо
витка при отсутствиинамагничивающих
сред, например, в воздухе)
ивеличинойэтого
тока[1][2][3].
Если в проводящем контуре течёт ток, то
ток создаёт магнитное
поле[3].
Величинамагнитного
потока, пронизывающего
одновитковый контур, связана с величиной
тока следующим образом[3]:
где L— индуктивность витка.
В случаекатушки,
состоящей из N витков предыдущее выражение
модифицируется к виду:
где 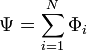
сумма магнитных потоков через все витки,
аL— уже индуктивность
многовитковой катушки. Ψ называютпотокосцеплениемили
полным магнитным потоком[4].
Коэффициент пропорциональностиLиначе
называетсякоэффициентом
самоиндукцииконтура или просто
индуктивностью[3].
Если поток, пронизывающий каждый из
витков одинаков, то Ψ = NΦ.
Соответственно,LN=L1N2(суммарный
магнитный поток увеличивается в N раз
и потокосцепление еще в N раз). Но в
реальных катушках магнитные поля в
центре и на краях отличаются, поэтому
используются более сложные формулы.
В системе единиц СИиндуктивность
измеряется вгенри[5],
сокращенно Гн, в системеСГС—
в сантиметрах (1 Гн = 109см)[3].
Контур обладает индуктивностью в один
генри, если при изменении тока на
одинамперв
секунду на выводах контура будет
возникать напряжение в одинвольт.
Реальный, не сверхпроводящий, контур
обладает омическим сопротивлением R,
поэтому на нём будет дополнительно
возникать напряжение U=I*R, где I —сила
тока, протекающего по контуру
в данное мгновение времени.
Символ L, используемый для
обозначения индуктивности, был взят в
честьЛенца
Эмилия Христиановича(Heinrich
Friedrich Emil Lenz)[источник не указан 447 дней].
Единица измерения индуктивности названа
в честьДжозефа
Генри(Joseph Henry)[6].
Сам термин индуктивность был
предложенОливером
Хевисайдом(Oliver Heaviside) в
феврале1886
года[источник не указан 447 дней].
Через индуктивность выражается ЭДС
самоиндукциив контуре,
возникающая при изменении в нём тока[3]:
.
При заданной силе тока индуктивность
определяет энергиюмагнитного
поля тока[3]:
.
Практически участки цепи со значительной
индуктивностью выполняют в виде катушек
индуктивности[3].
38. Энергия магнитного поля проводника с током
Магни́тное по́ле —
составляющая электромагнитного
поля,
появляющаяся при наличии изменяющегося
во времени электрического
поля.
Кроме того, магнитное поле может
создаваться током
заряженных частиц,
либо магнитными
моментами электронов в атомах (постоянные
магниты).
С точки зрения квантовой теории
поля электромагнитное
взаимодействие переносится
безмассовым бозон-фотоном (частицей,
которую можно представить как квантовое
возбуждение электромагнитного поля).
Основной характеристикой магнитного
поля является его сила, определяемая
вектором магнитной
индукции (вектор
индукции магнитного поля)[1].
В СИ магнитная индукция измеряется
в теслах (Тл),
в системе СГС в гауссах.
Магнитное
поле — это особый вид материи,
посредством которой осуществляется
взаимодействие между движущимися
заряженными частицами или телами,
обладающими магнитным
моментом.
Можно
также рассматривать магнитное поле,
как релятивистскую составляющую электрического
поля.
Точнее, магнитные поля являются
необходимым следствием существования
электрических полей испециальной
теории относительности.
Вместе, магнитное и электрическое поля
образуют электромагнитное
поле,
проявлениями которого являются свет и
прочие электромагнитные
волны.
Энергия магнитного поля
Приращение плотности энергии магнитного
поля равно:
где:
—напряжённость
магнитного поля,
—магнитная
индукция
В линейном тензорном приближении
(Bi= μ0μijHj)
плотность энергии равна:
где:
μij—тензормагнитной
проницаемости,
μii— диагональные компоненты
этого тензора,
μ0—магнитная
постоянная
В изотропном линейном магнетике:
где:
μ — относительная магнитная
проницаемость
В вакууме μ = 1 и:
Энергию магнитного поля в катушке
индуктивности можно найти по формуле:
где:
Φ — магнитный
поток,
I— ток,
L—индуктивностькатушки
или витка с током.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током |
| Напечатано:: | Гость |
| Дата: | Четверг, 25 Май 2023, 03:01 |
Оглавление
- Самоиндукция
- Наблюдение самоиндукции
- Энергия магнитного поля
- Примеры решения задач
- Упражнение 24
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. L = const, то
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
От теории к практике
Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции = 4,0 В?
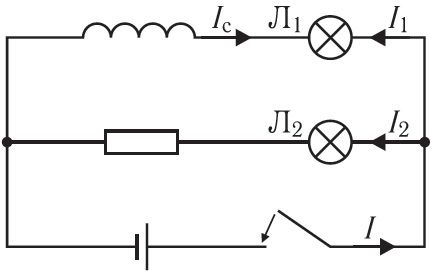
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л2 начинает светиться практически сразу, а лампочка Л1 — с заметным запаздыванием. При возрастании силы тока I1, созданного источником на участке, образованном катушкой и лампочкой Л1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции Iс направлен навстречу току источника. В результате рост силы тока I1 источника замедляется, и сила тока I1 — |Iс| не сразу достигает своего максимального значения.
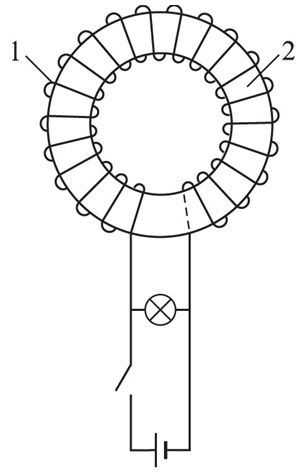
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений . Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.
Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
При замыкании цепи, состоящей из источника тока с ЭДС , катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции
.
Тогда в соответствии с законом Ома сила тока в цепи .
Значит, .
Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: .
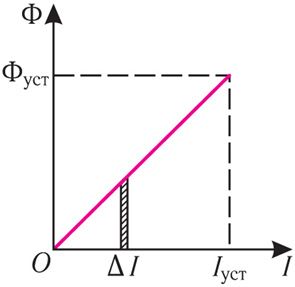
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):
δAдоп = ФΔI.
Полная дополнительная работа Адоп, равная сумме элементарных дополнительных работ δAдоп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).
Эта работа превращается в энергию магнитного поля катушки, поэтому:
где L — индуктивность контура; I — сила тока.
От теории к практике
Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки Wм = 1,2 Дж?
1. Что называют самоиндукцией?
2. В каких опытах можно наблюдать явление самоиндукции?
3. От чего зависит ЭДС самоиндукции?
4. Что называют индуктивностью? В каких единицах в СИ её измеряют?
5. Как вычислить энергию магнитного поля катушки с током?
6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?
Примеры решения задач
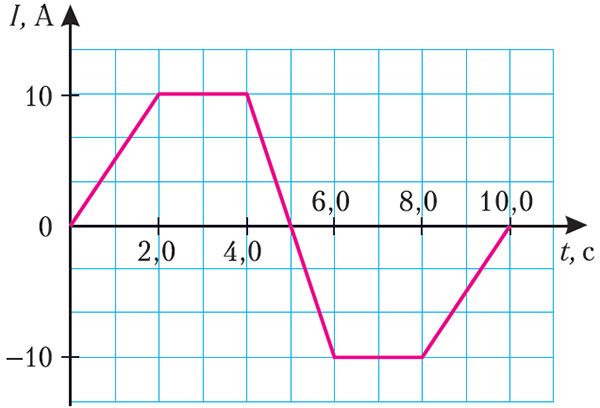
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
Дано:
L = 40 мГн = 4,0 · 10–2 Гн
— ?
Решение: ЭДС самоиндукции . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
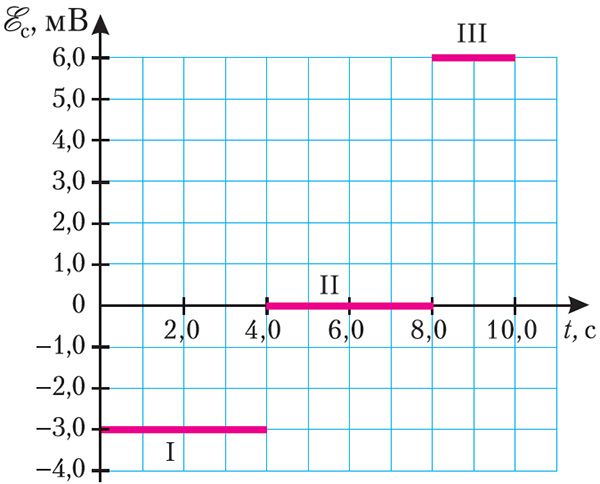
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
Дано:
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔII — ? ΔIII — ?
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции = –3,0 мВ, на участке III —
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
;
.
;
.
На участке II графика = 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки .
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Дано:
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
= ‒14,0 В
Фс — ?
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: . Следовательно,
. Тогда
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Упражнение 24
1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.
2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.
3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I1 = 2,0 А до I2 = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.
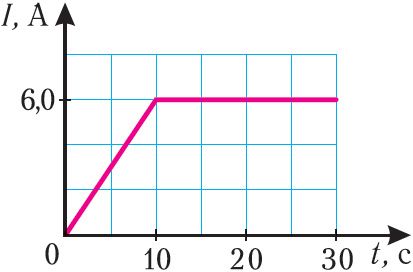
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t1 = 10 с и t2 = 20 с от момента начала отсчёта времени.
5. Сила тока в катушке равномерно уменьшилась от I1 = 10 А до I2 = 5,0 А. При этом энергия магнитного поля изменилась на ΔWм = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.
6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I1 = 8,0 А, если за промежуток времени t1 = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.
7. Энергия магнитного поля катушки с индуктивностью L1 = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L2 в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, .
- Подробности
- Обновлено 03.07.2018 17:41
- Просмотров: 1452
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на расчет индуктивности, самоиндукции, энергии магнитного поля тока.
Задача 1
Какова индуктивность витка проволоки, если при токе 6 А создается магнитный поток 12 мВб?
Задача 2
В катушке из 150 витков течет ток 7,5 А, и при этом создается магнитный поток 20 мВб.
Какова индуктивность катушки?
Задача 3
Через соленоид, индуктивность которого 0,4 мГн и площадь поперечного сечения 10 см2, проходит ток 0,5 А.
Какова индукция поля внутри соленоида, если он содержит 100 витков?
Задача 4
Определить индуктивность контура с током 1,2 А, если контур ограничивает площадь 20 см2, а магнитная индукция поля равна 0,8 Тл, причем вектор магнитной индукции направлен под углом 30o к плоскости контура.
Задача 5
Какая ЭДС самоиндукции возбуждается в обмотке электромагнита с индуктивностью 0,4 Гн при изменении силы тока на 5 А за 0,02 секунды?
Задача 6
Определить энергию магнитного поля катушки, если ее индуктивность 0,2 Гн, а ток в ней 12 А.
Задача 7
Какой должна быть сила тока в катушке с индуктивностью 0,5 Гн, чтобы энергия магнитного поля оказалась равной 1 Дж?
Задача 8
Найти энергию магнитного поля соленоида, индуктивность которого 0,02 Гн, а магнитный поток через него составляет 0,4 Вб.
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
→
2.3 Магнитное поле, индуктивность
2.3 Магнитное поле, индуктивность
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
Магнитное поле, индуктивность
Основные положения и соотношения
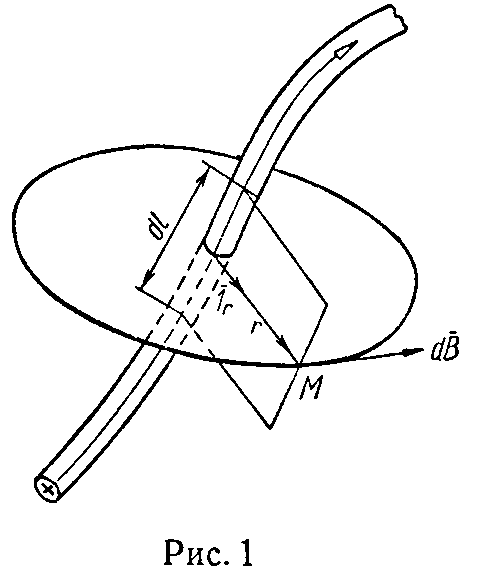
1. Закон Био — Савара — Лапласа выражает значение магнитной индукции, определяемой элементом тока I dl → на расстоянии r от него в однородной среде (рис. 1)
dB → =μ⋅ I⋅[ dl → × 1 r → ] 4π r 2 , (1)
здесь
1 r → – единичный вектор, направленный от центра элемента тока I dl → в точку М, в которой определяется магнитная индукция;
r — расстояние от центра элемента тока до той же точки;
µ — абсолютная магнитная проницаемость среды, равная µ0·µr;
µr — магнитная проницаемость (относительная магнитная проницаемость);
μ 0 =4π⋅ 10 −7 Гн м – магнитная постоянная.
В формуле (1) использовали векторное произведение [ a → × b → ]≡ a → × b →
Закон Био — Савара — Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био — Савара — Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
Связь между векторами напряженности магнитного поля и магнитной индукцией выражается формулой
B → =μ⋅ H → . (2)
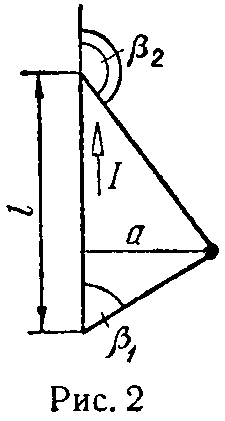
Величина напряженности магнитного поля тока, протекающего по прямому проводнику конечной длины l (рис. 2) в некоторой точке, находящейся на расстоянии a от проводника, равна
H= I 4π⋅a ⋅( cos β 1 −cos β 2 ). (3)
Направление вектора H → определяется правилом винта; так, в рассматриваемой на рис. 2 точке вектор H → направлен от читателя за чертеж.
Величина напряженности магнитного поля прямого и бесконечно длинного тока в точке, отстоящей на расстоянии a от оси провода, несущего ток, равна
H= I 2π⋅a . (4)
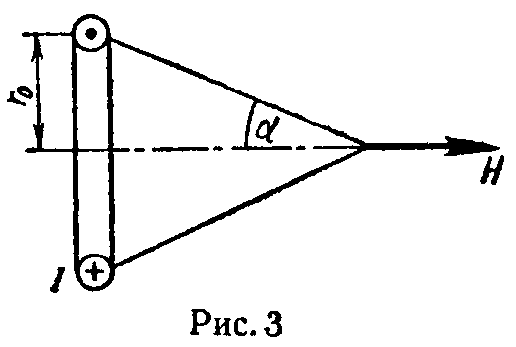
Величина напряженности магнитного поля кругового тока в некоторой точке на его оси (рис. 3) определяется по формуле
H= I 2 r 0 ⋅si n 3 α, (5)
здесь r0 — радиус витка, по которому протекает круговой ток, α — угол, под которым виден радиус витка из точки, в которой определяется напряженность поля.
Напряженность магнитного поля в центре плоскости витка определяется по формуле
H= I 2 r 0 . (6)
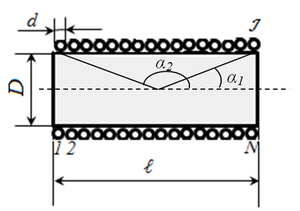
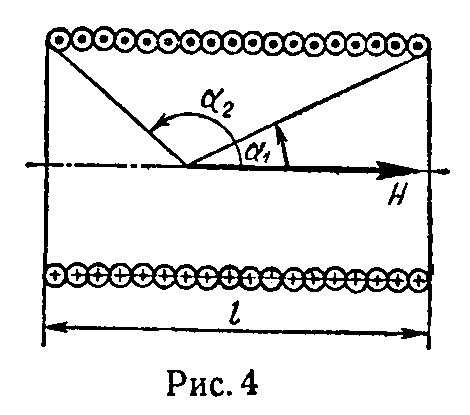
Напряженность магнитного поля соленоида. Величина напряженности магнитного поля в некоторой точке на оси цилиндрического соленоида (рис. 4)
H= w⋅I 2l ⋅( cos α 1 −cos α 2 ), (7)
здесь w — общее число витков соленоида.
Величина напряженности магнитного поля на оси очень длинного цилиндрического соленоида
H= w⋅I l . (8)
Направление вектора H → и здесь определяется правилом винта.
По этой же формуле находится напряженность магнитного поля на оси кольцевого соленоида (тороида). В этом случае l — длина средней линии магнитной индукции, считается совпадающей с кольцевой осью соленоида.
2. Закон полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
? H → dl → = ∑ I . (9)
Формулы (4) и (8) являются непосредственными результатами применения закона полного тока.
3. Поток вектора магнитной индукции сквозь поверхность S
Φ= ∫ S B → dS → . (10)
4. Сила Лоренца. Сила, испытываемая зарядом q, движущимся со скоростью v в магнитном поле с индукцией В, определяется по формуле
F → =q⋅[ v → × B → ]. (11)
Макроскопическим проявлением силы Лоренца является сила Ампера.
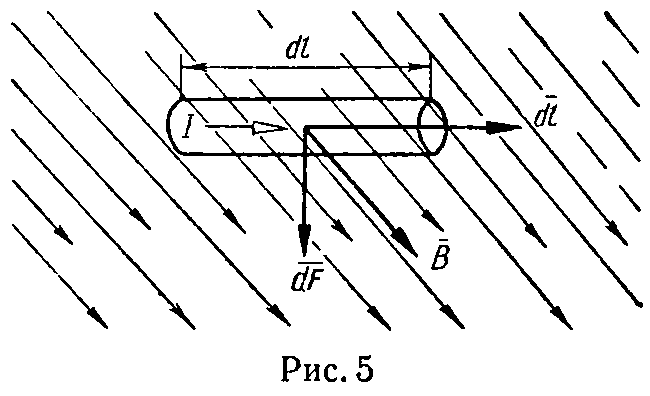
Закон Ампера. Сила (рис. 5), действующая на элемент провода dl → с током I , помещенный в магнитное поле с индукцией B → (сила Ампера),
dF → =I⋅[ dl → × B → ]. (12)
Прямолинейный проводник длиной l, помещенный в однородное магнитное поле с индукцией B → под углом α к вектору B → , испытывает силу
F → =I⋅[ l → × B → ]=I⋅l⋅B⋅sinα⋅ 1 n → , (13)
где 1 n → – единичный вектор, нормальный к плоскости, проведенной через векторы l → и B → .
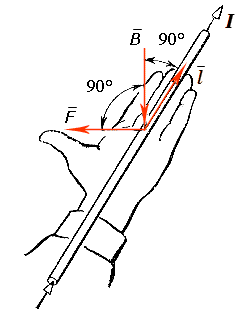
Направление силы Ампера F определяется правилом левой руки.
5. Работа сил поля при перемещении в нем на расстояние ds элемента проводника длиною dl с током I равна (рис. 6)
dW=I⋅dΦ, (14)
здесь dФ — магнитный поток через поверхность, описанную проводником при его перемещении.
Работа, производимая при перемещении замкнутого контура с неизменным по величине током в постоянном магнитном поле, определяется выражением
W=I⋅( Φ 2 − Φ 1 ), (15)
где Ф1 и Ф2 — величины магнитного потока, пронизывающего контур в начальном и конечном положениях.
6. Расчет магнитных цепей. Основанием к расчету служат: первый закон Кирхгофа для магнитных цепей и закон полного тока.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к контуру, образованному средними магнитными линиями магнитной цепи и имеет вид
F=ΣwI= ? H → dl → . (16)
Величина F называется магнитодвижущей силой (МДС).
Выражение
F=ΣwI= ∑ k=1 n Φ k R мk (17)
называют вторым законом Кирхгофа для магнитных цепей и формулируют следующим образом: алгебраическая сумма магнитодвижущих сил (ΣwI) в замкнутом контуре магнитной цепи равна алгебраической сумме магнитных напряжений ( ∑ k=1 n Φ k R мk ) в том же контуре.
В формуле (17) R мk = l k μ k S k – магнитное сопротивление участка цепи с сечением Sk, с длиною средней магнитной линии lk и с абсолютной магнитной проницаемостью материала µk.
Отметим, что для расчета стальной магнитной цепи формулой (17) пользуются редко, так как Rмk не может рассматриваться как постоянная величина (величина магнитной проницаемости стали и других ферромагнитных материалов зависит от их намагниченности).
При расчете магнитодвижущей силы для воздушного зазора напряженность магнитного поля определяется по формуле
H 0 = B μ 0 . (18)
7. Закон электромагнитной индукции. Величина индуктированной ЭДС
e=− dΨ dt , (19)
где Ψ — потокосцепление. Оно может быть выражено произведением величины магнитного потока на число витков, с которыми он сцеплен
Ψ= ∑ w⋅Φ . (20)
8. Общее выражение для статической индуктивности проводника, витка, катушки
L= Ψ I . (21)
9. ЭДС, индуктированная в прямолинейном проводнике, движущемся с равномерной скоростью v в однородном магнитном поле, равна
e = B·l·v·sinα, (22)
где α — угол между направлениями векторов v → и B → .
10. Величина ЭДС самоиндукции
e L =−L di dt . (23)
11. Индуктивность соленоида
L= μ⋅ w 2 ⋅S l , (24)
здесь w — число витков, S — сечение соленоида, l — длина средней линии магнитной индукции.
Эта же формула приближенно подходит для расчета индуктивности длинной однослойной катушки цилиндрической формы (l/D > 50), где l/D –отношение длины катушки к диаметру ее витков.
12. Для вычисления индуктивности коротких цилиндрических катушек без стального сердечника применяется формула
L=k⋅ μ 0 ⋅ w 2 ⋅S l , (25).
где коэффициент k является функцией отношения диаметра D катушки к ее длине l его значения приведены в таблице 1.
Таблица 1 — Значения коэффициент k(D/l)
|
D/l |
k |
D/l |
k |
|
0,00 |
1,0000 |
1,00 |
0,6884 |
|
0,10 |
0,9588 |
0,80 |
0.6581 |
|
0,20 |
0,9201 |
0,60 |
0.5697 |
|
0,40 |
0,8499 |
0,40 |
0,4719 |
|
0,60 |
0,7885 |
0,20 |
0,3108 |
|
0,80 |
0,7351 |
0,10 |
0,2033 |
|
1,00 |
0,6884 |
13. Индуктивность двухпроводной линии
L= μ 0 l π ln D r + μ⋅l 4π , (26)
здесь D — расстояние между осями проводов, r — радиус провода, l — длина линии, µ — абсолютная магнитная проницаемость проводов линии.
Для проводников, изготовленных не из ферромагнитных материалов, пользуются следующей приближенной формулой, в которой отсутствует слагаемое, выражающее внутреннюю индуктивность
L= μ 0 l π ln D r . (27)
Индуктивность однопроводной линии
L= μ 0 l 2π ln 2h r , (28)
где h — высота провода над землей.
14. Общее выражение для взаимной индуктивности двух контуров
M= w 1 Φ 21 I 2 = w 2 Φ 12 I 1 , (29)
здесь w1 и I1 — число витков и ток, проходящий в первом контуре, Ф21 — часть общего магнитного потока, определяемого током второго контура и пронизывающего первый контур, w2 и I2 — число витков и ток, проходящий во втором контуре, Ф12 — часть общего магнитного потока, определяемого током первого контура и пронизывающего второй контур.
15. Электродвижущая сила взаимоиндукции двух контуров с токами
e 1M =− w 1 d Φ 21 dt =−M d i 2 dt , e 2M =− w 2 d Φ 12 dt =−M d i 1 dt , (30)
здесь e1M — ЭДС, наведенная в первом контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф21, определяемого током во втором контуре, со скоростью d Φ 21 dt , e2M — ЭДС, наведенная во втором контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф12, определяемой током в первом контуре, со скоростью d Φ 12 dt .
16. Взаимная индуктивность двух кольцевых соленоидов, имеющих общий сердечник, число витков которых w1 и w2, определяется по приближенной формуле
M= μ w 1 w 2 S l , (31)
здесь S — сечение сердечника, l — длина средней линии магнитной индукции.
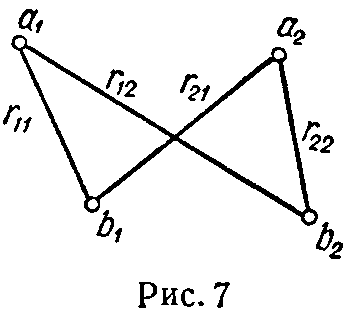
Взаимная индуктивность между двумя параллельными двухпроводными линиями a1a2 и b1b2 длиною l (рис. 7)
M= μ 0 l 2π ln r 12 r 21 r 11 r 22 . (32)
Расстояния считаются между осями проводов. Радиусы проводов предположены малыми по сравнению с расстояниями между ними.
17. Заряд, прошедший через проводящий контур. Количество индуктированного электричества, прошедшего через проводящий контур, имеющий w витков, при изменении сцепленного с ним магнитного потока от величины Ф1 до величины Ф2
Q= w r ( Φ 2 − Φ 1 ), (33)
здесь r — сопротивление контура, w — число витков.
18. Коэффициент магнитной связи двух контуров
k= M L 1 L 2 . (34)
Пределы изменения коэффициента магнитной связи
0 ≤ k ≤ 1.
Коэффициент рассеяния
σ = 1 — k2. (35)
19. Энергия магнитного поля
W= L⋅ I 2 2 = I⋅Ψ 2 , (36)
где Ψ — потокосцепление.
Удельная энергия магнитного поля (на единицу объема)
w= dW dV = B⋅H 2 = μ H 2 2 . (37)
Энергия магнитного поля может быть выражена через удельную энергию посредством интеграла
W= ∫ V B⋅H 2 dV . (38)
здесь V — объем пространства, занятый магнитным полем.
20. Полная магнитная энергия системы двух индуктивно связанных контуров с токами I1 и I2
W= L 1 I 1 2 2 + L 2 I 2 2 2 ±M⋅ I 1 I 2 . (39)
Упражнения и задачи
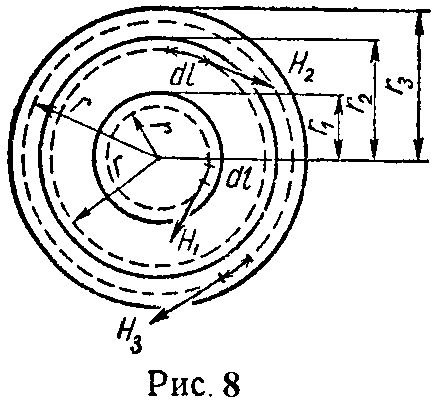
Задача 1. Вычислить и построить кривую, зависимости напряженности магнитного поля неограниченно длинного коаксиального кабеля (рис. 
Радиус внутреннего проводника r1 = 2 мм, радиусы трубы r2 = 7,2 мм и r3 = 7,5 мм.
Плотность тока по сечению каждого проводника распределена равномерно.
Решение
Для определения напряженности магнитного поля (ввиду симметрии) воспользуемся законом полного тока.
Область внутреннего проводника (0 ≤ r ≤ r1)
Проведем окружность радиуса r < r1 с центром на оси провода. В любой ее точке напряженность H1 вследствие симметрии имеет одно и то же значение и совпадает по направлению с элементом длины окружности . Беря линейный интеграл напряженности магнитного поля вдоль этой окружности, по закону полного тока получим
? H 1 → dl → = ? H 1 dlcos( H 1 → , dl → ) = H 1 ⋅ ? dl = H 1 ⋅2πr=I( r ),
где под I(r) надо понимать ток, проходящий в части сечения проводника, находящейся внутри контура циркуляции.
Плотность тока во внутреннем проводнике
δ 1 = I π r 1 2 .
Ток, проходящий через часть сечения проводника, имеющую радиус r < r1,
I( r )= δ 1 π r 2 = I⋅ r 2 r 1 2 .
Итак,
H 1 ⋅2πr= I⋅ r 2 r 1 2 ,
отсюда
H 1 = I⋅r 2π r 1 2 .
После подстановки числовых значений получим
H 1 = I⋅r 2π r 1 2 = 1⋅r 2π⋅ 0,002 2 =39800⋅r ( А м ).
Область полости трубы (r1 ≤ r ≤ r2)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
? H 2 → dl → = ? H 2 dl = H 2 ⋅ ? dl = H 2 ⋅2πr=I,
отсюда
H 2 = I 2πr = 0,159 r ( А м ).
Область трубы (r2 ≤ r ≤ r3)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
? H 3 → dl → = ? H 3 dl = H 3 ⋅ ? dl = H 3 ⋅2πr= ∑ I .
Здесь под ΣI надо понимать сумму токов, находящихся внутри окружности радиуса r, т. е. весь ток I, проходящий по внутреннему проводу, и ток, проходящий по части сечения кольца трубы, обходимой контуром циркуляции, причем этот последний ток должен быть взят со знаком минус (так как по трубе протекает обратный ток).
Плотность тока в трубе
δ 2 = I π( r 3 2 − r 2 2 ) ; ∑ I =I− δ 2 ( π r 2 −π r 2 2 )=I⋅ r 3 2 − r 2 r 3 2 − r 2 2 .
Итак,
H 3 ⋅2πr=I⋅ r 3 2 − r 2 r 3 2 − r 2 2 ,
отсюда
H 3 =I⋅ r 3 2 − r 2 2π( r 3 2 − r 2 2 )⋅r = 2,03 r −36100⋅r ( А м ),
Область пространства вне кабеля (r3 ≤ r)
Для всех точек пространства вне кабеля напряженность магнитного поля H4 = 0. Это вытекает из закона полного тока при любом контуре интегрирования, охватывающем весь кабель.
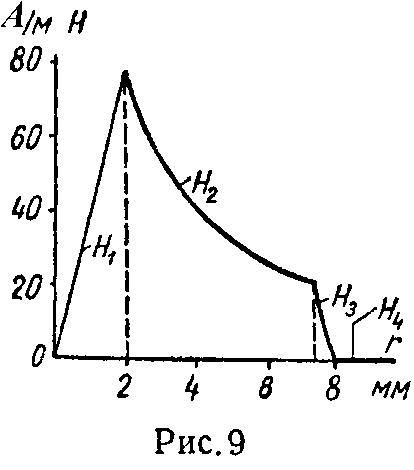
На рис. 9 представлена кривая изменения напряженности магнитного поля в функции r.
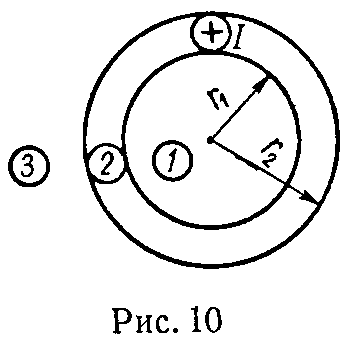
Задача 2. Вдоль длинного трубчатого провода, радиусы сечения которого r1 и r2, протекает постоянный ток I (рис. 10).
Вычислить и построить кривую зависимости напряженности магнитного поля в функции r — расстояния от точки до оси провода для областей 1 (внутри трубы), 2 (в стенках трубы), 3 (вне трубы). Даны: r1 = 2 см; r2 = 3 см, I = 10 А.
Ответ: внутри трубы (0 ≤ r ≤ r1) H1 = 0; в стенках трубы (r1 ≤ r ≤ r2) H 2 = r 2 −4 πr А см ; вне трубы (r2 ≤ r) H 3 = 5 πr А см .
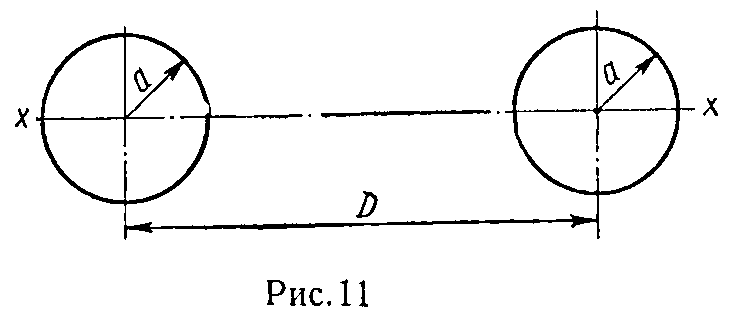
Задача 3. Построить кривую напряженности магнитного поля вдоль оси x для двухпроводной линии (рис. 11), оси проводов которой отстоят друг от друга на расстоянии D = 30 см.
Радиус проводов a = 4 мм. Ток в прямом и обратном проводе I = 200 А. Весь ток, протекающий в проводе, следует считать сосредоточенным в его оси.
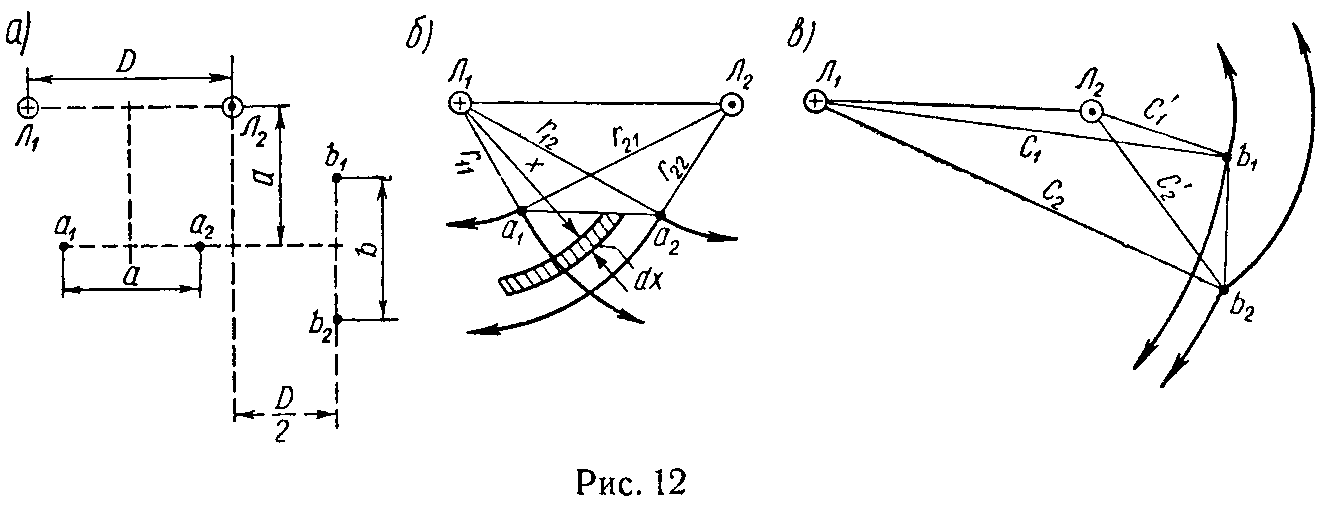
Задача 4. Два провода линии электропередачи Л1 и Л2 и две пары телефонных проводов (a1a2 и b1b2 расположены параллельно друг другу (рис. 12, а).
Если по проводам линии передачи проходит ток I = 150 А, то чему будет равно потокосцепление на 1 км с телефонной линией a1a2 и с телефонной линией b1b2. Даны: D = 90 см; a = b = 30 см.
Решение
Найдем потокосцепление линии Л1Л2 с линией a1a2 (рис. 12, б). Поток, определяемый током, проходящим через провод Л1, и пронизывающий линию a1a2, с учетом формул (2), (4) и того, что dS = ldx, где l — длина линии, будет равен
Φ Л 1 = ∫ r 11 r 12 BdS = ∫ r 11 r 12 μ I 2πx ldx = μ⋅I⋅l 2π ln r 12 r 11 .
Поток, определяемый током, проходящим через провод Л2, будет равен
Φ Л 2 = μ⋅I⋅l 2π ln r 21 r 22 = Φ Л 1 .
Так как
r 11 = r 22 = 30 2 + 30 2 =42,4 см и r 12 = r 21 = 30 2 + 60 2 =67 см,
то общий поток
Φ= Φ Л 1 + Φ Л 2 =2 μ 0 ⋅I⋅l 2π ln r 12 r 11 =2 4π⋅ 10 −7 ⋅150⋅ 10 3 2π ln 67 42,4 =27,5⋅ 10 −3 Вб.
Аналогично найдем, что потокосцепление линии Л1Л2 с линией b1b2 (рис. 12, в) будет равно
Φ= μ 0 ⋅I⋅l 2π ln c 1 ⋅ c ′ 2 c 2 ⋅ c ′ 1 =7,4⋅ 10 −3 Вб.
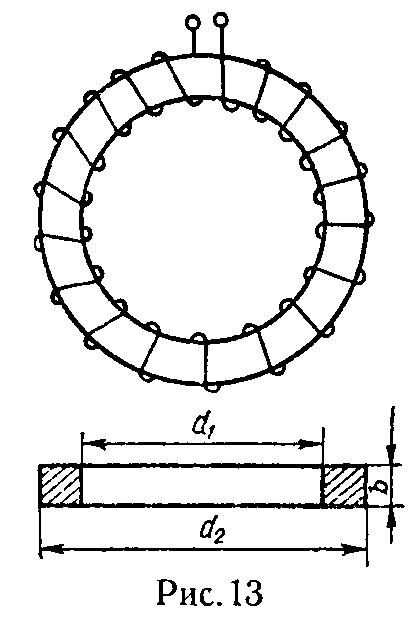
Задача 5. На кольцевой эбонитовый сердечник намотано w = 800 витков, по которым проходит ток I = 10 А (рис. 13).
Учитывая неравномерность индукции по сечению сердечника, вычислить значение магнитного потока, проходящего через сердечник.
Внутренний диаметр сердечника d1 = 20 см, внешний диаметр d2 = 25 см, толщина сердечника b = 4 см.
Сравнить полученные результаты с теми, которые будут, если предположить, что индукция по всему сечению сердечника неизменна и равна индукции, соответствующей осевой линии.
Указание. Найти напряженность магнитного поля в любой точке сечения сердечника, пользуясь законом полного тока.
Ответ: Φ= μIwb 2π ln d 2 d 1 ; Φ приб = μIw l ср S, где S= d 2 − d 1 2 b.
Задача 6. Прямолинейный проводник, длина которого равна 40 см, перемещается со скоростью 25 м/сек под углом α = 30° к линиям однородного магнитного поля, имеющего магнитную индукцию, равную 1 Вб/м2. Определить величину ЭДС, индуктированной в проводнике.
Ответ: 5 В.
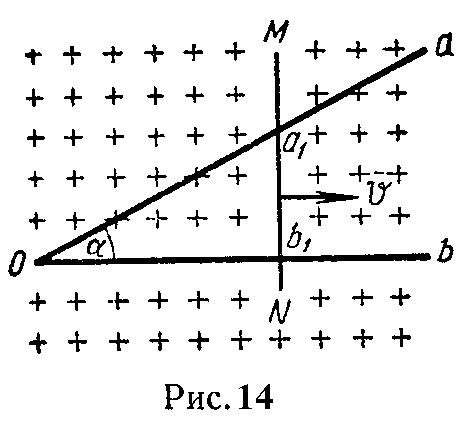
Задача 7. В однородном магнитном поле, индукция которого B, находится проволока aOb, изогнутая под углом α, по которой скользит проводник MN с равномерной скоростью v (рис. 14).
Вектор магнитной индукции перпендикулярен плоскости угла aOb. Все проводники обладают сопротивлением r0 на единицу длины. Найти выражения для наводимой ЭДС и тока, протекающего в контуре a1Ob1.
Решение
Обозначим отрезок a1b1 через h, а переменный отрезок Ob1 — через x.
Площадь треугольника a1Ob1 равна
S= x⋅h 2 = x 2 tgα 2 .
Магнитный поток, пронизывающий контур треугольника,
Φ=B⋅S= B 2 tgα⋅ x 2 .
Имея в виду, что dx/dt = v, по формуле (19) найдем выражение для наводимой ЭДС
e=− dΦ dt =− dΦ dx dx dt =− 2x⋅tgα⋅B 2 ⋅v=B⋅v⋅x⋅tgα;
ЭДС растет пропорционально x, ибо этой величине пропорциональна активная часть a1b1 перемещающегося проводника MN.
Сопротивление контура проводника a1Ob1a1
r= r 0 ⋅( x+h+ x cosα )= r 0 ⋅x⋅( 1+tgα+ 1 cosα ).
Заметим, что величина сопротивления также возрастает пропорционально расстоянию x.
Искомый ток
i= e r =− B⋅v⋅sinα r 0 ⋅( 1+sinα+cosα ) =const,
т.е. по контуру протекает постоянный ток.
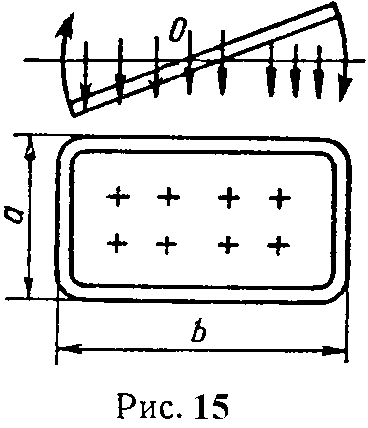
Задача 8. В однородном магнитном поле, индукция которого В = 0,5 Вб/м2, вокруг оси О вращается с равномерной скоростью прямоугольная рамка (рис. 15). Построить кривые изменения магнитного потока, пронизывающего рамку и наводимой в рамке ЭДС в функции времени. Рамка делает 1500 об/мин, ее размеры: a = 10 см, b = 20 см.
Как изменятся частота и величина максимальной ЭДС, наведенной в рамке, если: а) индукцию увеличить в 2 раза, б) сторону a увеличить в 2 раза, в) скорость вращения увеличить в 2 раза.
Ответ: Ф = 0,01cos50πt Вб, e = 1,57sin50πt В; а) и б) частота не изменится, Em увеличится в 2 раза; в) частота и Em увеличатся в 2 раза.
Задача 9. Круглый виток, радиус которого равен 5 см, находится в однородном магнитном поле, перпендикулярном плоскости витка, и изменяется с течением времени по уравнению В = Вmsinωt. Построить кривые изменения во времени магнитного потока, пронизывающего виток и наводимой в нем ЭДС, если Вm = 8000 Гс и ω = 628 1/с.
Единица индукции магнитного поля в системе единиц СИ Тесла (Тл), а в системе единиц СГСМ Гаусс (Гс). Соотношение между единицами: 1 Тл = 10000 Гс.
Ответ: Ф = 6,28·10–3sinωt Вб, e = –3,95cosωt В.
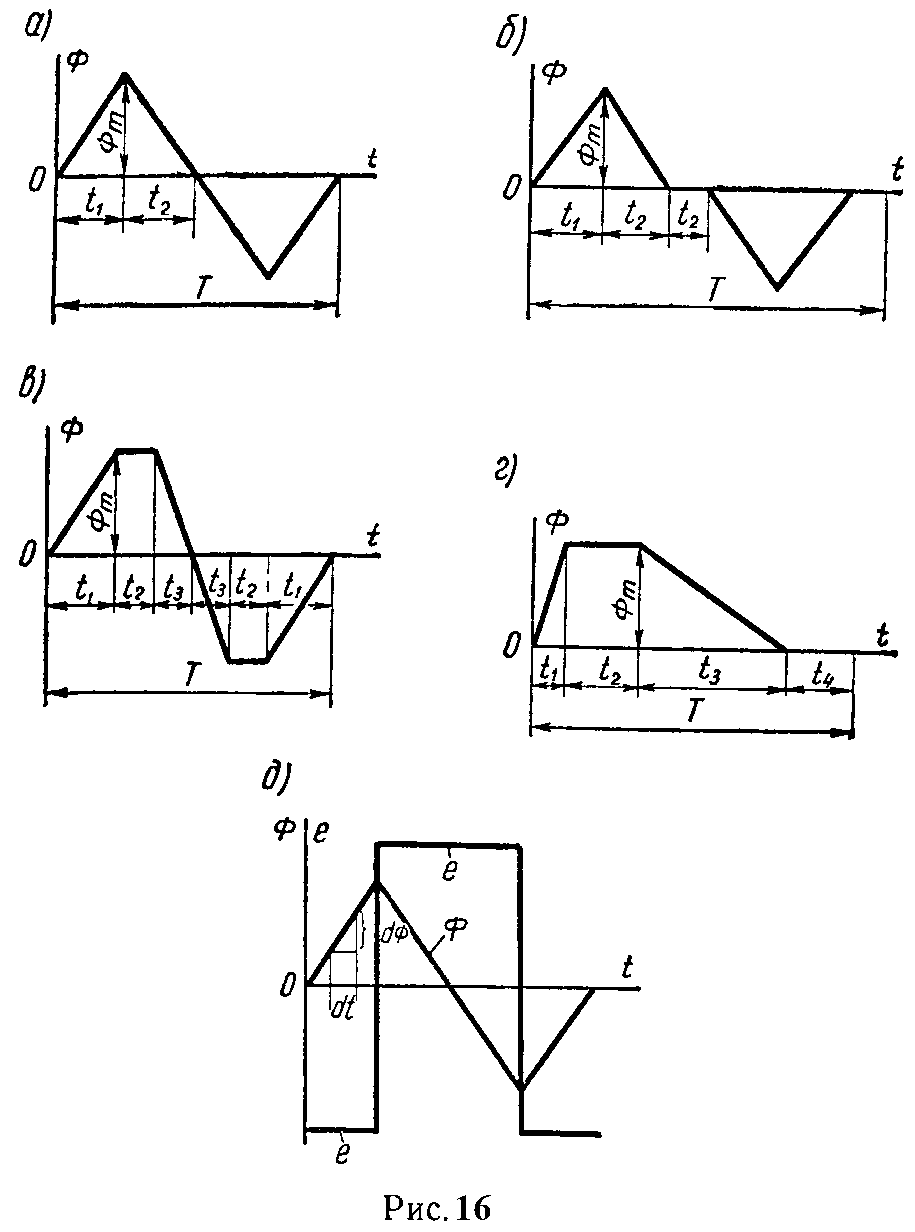
Задача 10. Построить кривую ЭДС, наводимой магнитным потоком в катушке, имеющей w =100 витков. Поток в функции времени изменяется согласно рис. 16, а, б, в, г.
Во всех случаях Фm = 10–2 Вб. Данные кривых:
а) для рис. 16, a t1 = t2 = 0,005 с;
б) для рис. 16, б t1 = 0,005 с, t2 = 0,0025 с;
в) для рис. 16, в t1 = 0,005 с, t2 = t3 = 0,0025 с;
г) для рис. 16, г t1 = 0,0025 с, t2 = t4 = 0,005 с; t3 = 0,01 с.
Решение
а) Наводимая ЭДС определяется по формуле (19).
На первом участке в интервале времени от нуля до t1 поток возрастает; за время dt происходит положительное приращение потока dФ (рис. 16, д). Вследствие линейного характера кривой отношение dФ/dt есть величина постоянная.
Величина наводимой ЭДС будет равна
e=−w dΦ dt =−w Φ m t 1 =−100 10 −2 0,005 =−200 В.
На втором участке t2 происходит спад кривой потока по прямой линии и, следовательно, dФ/dt также есть величина постоянная, но имеющая отрицательный знак; за время dt поток получает отрицательное приращение (dФ < 0); наводимая ЭДС равна
e=−w dΦ dt =+200 В.
На третьем участке за время dt поток продолжает убывать; и dФ/dt есть величина отрицательная; наводимая ЭДС равна +200 В; на четвертом участке магнитный поток возрастает с той же скоростью, что и на первом участке; наводимая ЭДС равна –200 В.
На рис. 16, д начерчена кривая наводимой ЭДС.
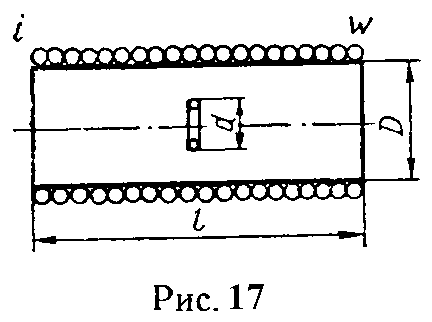
Задача 11. В центре цилиндрической катушки длиною l = 30 см и диаметром D = 10 см, состоящей из w = 400 витков, помещен виток, ось которого совпадает с осью катушки (рис. 17).
По катушке проходит ток
i = Imsinωt (Im = 4 А, ω = 314 с–1).
Определить взаимную индуктивность катушки и витка и ЭДС, наводимую в витке, если диаметр витка d = 0,5 см.
Ввиду малости размеров витка по сравнению с размерами катушки при расчете принять, что магнитная индукция, определяемая током в катушке во всех точках, лежащих в плоскости витка, будет такой же, как и в центре витка.
Полагая, что виток, перпендикулярный к оси цилиндрической катушки, расположен на расстоянии x от ее центра, построить кривую зависимости взаимной индуктивности катушки и витка в функции x.
Для построения кривой подсчет произвести для различных точек при изменении x от нуля до +l (соседние значения x брать через каждые 5 см).
Ответ: M = 31,2·10–9 Гн = 31,2 нГн; e = –39,2cos314t мкВ.
|
x, см |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
M, нГн |
31,2 |
30,7 |
26,3 |
16,1 |
4,63 |
1,62 |
0,72 |
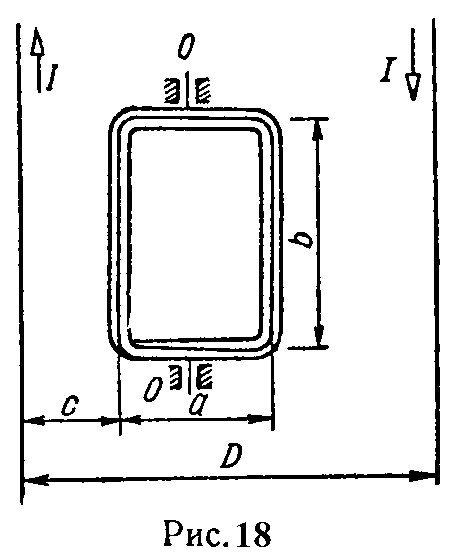
Задача 12. Катушка прямоугольной формы, средние размеры сторон которой равны a = 8 см, b = 15 см, содержащая w = 20 витков тонкой проволоки, находится в плоскости проводов двухпроводной линии передачи энергии, по которой проходит ток I = 100 А (рис. 18).
Расстояние между осью левого провода и серединой ближайшей стороны катушки c = 2 см. Расстояние между проводами линии D = 20 см.
Чему равна энергия потока взаимной индукции линии и катушки? Какова сила, действующая на катушку, если по ней проходит ток I = 0,5 А? Определить количество индуктированного в рамке электричества при ее повороте вокруг оси OO на 180°, если сопротивление катушки r = 0,08 Ом.
Примечание. Следует иметь в виду, что энергия потока взаимной индукции
W= w⋅Φ⋅I 2 ,
где Ф — магнитный поток, пронизывающий катушку, а I — ток в линии, определяющий этот поток.
Ответ: 6,6 мДж; 0,109 Гн; 33·10–4 Кл.
Задача 13. Определить индуктивность катушки, если известно, что при прохождении через нее синусоидального тока i = Imsinωt амплитуда (максимальная величина) наведенной ЭДС самоиндукции равна Em.
Дано Im = 2 А; ω = 5000 с–1; Em = 200 В.
Решение
По формуле (23) находим выражение для мгновенной величины электродвижущей силы самоиндукции, наводимой в катушке,
e L =−L di dt =−ωL I m cosωt.
Коэффициент при cosωt является амплитудой ЭДС самоиндукции, наведенной в катушке, т.е.
E m =ωL I m ,
откуда
L= E m ω I m = 200 5000⋅2 =0,02 Гн.
Задача 14. Определить индуктивность цилиндрической катушки без стального сердечника, имеющей w витков, длину l и сечение S. Расчет провести при следующих данных: a) w1 = 300, l1 = 60 см, S1 = 1 см2; б) w2 = 200, l2 = 60 см, S2 = 10 см2.
Решение
Индуктивность катушки вычисляем по формуле (25) с учетом коэффициента k, являющегося функцией отношения диаметра катушки к ее длине; значения k приведены в таблице 1.
а) Диаметр катушки найдем из формулы
S 1 = π D 1 2 4 ; D 1 = 4 S 1 π =1,13 см;
затем определяем коэффициент k1
k 1 = l 1 D 1 = 60 1,13 ≈53.
Так как k1 >50, то индуктивность находим по формуле (24)
L 1 = μ 0 ⋅ w 1 2 ⋅ S 1 l 1 = 4π⋅ 10 −7 ⋅ 300 2 ⋅1⋅ 10 −4 0,6 =18,8⋅ 10 −6 Гн=18,8 мкГн.
б) Найдем D2 и k2
D 2 = 4 S 2 π =3,57 см; k 2 = l 2 D 2 = 60 3,57 ≈16,8; D 2 l 2 = 3,57 60 =0,0595.
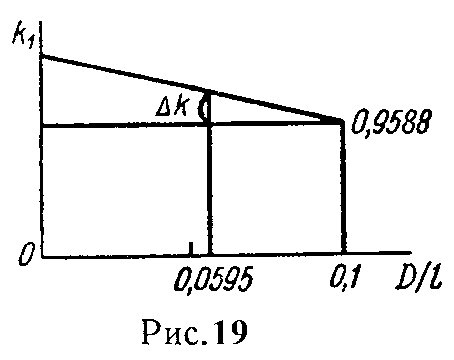
По таблице 1 находим, что отношению D/l = 0 соответствует k = 1, а отношению D/l = 0,1 соответствует k = 0,9588; путем интерполирования находим k, соответствующее отношению D2/l2 = 0,0595.
Из рис. 19 определяем
Δk 1−0,9588 = 0,1−0,0595 0,1 ,
откуда Δk = 0,0167, следовательно,
k = 0,9588 + Δk = 0,9588 + 0,0167 = 0,9755,
по формуле (25) находим индуктивность
L 2 =k μ 0 ⋅ w 2 2 ⋅ S 2 l 2 =81,5⋅ 10 −6 Гн=81,5 мкГн.
Задача 15. Индуктивность короткой цилиндрической катушки (для которой D:l = 1), имеющей 500 витков, равна 0,01 Гн. Определить индуктивность катушки, имеющей то же число витков и такую же длину, но у которой отношение D:l = 0,4.
Ответ: 2 мГн.
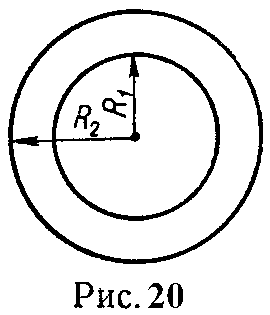
Задача 16. Определить индуктивность катушки, состоящей из 400 витков, намотанной на кольцевой сердечник, изготовленный из листовой электротехнической стали Э11, если ток I = 1 А. Сердечник имеет квадратное сечение. Радиусы: R1 = 3 см, R2 = 4 см.
Чему будет равна индуктивность, если в тороиде сделать зазор δ = 0,5 мм (рис. 20).
Указание. Надо рассчитать магнитную цепь, а для определения L воспользоваться формулой (21).
Ответ: 57,4 мГн; 32,8 мГн.
Задача 17. Катушка из 600 витков навита на стальной тороид, поперечное сечение которого равно 40 см2. Индуктивность катушки равна L1 = 2,5 Гн. Чему равна длина воздушного промежутка, который необходимо сделать в сердечнике для уменьшения индуктивности до 2 Гн?
При решении задачи принять, что магнитная проницаемость сердечника постоянна и очень велика по сравнению с единицей.
Решение
Магнитное сопротивление катушки без зазора
R 1 = l μS .
Для уменьшения индуктивности катушки в 1,25 раза ее магнитное сопротивление должно увеличиться в 1,25 раза, т. е. положив сечение пути потока в воздухе равным с сечением сердечника, получим
R 2 = l μS + δ μ 0 S =1,25 R 1 =1,25 l μS .
где δ — длина воздушного зазора, отсюда
δ S =0,25 l μ r S , l μ r =4δ.
Индуктивность катушки, определяемая по формуле (24), равна
L 1 = μ r μ 0 ⋅ w 2 ⋅S l ,
отсюда
l μ r = μ 0 ⋅ w 2 ⋅S L 1 .
Сравнивая два выражения для отношения l к µr, получим
4δ= μ 0 ⋅ w 2 ⋅S L 1 .
Отсюда рассчитывается необходимая длина воздушного зазора
δ= μ 0 ⋅ w 2 ⋅S 4 L 1 = 4π⋅ 10 −7 ⋅ 600 2 ⋅40⋅ 10 −4 4⋅2,5 =0,00018 м=0,18 мм.
Задача 18. На сердечник, изготовленный из листовой электротехнической стали Э11, имеющий регулируемый воздушный зазор, намотана катушка. Когда воздушный промежуток уменьшен до нуля, индуктивность катушки равна 3,5 Гн. При каком воздушном зазоре индуктивность катушки будет равна 2,5 Гн, если при зазоре в 1 мм ее индуктивность равна 2 Гн?
Принять, что абсолютная магнитная проницаемость сердечника постоянна.
Ответ: 0,53 мм.
Задача 19. Определить индуктивность 1 км воздушной медной двухпроводной линии, радиус проводов которой равен 2 мм и расстояние между осями проводов равно 30 см.
Ответ: 2 мГн.
Задача 20. Определить индуктивность 1 км воздушной медной однопроводной линии, радиус провода которой равен 2,5 мм. Расстояние провода от земли 5 м.
Ответ: 1,656 мГн.
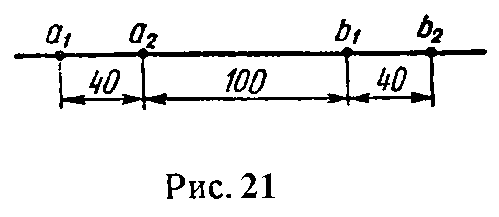
Задача 21. Найти взаимную индуктивность на 1 км между двумя параллельными линиями a1a2 и b1b2 (рис. 21). Радиусы проводов считать малыми по сравнению с расстояниями между их осями, заданными на рис. 21.
Решение
Расчет взаимной индуктивности проведем по формуле (32). Чтобы ею воспользоваться найдем расстояния: от оси первого провода первой линии до оси первого провода второй линии
r11 = a1b1 = 140 см;
от оси первого провода первой линии до оси второго провода второй линии
r12 = a1b2 = 180 см;
от оси второго провода первой линии до оси первого провода второй линии
r21 = a2b1 = 100 см;
и, наконец, от оси второго провода первой линии до оси второго провода второй линии
r22 = a2b2 = 140 см.
Искомая взаимная индуктивность
M= μ 0 l 2π ln r 11 r 22 r 12 r 21 = 4π⋅ 10 −7 2π ln 140⋅140 180⋅100 =17,2⋅ 10 −6 Гн=17,2 мкГн.
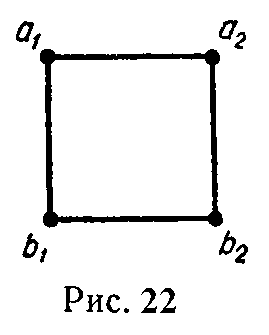
Задача 22. Четыре длинных прямых параллельных провода расположены в вершинах квадрата (рис. 22).
Провода a1a2 образуют одну цепь, провода b1b2 — другую. Чему равна взаимная индуктивность этих цепей на 1 км, если сторона квадрата равна 20 см? Радиусы проводов считать достаточно малыми (например, 1,5–2 мм).
Ответ: 0,1386 мГн.
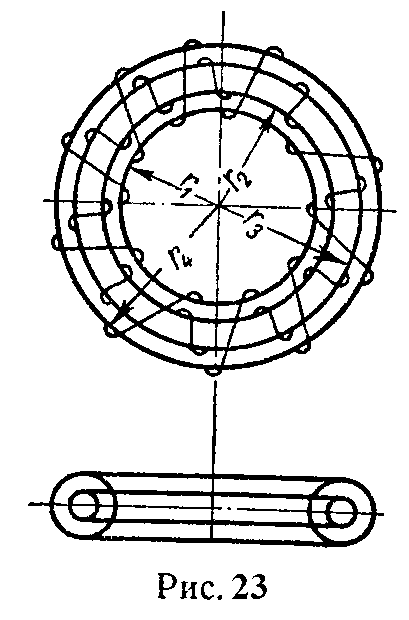
Задача 23. Найти взаимную индуктивность двух катушек, изображенных на рис. 23.
Число витков наружной катушки w1 = 200, число витков внутренней катушки w2 = 500; r1 = 8 см, r2 = 10 см, r3 = 12 см, r4= 14 см.
Решение
Взаимная индуктивность определяется по формуле (31), в которой под S надо понимать ту площадь, которая пронизывается потоком, сцепленным как с током первой так и с током второй катушки, т.е. площадь сечения меньшей катушки S2 равна
S 2 = π d 2 2 4 = π ( r 3 − r 2 ) 2 4 = 3,14⋅ 0,02 2 4 =3,14⋅ 10 −4 м 2 .
Полагая распределение магнитной индукции равномерным по сечениям обеих катушек, найдем
M= μ 0 w 1 w 2 S 2 2π r 1 + r 4 2 = 4π⋅ 10 −7 ⋅200⋅500⋅3,14⋅ 10 −4 2π⋅0,11 =57⋅ 10 −6 Гн=57 мкГн.
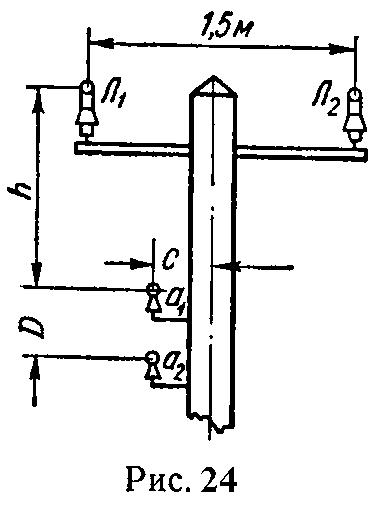
Задача 24. Под линией электропередачи Л1Л2 подвешены бронзовые провода линии связи a1a2 (рис. 24).
Определить индуктивность одного километра линии a1a2, диаметр проводов которой d = 3 мм, а расстояние между осями проводов D = 30 см.
Чему равна взаимная индуктивность на 1 км длины между линиями Л1Л2 и a1a2, если расстояния равны: h = 100 см, c = 25 см.
Какая электродвижущая сила наводится в линии связи, если по линии электропередачи протекает ток
i = Imsinωt,
где Im = 600 А, ω = 314 с–1.
Ответ: L = 2,12 мГн, M = 14 мкГн; e = –2,54cosωt В.
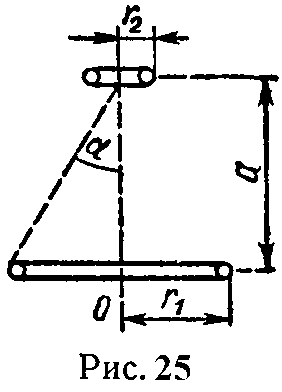
Задача 25. Определить взаимную индуктивность двух круговых витков, имеющих общую ось (рис. 25).
Радиусы витков r1 = 4 см, r2 = 0,5 см. Принять, что напряженность магнитного поля, определяемая током в большем витке во всех точках, лежащих в плоскости второго витка (внутри его), будет такой же, как и в центре второго витка.
Задачу решить для двух случаев: а) a = 0, б) a = 3 см.
На какое расстояние от центра 0 надо удалить второй виток, чтобы взаимная индуктивность составляла 1% от взаимной индуктивности в случае, когда плоскости витков совпадают.
Указание. Положив, что по большему витку проходит ток I, надо вычислить напряженность магнитного поля, созданную этим током в центре меньшего витка; умножив найденное значение H на магнитную постоянную и площадь, ограниченную меньшим витком, найти величину магнитного потока, пронизывающего этот виток. Разделив этот поток на ток I, получают искомую взаимную индуктивность (формула 29).
Ответ: а) 1,23 нГн; б) 0,63 нГн, 18,2 см.
Задача 26. На кольцо, изготовленное из литой стали, средний диаметр которого равен 25 см, навиты две катушки. Радиус поперечного сечения кольца 2 см. В первой катушке 250 витков, во второй — 500 витков. Относительную магнитную проницаемость стали принять постоянной и равной 1000. Определить индуктивность каждой катушки и их взаимную индуктивность (полагая распределение магнитной индукции в сечении кольца равномерным).
Ответ: L1 = 125,6 мГн; L2 = 502,4 мГн; M = 251,2 мГн.
Задача 27. Цилиндрическая катушка длиною в 1 м и диаметром в 10 см имеет 1000 витков. Вторая катушка, поперечное сечение которой 0,5 см2, а длина 1 см, имеет 10 витков. Катушки расположены так, что их оси совпадают.
Принять, что магнитная индукция, определяемая током первой катушки во всех точках, лежащих внутри второй катушки, будет такой же, как и в центре второй катушки. Определить взаимную индуктивность катушек, в случаях: а) когда их центры совпадают, б) когда центр второй катушки расположен на одном из концов первой катушки, в) когда их центры удалены друг от друга на 60 см.
Ответ: а) 0,625 мкГн; б) 0,314 мкГн; в) 0,033 мкГн.
Задача 28. Определить взаимную индуктивность двух катушек, индуктивности которых 0,04 и 0,16 Гн, а коэффициент связи равен 0,75.
Ответ: M = 0,06 Гн.
Задача 29. Определить коэффициент рассеяния двух катушек, индуктивности которых 30 и 120 мГн, а взаимная индуктивность равна 0.03 Гн.
Ответ: σ = 0,75.
Задача 30. Определить энергию магнитного поля цилиндрической катушки, содержащей 500 витков. Длина катушки равна 10 см. диаметр равен тоже 10 см; по виткам катушки проходит ток в 2 А. Среда — воздух.
Указание. Сначала следует вычислить индуктивность катушки по формуле (25), а затем энергию магнитного поля по формуле (36).
Ответ: 0,034 Дж.
Задача 31. Чему равна энергия магнитного поля катушки, имеющей 1000 витков и индуктивность которой равна 2 мГн, если магнитный поток, определяемый проходящим по катушке током, равен 2·10–5 Вб.
Ответ: 0,1 Дж.
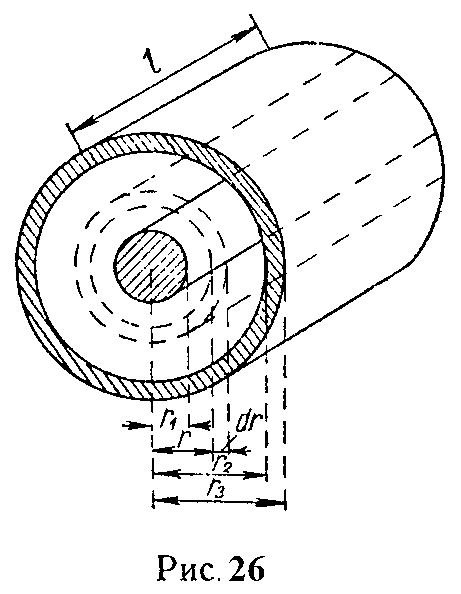
Задача 32. Исходя из выражения интеграла магнитной энергии
W= ∫ V μ H 2 2 dV ,
определить полную индуктивность коаксиального кабеля длиною l = 1 км, радиус внутреннего проводника которого r1 = 2 мм, внутренний радиус внешнего проводника r2 = 7,2 мм, внешний радиус внешнего проводника r3 = 7,5 мм (рис. 26).
Относительную магнитную проницаемость материала внутреннего и внешнего проводника, а также пространства между проводниками принять равной 1.
Определить энергию магнитного поля на 1 м длины кабеля, запасаемую во внутреннем проводе, между проводом и трубой и внутри трубы, если I = 1 А.
Указание. Индуктивность следует определить из выражения
L⋅ I 2 2 = ∫ V μ H 2 2 dV ,
которое следует применить по отдельности к области внутри внутреннего проводника, к полости трубы и к области внешнего проводника. При расчете энергии каждый раз надо рассматривать малый трубчатообразный объем (рис. 26)
dV = 2πr·dr·l.
Значение напряженности поля в каждой из областей было найдено в задаче 1.
В результате решения должно быть получено для внутренней индуктивности внутреннего проводника L’ = 0,05 мГн, то же для внешнего проводника L» = 0,0045 мГн, и для внешней индуктивности Lвне = 0,256 мГн. Полная индуктивность
L = L’ + L» + Lвне = 0,31 мГн.
Искомую энергию следует определять по формуле (36).
Задача 33. По двум катушкам, индуктивности которых равны L1 = 0,5 Гн, L2 = 1 Гн, а их взаимная индуктивность составляет M = 0,5 Гн, проходят токи I1 = 6 А, I2 = 4 А. Определить полную магнитную энергию этой системы.
Ответ: 29 Дж.

энергия магнитного поля,
коэффициент магнитной связи,
взаимная индуктивность,
индуктивность однопроводной линии,
индуктивность двухпроводной линии,
индуктивность соленоида,
ЭДС самоиндукции,
индуктивность,
закон электромагнитной индукции,
второй закон Кирхгофа для магнитных цепей,
первый закон Кирхгофа для магнитных цепей,
сила Ампера,
закон Ампера,
сила Лоренца,
закон полного тока,
магнитная постоянная,
закон Био Савара Лапласа