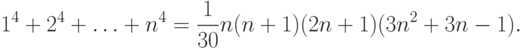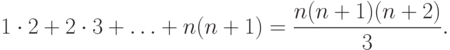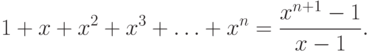-
Суть метода математической индукции.
Во
многих разделах арифметики, алгебры,
геометрии, анализа приходится доказывать
истинность предложений А(n),
зависящих от натуральной переменной.
Доказательство истинности предложения
А(n)
для всех значений переменной часто
удается провести методом математической
индукции, который основан на следующем
принципе.
Предложение
А(n)
считается истинным для всех натуральных
значений переменной, если выполнены
следующие два условия:
-
Предложение
А(n)
истинно для n=1. -
Из
предположения, что А(n)
истинно для n=k
(где k
– любое натуральное число), следует,
что оно истинно и для следующего значения
n=k+1.
Этот принцип называется принципом
математической индукции. Обычно он
выбирается в качестве одной из аксиом,
определяющих натуральный ряд чисел, и,
следовательно, принимается без
доказательства.
Под
методом математической индукции понимают
следующий способ доказательства. Если
требуется доказать истинность предложения
А(n)
для всех натуральных n,
то, во-первых, следует проверить истинность
высказывания А(1) и, во-вторых, предположив
истинность высказывания А(k),
попытаться доказать, что высказывание
А(k+1)
истинно. Если это удается доказать,
причем доказательство остается
справедливым для каждого натурального
значения k,
то в соответствии с принципом математической
индукции предложение А(n)
признается истинным для всех значений
n.
Метод математической
индукции широко применяется при
доказательстве теорем, тождеств,
неравенств, при решении задач на
делимость, при решении некоторых
геометрических и многих других задач.
-
Метод математической
индукции в решении задач на делимость.
С помощью метода математической индукции
можно доказывать различные утверждения,
касающиеся делимости натуральных чисел.
Следующее
утверждение можно сравнительно просто
доказать. Покажем, как оно получается
с помощью метода математической индукции.
Пример
1. Если n
– натуральное число, то число
четное.
При
n=1
наше утверждение истинно:
—
четное число. Предположим, что
— четное число. Так как
,a
2k
– четное число, то и
четное.
Итак, четностьдоказана приn=1,
из четности
выведена четность
.Значит,
четно при всех натуральных значенияхn.
Пример
2. Доказать
истинность предложения
A(n)={число
5кратно 19},n
– натуральное число.
Решение.
Высказывание
А(1)={число
кратно
19} истинно.
Предположим,
что для некоторого значения n=k
А(k)={число
кратно 19} истинно. Тогда, так как
,
очевидно, что и A(k+1)
истинно. Действительно, первое слагаемое
делится на 19 в силу предположения, что
A(k)
истинно; второе слагаемое тоже делится
на 19, потому что содержит множитель 19.
Оба условия принципа математической
индукции выполнены, следовательно,
предложение A(n)
истинно при всех значениях n.
-
Применение метода математической индукции к суммированию рядов.
Пример
1. Доказать
формулу
,
n
– натуральное число.
Решение.
При
n=1
обе части равенства обращаются в единицу
и, следовательно, первое условие принципа
математической индукции выполнено.
Предположим,
что формула верна при n=k,
т.е.
.
Прибавим
к обеим частям этого равенства
и преобразуем правую часть. Тогда получим
Таким
образом, из того, что формула верна при
n=k,
следует, что она верна и при n=k+1.
Это утверждение справедливо при любом
натуральном значении k.
Итак, второе условие принципа математической
индукции тоже выполнено. Формула
доказана.
Пример
2. Доказать,
что сумма n
первых чисел натурального ряда равна
.
Решение.
Обозначим
искомую сумму
,
т.е..
При
n=1
гипотеза верна.
Пусть
.
Покажем, что.
В самом деле,
.
Задача решена.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Метод математической индукции. Индукция по структуре объекта.
Комбинаторика: число размещений, перестановок и сочетаний.
Принцип включения и исключения
Метод математической индукции
Математическая индукция — это весьма общий метод,
который позволяет доказывать утверждения, зависящие от целочисленных параметров. Его можно сформулировать следующим образом.
Пусть P(n) — это некоторое утверждение, зависящее от
целочисленного параметра n. Пусть, во-первых,
утверждение P(n0) справедливо и пусть, во-вторых, для любого k >= n0 из справедливости P(k) следует справедливость P(k+1).
Тогда утверждение P(n) справедливо для всех n >= n0.
Таким образом доказательство «по индукции» состоит из двух этапов.
- Базис (или основание) индукции состоит в доказательстве утверждения P(n0) для некоторого начального значения n0 ( обычно n0=1, но это не обязательно).
- Шаг индукции состоит в предположении справедливости P(n) при n=k >= n0 и доказательстве из этого предположения справедливости утверждения P(k+1) .
Рассмотрим несколько примеров применения метода математической индукции.
Пример 1. Доказать, что при n>= 1
-
Базис индукции. При n=1 имеем
.
-
Шаг индукции. Допустим, что при n=k
Докажем тогда, что при n=k+1
Действительно,
Таким образом, наше утверждение выполненопри всех n>= 1.
Пример 2. Доказать, что для любого 
выполнено неравенство (1+x)n > 1 +nx (это неравенство называют неравенством Бернулли).
-
Базис индукции. При
, учитывая, что
, имеем (1+x)2=1 +2x +x2 > 1+2x.
- Шаг индукции. Допустим, что при n=k неравенство справедливо, т.е. (1+x)k > 1 +kx. Покажем, что тогда оно выполнено и при n=k+1. Действительно, так как 1+x > 0, то умножив обе части на 1+x > 0, получим (1+x)k(1+x)=(1+x) k+1 > (1+kx)(1+x)=1+ (k+1)x +kx2> 1+(k+1)x, что и требовалось.
В обычном понимании слово «индукция» означает переход от частных случаев
к некоторому общему утверждению, а «дедукция» — получение результатов для
частных случаев из некоторых общих утверждений, законов. В этом смысле
метод математической индукции является дедуктивным,
с его помощью доказываются общие утверждения (равенства, неравенства и т.п.).
Он не дает способа для выдвижения общей гипотезы
или угадывания общего правила или формулы по наблюдениям
за отдельными частными случаями. Но этот метод позволяет проверять
выдвинутые гипотезы. Для неверной гипотезы проверка провалится
на шаге индукции.
Отметим также, что приведенная формулировка принципа математической индукции
допускает разные эквивалентные варианты. В ряде случаев мы будем использовать
вариант, в котором шаг индукции состоит в предположении справедливости P(n) при всех n <= k и доказательстве из этого
предположения справедливости утверждения P(k+1).
Такая формулировка будет использоваться, в частности, при доказательствах
индукцией по построению объекта.
В дискретной математике и в информатике многие классы объектов определяются
индуктивно. В таких определениях явно или неявно участвует некоторая
функция, задающая «сложность» объекта, и индукция идет по значениям этой функции.
На базисном шаге определяются объекты минимальной сложности (обычно они имеют
сложность 0), а индукционный шаг определения заключается в том,
что из объектов меньшей сложности
с помощью некоторых операций (операторов, конструкций) строятся объекты
большей сложности.
Для доказательства некоторого свойства объектов индуктивно определенного класса метод математической индукции применяется в следующем виде.
- Базис индукции состоит в проверке требуемого свойства у объектов минимальной сложности.
- Шаг индукции состоит в предположении справедливости доказываемого свойства
- у всех объектов класса, имеющих сложность <= k, и проверке того, что все объекты большей сложности (обычно, сложности k+1 ), получаемые из них с помощью используемых при определении класса операций, также обладают требуемым свойством.
Рассмотрим эту схему на примере простых арифметических выражений.
Пример 2.1.
Пусть V ={x, y, z} — множество переменных, O={+, -, *, / } — список операций.
Определим индуктивно множество 
( слов) в объединенном алфавите 
арифметическими формулами. Одновременно будем определять меру сложности
этих формул, назывемую их глубиной. Глубину формулы 
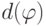
-
Базис индукции. Каждая переменная
является арифметической формулой глубины 0, т.е.
и d(v)=0.
-
Шаг индукции. Пусть
и
— арифметические формулы глубины
и
, соответственно. Тогда выражения
также являются арифметическими формулами из
и каждая из этих формул имеет глубину.
Пусть w=w1w2 … wn — произвольное слово в алфавите 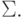
Докажем, что в каждой арифметической формуле из
скобки расставлены правильно.
-
Базис индукции.
. Формула глубины 0 является переменной
. В ней нет скобок и поэтому они расставлены правильно.
-
Шаг индукции. Пусть утверждение справедливо для всех формул из
глубины <= k и
— произвольная формула глубины
. Тогда она имеет одну из четырех форм (а), (б), (в) или (г). Предположим, что
. Тогда из определения глубины следует, что
и
, и по индукционному предположению в обеих формулах
и
скобки расставлены правильно. Покажем, что и в
скобки расставлены правильно. Пусть
и
. Тогда
,
здесь M= m1+m2 +3 и все символы vi, wj принадлежат алфавиту
Для каждого 1 < i <= m1+1 число левых скобок в t1 … ti
на 1 больше числа левых скобок в v1… vi-1, и следовательно, больше числа
правых скобок в этом слове, так все они входят в v1… vi-1.
Это же справедливо для слова t1t2 … tm1+2, заканчивающегося символом +.
При m1+2 < i < M
разница между числом левых и правых скобок в t1 … ti не меньше 1,
так как t1= (, а ви
скобки расставлены правильно.
Во всем словечисло левых и правых скобок совпадает, так как
к скобками
добавилась одна левая и одна правая скобка.
Таким образом, вскобки расставлены правильно. Случаи (б), (в) и (г)
рассматриваются аналогично.
Задачи
Задача 2.1. Доказать, что
Задача 2.2. Доказать, что
Задача 2.3. Доказать, что
Задача 2.4. Доказать, что n различных прямых на плоскости разбивают ее на области,
которые можно закрасить белой и черной красками так, что смежные области
будут закрашены разными красками.
Задача 2.5. Найдите ошибку в следующем доказательстве «по индукции» утверждения:
для всех n >= 1 справедливо неравенство 3n > 3(n +1) +1 .
Доказательство Пусть для некоторого k >= 1 неравенство справедливо, т.е. 3k > 3(k +1) +1 (*).
Докажем, что оно верно и для n=k+1, т.е. 3k+1 > 3(k+2) +1. Для этого заметим, что для любого k >= 1 верно неравенство 2 cdot 3k > 3. Прибавив его левую и правую часть к соответствующим частям неравенства (*), получим 3k + 2 x 3k > 3(k +1) +1+3 или 3 k+1 > 3(k+2) +1, что и требовалось.
Установите, при каких n справедливо неравенство 3n > 3(n +1)+1.
Содержание
Математическая индукция
Математическая индукция — Википедия
Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.

Фактически мы просто верим, что метод доказательства по индукции работает, убедившись на многих проверяемых примерах.
Формулировка
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: $ P_{1},P_{2},ldots ,P_{n},P_{n+1},ldots$.
Допустим, что
-
Установлено, что $ P_{1}$ верно. (Это утверждение называется базой индукции.)
-
Для любого n доказано, что если верно $ P_{n}$, то верно $ P_{n+1}$. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений $ P_{1}, P_{2}, P_{3}, ldots$. Если для любого натурального $n$ из того, что истинны все $P_{1}, P_{2}, P_{3} ,ldots, P_{n-1}$, следует также истинность $P_{n}$, то все утверждения в этой последовательности истинны, то есть $(forall nin {mathbb {N} }){Big (}(forall iin {1;dots ;n-1})P_{i}longrightarrow P_{i+1}{Big )}longrightarrow (forall nin {mathbb {N} })P_{n}$.
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при $n=1$ импликация $ (forall iin {1;dots ;n-1})P_{i}longrightarrow P_{n}$ эквивалентна $P_{1}$.
Из книги Виленкина
Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И тем не менее этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.
Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге.
…
В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломаного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство |AB| + |BC| >= |AC|.
…
Но из данной системы аксиом можно вывести очень много утверждений. И отбор тех утверждений, которые надо доказывать, вновь подсказывается индукцией. Именно она позволяет отделить полезные теоремы от бесполезных, указывает, какие теоремы могут оказаться верными, и даже помогает наметить путь доказательства. Как правило, справедливость теоремы сначала делается очевидной из опыта и наглядных соображений и лишь потом получает дедуктивное подтверждение. Лишь после того, как на многочисленных примерах убедились, что сумма чисел не изменяется при перестановке слагаемых, возникла потребность вывести это утверждение из аксиом арифметики.
…
индукция может привести и к ошибочным выводам [строго говоря, не индукция, а обобщение опытных данных]. Например, французский математик XVII века Пьер Ферма, рассматривая числа
$2^{2^1} + 1 = 5, 2^{2^2} + 1 = 17, 2^{2^3} + 1 = 257, 2^{2^4} + 1 = 65537$,
пришел к выводу, что при любом натуральном значении n число
$2^{2^n} + 1$ является простым. Проверить справедливость этого утверждения при n = 5 он не смог, так как не сумел выяснить, имеет ли число $2^{32}+1$ нетривиальные делители. Но Эйлеру удалось показать, что это число делится на 641.
В теории чисел доказывается, что если р — простое число, то $2^{p-1}-1$ делится на р. Но ни для одного из простых чисел, меньших 1000, $2^{p-1} — 1$ не делится на $p^2$. Поэтому возникла гипотеза, что вообще ни для одного простого числа р число $2^{p-1}-1$ не делится на $p^2$. Однако оказалось, что $2^{1093-1}-1$ делится на $1093^2$. Существуют примеры, когда число, опровергающее гипотезу, настолько велико, что найти его перебором практически невозможно. Например, первое значение n такое, что число $991n^2 + 1$ является точным квадратом, насчитывает 29 десятичных знаков. Поэтому, если бы кто-нибудь сформулировал гипотезу: число $991n^2+ 1$ никогда не является точным квадратом, то для опровержения этого утверждения ему пришлось бы перебрать столь много чисел, что это оказалось бы не под силу самой быстродействующей вычислительной машине (разумеется, опровергающее гипотезу число было найдено иным путем).
Из сказанного выше следует, что угаданный с помощью индукции результат подлежит дедуктивному доказательству. В некоторых случаях такое доказательство можно провести, разобрав конечное число случаев, исчерпывающих все возможности.




Примеры
Задача
Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
$ 1+q+cdots +q^{n}={frac {1-q^{n+1}}{1-q}}.$

Комментарий: истинность утверждения $P_{n}$ в этом доказательстве — то же, что истинность равенства
$ 1+q+cdots +q^{n}={frac {1-q^{n+1}}{1-q}}.$
Сумма квадратов первых n натуральных чисел
Некоторые конечные числовые ряды
Натуральные числа: n, k.
n — число членов ряда
Сумма первых n натуральных чисел

Сумма первых n четных натуральных чисел
$$2+4+6+ldots+2n = n(n+1)$$
Сумма первых n нечетных натуральных чисел
$$1+3+5+ldots+(2n-1) = n^2$$
Сумма n натуральных чисел, начиная с k

Сумма кубов первых n натуральных чисел

Сумма квадратов первых n нечетных натуральных чисел

Сумма кубов первых n нечетных натуральных чисел



Задача — разрезание квадрата на квадраты
Пример применения полной индукции.
При $n >= 6$ любой квадрат можно разрезать на n квадратов.




Научились разрезать на 6,7,8,9 частей. А дальше хочется применить индукцию.
Пусть есть квадрат, разрежем его на 4 части, а одну из частей — на n-2 части. Это не обычная индукция, так как мы опираемся не на предыдущий шаг, а на один из предыдущих доказанных фактов. Тогда мы получим n-2+3 = n+1 часть.
Получается здесь индукционный переход от доказанных утверждений при n, n-1 и n-2 к n+1.
Основная теорема арифметики
Каждое натуральное число $n>1$ можно представить в виде $ n=p_{1}cdot ldots cdot p_{k}$, где $ p_{1},ldots ,p_{k}$ — простые числа, причём такое представление единственно, если не учитывать порядок следования множителей.
Доказательство
Существование: Докажем существование разложения числа $n$ на простые множители, предполагая, что оно уже доказано для любого другого числа, меньшего $n$. Если $n$ — простое, то существование доказано. Если $n$ — составное, то оно может быть представлено в виде произведения двух чисел $a$ и $b$, каждое из которых больше 1, но меньше $n$. Числа $a$ и $b$ либо являются простыми, либо могут быть разложены в произведение простых (уже доказано ранее). Подставив их разложение в $ n=acdot b$, получим разложение исходного числа $ n$ на простые. Существование доказано.
Единственность — от противного, см Основная теорема арифметики — Википедия
Шапошников С. В. — Математический анализ I — Основная теорема арифметики — YouTube
Литература
А. Шень. Математическая индукция. — МЦНМО, 2004. 2016.
Головина, Яглом. Индукция в геометрии. 1961
Н. Я. Виленкин. Индукция. Комбинаторика. — Пособие для учителей. — М.: Просвещение, 1976. — 48 с.
Book of proof (Книга доказательств) — глава про математическую индукцию как метод доказательства.
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Существует метод рассуждений, который позволяет заменить неосуществимый бесконечный перебор доказательством того, что если утверждение истинно в одном случае, то оно окажется истинным и в следущем за ним случае. Этот метод носит название математической индукции (или рассуждением от $n$ к $n+1$)
Основы метода математической индукции
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ — натуральное число) справедливо при $forall n in N$, если:
- Утверждение $P(n)$ справедливо при $n=1$.
- Для $forall k in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с помощью метода математической индукции проводится в два этапа:
- База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
- Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
- Доказательство делимости и кратности
- Доказательство равенств и тождеств
- Задачи с последовательностями
- Доказательство неравенств
- Нахождение суммы и произведения
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Лучшее спасибо — порекомендовать эту страницу
Математическая индукция: задачи и решения
Доказательство кратности и делимости
Задача 1. Докажите, что $5^n-4n+15$ делится на 16 при всех $n in N_0$.
Задача 2. Доказать, что при любом натуральном $n$ число $a_n$ делится на $b$.
$$a_n = 2n^3+3n^2+7n, quad b=6.$$
Задача 3. Докажите методом математической индукции: $4^{2n-1} + 1$ кратно 5 для всех $n ge 1$.
Задача 4. Используя метод математической индукции, докажите, что для любого натурального числа истинно следующее утверждение: $6^{2n-2}+3^{n+1}+3^{n-1}$ кратно 11.
Доказательство равенств и неравенств
Задача 5. Доказать равенство
$$
1^2+2^2+…+n^2 = frac{n(n+1)(2n+1)}{6}.
$$
Задача 6. Доказать методом математической индукции:
$$
p+(p+1)+(p+2)+…+(p+n) = frac{(2p+n)(n+1)}{2}.
$$
Задача 7. Доказать неравенство:
$$
frac{1}{n+1}+frac{1}{n+2}+…+frac{1}{2n} gt frac{13}{24} quad (n gt 1).
$$
Задача 8. Доказать утверждение методом математической индукции:
$$
left(1-frac{1}{4}right)left(1-frac{1}{9}right)left(1-frac{1}{16}right)cdot … cdotleft(1-frac{1}{n^2}right) =frac{n+1}{2n} quad (n ge 2).
$$
Задача 9. Доказать неравенство:
$$ 2!cdot 4! cdot … cdot (2n)! gt [(n+1)!]^n quad (n gt 2).$$
Задача 10. Докажите методом математической индукции неравенство Бернулли: $(1+a)^n gt 1 + acdot n$ для всех $nin N$ и $a gt -1$, $a in R$.
Вычисление сумм
Задача 11. Доказать методом математической индукции:
$$
1^2+3^2+5^2+…+(2n-1)^2 = frac{n(4n^2-1)}{3}.
$$
Задача 12. Найдите сумму
$$1 cdot 1! + 2 cdot 2! + . . . + 2012 cdot 2012! + 2013 cdot 2013!$$
Заказать решение
Если вам нужна помощь с решением задач по любым разделам математики, обращайтесь в МатБюро. Выполняем контрольные и практические работы, ИДЗ и типовые расчеты на заказ. Стоимость задания от 60 рублей, оформление производится в Word, срок от 2 дней.
Заказать решение задач по математике легко!
Полезные ссылки о ММИ
- ММИ: краткая теория и примеры решений Страничка виртуальной школы юного математика. Разобраны примеры (в том числе для геометрии) и даны задачи для самостоятельной работы.
- Виленкин Н.Я. Индукция. Комбинаторика Классическое пособие по методу математической индукции и комбинаторике (базовые понятия и примеры задач).
- Математическая индукция. Основные определения и 10 разобранных решений.
- Николаева С.А. Метод математической индукции: методическое пособие для учителей и учащихся.
- А. Шень Математическая индукция. Пособие для школьников, разобраны 29 задач, из них 19 с полным решением.
Кратенький видеоурок о ММИ
Метод математической индукции
- Принцип математической индукции
- Примеры
п.1. Принцип математической индукции
Рассмотрим бесконечную последовательность утверждений, которую можно отобразить на множество натуральных чисел, т.е., попросту, пронумеровать:
P1, P2, … , Pn , …
Допустим, что
1) утверждение P1 верно (P1 называют базой индукции);
2) для любого n доказано, что, если верно Pn, то верно Pn+1
(истинность Pn → Pn+1, ∀n называют индуктивным переходом).
Тогда все утверждения последовательности P1, P2, … , Pn , … верны.
Говорят, что мы провели «доказательство утверждения Pn индукцией по n».
Принцип математической индукции используется для доказательства различных формул.
Например:
Докажем, что сумма первых n натуральных чисел равна (mathrm{S_n=1+2+…+n=frac{n(n+1)}{2}})
1) Для базы индукции (mathrm{n=1, S_1=frac{1cdot 2}{2}=1}) – верно
2) Допустим что при некотором (mathrm{n S_n=frac{n(n+1)}{2}.}) Найдём Sn+1: begin{gather*} mathrm{ S_{n+1}=(1+2+…+n)+n+1=S_n+n+1=frac{n(n+1)}{2}+(n+1)= }\ mathrm{ =frac{n(n+1)+2(n+1)}{2}=frac{(n+1)(n+2)}{2} } end{gather*} т.е. для Sn+1 формула также справедлива. Индуктивный переход выполняется. Следовательно, по принципу математической индукции (mathrm{S_n=frac{n(n+1)}{2}, forall nin mathbb{N}}).
Что и требовалось доказать.
п.2. Примеры
Пример 1. Докажите, что сума кубов первых n натуральных чисел равна (mathrm{S_n=frac{n^2(n+1)^2}{4}})
1) Для базы индукции (mathrm{n=1, S_1=frac{1^2(1+1)^2}{4}=1}) – верно
2) Допустим, что при некотором (mathrm{n, S_n=frac{n^2(n+1)^2}{4}}). Найдём Sn+1: begin{gather*} mathrm{ S_{n+1}=underbrace{1^3+2^3+3^3+…+n^3}_{S_n}+(n+1)^3=S_n+(n+1)^3= }\ mathrm{ =frac{n^2(n+1)^2}{4}+(n+1)(n+1)^2=frac{n^2(n+1)^2+4(n+1)(n+1)^2}{4} }\ mathrm{ =frac{(n+1)^2(n^2+4(n+1))}{4}=frac{(n+1)^2(n^2+4n+4)}{4}=frac{(n+1)^2(n+2)^2}{4} } end{gather*} т.е. для Sn+1 формула также справедлива. Индуктивный переход выполняется. Следовательно, по принципу математической индукции сумма кубов (mathrm{S_n=frac{n^2(n+1)^2}{4}, forall nin mathbb{N}}). Что и требовалось доказать.
Заметим, что согласно доказанной формуле сумма кубов является точным квадратом суммы первых степеней: $$ mathrm{ 1^3+2^3+3^3+…+n^3=left(frac{n(n+1)}{2}right)^2=(1+2+3+…+n)^2 } $$
Пример 2. Докажите формулу Архимеда $$ mathrm{1^2+2^2+3^2+…+n^2=frac{n(n+1)(2n+1)}{6}} $$
1) Для базы индукции (mathrm{n=1, S_1=frac{1(1+1)(2+1)}{6}=1}) – верно
2) Допустим, что при некотором (mathrm{n, S_n=frac{n(n+1)(2n+1)}{6}}). Найдём Sn+1: begin{gather*} mathrm{ S_{n+1}=underbrace{1^2+2^2+3^2+…+n^2}_{S_n}+(n+1)^2=S_n+(n+1)^2= }\ mathrm{ =frac{n(n+1)(2n+1)}{6}+(n+1)^2=frac{n(n+1)(2n+1)+6(n+1)^2}{6} }\ mathrm{ =frac{(n+1)left(n(2n+1)+6(n+1)right)}{6}=frac{(n+1)(2n^2+7n+6)}{6}= }\ mathrm{ =frac{(n+1)(n+2)(2n+3)}{6}=frac{(n+1)left((n+1)+1right)(2(n+1)+1)}{6} } end{gather*} т.е. для Sn+1 формула также справедлива. Индуктивный переход выполняется. Следовательно, по принципу математической индукции сумма квадратов (mathrm{S_n=frac{n(n+1)(2n+1)}{6}, forall ninmathbb{N}}). Что и требовалось доказать.
Пример 3. Докажите, что любой член последовательности an = 15n + 6 делится на 7.
1) Для базы индукции n=1, a1 = 15 + 6 = 21 – делится на 7, верно
2) Допустим, что при некотором (mathrm{n, a_n=15^n+6 text{ делится на 7, т.е. } frac{a^n}{7}=k, kinmathbb{N}}). Рассмотрим дробь (mathrm{frac{a_{n+1}}{7}}): begin{gather*} mathrm{ frac{a_{n+1}}{7}=frac{15^{n+1}+6}{7}=frac{15cdot 15^n+6}{7}=frac{(14+1)cdot 15^n+6}{7}= }\ mathrm{ =frac{14cdot 15^n+overbrace{(15^n+6)}^{=a_n}}{7}=frac{14cdot 15^n}{7}+frac{a_n}{7}=2cdot 15^n+k }end{gather*} Получаем натуральное число. Значит, an+1 также делится на 7. Индуктивный переход выполняется.
Следовательно, по принципу математической индукции an = 15n + 6 делится на 7 при любом натуральном (mathrm{ninmathbb{N}}). Что и требовалось доказать.
Пример 4. Докажите, что любой член последовательности an = 7n + 12n делится на 18 с остатком 1.
1) Для базы индукции n=1, a1 = 71 + 12 · 1 = 19 – делится на 18 с остатком 1, верно
2) Допустим, что при некотором $a_n=7^n+12n$ делится на 18 с остатком 1, т.е. $frac{a_n-1}{18}=k$, $k in mathbb {N}$ Рассмотрим дробь (mathrm{frac{a_{n+1}-1}{18}}): begin{gather*} mathrm{ frac{a_{n+1}-1}{18}=frac{7^{n+1}+12(n+1)-1}{18}=frac{7cdot 7^n+12n-1+12}{18}= }\ mathrm{ =frac{7^n + 12n-1}{18}+frac{6cdot 7^n+12}{18}=k+frac{7^n+2}{3} }end{gather*} Решаем подзадачу. Докажем, что (mathrm{b_n=frac{7^n+2}{3}}) всегда является натуральным числом.
1) Для базы индукции n=1, (mathrm{b_1=frac{7+2}{3}=3}) – верно
2) Допустим, что при некотором (mathrm{n, b_n=frac{7^n+2}{3}=m inmathbb{N}}). Рассмотрим (mathrm{b_{n+1}}): begin{gather*} mathrm{ b_{n+1}=frac{7^{n+1}+2}{3}=frac{7cdot 7^n+2}{3}=frac{7^n+2}{3}+frac{6cdot 7^n}{3}=m+2cdot7^n }end{gather*} Получили натуральное число. Индуктивный переход для подзадачи выполняется.
Значит, (mathrm{b_n=frac{7^n+2}{3}}). всегда является натуральным числом.
Возвращаемся к основной задаче: (mathrm{frac{a_{n+1}-1}{18}=k+frac{7^n+2}{3}=k+minmathbb{N}}).
Значит, an+1 делится на 18 с остатком 1. Индуктивный переход для основной задачи выполняется.
Следовательно, по принципу математической индукции an = 7n + 12n делится на 18 с остатком 1 при любом натуральном (mathrm{ninmathbb{N}}). Что и требовалось доказать.

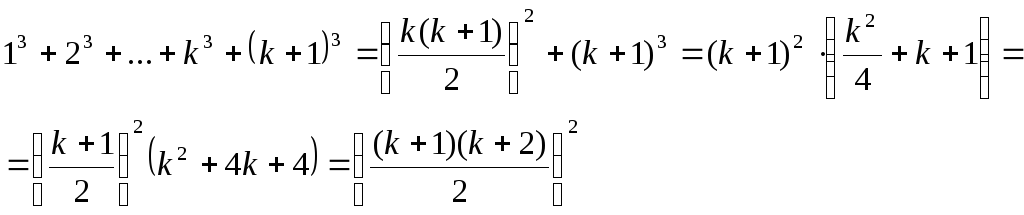
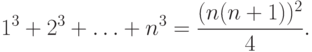
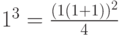 .
.
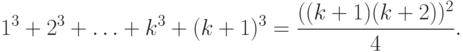
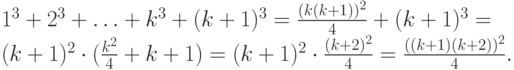
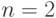 , учитывая, что
, учитывая, что 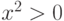 , имеем
, имеем 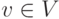 является арифметической формулой глубины 0, т.е.
является арифметической формулой глубины 0, т.е.  и
и 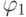 и
и 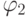 — арифметические формулы глубины
— арифметические формулы глубины 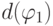 и
и 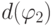 , соответственно. Тогда выражения
, соответственно. Тогда выражения
 .
. . Формула глубины 0 является переменной
. Формула глубины 0 является переменной  . Тогда она имеет одну из четырех форм (а), (б), (в) или (г). Предположим, что
. Тогда она имеет одну из четырех форм (а), (б), (в) или (г). Предположим, что 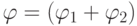 . Тогда из определения глубины следует, что
. Тогда из определения глубины следует, что 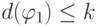 и
и 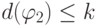 , и по индукционному предположению в обеих формулах
, и по индукционному предположению в обеих формулах  и
и  . Тогда
. Тогда 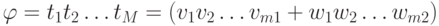 ,
,