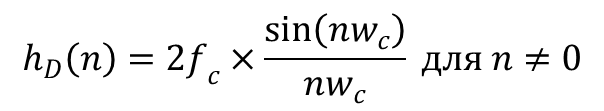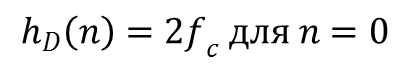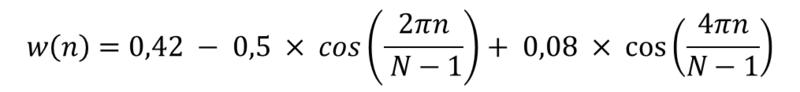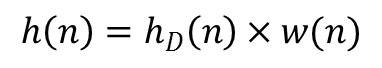-
И мпульсная характеристика и системная
функция цифрового
фильтра
-
Импульсная
характеристика фильтра. Понятие о
нерекурсивных и рекурсивных цифровых
фильтрах
Цифровым
фильтром дискретного
сигнала называется линейная
частотно-избирательная система,
реализуемая на основе вычислительного
устройства.
Пусть
при действии на входе цифрового фильтра
последовательности отсчетов xn
на его выходе действует последовательность
yn (рисунок 3.1).

Рисунок 3.1
Если
n-ый отсчет выходного
сигнала фильтра yn
зависит только от отсчетов входного
сигнала в данный и предшествующие
моменты дискретного времени xn,
xn-1,
..и т.д., то такой фильтр называется
нерекурсивным.
Если
n-ый отсчет выходного
сигнала фильтра yn
зависит не только от отсчетов входного
сигнала в данный и предшествующие
моменты дискретного времени xn,
xn-1
..и т.д., но и от отсчетов выходного сигнала
в предшествующие моменты времени yn-1,
yn-2,
..и т.д., то такой фильтр называется
рекурсивным.
Импульсной
характеристикой цифрового фильтра
называется выходной сигнал фильтра при
действии на его входе единичного отсчета
и при нулевых начальных условиях (рисунок
3.2).
Фильтр
с конечной импульсной характеристикой
называется КИХ — фильтром (КИХ — конечная
импульсная характеристика). Фильтр с
бесконечной импульсной характеристикой
называют БИХ — фильтром.
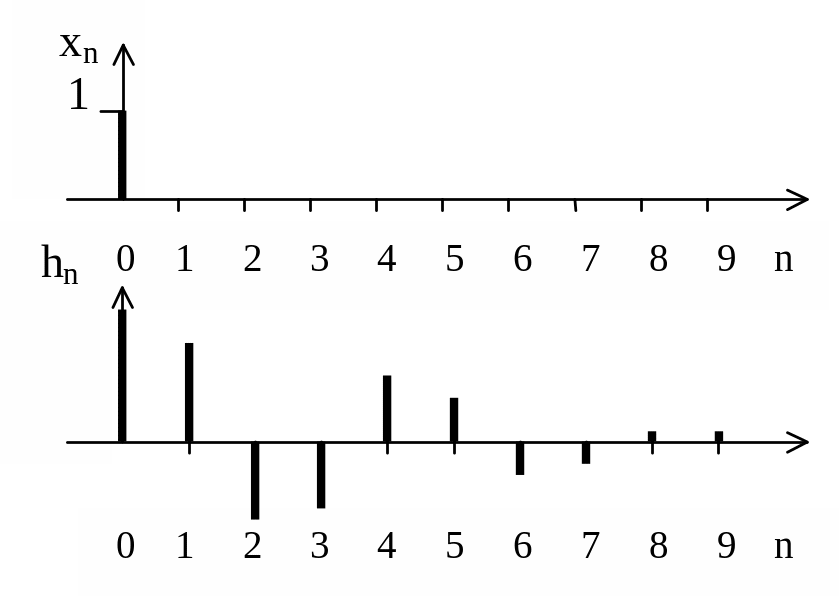
Рисунок
3.2 — Единичный отсчет xn
и импульсная
характеристика hn
3.2.
Определение выходного сигнала фильтра
по
входному сигналу и импульсной
характеристике
Определение
выходного сигнала цифрового фильтра
по входному сигналу и импульсной
характеристике основано на определении
импульсной характеристики и принадлежности
фильтра к линейным системам, для которых
справедлив принцип суперпозиции.
На
рисунке 3.3 приведен пример определения
выходного сигнала фильтра в случае,
когда входной сигнал xn
содержит два отсчета x0
= 2 и x1=
2, а импульсная характеристика 3 отсчета
h0 =
1, h1=0.5,
h2 =
0.25.
Сначала определим реакцию фильтра на
отсчет x0, считая,
что x1=0. Если бы
вместо x0 действовал
единичный отсчет, то выходным сигналом
была бы импульсная характеристика.

Рисунок 3.3 – Определение выходного
сигнала фильтра по входному сигналу и
импульсной характеристике
Так как фильтр линейная система, то при
входном отсчете в x0
раз больше единичного, выходной
сигнал будет представлять собой
импульсную характеристику, все отсчеты
которой умножены на x0,
— x0 hn.
Определим реакцию фильтра на отсчет
сигнала x1 при x0
=0. При x1=1 выходной
сигнал фильтра представлял бы собой
импульсную характеристику, запаздывающую
на один отсчет hn-1.
При отсчете x1,
отличном от единицы, реакцией фильтра
будет запаздывающая на один отсчет
импульсная характеристика, все отсчеты
которой умножены на x1,
— x1 hn-1.
Согласно принципу суперпозиции полученные
реакции суммируются.
В результате
,
,
…..
В общем случае
(3.1)
Согласно последнему соотношению
Однако в рассмотренном примере x2
= 0, поэтому, как видно из рисунка,
В общем случае
В данном примере x2
= x3 = 0, h3
= 0, поэтому
Соотношение 3.1 представляет собой
дискретную свертку последовательностей
xn и
hn,
т.е. выходной сигнал фильтра представляет
собой дискретную свертку входного
сигнала и импульсной характеристики
фильтра.
На рисунке 3.4 дано графическое представление
дискретной свертки при конечной
импульсной характеристике фильтра,
содержащей N+1 отсчет. Из
рисунка видно, что yn
зависит только от отсчетов входного
сигнала xn,
xn-1,
.. xn—N,
следовательно,
данный фильтр является нерекурсивным.
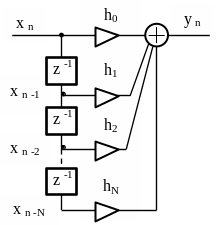
Рисунок 3.4 – Нерекурсивный цифровой
фильтр
Z – преобразование
дискретной свертки (3.1) входного сигнала
xn и
импульсной характеристики hn
равно произведению Z –
преобразований этих последовательностей.
Y(z) = H(z)
X(z),
где
Системной функцией цифрового фильтра
называется отношение Z
– преобразования Y(z)
выходного сигнала фильтра yn
к Z – преобразованию
X(z)
входного сигнала xn.
Из предыдущих соотношений следует, что
системная функция H(z)
представляет собой Z
– преобразование импульсной характеристики
фильтра
(3.2)
Для нерекурсивного фильтра с конечной
импульсной характеристикой имеем
Следовательно, системная функция
нерекурсивного цифрового фильтра
представляет собой полином степени N
комплексной переменной z
-1. Коэффициенты этого полинома
являются отсчетами импульсной
характеристики фильтра.
. В рекурсивном фильтре (рисунок 3.5) n
– ый отсчет выходного сигнала фильтра
yn
связан линейными соотношениями с
отсчетами входного сигнала в данный и
предшествующие моменты дискретного
времени xn,
xn-1,
..xn—N
и отсчетами выходного сигнала в
предшествующие моменты времени yn-1,
yn-2,
.. yn—N.
Соответствующие коэффициенты
пропорциональности B0,
B1, .. BN,
A1, A2,
.. AN
определяют свойства фильтра.
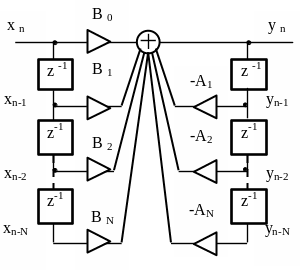
Рисунок
3.5 – Прямая форма программной реализации
рекурсивного фильтра
Согласно схеме
Выразим Z — преобразование
выходного сигнала Y(z)
через Z-преобразование
входного сигнала
Из последнего соотношения получим
Таким образом,
системная функция цифрового фильтра в
общем случае представляет собой
дробно-рациональную функцию. Полином
числителя описывает нерекурсивную
часть фильтра, а полином знаменателя –
рекурсивную.
Нулем системной функции называется
значение комплексной переменной z,
при котором системная функция равна
нулю.
Полюсом системной функции называется
значение комплексной переменной z,
при котором системная функция равна
бесконечности.
Задача №3.1
На входе фильтра действует сигнал
Выходной сигнал фильтра представляет
собой единичный отсчет
Определите системную функцию и импульсную
характеристику фильтра.
Решение задачи №3.1
Для нахождения системной функции
определим Z – преобразования
входного и выходного сигналов
Системная функция определяется
соотношением
Так как коэффициенты системной функции
нерекурсивного фильтра являются
отсчетами его импульсной характеристики,
находим:
Импульсная характеристика фильтра
приведена на рисунке 3.6.
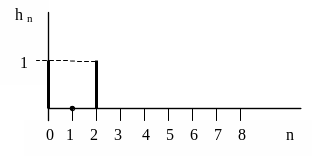
Рисунок 3.6 — Импульсная характеристика
фильтра
Задача №3.2
Определите системную функцию и импульсную
характеристику цифрового фильтра
рисунка 3.7. Определите выходной сигнал
фильтра при действии на входе сигнала
Постройте графики входного сигнала xn,
импульсной характеристики hn,
и выходного сигнала yn.
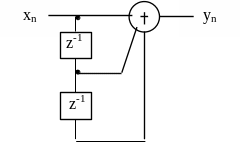
Рисунок 3.7
Решение задачи
№3.2
Из рисунка 3.7 следует, что
Выразим Z – преобразование
выходного сигнала фильтра через Z
– преобразование входного сигнала
Определим системную функцию фильтра
Коэффициенты системной функции
нерекурсивного цифрового фильтра
являются отсчетами его импульсной
характеристики, поэтому
Определим Z – преобразования
входного и выходного сигналов фильтра
Коэффициенты прямого Z –
преобразования выходного сигнала
фильтра являются отсчетами этого
сигнала.
Следовательно,
.
Временные диаграммы импульсной
характеристики, входного и выходного
сигналов приведены на рисунке 3.8.
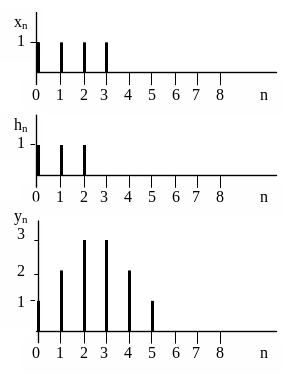
Рисунок 3.8 – Временные диаграммы
импульсной
характеристики, входного и выходного
сигналов
Задача №3.3
Определите системную функцию цифрового
фильтра рисунка 3.9 и найдите полюсы и
нули этой функции при
А = 0.9.
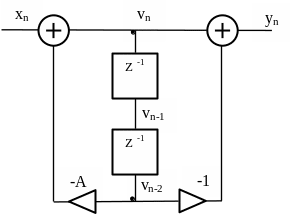
Рисунок 3.9
Решение задачи №3.3
Из схемы следует, что
Данный фильтр является рекурсивным,
так как n -ый отсчет сигнала
на выходе одного из сумматоров vn
зависит не только от отсчета входного
сигнала xn,
но и от задержанного на два интервала
дискретизации отсчета vn-2
этого же сигнала.
Выразим Z – преобразование
выходного сигнала фильтра через Z
– преобразование входного сигнала
Из первого уравнения выразим V(z)
через X(z),
подставим во второе уравнение и получим
Разделив Y(z)
на X(z), найдем
системную функцию
Системная функция H(z)
представляет собой дробно-рациональную
функцию. Знаменатель функции описывает
рекурсивную часть фильтра, а числитель
– нерекурсивную.
Для определения полюсов системной
функции знаменатель приравняем нулю и
найдем корни полученного квадратного
уравнения
Откуда
Для определения нулей системной функции
числитель приравняем нулю
Откуда
Задача №3.4
Определите импульсную характеристику
(с нулевого по третий отсчет) цифрового
фильтра рисунка 3.10 при
A
= — 0.5.

Рисунок 3.10
Решение задачи
№3.4
Учтем, что выходной сигнал фильтра yn
представляет собой импульсную
характеристику hn
при условии, что на входе фильтра
действует единичный отсчет
Заполним таблицу, учитывая, что
и
y-1=
0.
|
n |
xn |
yn = |
yn-1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0.500 |
1 |
|
2 |
0 |
0.250 |
0.500 |
|
3 |
0 |
0.125 |
0.250 |
Задача №3.5
На рисунке 3.11 приведена импульсная
характеристика цифрового фильтра.
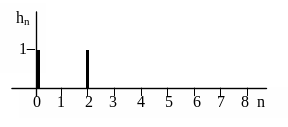
Рисунок 3.11 – Импульсная характеристика
фильтра
На входе фильтра действует сигнал
Определите сигнал на выходе фильтра.
Решение задачи
№3.5
Выходной сигнал фильтра yn
представляет собой дискретную свертку
входного сигнала xn
и импульсной характеристики hn
При n>1
Отсчеты y0 и y1
определяют переходной процесс на выходе
фильтра. В установившемся режиме выходной
сигнал фильтра равен нулю.
Задача №3.6
Определите системную функцию цифрового
фильтра рисунка 3.12.
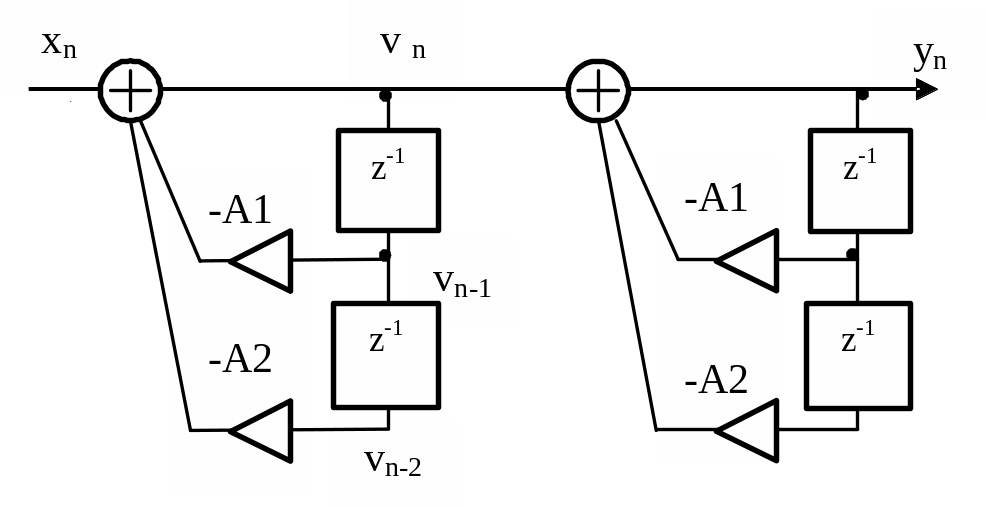
Рисунок 3.12
Решение задачи
№3.6
Согласно определению
где Y(z)
и X(z) — Z
– преобразования сигналов yn
и xn
соответственно.
Преобразуем последнее выражение, умножив
числитель и знаменатель дроби на Z
– преобразование V(z)
сигнала vn
где
— системная функция первого звена
фильтра,
— системная функция второго звена
фильтра.
Из рисунка видно, что звенья фильтра
одинаковы, поэтому H2(z)
= H1(z).
Следовательно,
Для определения системной функции
первого звена запишем выражение для
выходного сигнала фильтра
Воспользовавшись свойствами Z
– преобразования, получим
Обратите внимание на то, что в выражении
для H1(z)
перед коэффициентами A1
и A2 стоит знак «плюс», а
на схеме – «минус».
Системная функция фильтра определяется
соотношением
Задача №3.7
Импульсная характеристика цифрового
фильтра описывается соотношением
где α>0.
Определите системную функцию и приведите
схему фильтра (графическое представление
алгоритма цифровой фильтрации).
Решение задачи №3.7
Системная функция цифрового фильтра
H(z) представляет
собой Z – преобразование
его импульсной характеристики hn
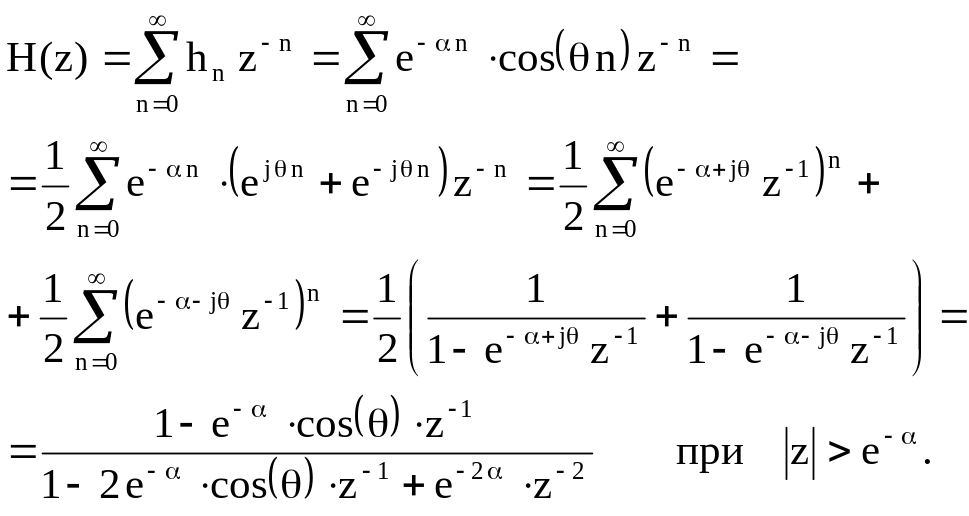
Обозначим
Тогда
Представим H(z)
в виде произведения двух системных
функций:
где
Такое представление системной функции
соответствует последовательному
соединению двух звеньев фильтра:
рекурсивного звена второго порядка с
системной функцией HA(z)
и нерекурсивного звена первого порядка
с системной функцией HB(z)
(рисунок 3.13). Заметим, что если в знаменателе
системной функции перед коэффициентами
A1 и A2 стоит
знак «+», то на схеме ему соответствует
знак «-».
Из рисунка видно, что одна и та же
переменная vn
действует на входе двух элементов
задержки, поэтому один из них можно
исключить и получить каноническую форму
фильтра, приведенную на рисунке 3.14.
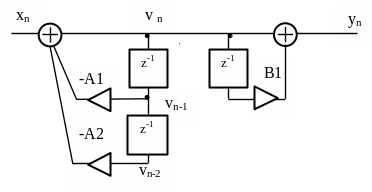
Рисунок 3.13 – Представление цифрового
фильтра
в виде последовательного соединения
двух звеньев
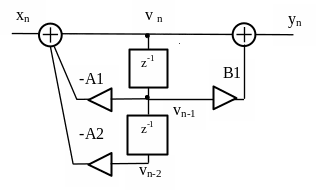
Рисунок 3.14 – Каноническая форма фильтра
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10.06.20155.07 Mб14Методичка_ВТиИТ.rtf
- #
Введение
Цифровой фильтр – фильтр, обрабатывающий цифровой сигнал с целью выделения и (или) подавления определённых частот этого сигнала.
- Разделяют два больших класса цифровых фильтров:
- Фильтры с конечной импульсной характеристикой (КИХ-фильтры, FIR)
- Фильтры с бесконечной импульсной характеристикой (БИХ-фильтры, IIR)
Зачем они нужны? Чем нас не устраивают аналговые фильтры? Давайте рассмотрим преимущества и недостатки цифровых фильтров.
Преимущества цифровых фильтров:
- Высокая точность и воспроизводимость (у аналоговых фильтров это определяется разбросом номиналов компонентов)
- Гибкость (можно изменять характеристику, не затрагивая аппаратную часть)
- Компактность (например, аналоговые ФНЧ могут занимать много места, в то время как цифровые имеют одинаковые габариты при любой форме АЧХ в пределах одной частоты дискретизации)
Недостатки цифвровых фильтров:
- Сложность работы в реальном времени (все вычисления должны пройти менее, чем за один период дискретизации)
- Высокая стоимость
Начнём изучение фильтров с наиболее простого типа — КИХ-фильтров.
КИХ-фильтры
Давайте сразу рассмотрим пример. Сгенерируем в Matlab зашумлённый сигнал частотой 0.5 Гц, оцифрованный с частотй дискретизации 10 Гц. Для начала, объявим переменную fs, которой присвоим значение частоты дискретизации, создадим массив временных отсчётов ts, и переменную N, которой присвоим количество получившихся отсчётов:
fs = 10; ts = 0: 1/fs : 10-1/fs; N = length(ts);
Теперь создадим сам синусоидальный сигнал x с частотой 0.5 Гц, зашумлённый случайным сигналом, амплитуда которого изменяется в диапазоне от a=-0.01 до b=0.1:
a = -0.01; b = 0.1; x = (a + (b - a) * rand(1, N)).*sin(2*pi*0.5*ts);
Построим график сигнала x:
plot(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал x(n)');
И получим результат:
Возьмём первые пять отсчётов с x(1) по x(5), найдём их среднее арифметическое, запишем его в новый массив в элемент y(1), затем возьмём отсчёты с x(2) по x(6), также рассчитаем их среднее значение и запишем его в элемент y(2) и так далее, пока не пройдём по всему сигналу:
y = zeros(1,N+6); for i = 6 : length(x) y(i) = (x(i-1) + x(i-2) + x(i-3) + x(i-4) + x(i-5))/5; end
А теперь построим сигналы x и y друг под другом в одном окне:
subplot(2,1,1);
plot(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал x(n)');
subplot(2,1,2);
plot(y(1:100)), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал y(n)');
Результаты выполнения получившегося скрипта показаны ниже:
И что же мы видим? Сигнал y(n) (на рисунке снизу) похож на сигнал x(n) (сверху), однако имеет некоторую задержку и более гладкую форму. Получается, что мы только что применили к сигналу x(n) фильтр нижних частот (ФНЧ)! Спроектированный нами фильтр называется скользящее среднее. Уравнение данного фильтра имеет вид:
(1)
А его структурная схема выглядит так:
В каждый момент времени берётся текущий отсчёт и 4 предыдущих, каждый из которых домножается на коэффициент 1/5, затем эти результаты складываются и полученная сумма поступает на выход. Процедура повторяется, пока весь сигнал не будет обработан.
Свёртка
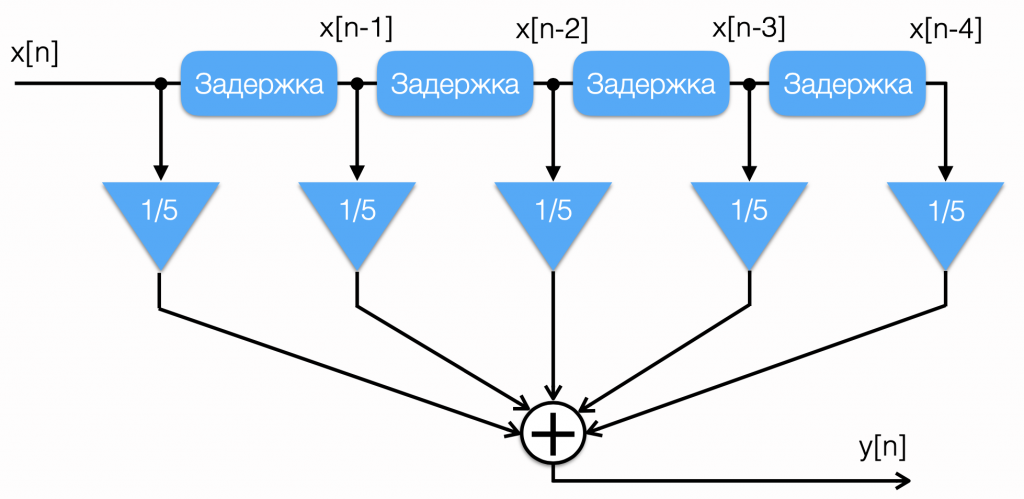
А что, если вместо коэффициентов 1/5 взять что-то другое? На самом деле, уравнение (1) представляет собой частный случай операции свёртки:
(2)
где ,
— длина
,
— длина
Это уравнение и является уравнением КИХ-фильтра. Его структурная схема выглядит так:
Теорема о свёртке
Со свёрткой связана следующая теорема:
Если два сигнала
и
имеют дискретные преобразования Фурье (ДПФ)
и
соответственно, то свёртка этих сигналов во временной области
эквивалентна произведению их спектров в частотной области
(и наоборот):
(3)
И действует это в обе стороны. Получается, что, когда мы делаем свёртку исходного сигнала с коэффициентами фильтра, мы перемножаем амплитудно-частотную характеристику (АЧХ) исходного сигнала и АЧХ фильтра, тем самым убираем ненужные частоты. А это и есть фильтрация.
Мы выше говорили: “фильтры с конечной импульсной характеристикой, фильтры с бесконечной импульсной характеристикой”. А что же такое “импульсная характеристика”? Давайте вспомним на примере фильтров.
Импульсная характеристика КИХ-фильтра
Импульсная характеристика фильтра — это выходная последовательность фильтра во временной области при подаче на вход фильтра дельта-функции, или функции Дирака — единственного отсчёта, равного единице (единичного импульса), которому предшествуют и за которым следуют нулевые отсчёты.
Возьмём предыдущий пример из Matlab и вместо исходного сигнала x подставим в него функцию Дирака:
clear;
fs = 10;
ts = 0: 1/fs : 10-1/fs;
N = length(ts);
x = zeros(N,1);
x(5) = 1;
subplot(2,1,1);
stem(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Функция Дирака');
y = zeros(1,N+6);
for i = 6 : length(x)
y(i) = (x(i-1) + x(i-2) + x(i-3) + x(i-4) + x(i-5))*1/5;
end
subplot(2,1,2);
stem(y(1:100)), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Импульсная характеристика');
Результат выполнения скрипта показан ниже:
Из рисунка видно, что импульсная характеристика фильтра представляет собой 5 отсчётов амплитудой 0.2 (или 1/5). Получается, что мы с вами видим ни что иное, как коэффициенты фильтра. Поэтому коэффициенты КИХ-фильтра также называют его импульсной характеристикой.
Проектирование КИХ-фильтров
Теперь возникает вопрос: как рассчитать коэффициенты, чтобы получить требуемую АЧХ фильтра? Самый простой способ: “рисуем” необходимую АЧХ в частотной области, делаем обратное ДПФ от этой АЧХ и получаем набор коэффициентов во временной области. Наверняка, каждый из вас мечтает увидеть фильтр с идеально прямоугольной АЧХ. Возможно ли такое? Давайте разбираться. Что из себя представляет ДПФ от идеально прямоугольного сигнала? Правильно, функцию , которую мы рассматривали, когда изучали растекание спектра ДПФ:
Данная функция бесконечна во временной области, поэтому для реализации идеально прямоугольной АЧХ нам потребуется бесконечное количество коэффициентов фильтра. Получается, чем больше мы используем коэффициентов h[n], тем больше АЧХ фильтра будет похожа на прямоугольную. Вроде бы логично — возьми побольше коэффициентов, получишь хороший фильтр. Но не всё так просто: в реальности мы не можем увеличивать количество коэффициентов фильтра, т.к. это приведёт к дополнительным операциям перемножения, каждая из которых вызывает задержку. Для того, чтобы система работала в реальном времени, нужно, чтобы все вычисления по формуле (2) производились за время, не превышающее один период дискретизации. Вот и простейшее ограничение.
Давайте попробуем на примере. Создадим сигнал x(n), состоящий из N нулевых отсчётов, затем присвоим первым 200 отсчтётам значение 1. Это будет наша требуемая форма АЧХ:
clear; fs = 1000; % частота дискретизации ts = 0:1/fs:1-1/fs; % массив временных отсчётов N = length(ts); % длина массива временных отсчётов x = zeros(N,1); x(1:200) = 1;
Рассчитаем ОДПФ от сигнала x(n), для удобства сдвинем его с помощью ifftshift, отбросим мнимую часть и присвоим полученный результат сигналу y(n). Далее построим графики сигнала x(n), и, чтобы лучше рассмотреть сигнал у(n), график его 200 центральных отсчётов.
y = real(ifftshift(ifft(x)));
subplot(2,1,1);
plot(x), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('Ожидаемая АЧХ, x(n)');
subplot(2,1,2);
plot(N/2-100:N/2+100-1,y(N/2-100:N/2+100-1)), grid on;
xlabel('Временные отсчёты');
ylabel('Амплитуда');
title('Фрагмент полученной импульсной характеристики, y(n)');
Результат выполнения скрипта показан ниже:
Теперь давайте анализировать реальную АЧХ от спроектированного фильтра. Для этого создадим сигнал a(n), состоящий из N нулевых отсчётов, затем присвоим первому отсчёту 1. Таким образом, получим функцию Дирака, спектр которой является константой на всей частотной оси:
a = zeros(N,1); a(1) = 1;
Теперь попробуем пропустить функцию Дирака через спроектированный ранее фильтр y(n), при этом будем использовать разное количество отсчётов y(n):
figure;
Nf1 = 5;
af1 = filter(y(N/2-Nf1:N/2+Nf1-1),1,a);
subplot(2,2,1);
plot(abs(fft(af1))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=10');
Nf2 = 10;
af2 = filter(y(N/2-Nf2:N/2+Nf2-1),1,a);
subplot(2,2,2);
plot(abs(fft(af2))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=20');
Nf3 = 25;
af3 = filter(y(N/2-Nf3:N/2+Nf3-1),1,a);
subplot(2,2,3);
plot(abs(fft(af3))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=50');
Nf4 = 50;
af4 = filter(y(N/2-Nf4:N/2+Nf4-1),1,a);
subplot(2,2,4);
plot(abs(fft(af4))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=100');
Результат выполнения скрипта показан ниже:
Из графиков видно, что, чем больше мы используем отсчётов нашего фильтра (а количество отсчётов – это порядок цифрового фильтра), тем более его характеристика становится похожа на идеальную. Однако, стоит обратить внимание, что на вершине АЧХ всех наших фильтров видны пульсации независимо от того, сколько используется отсчётов в импульсной характеристике. Эти пульсации называются пульсации Гиббса и возникают из-за медленной сходимости ряда Фурье, которая обусловлена наличием разрыва функции на частоте среза полосы пропускания фильтра. С увеличением числа отсчетов уменьшается длительность выбросов на вершине АЧХ, но их амплитуда не меняется и составляет примерно 9% от амплитуды АЧХ на частоте среза.
Окна при проектировании КИХ-фильтров
Запишем выражение (3) следующим образом:
(4)
где:
Получается, что, когда мы берём какое-то ограниченное количество отсчётов от импульсной характеристики идеального фильтра, мы умножаем эту импульсную характеристику на прямоугольное окно, спектр которого мы рассматривали выше. Эта процедура во временной области эквивалентна свёртке спектра идеальной характеристики и спектра ограниченной импульсной характеристики в частотной области. Ниже приведён листинг, моделирующий выражение (4):
clear;
fs = 100; % частота дискретизации
ts = -20:1/fs:20-1/fs; % временные отсчёты
N = length(ts); % длина массива временных отсчётов
% Идеальный прямоугольный спектр от бесконечного числа отсчётов
Hinf = zeros(N,1);
Hinf(N/2-750:N/2+749) = 1;
% Спектр прямоугольного окна - sinc(x)
W = sinc(ts);
subplot(2,1,1);
plot(Hinf), grid on, hold on;
plot(W);
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра с бесконечной характеристикой Hinf(n) и окна W(n)');
% Свёртка спектров
c = conv(Hinf, W);
subplot(2,1,2);
plot(c), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('Свёртка Hinf(n) и W(n)');
Результат выполнения скрипта показан ниже:
Чтобы уменьшить амплитуду пульсаций, как и в случае с ДПФ, при проектировании КИХ-фильтров используют окна, отличные от прямоугольного. Давайте модифицируем наш листинг “Анализ АЧХ фильтра, часть 4” и добавим в строчках 26, 34, 42, 50 умножение на окно Хэмминга:
... af1 = filter(y(N/2-Nf1:N/2+Nf1-1).*hamming(Nf1*2),1,a); ... af2 = filter(y(N/2-Nf2:N/2+Nf2-1).*hamming(Nf2*2),1,a); ... af3 = filter(y(N/2-Nf3:N/2+Nf3-1).*hamming(Nf3*2),1,a); ... af4 = filter(y(N/2-Nf4:N/2+Nf4-1).*hamming(Nf4*2),1,a); ...
Полученные результаты показаны ниже:
Другое дело! Пульсации ушли, однако АЧХ фильтра стала более “заваленной”. Выбор типа окна зависит от конкретной решаемой задачи. Самые распространённые: параметрическое окно Кайзера, Чебышёва, окно Блэкмана, Хэмминга и др.
БИХ-фильтры
Основное отличие в структуре БИХ-фильтра от КИХ-фильтра — наличие обратной связи. Что такое обратная связь? Это когда на вход устройства подаётся сигнал, пропорциональный сигналу на его выходе. Таким образом, значение выходного сигнала БИХ-фильтра зависит не только от текущего и предыдущего значения входного сигнала, но и от предыдущего значения выходного сигнала. Это одновременно и плюс, и минус: наличие обратной связи позволяет значительно сократить количество отсчётов (а значит, и порядок фильтра, а как следствие – количество умножений), однако может привести к неустойчивости его работы, или вообще превратить фильтр в генератор. Из-за того, что при отсутствии входного сигнала на выходе БИХ-фильтра может генерироваться бесконечное количество отсчётов, его и прозвали фильтром с бесконечной импульсной характеристикой.
Давайте на примере сравним, сколько же потребуется коэффициентов КИХ- и БИХ-фильтра для реализации одинаковой АЧХ. Спроектируем с помощью filterDesigner два ФНЧ со следующими параметрами:
В результате получили два фильтра, АЧХ и ФЧХ которых представлены ниже:
Из рисунка видно, что АЧХ фильтров действительно схожи, однако, для реализации КИХ-фильтра нам потребовалось 222 коэффициента, а для реализации БИХ-фильтра — всего 41. Получается, что в случае с БИХ-фильтром, операций умножения требуется в 5 раза меньше.
Следует также обратить внимание на график фазы. У КИХ-фильтров ФЧХ гарантированно линейная, у БИХ-фильтров она гарантированно нелинейная, о чём нужно помнить.
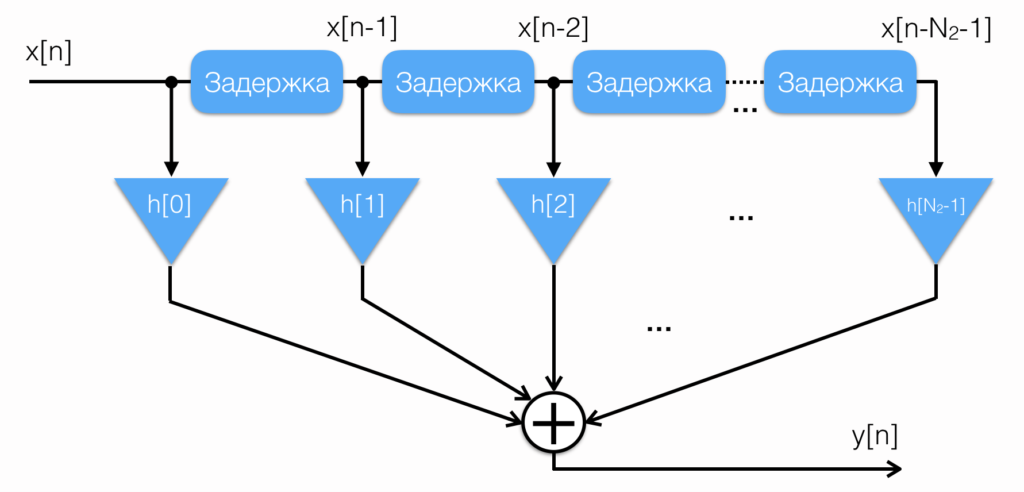
Рассмотрим структуру БИХ-фильтра:
Он состоит из двух частей: прямой и обратной связи. Прямая связь повторяет структурную схему КИХ фильтра, обратная связь напоминает зеркальную копию прямой связи.
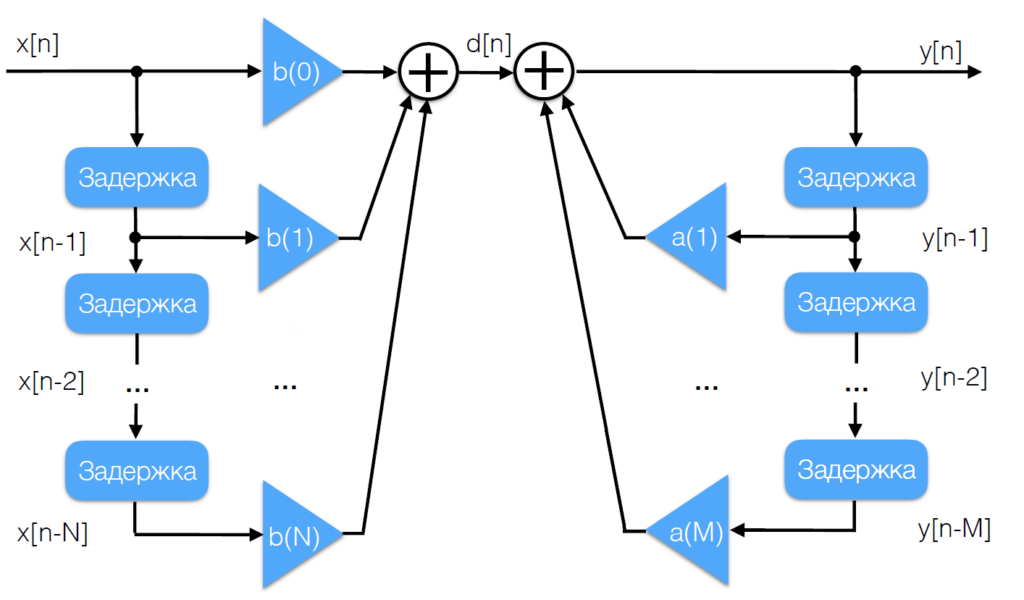
Таким образом, разностное уравнение БИХ-фильтра имеет вид:
(5)
где:
При проектировании БИХ-фильтров используют z-преобразование, корни которого идут от преобразования Лапласа. Второе преобразование вам точно знакомо, его должны были изучать на курсе математического анализа. Давайте вспомним, что это такое, а затем перейдём к изучению z-преобразования. Но это на следующей лекции.
Скачать конспект в pdf: Digital Filters Lecture – V.V. Leonidov.pdf
Основы цифровой обработки сигналов: АЧХ и ФЧХ, Цифровые фильтры, КИХ и БИХ фильтры
Рассмотрены 3 темы по основам цифровой обработки сигналов: АЧХ и ФЧХ, цифровые фильтры, КИХ и БИХ фильтры
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- АЧХ и ФЧХ,
- Цифровые фильтры,
- КИХ и БИХ фильтры.
АЧХ и ФЧХ
В этом видео мы поговорим о таких характеристиках линейных стационарных систем, как амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). В предыдущей публикации мы рассмотрели различные способы описания линейных стационарных дискретных систем. Разностное уравнение показывает, как вычислять значения отсчётов на выходе системы, передаточная функция описывает динамику в зэд области, импульсная характеристика нужна для свёртки с входным сигналом. Но ни одно из рассмотренных описаний не даёт нам понимания, как же именно наша система будет преобразовывать сигнал. А это хотелось бы знать до того, как мы подадим входное воздействие.
Именно поэтому для описания систем используют частотные характеристики. А именно – амплитудно-частотную характеристики (АЧХ) и фазочастотную характеристику (ФЧХ). Как вы уже поняли, это характеристики системы, но для их лучшего понимания мы можем обратиться к характеристикам сигнала.
Давайте для простоты начнём с АЧХ. У сигнала есть амплитудный спектр, то есть зависимость энергии сигнала в зависимости от частоты. А у системы есть АЧХ, говоря простыми словами, зависимость коэффициента усиления от частоты.
В частотной области спектр сигнала должен пройти через АЧХ системы, при этом его спектр исказится, подобно тому, как брусок пластилина изменит своё сечение при прохождении через определённую формочку.
Давайте рассмотрим влияние АЧХ и ФЧХ на отдельные спектральные составляющие сигнала, или синусоиды. Допустим, у нас есть сигнал, состоящий из двух отдельных синусоид. При прохождении через систему с АЧХ представленной формы, синусоида меньшей частоты не изменит своей амплитуды, в то время как синусоида большей частоты станет меньше по уровню, так как этой частоте соответствует коэффициентт усиления меньше единицы. АЧХ системы может усиливать сигнал в одних полосах и подавлять в других.
Фазочастотная характеристика показывает зависимость фазового сдвига от частоты. Подобно тому, как мы можем отразить фазовый спектр сигнала. Но в случае с ФЧХ, к начальной фазе сигнала на конкретной частоте добавится сдвиг, определяемый ФЧХ. Проще говоря, синусоида не только изменит свою амплитуду, но и сдвинется на временной оси.
АЧХ и ФЧХ наглядно демонстрируют нам, как система изменяет проходящий через неё сигнал. Но откуда мы получаем эти характеристики, и связанны ли они с разностным уравнением, или передаточной функцией? На самом деле да, связаны.
Если мы отобразим передаточную функцию на комплексной плоскости в виде трёхмерной поверхности, с учётом нулей и полюсов, и наложим на неё окружность единичного радиуса, то проекция или разворот этой кривой с учётом всех взлётов и падений и есть ни что иное, как форма амплитудно-частотной характеристики системы.
Как вы видите, кривая строится также и в области отрицательных частот. А о способах определения АЧХ системы я рекомендую Вам поискать дополнительную информацию самостоятельно.
Мы же подошли к основному смыслу рассматриваемых систем. Задачи линейных стационарных систем – изменять амплитуду и фазу входных сигналов. И процесс этот называется фильтрацией. К примеру, удаление нежелательной высокочастотной составляющей в сигнале и усиление полезной низкочастотной – типичная задача для линейной стационарной системы. Отныне и в дальнейшем мы будем называть такие системы фильтрами. И в следующих публикациях мы познакомимся с различными типами дискретных фильтров. Пока что нам важно усвоить, что для описания фильтра нам достаточно знать его коэффициенты a и b.
Давайте перейдём в MATLAB и проанализируем фильтр с коэффициентами из прошлой публикации.
Начнем мы с формирования входного воздействия. В нашем случае, это будет ЛЧМ сигнал, то есть так называемый сигнал с линейной частотной модуляцией. Давайте запустим секцию и посмотрим как он выглядит во временной области.
Вы видите, что это сигнал, у которого частота нарастает с ростом времени. Подобный тип сигнала позволит нам достаточно наглядно во временной области посмотреть на работу нашего фильтра.
Теперь давайте посмотрим, как же выглядит амплитудно-частотные и фазо-частотные характеристики при заданных коэффициентах b и a. Для этого мы воспользуемся встроенной функцией freqz. Это функция отображает сразу АЧХ и ФЧХ, также в этой секции мы высчитываем нули и полюса нашей передаточной функции и отображаем их на нуль-полюсной диаграмме. Из форм АЧХ мы сразу можем понять, что данный фильтр представляет собой фильтр нижних частот, то есть он пропускает частоты меньше 2 кГц, а начиная с 2 кГц он начинает постепенно подавлять, и высокочастотные компоненты будут уже гораздо меньше по уровню нежели низкочастотные. Нуль-полюсная диаграмма конечно не настолько наглядно показывает нам, что же будет происходить с сигналом при прохождении через наш фильтр.
В следующей секции мы будем строить трёхмерный вид передаточной функции на комплексной плоскости. Все длинные формулы вычисления я убрал в функцию helperfunk2, мы также будем прилагать её в описании к этому видео. Так что если хотите проанализировать ее, можете это сделать, но сейчас я на это время тратить не буду. Я просто запущу эту секцию, и мы посмотрим на вид нашей передаточной функции на комплексной плоскости.
Я специально отразил здесь 2 версии этой проекции, то есть в данном случае у нас здесь просто показаны 2 явных полюса и 1 ноль.
Если приблизить передаточную функцию, то мы явно увидим нашу кривую, которая при развороте даёт нам уже форму нашей АЧХ.
Если мы посмотрим на вид этого разворота, конкретно в области положительных частот, то он по форме очень напоминает то, что выдавала нам функция freqz. То есть здесь мы также наблюдаем АЧХ фильтра нижних частот.
Пришло время отфильтровать наш сигнал. Для этого мы воспользуемся встроенной функцией filter, которой мы просто передаём наши наборы коэффициентов фильтра и входное воздействие х. Затем мы отобразим отфильтрованный сигнал на одном графике с исходным. Давайте запустим эту секцию.
И как мы видим в момент времени t=1 сек, когда частота нашего сигнала доходит до 4 кГц, его амплитуда становится минимальной. Ну и завершении этого скрипта давайте попробуем вычислить выход нашего фильтра при помощи свертки. Для этого сперва мы вычисляем нашу импульсную характеристику фильтра при помощи встроенной функций impz, а затем при помощи функции conv определяем выход нашего фильтра.
В данном случае я накладываю выход функции filter и выход функции conv друг на друга. Как видите, они точно совпадают.
Наверх
Цифровые фильтры
В этой публикации мы начинаем знакомиться с цифровыми фильтрами. В прошлых публикациях мы познакомились с описанием линейных стационарных дискретных систем, в данном и последующих видео мы будем знакомиться с применением подобных систем для задач цифровой обработки сигналов и фильтрации, в частности.
Для начала давайте вспомним, что делает фильтр в соответствии с задачами цифровой обработки. Например, он может пропускать сигналы в определённой полосе частот, и подавлять в других полосах. Он может быть частью эквалайзера, усиливая или подавляя сигнал в выбранной полосе. Помимо этого, фильтры могут быть использованы для изменения фазы сигнала, дифференцирования, изменения частоты дискретизации, но об этом мы пока не говорим. А сосредоточимся мы именно на свойствах частотной избирательности цифровых фильтров.
Давайте вспомним знакомый нам пример фильтра из предыдущих публикаций – скользящее среднее. Только в этот раз мы представим осредняющие коэффициенты как импульсную характеристику нашей линейной дискретной системы. Как ведёт себя подобный фильтр с точки зрения частотной избирательности? Давайте разберёмся в MATLAB.
В данном скрипте мы будем осуществлять осреднение входного сигнала, но теперь – через операцию свёртки сигнала с импульсной характеристикой линейной дискретной системы. Длина импульсной характеристики h может варьироваться через переменную num. Создаём сумму двух синусоид, медленной, которую мы считаем полезным сигналом, и быстрой, большей частоты и меньшей амплитуды, которая будет зашумлять первую. Сумму s мы затем сворачиваем с вектором h. Запускаем секцию скрипта и наблюдаем эффект осреднения входного сигнала.
Если импульсную характеристику сделать длиннее, то сигнал осредняется ещё сильнее, и задержка выхода относительно входа также увеличивается.
Но что здесь происходит с точки зрения частотной избирательности? Быстро меняющаяся синусоида подавляется, так как близко расположенные отсчёты входного сигнала приравниваются к среднему значению попавших в окно осреднения. Медленно изменяющийся сигнал при подобной операции искажается меньше, а это значит, что относительно плавно изменяющаяся первая синусоида на выходе подобного фильтра будет иметь большую амплитуду. С точки зрения частотной избирательности, подобная система пропускает сигналы меньшей частоты, и подавляет сигналы большей частоты.
Давайте убедимся в этом, оценив АЧХ фильтра. Воспользуемся функцией freqz. Как мы видим по форме АЧХ, это действительно фильтр нижних частот. В данной публикации мы рассмотрим параметры частотно-избирательных цифровых фильтров, и очертим основные этапы проектитования фильтров. И тут нужно сделать одно пояснение. Несмотря на то, что в предыдущих публикациях я говорил, что линейные дискретные системы мы можем смело называть фильтром, и часто в инженерных кругах так и делают, между ними всё же есть различие. Формально, линейной дискретной системой мы называем математическое описание, а фильтром – устройство. Фильтры строятся на основе описания линейной дискретной системы, но, помимо этого, также определяются способом их реализации – архитектурой, квантованием, платформой – например, цифровой фильтр может быть реализован программно, в виде кода, или аппаратно, как цифровая схема.
Давайте попробуем очертить основные параметры цифровых фильтров. Во-первых, сюда относятся параметры линейной дискретной системы, такие как передаточная функция или разностное уравнение, то есть по сути – коэффициенты фильтра. Тесно связанные с коэффициентами АЧХ и ФЧХ определяют функцию фильтра, например, тип его частотной избирательности, и об этом мы подробно поговорим в этом видео.
Импульсная характеристика также относится к параметрам линейной системы, но мы чаще говорим о классификации фильтров в зависимости от их импульсной характеристик. Мы различаем фильтры с конечной импульсной хар-кой – КИХ фильтры, и фильтры с бесконечной импульсной характеристикой – БИХ фильтры. О разнице между ними я расскажу с следующей публикации.
Помимо этого, у фильтров есть дополнительные характеристики, вытекающие из вышеперечисленных – например, переходная функция, групповая и фазовые задержки, нуль-полюсная диаграмма и прочие.
Фильтры могу различаться по своей архитектуре, а она тесно связана с реализацией устройства в железе. Также, большинство реальных фильтров работают в целочисленной арифметике, и при их реализации надо обязательно учитывать эффекты квантования.
Цифровые фильтры могут быть классифицированы по перечисленным характеристикам.
Давайте рассмотрим классификацию фильтров по их частотной избирательности, то есть по АЧХ. С точки зрения своей функции частотно-избирательной цепи, фильтры могут разделяться на множество типов. Рассмотрим основные, наиболее распространённые типы.
Во-первых, это фильтры нижних и верхних частот. Как вы понимаете из названия, фильтр нижних частот пропускает низкие частоты, до определённой частоты среза, и подавляет высокие частоты. Фильтр верхних частот исполняет обратную функцию.
Также существуют полосно-пропускающие и полосно-заграждающие фильтры. Первые пропускают сигнал только в определённой полосе частот, вторые могут подавлять сигнал в определённой полосе частот, и пропускать во всех остальных.
Ну и частным случаем полосовых фильтров могут считаться резонансные фильтры, пропускающие или подавляющие сигнал только на одной конкретной частоте.
Требования к частотной избирательности фильтра в зависимости от накладываемой на него задачи можно записать в виде спецификации к его частотным характеристикам.
Давайте познакомимся со спецификацией на примере фильтра нижних частот. У АЧХ подобного фильтра можно выделить три основные полосы, а именно – полосу пропускания, полосу перехода, и полосу заграждения.
Полоса пропускания фильтра, или passband, – это тот диапазон частот, в котором в идеале находится наш полезный сигнал. Его мы хотим пропустить по возможности без искажений. Границей полосы пропускания для ФНЧ является частота Fp, или Fpass. Она отсчитывается по уровню минус три децибела от максимума.
Усиление сигнала в полосе пропускания, опять-таки в идеале, должно быть постоянным. Но на практике зачастую присутствуют определённые нестабильности усиления, или пульсации. Уровень допустимых пульсаций в полосе пропускания определяется параметром Apass, и измеряется в децибелах.
Полоса заграждения, или stopband, – это тот диапазон частот, в котором сигнал должен гарантированно ослабляться не менее чем на Ast децибел. Начинается полоса заграждения с частоты Fst.
А между этими полосами находится переходная полоса, или transition band, усиление в этой полосе плавно спадает. Кстати, чем более резкий переход у фильтра от полосы пропускания к полосе заграждения, то есть чем уже полоса перехода, тем больший порядок должен иметь фильтр. А порядок – это количество коэффициентов фильтра, и оно связано с количеством умножителей, необходимых для реализации.
Так что фильтры с крутыми спадами обычно более сложные и дорогие, поэтому перед проектировщиком всегда стоит задача поиска компромисса между соответствием формы частотной характеристики некой идеальной, и стоимостью реализации устройства.
Давайте также рассмотрим этапы проектирования того самого устройства – цифрового фильтра. Начинаем мы с определения спецификации фильтра, исходя из его задачи. Затем нам надо понять, хотим мы использовать для этого КИХ или БИХ фильтр. Как и говорил, о разнице между ними – в следующей публикации. Затем нам необходимо на основе спецификации и типа фильтра подсчитать коэффициенты, то есть те значения, на которые мы будем умножать отсчёты входного и, возможно, выходного сигналов.
Процесс, который является ключевым здесь – переход от спецификации к коэффициентам! Сложная в прошлом вычислительная задача в современном мире решается очень просто – при помощи MATLAB. Большинство инженеров занимаются расчётом коэффициентов фильтров именно в MATLAB с использованием средств Signal Processing Toolbox.
Давайте пройдём путь до подсчёта коэффициентов по заданной спецификации в livescript, пока что не затрагивая реализацию. Для начала импортируем и прослушаем аудиофайл, который будет нашим входным сигналом.
Затем перейдём к спецификации.
Я хочу попробовать создать полосно-заграждающий фильтр, который слегка подавит так называемую середину. Полоса заграждения будет лежать в пределах от 1000 до 4000 Гц. Подавление в полосе будет всего лишь 10 дБ, а уровень допустимых пульсаций в полосах пропускания составит 1 дБ. Для аудио-фильтра это весьма много, но для нашего примера это не так критично.
Затем мы формируем объект спецификации d. Для этого мы передаём функции fdesign тип отклика – bandstop, и все наши значения параметров.
Затем на основе объекта спецификации мы уже будем счиать коэффициенты, которые будут храниться в объекте фильтра Hd . Подсчитываем мы их командой design. Ей мы передаём объект спецификации и тип фильтра. У нас это КИХ фильтр типа equiripple.
На основе подсчитанных коэффициентов MATLAB вычисляет характеристики фильтра и мы можем их посмотреть в программе Filtel Visualization Tool.
Здесь мы сразу наглядно оцениваем АЧХ фильтра и соответствие её спецификации. Маска спецификации отрисовывается красными пунктирными линиями. Так же нам доступны выизуализации фазочастотной характеристики, групповой и фазовой задержек, импульсной и переходной характеристик, нуль-полюсная диаграмма, значения коэффициентов и сводная информация, включающая также стоимость реализации фильтра.
Если мы отразим значения коэффициентов числителя передаточной функции фильтра на графике, то мы можем заметить, что это – импульсная характеристика.
Для КИХ-фильтров это всегда так, но подробнее об этом мы поговорим в следующей публикации.
А сейчас нам осталось только применить фильтр к входному аудиофайлу и прослушать результат. Ну а если вам интересно посмотреть на спектр сигнала до и после фильтрации – попробуйте сделать это самостоятельно, команды вы знаете. Просто добавьте их в livescript.
Наверх
КИХ и БИХ фильтры
В данной публикации мы поговорим о КИХ и БИХ фильтрах, о разнице между ними и мотивациях применения. Начнём с КИХ-фильтров. По определению, КИХ – это фильтр с конечной импульсной характеристикой. По английский это произносится как FIR Filter, от final impulse response. КИХ фильтры – нерекурсивные, а это значит, что для вычисления значения на выходе фильтра используются только текущее и задержанные значения входа. В разностном уравнении есть только коэффициенты при x. Передаточная функция в знаменателе имеет константу, часто единицу. А схема фильтра не имеет обратных связей.
Если вы вспомните схему для подсчёта дискретной свёртки из предыдущих публикаций, то она очень похожа на представленную схему КИХ-фильтра. Вектор входных отсчётов формируется при помощи линий задержки, или регистров, перемножение отсчётов сигнала на отсчёты импульсной характеристики осуществляется в умножителях, а сумматоры потом объединяют всё в отсчёт выходного сигнала. Отсчёты импульсной характеристики КИХ-фильтра – это и есть вектор коэффициентов b. То есть мы указываем импульсную характеристику явно, и она по понятным причинам конечна.
Теперь поговорим о преимуществах и недостатках применения КИХ-фильтров.
Начнём с преимуществ:
- они могут обладать линейной фазой, и это очень важно, так как задача компенсации фазового набега заметно упрощается;
- они всегда устойчивы, то есть даже при очень большом уровне входного сигнала при его выключении через некоторое время сигнал на выходе гарантированно затухнет. Это прямое следствие того, что схемы КИХ-фильтров не содержат обратных связей
- ну и фактически имея достаточный порядок фильтра, мы можем сформировать произвольный частотный или фазовый отклик
Основной существенный недостаток КИХ-фильтров:
- Они до роже в реализации, чем БИХ-фильтры со схожей АЧХ.
Мы говорим, что КИХ-фильтры обычно бывают больших порядков, а порядок фильтра влияет на количество ресурсов, требуемых для его реализации. О каких ресурсах мы говорим? Когда мы рассматриваем аппаратную реализацию, то есть цифровую схему, то речь идёт о базовых блоках для построения фильтров – умножителях, сумматорах и регистрах, или линиях задержки. Иногда там ещё используются мультиплексоры.
Кратко расскажу об одном из методов синтеза КИХ-фильтров, наиболее наглядном. Под синтезом мы понимаем процесс получения коэффициентов. И так как коэффициенты КИХ-фильтра – это его импульсная характеристика, то мы можем нарисовать идеальную форму АЧХ, (к примеру, здесь мы идём от идеальной АЧХ фильтра нижних частот) и при помощи обратного быстрого преобразования Фурье получить соответствующую ей идеальную импульсную характеристику. Она получится бесконечная.
Затем эту импульсную характеристику мы перемножаем с оконной функцией конечной длительности, то есть формируем конечную импульсную характеристику. При ограничении количества отсчётов, форма АЧХ отклоняется от идеальной, появляются пульсации и переходные полосы. Вспоминаем эффект Гиббса. А вообще методы синтеза фильтров – это отдельная наука, в рамках данного курса мы её не охватим.
А в рамках этой публикации мы познакомимся с БИХ-фильтрами, фильтрами с бесконечной импульсной характеристикой. По-английски они называются IIR (Infinite impulse response). Кстати, БИХ-фильтры могут быть как аналоговые, так и цифровые. КИХ-фильтры могут быть только цифровыми.
БИХ фильтры – рекурсивные, для вычисления значения на выходе фильтра используются как значения входа, так и задержанные значения выхода. Передаточная функция представляется в стандартном дробно-рационально виде, а схема фильтра содержит обратные связи.
Из преимуществ БИХ-фильтров можно отметить:
- относительную простоту реализации по сравнению с КИХ-фильтрами (мы убедимся в этом на примере),
- относительную простоту синтеза на основе аналоговых прототипов.
В качестве недостатков:
- могут быть неустойчивыми. Если коэффициент в цепи обратной связи будет больше единицы, может образоваться положительная обратная связь, фильтр может завестись, и сигнал на его выходе может продолжаться и усиливаться даже после выключения входного воздействия,
- они не могут обладать линейной фазой,
- мы не можем сформировать произвольную АЧХ и ФЧХ, по сути, мы выбираем АЧХ из типов, основывающихся на аналоговых прототипах, чаще всего это стандартные фильтры нижних и верхних частот, полосовые и так далее. Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.
Синтезируются БИХ-фильтры при помощи преобразования непрерывной передаточной характеристики аналогового прототипа в дискретную характеристику цифрового фильтра. В детали билинейного преобразования тоже не лезем.
А поговорим мы про автоматизацию задания спецификации и синтеза самых разнообразных фильтров в MATLAB. Конкретно – про интерактивное приложение Filter Designer App, ранее называлось FDA Tool. Это приложение в составе Signal Processing Toolbox для анализа, синтеза, квантования фильтров, создания многоскоростных систем, импорта и экспорта коэффициентов и многого другого. Инженеры по всему миру не один десяток лет используют именно это приложение для быстрого проектирования цифровых фильтров, очень его любят и уважают, вполне заслуженно.
Давайте воспользуемся им для фильтрации зашумлённого музыкального файла. Во-первых, загрузим аудиоданные. Я это сделаю, просто кликнув дважды по mp3-файлу. Именя переменных оставляем по-умолчанию. Ну и сразу прослушаем аудио. Мы слышим Дебюсси с наложенными на него ударными из другой композиции.
Посмотрим на этот сигнал в Signal Analyzer. Выберем наш вектор, отобразим его во временной области, укажем частоту дискретизации, чтобы наблюдать сигнал в реальных секундах и герцах. И отобразим спектр.
Курсор поможет нам понять, где проходит граница полезного сигнала и помехи. Граница расположена в районе 2.2 кГц. Свернём Signal Analyzer и откроем инструмент Filter Designer. Попробуем разработать в нём подходящий цифровой фильтр.
Выбираем тип отклика мы оставляем lowpass, то есть фильтр нижних частот. Пока что попробуем реализовать его в виде КИХ-фильтра equiripple. Указываем частоту дискретизации, границу полосы пропускания и начало полосы заграждения. На переходную полосу мы оставляем всего лишь 200 Герц, это достаточно крутой спад. Пульсации для аудио-фильтра мы зададим не более 0.1 децибела, а подавление оставим на уровне 80. Нажимаем кнопку Design Filter.
И наблюдаем АЧХ. Форма вполне соответствует спецификации, фазочастотная характеристика линейна в полосе пропускания, групповая и фазовая задержки – константы, тут же можем оценить форму импульсной характеристики и переходной функции,
Но на вкладке информации мы можем увидеть, что фильтр требует очень много ресурсов, более семи сотен умножителей, сумматоров и регистров.
Проверим, будет ли БИХ-фильтр экономичнее. Выберем самый экономичный вариант, эллиптический БИХ-фильтр, наблюдаем форму его АЧХ, и в информации видим, что ресурсов подобный фильтр требует в тридцать раз меньше! Это серьёзная разница.
Но за неё придётся поплатиться нелинейностью фазы, а также зависящими от частоты групповой и фазовой задержками. Но наш БИХ-фильтр устойчив, все его полюса находятся внутри окружности единичного радиуса на нуль-полюсной диаграмме.
И в информации о структуре фильтра мы видим надпись Second Order Sections. Покажем структуру в центре документации.
Секции второго порядка – это каскадный способ построения БИХ-фильтров из меньших фильтров второго порядка. Оставим всё как есть, убедимся, что форма АЧХ нас устраивает, а фаза для задачи фильтрации аудио не так критична.
И теперь мы экспортируем вычисленные коэффициенты фильтра в рабочее пространство MATLAB в виде так называемой sos матрицы и вектора усилений для каждого каскада. Каждая секция содержит шесть коэффициентов, они объединяются в матрицу размером n на 6. При желании мы можем преобразовать такую форму преставления в привычные нам коэффициенты передаточной функции. Воспользуемся функцией sos2tf и получим общую дробь для всего фильтра. Теперь отфильтруем входной сигнал data, и оценим результат в Signal Analyzer. Добавим вектор y, укажем ему частоту дискретизации, чтобы на временной оси его можно было отрисовать.
Видим явное уменьшение амплитуды на всём промежутке, и на спектре после 2,2 кГц мы наблюдаем серьёзное подавление. Проверим, удалось ли нам освободить Дебюсси. Прослушаем выход фильтра командой sound. В целом, получилось неплохо.
Построение цифрового фильтра с конечной импульсной характеристикой
Время на прочтение
3 мин
Количество просмотров 121K
Вступление издалека
Недавно передо мной встала достаточно интересная задача, с которой я раньше никогда не сталкивался — борьба с шумом. Мы принимали сигнал с датчиков на аналогово-цифровой преобразователь (АЦП)
А так как данная тема для меня была (хотя и сейчас есть кое-где) темным лесом, я пошел мучить вопросами гугл, мне показалось освещена эта тема не очень подробно и доступно, поэтому решил написать статью с примером разработки и готовым исходником.
Ближе к делу
Цифровые фильтры могут быть двух видов – с конечной и с бесконечной импульсной характеристикой (КИХ и БИХ). Для решения моей задачи подходит КИХ-фильтр, поэтому про него и расскажу.
Для начала посмотрим как же он работает:
Здесь показан пример фильтра нижних частот, как видно на рисунке, этот фильтр пропускает нижние частоты, а все остальные старается отсечь (подавление), или хотя бы ослабить (переход). Отклонения в полосе пропускания и полосе подавления выбираются в зависимости от принимаемого сигнала, но при использовании различных весовых функций, на них могут накладываться определенные ограничения. Например, если используется весовая функция Хэмминга, то эти отклонения будут равны между собой.
Ширина полосы перехода ∆F зависит от длины фильтра и от весовой функции (для функции Блэкмена ∆F=5,5|N).
Работает фильтр довольно просто: фильтр получает значения, с помощью коэффициентов преобразует их и выдаёт выходную последовательность, тогда с формулой самого фильтра всё понятно:
Она реализуется через цикл, но постойте, а где же взять нужные коэффициенты? Вот тут-то как раз и зарыта собака (и не одна).
Параметры фильтра
Естественно для разных фильтров нужны разные коэффициенты, и для этого нужно определиться с параметрами фильтра, это обычно сначала делается теоретически (с умным видом прикидываем какая у нашего сигнала частота, потом частоты, которые надо отсеивать), а потом изучаем АЧХ реальных измерений (и осознаем, как сильно мы ошибались).
По этим АЧХ мы определяемся с идеальной частотной характеристикой (какие частоты проходят свободно, какие мы убираем и как сильно), теперь нам нужна идеальная импульсная характеристика её можно посчитать как Фурье-образ от идеальной частотной:
где H_D(w) – идеальная характеристика.
Но можно пойти и по более простому пути – есть уже заранее вычисленные идеальные импульсные характеристики, например для фильтра нижних частот формула выглядит следующим образом:
где fc и wc – частота среза.
Итак, осталось уже немного идеал идеалом, а мы имеем дело с практикой, и нам нужна «реальная» импульсная характеристика. Для её расчета нам понадобится весовая функция w(n), их есть несколько разновидностей, в зависимости от требований к фильтру (Хэмминга, Хеннинга, Блэкмена, Кайзера, о них не говорю, ибо статья и так большая), в нашем случае я использую функцию Блэкмена:
где N – длина фильтра, т.е. количество коэффициентов.
Теперь надо перемножить идеальную импульсную характеристику и весовую функцию:
Финишная прямая
Теперь мы готовы рассчитать выходные значения, по формуле фильтра, она самая первая в этой статье, ну вот и всё, в завершение привожу исходный код фильтра:
void Filter (const double in[], double out[], int sizeIn)
{
const int N = 20; //Длина фильтра
long double Fd = 2000; //Частота дискретизации входных данных
long double Fs = 20; //Частота полосы пропускания
long double Fx = 50; //Частота полосы затухания
long double H [N] = {0}; //Импульсная характеристика фильтра
long double H_id [N] = {0}; //Идеальная импульсная характеристика
long double W [N] = {0}; //Весовая функция
//Расчет импульсной характеристики фильтра
double Fc = (Fs + Fx) / (2 * Fd);
for (int i=0;i<N;i++)
{
if (i==0) H_id[i] = 2*M_PI*Fc;
else H_id[i] = sinl(2*M_PI*Fc*i )/(M_PI*i);
// весовая функция Блекмена
W [i] = 0.42 - 0.5 * cosl((2*M_PI*i) /( N-1)) + 0.08 * cosl((4*M_PI*i) /( N-1));
H [i] = H_id[i] * W[i];
}
//Нормировка импульсной характеристики
double SUM=0;
for (int i=0; i<N; i++) SUM +=H[i];
for (int i=0; i<N; i++) H[i]/=SUM; //сумма коэффициентов равна 1
//Фильтрация входных данных
for (int i=0; i<sizeIn; i++)
{
out[i]=0.;
for (int j=0; j<N-1; j++)// та самая формула фильтра
if(i-j>=0)
out[i]+= H[j]*in[i-j];
}
}При подготовке статьи использовались:
Основные характеристики и параметры фильтров. analogiu.ru/6/6-5-2.html
Айфичер Э. Джервис Б. Цифровая обработка сигналов. Практический подход. 2-е издание
В предыдущей статье рассмотрели оптимальный прием сигналов и ансамбль сигнала. В этой статье поговорим о согласованном фильтре, его свойствах и АЧХ и ФЧХ характеристиках.
Согласованный фильтр
Согласованный фильтр — линейный оптимальный фильтр, позволяющий получить максимальное отношение сигнал/шум на выходе фильтра для сигналов известной формы.
Линейный фильтр вносит линейные искажения. Если на нелинейное устройство подать моногармонический сигнал (обычную синусоиду) с одной частотой, то на выходе устройства, посмотрев на спектр, увидим новые спектральные составляющие, гармоники. У линейного устройства новые спектральные составляющие не появляются. На выходе любого линейного устройства, те же самые спектральные составляющие, что и на его входе, без добавления новых гармоник, у этих устройств изменяются только амплитуда и фаза.
Оптимальный фильтр, оптимальный это значит, что он достигает какого-то наилучшего качества. Если мы говорим про оптимальность, то мы должны говорить и про критерий оптимальности, т.е. что у нас достигается наилучшим способом. В данном случае критерием оптимальности является отношение сигнал/шум.
Для каждого сигнала существует свой согласованный фильтр. Сигнал на выходе любого линейного фильтра, в том числе и согласованного, определяется выражением:
Свойства согласованного фильтра
Для любого линейного фильтра сигнал на выходе определяется через свертку сигнала на входе и его импульсной характеристики.
Импульсная характеристика фильтра это реакция фильтра (т.е. то что мы получим на выходе фильтра), на дельта импульс.
Если на вход фильтра подадим дельта импульс, то на выходе получим отклик, этот отклик и есть импульсная характеристика.
Дельта импульс это математическая абстракция, это импульс, который имеет бесконечно большую амплитуду, бесконечно малую длительность и площадь этого импульса равна единице. На практике, такой дельта импульс можно заменить коротким импульсом. Спектр дельта импульса равномерен и бесконечен.
Импульсная характеристика согласованного фильтра
Импульсная характеристика СФ имеет отзеркаленную форму сигнала, для которого фильтр согласован:
- где Ts – длительность сигнала;
- s – сигнал;
- k – константа, сигнал можно умножать на любую константу.
- В формуле t со знаком минус, сигнал отзеркалили по времени.
Не важно какую амплитуду имеет сигнал, если по форме сигнал повторяет импульсную характеристику, то фильтр будет согласован для этого сигнала. На картинке ниже представлено два примера. Есть треугольный сигнал, осциллограмма в виде треугольного импульса.
Какой фильтр будет для него согласован? Тот который имеет импульсную характеристику повторяющую форму сигнала, но отзеркаленную.
Другой пример, выше, затухающая синусоида сигнала. Чтобы спроектировать согласованный фильтр для такого сигнала, нужно взять форму сигнала и отзеркалить ее и получится импульсная характеристика.
Если у сигнала меняется амплитуда, становится больше или меньше, импульсная характеристика не меняется, фильтр всё равно будет согласован.
Частотные характеристики согласованного фильтра
Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала.
- где H(f) – частотная передаточная характеристика фильтра;
- S(f) – Фурье-образ сигнала;
- T – длительность сигнала;
- k – константа.
Комплексная экспонента е^-i2πTf говорит о сдвиге фаз, возникшем в результате задержки сигнала в фильтре на время T. Откуда взялась комплексная экспонента? Любой фильтр вносит задержку, а комплексная экспонента поворачивает фазу сигнала.
Эта функция H(f) комплексная, у нее есть мнимая и реальная части. Формула с точностью до постоянного множителя (константы) повторяет Фурье-образ сигнала S(f). Единственное, нужно взять Фурье-образ и сделать над ним комплексное сопряжение. Фурье-образ сигнала это результат преобразования Фурье. Это комплексный спектр сигнала.
Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала с точностью до какого-то постоянного коэффициента. Импульсная характеристика повторяет форму сигнала, частотная характеристика повторяет спектр сигнала, только комплексно сопряжена.
Комплексное сопряжение. Если есть комплексное число в котором есть реальная и мнимая часть, то комплексное число сопряженное, это число у которого меняется знак мнимой части. c=a+jb и c=a-jb.
АЧХ и ФЧХ согласованного фильтра
Из передаточной характеристики H(f) получаем АЧХ и ФЧХ. Чтобы получить АЧХ нужно у этой функции взять модуль. АЧХ согласованного фильтра с точностью до постоянного коэффициента k повторяет амплитудный спектр сигнала:
ФЧХ согласованного фильтра повторяет фазовый спектр сигнала с обратным знаком и с учетом задержки:
где ψs(f) — фазовый спектр сигнала.
На картинке выше есть амплитудный и фазовый спектр. Чтобы получить согласованный фильтр, нужно взять фильтр, который имеет АЧХ повторяющий амплитудный спектр сигнала и ФЧХ повторяющий фазовый спектр сигнала, но с обратным знаком. Наклон, который появился на графике “ФЧХ согласованного фильтра” появился из-за задержки сигнала.
Отклик согласованного фильтра
Предположим, есть сигнал, который имеет прямоугольную форму, для него спроектирован согласованный фильтр, который будет иметь импульсную характеристику в виде прямоугольного импульса.
Если на вход согласованного фильтра подать прямоугольный импульс, то на выходе получится сигнал, который определяется через свёртку.
Отклик СФ на сигнал определяется свёрткой импульсной характеристики h(t) и сигналом s(t).
Свёртка это перемножение двух функций в различный момент сдвига друг относительно друга и затем функции нужно их проинтегрировать.
На картинке, зафиксировали положение импульсов. Есть один импульс s(t) на входе и вторая импульсная характеристика согласованного фильтра h(t). В конкретный момент времени нужно вычислить площадь, которая образуется пересечением и эта площадь — значение сигнала на выходе в какой-то конкретный момент времени. И нужно постепенно смещать этот импульс и снова вычислять площадь и так далее. В итоге получим функцию, это и есть свертка.
Сигнал проходя через согласованный фильтр не сохраняет свою форму.
С точки зрения приема сигнала важна не его форма, а значение сигнала. В следующей статье расскажем про приемники.


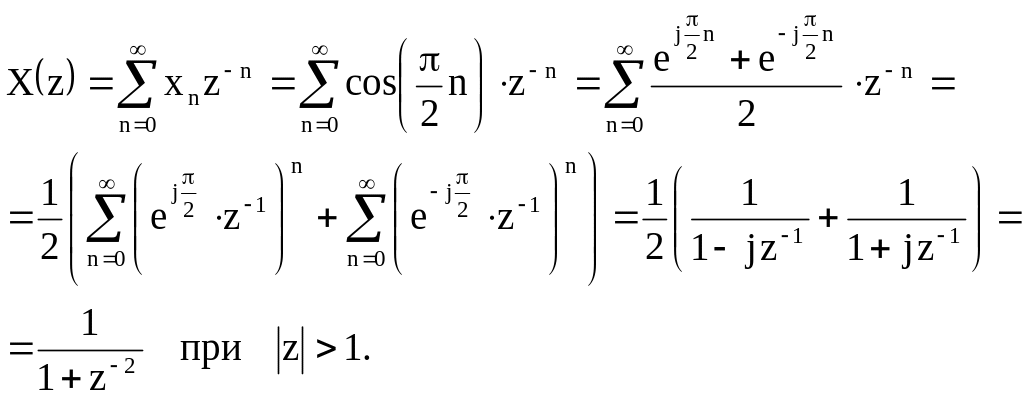
![Rendered by QuickLaTeX.com begin{equation*} y[n]=sumlimits_{k=0}^{M-1} h(k) cdot x(n-k) text{, где} sumlimits_{k=0}^M h(k) = 1 end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-b1bdff669d80da2fe4508b625186fae0_l3.png)
![Rendered by QuickLaTeX.com begin{equation*} y[n] = x[n] ast h[n]=sumlimits_{k=0}^{M-1} h(k) cdot x(n-k), end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-c92c6e0ed841a43340c6de002b1b1e2a_l3.png)
![Rendered by QuickLaTeX.com begin{equation*} y[n] = sumlimits_{i=0}^{N} b(i) cdot x(n-i) - sumlimits_{k=1}^{M} a(k) cdot y(n-k), end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-8be774d473e364fbb980013abfee0d2b_l3.png)