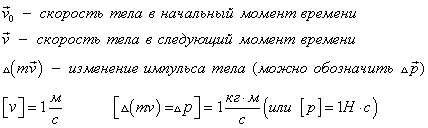I. Механика
Тестирование онлайн
Импульс тела
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Импульс это векторная величина, которая определяется по формуле
Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.
Направление вектора импульса всегда совпадает с направлением вектора скорости.
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Импульс силы
Это векторная величина, которая определяется по формуле
Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела
Вывод второго закона Ньютона в общем виде
График F(t). Переменная сила
Импульс в физике
Любое тело, обладающее скоростью, обладает импульсом.
Тело всегда движется туда, куда направлен вектор его скорости.
Импульс тела – это вектор. Он сонаправлен с вектором скорости тела.
Покоящееся тело импульса не имеет — если тело не движется, его импульс равен нулю.
Физики различают два вектора – импульс тела и импульс силы.
Импульса тела, формула
Возьмем вектор ( vec{v} ) скорости тела (рис. 1), умножим его на ( m ) массу тела (масса — скаляр), получим новый вектор, обозначим его ( p ). Длина этого вектора отличается от длины скорости, а направление – совпадает.
Подробнее о умножении вектора на число написано тут.
Рис. 1. Вектор скорости тела умножаем на скаляр — массу тела, получаем вектор импульса тела
[ large boxed{ vec{v} cdot m = vec{p} }]
( vec{v} left( frac{ text{м}}{с} right) ) – скорость тела, вектор
( m left( text{кг} right) ) – масса тела, скаляр (просто число)
( vec{p} left( text{кг} cdot frac{ text{м}}{c} right) ) – импульс тела, вектор, он сонаправлен со скоростью тела
Если тело не движется, оно импульсом не обладает ( vec{p} = 0 ).
Импульс силы, формула
На тело может действовать сила, например, когда тело соударяется с каким-то другим телом. Тела взаимодействуют с помощью сил. Что такое сила, написано тут.
Действие происходит не мгновенно, а в течение какого-то промежутка времени.
Возьмем вектор ( vec{F} ) силы, действующей на тело (рис. 2), умножим его на ( Delta t ) кусочек времени, в течение которого сила действовала (время — скаляр), получим новый вектор. Для этого вектора не придумали специального обозначения.
Рис. 2. Вектор силы, действующей на тело, умножаем на скаляр – промежуток времени, в течение которого сила действовала, получаем вектор импульса силы
[ large boxed{overrightarrow {F cdot Delta t }}]
( vec{F} left( H right) ) – сила, действующая на тело, вектор
( Delta t left( c right) ) – время воздействия силы (просто число). Можно пояснить так:
Пусть сила действовала несколько секунд. Тогда ( Delta t = t — t_{0} ) – разница между двумя положениями секундной стрелки на часах.
- ( t left( c right) ) – конечное положение стрелки,
- ( t_{0} left( c right) ) – начальное положение стрелки.
Длины векторов силы и импульса силы отличаются, а направления – совпадают.
Если сила не действует ( vec{F} = 0 ), то вектор импульса силы отсутствует ( vec{F} cdot Delta t = 0 ).
Импульс тела и импульс силы связаны. В этой статье подробно описана связь между этими векторами.
Оценка статьи:
Загрузка…
Импульс силы
Импульс силы — это изменение импульса (количества движения) тела.
Импульс силы обусловлен ускорением (изменением скорости) или воздействием силы.
Если
| Δp | изменение импульса тела (Импульс силы), | Ньютон·секунда |
|---|---|---|
| m | масса тела, | кг |
| Δu | изменение скорости тела, | метр/секунда |
| F | постоянная сила, ускоряющая тело, | Ньютон |
| Δt | продолжительность действия силы, | секунд |
то
[ vector{F} = mvector{a} = m frac{ Δvector{u} }{Δt} ]
[ Δvector{p} = mvector{u} = vector{F}Δt ]
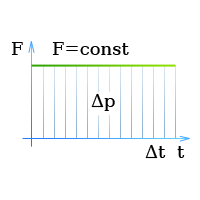
Произведение FΔt и называется импульсом силы.
Импульс силы — сила постоянна во времени
Единица СИ импульса силы:
[
[FΔt] = text{Ньютон} cdot text{сек} = text{кг} cdot text{м/сек}
]
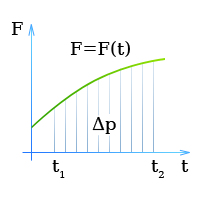
Если сила меняется со временем, т.е.
Импульс силы — сила меняется со временем
[ vector{F} = vector{F}(t) ]
то
Импульс силы — равен интегралу от силы по времени.
[ Δvector{p} = mvector{u} = int_{t_1}^{t_2} vector{F}dt ]
Из [5] вытекает следующее определение силы:
[ dvector{p} = vector{F} dt ]
откуда
[ vector{F} = frac{ dvector{p} }{ dt } ]
Мгновенное значение силы равно первой производной импульса тела по времени.
Импульс силы |
стр. 475 |
|---|
История открытия
Слово «импульс» в переводе с латинского означает «толчок». В некоторых книгах вместо этого термина используется термин «количество движения». Это понятие ввели в науку тогда же, когда Исаак Ньютон открыл и сформулировал законы, которые позже были названы в его честь.
Впервые слово «импульс» использовал учёный Рене Декарт в начале XVII века. Тогда в физике ещё не применялось понятие массы. Декарт определил эту математическую величину как произведение скорости тела и его «величины». В дальнейшем Ньютон уточнил формулировку Декарта. Согласно его определению, импульс (или количество движения) пропорционален величине скорости и массы движущегося тела.
Определение и свойства
Импульсом силы в физике принято называть величину, равную произведению этой силы на время. Фактически она представляет собой следующую закономерность F∆t = ∆P (формула импульса силы). Отсюда можно вычислить, в чём измеряется импульс силы — эти единицы называются ньютон-секундами. С помощью этого произведения можно описать следующие физические явления:
- Полёт выпущенной из лука стрелы. Чем дольше она взаимодействует с тетивой лука, тем больше изменяется её движение и тем выше конечная скорость полёта.
- Две точки или два шарика, сталкивающиеся друг с другом (упругий удар). Согласно третьему закону Ньютона, эти тела при ударе имеют равные модули силы. Следовательно, модули импульса тоже должны быть равными. При этом масса шариков может быть неодинаковой.
В релятивистской физике соотношение кинетической энергии и количества движения электрона характеризуется выражением p = (T2 + 2Tmc2)½/c.
Силы одинаковой величины, которые действуют на протяжении одинакового отрезка времени, вызывают одинаковые импульсы силы. Причём этот показатель не зависит от массы тела.
Для показателя изменения справедливо и обратное утверждение. Сумма сил, которые действуют на тело, равна отношению импульса силы ко времени.
В переводе с латинского слово «импульс» означает «толчок». Этот термин в некоторых источниках заменён на «количество движения».
Импульс силы направлен в ту же сторону, что и вектор скорости движения.
Импульс тела
Согласно современному определению, импульсом тела принято называть физическую величину, которая равняется произведению массы и скорости: P = mV, где P и V являются векторными величинами.
Направление вектора этого параметра сонаправлено с вектором скорости. Общепринятой единицей измерения в системе СИ принято считать 1 кг*м/с. Такие характеристики имеет тело массой в 1 кг, движущееся в пространстве со скоростью 1 м/с.
Этот показатель используется в физике для описания механического движения материальной точки. В быту люди оценивают движение тела через его скорость. Чем больше скорость, с которой перемещается тело в пространстве, тем больше его «количество движения». Если тело встречает на своём пути преграду, их взаимодействие зависит не только от скорости, но и от массы.
Например, по дороге с одинаковой скоростью движется мотоцикл и грузовик с кузовом, полным камня. При столкновении с забором или другой преградой разрушения от грузовика будут гораздо больше, чем от мотоцикла. Отсюда видно, что одной скорости недостаточно для характеристики движения, поэтому используется понятие «импульс тела».
Взаимодействие в замкнутой системе
Если два физических тела взаимодействуют между собой, одно из них может частично или полностью передавать другому свой импульс. Если при этом на объекты не действуют дополнительные факторы, такую систему принято называть замкнутой.
При таких условиях векторная сумма импульсов всех объектов системы будет сохраняться. При этом она не зависит от характера и количества взаимодействий между участниками системы. Это правило получило название закона сохранения импульса, формула которого выглядит как p1 +p2 = p1′ +p2′. Оно выведено из второго и третьего законов Ньютона.
В качестве примера можно взять 2 произвольных взаимодействующих объекта, на которые не действуют никакие внешние факторы:
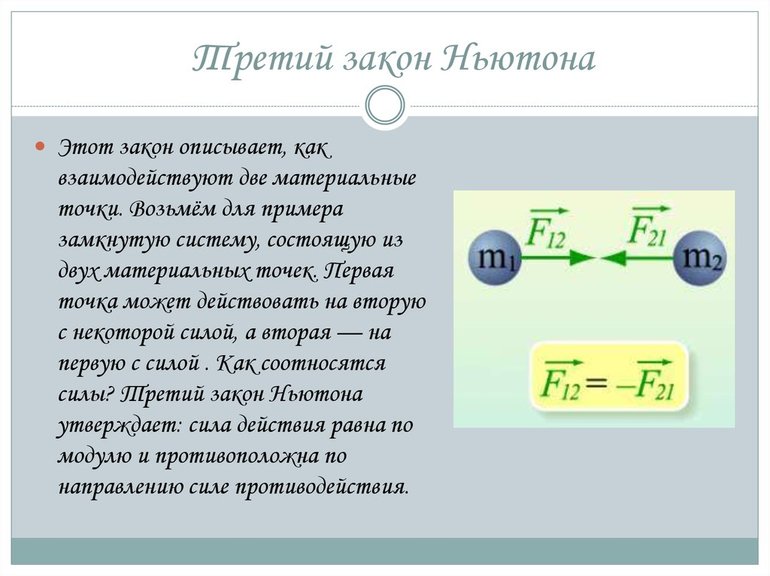
- Силы взаимодействия тел обозначаются как F1 и F2.
- Согласно 3-му закону Ньютона, F2 = — F1.
- Если объекты взаимодействуют в течение момента времени t, то параметры их сил имеют одинаковые модули, но их векторы направлены в противоположные стороны: F2t = — F1t.
- Если применить к этой системе второй закон Ньютона, станет видно, что при взаимодействии этих тел их суммарный импульс останется неизменным.
Таким образом, при парном взаимодействии тел в замкнутой системе внутренние силы не меняют векторную сумму всех импульсов, входящих в неё. С помощью этого правила можно находить скорости объектов в закрытой системе, даже если неизвестны показатели действующих сил. В качестве примера можно рассмотреть реактивное движение:
- Во время выстрела из артиллерийского орудия возникает эффект отдачи — снаряд движется в одном направлении, а пушка откатывается в противоположную.
- В этом случае пушка и снаряд — это два объекта одной системы.
- Скорость пушки зависит от соотношения массы её и ядра и от скорости снаряда.
- Скорости пушки и снаряда можно обозначить как V и v, а массу как M и m.
- Формулу в этом случае можно записать как уравнение MV + mv =0.
Если тело или частица сохраняет неподвижность, количество движения равняется нулю. Напротив, любая движущаяся точка обладает показателем, отличным от 0. Количество движения тела изменяется пропорционально его скорости.
Закон сохранения может оказаться справедливым и для незамкнутой системы. Это возможно, если сила или время внешнего воздействия стремится к нулю. В этом случае внешними показателями можно пренебречь.
Принцип решения задач
Приведённый закон часто используется для решения физических задач. Общая схема их решения выглядит следующим образом:
- Записываются имеющиеся условия.
- Делается схематическое изображение. Обязательно указываются векторы скоростей.
- На рисунке определяется координатная ось для проецирования.
- Формула закона записывается в векторной форме.
- Далее те же показатели отражаются в проекции на оси.
- Проводятся вычисления и записывается ответ.
Выведение законов Ньютона
Известно, что импульс силы равняется изменению импульса тела:
Ft = mv—mv0, тогда Ft = m (v—v0). Отсюда следует, что F = m (v—v0)/t.
Отношение изменения скорости ко времени — это показатель ускорения. Таким образом, сила зависит от ускорения. Если записать уравнение как a = (v—v0)/t, можно вывести формулу второго закона: F = ma.
Можно сформулировать закон и по-другому: сила, которая была приложена к физическому объекту, равняется отношению изменения величины импульса к отрезку времени, за который он изменился.
Третий закон Ньютона выводится исходя из закона сохранения импульса. Для нахождения используются векторные показатели скоростей, то есть скорость может иметь различное направление.
Время в закрытой системе для двух взаимодействующих объектов является величиной одинаковой. Исходя из этого, формулировка третьего закона звучит следующим образом: два объекта взаимодействуют, при этом имеют одинаковую величину силы, но противоположные по направленности векторы, которые идут по направлению к друг другу. Отсюда следует, что модульные значения этих сил равнозначны.
Применение этих законов затруднительно при оценке кратковременного взаимодействия объектов (удара). В этом случае удобнее использовать для расчётов закономерности сохранения силы и количества движения.
Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.
Векторную величину Ft, равную произведению силы на время ее действия, называют импульсом силы. Векторную величину р=mv, равную произведению массы тела на его скорость, называют импульсом тела.
Формула для нахождения импульса тела вытекает из всем извесного Второго закона Ньютона
А ускорение найдем через разность скоростей на время.
Отсюда и получается, что импульс силы
Из импульса силы вытекает закон сохранения импульса
Так же есть:
Импульс тела
В Формуле мы использовали :
— Импульс силы
— Масса тела
— Сила приложенная к телу
— Время действия силы
— Конечная скорость тела
— Начальная скорость тела