Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.2k
Инженеры-взрывотехники проводят испытание новых видов взрывчатки в открытом снизу толстостенном цилиндрическом «колоколе» массой M и радиусом R, стоящем на земле. Внутри колокола на его оси на высоте h от поверхности земли взрывается заряд массой m. Заряд разрывается на множество мелких осколков, разлетающихся с одинаковыми скоростями равномерно во все стороны. Считая, что все осколки либо уходят в землю, либо застревают в стенках колокола, что масса колокола много больше массы осколков, и что все осколки долетают до колокола практически одновременно, найти высоту, на которую он подпрыгнет над землей. Суммарная кинетическая энергия осколков E.
Спрятать решение
Решение.
Поскольку осколки застревают в колоколе, они передают ему свой импульс. А так как суммарный импульс осколков равен нулю, то если бы колокол окружал заряд со всех сторон, то после взрыва он бы не двигался. Поэтому движение колокола связано с тем, что часть осколков попадают в землю и не передают колоколу свой импульс. По закону сохранения импульса импульс осколков попадающих в колокол, равен импульсу осколков, попадающих в землю. Найдем последний.
В землю попадут все осколки, которые движутся после взрыва в конусе, опирающемся на основание колокола, с вершиной в точке взрыва (см. рисунок). Пусть при взрыве образовалось N осколков (по условию число N много больше единицы N − 1 ). Поскольку суммарная энергия осколков E, то скорость каждого осколка можно найти из соотношения
— масса каждого осколка, v — его скорость). Но т. к.
(m — масса всего заряда), то скорости всех осколков равны
Рассмотрим теперь осколки, движущиеся внутри бесконечно узкого конуса с углом раствора расположенного под углом
к вертикали (см. рисунок). Количество осколков, которые движутся внутри этого конуса
так относится к полному числу осколков N, как относится площадь основания этого конуca
к площади сферы, радиус которой равен высоте конуса
Импульс этих осколков можно найти как
Суммарный импульс этих осколков направлен вертикально вниз и равен сумме вертикальных проекций импульсов осколков, попадающих в землю. Поэтому импульс осколков, попавших в землю равен
Но величина равна проекции площади основания рассматриваемого конуса на поверхность земли. Поэтому
Отсюда находим суммарный импульс осколков, ушедших в землю
Такой же импульс (на направленный вверх) получит колокол, и, следовательно, по закону сохранения импульса его скорость сразу после взрыва заряда будет равна
(здесь мы пренебрегли массой осколков, застрявших в колоколе). Высоту подъема колокола теперь можно найти по закону сохранения энергии
Ответ:
Спрятать критерии
Критерии проверки:
Классификатор: Механика. Баллистическое движение
Добавил:
Вуз:
Предмет:
Файл:
Скачиваний:
4
Добавлен:
11.09.2022
Размер:
254.98 Кб
Скачать

Закон сохранения импульса
Цель работы: Проверка закона сохранения импульса. Изучение движения осколков разорвавшегося тела. Определение начального импульса разорвавшегося тела.
1. Теоретическое содержание
Импульс тела – это векторная физическая величина, численно равная произведению массы тела на его скорость. Направление вектора импульса тела совпадает с направлением вектора его скорости.
Согласно закону сохранения импульса суммарный импульс замкнутой системы тел сохраняется, то есть остается постоянным при любых взаимодействиях тел внутри системы. Числовое значение и направление суммарного импульса замкнутой системы всегда одинаковы в любые моменты времени.
Система тел считается замкнутой, если на нее не действуют внешние силы или действие этих сил скомпенсировано.
В данной работе рассматривается тело массой m0 , движущееся
|
равномерно и прямолинейно в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
горизонтальном направлении |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
v1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
со |
скоростью |
v0 . Следова- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
m1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
тельно, внешние силы отсут- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ствуют или их действие m0 |
0 |
α1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
v |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
скомпенсировано. В некото- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
рый |
момент |
времени |
тело |
α2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
распадается (разрывается) на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
два осколка массами m1 и m2 . |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Каждый осколок также дви- |
m2 |
v |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
жется равномерно и прямоли- |
Рис. 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
нейно со скоростями vr1 |
и v 2 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
направленными под углами α1 и α2 |
к направлению движения первона- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
чального тела, соответственно (рис. 1). |
3

До разрыва замкнутая система состояла из одного тела массой m0 и обладала импульсом p0 = m0v0 . После разрыва система состоит из
|
двух тел: осколка массой m1 |
с импульсом p1 = m1v1 и осколка массой |
|
m2 с импульсом p2 = m2v 2 . |
Согласно закону сохранения импульсы |
системы до разрыва и после разрыва должны быть одинаковы. То есть векторная сумма импульсов осколков p1 и p2 должна быть равна им-
пульсу первоначального тела p0 . Тогда для данной системы тел закон
сохранения импульса имеет вид:
p0 = p1 + p2
или
|
r |
m0v0 = m1v1 + m2v 2 . |
|
Импульсы осколков p1 |
и p2 складываются |
по правилу треугольников. Суммарный импульс осколков pr можно определить из теоремы коси-
|
нусов (рис. 2): |
||||
|
p 2 = p 2 |
+ p 2 |
− 2 p p |
2 |
cos β . |
|
1 |
2 |
1 |
||
|
В треугольнике |
β =180 −α1 −α2 ; |
cos(180 −α1 −α2 ) = −cos(α1 +α2 ) .
Тогда теорема косинусов примет вид:
|
p 2 = p 2 |
+ p 2 |
+ 2 p p |
2 |
cos(α |
1 |
+α |
2 |
) , |
Рис. 2 |
|
1 |
2 |
1 |
а числовое значение суммарного импульса p осколков равна
p = 
В данной работе необходимо убедиться, что закон сохранения импульса выполняется: суммарный импульс осколков p равен импуль-
су p0 первоначального тела при любом движении осколков. Суммарная масса осколков m1 и m2 равна массе первоначального
тела m0 = m1 + m2 . Каждый осколок представляет собой часть первона-
чального тела. Относительная масса первого осколка k1 = m1 ; относи- m0
тельная масса второго осколка k2 = m2 =1 − k1. m0
Чтобы вычислить суммарный импульс p осколков, необходимо знать массы осколков m1 = k1m0 и m2 =(1 − k1 )m0 , скорости осколков
4

v1 и v 2 , а также углы α1 и α2 между направлением движения первоначального тела и направлениями движения осколков.
2.Модель экспериментальной установки
Вданной работе с помощью средств компьютерной графики моделируется процесс равномерного прямолинейного движения тела. Тело движется на фоне транспортира вдоль его горизонтального диаметра. Когда тело достигает центра транспортира, оно разрывается на два осколка. Осколки тоже движутся равномерно и прямолинейно от центра к краю транспортира. По краю транспортира установлены «ловушки». Радиус транспортира 10 м. Транспортир используется для определения углов между направлением движения первоначального тела и направле-
ниями движения осколков. Точность измерения углов составляет 1°. Для определения времени движения осколков используются секундомеры, способные измерять время с точностью до 1 микросекунды. При указанных условиях погрешность определения суммарного импульса осколков в эксперименте не превышает 3-7%.
Работа выполняется на IBM-совместимом персональном компьютере в виде самостоятельного Windows-приложения. Для удобства выполнения работы в программе предусмотрены три раздела: кратное описание работы; порядок выполнения работы и эксперимент. Переключение между разделами осуществляется с помощью кнопок «Ход работы» и «Эксперимент». Нажатие этих кнопок в зависимости от контекста работы программы приводит либо к вызову соответствующих разделов, либо к возвращению в раздел описания. Раздел программы «Эксперимент» содержит панель инструментов с кнопками для выбора первоначального тела, бегунок прокрутки для регулирования относительной массы первого осколка и два секундомера для измерения времени движения осколков.
|
Варианты выполнения работы |
||||||||
|
Вариант |
Тело |
Вариант |
Тело |
Вариант |
Тело |
|||
|
1 |
Тело A |
5 |
Тело E |
8 |
Тело H |
|||
|
2 |
Тело B |
6 |
Тело F |
9 |
Тело I |
|||
|
3 |
Тело C |
7 |
Тело G |
10 |
Тело J |
|||
|
4 |
Тело D |
5
Соседние файлы в папке МодМ-03
- #
- #
- #
11.09.2022110 б0ModM-03_02.jpg.uid-zps
- #
- #
- #
- #
11.09.202236.86 Кб0МодМ-03 (1).xls
- #
11.09.202230.72 Кб0МодМ-03.xls
Импульс тела. Закон сохранения импульса
1. Опыты и наблюдения свидетельствуют о том, что результат действия силы (взаимодействия) зависит от времени её действия. Так, если к штативу на нити подвесить
тяжёлую гирю, к которой привязана ещё одна нить снизу, и резко дернуть нижнюю нить, то она оборвётся, а верхняя нить останется целой. Если же теперь медленно потянуть
нижнюю нить, то оборвётся верхняя нить. Поэтому для характеристики действия силы вводят величину, называемую импульсом силы.
Импульсом силы называют векторную величину, равную произведению силы и времени её действия ( (vec{F}t) ). Импульс силы является мерой действия силы за некоторый промежуток времени.
Единица импульса силы ( [,Fcdot t,] ) = 1 Н · с.
2. С другой стороны, результат действия силы зависит и от характеристик тела, на которое эта сила действует.
Зависимость результата действия силы от массы тела можно проиллюстрировать с помощью следующего простого примера. Летящий с некоторой скоростью футбольный мяч, ударяясь о пустую картонную коробку, сдвинет её с места, а, ударяясь о такую же коробку, заполненную металлическими предметами, скорее всего, отскочит от неё, а коробка при этом останется неподвижной.
Пуля, летящая со скоростью 2 м/с, при попадании в деревянную стенку в лучшем случае оставит на ней вмятину, а пуля, летящая со скоростью 200 м/с, стенку пробьёт. Таким образом, результат действия силы зависит от массы и скорости взаимодействующих тел.
3. Величину, равную произведению массы тела и его скорости, называют импульсом тела, ( vec{p}=mvec{v} ) — импульс тела (или просто импульс). Единица импульса ( [,p,] ) = 1 кг · м/с2.
Импульс — величина векторная, поскольку масса — величина скалярная, а скорость — векторная.
Импульс — величина относительная, его значение зависит от выбора системы отсчёта, поскольку относительной величиной является скорость.
4. Импульс силы и изменение импульса тела связаны между собой.
Запишем второй закон Ньютона: ( vec{F}=mvec{a} ).
Подставим в формулу выражение для ускорения ( vec{a}=frac{vec{v}-vec{v}_0}{t} ), ( vec{F}=frac{m(vec{v}-vec{v}_0)}{t} ) или ( vec{F}t=mvec{v}-mvec{v}_0 ).
В левой части равенства стоит импульс силы; в правой части — разность конечного и начального импульсов тела, т.е. изменение импульса тела. ( vec{F}t=Delta(mvec{v}) ).
Таким образом, импульс силы равен изменению импульса тела.
Это иная формулировка второго закона Ньютона. Именно в таком виде сформулировал свой закон Ньютон.
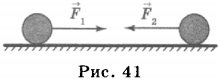
5. Взаимодействующие между собой тела образуют систему тел. Между телами системы действуют силы взаимодействия: на одно тело — сила ( vec{F}_1 ), на другое тело — сила ( vec{F}_2 ). При этом сила равна силе и направлена противоположно ей: ( vec{F}_1=-vec{F}_2 ) (рис. 41).
Силы, с которыми тела системы взаимодействуют между собой, называют внутренними силами.
Помимо внутренних сил, на тела системы действуют внешние силы. Так взаимодействующие тела притягиваются к Земле. Сила тяготения является в данном случае внешней силой. Если тела движутся, то на них действует сила сопротивления воздуха, сила трения. Они тоже являются внешними силами по отношению к системе, которая в данном случае состоит из двух тел. Ни Земля, ни воздух в эту систему тел не входят.
Внешними силами называются силы, которые действуют на тела системы со стороны других тел.
Будем рассматривать такую систему тел, на которую не действуют внешние силы.
Замкнутой системой тел называют систему тел, взаимодействующих между собой и не взаимодействующих с другими телами. В замкнутой системе действуют только внутренние силы, внешние силы на неё не действуют.
6. Рассмотрим взаимодействие двух тел, составляющих замкнутую систему. Масса первого тела ( m_1 ), его скорость до взаимодействия ( vec{v}_{01} ), после взаимодействия ( vec{v}_{1} ). Масса второго тела ( m_1 ), его скорость до взаимодействия ( vec{v}_{02} ), после взаимодействия ( vec{v}_{2} ). Для этих тел справедливо равенство:
[ m_1vec{v}_{01}+m_1vec{v}_{02}=m_1vec{v}_{1}+m_1vec{v}_{2} ]
В левой части равенства стоит сумма импульсов тел до взаимодействия, в правой части — сумма импульсов тел после взаимодействия. Как видно, импульс каждого тела при взаимодействии изменился, а сумма импульсов осталась неизменной.
Геометрическая сумма импульсов тел, входящих в замкнутую систему, остаётся постоянной при любых взаимодействиях тел этой системы между собой.
В этом состоит закон сохранения импульса.
7. Замкнутая система — это идеализация. В реальном мире нет таких систем, на которые не действовали бы внешние силы. Однако в ряде случаев реальные системы взаимодействующих тел можно рассматривать как замкнутые. Это возможно, когда внутренние силы много больше внешних сил, или когда время взаимодействия мало, или когда внешние силы уравновешивают друг друга. Кроме того, в ряде случаев равна нулю проекция внешних сил на какое-либо направление. В этом случае закон сохранения импульса выполняется для проекций импульсов взаимодействующих тел на это направление.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Тело двигалось под действием силы 10 Н в течение 5 с. Чему равно изменение импульса тела?
1) 2 Н/с
2) 5 Н·с
3) 50 Н·с
4) нельзя дать ответ, т.к. неизвестны масса и скорость тела
2. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся в ту же сторону с той же скоростью?
1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с
3. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся с той же скоростью, но в противоположную сторону?
1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с
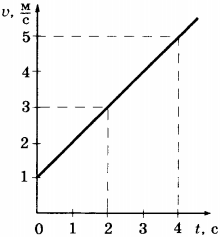
4. На графике показаны изменения скорости велосипедиста с течением времени. Чему равно изменение импульса велосипедиста через 4 с после начала движения, если его масса 50 кг?
1) 200 кг·м/с
2) 2500 кг·м/с
3) 2000 кг·м/с
4) 2500 кг·м/с
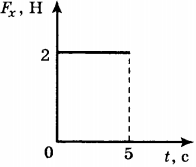
5. Тело движется в положительном направлении оси ( Ox ). На рисунке представлен график зависимости от времени ( t ) проекции силы ( F_x ), действующей на тело. В интервале времени от 0 до 5 с проекция импульса тела на ось ( Ox )
1) уменьшается на 5 кг·м/с
2) не изменяется
3) увеличивается на 10 кг·м/с
4) увеличивается на 5 кг·м/с
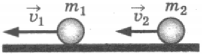
6. Два шара массой ( m_1 ) и ( m_2 ) движутся в одном направлении со скоростями соответственно ( x_1 ) и ( x_2 ) по гладкому горизонтальному столу (см. рисунок). Полный импульс ( p ) системы шаров равен по модулю
1) ( p=m_2x_2-m_1x_1 ) и направлен налево ←
2) ( p=m_1x_1-m_2x_2 ) и направлен вправо →
3) ( p=m_1x_1+m_2x_2 ) и направлен налево ←
4) ( p=m_1x_1-m_2x_2 ) и направлен вправо →
7. Два шарика массой 50 г и 100 г движутся со скоростью 0,6 м/с и 0,4 м/с соответственно. Направления движения шариков составляют угол 90°. Модуль суммарного импульса шариков равен
1) 0,15 кг·м/с
2) 0,07 кг·м/с
3) 0,05 кг·м/с
4) 0,01 кг·м/с
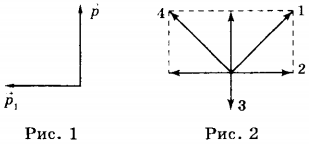
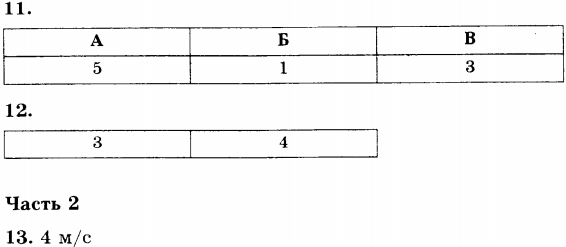
8. Снаряд, импульс которого ( vec{p} ) был направлен вертикально вверх, разорвался на два осколка. Импульс одного осколка ( vec{p}_1 ) в момент взрыва был направлен горизонтально (рис. 1). Какое направление имел импульс ( vec{p}_2 ) второго осколка (рис. 2)?
1) 1
2) 2
3) 3
4) 4
9. Масса мальчика в 3 раза меньше массы лодки. В момент прыжка с неподвижной лодки скорость мальчика равна 1,5 м/с. При этом лодка приобретает скорость, равную
1) 4,5 м/с
2) 2 м/с
3) 0,5 м/с
4) 0 м/с
10. Закон сохранения импульса справедлив:
А. Для замкнутой системы тел
Б. Для любой системы тел.
Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
11. Установите соответствие между физическими величинами (в левом столбце таблицы) и их единицами (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами
ВЕЛИЧИНА
A. Импульс
Б. Скорость
B. Ускорение
ЕДИНИЦА
1) метр/секунда (1 м/с)
2) ньютон (1 Н)
3) метр/секунда2 (1 м/с2)
4) джоуль (1 Дж)
5) ньютон·секунда (1 Н·с)
12. Из приведённого перечня выберите 2 правильных утверждения и запишите их номера в таблицу.
1) Закон сохранения импульса справедлив для любой системы тел.
2) Импульс тела — величина скалярная.
3) Закон сохранения импульса справедлив для замкнутой системы тел.
4) Изменение импульса тела равно импульсу силы.
5) Закон сохранения импульса не применим к незамкнутой системе тел ни при каких условиях.
Часть 2
13. Снаряд летит горизонтально и разрывается на два осколка массой 2 кг и 3 кг. С какой скоростью летел снаряд, если первый осколок в результате разрыва приобрёл скорость 50 м/с, второй 40 м/с? Скорости осколков направлены горизонтально в противоположную сторону.
Ответы
Импульс тела. Закон сохранения импульса
3.1 (62.45%) 49 votes
«Я принимаю, что во Вселенной…
есть известное количество движения,
которое никогда не увеличивается,
не уменьшается, и, таким образом,
если одно тело приводит в движение
другое, то теряет столько своего
движения, сколько его сообщает»
Рене Декарт
Данная тема посвящена изучению методов решения задач на закон
сохранения импульса.
Задача 1. Железнодорожная платформа движется со
скоростью 2,5 м/с. Из орудия, закрепленного на платформе, производится выстрел.
Масса снаряда 25 кг, его скорость 700 м/с, а масса платформы с орудием 20000
кг. Определите скорость платформы после выстрела, если выстрел произведен: а) в
направлении движения платформы; б) в противоположном направлении; в) ствол
орудия во время выстрела составляет угол 60о с направлением
движения. Считать, что силы сопротивления движению пренебрежимо малы.
|
ДАНО: |
РЕШЕНИЕ: Запишем закон сохранения импульса: Импульсы тел до взаимодействия: Импульсы тел после взаимодействия: а) Запишем закон сохранения импульса в проекциях на ось Ох: Преобразуем данное уравнение Тогда искомая скорость платформы б) Рассмотрим случай, когда выстрел произведён в Запишем закон сохранения импульса в проекциях на ось Ох: Преобразуем данное уравнение Тогда в) Рассмотрим случай, когда ствол орудия во время выстрела Запишем закон сохранения импульса в проекциях на ось Ох: Преобразуем последнюю формулу Тогда искомая скорость |
Задача 2. Зенитный снаряд, выпущенный вертикально
вверх, разорвался в верхней точке траектории на три осколка. Первый осколок
массой 9 кг имел скорость 60 м/с, направленную вертикально вверх, скорость
второго равна 40 м/с и направлена горизонтально, а его масса 18 кг. Масса
третьего осколка 4,5 кг. Найдите величину и направление вектора скорости
меньшего осколка.
|
ДАНО: |
РЕШЕНИЕ: Если длительность процесса взаимодействия настолько мала, Чтобы указанная векторная сумма импульсов осколков была Закон сохранения импульса в проекциях на ось Ох: Закон сохранения импульса в проекциях на ось Оу: И разделим почленно второе уравнение на первое, помня о Тогда угол a Скорость меньшего осколка (1 способ): Для того чтобы определить скорость меньшего осколка, можно Скорость меньшего осколка (2 способ): Возведём почленно в квадрат левые и правые части уравнений |
Ответ: α
= 36,9о; υ3 = 200 м/с.
Задача 3. Длина лодки 6 м. Человек, масса которого
вдвое меньше массы лодки, переходит с носа лодки на корму. На какое расстояние
относительно воды переместится лодка, если сопротивлением воды при движении
лодки можно пренебречь.
|
ДАНО: |
РЕШЕНИЕ: Запишем закон сохранения импульса: Закон сохранения импульса в проекциях на ось Ох: Запишем закон сложения скоростей Закон сложения скоростей в проекциях на ось Ох: Тогда Так как движение лодки и человека равномерное, то: Следовательно |
|
|
Ответ: 2 м.
Задача 4. Человек, сидящий в лодке, бросает камень
вдоль нее под углом 60о к горизонту. Масса камня составляет 1 кг,
масса человека и лодки — 150 кг, начальная скорость камня относительно берега
равна 10 м/с. Определите расстояние между точкой падения камня и лодкой в
момент, когда камень коснется воды.
|
ДАНО: |
РЕШЕНИЕ: Расстояние между точкой падения камня и лодкой: Дальность полета камня: Расстояние, пройденное лодкой: где время полёта камня Закон сохранения импульса: Запишем закон сохранения импульса в проекциях на ось Ох: Тогда искомое расстояние |
|
|
Ответ: 8,8 м.