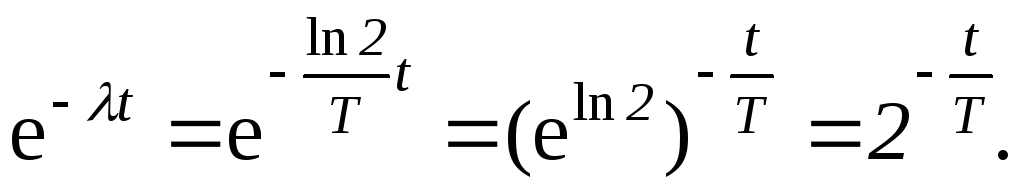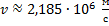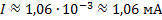Электрон
в атоме движется. Поскольку это движение
не прямолинейное, электрон
обладает моментом импульса
В начале
прошлого века при создании модели атома
Н.Бор допустил, что стационарными
состояниями атома являются только
такие, в которых момент импульса равен
целому кратному постоянной Планка h,
деленной на 2π. Это позволило Н.Бору
рассчитать наблюдаемые линии спектра
водорода.
Момент
импульса, обусловленный перемещением
в пространстве, называют орбитальным.
Согласно квантовой теории модуль вектора
орбитального момента равен
где l —
орбитальное квантовое число, принимающее
значения 0, 1, 2,… Таким образом, момент
импульса электрона L,
как и энергия, квантуется,
т.е. принимает дискретныезначения.
Из квантовой теории следует еще один
важный вывод: проекция момента импульса
электрона на какое-либо заданное направление
в пространстве z(например,
на направление силовых линий магнитного
или электрического поля) также квантуется
по правилу:
Электрон,
движущийся вокруг ядра, представляет
собой элементарный круговой электрический
ток. Согласно классической теории
электромагнитных явлений, замкнутый
ток является источником магнетизма. Из
опыта следует, что магнитное действие
замкнутого тока (контура с током)
определено, если известно произведение
силы тока i на
площадь контура S.
Это произведение носит название МАГНИТНОГО
МОМЕНТА. Обозначим
его μ. μ
= iS. Найдем связь
магнитного момента с моментом импульса L.
В качестве примера рассмотрим движение
частицы с массой m и
зарядом q по
окружности радиуса r с
частотой ν.
Для
микрочастиц квантовая теория приводит
к такой же связи орбитального механического
и магнитного моментов электрона.
Теперь q = e (e<0!)
— заряд электрона, m —
его масса).
Опытные
данные (тонкое расщепление спектральных
линий, результаты опыта Штерна и Герлаха
— об этом позднее скажем) говорили о том,
что электрон в состоянии 1s (орбитальное
квантовое число l =
0, и, следовательно, L =
0) имеет ненулевой момент импульса S,
не связанный с перемещением частицы
как целого. Этот момент импульса назвали
спиновым (спин,
английское spin, вращение). При введении
понятия «Спин» предполагалось, что
электрон можно рассматривать как
«вращающийся волчок», а его Спин —
как характеристику такого вращения.
Спиновое
квантовое число для электрона s =
1/2 (то же значение для протона, нейтрона
и еще ряда частиц). Квантовое число
проекции .
Т.е. проекций только две.
Спиновому
моменту импульса пропорционален спиновый
магнитный момент μs
БИЛЕТ
21
-
Распределение
электронов по энергетическим уровням.
Принцип Паули
Если
тождественные частицы имеют одинаковые
квантовые числа, то их волновая функция
симметрична относительно перестановки
частиц. Отсюда следует, что два одинаковых
фермиона, входящих в одну систему, не
могут находиться в одинаковых состояниях,
т.к. для фермионов волновая функция
должна быть антисимметричной. Фермионы
– частицы, обладающие полуцелым сплином.
Принцип
Паули: В определённом состоянии может
находиться не более одного фермиона.
Для электрона это значит, что в состоянии
с заданными квантовыми числами (n,l,m,
может находиться не более одного
электрона. Принцип Паули позволяет
объяснить, почему электроны в атоме не
переходят все сразу в основное состояние
с моментальной энергией. На основе
принципа Паули объясняется периодическая
система.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры решения задач
Решение.Так как кинетическая энергия электрона (0.5 МэВ) почти равна его энергии покоя (0.511 МэВ), то скорость электрона близка к скорости света и, следовательно, задачу нужно решать по формулам релятивистской механики.
Длина волны де Бройля выражается формулой

где h– постоянная Планка; p– импульс электрона.
Импульс электрона определим из формулы, связывающей энергию частицы с ее импульсом:


Полная энергия электрона равна сумме его энергии покоя и кинетической энергии


Подставив в формулу (1) вместо импульса рэлектрона его значение по формуле (5), получим

При числовом подсчете по формуле (6) нет необходимости выражать энергию покоя и кинетическую энергию в единицах системы СИ. Значения энергии можно взять в мегаэлектрон-вольтах, если предварительно выразить постоянную Планка в мегаэлектрон-вольтах в секунду:
Можно поступить иначе, выразив постоянную Планка hчерез комптоновскую длину волныλkэлектрона. Как известно, длина волны Комптона
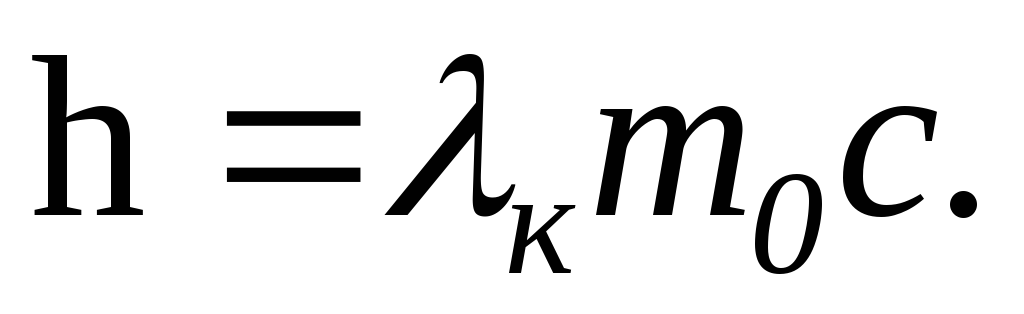
Подставив в формулу (6) вместо hего значение по формуле (7) и учтя, чтоm0с 2 = Е0, получим

Комптоновская длина волны электрона λк = 0.0242Ǻ.Сделав подстановку чисел, получим искомую длину волны де Бройля:

Пример 2. Угол рассеяния фотона в результате эффекта Комптона составляет 180. Определить кинетическую энергию электрона отдачи, если энергия фотона до рассеяния равна 0.51 МэВ.
Решение.При эффекте Комптона электрон отдачи получает энергию от фотона
Т = ε1 – ε2, (1)
где ε1– энергия падающего фотона;ε2– энергия рассеянного фотона.
Энергию рассеянного фотона найдем, воспользовавшись уравнением Комптона
которое для случая рассеяния под углом Θ = 180примет вид
Выразив длины волн через энергию фотонов, получим
Разделив обе части равенства на hc, найдем
или, приняв во внимание, что m0с 2 есть энергия покоя электронаЕ0,

Подставив числовые значения ε1иЕ0, получим

Подставив значения ε1иε2в (1) и произведя вычисления, найдем кинетическую энергию электрона отдачи:
Т = 0.51 – 0.17 = 0.34 МэВ.
Пример 3. Какое наименьшее напряжение надо приложить к рентгеновской трубке, чтобы получить наименьшую длину волны в серии L, если антикатод сделан из железа и постоянная экранирования равна 7.5 (по Мозли)?
Решение.Характеристическое рентгеновское излучение наблюдается всякий раз, когда заполняются места во внутренних слоях электронной оболочки атома, освобожденные электронами вследствие вырывания их бомбардирующими антикатод электронами. Энергия, необходимая для возбуждения какой-либо серии (К, L, М, …), определяется работой вырывания электрона из соответствующего слоя и равна максимальной энергии кванта, соответствующего этой серии.
Так, все линии серии Lпоявляются, если освобождается место во втором от ядра слое – слоеL. Следовательно, наименьшую длину волны или максимальную частоту для этой серии определим по формуле Мозли из условия, чтоn = ∞, k = 2, Z = 26:
где b– постоянная экранирования. Для этой серии у всех элементовbодинакова и равна 7.5 (по Мозли).

Из сказанного выше следует, что

При таком напряжении на трубке появятся все линии серии L, и более мягкие, а линии серииKнаблюдаться не будут.
Пример 4. Электрон, имеющий скорость 10 6 м/с, влетает в камеру Вильсона. Приняв размер зерна фотоэмульсии порядка 10 –6 м, найдите неопределенность в скорости. Сравните Vх и ΔVх.
Решение.Ширина трека 10 –6 м, следовательно, неопределенность в координатеΔх = 10 –6 . Используя соотношение неопределенности Гейзенберга, запишем

Из неопределенности импульса определим неточность в скорости:

Таким образом, в этом случае можно говорить о траектории частицы в классическом смысле.
Пример 5. Определить возможные значения орбитального момента импульса Мl электрона в возбужденном атоме водорода, если энергия возбуждения ε = 12.09 эВ.
Решение.Орбитальный момент импульсаМlэлектрона определяется квантовым числом по формуле
где l– орбитальное квантовое число (l = 0, 1, 2 ,…, n – 1).
Найдем главное квантовое число nс помощью формулы, определяющей собственные значения энергии электрона в атоме водорода:
где n– главное квантовое число (n = 1, 2, 3,…).
Учтем, что при n = 1 E = –13.6эВ. Тогда

Энергия возбуждения εесть квант энергии, поглощенный атомом при переходе из основного состояния (n = 1) в возбужденное. Следовательно,
Подставив числовые значения величин, выраженные в электрон-вольтах, получим
откуда n = 3. Следовательно,l = 0, 1, 2.
Теперь найдем возможные значения Мl:
при l = 0 Ml = 0,
при l = 1 Ml = (h/2π)
при l = 2 Ml= (h/2π)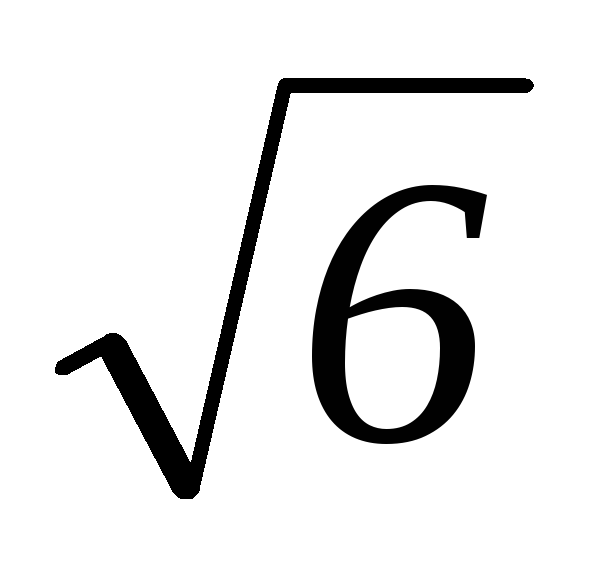
Пример 6. Первоначально покоившийся атом водорода испустил фотон, длина волны которого соответствует максимальной длине волны в серии Бальмера. Определить скорость V движения атома водорода (h = 6.62 10 –34 ·Дж с; М = 1.672 10 –24 г; R = 109677 см –1 ).
Решение. По закону сохранения импульса, импульс испущенного фотона равен импульсу атома, поэтому
Максимальную частоту фотона можно определить, используя формулу Бальмера для случая n = 3(длина волны в этом случае будет максимальной):
Значит, скорость отдачи
Пример 7. Радиоактивный натрий 11Νa 24 распадается, выбрасывая β-частицы. Период полураспада 14,8 ч. Вычислить количество атомов, распавшихся в 1 мг данного радиоактивного препарата:
а) за 10 ч;
б) за 0,01 с.
Решение. а) Число радиоактивных атомов убывает со временем по закону
где Ν– число нераспавшихся радиоактивных атомов черезtсекунд с момента начала отсчета;Ν0– число радиоактивных атомов к моменту начала отсчета;λ– постоянная радиоактивного распада.
Число распавшихся атомов

Выразив λчерез период полураспадаТ, преобразуем выражение е -λt :
После преобразования равенство (1) будет иметь вид

В нашем случае Ν0– число атомов в 1 мг11Νa 24 . В одном килограмм-атоме11Νa 24 содержится 6.0210 26 (число Авогадро) атомов; в 1 мг содержится
Подставив числовые значения в формулу (2), получим

б) Вторая часть задачи решается аналогично, однако здесь встречаются трудности в вычислении выражения2 – t / T .
Для решения этой части задачи заметим, что при λΔt<<1вместо (2) можно воспользоваться соотношением
ΔN = N0 λ Δt. (3)
Заменив в формуле (3) λчерез
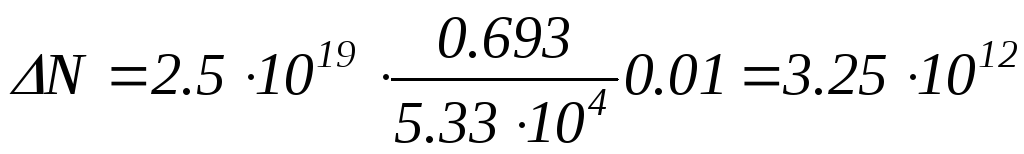
Пример 8. Найти активность радона, образовавшегося из m0 = 1 г радия 
Решение. Активность препарата измеряется числом ядер, распадающихся в единицу времени:

где dN– число радиоактивных ядер, распадающихся за промежуток времениdt;λ– постоянная радиоактивного распада.
Если радиоизотоп А1с постоянной распадаλ1превращается в радиоизотопА2с постоянной распадаλ2, то число ядер радиоизотопаА2изменяется со временем по закону
где N1(0) – число ядер радиоизотопаА1 в моментt = 0.
Для искомой активности запишем
Входящие сюда величины выразим через данные m0,μ,T1,T2по формулам
T λ = ln2,
где NA– число Авогадро; m0– начальная масса препарата;μ– молярная масса изотопа.
Произведя сокращения, имеем
Это общая формула, выражающая закон изменения со временем активности одного радиоизотопа (дочернего), полученного в процессе распада другого (материнского). Формулу можно упростить, если учесть вытекающие из условия соотношения Т1>>T2 и T1>>t. Из первого неравенства следует, что можно пренебречь величиной Т2 в разности T1 – T2. В силу второго неравенства можно принять за единицу первый член, стоящий в скобках. Тогда найдем
Произведя расчет, получим

Определить импульс электрона, если он движется со скоростью, равной 0,6 скорости света
Определить импульс электрона, если он движется со скоростью, равной 0,6 скорости света.
Задача №11.5.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Релятивистский импульс электрона (p), т.е. импульс электрона, движущегося относительно наблюдателя с некоторой скоростью (upsilon), можно определить по формуле:
Здесь (m_e) – масса покоя электрона, равная 9,1·10 -31 кг, (upsilon) – скорость движения электрона относительно наблюдателя, (c) – скорость света в вакууме, равная 3·10 8 м/с.
По условию задачи электрон движется со скоростью, равной 0,6 скорости света в вакууме, то есть (upsilon = 0,6c), поэтому формула (1) примет следующий вид:
Задача решена в общем виде, нам остается только подставить численные данные в указанную формулу и посчитать численный ответ:
[p = frac<3> <4>cdot 9,1 cdot <10^< – 31>> cdot 3 cdot <10^8>= 2,05 cdot <10^< – 22>>;кг cdot м/с]
Ответ: 2,05·10 -22 кг·м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Большая Энциклопедия Нефти и Газа
Импульсами электронов воздействовали на бензол, толуол, хлорбензол, и-ксилол и мезитилен. Во всех случаях осциллограммы показывают поглощение, связанное со свободными радикалами и спадающее к нулю менее чем за 1 мсек. Уменьшение происходит по второму порядку и, как полагают, вызвано рекомбинацией радикалов. [4]
Поскольку импульсы сталкивающихся электронов ( в системе центра инерции) взаимно противоположны, то одинаковым спиральностям ( Kt A2) отвечают антипараллельные спины, а различным спиральностям ( Я) — 2) — параллельные спины. [5]
Момент импульса электронов в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса электрона. [6]
Рд — импульсы электрона и дырки соответственно, a fe ЛуО — импульс, который должен быть унесен какой-либо выделившейся частицей. [7]
Определим теперь импульс электрона в данном энергетическом состоянии внутри кристалла. [8]
Вычисляя изменение импульса электрона , можно считать, что v и vc одинаковы, масса мишени бесконечно большая, а передача энергии отсутствует. [10]
Поскольку квадрат импульса электрона р2 равен K2k2, величина представляет собой кинетическую энергию свободного электрона. Свободным ложно считать электрон, движущийся в постоянном потенциальном поле U ( г) const. Зонный характер спектра исчезает ( см. фиг. Введение эффективной массы сохраняет квадратичную связь между энергией и волновым вектором Е ( k) — kz и меняет только константу пропорциональности. Это позволяет интерпретировать второй член в выражении (1.12) приближенно как кинетическую энергию электрона в кристалле, так что состояния электрона внутри данной зоны различаются по существу импульсами и значениями кинетической энергии трансляционного движения. Такое рассмотрение позволяет легко представить условия, при которых в кристалле возникает электрический ток. [11]
Полный момент импульса электрона является суммой орбитального и спинового моментов. [12]
Изменение величины импульса электронов определяется размером отрезка ординаты, отсекаемой сепаратрисой на плоскости импульс — фаза и лежащей внутри нее. [13]
Компонента момента импульса электронов вдоль межъядерной оси обозначается через Л и принимает целочисленные значения. [14]
Таким образом, импульс электрона растет пропорционально средней магнитной индукции. [15]
Как найти импульс электрона и энергию электрона если известна его скорость. скорость равно 2* 10 в 8 степени
Мы отправили письмо со ссылкой на смену пароля на username@mail.ru.
Если письма нет, проверь папку «Спам».
Чтобы вопрос опубликовался, войди или зарегистрируйся
Нужна регистрация на Учи.ру
«Ваш урок» теперь называется Учи.Ответы. Чтобы зайти на сайт, используй логин и пароль от Учи.ру. Если у тебя их нет, зарегистрируйся на платформе.
Условие задачи:
Определить импульс фотона, соответствующего рентгеновскому излучению с частотой 3·1017 Гц.
Задача №11.1.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=3 cdot 10^{17}) Гц, (p-?)
Решение задачи:
Запишем формулу длины волны де Бройля (lambda):
[lambda = frac{h}{p}]
В этой формуле (h) – это постоянная Планка, равная 6,62·10-34 Дж·с.
Откуда выразим импульс фотона (p):
[p = frac{h}{lambda };;;;(1)]
Известно, что частоту колебаний (nu) можно выразить через скорость света (c), которая равна 3·108 м/с, и длину волны (lambda) по следующей формуле:
[nu = frac{c}{lambda }]
Из этой формулы выразим длину волны (lambda):
[lambda = frac{c}{nu }]
Это выражение подставим в формулу (1), тогда имеем:
[p = frac{{hnu }}{c}]
Посчитаем численный ответ задачи:
[p = frac{{6,62 cdot {{10}^{ – 34}} cdot 3 cdot {{10}^{17}}}}{{3 cdot {{10}^8}}} = 6,62 cdot {10^{ – 25}}; кг cdot м/с]
Ответ: 6,62·10-25 кг·м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
11.1.14 Найти массу фотона излучения с длиной волны 1 мкм
11.1.16 С какой скоростью должен двигаться электрон, чтобы его импульс был равен
11.1.17 При какой длине волны излучения масса фотона равна массе покоя электрона?
Импульс фотона
Используя формулу массы фотона, можно получить формулу импульса фотона р = mc.
Если
| p | импульс фотона, | (кг × м)/с |
|---|---|---|
| h | постоянная Планка, 6,626 × 10-34, | Дж × с |
| ν | частота излучения, | Гц = 1/с |
| λ | длина волны излучения в вакууме, | м |
| c | скорость света в вакууме, 3 × 108 | м/с |
то
[ p=frac{hν}{c}=frac{h}{λ}]
Экспериментальные доказательства квантовых свойств излучения и корпускулярной природы фотона основываются на:
а) фотоэлектрическом эффекте: скорость испускаемых фотоэлектронов не зависит от интенсивности света, но зависит от его частоты. Если частота оказывается ниже граничного значения, то электроны не испускаются;
б) эффекте Комптона: при столкновении фотона с электроном часть энергии и импульса фотона передается электрону. Потеря фотоном энергии приводит к уменьшению его частоты. Скорость электрона после соударения определяется на основе закона сохранения импульса.
Вычислить, найти импульс фотона через частоту
Вычислить, найти импульс фотона через длину волны
Импульс фотона |
стр. 731 |
|---|
Решение задач по теме «Модель атома Н. Бора»
Задача 1
Определите скорость v и ускорение a электрона на первой боровской орбите, радиус которой определяется формулой 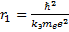
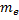
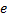
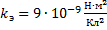
Дано: 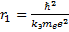
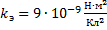
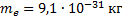
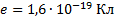
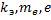
Найти: 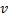
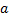
Решение
В формуле радиуса первой боровской орбиты:
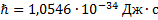
Радиус окружности, по которому происходит движение, равен:
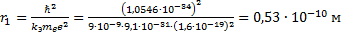
Рис. 1. Иллюстрация к задаче №1
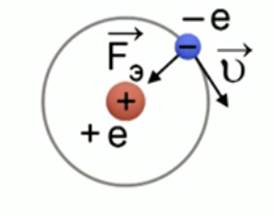
Согласно модели Бора, вокруг ядра атома водорода, заряд которого 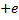
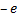
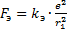
Также эта сила является центростремительной, то есть:
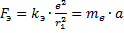
Следовательно, ускорение равно:
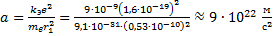
Центростремительное ускорение равно:
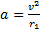
Отсюда скорость равна:
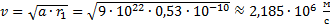
Ответ: 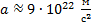
Задача 2
Найти силу электрического тока, который вызывает электрон, двигаясь по первой боровской орбите.
Дано: 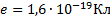
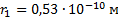
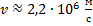
Найти: 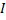
Решение
Известно, что сила тока равна:
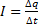
Для данной задачи:
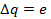
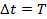
Период обращения электрона равен:
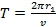
Следовательно, сила тока, возникающего при движении электрона по орбите радиусом 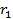
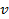
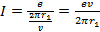
Подставим в данное выражение известные данные:
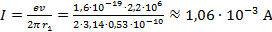
Ответ:
Задача 3
Найти максимальную частоту, максимальную длину волны и максимальный импульс фотона в видимой части спектра, излучённого при переходе электрона на второй энергетический уровень в атоме водорода.
Дано: 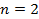
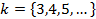
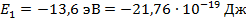
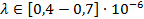
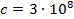
Найти: 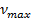
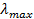
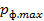
Решение
Согласно второму постулату Бора:
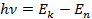
где 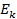
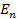
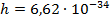
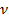
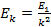
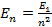
Следовательно, частота излучения фотона равна:

Частота и длина волны связаны следующим соотношением:
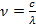
Зная световой диапазон в длинах волн (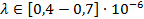
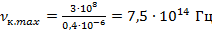
Более высокие частоты относятся к ультрафиолетовой части спектра и человеческим глазом не фиксируются.
Минимальное значение частоты при излучении будет при 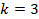
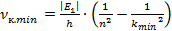
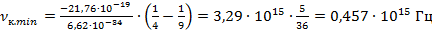
Подставим данное значение в формулу связи между длиной волны и частотой. Если частота минимальная, то значение длины волны будет максимальное:
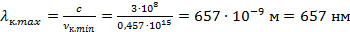
Данное значение входит в световой диапазон – это красная линия в излучении атома водорода.
Для того чтобы вычислить максимальное значение частоты фотона в видимой части спектра, необходимо подставлять значения k от 4-х и выше.
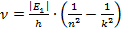
Если подставить значение 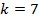
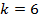
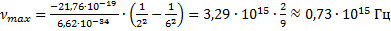
Мы попали в световой диапазон, так как он ограничивается значением 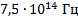
Полученная максимальная частота соответствует минимальной длине волны, равной:
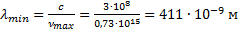
Минимальная длина волны была найдена для определения максимального импульса фотона.
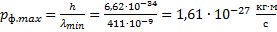
Ответ: ;
;
.