До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
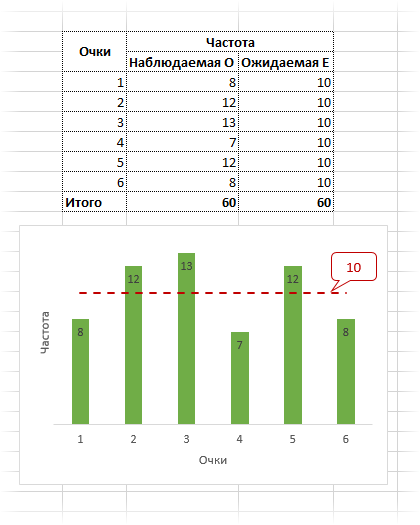
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
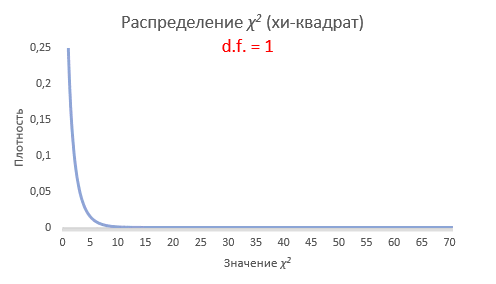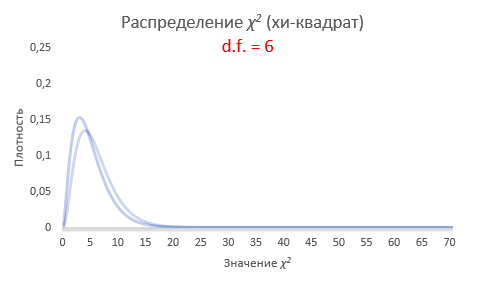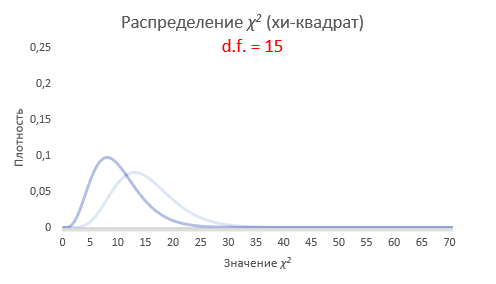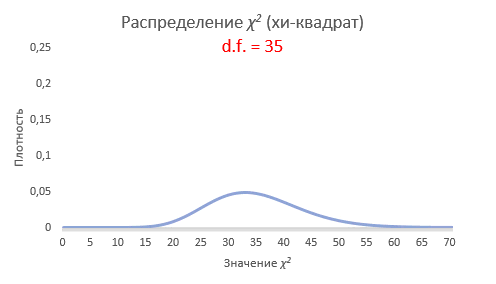
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
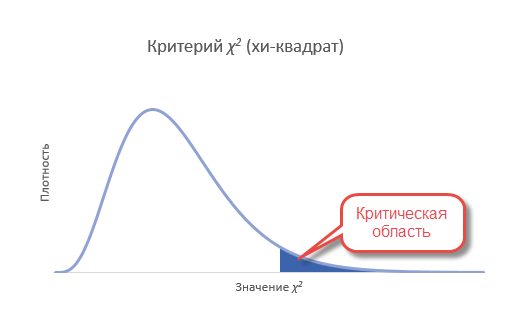
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
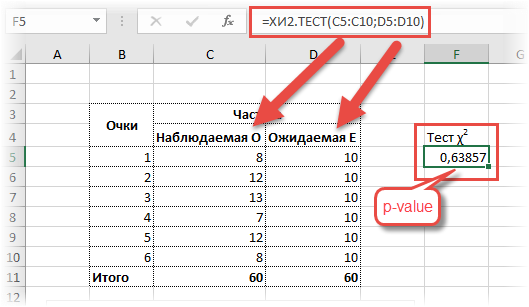
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
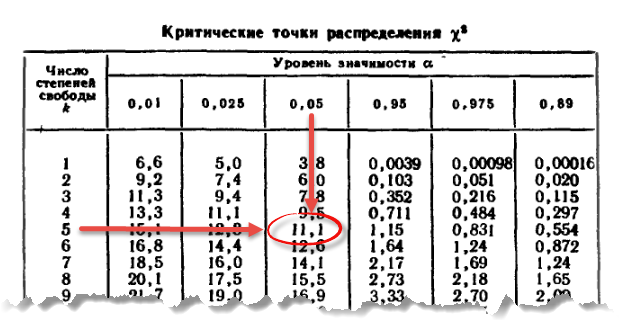
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
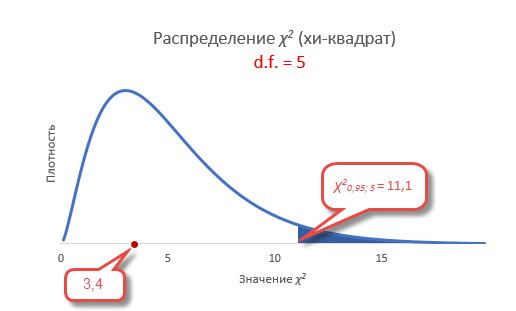
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
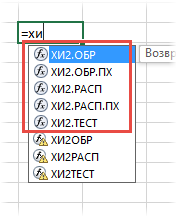
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
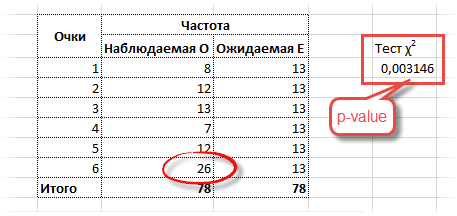
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
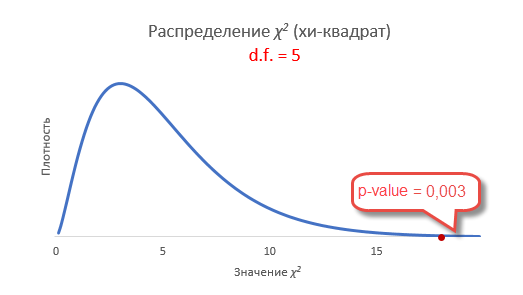
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
Ниже представлена таблица значений критических точек распределения χ2 (хи-квадрат) критерия Пирсона, широко используемые в задачах математической статистики, таких как построение доверительных интервалов,
проверка статистических гипотез и непараметрическое оценивание.
|
Число степеней свободы k |
Уровень значимости α | |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,6 | 5 | 3,8 | 0,0039 | 0,00098 | 0,00016 |
| 2 | 9,2 | 7,4 | 6 | 0,103 | 0,051 | 0,02 |
| 3 | 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 |
| 6 | 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 |
| 7 | 18,5 | 16 | 14,1 | 2,17 | 1,69 | 1,24 |
| 8 | 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19 | 16,9 | 3,33 | 2,7 | 2,09 |
| 10 | 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 |
| 11 | 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 23,3 | 21 ,0 | 5,23 | 4,4 | 3,57 |
| 13 | 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 27,5 | 25 | 7,26 | 6,26 | 5,23 |
| 16 | 32 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 |
| 19 | 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,9 |
| 22 | 40,3 | 36,8 | 33,9 | 12,3 | 11 | 9,54 |
| 23 | 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 |
| 24 | 43 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 45,7 | 42,6 | 17,7 | 16 | 14,3 |
| 30 | 50,9 | 47 | 43,8 | 18,5 | 16,8 | 15 |
Пример решения задачи
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.6, 3.4, 2.0.
Проверить
гипотезу
: дисперсия равна
10.0.
Используются
таблицы распределения хи-квадрат.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Вычислим
среднее и
исправленную дисперсию:
Для
того, чтобы при заданном уровне значимости
проверить нулевую гипотезу
о равенстве неизвестной генеральной дисперсии
гипотетическому значению
при конкурирующей гипотезе
вычисляем наблюдаемое значение критерия:
При
уровне значимости
находим:
— нет
оснований отвергнуть нулевую гипотезу
В этом руководстве объясняется, как читать и интерпретировать таблицу распределения хи-квадрат .
Что такое таблица распределения хи-квадрат?
Таблица распределения хи-квадрат — это таблица, которая показывает критические значения распределения хи-квадрат. Чтобы использовать таблицу распределения хи-квадрат, вам нужно знать только два значения:
- Степени свободы для теста хи-квадрат
- Альфа-уровень для теста (обычно выбираются 0,01, 0,05 и 0,10).
На следующем изображении показаны первые 20 строк таблицы распределения хи-квадрат со степенями свободы в левой части таблицы и альфа-уровнями в верхней части таблицы:
Примечание. Полную таблицу распределения хи-квадрата с большим количеством степеней свободы вы можете найти здесь .
Критические значения в таблице часто сравнивают со статистикой теста Хи-квадрат. Если статистика теста больше критического значения, найденного в таблице, то вы можете отклонить нулевую гипотезу теста хи-квадрат и сделать вывод, что результаты теста статистически значимы.
Примеры использования таблицы распределения хи-квадрат
Мы продемонстрируем, как использовать таблицу распределения хи-квадрат со следующими тремя типами тестов хи-квадрат:
- Тест хи-квадрат на независимость
- Тест хи-квадрат на качество подгонки
- Тест хи-квадрат на однородность
Тест хи-квадрат на независимость
Мы используем тест Хи-квадрат на независимость , когда хотим проверить, существует ли значительная связь между двумя категориальными переменными.
Пример: предположим, мы хотим знать, связан ли пол с предпочтениями политической партии. Мы берем простую случайную выборку из 500 избирателей и опрашиваем их об их предпочтениях в отношении политических партий. Используя уровень значимости 0,05, мы проводим тест хи-квадрат на независимость, чтобы определить, связан ли пол с предпочтениями политической партии. В следующей таблице представлены результаты опроса:
Оказывается, статистика теста для этого теста хи-квадрат составляет 0,864.
Затем мы можем найти критическое значение для теста в таблице распределения хи-квадрат. Степени свободы равны (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, и проблема подсказала нам, что мы должны использовать альфа-уровень 0,05. Таким образом, по таблице распределения хи-квадрат критическое значение теста равно 5,991 .
Поскольку наша тестовая статистика меньше нашего критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует связь между полом и предпочтениями политических партий.
Тест хи-квадрат на качество подгонки
Мы используем критерий пригодности хи-квадрат , когда хотим проверить, следует ли категориальная переменная гипотетическому распределению.
Пример: Владелец магазина утверждает, что 30 % всех его покупателей на выходных посещают его в пятницу, 50 % — в субботу и 20 % — в воскресенье. Независимый исследователь посещает магазин в случайные выходные и обнаруживает, что 91 покупатель посещает его в пятницу, 104 — в субботу и 65 — в воскресенье. Используя уровень значимости 0,10, мы проводим критерий хи-квадрат на соответствие, чтобы определить, согласуются ли данные с заявлением владельца магазина.
В этом случае тестовая статистика оказывается равной 10,616.
Затем мы можем найти критическое значение для теста в таблице распределения хи-квадрат. Степени свободы равны (#outcomes-1) = 3-1 = 2, и задача подсказала нам, что мы должны использовать альфа-уровень 0,10. Таким образом, по таблице распределения хи-квадрат критическое значение теста равно 4,605 .
Поскольку наша тестовая статистика больше нашего критического значения, мы отклоняем нулевую гипотезу. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что истинное распределение покупателей, заходящих в этот магазин по выходным, не равно 30% в пятницу, 50% в субботу и 20% в воскресенье.
Тест хи-квадрат на однородность
Мы используем тест хи-квадрат на однородность , когда хотим формально проверить, есть ли разница в пропорциях между несколькими группами.
Пример. Баскетбольный тренировочный центр хочет проверить, улучшат ли две новые тренировочные программы долю игроков, прошедших сложный тест по стрельбе. 172 игрока случайным образом распределяются по программе 1, 173 — по программе 2 и 215 — по текущей программе. После использования тренировочных программ в течение одного месяца игроки проходят тест по стрельбе. В таблице ниже показано количество игроков, прошедших тест на стрельбу, в зависимости от того, какую программу они использовали.
Используя уровень значимости 0,05, мы проводим критерий хи-квадрат на однородность, чтобы определить, является ли процент сдачи одинаковым или для каждой тренировочной программы.
Оказывается, статистика теста для этого теста хи-квадрат равна 4,208.
Затем мы можем найти критическое значение для теста в таблице распределения хи-квадрат. Степени свободы равны (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, и проблема подсказала нам, что мы должны использовать альфа-уровень 0,05. Таким образом, по таблице распределения хи-квадрат критическое значение теста равно 5,991 .
Поскольку наша тестовая статистика меньше нашего критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что три программы обучения дают разные результаты.
Вступление
«Наука продвигается, предлагая и проверяя гипотезы, а не объявляя вопросы неразрешимыми» — Ник Мацке
Давайте начнем с тематического исследования. Я хочу, чтобы вы прямо сейчас подумали о вашем любимом ресторане. Допустим, вы хотите предсказать количество людей, приезжающих на обед пять дней в неделю. В конце недели вы заметили, что ожидаемое количество отличался от фактического.
Похоже на главную проблему статистики? Это идея!
Итак, как вы будете проверять статистическую значимость между наблюдаемыми и ожидаемыми значениями? Помните, что это категориальная переменная — «дни недели» — с пятью категориями [понедельник, вторник, среда, четверг, пятница].
Один из лучших способов справиться с этим — использовать критерий хи-квадрат.
Мы всегда можем выбрать z-тесты, t-тесты или ANOVA, когда имеем дело с непрерывными переменными. Но ситуация становится более сложной при работе с категориальными функциями (как подтвердит большинство ученых!). Я обнаружил, что тест хи-квадрат очень полезен в моих собственных проектах.
Итак, давайте углубимся в статью, чтобы понять все о тесте хи-квадрат, что это такое, как он работает и как мы можем реализовать его в R.
Если вы новичок в области статистики и данных, я бы порекомендовал следующие ресурсы, чтобы получить исчерпывающий обзор этих двух общих тем:
Я уверен, что вы уже сталкивались с категориальными переменными, даже если вы не могли их интуитивно распознать. С ними может быть сложно разобраться в мире наук о данных, поэтому давайте сначала определим их.
Категориальные переменные попадают в особую категорию тех переменных, которые можно разделить на конечные категории. Эти категории обычно являются именами или ярлыками. Эти переменные также называются качественными переменными, поскольку они отображают качество или характеристики этой конкретной переменной.
Например, категория «Жанр фильма» в списке фильмов может содержать категориальные переменные — «Боевик», «Фэнтези», «Комедия», «Мелодрама» и т. д.
Существует два типа категориальных переменных:
Номинальная переменная: не имеет естественного упорядочения по своим категориям. У них могут быть две или более категории. Например, семейное положение (холост, женат, разведен); пол (мужской, женский, трансгендерный) и т. д.
Порядковая переменная: переменная, для которой категории могут быть размещены в определенном порядке. Например, удовлетворенность клиентов (отлично, очень хорошо, хорошо, средне, плохо) и т. д.
Когда данные, которые мы хотим проанализировать, содержат переменные этого типа, мы обращаемся к критерию хи-квадрат, обозначенному χ², чтобы проверить нашу гипотезу.
Что такое критерий хи-квадрат и почему мы его используем?
Критерий хи-квадрат — это критерий статистической значимости для категориальных переменных.
Давайте научимся использовать хи-квадрат на интуитивном примере.
Исследователь интересуется взаимоотношениями между приемом абитуриентов на статистический факультет известного университета и их оценкой C.G.P.A (итоговая оценка).
Он получает записи о зачислении за последние пять лет из базы данных (случайным образом). Он записывает, сколько абитуриентов попало в каждую из следующих групп: категории баллов — 9-10, 8-9, 7-8, 6-7 и ниже 6.
Если нет никакой связи между процентом зачисления и C.G.P.A., тогда принятые абитуриенты должны быть в равной степени распределены по разным категориям C.G.P.A. (т.е. в каждой категории должно быть одинаковое количество абитуриентов).
Тем не менее, если абитуриенты, имеющие C.G.P.A более 8, с большей вероятностью будут зачислены, то в высшей категории C.G.P.A. будет больше абитуриентов по сравнению с более низкими категориями C.G.P.A. В этом случае собранные данные будут составлять наблюдаемые частоты.
Таким образом, вопрос в том, являются ли эти частоты случайными?
Здесь вступает в дело тест хи-квадрат! Он помогает нам ответить на поставленный выше вопрос, сравнивая наблюдаемые частоты с частотами, которые можно получить случайно.
Критерий хи-квадрат в проверке гипотез используется для проверки гипотезы о распределении наблюдений/частот по различным категориям.
Примечание. Я настоятельно рекомендую ознакомиться с этой статьей, если вам нужно освежить свои концепции проверки гипотез.
Мы находимся почти на стадии реализации тестов хи-квадрат, но есть еще одна вещь, которую мы должны изучить, прежде чем попасть туда.
Допущения теста Хи-квадрат
Как и любой другой статистический тест, тест хи-квадрат имеет несколько собственных предположений:
- χ2 предполагает, что данные для исследования получены путем случайного отбора, то есть они выбираются из популяции случайным образом.
- Категории являются взаимоисключающими, то есть каждый предмет относится только к одной категории. Например, из приведенного выше примера, число людей, которые обедали в вашем ресторане в понедельник, не может быть включено в категорию вторника.
- Данные должны быть представлены в виде частот или количеств определенной категории, а не в процентах.
- Данные не должны состоять из парных выборок или групп, то есть мы можем сказать, что наблюдения должны быть независимы друг от друга.
- Когда более 20% ожидаемых частот имеют значение меньше 5, то хи-квадрат не может использоваться. Чтобы решить эту проблему, нужно либо объединить категории, только если это уместно, или получить больше данных.
Типы тестов хи-квадрат (с вычислениями вручную и с реализацией в R)
Тест хи-квадрат на адекватность модели
Это непараметрический тест. Обычно мы используем его, чтобы определить, насколько значительно наблюдаемое значение данного события отличается от ожидаемого значения. В этом случае у нас есть категориальные данные для одной независимой переменной, и мы хотим проверить, является ли распределение данных аналогичным или отличным от распределения ожидаемых значений.
Давайте рассмотрим приведенный выше пример, в котором ученый-исследователь интересовался взаимоотношениями между приемом студентов на факультет статистики известного университета и их C.G.P.A.
В этом случае независимой переменной является C.G.P.A с категориями 9-10, 8-9, 7-8, 6-7 и ниже 6.
Статистический вопрос здесь заключается в следующем: одинаково ли распределены наблюдаемые частоты принятых студентов для разных категорий C.G.P.A (так, чтобы наше теоретическое распределение частот содержало одинаковое количество студентов в каждой из категорий C.G.P.A).
Мы упорядочим эти данные, используя таблицу сопряженности, которая будет состоять из наблюдаемых и ожидаемых значений, как показано ниже:
|
C.G.P.A |
||||||
|
10-9 |
9-8 |
8-7 |
7-6 |
менее 6 |
всего |
|
|
Наблюдаемая частота принятых студентов |
30 |
35 |
20 |
10 |
5 |
100 |
|
Ожидаемая частота принятых студентов |
20 |
20 |
20 |
20 |
20 |
100 |
После построения таблицы сопряженности следующая задача — вычислить значение статистики хи-квадрат. Формула для хи-квадрат имеет вид:
где,
χ 2 = значение хи-квадрат
Oi = наблюдаемая частота
Ei = ожидаемая частота
Давайте посмотрим на пошаговый подход для вычисления значения хи-квадрат:
Шаг 1: Вычтите каждую ожидаемую частоту из соответствующей наблюдаемой частоты. Например, для категории C.G.P.A 10-9 это будет «30-20 = 10». Примените аналогичную операцию для всех категорий.
Шаг 2: возведите в квадрат каждое значение, полученное на шаге 1, то есть (O-E)2. Например: для категории C.G.P.A 10-9 значение, полученное на шаге 1, равно 10. Оно становится равным 100 при возведении в квадрат. Примените аналогичную операцию для всех категорий.
Шаг 3: Разделите все значения, полученные на шаге 2, на соответствующие ожидаемые частоты, то есть (O-E)2
/E. Например: для категории C.G.P.A 10-9 значение, полученное на шаге 2, равно 100. При делении его на соответствующую ожидаемую частоту, равную 20, оно становится равным 5. Примените аналогичную операцию для всех категорий.
Шаг 4: Сложите все значения, полученные на шаге 3, чтобы получить значение хи-квадрат. В этом случае значение хи-квадрат получается равным 32,5.
Шаг 5: После того, как мы вычислили значение хи-квадрат, следующая задача — сравнить его с критическим значением хи-квадрат. Мы можем найти его в приведенной ниже таблице хи-квадрат для различного количества степеней свободы (количество категорий — 1) и уровня значимости:
В этом случае степени свободы 5-1 = 4. Таким образом, критическое значение при уровне значимости 5% составляет 9,49.
Полученное нами значение 32,5 намного больше, чем критическое значение 9,49. Поэтому можно сказать, что наблюдаемые частоты значительно отличаются от ожидаемых частот. Другими словами, C.G.P.A связан с количеством зачислений на факультет статистики.
Давайте еще больше укрепим наше понимание, выполнив тест хи-квадрат в R.
Тест хи-квадрат на адекватность модели в R
Давайте реализуем критерий пригодности хи-квадрат в R. Время запустить RStudio!
Постановка задачи
Давайте разберемся с постановкой задачи, прежде чем погрузиться в R.
Организация утверждает, что опыт работы сотрудников разных отделов распределяется по следующим категориям:
11 — 20 лет = 20%
21 — 40 лет = 17%
6 — 10 лет = 41% и
До 5 лет = 22%
Произведена случайная выборка из 1470 сотрудников. Предоставляет ли эта случайная выборка доказательства против жалоб на компанию?
Вы можете скачать данные здесь.
Формулирование гипотезы
Нулевая гипотеза: истинные пропорции опыта работы сотрудников различных отделов распределены по следующим категориям: 11–20 лет = 20%, 21–40 лет = 17%, 6–10 лет = 41% и до 5 лет. = 22%
Альтернативная гипотеза: распределение опыта сотрудников разных отделов отличается от того, что заявляет организация
Давайте начнем!
Шаг 1. Сначала импортируйте данные
Шаг 2: Подтвердите их правильность в R:
# Шаг 1 — Импорт данных
#Импорт данных csv
data<-read.csv(file.choose())
#Шаг 2: Подтвердите их правильность в R:
#Количество строк и столбцов
dim(data)
#Посмотрим первые 10 rows строк из набора данных
head(data,10)
Вывод:
#Количество строк и столбцов
[1] 1470 2
#Посмотрим первые 10 rows строк из набора данных
age.intervals Experience.intervals
1 41 — 50 6 — 10 Years
2 41 — 50 6 — 10 Years
3 31 — 40 6 — 10 Years
4 31 — 40 6 — 10 Years
5 18 — 30 6 — 10 Years
6 31 — 40 6 — 10 Years
7 51 — 60 11 — 20 Years
8 18 — 30 Upto 5 Years
9 31 — 40 6 — 10 Years
10 31 — 40 11 — 20 Years
Шаг 3: Создайте таблицу сопряженности для ожидаемых частот:
# Шаг 3 — Рассчитать долю опыта работы сотрудников
# Таблица сопряженности для наблюдаемых частот
prop.table((table(data$Experience.intervals)))
Вывод:
11 — 20 Years 21 — 40 Years 6 — 10 Years Upto 5 Years
0.2312925 0.1408163 0.4129252 0.2149660
Шаг 4: Рассчитать значение хи-квадрат:
# Шаг 4 — Рассчитать значение хи-квадрат
chisq.test(x = table(data$Experience.intervals),
p = c(0.2, 0.17, 0.41, 0.22))
Вывод:
Chi-square test for given probabilities
data: table(data$Experience.intervals)
X-squared = 14.762, df = 3, p-value = 0.002032
Значение р здесь меньше 0,05. Поэтому мы отвергнем нашу нулевую гипотезу. Следовательно, распределение опыта работы сотрудников разных отделов отличается от того, что заявляет компания.
Критерий хи-квадрат для независимости
Второй тип теста хи-квадрат — это критерий согласия Пирсона. Этот тест используется, когда у нас есть категориальные данные для двух независимых переменных, и мы хотим увидеть, есть ли какая-либо связь между переменными.
Давайте возьмем другой пример. Учитель хочет знать ответ на вопрос, связан ли результат теста по математике с полом человека, проходящего тест. Или, другими словами, он хочет знать, показывают ли мужчины результаты, отличные от женщин.
Итак, вот две категориальные переменные: пол (мужской и женский) и результат теста по математике (успешно или не успешно). Давайте теперь посмотрим на таблицу сопряженности:
| Boys | Girls | |
| Pass | 17 | 20 |
| Fail | 8 | 5 |
Изучив приведенную выше таблицу непредвиденных обстоятельств, мы можем видеть, что у девочек сравнительно более высокий уровень прохождения теста, чем у мальчиков. Однако, чтобы проверить, является ли эта наблюдаемая разница значимой или нет, мы выполним тест хи-квадрат.
Шаги для вычисления значения хи-квадрат следующие:
Шаг 1: Рассчитать суммарные значения по строкам и столбцам приведенной выше таблицы сопряженности:
| Boys | Girls | Total | |
| Pass | 17 | 20 | 37 |
| Fail | 8 | 5 | 13 |
| Total | 25 | 25 | 50 |
Шаг 2: Рассчитайте ожидаемую частоту для каждой отдельной ячейки путем умножения суммы по строке на сумму по столбцу и делению на общее число наблюдений:
Ожидаемая частота = (сумма по строке x сумма по столбцу) / общая сумма
Для первой ячейки ожидаемая частота будет (37 * 25) / 50 = 18,5. Теперь напишите их ниже наблюдаемых частот в скобках:
| Boys | Girls | Total | |
| Pass | 17 (18.5) |
20 (18.5) |
37 |
| Fail | 8 (6.5) |
5 (6.5) |
13 |
| Total | 25 | 25 | 50 |
Шаг 3: Рассчитать значение хи-квадрат по формуле:
Рассчитайте правую часть каждой ячейки. Например, для первой ячейки
((17-18,5)^2)/18,5 = 0,1216.
Шаг 4: Затем сложите все значения, полученные для каждой ячейки. В этом случае значения будут:
0.1216+0.1216+0.3461+0.3461 = 0.9354
Шаг 5: Рассчитать степени свободы, т. е.
(Количество строк-1) * (количество столбцов-1) = 1 * 1 = 1
Следующая задача — сравнить его с критическим значением хи-квадрат из таблицы, которую мы видели выше.
Расчетное значение хи-квадрат составляет 0,9354, что меньше критического значения 3,84. Таким образом, в этом случае мы не можем отклонить нулевую гипотезу. Это означает, что между этими двумя переменными нет существенной связи, т. е. у мальчиков и девочек статистически схожая картина прохождения/неудач в их математических тестах.
Давайте еще больше укрепим наше понимание, выполнив тест хи-квадрат в R.
Тест хи-квадрат на независимость в R
Постановка задачи
Отдел кадров организации хочет проверить, зависят ли возраст и опыт сотрудников друг от друга. Для этой цели, собирается случайная выборка из 1470 сотрудников с учетом их возраста и опыта. Вы можете скачать данные здесь.
Формулирование гипотезы
Нулевая гипотеза: возраст и опыт — две независимые переменные
Альтернативная гипотеза: возраст и опыт — две зависимые переменные
Давайте начнем!
Шаг 1. Сначала импортируйте данные
Шаг 2: Подтвердите их правильность в R:
# Шаг 1 — Импорт данных
# Импорт данных csv
data<-read.csv(file.choose())
# Шаг 2 — проверка данных на корректность
# Число строк и столбцов
dim(data)
#Выводим первые 10 строк набора данных
head(data,10)
Вывод:
# Число строк и столбцов
[1] 1470 2
> # Выводим первые 10 строк набора данных
age.intervals Experience.intervals
1 41 — 50 6 — 10 Years
2 41 — 50 6 — 10 Years
3 31 — 40 6 — 10 Years
4 31 — 40 6 — 10 Years
5 18 — 30 6 — 10 Years
6 31 — 40 6 — 10 Years
7 51 — 60 11 — 20 Years
8 18 — 30 Upto 5 Years
9 31 — 40 6 — 10 Years
10 31 — 40 11 — 20 Years
Шаг 3: Постройте таблицу сопряженности и вычислите значение хи-квадрат:
# Шаг 3 — Создание таблицы и вычисление значение хи-квадрат
ct<-table(data$age.intervals,data$Experience.intervals)
ct
chisq.test(ct)
Вывод:
ct<-table(data$age.intervals,data$Experience.intervals)<-table age.intervals=»» data=»» font=»» xperience.intervals=»»>
> ct
11 — 20 Years 21 — 40 Years 6 — 10 Years Upto 5 Years
18 — 30 22 0 172 192
31 — 40 190 20 308 101
41 — 50 85 112 110 15
51 — 60 43 75 17 8
> chisq.test(ct)
Pearson’s Chi-squared test
data: ct
X-squared = 679.97, df = 9, p-value < 2.2e-16
Значение р здесь меньше 0,05. Поэтому мы отвергнем нашу нулевую гипотезу. Мы можем сделать вывод, что возраст и опыт являются двумя зависимыми переменными, то есть, по мере того, как опыт увеличивается, возраст также увеличивается (и наоборот).