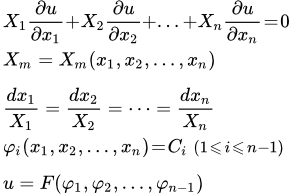Как найти характеристики дифференциального уравнения

From Wikipedia, the free encyclopedia

In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation. The method is to reduce a partial differential equation to a family of ordinary differential equations along which the solution can be integrated from some initial data given on a suitable hypersurface.

Characteristics of first-order partial differential equation[edit]

For a first-order PDE (partial differential equation), the method of characteristics discovers curves (called characteristic curves or just characteristics) along which the PDE becomes an ordinary differential equation (ODE).^[1] Once the ODE is found, it can be solved along the characteristic curves and transformed into a solution for the original PDE.

For the sake of simplicity, we confine our attention to the case of a function of two independent variables x and y for the moment. Consider a quasilinear PDE of the form

$a(x,y,z){frac {partial z}{partial x}}+b(x,y,z){frac {partial z}{partial y}}=c(x,y,z).$

(1)

Suppose that a solution z is known, and consider the surface graph z = z(x,y) in R³. A normal vector to this surface is given by

$left({frac {partial z}{partial x}}(x,y),{frac {partial z}{partial y}}(x,y),-1right).,$

As a result,^[2] equation (1) is equivalent to the geometrical statement that the vector field

is tangent to the surface z = z(x,y) at every point, for the dot product of this vector field with the above normal vector is zero. In other words, the graph of the solution must be a union of integral curves of this vector field. These integral curves are called the characteristic curves of the original partial differential equation and are given by the Lagrange–Charpit equations^[3]

${displaystyle {begin{array}{rcl}{frac {dx}{dt}}&=&a(x,y,z),\{frac {dy}{dt}}&=&b(x,y,z),\{frac {dz}{dt}}&=&c(x,y,z).end{array}}}$

A parametrization invariant form of the Lagrange–Charpit equations^[3] is:

${displaystyle {frac {dx}{a(x,y,z)}}={frac {dy}{b(x,y,z)}}={frac {dz}{c(x,y,z)}}.}$

Linear and quasilinear cases[edit]

Consider now a PDE of the form

$sum _{i=1}^{n}a_{i}(x_{1},dots ,x_{n},u){frac {partial u}{partial x_{i}}}=c(x_{1},dots ,x_{n},u).$

For this PDE to be linear, the coefficients a_i may be functions of the spatial variables only, and independent of u. For it to be quasilinear,^[4] a_i may also depend on the value of the function, but not on any derivatives. The distinction between these two cases is inessential for the discussion here.

For a linear or quasilinear PDE, the characteristic curves are given parametrically by

$(x_{1},dots ,x_{n},u)=(x_{1}(s),dots ,x_{n}(s),u(s))$

such that the following system of ODEs is satisfied

${frac {dx_{i}}{ds}}=a_{i}(x_{1},dots ,x_{n},u)$

(2)

${frac {du}{ds}}=c(x_{1},dots ,x_{n},u).$

(3)

Equations (2) and (3) give the characteristics of the PDE.

Proof for quasilinear Case[edit]

In the quasilinear case, the use of the method of characteristics is justified by Grönwall’s inequality. The above equation may be written as

We must distinguish between the solutions to the ODE and the solutions to the PDE, which we do not know are equal a priori. Letting capital letters be the solutions to the ODE we find

Examining ${displaystyle Delta (s)=|u(mathbf {X} (s))-U(s)|^{2}}$ , we find, upon differentiating that

which is the same as

We cannot conclude the above is 0 as we would like, since the PDE only guarantees us that this relationship is satisfied for
, ,
and we do not yet know that .

However, we can see that

since by the PDE, the last term is 0. This equals

By the triangle inequality, we have

Assuming are at least ${displaystyle C^{1}}$ , we can bound this for small times. Choose a neighborhood Omega around small enough such that are locally Lipschitz. By continuity, will remain in Omega for small enough . Since , we also have that will be in Omega for small enough by continuity. So, and for ${displaystyle sin [0,s_{0}]}$ . Additionally, for some for ${displaystyle sin [0,s_{0}]}$ by compactness. From this, we find the above is bounded as

${displaystyle |Delta '(s)|leq C|u(mathbf {X} (s))-U(s)|^{2}=C|Delta (s)|}$

for some . It is a straightforward application of Grönwall’s Inequality to show that since we have for as long as this inequality holds. We have some interval such that in this interval. Choose the largest epsilon such that this is true. Then, by continuity, . Provided the ODE still has a solution in some interval after epsilon , we can repeat the argument above to find that in a larger interval. Thus, so long as the ODE has a solution, we have .

Fully nonlinear case[edit]

Consider the partial differential equation

$F(x_{1},dots ,x_{n},u,p_{1},dots ,p_{n})=0$

(4)

where the variables p_i are shorthand for the partial derivatives

$p_{i}={frac {partial u}{partial x_{i}}}.$

Let (x_i(s),u(s),p_i(s)) be a curve in R²ⁿ⁺¹. Suppose that u is any solution, and that

$u(s)=u(x_{1}(s),dots ,x_{n}(s)).$

Along a solution, differentiating (4) with respect to s gives

$sum _{i}(F_{x_{i}}+F_{u}p_{i}){dot {x}}_{i}+sum _{i}F_{p_{i}}{dot {p}}_{i}=0$

${dot {u}}-sum _{i}p_{i}{dot {x}}_{i}=0$

$sum _{i}({dot {x}}_{i}dp_{i}-{dot {p}}_{i}dx_{i})=0.$

The second equation follows from applying the chain rule to a solution u, and the third follows by taking an exterior derivative of the relation $du-sum _{i}p_{i},dx_{i}=0$ . Manipulating these equations gives

${dot {x}}_{i}=lambda F_{p_{i}},quad {dot {p}}_{i}=-lambda (F_{x_{i}}+F_{u}p_{i}),quad {dot {u}}=lambda sum _{i}p_{i}F_{p_{i}}$

where λ is a constant. Writing these equations more symmetrically, one obtains the Lagrange–Charpit equations for the characteristic

${frac {{dot {x}}_{i}}{F_{p_{i}}}}=-{frac {{dot {p}}_{i}}{F_{x_{i}}+F_{u}p_{i}}}={frac {dot {u}}{sum p_{i}F_{p_{i}}}}.$

Geometrically, the method of characteristics in the fully nonlinear case can be interpreted as requiring that the Monge cone of the differential equation should everywhere be tangent to the graph of the solution. The second order partial differential equation is solved with Charpit method .

Example[edit]

As an example, consider the advection equation (this example assumes familiarity with PDE notation, and solutions to basic ODEs).

${displaystyle a{frac {partial u}{partial x}}+{frac {partial u}{partial t}}=0}$

where is constant and is a function of and . We want to transform this linear first-order PDE into an ODE along the appropriate curve; i.e. something of the form

${displaystyle {frac {d}{ds}}u(x(s),t(s))=F(u,x(s),t(s)),}$

where is a characteristic line. First, we find

${frac {d}{ds}}u(x(s),t(s))={frac {partial u}{partial x}}{frac {dx}{ds}}+{frac {partial u}{partial t}}{frac {dt}{ds}}$

by the chain rule. Now, if we set ${frac {dx}{ds}}=a$ and ${frac {dt}{ds}}=1$ we get

${displaystyle a{frac {partial u}{partial x}}+{frac {partial u}{partial t}}}$

which is the left hand side of the PDE we started with. Thus

${displaystyle {frac {d}{ds}}u=a{frac {partial u}{partial x}}+{frac {partial u}{partial t}}=0.}$

So, along the characteristic line , the original PDE becomes the ODE ${displaystyle u_{s}=F(u,x(s),t(s))=0}$ . That is to say that along the characteristics, the solution is constant. Thus, ${displaystyle u(x_{s},t_{s})=u(x_{0},0)}$ where $(x_{s},t_{s}),$ and ${displaystyle (x_{0},0)}$ lie on the same characteristic. Therefore, to determine the general solution, it is enough to find the characteristics by solving the characteristic system of ODEs:

In this case, the characteristic lines are straight lines with slope , and the value of remains constant along any characteristic line.

Characteristics of linear differential operators[edit]

Let X be a differentiable manifold and P a linear differential operator

$P:C^{infty }(X)to C^{infty }(X)$

of order k. In a local coordinate system xⁱ,

$P=sum _{|alpha |leq k}P^{alpha }(x){frac {partial }{partial x^{alpha }}}$

in which α denotes a multi-index. The principal symbol of P, denoted σ_P, is the function on the cotangent bundle T^∗X defined in these local coordinates by

$sigma _{P}(x,xi )=sum _{|alpha |=k}P^{alpha }(x)xi _{alpha }$

where the ξ_i are the fiber coordinates on the cotangent bundle induced by the coordinate differentials dxⁱ. Although this is defined using a particular coordinate system, the transformation law relating the ξ_i and the xⁱ ensures that σ_P is a well-defined function on the cotangent bundle.

The function σ_P is homogeneous of degree k in the ξ variable. The zeros of σ_P, away from the zero section of T^∗X, are the characteristics of P. A hypersurface of X defined by the equation F(x) = c is called a characteristic hypersurface at x if

$sigma _{P}(x,dF(x))=0.$

Invariantly, a characteristic hypersurface is a hypersurface whose conormal bundle is in the characteristic set of P.

Qualitative analysis of characteristics[edit]

Characteristics are also a powerful tool for gaining qualitative insight into a PDE.

One can use the crossings of the characteristics to find shock waves for potential flow in a compressible fluid. Intuitively, we can think of each characteristic line implying a solution to along itself. Thus, when two characteristics cross, the function becomes multi-valued resulting in a non-physical solution. Physically, this contradiction is removed by the formation of a shock wave, a tangential discontinuity or a weak discontinuity and can result in non-potential flow, violating the initial assumptions.^[5]

Characteristics may fail to cover part of the domain of the PDE. This is called a rarefaction, and indicates the solution typically exists only in a weak, i.e. integral equation, sense.

The direction of the characteristic lines indicates the flow of values through the solution, as the example above demonstrates. This kind of knowledge is useful when solving PDEs numerically as it can indicate which finite difference scheme is best for the problem.

Notes[edit]

^ Zachmanoglou, E. C.; Thoe, Dale W. (1976), «Linear Partial Differential Equations : Characteristics, Classification, and Canonical Forms», Introduction to Partial Differential Equations with Applications, Baltimore: Williams & Wilkins, pp. 112–152, ISBN 0-486-65251-3
^ John, Fritz (1991), Partial differential equations (4th ed.), Springer, ISBN 978-0-387-90609-6
^ ^a ^b Delgado, Manuel (1997), «The Lagrange-Charpit Method», SIAM Review, 39 (2): 298–304, Bibcode:1997SIAMR..39..298D, doi:10.1137/S0036144595293534, JSTOR 2133111
^ «Partial Differential Equations (PDEs)—Wolfram Language Documentation».
^ Debnath, Lokenath (2005), «Conservation Laws and Shock Waves», Nonlinear Partial Differential Equations for Scientists and Engineers (2nd ed.), Boston: Birkhäuser, pp. 251–276, ISBN 0-8176-4323-0

References[edit]

Courant, Richard; Hilbert, David (1962), Methods of Mathematical Physics, Volume II, Wiley-Interscience
Evans, Lawrence C. (1998), Partial Differential Equations, Providence: American Mathematical Society, ISBN 0-8218-0772-2
Polyanin, A. D.; Zaitsev, V. F.; Moussiaux, A. (2002), Handbook of First Order Partial Differential Equations, London: Taylor & Francis, ISBN 0-415-27267-X
Polyanin, A. D. (2002), Handbook of Linear Partial Differential Equations for Engineers and Scientists, Boca Raton: Chapman & Hall/CRC Press, ISBN 1-58488-299-9
Sarra, Scott (2003), «The Method of Characteristics with applications to Conservation Laws», Journal of Online Mathematics and Its Applications.
Streeter, VL; Wylie, EB (1998), Fluid mechanics (International 9th Revised ed.), McGraw-Hill Higher Education

External links[edit]

Prof. Scott Sarra tutorial on Method of Characteristics
Prof. Alan Hood tutorial on Method of Characteristics

Источник

Линейные дифференциальные уравнения в частных производных первого порядка

Линейные однородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_n – заданные функции переменных x ₁ , x ₂ , . x_n .

Чтобы решить линейное однородное уравнение в частных производных первого порядка:

необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ ₁( x ₁ , x ₂ , . x_n ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n ) = C ₂ ,
.
φ_{n- 1} ( x ₁ , x ₂ , . x_n ) = C_{n- 1} ,
где C_k – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_{n+ 1} – заданные функции от переменных x ₁ , x ₂ , . x_n и z .

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ ₁( x ₁ , x ₂ , . x_n , z ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n , z ) = C ₂ ,
.
φ_n ( x ₁ , x ₂ , . x_n , z ) = C_n .
После чего сразу получаем общий интеграл в неявном виде:

где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ ₁ = F ( φ ₂ , φ ₃ , . φ_n ) ,
φ ₂ = F ( φ ₁ , φ ₃ , . φ_n ) ,
и т. д.

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение:

Здесь переменные уже разделены, интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда

Подставим во второе уравнение:

Или:

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение C₁ = x y 2 :

Итак, мы нашли два интеграла уравнения характеристик:

Общее решение исходного уравнения в частных производных имеет вид:

где F — произвольная функция от двух аргументов F(φ₁, φ₂) . Найдем ее вид из граничного условия
при .

Рассматриваем решение на границе.
Положим x y = –1 :

Отсюда

На границе
.

Итак, мы нашли, что на границе функция F имеет вид:
F ( φ ₁ , φ ₂ ) = φ ₁ φ ₂ .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:

Общее решение:

где F — произвольная функция от двух аргументов F ( φ ₁ , φ ₂ ) .

Неоднородное уравнение

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение:

Умножаем на 2 z и интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда
x = C ₁ y

Подставим во второе уравнение:

Или:

Замечаем, что , тогда

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение и преобразуем:

Итак, мы нашли два интеграла уравнения характеристик:

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:

Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ ₁ , φ ₂) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ ₁ = F ( φ ₂) ,
где F — произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем

Итак, мы нашли, что на границе:

.
Подставим в выражение общего интеграла:
φ ₁ = F ( φ ₂)
.
Сделаем подстановку
:
.

Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ₁ и φ₂ :

.
Умножим на a 2 y 2 .

Автор: Олег Одинцов . Опубликовано: 23-09-2014

Свойства общего решения дифференциального уравнения

Раздел 8. Дифференциальные уравнения

Общая характеристика дифференциальных уравнений

Определение обыкновенного дифференциального уравнения

И дифференциального уравнения в частных производных

Решение различных геометрических, физических и экономических задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту или иную задачу, с некоторой функцией этих переменных и производными этой функции различных порядков.

В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.

Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S, т.е.

Тогда получаем: — уравнение связывающее функцию с независимой переменной t и производной второго порядка функции .

Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, неизвестные функции и производные различных порядков от неизвестных функций по независимым переменным.

Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Пример. — обыкновенное дифференциальное уравнение 1 – го порядка. Общий вид: .

— обыкновенное дифференциальное уравнение 2 – го порядка. Общий вид:

— дифференциальное уравнение в частных производных первого порядка.

Определение. Общим решениемдифференциального уравнения называется дифференцируемая функция одного или нескольких аргументов, которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

В дальнейшее будем рассматривать дифференциальные уравнения, содержащие неизвестную функцию одного независимого аргумента.

Свойства общего решения дифференциального уравнения

1) Любое дифференциальное уравнение имеет бесконечное множество решений. 2) При задании начальных условий , существует такое значение , при котором решением дифференциального уравнения является функция .

Определение. Решение вида называется частным решениемдифференциального уравнения.

Определение. Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида , удовлетворяющего начальным условиям .

Теорема Коши (о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция непрерывна в некоторой области D в плоскости и имеет в этой области непрерывную частную производную , то какова бы не была точка в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку и принимающее при значение , т.е. существует единственное решение дифференциального уравнения.

Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Пример. Найти общее решение дифференциального уравнения .

Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

; ; /

;

; ; ; ; —

общее решение исходного дифференциального уравнения.

Допустим, заданы некоторые начальные условия: , тогда

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

Определение. Интегральной кривойназывается график решения дифференциального уравнения на плоскости .

Определение. Особым решениемдифференциального уравнения называется такое решение, во всех точках которого условие единственности решения задачи Коши не выполняется, т.е. в окрестности некоторой точки существует не менее двух интегральных кривых.

Особые решения не зависят от постоянной С.

Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.

Отметим, что не каждое дифференциальное уравнение имеет особые решения.

Пример. Найти общее решение дифференциального уравнения: Найти особое решение, если оно существует. Имеем

; ; ; ; ; .

Данное дифференциальное уравнение имеет также особое решение .

Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.

Метод характеристик при решение задачи коши для уравнений гиперболического типа

Стерлитамакский филиал Башкирский государственный университет

NovaInfo58, с. 11-15
Опубликовано 25 января 2017
Раздел: Физико-математические науки
Просмотров за месяц: 78
CC BY-NC

Аннотация

В статье рассматривается решение задачи Коши для уравнения гиперболического типа. Продемонстрировано решение данного уравнения методом характеристик.

Ключевые слова

Текст научной работы

Многие задачи физики, в частности механики, приводят к исследованию дифференциальных уравнений в частных производных второго порядка. Так, например, при изучении различных видов волн: звуковых, электромагнитных и других колебательных явлений приходят к волновому уравнению

где u=u(x,y,z,t), a — скорость распространения волны в данной среде. В одномерном случае это уравнение примет вид

которое является уравнением вынужденных колебаний однородной струны [1, 12].

В одномерном случае рассмотрим уравнение струны [2, 26]:

Задача Коши: Найти решение u(x,y) данного уравнения, удовлетворяющее начальным условиям:

Задача Коши для уравнения струны является математической моделью физической задачи о колебаниях настолько большой струны, что влияние ее концов уже не сказывается на колебаниях других точек струны. По этой причине в этой задаче отсутствуют граничные условия.

Приведем уравнение (1) к каноническому виду. Для этого составим уравнение характеристик

где A=0, 2B=e y , C=-1. Вычислим D=B^2-AC=frac><4>>0

. Следовательно, уравнение (1) является уравнением гиперболического типа.

Подставляя в уравнение характеристик наши значения, получим:

источники:

http://megaobuchalka.ru/8/45486.html

http://novainfo.ru/article/10861

Источник

Уравнения характеристик и общие интегралы

Рассмотрим теперь задачу преобразования
исходного уравнения в частных производных
к более простому виду, например,
преобразуем так, чтобы в преобразованном
уравнении коэффициенты

в области

оказались равными нулю, то есть

=0.

Представим эти
уравнения в виде:

Разрешив их
относительно

и

,
получим:

и

,
(8)

где

.
Квадратные уравнения имеют одинаковые
коэффициенты, следовательно, будут
иметь одинаковые корни. Обозначим эти
корни как

и

.

В этих выражениях
предполагается, что

.
Если это условие не выполнено, то
уравнения будут линейными, и будут иметь
простые решения. Решения квадратных
уравнений можно записать в виде

,

.
(9)

Докажем, что
система уравнений в частных производных
(10) эквивалентна системе обыкновенных
дифференциальных уравнений:

и

.
(10)

В самом деле,
пусть функции

есть общие интегралы уравнений (10), то
есть, постоянны вдоль решения этой
системы.

Тогда полное
приращение этих функций вдоль решения
будет равен нулю:

Откуда
получим

В силу
равенств (10) получим

Преобразуя
эти равенства, получим

,

.
То есть, все решения системы (10) являются
также решениями системы (9). Можно
доказать, что верно и обратное утверждение.
Следовательно, системы (9) и (10) эквивалентны.

Общие интегралы
уравнений (10)

образуют два семейства кривых, называемых
характеристиками уравнения (3).
Уравнения (10) называются дифференциальными
уравнениями характеристик.

Канонический вид гиперболических, параболических и эллиптических уравнений

При помощи
общих интегралов определяются новые
переменные и, поэтому форма записи
уравнения в новых переменных будет
зависеть от дискриминанта

.
Рассмотрим все возможные случаи

.

1) Дискриминант

в области

.
Гиперболический тип уравнения. В этом
случае правые части уравнений (10) будут
действительными и различными функциями.
Решая эти дифференциальные уравнения
найдем два общих интеграла

и

.
Тогда, согласно доказанному выше, полагая
в качестве новых переменных

,

,
получим

и в новых переменных исходное уравнение
будет иметь следующий вид

.

Преобразуя,
получим

Это и есть
каноническая форма гиперболического
уравнения. Приведем еще одну каноническую
форму для гиперболических уравнений.
Для этого введем новые переменные

Вычислим
частные производные

Подставляя
эти выражения в первую каноническую
форму, получим

Это вторая
каноническая форма для гиперболических
уравнений.

2) Дискриминант

в области

.
Параболический тип уравнений. В этом
случае решения уравнений (10) совпадают
и в результате решения этих уравнений
получим только один общий интеграл

.
Возьмем в качестве новой переменной

.
В качестве второй переменной возьмем
любую функцию

,
функционально не зависящую от

,
то есть такую, что

При таком
выборе получим

При этом

в силу произвольности

.
Кроме того,

Учитывая
это, получим

,

.

Получили
каноническую форму для параболических
уравнений.

3) Пусть
дискриминант

в области

.
Эллиптический тип уравнений. В этом
случае правые части уравнений (10) будут
комплексными функциями. Тогда общий
интеграл также будет комплексной
функцией. Обозначим эту функцию через

.
Сопряженная к ней

также будет общим интегралом. Тогда
можно ввести новые комплексные переменные

,

.

В
результате введения этих переменных,
как и в случае гиперболических уравнений,
получим

—
канонический вид эллиптических уравнений.
Рассмотрим также и другую каноническую
форму с вещественными переменными. Для
этого введем новые, вещественные
переменные

Откуда
получим

.
Вычисляя коэффициенты по формулам (6)
получим вторую каноническую форму для
эллиптических уравнений

Пример
1. Уравнение в частных производных

,
заданное в области

,
преобразовать к каноническому виду.

Решение.
Вычислим дискриминант данного уравнения

Следовательно,
данное уравнение гиперболического
типа. Составим характеристическое
уравнение

Откуда получим

,

.
Решим эти дифференциальные уравнения
методом разделения переменных:

Откуда, интегрируя,
получим

или

.
Аналогично решим второе уравнение

Таким образом,
общие интегралы будут такими
.
Введем, согласно общей теории
преобразований, новые переменные

По
формулам (5) для частных производных

найдем выражения в новых переменных:

Подставляя эти
выражения в исходное уравнение, получим
канонический вид в новых переменных:

Пример
2. Преобразовать в канонический вид
уравнение

Решение.
Вычислим дискриминант

.
Дискриминант равен нулю и, следовательно,
уравнение параболическое. Составим
характеристическое уравнение:

или

Откуда

и общий интеграл этого уравнения будет

Введем новые
переменные

и найдем выражения для частных производных
в новых переменных

Подставляя в
исходное уравнение эти выражения,
получим

— канонический вид исходного уравнения.

Пример 3. Преобразовать в канонический
вид уравнение

Решение.
Вычислим дискриминант

Следовательно, уравнение эллиптическое.
Составим характеристическое уравнение

Решая это уравнение, получим

Откуда

,

Тогда общими интегралами будут

Обозначим через

и введем новые переменные

Вычисляя по формулам (5) частные производные
и подставляя их в исходное уравнение,
получим

— каноническая форма для исходного
уравнения.

Пример 4.
Уравнение в частных производных

,
заданное в области

,
преобразовать к каноническому виду.

Решение.
Вычислим дискриминант

.
Следовательно, уравнение является
гиперболическим. Составим уравнения
характеристик

,

.

Решим эти
уравнения методом разделения переменных.
Преобразуем к виду

и интегрируя, получим

;

Следовательно,
интегралами будут

и

.
Новыми переменными в этом случае будут

и

.

По формулам (6)
вычислим коэффициенты нового уравнения:

,

,

Подставим их в
уравнение (5а) и получим:

Выразим x и
y через

и  и получим
канонический вид исходного уравнения

Пример
5. Уравнение

,

преобразовать к канонической форме.

Решение.
Вычислим дискриминант

.
Составим
характеристические уравнения:

,

.

Решим их методом
разделения переменных:

Интегрируя,
получим

,

.
Следовательно, новыми переменными будут

Введем вещественные
переменные

и

.

Вычисляя все
коэффициенты нового уравнения по
формулам (6) получим искомый канонический
вид

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Численные методы решения уравнений в частных производных

Метод прямых

Основная идея метода состоит в сведении проблемы решения уравнений в частных производных к решению системы обыкновенных дифференциальных уравнений. Он используется в основном для решения уравнений эллиптического и параболического типов. В методе прямых, в отличие от метода сеток, не все дифференциальные операторы, входящие в исходную дифференциальную задачу, заменяются разностными. Обычно для аппроксимации выбирается оператор, соответствующий пространственной переменной в задаче теплопроводности или соответствующий неравноправному направлению в задачах с эллиптическими уравнениями. Тем самым дифференциальная задача заменяется дифференциально-разностной с меньшим числом непрерывных переменных (понижается размерность дифференциальной задачи). В связи с этим данный метод можно рассматривать как предельный случай метода сеток, когда шаги сетки по определенным независимым переменным стремятся к нулю.

Основную идею конструирования метода прямых рассмотрим на примере нахождениия решения u(x,y) уравнения:

$begin{gathered}A(x,y)frac{partial^2 u(x,y)}{partial x^2}+ 2B(x,y)frac{partial^2 u(x,y)}{partial y,partial x}+ C(x,y) frac{partial^2 u(x,y)}{partial y^2}+ D(x,y)frac{partial u(x,y)}{partial x},+\[2pt] +,E(x,y)frac{partial u(x,y)}{partial y}+ F(x,y)u(x,y)= G(x,y),quad (x,y)in Omega= (0,L)times (0,M), end{gathered}$

(8.59)

с краевыми условиями

$begin{aligned}& (x,0)= varphi(x), & & u(x,M)= psi(x),\ & (0,y)= Phi(y), & & u(L,y)= Psi(y) end{aligned}$

(8.60)

на границах области прямоугольной формы (рис. 8.15), где varphi(x),psi(x), Phi(x), Psi(x) — заданные функции. Пусть выполнено условие B^2-AC<0 эллиптичности уравнения для всех (x,y)in Omega . Отсюда следует, что A(x,y)ne 0,~ C(x,y)ne 0 .

Нахождение решения ДУ в частных производных на границах области

Для решения задачи выберем на отрезке [0,M] точки $y_{j}= j,h,~ 0 leqslant j leqslant J,~ J,h=M$ , и проведем через них прямые, параллельные оси . На каждой прямой дифференциальное уравнение в частных производных (8.59) приближенно заменим обыкновенным дифференциальным уравнением для функций $u(x,y_{j})$ . Для этого аппроксимируем частные производные по ycolon

$begin{gathered}left.{frac{partial widehat{u}(x,y)}{partial y}}right|_{y=y_{j}}= frac{widehat{u}(x,y_{j+1})-widehat{u}(x,y_{j-1})}{2h},,\[2pt] left.{frac{partial^2 widehat{u}(x,y)}{partial y^2}}right|_{y=y_{j}}= frac{widehat{u}(x,y_{j+1})-2,widehat{u}(x,y_{j})+ widehat{u}(x,y_{j-1})}{h^2},,\[2pt] left.{frac{partial^2 widehat{u}(x,y)}{partial y, partial x}}right|_{y=y_{j}}= frac{widehat{u}_{x}(x,y_{j+1})-widehat{u}_{x}(x,y_{j-1})}{2h},. end{gathered}$

(8.61)

Введем обозначения

$begin{gathered}widehat{u}(x,y_{j})= widehat{u}_{j}(x),qquad frac{partial widehat{u}(x,y_{j})}{partial x}= widehat{u},'_{j}(x),qquad frac{partial^2 widehat{u}(x,y_{j}) }{partial x^2}= widehat{u},''_{j}(x),\[4pt] A(x,y_{j})= A_{j}(x),qquad B(x,y_{j})= B_{j}(x),qquad C(x,y_{j})= C_{j}(x)quad text{etc.}end{gathered}$

(8.62)

На прямых, описываемых уравнениями $y_{j}=text{const},~ j=1,ldots,J-1$ , получаем

$begin{gathered} A_{j}(x)widehat{u},''_{j}(x)+ B_{j}(x)frac{widehat{u},'_{j+1}(x)-widehat{u},'_{j-1}(x)}{h}+ C_{j}(x) frac{widehat{u}_{j+1}(x)-2,widehat{u}_{j}(x)+ widehat{u}_{j-1}(x)}{h^2}+ D_{j}(x) widehat{u},'_{j}(x)+\[2pt] E_{j}(x) frac{widehat{u}_{j+1}(x)-widehat{u}_{j-1}(x)}{2h}+ F_{j}(x) widehat{u}_{j}(x)= G_{j}(x),quad j=1,ldots,J-1;~ 0<x<L. end{gathered}$

Здесь $widehat{u}_{1}(x),ldots, widehat{u}_{J-1}(x)$ — приближенное решение задачи на прямых $y=y_1=text{const},ldots, y=y_{J-1}= text{const},$ $A_{j}(x),ldots, G_{j}(x)$ — коэффициенты уравнения (8.59) на этих прямых. В силу краевых условий находим

$begin{gathered}widehat{u}_{0}(x)= u(x,0)= varphi(x),qquad widehat{u}_{J}(x)= u(x,M)= psi(x),\[4pt] widehat{u}_{j}(0)= Phi(y_{j})= Phi(j,h),quad widehat{u}_{j}(L)= Psi(y_{j})= Psi(j,h),quad j=1,ldots,J-1. end{gathered}$

(8.63)

Таким образом, от линейного дифференциального уравнения в частных производных (8.59) и краевыми условиями (8.60) переходим к дифференциально-разностной краевой задаче (8.62),(8.63) для системы из (n-1) обыкновенных дифференциальных уравнений (8.62) относительно (n-1) неизвестных функций $widehat{u}_{1}(x),ldots, widehat{u}_{J-1}(x)$ . В результате ее решения можно найти законы изменения искомой функции u(x,y) вдоль прямых $y_{j}=text{const},$ j=0,1,ldots,J , то есть $widehat{u}(x,y_{j}),~ j=0,1,ldots,J$ . Значения функции в промежуточных точках по у может быть найдено с помощью интерполяции. Система (8.62),(8.63) называется системой уравнений метода прямых.

Замечания

1. В зависимости от выбора аппроксимационных формул для производных по у можно получить различные системы метода прямых, отличающиеся порядком аппроксимации.

2. Метод прямых удобнее применять в том случае, когда коэффициенты в уравнении (8.59) не зависят от . Тогда система (8.62) будет системой с постоянными коэффициентами.

3. Если расчетная область отлична от прямоугольника, при реализации метода возникают трудности, связанные с тем, что функции $u_{j}(x)$ определены на различных множествах.

4. При решении нестационарных уравнений дискретизация проводится по пространственным переменным, а время остается непрерывной переменной.

5. На практике система дифференциальных уравнений (8.62) из-за большого числа должна решаться численно, поэтому потребуется вводить шаг не только по .

6. Если изменение искомой функции внутри множества Omega в направлении не велико, то можно ограничиться одной или двумя прямыми.

Пример 8.9. Составить уравнения метода прямых для решения одномерной задачи теплопроводности (где psi(x) — заданная функция)

$begin{aligned}& u_{t}=a^2cdot u_{xx},quad 0<x<1,quad 0<t<1,\ & u(x,0)= psi(x),quad 0 leqslant x leqslant 1,\ & u(0,t)= u(1,t)=0,quad 0<t leqslant 1. end{aligned}$

Решение, формула (8.64)

Прямые, параллельные оси

Для решения задачи выберем на отрезке [0,1] точки $x_{i}= i,h,~ i=0,1,ldots, I;~ I,h=1$ и проведем через них прямые, параллельные оси (рис. 8.16). На каждой прямой приближенно заменим уравнение теплопроводности обыкновенным дифференциальным уравнением для функции $u(x_{i},t)$ . Для этого заменим частную производную $u_{xx}$ по формуле

$left.{frac{partial^2 widehat{u}}{partial x^2}}right|_{x=x_{i}}= frac{widehat{u}(x_{i-1},t)-2,widehat{u}(x_{i},t)+ widehat{u}(x_{i+1},t)}{h^2}$

и введем обозначения $widehat{u}(x_{i},t)= widehat{u}_{i}(t),~ frac{partial widehat{u}(x_{i}, t)}{partial t}= widehat{u},'_{i}(t)$ .

Тогда на прямых $x_{i}=text{const},~ i=1,ldots,I-1$ , получаем систему и

$begin{gathered}widehat{u},'_{i}(t)= a^2cdot frac{widehat{u}(x_{i-1},t)-2,widehat{u}(x_{i},t)+ widehat{u}(x_{i+1},t)}{h^2},,quad 1 leqslant i leqslant I-1,\[4pt] begin{aligned}& widehat{u}_{0}(t)= u(0,t)=0, & & 0<t leqslant 1,\ & widehat{u}_{I}(t)= u(1,t)=0, & & 0<t leqslant 1 end{aligned} end{gathered}$

(8.64)

с начальными условиями $widehat{u}_{i}(0)= psi(x_{i})= psi(i,h),~ i=1,2,ldots,I-1$ . Полученную систему дифференциальных уравнений можно записать в векторно-матричной форме:

$frac{d}{dt}! begin{pmatrix}widehat{u}_1\ vdots\ vdots\ widehat{u}_{I-1} end{pmatrix}= frac{a^2}{h^2}! begin{pmatrix}-1&1&cdots& 0&0\ 1&-2&1&cdots&0\ vdots& vdots& vdots& vdots& vdots\ vdots& vdots& 1&-2&1\ 0&0&cdots& 1&-2 end{pmatrix}!cdot! begin{pmatrix}widehat{u}_1\ vdots\ vdots\ widehat{u}_{I-1}end{pmatrix}!.$

Задача имеет аналитическое решение

$widehat{u}(t)= H^{-1}cdot! begin{pmatrix}exp dfrac{lambda_1a^2t}{h^2}&0&0\ 0&ddots&0\ 0&0& exp dfrac{lambda_{I-1}a^2t}{h^2} end{pmatrix}!cdot H,u(0),$

где $u(0)= begin{pmatrix}psi(h)\ psi(2h)\ vdots\ psi bigl((I-1)hbigr)end{pmatrix}!,~ lambda_{i}=-left(2cos frac{pi,i}{n}+ 2right)!,~ i=1,ldots,I-1$ — собственные значения матрицы системы, элементы матрицы (собственные векторы матрицы ) равны $H_{ik}= sin frac{pi,ik}{n},,$ i=1,ldots,I-1, k=1,ldots,I-1 .

Заметим, что при численном решении системы обыкновенных дифференциальных уравнений при увеличении числа (улучшении точности) коэффициент жесткости системы увеличивается. При больших значениях справедливо $S= frac{max_{i}|lambda_{i}|}{min_{i}|lambda_{i}|}cong frac{4I^2}{pi^2}$ .

Метод характеристик

Данный метод применяется при численном решении уравнений математической физики, описывающих различные процессы в газовой динамике, теории упругости, прочности и других прикладных областях. При его использовании в процессе решения задачи имеется возможность выделять в расчетных областях особые поверхности или линии, отделяющие области с одними свойствами от областей с другими свойствами.

Рассмотрим основные идеи метода на примере задачи Коши для квазилинейной системы дифференциальных уравнений m-го порядка с двумя независимыми переменными x,,tcolon

$begin{aligned}&begin{aligned}&a_{11} frac{partial u_{1}(x,t)}{partial t}+ ldots+a_{1m} frac{partial u_{m}(x,t)}{partial t}+ b_{11} frac{partial u_{1}(x,t)}{partial x}+ldots+b_{1m} frac{partial u_{m}(x,t)}{partial x}= f_1(x,t,u),\[-2pt] &quadvdots\[-4pt] &a_{m1} frac{partial u_{1}(x,t)}{partial t}+ ldots+a_{mm} frac{partial u_{m}(x,t)}{partial t}+ b_{m1} frac{partial u_{1}(x,t)}{partial x}+ldots+b_{mm} frac{partial u_{m}(x,t)}{partial x}= f_m(x,t,u),end{aligned}\[4pt] &begin{aligned}& u_1(x,0)= varphi_1(x), & & xin mathbb{R},\[-2pt] & quadvdots\[-4pt] & u_m(x,0)= varphi_m(x), & & xin mathbb{R}, end{aligned} end{aligned}$

где $a_{ij}=a_{ij}(x,t,u),~ b_{ij}=b_{ij}(x,t,u),~ i=1,ldots,m;~ j=1,ldots,m;~ D=Rtimes (0,T),~ T>0$ — заданный момент времени. Перепишем систему в векторно-матричном виде

$begin{gathered}A(x,t,u)frac{partial u(x,t)}{partial t}+ B(x,t,u)frac{partial u_{1}(x,t)}{partial x}= f(x,t,u),quad (x,t)in D,\[2pt] u(x,0)= varphi(x),quad xin mathbb{R}, end{gathered}$

(8.65)

где $A(x,t,u)= bigl(a_{ij}(x,t,u)bigr),~ B(x,t,u)= bigl(b_{ij}(x,t,u)bigr)$ — матрицы размеров $(mtimes m),~ f(x,t,u)= begin{pmatrix}f_1(x,t,u)\vdots\ f_m(x,t,u) end{pmatrix}$ — вектор-функция, $u(x,t)= begin{pmatrix}u_1(x,t)\ vdots\ u_m(x,t) end{pmatrix}$ — искомая вектор-функция правых частей, $varphi(x)= begin{pmatrix} varphi_1(x)\ vdots\ varphi_m(x) end{pmatrix}$ — заданная вектор-функция.

Пусть известно, что система (8.65) имеет гладкое решение в области и на некоторой кривой gamma оно задано и равно $Bigl.{u(x,t)}Bigr|_{gamma}$ (рис. 8.17). Рассмотрим задачу о нахождении решения в окрестности кривой gamma .

График кривой, проходящей через точку

Выберем на кривой gamma произвольную точку (x_0,t_0) , а вектор бесконечно малого смещения вдоль этой кривой из точки обозначим (dx,dt) . Присоединим к уравнениям (8.65) выражение для полного дифференциала (для упрощения записи опустим аргументы):

$A,frac{partial u}{partial t}+ B,frac{partial u}{partial x}=f,qquad du= frac{partial u}{partial x},dx+ frac{partial u}{partial t},dt,.$

Умножим первое уравнение на , а из второго выразим $frac{partial u}{partial t},dtcolon$

$A,frac{partial u}{partial t},dt+ B,frac{partial u}{partial x},dt= f,dt,qquad frac{partial u}{partial t},dt= du-frac{partial u}{partial x},dx,.$

Подставляя второе уравнение в первое, имеем $A,du-A,frac{partial u}{partial x},dx+ B,frac{partial u}{partial x},dt= f,dt$ или

$(B,dt-A,dx)cdot frac{partial u}{partial x}= f,dt-A,du,.$

(8.66)

Если определитель матрицы (B,dt-A,dx) отличен от нуля в каждой точке кривой gamma , то частная производная $frac{partial u}{partial x}$ и, следовательно, частная производная $frac{partial u}{partial t}$ определяются однозначно. В этом случае можно найти решение в окрестности кривой $gammacolon, Bigl.{u(x,t)= u(x,t)}Bigr|_{gamma}+ du$ , что соответствует разложению искомого решения по формуле Тейлора до членов первого порядка. Если определитель матрицы (B,dt-A,dx) в каждой точке кривой gamma равен нулю, то в силу предположения о существовании решения производные $frac{partial u}{partial x},, frac{partial u}{partial t}$ и, следовательно, функция u(x,t) , находятся неоднозначно. В этом случае кривая у называется характеристикой. Приравнивая определитель матрицы (B,dt-A,dx) к нулю и предполагая, что dtne0 вдоль кривой gamma , получаем соотношение

$left|B-Acdot frac{partial u}{partial t}right|=0quad text{ili}quad |B-A lambda|=0,$

(8.67)

где $lambda(x,t,u)= frac{partial u}{partial t}$ . Линии, задаваемые дифференциалами смещения dx,,dt , вдоль которых справедливо (8.67), являются характеристиками. Анализ разрешимости уравнения (8.67) позволяет ввести классификацию систем вида (8.65).

Если уравнение (8.67) имеет различных действительных корней, то система (8.65) называется гиперболической; если их число меньше , то система называется параболической; если уравнение не имеет действительных корней, то — эллиптической. В дальнейшем будем рассматривать только гиперболические системы, т.е. имеющие различных характеристик:

$left(frac{dx}{dt}right)_{i}= lambda_{i}(x,t,u),quad i=1,2,ldots,m,$

(8.68)

где функции $lambda_{i}(x,t,u)$ задают характеристические направления в каждой точке кривой gamma .

Вдоль характеристик решение системы должно удовлетворять характеристическим соотношениям (соотношениям совместности), которые получаются в результате приравнивания к нулю определителя m-го порядка расширенной матрицы, т.е.

bigl(B,dt-A,dx,, f,dt-A,dubigr).

(8.69)

При этом следует избегать случаев получения тривиальных тождеств. Характеристические соотношения связывают дифференциалы искомых функций с дифференциалами независимых переменных вдоль характеристик.

Этот способ получения характеристических соотношений основан на применении теоремы Кронекера-Капелли: решение системы (8.66) существует тогда и только тогда, когда ранг матрицы (B,dt-A,dx) этой системы равен рангу расширенной матрицы. Предполагается, что решение существует и определитель матрицы системы (m-го порядка) вдоль характеристик равен нулю. Поэтому должен быть равен нулю определитель расширенной матрицы, составленный из произвольных столбцов.

В результате описан принцип получения характеристических уравнений (уравнений характеристик и характеристических соотношений). Их вывод составляет первый этап метода характеристик. Основные идеи первого, а также второго этапа, связанного с конструированием численной схемы, рассмотрим на примере линейной задачи Коши для одномерного волнового уравнения, описывающего распространение плоских звуковых волн в покоящейся среде.

Пример 8.10. Получить соотношения метода характеристик для решения линейной задачи Коши

$frac{partial^2 varphi(x,t)}{partial t^2} = frac{partial^2 varphi(x,t)}{partial x^2},,quad (x,t)in mathbb{R}times (0;T),quad varphi(x,0)=x^2+x,quad varphi_t(x,0)=cos x,quad xin mathbb{R}.$

Решение, формулы (8.70)-(8.77)

Данная задача, в частности, описывает процесс распространения звуковых волн в спокойной среде (отсутствуют источники и стоки), следовательно, решаемое уравнение можно рассматривать как уравнение акустики.

Для применения метода характеристик сначала сведем задачу к виду (8.65), т.е. к системе двух уравнений первого порядка. Для этого введем новые искомые функции

$nu(x,t)= frac{partial varphi(x,t)}{partial t},qquad p(x,t)= frac{partial varphi(x,t)}{partial x},.$

Здесь nu(x,t),,p(x,t) — отклонения скорости и давления от их значений в невозмущенной среде, вызванные распространением звуковых волн, varphi(x,t) — потенциал функции nu(x,t) . Тогда уравнение можно представить в форме

$frac{partial }{partial t}! left(frac{partial varphi(x,t)}{partial t}right)= frac{partial }{partial x}! left(frac{partial varphi(x,t)}{partial x}right)quad text{ili}quad frac{partial nu(x,t)}{partial t}-frac{partial p(x,t)}{partial x}=0.$

Предполагая, что задача имеет гладкое решение (т.е. рассматриваемая функция имеет столько непрерывных производных, сколько нужно для законности приводимых преобразований), воспользуемся свойством, справедливым для дважды непрерывно дифференцируемых функций:

$frac{partial^2 varphi(x,t)}{partial x,partial t}= frac{partial^2 varphi(x,t)}{partial t,partial x}quad text{ili}quad frac{partial p(x,t)}{partial t}= frac{partial nu(x,t)}{partial x},.$

В результате от исходной задачи для волнового уравнения переходим к задаче для системы двух дифференциальных уравнений с начальными условиями относительно новых искомых функций:

$left{begin{aligned}& frac{partial nu(x,t)}{partial t}-frac{partial p(x,t)}{partial x}=0, & & nu(x,0)=cos x,\ & frac{partial p(x,t)}{partial t}-frac{partial nu(x,t)}{partial x}=0, & & p(x,0)=2x+1. end{aligned}right.$

Запишем систему в виде (8.65)

$Acdot frac{partial u}{partial t}+ Bcdot frac{partial u}{partial x}=0,quad u(x,0)= begin{pmatrix}cos x\ 2x+1end{pmatrix}!,$

(8.70)

где $A=begin{pmatrix}1&0\0&1end{pmatrix}!,~ B=begin{pmatrix}0&-1\-1&0end{pmatrix}!,~ u=begin{pmatrix}nu\p end{pmatrix}!,~ m=2$ . Для решения задачи (8.70) применим метод характеристик, содержащий два этапа.

Первый этап. Нахождение характеристик и вывод характеристических соотношений. Для этого решим уравнение (8.67), записанное для (8.70):

$|B-Acdot lambda|= begin{vmatrix}-lambda&-1\-1&-lambda end{vmatrix}=0.$

Получаем $lambda^2-1=0,~ lambda_{1,2}=pm1$ , т.е. два направления характеристик:

${left(frac{dx}{dt}right)!}_{1}= lambda_1=1;quad {left(frac{dx}{dt} right)!}_{2}= lambda_2=-1.$

(8.71)

Интегрируя, найдем общие решения полученных дифференциальных уравнений. Для первого уравнения x=t+text{const} , а для второго x=-t+text{const} . Им соответствуют два семейства характеристик (в данной задаче прямых линий). Их принято обозначать буквой $C^{+}$ с верхним индексом «+» для семейства характеристик, имеющих меньший угол с положительным направлением оси Ох по сравнению с соответствующим углом для характеристик семейства $C^{-}$ . В данной задаче характеристики семейства $C^{+}$ имеют положительный наклон, а характеристики семейства $C^{-}$ — отрицательный наклон (рис. 8.18). Условно их также называют характеристиками первого и второго семейств соответственно.

Семейства наклонных прямых

Для получения характеристических соотношений запишем расширенную матрицу (в решаемой задаче $f=begin{pmatrix}0\0 end{pmatrix}$ ):

$bigl(B,dt-A,dx,, f,dt-A,,dubigr)= left(underbrace{begin{pmatrix}0&-dt\-dt&0 end{pmatrix}}_{B,dt}-underbrace{begin{pmatrix}dx&0\ 0&dx end{pmatrix}}_{A,dx},-underbrace{begin{pmatrix}1&0\ 0&1 end{pmatrix}!! begin{pmatrix}dnu\ dpend{pmatrix}}_{A,du} right)= begin{pmatrix}-dx&-dt-dnu\-dt&-dx&-dp end{pmatrix}!.$

Приравнивая определитель матрицы, составленной из последних двух столбцов, нулю, получаем

$begin{vmatrix}-dt&-dnu\-dx&-dp end{vmatrix}= dpcdot dt-dnucdot dx=0.$

Поделив на (предполагается, что dtne 0 ), имеем $dp-dnu, frac{dx}{dt}=0$ . Так как на прямых семейства $C^{+}$ выполняется равенство ${left( frac{dx}{dt} right)!}_{1}= lambda_1=1$ , то соответствующие характеристическое соотношение имеет вид

dp-dnu=0.

(8.72)

Аналогично на прямых семейства $C^{-}$ справедливо ${left( frac{dx}{dt} right)!}_{2}= lambda_2=-1$ и

dp+ dnu=0.

(8.73)

Обыкновенные дифференциальные уравнения (8.71)–(8.73) образуют систему уравнений метода характеристик. Полученные характеристические соотношения (8.72), (8.73) в данной задаче могут быть проинтегрированы. В результате получаются конечные соотношения, называемые инвариантами Римана. Далее они будут использованы при построении численной схемы

p-nu=text{const} (вдоль семейства $C^{+}$ ),

p+nu=text{const} (вдоль семейства $C^{-}$ ),

Результатом первого этапа является получение уравнений характеристик и характеристических соотношений (следствий из них):

$begin{aligned}& {left( frac{dx}{dt} right)!}_{1}=1 & & (x=t+text{const}); & & p-nu=text{const},\ & {left( frac{dx}{dt} right)!}_{2}=-1 & & (x=-t+text{const}); & & p+nu=text{const}.end{aligned}$

(8.74)

К системе (8.74) следует добавить начальные условия nu(x,0)=cos x,~ p(x,0)=2x+1 .

Второй этап. Конструирование численной схемы и вычисление значений искомых функций.

1. Для простоты изложения выделим на оси Ох отрезок [0;l] и на нем зададим три точки 0;0,5;1 (рис.8.19, а). Они соответствуют нулевому временному слою. Значения функций p(x,t),, nu(x,t) в этих точках будем обозначать $p_{i}^0,,nu_{i}^0,~ i=0,1,2$ , а сами точки $(x_{i},t^n)$ парами индексов (i,n) , где — номер точки по переменной , а — номер временного слоя. Для n=0 с учетом начальных условий nu(x,0)=cos x,~ p(x,0)=2x+1 получаем

$begin{aligned}& nu_{0}^{0}= nu(0;0)=1; & & nu_{1}^{0}= nu(0,!5;0)=0,!8776; & & nu_{2}^{0}= nu(1;0)=0,!5403;\[2pt] & p_{0}^{0}= p(0;0)=1; & & p_{1}^{0}= nu(0,!5;0)=2; & & p_{2}^{0}= p(1;0)=3. end{aligned}$

Конструкция численной схемы

2. Выведем разностные уравнения, определяющие положение точек на следующем временном слое и значения искомых функций в них. Система (8.74) заменяется системой разностных уравнений. Численное решение задачи строится на характеристической сетке, которая формируется одновременно с процессом нахождения решения. При этом обычно рассматривается трехточечный угловой шаблон с узлами «1»,»2″,»3″, составленный отрезками характеристик (из семейств $C^{+}$ и $C^{-}$ ), пересекающихся в рассчитываемой точке «3» (рис. 8.19,б). Назовем этот шаблон базовым. Предполагается, что положение узлов «1» , «2» и значения решения в узлах известны из начальных условий или рассчитаны на предыдущем шаге. Положение узла «3» и значение решения в нем подлежат определению.

Аппроксимируя производную по формулам

${left(frac{dx}{dt}right)}_{1}cong frac{x_3-x_1}{t_3-t_1}$ (вдоль характеристики из семейства $C^{+}$ с lambda_1=1 ),

${left(frac{dx}{dt}right)}_{2}cong frac{x_3-x_2}{t_3-t_2}$ (вдоль характеристики из семейства $C^{-}$ с lambda_2=-1 ),

получаем

x_3-x_1=t_3-t_1,qquad x_3-x_2=t_2-t_3.

(8.75)

Условие p-nu=text{const} вдоль характеристик из семейств $C^{+}$ записывается для лежащих на ней узлов «1» и «3»:

p_3-nu_3=p_1-nu_1,

(8.76)

а условие p-nu=text{const} вдоль характеристики из семейства $C^{-}$ записывается для лежащих на ней узлов «2» и «3»:

p_3+nu_3= p_2+nu_2.

(8.77)

Система (8.75)–(8.77) является замкнутой относительно искомых значений x_3,,t_3,,p_3,,nu_3 при известных x_1, t_1, x_2, t_2, p_1, nu_1, p_2, nu_2 . Формулы (8.75)–(8.77) являются базовыми для расчета всех точек, принадлежащих области . После совмещения узлов «1» и «2» базового шаблона с выбранными очередными узлами сетки в (8.75)–(8.77) подставляются конкретные величины в соответствии с принятыми обозначениями.

Чертеж углового шаблона

3. Производится расчет первого временного слоя. В решаемой задаче на нулевом временном слое угловой шаблон может занимать два положения (рис. 8.20, а,б). Для точки с номерами (0,1) первого рассчитываемого слоя узлы «1» и «2» углового шаблона совмещаются с узлами (0,0) и (1,0) (рис. 8,20,а). Поэтому система (8.75)–(8.77) имеет вид

$begin{aligned} & x_{0,1}-x_{0,0}= t_{0,1}-t_{0,0}, & & x_{0,1}-x_{1,0}= t_{1,0}-t_{0,1},\[2pt] & p_0^1-nu_0^1= p_0^0-nu_0^0, & & p_0^1+ nu_0^1= p_1^0+ nu_1^0. end{aligned}$

Подставляя $t_{0,0}=0,~ t_{1,0}=0,~ x_{0,0}=0,~ x_{1,0}=0,!5$ и известные значения p_0^0, p_1^0, nu_0^0, nu_1^0 на нулевом слое (см. п.1), получаем

$begin{gathered}x_{0,1}-0=t_{0,1}-0;qquad x_{0,1}-0,!5=0-t_{0,1};\[2pt] p_0^1-nu_0^1=1-1=0;qquad p_0^1+nu_0^1=2+ 0,!8776= 2,!8776. end{gathered}$

Решение этой системы: $x_{0,1}=0,!25;~ t_{0,1}=0,!25;~ p_0^1=1,!4388;~ nu_0^1=1,!4388$ .

Для второй точки первого слоя (рис. 8.20,б) с номерами (l;l) узлы «1» и «2» углового шаблона совмещаются с узлами (l;0) и (2;0) . Тогда система (8.75)–(8.77) имеет вид:

$begin{gathered}x_{1,1}-x_{1,0}=t_{1,1}-t_{1,0};qquad x_{1,1}-x_{2,0}= t_{2,0}-t_{1,1};\[2pt] p_1^1-nu_1^1= p_1^0-nu_1^0;qquad p_1^1+ nu_1^1= p_2^0+ nu_2^0. end{gathered}$

Подставляя $t_{1,0}=0,~ t_{2,0}=0,~ x_{1,0}=0,!5,~ x_{2,0}=1$ и известные значения p_1^0,nu_1^0,o_2^0,nu_2^0 на нулевом слое (см. п.1), получаем

$begin{gathered}x_{1,1}-0,!5=t_{11}-0;qquad x_{1,1}-1=0-t_{1,1};\[2pt] p_1^1-nu_1^1=2-0,!8776=1,!1224;qquad p_1^1+nu_1^1=3+0,!5403= 3,!5403. end{gathered}$

Отсюда $x_{1,1}= 0,!75;~ t_{1,1}= 0,!25; p_1^1= 2,!33135;~ nu_1^1= 1,!20895$ .

4. Для расчета точки (0,2) следующего временного слоя узлы «1» и «2» углового шаблона совмещаются с узлами (0,1) и (1,1) (рис.8.20,в). Тогда система (8.75)–(8.77) принимает вид:

$begin{gathered}x_{0,2}-x_{0,1}=t_{0,2}-t_{0,1};qquad x_{0,2}-x_{1,1}=t_{1,1}-t_{0,2};\[2pt] p_0^2-nu_0^2= p_0^1-nu_0^1;qquad p_0^2+nu_0^2= p_1^1+ nu_1^1. end{gathered}$

Подставляя значения с предыдущего слоя, имеем

$begin{gathered}x_{0,2}-0,!25=t_{0,2}-0,!25;qquad x_{0,2}-0,!75= 0,!25-t_{0,2};\[2pt] p_0^2-nu_0^2= 1,!4388-1,!4388;qquad p_0^2+ nu_0^2=2,!33135+ 1,!20895. end{gathered}$

Отсюда $x_{0,2}= 0,!5;~ t_{0,2}= 0,!5;~ p_0^2=nu_0^2= 1,!77015$ .

Очевидно (см. рис. 8.19,а), количество узлов на каждом последующем слое уменьшается на единицу. Расчет продолжается до замыкания области, так как на последнем слое останется один узел. В данном примере этим узлом является точка (0,2) .

Замечание. Рассмотренная в примере 8.10 задача является всего лишь модельной, выбранной для пояснения основных принципов конструирования метода характеристик и его численной реализации. В вычислительной практике, как правило, ставятся нелинейные задачи. Проиллюстрируем некоторые особенности их решения на следующем примере.

Пример 8.11. Получить соотношения метода характеристик для решения нелинейной задачи Коши

$begin{gathered}begin{aligned}&a_{11}frac{partial u_1(x,t)}{partial t}+ a_{12}frac{partial u_2(x,t)}{partial t}+ b_{11}frac{partial u_1(x,t)}{partial x}+ b_{12}frac{partial u_2(x,t)}{partial x}=f_1,\ &a_{21}frac{partial u_1(x,t)}{partial t}+ a_{22}frac{partial u_2(x,t)}{partial t}+ b_{21}frac{partial u_1(x,t)}{partial x}+ b_{22}frac{partial u_2(x,t)}{partial x}=f_2,end{aligned}quad (x,t)in D\[4pt] u_1(x,0)= varphi_1(x),quad u_2(x,0)= varphi_2(x),quad xin mathbb{R},end{gathered}$

где $a_{ij}=a_{ij}(x,t,u),~ b_{ij}=b_{ij}(x,t,u),~ f_{i}=f_{i}(x,t,u),~ i=1,2;~ j=1,2;~ varphi_{1}(x),~ varphi_2(x)$ — заданные функции; D=mathbb{R}times (0,T),~ T>0 — заданный момент времени.

[reshenie=Решение, формулы (8.78)-(8.80)]

Поставленная задача является частным случаем задачи (8.65) при m=2 . Применим метод характеристик, включающий два этапа.

Первый этап. Нахождение характеристик и характеристических соотношений. Уравнение (8.67) имеет вид

$|B-A lambda|= begin{vmatrix}b_{11}-lambda a_{11}& b_{12}-lambda a_{12}\ b_{21}-lambda a_{21}& b_{22}-lambda a_{22}end{vmatrix}=0$ или a,lambda^2+ b,lambda+c=0,

где $a=a_{11}a_{12}-a_{12}a_{21},~ b=a_{21}b_{12}+ a_{12}b_{21}-a_{11}b_{22}-a_{22}b_{11},~ c=b_{11}b_{22}-b_{12}b_{21}$ . Решая полученное уравнение, находим выражения для двух характеристических направлений в каждой точке расчетной области:

$begin{aligned}&{left(frac{dx}{dt}right)}_{1}= lambda_{1}(x,t,u_1,u_2)= frac{-b+ sqrt{b^2-ac}}{2a}quad (C^{+});\[2pt] &{left(frac{dx}{dt}right)}_{2}= lambda_{2}(x,t,u_1,u_2)= frac{-b-sqrt{b^2-ac}}{2a}quad (C^{-}). end{aligned}$

(8.78)

Сформируем расширенную матрицу

$bigl(B,dt-A,dx,, f,dt-A,dubigr)= begin{pmatrix}b_{11}dt-a_{11}dx& b_{12}dt-a_{12}dx& f_1dt-a_{11}du_1-a_{12}du_2\ b_{21}dt-a_{21}dx& b_{22}dt-a_{22}dx& f_2dt-a_{21}du_1-a_{22}du_2 end{pmatrix}$

Характеристические соотношения получаются в результате приравнивания нулю определителя второго порядка (m=2) , составленного из второго и третьего столбцов расширенной матрицы:

$begin{vmatrix}b_{12}dt-a_{12}dx& f_1dt-a_{11}du_1-a_{12}du_2\ b_{22}dt-a_{22}dx& f_2dt-a_{21}du_1-a_{22}du_2 end{vmatrix}=0.$

Раскрыв определитель и поделив на dtne0 , получим

$left(e-a,frac{dx}{dt}right)!du_1+ g,du_2+ h,dt+ q,dx=0,$

где $e=a_{11}b_{22}-a_{21}b_{12},~ g=a_{12}b_{22}-a_{22}b_{12},~ h=b_{12}f_2-b_{22}f_1,~ q=a_{22}f_1-a_{12}f_2$ . Последние два слагаемых перепишем в эквивалентной форме $h,dt+ q,dx= left(h+ q,frac{dx}{dt}right)!dt$ .

Поскольку для семейства характеристик $C^{+}$ выполняется равенство ${left(frac{dx}{dt}right)}_{1}= lambda_{1}$ , а для семейства $C^{-}$ — равенство ${left(frac{dx}{dt}right)}_{2}= lambda_{2}$ , то характеристические соотношения имеют вид

$begin{aligned}& (e-a lambda_1),du_1+ g,du_2+ (h+q lambda_1),dt=0quad (C^{+});\[2pt] & (e-a lambda_2),du_1+ g,du_2+ (h+q lambda_2),dt=0quad (C^{-}). end{aligned}$

(8.79)

В результате получена характеристическая система (8.78), (8.79) из четырех обыкновенных дифференциальных уравнений. Они позволяют найти значения t,x,u_1,u_2 вдоль характеристик.

Второй этап. Конструирование численной схемы. Как и в предыдущем примере, будем использовать трехточечный угловой шаблон (рис. 8.19, б). Предполагается, что в точках «1» и «2» известны значения t,x,u_1,u_2 из начальных данных или из расчета предыдущего слоя, т.е. $t_1,x_1,u_{11},u_{21}$ для точки «1» и $t_2,x_2,u_{12},u_{22}$ для точки «2». Здесь при обозначении значений функций u_1,u_2 , а далее и при обозначении других функций в точках шаблона первый нижний индекс соответствует номеру самой функции, а второй индекс — номеру точки в шаблоне. Требуется найти значения $t_3,x_3, u_{13}, u_{23}$ определяющие положение точки «3» и значения искомых функций в ней. Предполагается, что точки «1» и «2» близки друг к другу, поэтому заменим дифференциалы конечными приращениями, а производную $frac{dx}{dt}$ — конечноразностным отношением:

$begin{gathered}dtcong Delta t=t_3-t_1,quad dxcong Delta x=x_3-x_1,quad du_1cong Delta u_1=u_{13}-u_{11},quad du_2cong Delta u_2=u_{23}-u_{21},quad {left(frac{dx}{dt} right)}_{1}cong frac{x_3-x_1}{t_3-t_1}quad (C^{+});\[4pt] dtcong Delta t=t_3-t_2,quad dxcong Delta x=x_3-x_2,quad du_1cong Delta u_1=u_{13}-u_{12},quad du_2cong Delta u_2=u_{23}-u_{22},quad {left(frac{dx}{dt}right)}_{2}cong frac{x_3-x_2}{t_3-t_2}quad (C^{+}). end{gathered}$

В итоге уравнения характеристик являются уравнениями прямых, соединяющих точки «1» и «2» с точкой «3», а характеристическая система (8.78), (8.79) преобразуется к виду

$begin{gathered}begin{aligned}& x_3-x_1= (lambda_1)_1(t_3-t_1),\ & x_3-x_2= (lambda_2)_2(t_3-t_2),end{aligned}\[4pt] begin{aligned}& (e-a lambda_1)_1(u_{13}-u_{11})+ (g)_1(u_{23}-u_{21})+ (h+ q lambda_1)_1 (t_3-t_1)=0,\ & (e-a lambda_2)_2(u_{13}-u_{12})+ (g)_2(u_{23}-u_{22})+ (h+ q lambda_2)_2 (t_3-t_2)=0. end{aligned}end{gathered}$

(8.80)

Здесь нижние индексы 1 и 2 указывают, что значения всех функций, входящих в соответствующие выражения, подсчитываются в точке «1» или «2». Решая систему (8.80), можно найти значения $t_3,x_3,u_{13},u_{23}$ » определяющие положение точки «3» и значения искомых функций в ней. Сначала обычно решаются первые два уравнения и определяются значения t_3,x_3 , а затем — последние два уравнения, откуда находятся $u_{13},u_{23}$ .

Опишем теперь общую схему численного решения поставленной задачи Коши.

1. При t=0 на оси абсцисс задаются точки с некоторым шагом. В этих точках (на рис. 8.21 выделен фрагмент, содержащий точки 1-6) значения функций $u_{1},u_{2}$ определяются начальными данными, т.е. функциями varphi_1(x), varphi_2(x) .

Схема численного решения уравнения в частных производных

2. В соответствии с изложенной методикой последовательно рассчитываются координаты точек 7-11 и приближенные значения решения в них. При этом точки «1» и «2» углового шаблона последовательно совмещаются с точками 1 и 2, затем с точками 2 и 3, 3 и 4, 4 и 5, 5 и 6. Узлами выстраиваемой характеристической сетки служат точки пересечения характеристик (они образуют следующий временной слой).

3. Расчет слоев продолжается до достижения последней точки (точки 21) треугольной области.

Отметим, что дифференциальным уравнениям (8.78) соответствуют криволинейные характеристики, а точка «3» должна быть точкой пересечения этих криволинейных характеристик. При переходе от дифференциальных уравнений (8.78),(8.79) к разностным дифференциалы были заменены конечными разностями, а производные конечно-разностными отношениями. Вследствие этого криволинейные характеристики были аппроксимированы отрезками прямых. Решение системы (8.80) объявляется первым приближением, т.е. $t_3^{(1)}= t_3,~ x_3^{(1)}= x_3,$ $u_{13}^{(1)}= u_{13},~ u_{23}^{(1)}= u_{23},$ и может возникнуть необходимость в уточнении координат точки «3» и значений искомых функций в этой точке. Ограничимся изложением одного из возможных способов уточнения. После нахождения первого приближения следует найти средние арифметические значения:

$begin{aligned}& overline{lambda}_{1}= frac{(lambda_1)_1+ (lambda_1)_3}{2},,quad overline{lambda}_{2}= frac{(lambda_2)_2+ (lambda_2)_3}{2},,quad K_1= frac{(e-a lambda_1)_1+ (e-a lambda_1)_3}{2},,quad K_2= frac{(e-a lambda_2)_2+ (e-a lambda_2)_3}{2},,\[4pt] & overline{L}_{1}= frac{(g)_1+ (g)_3}{2},,quad overline{L}_{2}= frac{(g)_2+ (g)_3}{2},,quad M_1= frac{(h+ q lambda_1)_1+ (h+ q lambda_1)_3}{2},,quad M_2= frac{(h+ q lambda_2)_2+ (h+ q lambda_2)_3}{2},,end{aligned}$

где нижний индекс 3 указывает, что соответствующее выражение подсчитывается в найденной точке «3». Эти соотношения получаются, если при интегрировании дифференциальных уравнений применять правило трапеций. Затем решается система

$begin{gathered}x_{3}^{(2)}-x_{1}= overline{lambda}_{1}(t_{3}^{(2)}-t_{1}),\ x_{3}^{(2)}-x_{2}= overline{lambda}_{2}(t_{3}^{(2)}-t_{2}),\[4pt] K_1,bigl(u_{13}^{(2)}-u_{11}bigr)+ L_1,bigl(u_{23}^{(2)}-u_{21}bigr)+ M_1,bigl(t_{3}^{(2)}-t_{1}bigr)=0,\ K_2,bigl(u_{13}^{(2)}-u_{12}bigr)+ L_2,bigl(u_{23}^{(2)}-u_{22}bigr)+ M_2,bigl(t_{3}^{(2)}-t_{2}bigr)=0 end{gathered}$

относительно нового (второго) приближения $t_2^{(2)},,x_3^{(2)},, u_{13}^{(2)},, u_{23}^{(2)}$ . Описанный процесс продолжают до тех пор, пока решения, полученные при двух последовательных приближениях, не будут совпадать с заданной точностью. Как правило, если расстояние между точками «1» и «2» невелико, достаточно сделать два уточнения.

Замечания

1. Приведенные примеры иллюстрируют важное свойство метода характеристик, отличающее его от ранее рассмотренных разностных методов. Оно заключается в том, что расчеты осуществляются вдоль характеристик — линий, по которым распространяется информация об исходных данных, что придает методу четкий физический смысл.

2. Описанный метод расчета, когда точки следующего слоя заранее неизвестны, а вычисления ведутся вдоль характеристик семейств $C^{+}$ и $C^{-}$ , выделяемых в процессе расчета, называется классическим методом характеристик. Существуют модификации этого метода, когда точки следующего слоя задаются заранее, а для нахождения значений искомых функций в них характеристики выпускаются в направлении к известному слою. Такие методы называются сеточно-характеристическими.

Метод Годунова

В механике сплошных сред при решении задач, описывающихся квазилинейными дифференциальными уравнениями в частных производных, в расчетных областях могут возникать поверхности сильного разрыва, к которым относятся ударные волны, центрированные волны разрежения, поверхности контактного разрыва. На этих поверхностях терпят разрыв как искомые функции, характеризующие исследуемые процессы, так и их производные. При решении таких задач используются два класса численных схем, в одном из которых с использованием законов сохранения явно выделяются поверхности разрыва, а в другом эти поверхности явно не выделяются, а рассчитываются «насквозь» вместе с областями непрерывности. К последнему классу методов относится метод С. К. Годунова. Идею его конструирования рассмотрим на примере решения смешанной краевой задачи для уравнений акустики.

Пример 8.12. Получить соотношения метода Годунова для решения задачи

$frac{partial u(x,t)}{partial t}+ frac{1}{rho_0}cdot frac{partial p(x,t)}{partial x}=0,qquad frac{partial p(x,t)}{partial t}+ rho_0a_0^2cdot frac{partial u(x,t)}{partial x}=0$

с начальными условиями u(x,0)=psi_1(x),~ p(x,0)=psi_2(x),~ 0 leqslant x leqslant 1 ,
и краевыми условиями p(0,t)=varphi_1(t),~ p(1,t)=varphi_2(t),~ 0<t leqslant T .

Решение, формулы (8.81)-(8.90)

Система двух дифференциальных уравнений описывает распространение плоских звуковых волн (малых возмущений) в покоящейся среде. Здесь u(x,t),, p(x,t) — малые отклонения скорости и давления от их значений в невозмущенной среде, вызванные распространением звуковых волн; rho_0 — плотность невозмущенной среды; a_0 — скорость звука.

Рассмотрим основные этапы конструирования метода Годунова.

1. Введем разбиение отрезка [0;1] с шагом h=1!!not{phantom{|}},n , где — число промежутков. В результате получим узлы $x_{i},~ i=0,1,ldots,n$ , определяемые соотношением

$x_{i+1}=x_{i}+h,quad i=0,1,ldots,n-1;quad x_0=0,quad x_n=1.$

2. Заменим функции psi_1(x),, psi_2(x) на начальном слое t=0 кусочно-постоянными (пример описанной замены для некоторой произвольной функции изображен на рис. 8.22) путем их интегрального осреднения по формулам

$u_{1-1!not{phantom{|}},,2}= frac{1}{h} intlimits_{x_{i-1}}^{x_{i}} psi_1(x),dx,,quad p_{1-1!not{phantom{|}},,2}= frac{1}{h} intlimits_{x_{i-1}}^{x_{i}} psi_2(x),dx,,quad i=1,2,ldots,n.$

(8.81)

Здесь и далее все заданные или ранее рассчитанные функции снабжаются нижними полуцелыми индексами. Из рис. 8.22 видно, что полученная кусочно-постоянная функция имеет в узлах разрывы первого рода.

Кусочно-постоянные функции

3. Выберем шаг tau по времени и образуем следующий расчетный слой (t_1=tau) с теми же узлами $x_{i}$ (рис. 8.23). Таким образом, образуется совокупность прямоугольных ячеек. Предполагается, что искомые функции на горизонтальных и вертикальных границах образованных ячеек также являются постоянными.

Графики постоянных функций

На рассчитываемом слое при t=tau приближенное решение задачи также представляется в виде кусочно-постоянной функции, имеющей разрывы в узлах сетки, совпадающих с узлами на предыдущем слое. Это означает, что во времени на слоях t=text{const} сохраняется структура решения, изображенная на рис. 8.22. Значения искомых функций на рассчитываемом слое (верхних границах ячеек) обозначаются верхними полуцелыми индексами: $u^{1-1!not{phantom{|}},,2},, p^{1-1!not{phantom{|}},,2},$ i=1,2,ldots,n . На вертикальных границах ячеек значения функций обозначаются прописными буквами с нижними целыми индексами: $U_{i},,P_{i},~ i=0,ldots,n$ .

При i=0,~ i=n значения P_0 и P_n определяются краевыми условиями по формулам, аналогичным (8.81):

$P_0= frac{1}{tau} intlimits_{0}^{tau} varphi_1(t),dt,,quad P_n= frac{1}{tau} intlimits_{0}^{tau} varphi_2(t),dt,.$

(8.82)

Значения $U_1,ldots,U_{n-1},, P_1,ldots,P_{n-1}$ находятся в результате решения вспомогательной задачи о распаде произвольного разрыва, описанного в п.4, а значения U_0,,U_n определяются в п.5.

4. Выберем две соседние ячейки с узлами $x_{i-1},,x_{i}$ и $x_{i},,x_{i+1}$ (эти ячейки выделены на рис. 8.23 жирными линиями). С целью нахождения значений $U_{i},,P_{i}$ на внутренней границе ячеек при $x=x_{i}$ рассмотрим решение вспомогательной задачи, называемой задачей о распаде произвольного разрыва.

Дана система уравнений

$frac{partial u(x,t)}{partial t}+ frac{1}{rho_0}cdot frac{partial p(x,t)}{partial x}=0,qquad frac{partial p(x,t)}{partial t}+ rho_0a_0^2cdot frac{partial u(x,t)}{partial x}=0$

(8.83)

с начальными условиями вида

$u(x,0)= left{begin{aligned}&u_{i-1!not{phantom{|}},,2},quad x_{i-1} leqslant x<x_{i},\ &u_{i+1!not{phantom{|}},,2},quad x_{i} leqslant x<x_{i+1}, end{aligned}right.qquad p(x,0)= left{begin{aligned}&p_{i-1!not{phantom{|}},,2},quad x_{i-1} leqslant x<x_{i},\ &p_{i+1!not{phantom{|}},,2},quad x_{i} leqslant x<x_{i+1}. end{aligned}right.$

Требуется найти решение u(x,t),,p(x,t) при t>0 и $x=x_{i}$ , то есть $u(x_{i},t)=U_{i},~ p(x_{i},t)=P_{i}$ .

Заметим, что в данной задаче начальные данные имеют разрыв первого рода в точке $x_{i}$ . При t>0 они трансформируются, т.е. происходит распад разрыва, что обусловливает название рассматриваемой задачи. Для ее решения применим метод характеристик. Перепишем систему (8.83) в матричной форме

$Acdot frac{partial u(x,t)}{partial t}+ Bcdot frac{partial u(x,t)}{partial x}=0$ , где $A=begin{pmatrix}1&0\ 0&1 end{pmatrix}!,~~ B=begin{pmatrix}0& 1!!not{phantom{|}},rho_0\ rho_0a_0^2&0 end{pmatrix}!,~~ u=begin{pmatrix}u\p end{pmatrix}$ .

Для нахождения характеристических направлений используем условие

$|B-Acdot lambda|= begin{vmatrix}-lambda& 1!!not{phantom{|}},rho_0\ rho_0a_0^2&-lambdaend{vmatrix}=0$ . Отсюда ${left(frac{dx}{dt}right)!}^{+}= lambda^{+}= a_0,~~ {left(frac{dx}{dt}right)!}^{-}= lambda^{-}=-a_0$ .

Интегрируя последние уравнения, имеем

$x-a_0t=text{const}~(C^{+}),qquad x+a_0t=text{const}~(C^{-}).$

Если при t=0 выполняется условие $x=x_{i}$ , то из последних соотношений выделяются две прямые, исходящие из точки $x_{i}$ на начальном слое:

$x-a_0t=x_{i}~(C^{+}),qquad x+a_0t=x_{i}~(C^{-}).$

Для получения характеристических соотношений запишем расширенную матрицу (8.69) (учитывая, что fequiv 0 ):

$left(B,dt-A,dx,-A! begin{pmatrix}du\dpend{pmatrix}right)= begin{pmatrix}-dx&dfrac{1}{rho_0},dt&-dt\ rho_0a_0^2dt&-dx&-dp end{pmatrix}!.$

Приравнивая определитель матрицы, составленной из двух последних столбцов, нулю, получаем

$-dfrac{1}{rho_0},dp,dt-dx,du=0.$ Полагая dtne0 , разделим уравнение на $dtcolon,-dfrac{1}{rho_0},dp-frac{dx}{dt},du=0.$

Подставляя вместо $frac{dx}{dt}$ сначала $lambda^{+}=a_0$ , а затем $lambda^{-}=-a_0$ , получаем

$du+ dfrac{1}{rho_0,a_0},dp=0quad (C^{+}),qquad du-dfrac{1}{rho_0,a_0},dp= 0quad (C^{-}).$

Так как коэффициенты обоих уравнений постоянны, то их можно переписать в эквивалентной форме

$d! left(u+ dfrac{1}{rho_0,a_0},pright)=0quad (C^{+}),qquad d! left(u-dfrac{1}{rho_0,a_0},pright)=0quad (C^{-}).$

Интегрируя и обозначая постоянные интегрирования $I^{+},,I^{-}$ , имеем

$u+ dfrac{1}{rho_0,a_0},p=I^{+}quad (C^{+}),qquad u-dfrac{1}{rho_0,a_0},p=I^{-}quad (C^{-}).$

(8.84)

Полученные соотношения называются инвариантами Римана. Они показывают, что величина $u+ dfrac{1}{rho_0,a_0},p=I^{+}$ остается постоянной вдоль семейства $C^{+}$ , а величина $u-dfrac{1}{rho_0,a_0},p=I^{-}$ остается постоянной вдоль семейства $C^{-}$ .

Теперь, используя направления характеристик и сохраняющиеся вдоль них инварианты, построим численную схему решения задачи о распаде разрыва.

Семества прямых, исходящие из узлов сетки

Рассмотрим две характеристики $x-a_0t=x_{i-1}$ и $x-a_0t=x_{i}$ из семейства $C^{+}$ , исходящие из узлов $x_{i-1},,x_{i}$ , а также две характеристики $x+a_0t=x_{i}$ и $x+a_0t=x_{i+1}$ из семейства $C^{-}$ , исходящие из узлов $x_{i},,x_{i+1}$ (рис. 8.24). В результате пересечения указанных характеристик образуются области I, II, III , первые две из которых представлены треугольниками, а третья — четырехугольником. Вертикальная граница $(x_{i}= text{const})$ , разделяющая ячейки, на которой ищется решение задачи, располагается в области III. Покажем, что на этой границе искомое решение постоянно. Для этого выберем на ней произвольную точку (назовем ее точка 3) , а решение в ней обозначим $U_{i},, P_{i}$ . В эту точку приходит характеристика семейства $C^{+}$ , исходящая из точки 1 промежутка $(x_{i-1}, x_{i})$ . Точке 1 соответствуют заданные значения $u_{i-1!not{phantom{|}},,2},, p_{i-1!not{phantom{|}},,2}$ . Вдоль этой характеристики остается постоянной величина $u+ dfrac{1}{rho_0,a_0},p=I^{+}$ , то есть

$U_{i}+ frac{1}{rho_0,a_0}cdot P_{i}= u_{i-1!not{phantom{|}},,2}+ frac{1}{rho_0,a_0}cdot p_{i-1!not{phantom{|}},,2}.$

Кроме того, в точку 3 приходит характеристика семейства $C^{-}$ , исходящая из точки 2 промежутка $(x_{i},x_{i+1})$ . Точке 2 соответствуют заданные значения и $u_{i+ 1!not{phantom{|}},,2},, p_{i+ 1!not{phantom{|}},,2}$ . Вдоль этой характеристики остается постоянной величина $u-dfrac{1}{rho_0,a_0},p=I^{-}$ , то есть

$U_{i}-frac{1}{rho_0,a_0}cdot P_{i}= u_{i+ 1!not{phantom{|}},,2}-frac{1}{rho_0,a_0}cdot p_{i+ 1!not{phantom{|}},,2}.$

Разрешая систему из двух последних уравнений относительно $U_{i}$ и $P_{i}$ , получаем

$begin{gathered}U_{i}= frac{u_{i-1!not{phantom{|}},,2}+ u_{i+ 1!not{phantom{|}},,2}}{2}-frac{p_{i+ 1!not{phantom{|}},,2}-p_{i+ 1!not{phantom{|}},,2}}{2rho_0,a_0},\ P_{i}= frac{p_{i-1!not{phantom{|}},,2}+ p_{i+ 1!not{phantom{|}},,2}}{2}+ rho_0,a_0cdot frac{u_{i+ 1!not{phantom{|}},,2}-u_{i-1!not{phantom{|}},,2}}{2},,end{gathered}quad i=1,2,ldots,n-1.$

(8.85)

Поскольку точка 3 была выбрана произвольно на вертикальной границе ячейки, то полученные выражения определяют решение в любой точке этой границы (очевидно, решение постоянно вдоль границы), за исключением самой точки $x_{i}$ и точки пересечения характеристик, исходящих из точек $x_{i-1},, x_{i+1}$ . Таким образом, формулы (8.85) определяют «большие» величины $U_{i},, P_{i}$ на всех внутренних вертикальных границах ячеек.

Результаты решения данной вспомогательной задачи определяют шаг tau по времени. Действительно, влияние каждого из разрывов, относящихся к соседним узлам $x_{i-1},,x_{i}$ на слое t=0 , ограничивается характеристиками, исходящими из этих узлов. Физически это означает, что разрывы, возникшие при t=0 , распространяются со скоростью звука a_0 . Характеристики, исходящие из соседних узлов навстречу друг другу, пересекутся в точке с координатами $t=frac{h}{2a_0},~ x=frac{x_{i-1}+ x_{i}}{2}$ . От этой встречи разрывов возникнут новые волны, которые через следующий отрезок времени длительностью $frac{h}{2a_0}$ достигнут вертикальных границ $(x_{i-1}=text{const},~ x_{i}=text{const})$ соседних ячеек. Именно до этого момента, т.е. в течение времени $frac{h}{a_0}= frac{h}{2a_0}+ frac{h}{2a_0}$ , значения $U_{i},, P_{i}$ будут сохраняться неизменными и определяться по формулам (8.85). Таким образом, величина шага по времени должна выбираться из условия $tau< frac{h}{a_0}$ .

При i=0 для нахождения величины U_0 при известном P_0 используется инвариант Римана $u-frac{p}{rho_0 a_0}=I^{-}$ вдоль семейства $C^{-}$ (рис. 8.25). Поскольку на промежутке (0,x_1) заданы значения $u_{1!not{phantom{|}},,2},,p_{1!not{phantom{|}},,2}$ , то $U_0-frac{P_0}{rho_0a_0}= u_{1!not{phantom{|}},,2}-frac{p_{1!not{phantom{|}},,2}}{rho_0 a_0}$ . Отсюда получаем

$U_0= frac{1}{rho_0a_0}cdot P_0+ u_{1!not{phantom{|}},,2}-frac{1}{rho_0 a_0}cdot p_{1!not{phantom{|}},,2}.$

(8.86)

Семейства прямых, образующих прямоугольные области

При i=n для нахождения величины U_n при известном P_n используется инвариант Римана $u+frac{p}{rho_0a_0}=I^{+}$ вдоль семейства $C^{+}$ (рис. 8.25). Поскольку на последнем промежутке $(x_{n-1},1)$ заданы значения $u_{n-1!not{phantom{|}},,2},, p_{n-1!not{phantom{|}},,2}$ , то $U_n+frac{P_n}{rho_0a_0}= u_{n-1!not{phantom{|}},,2}+ frac{P_{n-1!not{phantom{|}},,2}}{rho_0a_0}$ . Отсюда получаем

$U_n=-frac{1}{rho_0a_0}cdot P_n+ u_{n-1!not{phantom{|}},,2}+ frac{1}{rho_0a_0}cdot p_{n-1!not{phantom{|}},,2}.$

(8.87)

На рис. 8.25 показаны две крайние ячейки с тремя характеристиками, одна из которых (верхняя) ограничивает область влияния начальных данных, заданных на промежутках (x_0,x_1) и $(x_{n-1},x_{n})$ соответственно.

6. Перейдем к задаче расчета искомых величин на следующем временном слое. Для этого рассмотрим одну ячейку (рис. 8.26), для которой известны значения приближенного решения $u_{i-1!not{phantom{|}},,2},, p_{i-1!not{phantom{|}},,2}$ на нижней границе и $U_{i-1},P_{i-1},U_{i},P_{i},$ i=1,2,ldots,n , на левой и правой вертикальных границах (см. п.4). Требуется определить значения $p^{i-1!not{phantom{|}},,2},, u^{i-1!not{phantom{|}},,2}$ на верхней границе ячейки.

Прямоугольная область и ячейка сетки

Для решения поставленной задачи перепишем уравнения (8.83) в так называемом дивергентном виде

$frac{partial u(x,t)}{partial t}+ frac{partial}{partial x}! left(frac{p(x,t)}{rho_0} right)=0,qquad frac{partial p(x,t)}{partial t}+ frac{partial}{partial x}bigl(rho_0a_0^2u(x,t) bigr)=0.$

(8.88)

Запишем двойной интеграл от левой и правой частей уравнений по поверхности ячейки. Для его нахождения применим формулу Грина перехода от двойного интеграла к криволинейному интегралу второго рода:

$iintlimits_{S}! left(frac{partial Phi_1}{partial t}+ frac{partial Phi_2}{partial x}right)!dx,dt= ointlimits_{gamma}bigl(Phi_1,dx-Phi_2,dtbigr),$

где — поверхность ячейки, а gamma — ее граница, обходимая против часовой стрелки. Таким образом, вместо системы (8.88) получается система интегральных уравнений

$ointlimits_{gamma}u,dx-frac{p}{rho_0},dt=0,qquad ointlimits_{gamma}p,dx-rho_0a_0^2u,dt=0.$

Проводя интегрирование, имеем

$begin{gathered}u_{i-1!not{phantom{|}},,2}h-frac{P_{i}}{rho_0}cdot tau-u^{i-1!not{phantom{|}},,2}h+ frac{P_{i-1}}{rho_0}cdot tau=0,\[4pt] p_{i-1!not{phantom{|}},,2}h-rho_0a_0^2U_{i}tau-p^{i-1!not{phantom{|}},,2}h+ rho_0a_0^2U_{i-1}tau=0. end{gathered}$

Из этих уравнений получаем

$begin{gathered}u^{i-1!not{phantom{|}},,2}= u_{i-1!not{phantom{|}},,2}-frac{tau}{h,rho_0}cdot (P_{i}-P_{i-1}),\[4pt] p^{i-1!not{phantom{|}},,2}= p_{i-1!not{phantom{|}},,2}-frac{tau}{h}cdot rho_0a_0^2(U_{i}-U_{i-1}). end{gathered}$

Таким образом, получены формулы для расчета первого временного слоя (t=tau) . После нахождения значений $u^{frac{1}{2}},p^{frac{1}{2}}, u^{frac{3}{2}}, p^{frac{3}{2}},ldots, u^{n-frac{1}{2}}, p^{n-frac{1}{2}}$ из условия $tau<frac{h}{a_0}$ выбирается очередной шаг и формируется новый временной слой (t_2=t_1+ tau) . Найденные значения используются в качестве опорных (они переобозначаются путем присвоения им соответствующих нижних индексов) для нахождения приближенного решения на следующем слое по формулам (8.85)–(8.87), (8.89). Заметим, что для вычисления P_0,,P_n вместо (8.82) используются формулы интегрального осреднения, аналогичные (8.81). Для расчета, например, второго временного слоя они имеют вид

$P_0= frac{1}{tau} intlimits_{t_1}^{t_2} varphi_1(t),dt,,qquad P_n= frac{1}{tau} intlimits_{t_1}^{t_2} varphi_2(t),dt,.$

(8.90)

Изложенная схема метода Годунова имеет первый порядок аппроксимации по tau и .

Замечание. Из процедуры интегрирования следует, что искомые значения $u^{n-1!not{phantom{|}},,2},, p^{n-1!not{phantom{|}},,2}$ соответствуют среднеинтегральным величинам

$u^{n-1!not{phantom{|}},,2}= frac{1}{h} intlimits_{x_{i-1}}^{x_{i}} u(x,tau),dx,,qquad p^{n-1!not{phantom{|}},,2}= frac{1}{h} intlimits_{x_{i-1}}^{x_{i}} p(x,tau),dx,.$

Приведем пример расчета по описанной схеме для частного случая рассматриваемой задачи (где rho_0=0,!123;~ a_0=0,!25 ):

$begin{gathered}begin{aligned}& frac{partial u(x,t)}{partial t}+ frac{1}{rho_0}cdot frac{partial p(x,t)}{partial x}=0,\ & frac{partial p(x,t)}{partial t}+rho_0a_0^2cdot frac{partial u(x,t)}{partial x}=0,end{aligned}qquad 0<x<1,quad 0<t<1,\[4pt] begin{aligned}& u(x,0)= psi_1(x)=sin x, & & p(x,0)=psi_2(x)= rho_0xsin x, & & 0 leqslant x leqslant 1,\ & p(0,t)= varphi_1(t)=0,!1t+ rho_0a_0^2sin t, & & p(1,t)= varphi_2(t)= 0,!1t+ rho_0a_0^2sin t, & & 0<t leqslant1, end{aligned} end{gathered}$

Решение

А. Выберем число промежутков n=2 . Тогда находится шаг $h=frac{1}{2}= 0,!5$ и вводятся узлы x_0=0;~ x_1=0,!5;~ x_2=1 . Зададим шаг tau= 0,!5 по времени из условия $tau< frac{h}{a_0}= frac{0,!5}{0,!25}=2$ . Сформируем две ячейки «A» и «B» первого временного слоя t_1=tau= 0,!5 (рис. 8.27).

Ячейки сетки в прямоугольной области

Б. Заменим функции psi_1(x)=sin x,~ psi_2(x)=rho_0xsin x кусочно-постоянными по формулам (8.81). Для вычисления интегралов используются квадратурные формулы трапеций:

$u_{i-1!not{phantom{|}},,2}= frac{1}{h}cdot frac{u_{i-1}+ u_{i}}{2}cdot h=frac{u_{i-1}+ u_{i}}{2},,qquad p_{i-1!not{phantom{|}},,2}= frac{1}{h}cdot frac{p_{i-1}+ p_{i}}{2}cdot h=frac{p_{i-1}+ p_{i}}{2},,quad i=1;2,$

где $u_{i}=sin x_{i},~ p_{i}=rho_0x_{i}sin x_{i}$ . Поэтому

$begin{aligned}& u_{1!not{phantom{|}},,2}cong frac{0+0,!479}{2}cong 0,!239; & & u_{3!not{phantom{|}},,2}cong frac{0,!479+ 0,!841}{2}cong 0,!660;\[2pt] <br />& p_{1!not{phantom{|}},,2}cong frac{0+0,!0294}{2}cong 0,!239; & & p_{3!not{phantom{|}},,2}cong frac{0,!479+ 0,!841}{2}cong 0,!660<br />end{aligned}$

В. Найдем значения P_0,,P_2 по формулам (8.82). Для вычисления интегралов, как и ранее, применяется формула трапеций:

$P_0cong frac{0+0,!0537}{2}cong 0,!0269;qquad P_2cong frac{0+0,!0463}{2}cong 0,!0231.$

Рассчитаем значение U_0 на левой границе ячейки «А» по формуле (8.86): $U_0=frac{P_0}{rho_0a_0}+ u_{1!not{phantom{|}},,2}-frac{p_{1!not{phantom{|}},,2} }{rho_0a_0}cong 0,!635$ и значение U_2 на правой границе ячейки по формуле (8.87): $U_2=-frac{P_2}{rho_0a_0}+ u_{3!not{phantom{|}},,2}+ frac{p_{3!not{phantom{|}},,2} }{rho_0a_0}cong 1,!476$ .

Г. Вычислим значения U_1,,P_1 на правой границе ячейки «А» (левой границе ячейки «В» ). По формулам (8.85) получаем

$U_1=frac{u_{1!not{phantom{|}},,2}+ u_{3!not{phantom{|}},,2}}{2}-frac{p_{3!not{phantom{|}},,2}-p_{1!not{phantom{|}},,2}}{2rho_0a_0}cong-0,!392;qquad frac{p_{1!not{phantom{|}},,2}+ p_{3!not{phantom{|}},,2}}{2}-rho_0a_0, frac{u_{3!not{phantom{|}},,2}-u_{1!not{phantom{|}},,2}}{2}cong 0,!0341.$

Д. Вычислим значения $u^{1!not{phantom{|}},,2},, p^{1!not{phantom{|}},,2},, u^{3!not{phantom{|}},,2},, p^{3!not{phantom{|}},,2}$ на верхних границах ячеек:

$begin{aligned}& u^{1!not{phantom{|}},,2}= u_{1!not{phantom{|}},,2}-frac{tau}{h,rho_0}(P_1-P_0)cong 0,!1805; & & p^{1!not{phantom{|}},,2}= p_{1!not{phantom{|}},,2}-frac{tau}{h},rho_0a_0^2(U_1-U_0)cong 0,!0226;\[4pt] & u^{3!not{phantom{|}},,2}= u_{3!not{phantom{|}},,2}-frac{tau}{h,rho_0}(P_2-P_1)cong 0,!749; & & p^{3!not{phantom{|}},,2}= p_{3!not{phantom{|}},,2}-frac{tau}{h},rho_0a_0^2(U_2-U_1)cong 0,!0521. end{aligned}$

Таким образом, первый слой полностью рассчитан.

Е. Для расчета второго слоя (t_2=t_1+tau) с шагом tau=0,!5 полученные значения $u^{1!not{phantom{|}},,2},, p^{1!not{phantom{|}},,2},, u^{3!not{phantom{|}},,2},, p^{3!not{phantom{|}},,2}$ переобозначим, для чего верхние индексы заменяются нижними:

$u_{1!not{phantom{|}},,2}=0,!1805;quad p_{1!not{phantom{|}},,2}= 0,!0226;quad u_{3!not{phantom{|}},,2}=0,!749;quad p_{3!not{phantom{|}},,2}= 0,!0521$

Сформируем две ячейки «С» и «D» второго временного слоя (см. рис. 8.27).

Ж. Найдем значения P_0,,P_2 по формулам (8.82). Для вычисления интегралов, как и ранее, применяется формула трапеций:

$P_0cong frac{0,0537+ 0,1065}{2}cong 0,!0801;qquad P_2cong frac{0,0463+ 0,00935}{2}cong 0,!0278.$

Рассчитаем значение U_0 на левой границе ячейки «С» по формуле (8.86):

$U_0= frac{1}{rho_0,a_0}cdot P_0+ u_{1!not{phantom{|}},,2}-frac{1}{rho_0, a_0}cdot p_{1!not{phantom{|}},,2}cong 2,!0504$

и значение U_2 на правой границе ячейки «D» по формуле (8.87):

$U_2=-frac{1}{rho_0,a_0}cdot P_2+ u_{3!not{phantom{|}},,2}+ frac{1}{rho_0,a_0}cdot p_{3!not{phantom{|}},,2}cong 0,!8651.$

3. Вычислим значения U_1,,P_1 на правой границе ячейки «С» (левой границе ячейки «D»). По формулам (8.85) получаем

$U_1= frac{u_{1!not{phantom{|}},,2}+ u_{3!not{phantom{|}},,2}}{2}-frac{p_{3!not{phantom{|}},,2}-p_{1!not{phantom{|}},,2}}{2,rho_0,a_0}cong-0,!0150;qquad P_1=frac{p_{1!not{phantom{|}},,2}+ p_{3!not{phantom{|}},,2}}{2}-rho_0a_0, frac{u_{3!not{phantom{|}},,2}-u_{1!not{phantom{|}},,2}}{2}cong 0,!02861.$

Вычислим значения $u^{1!not{phantom{|}},,2},, p^{1!not{phantom{|}},,2},, u^{3!not{phantom{|}},,2},, p^{3!not{phantom{|}},,2}$ на верхних границах ячеек «С» и «D»:

$begin{aligned}& u^{1!not{phantom{|}},,2}= u_{1!not{phantom{|}},,2}-frac{tau}{h,rho_0}(P_1-P_0)cong 0,!599; & & p^{1!not{phantom{|}},,2}= p_{1!not{phantom{|}},,2}-frac{tau}{h},rho_0,a_0^2(U_1-U_0)cong 0,!0385;\[2pt] & u^{3!not{phantom{|}},,2}= u_{3!not{phantom{|}},,2}-frac{tau}{h,rho_0}(P_2-P_1)cong 0,!7556; & & p^{3!not{phantom{|}},,2}= p_{3!not{phantom{|}},,2}-frac{tau}{h},rho_0,a_0^2(U_2-U_1)cong 0,!04533. end{aligned}$

Таким образом, второй слой полностью рассчитан и найдено приближенное решение поставленной задачи.

Замечание. Здесь рассмотрен пример методики конструирования метода С.К. Годунова и ее реализации для относительно простой линейной задачи. В нелинейном случае метод существенно усложняется. Для более глубокого изучения проблемы авторы рекомендуют, где данный метод применяется для различных классов нелинейных задач и задач с тремя и четырьмя независимыми переменными.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Characteristics of first-order partial differential equation[edit]

Linear and quasilinear cases[edit]

Proof for quasilinear Case[edit]

Fully nonlinear case[edit]

Example[edit]

Characteristics of linear differential operators[edit]

Qualitative analysis of characteristics[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Линейные дифференциальные уравнения в частных производных первого порядка

Линейные однородные уравнения в частных производных первого порядка

Линейные неоднородные уравнения в частных производных первого порядка

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Неоднородное уравнение

Свойства общего решения дифференциального уравнения

Метод характеристик при решение задачи коши для уравнений гиперболического типа

Аннотация

Ключевые слова

Текст научной работы

Уравнения характеристик и общие интегралы

Канонический вид гиперболических, параболических и эллиптических уравнений

Численные методы решения уравнений в частных производных

Метод прямых

Метод характеристик

Метод Годунова

Не пропустите также: