Как найти группы треугольников

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

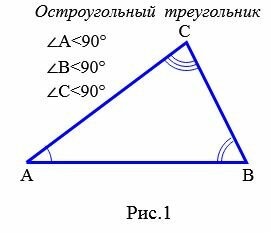
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

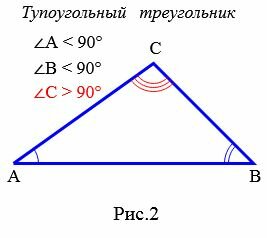
Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

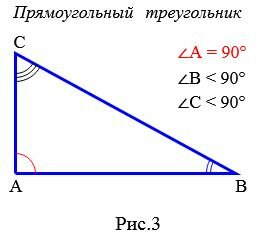
Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

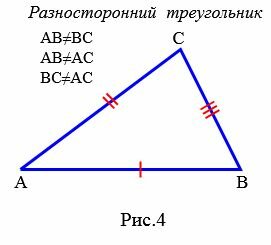
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

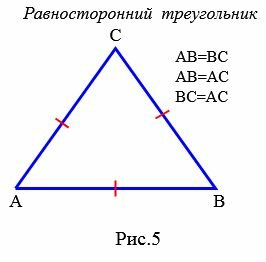
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

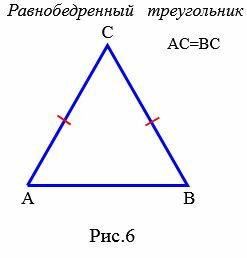
Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Поиск групп подобных треугольников среди массива треугольников по сторонам. Как реализовать?

Для начала, чтобы было проще искать, лучше сохранить стороны треугольников по возрастанию, то есть z[j].n
Затем, вспоминаем правило подобия треугольников с учётом сортировки длин сторон:

Перепишем эти условия для компьютера:

Поскольку вещественные вычисления на компьютере дают погрешность, то условия надо преобразовать (epsilon — константа, задающая точность вычислений):

Теперь начиная с первого треугольника, относим его к классу 1 проверяем его на подобие остальным и там, где треугольники подобны записываем их в класс 1.
Затем ищем треугольник, у которого класс не задан, относим его с следующему классу, проверяем его подобие остальным бесклассовым треугольникам, для подобных записываем тот же класс.
Продолжаем, пока все треугольники не будут отнесены к одному из классов.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

В математике группа треугольника — это группа, которая может быть представлена геометрически при помощи последовательных отражений относительно сторон треугольника. Треугольником может служить обычный евклидов треугольник, треугольник на сфере или гиперболический треугольник^[en]. Любая группа треугольника является группой симметрии паркета конгруэнтных треугольников в двумерном пространстве, на сфере или на гиперболической плоскости^[en].

Определение[править | править вики-текст]

Пусть l, m, n — целые числа, большие либо равные 2. Группа треугольника Δ(l,m,n) является группой движений евклидового пространства, двумерной сферы, вещественной проективной плоскости или гиперболической плоскости, порождённой отражениями относительно сторон треугольника с углами π/l, π/m and π/n (измеряемые в радианах). Произведение отражений относительно двух смежных сторон является вращением на угол, равный удвоенному углу между этими сторонами, 2π/l, 2π/m и 2π/n. Таким образом, если отражения обозначить буквами a, b и c, а углы между сторонами в циклическом порядке, как указано выше, имеют место следующие соотношения:

Существует теорема, что все другие соотношения между a, b, c являются следствием этих соотношений и что Δ(l,m,n) является дискретной группой^[en] движений соответствующего пространства. Эта группа треугольника является группой отражений^[en], допускающей задание

Абстрактная группа с этим заданием является группой Коксетера с тремя генераторами.

Классификация[править | править вики-текст]

Если заданы любые натуральные числа l, m, n > 1, в точности одна из классических двумерных геометрий (евклидова, сферическая или гиперболическая) допускает треугольник с углами (π/l, π/m, π/n) и пространство замощено отражениями этого треугольника. Сумма углов треугольника определяет тип геометрии по Формула Гаусса — Бонне: пространство евклидово, если сумма углов в точности равна π, сферическое, если превышает π и гиперболическое, если строго меньше π. Более того, любые два треугольника с заданными углами конгруэнтны. Каждая группа треугольника определяет замощение, которое обычно раскрашивается в два цвета, так что любые два соседних элемента мозаики имеют разные цвета.

В терминах чисел l, m, n > 1 существуют следующие возможности.

Евклидова плоскость[править | править вики-текст]

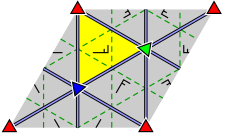
Группа треугольника является бесконечной группой симметрии некоторого паркета (или мозаики) евклидовой плоскости треугольниками, углы которых в сумме дают π (или 180°). С точностью до перестановок, тройка (l, m, n) является одной из троек (2,3,6), (2,4,4), (3,3,3). Соответствующие группы треугольников являются представителями группы рисунков обоев^[en].

(2,3,6)	(2,4,4)	(3,3,3)
Разделённый шестиугольный паркет[en]	Квадратный паркет «Тетракис»[en]	Треугольный паркет
Более детальные диаграммы с помеченными вершинами. Показано, как действуют отражения.

Сфера[править | править вики-текст]

Группа треугольника является конечной группой симметрии паркета на единичной сфере из сферических треугольников, или треугольников Мёбиуса, сумма углов которых в сумме дают число, большее π. С точностью до перестановки тройки (l,m,n) имеют вид (2,3,3), (2,3,4), (2,3,5) или (2,2,n), n > 1. Сферические группы треугольников можно сопоставить с группами симметрий правильных многогранников в трёхмерном евклидовом пространстве: Δ(2,3,3) соответствует тетраэдру, Δ(2,3,4) соответствует как кубу, так и октаэдра (они имеют одну и ту же группу симметрии), Δ(2,3,5) соответствует как додекаэдру, так и икосаэдру. Группы Δ(2,2,n), n > 1, диэдрической симметрии можно рассматривать как группы симметрии семейства диэдров, которые образуются двумя одинаковыми правильными n-угольниками, соединёнными вместе, или, двойственно, осоэдром, который образован объединением n двуугольников.

Сферический паркет^[en], соответствующий правильному многограннику, получается путём барицентрического подразделения многогранника и проекции полученных точек и прямых на описанную сферу. Для тетраэдра имеется четыре грани, и каждая грань является равносторонним треугольником, который делится на 6 меньших частей медианами, пересекающимися в центре. Получающаяся мозаика имеет 4 × 6=24 сферических треугольника (это сферический тетракисгексаэдр).

Эти группы конечны, что соответствует компактности сферы – площади дисков на сфере растут в терминах радиуса, но в конечном счёте покрывают всю сферу.

Треугольные замощения приведены ниже:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,n)
(2,3,3)	(2,3,4)	(2,3,5)

Сферические паркеты, соответствующие октаэдру и икосаэдру, а также диэдральным сферичесим мозаикам с чётным n, центрально симметричны. Поэтому каждая эта упаковка определяет паркет вещественной проективной плоскости, эллиптический паркет^[en]. Их группа симметрии является фактор-группой сферической группы треугольников по центральной симметрии (-I), которая является центральным элементом порядка 2. Поскольку проективная плоскость является моделью эллиптической геометрии, такие группы называются эллиптическими группами треугольника^[1].

Гиперболическая плоскость[править | править вики-текст]

Группа треугольника является бесконечной группой симметрии паркета на гиперболической плоскости^[en] из гиперболических треугольников, сумма углов которого меньше π. Все тройки, не перечисленные выше, представляют паркеты на гиперболической плоскости. Например, тройка (2,3,7) даёт группу треугольника (2,3,7). Существует бесконечно много таких групп. Ниже приведены паркеты, связанные с некоторыми малыми значениями.

Примеры прямоугольных треугольников (2 p q)
(2 3 7)	(2 3	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Примеры треугольников общего вида (p q r)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Гиперболические группы треугольников являются примерами неевклидовых кристаллографических групп^[en] и обобщены в теории Громова гиперболических групп.

Группы фон Дика[править | править вики-текст]

Обозначим через D(l,m,n) подгруппу с индексом 2 в Δ(l,m,n), сгенерированную словами чётной длины в генераторах. Такие подгруппы иногда называются «обычными» группами треугольников ^[2] или группами фон Дика, по имени Вальтера фон Дика^[en]. Сферические, евклидовы и гиперболические треугольники соответствуют элементам группы, сохряняющей ориентацию треугольников. Проективные (эллиптические) треугольники нельзя интерпретировать таким образом, поскольку проективная плоскость не имеет ориентации, и в ней нет «сохранения ориентации». Отражения, однако, локально сохраняют ориентацию (и любое многообразие локально ориентируемо, поскольку локально евклидово).^[3]

Группы D(l,m,n) определяются следующим заданием:

В терминах генераторов это x = ab, y = ca, yx = cb. Геометрически три элемента x, y, xy соответствуют вращениям на 2π/l, 2π/m и 2π/n вокруг трёх вершин треугольника.

Заметим, что D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l), так что D(l,m,n) не зависит от порядка чисел l,m,n.

Гиперболическая группа фон Дика — это группа Фукса^[en], дискретная группа, состоящая из сохраняющих ориентацию изометрий гиперболической плоскости.

Паркет с наложением[править | править вики-текст]

Подробное рассмотрение темы: Треугольник Шварца

Группы треугольников сохраняют паркетную укладку треугольниками, а именно фундаментальную область для действия (треугольника, определённого прямыми отражения), называемого треугольником Мёбиуса, и задаются тройкой целых чисел (l,m,n), соответствующих треугольникам (2l,2m,2n) с общей вершиной. Существуют также паркеты, образованные треугольниками с наложением, которые соответствуют треугольникам Шварца с рациональными числами (l/a,m/b,n/c), где знаменатели взаимно просты с числителями. Это соответствует сторонам под углом aπ/l (соотв.), что соответствует вращению на of 2aπ/l (соотв.), которое имеет порядок l и потому идентично элементу абстрактной группы, но различается, когда представляется в виде отражений.

Например, треугольник Шварца (2 3 3) даёт на сфере паркет плотности^[en] 1, в то время как треугольник (2 3/2 3) даёт на сфере паркет с плотностью 3, но с той же самой абстрактной группой. Эти симметрии паркетов с наложением не считаются группами треугольников.

История[править | править вики-текст]

Группы треугольников датируются по меньшей мере представлением икосаэдральной группы^[en] как группы вращений треугольника (2,3,5) Гамильтоном в 1856 в его статье об икосианах^[4].

Приложения[править | править вики-текст]

Внешние видеофайлы
	Искажённый модулярный паркет[5] – визуализация отображения (2,3,∞) → (2,3,7) путём трансформации соответствующих паркетов.

Группы треугольников возникают в арифметической геометрии^[en]. Модулярная группа, генерируемая двумя элементами, S и T, с соотношениями S² = (ST)³ = 1, является группой вращений треугольника (2,3,∞) и отображается во все группы треугольников (2,3,n) добавлением отношения Tⁿ = 1. Более обще, группа Гекке^[en] H_q, генерируемая двумя элементами, S и T, с соотношением S² = (ST)^q = 1 (нет отношения отдельно для T), является группой вращений треугольника (2,q,∞) и отображается во все группы треугольников (2,q,n) добавлением отношения Tⁿ = 1. Модулярная группа является группой Гекке H₃. В теории dessins d’enfants^[en] функция Белого^[en] позволяет получить замощение римановой поверхности, соответствующее некоторой группе треугольника.

Все 26 спорадических групп являются фактор-группами групп треугольника^[6], из которых 12 являются группами Гурвица^[en] (фактор-группа группы (2,3,7)).

Смотрите также[править | править вики-текст]

• Треугольник Шварца
• Отображение треугольника Шварца^[en] — это отображение треугольников в верхнюю полуплоскость^[en].
• Геометрическая теория групп

Примечания[править | править вики-текст]

Литература[править | править вики-текст]

Внешние ссылки[править | править вики-текст]

• Robert Dawson Некоторые сферические паркеты (Показано большое число интересных замощений сферы, большинство из которых не являются паркетами группы треугольников.)
• Elizabeth r chen triangle groups (2010) Обои на экран дисплея

В математике группа треугольников является группой это может быть реализовано геометрически посредством последовательностей отражений по сторонам треугольника . Треугольник может быть обычным евклидовым треугольником, треугольником на сфере или гиперболическим треугольником. Каждая группа треугольников представляет собой группу симметрии мозаики евклидовой плоскости, сферы или гиперболической плоскости на конгруэнтных треугольников, называемых треугольниками Мёбиуса, каждый из которых является фундаментальной областью для действия.

Содержание

• 1 Определение
• 2 Классификация
  • 2.1 Евклидов случай
  • 2.2 Сферический случай
  • 2.3 Гиперболический случай
    • 2.3.1 Гиперболическая плоскость
• 3 группы Фон Дейка
• 4 Перекрывающиеся плитки
• 5 История
• 6 Приложения
• 7 См. Также
• 8 Ссылки
• 9 Внешние ссылки

Определение

Пусть l, m, n будут целые числа больше или равные 2. Треугольная группа Δ (l, m, n) — это группа движений евклидовой плоскости, двумерной сферы, действительной проективной плоскость, или гиперболическая плоскость, образованная отражениями в сторонах треугольника с углами π / l, π / m и π / n (измеряется в радианах ). Произведение отражений в двух соседних сторонах представляет собой поворот на угол, который в два раза больше угла между этими сторонами, 2π / l, 2π / m и 2π / n. Следовательно, если образующие отражения помечены a, b, c и углы между ними в циклическом порядке такие, как указано выше, то выполняются следующие соотношения:

1. a 2 = b 2 = c 2 = 1 { displaystyle a ^ {2} = b ^ {2} = c ^ {2} = 1}
2. (ab) l = (bc) n = (ca) m = 1. { displaystyle (ab) ^ {l} = (bc) ^ {n} = (ca) ^ {m} = 1.}

Это теорема, что все другие отношения между a, b, c являются следствиями этих отношений и что Δ (l, m, n) — дискретная группа движений соответствующего пространства. Таким образом, группа треугольников — это группа отражений , которая допускает представление группы

Δ (l, m, n) = ⟨a, b, c ∣ a 2 = b 2 = c 2 = (ab) l = (bc) n = (ca) m = 1⟩. { displaystyle Delta (l, m, n) = langle a, b, c mid a ^ {2} = b ^ {2} = c ^ {2} = (ab) ^ {l} = (bc) ^ {n} = (ca) ^ {m} = 1 rangle.}

Абстрактная группа с этим представлением — это группа Кокстера с тремя образующими.

Классификация

Для любых натуральных чисел l, m, n>1 ровно одна из классических двумерных геометрий (евклидова, сферическая или гиперболическая) допускает треугольник с углами (π / l, π / m, π / n), а пространство выложено отражениями треугольника. Сумма углов треугольника определяет тип геометрии по теореме Гаусса – Бонне : она евклидова, если сумма углов равна точно π, сферическая, если она превышает π, и гиперболическая, если она строго меньше чем π. Более того, любые два треугольника с данными углами конгруэнтны. Каждая группа треугольников определяет мозаику, которая обычно окрашивается в два цвета, так что любые две соседние плитки имеют противоположные цвета.

В терминах чисел l, m, n>1 возможны следующие варианты.

Евклидов случай

1 l + 1 m + 1 n = 1. { displaystyle { frac {1} {l}} + { frac {1} {m}} + { frac {1} {n}} = 1.}

Группа треугольников — это бесконечная группа симметрии некоторой мозаики (или мозаики) евклидовой плоскости треугольниками, сумма углов равна π (или 180 °). С точностью до перестановок тройка (l, m, n) является одной из троек (2,3,6), (2,4,4), (3,3,3). Соответствующие группы треугольников являются экземплярами групп обоев.

(2,3,6)	(2,4,4)	(3,3,3)
Разделенная пополам шестиугольная мозаика	квадратная мозаика тетракиса	треугольная мозаика
Более подробные диаграммы, помеченные вершины и показывающие, как работает отражение:

Сферический случай

1 l + 1 m + 1 n>1. { displaystyle { frac {1} {l}} + { frac {1} {m}} + { frac {1} {n}}>1.}

Группа треугольников является конечной группой симметрии замощение единичной сферы сферическими треугольниками или треугольниками Мёбиуса, сумма углов которых дает число больше π. С точностью до перестановок тройка (l, m, n) имеет вид (2, 3,3), (2,3,4), (2,3,5) или (2,2, n), n>1. Сферические треугольные группы можно отождествить с группами симметрии правильных многогранников в трехмерном евклидовом пространстве: Δ (2,3,3) соответствует тетраэдру, Δ (2,3,4) как кубу, так и октаэдр (которые имеют одинаковую группу симметрии), Δ (2,3,5) как для додекаэдра, так и для икосаэдра. Группы Δ (2, 2, n), n>1 диэдральной симметрии можно интерпретировать как группы симметрии семейства диэдров, которые представляют собой вырожденные твердые тела, образованные двумя идентичными правильными n-угольниками, соединенными вместе, или двойными хозоэдрами, которые образованы путем соединения n двуугольников вместе в двух вершинах.

сферическая мозаика, соответствующая правильному многограннику, получается путем формирования барицентрического подразделения многогранника и проецирования полученных точек и линий на описанную сферу. В случае тетраэдра есть четыре грани, и каждая грань представляет собой равносторонний треугольник, который разделен на 6 меньших частей медианами, пересекающимися в центре. Результирующая мозаика имеет 4 × 6 = 24 сферических треугольника (это сферический куб Дисдиакиса ).

Эти группы конечны, что соответствует компактности сферы — площади дисков в сфере сначала увеличиваются по радиусу, но в конечном итоге покрывают всю сферу.

Треугольные мозаики изображены ниже:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2, n)
(2,3,3)	(2,3,4)	(2,3,5)

Сферические мозаики, соответствующие октаэдру и икосаэдру, и двугранные сферические мозаики с четным n центрально-симметричными. Следовательно, каждый из них определяет замощение реальной проективной плоскости, эллиптическое замощение. Его группа симметрии — это фактор группы сферических треугольников по отражению через начало координат (-I), который является центральным элементом порядка 2. Поскольку проективная плоскость является моделью эллиптической геометрии, такие группы называются эллиптическими треугольными группами.

Гиперболический случай

1 l + 1 m + 1 n < 1. {displaystyle {frac {1}{l}}+{frac {1}{m}}+{frac {1}{n}}<1.}

Треугольная группа — это бесконечная группа симметрии мозаики гиперболическая плоскость — гиперболическими треугольниками, сумма углов которых меньше π. Все тройки, не указанные в списке, представляют собой мозаики гиперболической плоскости. Например, тройка (2,3,7) дает треугольную группу (2,3,7). Таких групп бесконечно много; мозаики, связанные с некоторыми маленькими значениями:

гиперболическая плоскость

Пример прямоугольных треугольников (2 pq)
. (2 3 7)	. (2 3	. (2 3 9)	. (2 3 ∞)
. (2 4 5)	. (2 4 6)	. (2 4 7)	. (2 4	. (2 4 ∞)
. (2 5 5)	. (2 5 6)	. (2 5 7)	. (2 6 6)	. (2 ∞ ∞)
Пример общих треугольников (pqr)
. (3 3 4)	. (3 3 5)	. (3 3 6)	. (3 3 7)	. (3 3 ∞)
. (3 4 4)	. (3 6 6)	. (3 ∞ ∞)	. (6 6 6)	. (∞ ∞ ∞)

Гиперболические треугольные группы являются примерами неевклидовой кристаллографической группы и были обобщены в теории Громова гиперболических групп.

групп Фон Дейка

Обозначим D (l, m, n) подгруппа из индекса 2 в Δ (l, m, n), порожденная словами четной длины в генераторах. Такие подгруппы иногда называют «обычными» треугольными группами или группами фон Дейка после Вальтера фон Дейка. Для сферических, евклидовых и гиперболических треугольников они соответствуют элементам группы, которые сохраняют ориентацию треугольника — группу вращений. Для проективных (эллиптических) треугольников их нельзя так интерпретировать, поскольку проективная плоскость неориентируема, поэтому нет понятия «сохраняющий ориентацию». Однако отражения локально меняют ориентацию (и каждое многообразие является локально ориентируемым, поскольку локально евклидово): они фиксируют линию, и в каждой точке линии отражается поперек линии.

Группа D (l, m, n) определяется следующим представлением:

D (l, m, n) = ⟨x, y ∣ xl, ym, (xy) n⟩. { displaystyle D (l, m, n) = langle x, y mid x ^ {l}, y ^ {m}, (xy) ^ {n} rangle.}

В терминах генераторов выше это x = ab, y = ca, yx = cb. Геометрически три элемента x, y, xy соответствуют поворотам на 2π / l, 2π / m и 2π / n вокруг трех вершин треугольника.

Обратите внимание, что D (l, m, n) ≅ D (m, l, n) ≅ D (n, m, l), поэтому D (l, m, n) не зависит от порядка l, m, n.

Гиперболическая группа фон Дейка — это фуксова группа, дискретная группа, состоящая из сохраняющих ориентацию изометрий гиперболической плоскости.

Перекрывающиеся мозаики

Группы треугольников сохраняют мозаику треугольниками, а именно фундаментальную область для действия (треугольник, определяемый линиями отражения), называемый Треугольник Мёбиуса, и задаются тройкой целых чисел (l, m, n), — целые числа соответствуют (2l, 2m, 2n) треугольникам, сходящимся в вершине. Также существуют мозаики из перекрывающихся треугольников, которые соответствуют треугольникам Шварца с рациональными числами (l / a, m / b, n / c), где знаменатели взаимно просты с числителями.. Это соответствует ребрам, сходящимся под углами aπ / l (соответственно), что соответствует повороту на 2aπ / l (соответственно), который имеет порядок l и, таким образом, идентичен как абстрактный элемент группы, но отличается, когда представлен отражение.

Например, треугольник Шварца (2 3 3) дает мозаику сферы с плотностью 1, а треугольник (2 3/2 3) дает мозаику с плотностью 3, но с той же абстрактной группой. Эти симметрии перекрывающихся мозаик не считаются треугольными группами.

История

Треугольные группы датируются, по крайней мере, тем, что группа икосаэдра была представлена ​​как (вращательная) (2,3,5) группа треугольников Уильямом Роуэн Гамильтон в 1856 году в своей статье о икозиевом исчислении.

Приложения

Внешнее видео
Деформированное модульное мозаичное покрытие — визуализация карты (2,3, ∞) → (2, 3,7) путем преобразования связанных мозаик.

Группы треугольников возникают в арифметической геометрии. Модульная группа порождается двумя элементами, S и T, с учетом соотношений S² = (ST) ³ = 1 (нет связи на T), является группой треугольников вращения (2,3, ∞) и отображается на все треугольные группы (2, 3, n) путем добавления отношения T = 1. В более общем смысле, группа Гекке Hqпорождается двумя элементами, S и T, при соблюдении соотношений S = ( ST) = 1 (нет отношения к T), является вращательной треугольной группой (2, q, ∞) и отображается на все треугольные группы (2, q, n) путем добавления отношения T = 1, модулярная группа является группой Гекке. группа H 3. В теории Гротендика детских рисунков функция Белого приводит к мозаике римановой поверхности с помощью областей отражения. группы треугольников.

Все 26 спорадических групп являются факторами треугольных групп, из которых 12 являются группами Гурвица (факторами группы (2,3,7)).

См. Также

Ссылки

Внешние ссылки

• Роберт Доусон Некоторые сферические мозаики (без даты, до 2004 г.) (Показывает ряд интересных мозаичных мозаик, большинство из которых не являются мозаиками группы треугольников.)
• Элизабет Рчен треугольные группы (2010) фоновые изображения рабочего стола

В этой статье использованы материалы из треугольных групп с сайта PlanetMath, который находится под лицензией Creative Commons Лицензия с указанием авторства / совместного использования.

From Wikipedia, the free encyclopedia

This article is about a geometric concept. For Weihai, China-based tire manufacturing company, see Triangle Group.

In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action.

Definition[edit]

Let l, m, n be integers greater than or equal to 2. A triangle group Δ(l,m,n) is a group of motions of the Euclidean plane, the two-dimensional sphere, the real projective plane, or the hyperbolic plane generated by the reflections in the sides of a triangle with angles π/l, π/m and π/n (measured in radians). The product of the reflections in two adjacent sides is a rotation by the angle which is twice the angle between those sides, 2π/l, 2π/m and 2π/n. Therefore, if the generating reflections are labeled a, b, c and the angles between them in the cyclic order are as given above, then the following relations hold:

It is a theorem that all other relations between a, b, c are consequences of these relations and that Δ(l,m,n) is a discrete group of motions of the corresponding space. Thus a triangle group is a reflection group that admits a group presentation

An abstract group with this presentation is a Coxeter group with three generators.

Classification[edit]

Given any natural numbers l, m, n > 1 exactly one of the classical two-dimensional geometries (Euclidean, spherical, or hyperbolic) admits a triangle with the angles (π/l, π/m, π/n), and the space is tiled by reflections of the triangle. The sum of the angles of the triangle determines the type of the geometry by the Gauss–Bonnet theorem: it is Euclidean if the angle sum is exactly π, spherical if it exceeds π and hyperbolic if it is strictly smaller than π. Moreover, any two triangles with the given angles are congruent. Each triangle group determines a tiling, which is conventionally colored in two colors, so that any two adjacent tiles have opposite colors.

In terms of the numbers l, m, n > 1 there are the following possibilities.

The Euclidean case[edit]

The triangle group is the infinite symmetry group of a certain tessellation (or tiling) of the Euclidean plane by triangles whose angles add up to π (or 180°). Up to permutations, the triple (l, m, n) is one of the triples (2,3,6), (2,4,4), (3,3,3). The corresponding triangle groups are instances of wallpaper groups.

(2,3,6)	(2,4,4)	(3,3,3)
bisected hexagonal tiling	tetrakis square tiling	triangular tiling
More detailed diagrams, labeling the vertices and showing how reflection operates:

The spherical case[edit]

The triangle group is the finite symmetry group of a tiling of a unit sphere by spherical triangles, or Möbius triangles, whose angles add up to a number greater than π. Up to permutations, the triple (l,m,n) has the form (2,3,3), (2,3,4), (2,3,5), or (2,2,n), n > 1. Spherical triangle groups can be identified with the symmetry groups of regular polyhedra in the three-dimensional Euclidean space: Δ(2,3,3) corresponds to the tetrahedron, Δ(2,3,4) to both the cube and the octahedron (which have the same symmetry group), Δ(2,3,5) to both the dodecahedron and the icosahedron. The groups Δ(2,2,n), n > 1 of dihedral symmetry can be interpreted as the symmetry groups of the family of dihedra, which are degenerate solids formed by two identical regular n-gons joined together, or dually hosohedra, which are formed by joining n digons together at two vertices.

The spherical tiling corresponding to a regular polyhedron is obtained by forming the barycentric subdivision of the polyhedron and projecting the resulting points and lines onto the circumscribed sphere. In the case of the tetrahedron, there are four faces and each face is an equilateral triangle that is subdivided into 6 smaller pieces by the medians intersecting in the center. The resulting tesselation has 4 × 6=24 spherical triangles (it is the spherical disdyakis cube).

These groups are finite, which corresponds to the compactness of the sphere – areas of discs in the sphere initially grow in terms of radius, but eventually cover the entire sphere.

The triangular tilings are depicted below:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,n)
(2,3,3)	(2,3,4)	(2,3,5)

Spherical tilings corresponding to the octahedron and the icosahedron and dihedral spherical tilings with even n are centrally symmetric. Hence each of them determines a tiling of the real projective plane, an elliptic tiling. Its symmetry group is the quotient of the spherical triangle group by the reflection through the origin (-I), which is a central element of order 2. Since the projective plane is a model of elliptic geometry, such groups are called elliptic triangle groups.^[1]

The hyperbolic case[edit]

The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane by hyperbolic triangles whose angles add up to a number less than π. All triples not already listed represent tilings of the hyperbolic plane. For example, the triple (2,3,7) produces the (2,3,7) triangle group. There are infinitely many such groups; the tilings associated with some small values:

Hyperbolic plane[edit]

Example right triangles (2 p q)
(2 3 7)	(2 3	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Example general triangles (p q r)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Hyperbolic triangle groups are examples of non-Euclidean crystallographic group and have been generalized in the theory of Gromov hyperbolic groups.

Von Dyck groups[edit]

Denote by D(l,m,n) the subgroup of index 2 in Δ(l,m,n) generated by words of even length in the generators. Such subgroups are sometimes referred to as «ordinary» triangle groups^[2] or von Dyck groups, after Walther von Dyck. For spherical, Euclidean, and hyperbolic triangles, these correspond to the elements of the group that preserve the orientation of the triangle – the group of rotations. For projective (elliptic) triangles, they cannot be so interpreted, as the projective plane is non-orientable, so there is no notion of «orientation-preserving». The reflections are however locally orientation-reversing (and every manifold is locally orientable, because locally Euclidean): they fix a line and at each point in the line are a reflection across the line.^[3]

The group D(l,m,n) is defined by the following presentation:

In terms of the generators above, these are x = ab, y = ca, yx = cb. Geometrically, the three elements x, y, xy correspond to rotations by 2π/l, 2π/m and 2π/n about the three vertices of the triangle.

Note that D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l), so D(l,m,n) is independent of the order of the l,m,n.

A hyperbolic von Dyck group is a Fuchsian group, a discrete group consisting of orientation-preserving isometries of the hyperbolic plane.

Overlapping tilings[edit]

Triangle groups preserve a tiling by triangles, namely a fundamental domain for the action (the triangle defined by the lines of reflection), called a Möbius triangle, and are given by a triple of integers, (l,m,n), – integers correspond to (2l,2m,2n) triangles coming together at a vertex. There are also tilings by overlapping triangles, which correspond to Schwarz triangles with rational numbers (l/a,m/b,n/c), where the denominators are coprime to the numerators. This corresponds to edges meeting at angles of aπ/l (resp.), which corresponds to a rotation of 2aπ/l (resp.), which has order l and is thus identical as an abstract group element, but distinct when represented by a reflection.

For example, the Schwarz triangle (2 3 3) yields a density 1 tiling of the sphere, while the triangle (2 3/2 3) yields a density 3 tiling of the sphere, but with the same abstract group. These symmetries of overlapping tilings are not considered triangle groups.

History[edit]

Triangle groups date at least to the presentation of the icosahedral group as the (rotational) (2,3,5) triangle group by William Rowan Hamilton in 1856, in his paper on icosian calculus.^[4]

Applications[edit]

External video
Warped modular tiling[5] – visualization of the map (2,3,∞) → (2,3,7) by morphing the associated tilings.

Triangle groups arise in arithmetic geometry. The modular group is generated by two elements, S and T, subject to the relations S² = (ST)³ = 1 (no relation on T), is the rotational triangle group (2,3,∞) and maps onto all triangle groups (2,3,n) by adding the relation Tⁿ = 1. More generally, the Hecke group H_q is generated by two elements, S and T, subject to the relations S² = (ST)^q = 1 (no relation on T), is the rotational triangle group (2,q,∞), and maps onto all triangle groups (2,q,n) by adding the relation Tⁿ = 1 the modular group is the Hecke group H₃. In Grothendieck’s theory of dessins d’enfants, a Belyi function gives rise to a tessellation of a Riemann surface by reflection domains of a triangle group.

All 26 sporadic groups are quotients of triangle groups,^[6] of which 12 are Hurwitz groups (quotients of the (2,3,7) group).

See also[edit]

• Schwarz triangle
• The Schwarz triangle map is a map of triangles to the upper half-plane.
• Geometric group theory

References[edit]

External links[edit]

• Elizabeth r chen triangle groups (2010) desktop background pictures

This article incorporates material from Triangle groups on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Эта статья о геометрической концепции. Для Weihai, китайской компании по производству шин, см. Triangle Group .

В математике , А треугольник группа представляет собой группу , которая может быть реализована геометрически последовательностями отражений поперек сторон треугольника . Треугольник может быть обычным евклидовым треугольником, треугольником на сфере или гиперболическим треугольником . Каждый треугольник группа является группа симметрии из черепицы в евклидовой плоскости , в сфере , или гиперболической плоскости по конгруэнтным треугольникам называется Мёбиус треугольники , каждая из которых является фундаментальной областью для действия.

Определение

Пусть l , m , n — целые числа, большие или равные 2. Треугольная группа Δ ( l , m , n ) — это группа движений евклидовой плоскости, двумерной сферы, действительной проективной плоскости или гиперболической плоскости. плоскость, образованная отражениями в сторонах треугольника с углами π / l , π / m и π / n (измеренными в радианах ). Произведение отражений в двух соседних сторонах представляет собой поворот на угол, который в два раза больше угла между этими сторонами, 2π / l , 2π / m и 2π / n . Следовательно, если образующие отражения обозначены как a , b , c, а углы между ними в циклическом порядке такие, как указано выше, то выполняются следующие соотношения:

Это теорема, что все остальные отношения между a, b, c являются следствиями этих отношений и что ∆ ( l, m, n ) — дискретная группа движений соответствующего пространства. Таким образом, треугольная группа — это группа отражений , допускающая групповое представление.

Абстрактная группа с таким представлением — это группа Кокстера с тремя образующими.

Классификация

Для любых натуральных чисел l ,  m ,  n  > 1 ровно одна из классических двумерных геометрий (евклидова, сферическая или гиперболическая) допускает треугольник с углами (π / l, π / m, π / n) и пространство выложено отражениями треугольника. Сумма углов треугольника определяет тип геометрии по теореме Гаусса – Бонне : она евклидова, если сумма углов точно равна π, сферическая, если она превышает π, и гиперболическая, если она строго меньше π. Более того, любые два треугольника с заданными углами конгруэнтны. Каждая группа треугольников определяет мозаику, которая обычно окрашивается в два цвета, так что любые две соседние плитки имеют противоположные цвета.

В терминах чисел l ,  m ,  n  > 1 возможны следующие варианты.

Евклидов случай

Группа треугольников — это группа бесконечной симметрии определенной мозаики (или мозаики) евклидовой плоскости треугольниками, углы которых в сумме составляют π (или 180 °). С точностью до перестановок тройка ( l ,  m ,  n ) является одной из троек (2,3,6), (2,4,4), (3,3,3). Соответствующие группы треугольников являются экземплярами групп обоев .

(2,3,6)	(2,4,4)	(3,3,3)
пополам шестиугольная мозаика	квадратная плитка тетракис	треугольная черепица
Более подробные диаграммы, помеченные вершинами и показывающие, как работает отражение:

Сферический корпус

Группа треугольников — это конечная группа симметрии замощения единичной сферы сферическими треугольниками или треугольниками Мёбиуса , сумма углов которых дает число больше π. С точностью до перестановок тройка ( l , m , n ) имеет вид (2,3,3), (2,3,4), (2,3,5) или (2,2, n ), n  > 1. Сферические треугольные группы можно отождествить с группами симметрии правильных многогранников в трехмерном евклидовом пространстве: ∆ (2,3,3) соответствует тетраэдру , ∆ (2,3,4) — как кубу, так и октаэдр (которые имеют ту же самую группу симметрии), Δ (2,3,5) как к додекаэдра и икосаэдра . Группы диэдральной симметрии Δ (2,2, n ), n  > 1, можно интерпретировать как группы симметрии семейства диэдров , которые представляют собой вырожденные твердые тела, образованные двумя одинаковыми правильными n -угольниками, соединенными вместе, или двойными хозоэдрами , которые образованы соединением n двуугольников в двух вершинах.

Сферические плиточный , соответствующие правильный многогранник получаются путем формирования барицентрического подразделения многогранника и проецирования полученных точек и линий на описанной сферу. В случае тетраэдра есть четыре грани, и каждая грань представляет собой равносторонний треугольник, который разделен на 6 меньших частей медианами, пересекающимися в центре. Полученная мозаика имеет 4 × 6 = 24 сферических треугольника (это сферический куб Дисдиакиса ).

Эти группы конечны, что соответствует компактности сферы — площади дисков в сфере сначала увеличиваются по радиусу, но в конечном итоге покрывают всю сферу.

Треугольные мозаики изображены ниже:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2, п)
(2,3,3)	(2,3,4)	(2,3,5)

Сферические мозаики, соответствующие октаэдру и икосаэдру, и двугранные сферические мозаики с четным n , центрально-симметричны . Следовательно, каждый из них определяет замощение реальной проективной плоскости, эллиптическое замощение . Его группа симметрии — это фактор группы сферических треугольников по отражению через начало координат (- I ), который является центральным элементом порядка 2. Поскольку проективная плоскость является моделью эллиптической геометрии , такие группы называются группами эллиптических треугольников.

Гиперболический случай

Группа треугольников — это бесконечная группа симметрии замощения гиперболической плоскости гиперболическими треугольниками, сумма углов которых дает число меньше π. Все тройки, не указанные в списке, представляют собой мозаики гиперболической плоскости. Например, тройка (2,3,7) дает группу треугольников (2,3,7) . Таких групп бесконечно много; мозаики, связанные с некоторыми небольшими значениями:

Гиперболическая плоскость

Модель диска Пуанкаре фундаментальных треугольников области

Пример прямоугольных треугольников (2 шт.)
(2 3 7)	(2 3	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Пример общих треугольников (pqr)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Гиперболические треугольные группы являются примерами неевклидовой кристаллографической группы и были обобщены в теории гиперболических групп Громова .

Группы фон Дейка

Обозначим через D ( л , м , п ) подгруппа из индекса 2 в А (л, т, п) , порожденный словами четной длины от образующих. Такие подгруппы иногда называют «обычными» треугольными группами или группами фон Дейка в честь Вальтера фон Дейка . Для сферических, евклидовых и гиперболических треугольников они соответствуют элементам группы, сохраняющей ориентацию треугольника — группе вращений. Для проективных (эллиптических) треугольников их нельзя так интерпретировать, поскольку проективная плоскость неориентируема, поэтому нет понятия «сохраняющий ориентацию». Однако отражения локально меняют ориентацию (и каждое многообразие является локально ориентируемым, поскольку локально евклидово): они фиксируют линию, и в каждой точке линии отражается поперек линии.

Группа D ( l , m , n ) определяется следующим представлением:

В терминах генераторов, приведенных выше, это x = ab, y = ca, yx = cb . Геометрически три элемента x , y , xy соответствуют поворотам на 2π / l , 2π / m и 2π / n вокруг трех вершин треугольника.

Обратите внимание, что D ( l , m , n ) ≅ D ( m , l , n ) ≅ D ( n , m , l ), поэтому D ( l , m , n ) не зависит от порядка l , m , n .

Гиперболическая группа фон Дейка — это фуксова группа , дискретная группа, состоящая из сохраняющих ориентацию изометрий гиперболической плоскости.

Перекрывающиеся плитки

Группы треугольников сохраняют мозаику из треугольников, а именно фундаментальную область действия (треугольник, определяемый линиями отражения), называемый треугольником Мёбиуса , и задаются тройкой целых чисел ( l , m , n ) — целыми числами соответствуют (2 l , 2 m , 2 n ) треугольника, сходящегося вместе в вершине. Также существуют мозаики из перекрывающихся треугольников, которые соответствуют треугольникам Шварца с рациональными числами ( l / a , m / b , n / c ), знаменатели которых взаимно просты с числителями. Это соответствует ребрам, пересекающимся под углами a π / l (соответственно), что соответствует повороту на 2 a π / l (соответственно), который имеет порядок l и, таким образом, идентичен как абстрактный элемент группы, но отличается, когда представлен отражением.

Например, треугольник Шварца (2 3 3) дает разбиение сферы с плотностью 1, а треугольник (2 3/2 3) дает разбиение сферы с плотностью 3, но с той же абстрактной группой. Эти симметрии перекрывающихся мозаик не считаются треугольными группами.

История

Группы треугольников относятся, по крайней мере, к представлению группы икосаэдра как группы (вращательных) (2,3,5) треугольников Уильямом Роуэном Гамильтоном в 1856 году в его статье по икозианскому исчислению .

Приложения

Внешнее видео
Warped modular tiling — визуализация карты (2,3, ∞) → (2,3,7) путем морфинга связанных мозаик.

Группы треугольников возникают в арифметической геометрии . Модульная группа порождается два элементами, S и Т , при условии отношений S ² = ( ST ) ³ = 1 (никакого отношения на Т ), является вращательным треугольник группы (2,3, ∞) и отображает на все треугольник групп (2,3, n ) путем добавления отношения T ⁿ = 1. В более общем смысле, группа Гекке H _q порождается двумя элементами, S и T , с учетом соотношений S ² = ( ST ) ^q = 1 (no отношение на T ), представляет собой группу треугольников вращения (2, q , ∞) и отображается на все треугольные группы (2, q , n ) путем добавления отношения T ⁿ = 1, модулярная группа является группой Гекке H ₃ . В Гротендик теории «s из детских рисунков струкция , функция Belyi приводит к тесселяции на римановой поверхности с помощью отражения областей треугольной группы.

Все 26 спорадических групп являются факторами треугольных групп, из которых 12 являются группами Гурвица (факторами группы (2,3,7)).

Смотрите также

• Треугольник Шварца
• Карта треугольника Шварца — это карта треугольников в верхнюю полуплоскость .
• Геометрическая теория групп

Рекомендации

внешняя ссылка

• Роберт Доусон Некоторые сферические мозаики (без даты, ранее 2004 г.) (Показывает ряд интересных мозаичных мозаик, большинство из которых не являются мозаиками группы треугольников.)
• Треугольники группы елизаветы рчен (2010) обои на рабочий стол

Эта статья включает материалы групп Triangle на PlanetMath , которые находятся под лицензией Creative Commons Attribution / Share-Alike License .