Как найти гравитационный радиус луны

From Wikipedia, the free encyclopedia

Radial gravity anomaly at the surface of the Moon in mGal

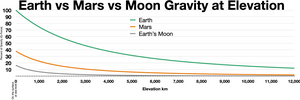
The acceleration due to gravity on the surface of the Moon is approximately 1.625 m/s², about 16.6% that on Earth’s surface or 0.166 ɡ.^[1] Over the entire surface, the variation in gravitational acceleration is about 0.0253 m/s² (1.6% of the acceleration due to gravity). Because weight is directly dependent upon gravitational acceleration, things on the Moon will weigh only 16.6% (= 1/6) of what they weigh on the Earth.

Gravitational field[edit]

The gravitational field of the Moon has been measured by tracking the radio signals emitted by orbiting spacecraft. The principle used depends on the Doppler effect, whereby the line-of-sight spacecraft acceleration can be measured by small shifts in frequency of the radio signal, and the measurement of the distance from the spacecraft to a station on Earth. Since the gravitational field of the Moon affects the orbit of a spacecraft, one can use this tracking data to detect gravity anomalies.

Most low lunar orbits are unstable. Detailed data collected has shown that for low lunar orbit the only «stable» orbits are at inclinations near 27°, 50°, 76°, and 86°.^[2] Because of the Moon’s synchronous rotation it is not possible to track spacecraft from Earth much beyond the limbs of the Moon, so until the recent Gravity Recovery and Interior Laboratory (GRAIL) mission the far-side gravity field was not well mapped.

The missions with accurate Doppler tracking that have been used for deriving gravity fields are in the accompanying table. The table gives the mission spacecraft name, a brief designation, the number of mission spacecraft with accurate tracking, the country of origin, and the time span of the Doppler data. Apollos 15 and 16 released subsatellites. The Kaguya/SELENE mission had tracking between 3 satellites to get far-side tracking. GRAIL had very accurate tracking between 2 spacecraft and tracking from Earth.

Missions Used for Lunar Gravity

Mission	ID	Number	Source	Years
Lunar Orbiter 1	LO1	1	US	1966
Lunar Orbiter 2	LO2	1	US	1966–1967
Lunar Orbiter 3	LO3	1	US	1967
Lunar Orbiter 4	LO4	1	US	1967
Lunar Orbiter 5	LO5	1	US	1967–1968
Apollo 15 Subsatellite	A15	1	US	1971–1972
Apollo 16 Subsatellite	A16	1	US	1972
Clementine	Cl	1	US	1994
Lunar Prospector	LP	1	US	1998–1999
Kaguya/SELENE	K/S	3	Japan	2007–2009
Chang’e 1	Ch1	1	China	2007–2009
GRAIL	G	2	US	2012
Chang’e 5T1	Ch1T1	1	China	2015–2018

The accompanying table below lists lunar gravity fields. The table lists the designation of the gravity field, the highest degree and order, a list of mission IDs that were analyzed together, and a citation. Mission ID LO includes all 5 Lunar Orbiter missions. The GRAIL fields are very accurate; other missions are not combined with GRAIL.

Lunar Gravity Fields

Designation	Degree	Mission IDs	Citation
LP165P	165	LO A15 A16 Cl LP	^[3]
GLGM3	150	LO A15 A16 Cl LP	^[4]
CEGM01	50	Ch 1	^[5]
SGM100h	100	LO A15 A16 Cl LP K/S	^[6]
SGM150J	150	LO A15 A16 Cl LP K/S	^[7]
CEGM02	100	LO A15 A16 Cl LP K/S Ch1	^[8]
GL0420A	420	G	^[9]
GL0660B	660	G	^[10]
GRGM660PRIM	660	G	^[11]
GL0900D	900	G	^[12]
GRGM900C	900	G	^[13]
GRGM1200A	1200	G	^[14]
CEGM03	100	LO A15 A16 Cl LP Ch1 K/S Ch5T1	^[15]

A major feature of the Moon’s gravitational field is the presence of mascons, which are large positive gravity anomalies associated with some of the giant impact basins. These anomalies significantly influence the orbit of spacecraft around the Moon, and an accurate gravitational model is necessary in the planning of both crewed and uncrewed missions. They were initially discovered by the analysis of Lunar Orbiter tracking data:^[16] navigation tests prior to the Apollo program showed positioning errors much larger than mission specifications.

Mascons are in part due to the presence of dense mare basaltic lava flows that fill some of the impact basins.^[17] However, lava flows by themselves cannot fully explain the gravitational variations, and uplift of the crust-mantle interface is required as well. Based on Lunar Prospector gravitational models, it has been suggested that some mascons exist that do not show evidence for mare basaltic volcanism.^[3] The huge expanse of mare basaltic volcanism associated with Oceanus Procellarum does not cause a positive gravity anomaly. The center of gravity of the Moon does not coincide exactly with its geometric center, but is displaced toward the Earth by about 2 kilometers.^[18]

Mass of Moon[edit]

The gravitational constant G is less accurate than the product of G and masses for Earth and Moon. Consequently, it is conventional to express the lunar mass M multiplied by the gravitational constant G. The lunar GM = 4902.8001 km³/s² from GRAIL analyses.^[12]^[11]^[19] The mass of the Moon is M = 7.3458 × 10²² kg and the mean density is 3346 kg/m³. The lunar GM is 1/81.30057 of the Earth’s GM.^[20]

Theory[edit]

For the lunar gravity field, it is conventional to use an equatorial radius of R = 1738.0 km. The gravity potential is written with a series of spherical harmonic functions P_nm. The gravitational potential V at an external point is conventionally expressed as positive in astronomy and geophysics, but negative in physics. Then, with the former sign,

${displaystyle V=left({frac {GM}{r}}right)-left({frac {GM}{r}}right)sum left({frac {R}{r}}right)^{n}J_{n}P_{n,0}(sin phi )+left({frac {GM}{r}}right)sum left({frac {R}{r}}right)^{n}[C_{n,m}P_{n,m}(sin phi )cos(mlambda )+S_{n,m}P_{n,m}(sin phi )sin(mlambda )]}$

where r is the radius to an external point with r ≥ R, φ is the latitude of the external point, and λ is the east longitude of the external point. Note that the spherical harmonic functions P_nm can be normalized or unnormalized affecting the gravity coefficients J_n, C_nm, and S_nm. Here we will use unnormalized functions and compatible coefficients. The P_n0 are called Legendre polynomials and the P_nm with m≠0 are called the Associated Legendre polynomials, where subscript n is the degree, m is the order, and m ≤ n. The sums start at n = 2. The unnormalized degree-2 functions are

${displaystyle {begin{aligned}P_{2,0}&={frac {3}{2}}sin ^{2}!phi -{frac {1}{2}}\[1ex]P_{2,1}&=3sin phi cos phi \[1ex]P_{2,2}&=3cos ^{2}phi end{aligned}}}$

Note that of the three functions, only P₂₀(±1)=1 is finite at the poles. More generally, only P_n0(±1)=1 are finite at the poles.

The gravitational acceleration of vector position r is

${displaystyle {begin{aligned}{frac {d^{2}r}{dt^{2}}}&=nabla V\[1ex]&={partial V over partial r}e_{r}+{frac {1}{r}}{partial V over partial phi }e_{phi }+{frac {1}{rcos phi }}{partial V over partial lambda }{e_{lambda }}end{aligned}}}$

where e_r, e_φ, and e_λ are unit vectors in the three directions.

Gravity coefficients[edit]

The unnormalized gravity coefficients of degree 2 and 3 that were determined by the GRAIL mission are given in Table 1.^[12]^[11]^[19] The zero values of C₂₁, S₂₁, and S₂₂ are because a principal axis frame is being used. There are no degree-1 coefficients when the three axes are centered on the center of mass.

Lunar Gravity Coefficients

nm	J_n	C_nm	S_nm
20	203.3 × 10⁻⁶	—	—
21	—	0	0
22	—	22.4 × 10⁻⁶	0
30	8.46 × 10⁻⁶	—	—
31	—	28.48 × 10⁻⁶	5.89 × 10⁻⁶
32	—	4.84 × 10⁻⁶	1.67 × 10⁻⁶
33	—	1.71 × 10⁻⁶	−0.25 × 10⁻⁶

The J₂ coefficient for an oblate shape to the gravity field is affected by rotation and solid-body tides whereas C₂₂ is affected by solid-body tides. Both are larger than their equilibrium values showing that the upper layers of the Moon are strong enough to support elastic stress. The C₃₁ coefficient is large.

Simulating lunar gravity[edit]

In January 2022 China was reported by the South China Morning Post to have built a small (60 centimeters in diameter) research facility to simulate low lunar gravity with the help of magnets.^[21]^[22] The facility was reportedly partly inspired by the work of Andre Geim (who later shared the 2010 Nobel Prize in Physics for his research on graphene) and Michael Berry, who both shared the Ig Nobel Prize in Physics in 2000 for the magnetic levitation of a frog.^[21]^[22]

References[edit]

^ C. Hirt; W. E. Featherstone (2012). «A 1.5 km-resolution gravity field model of the Moon». Earth and Planetary Science Letters. 329–330: 22–30. Bibcode:2012E&PSL.329…22H. doi:10.1016/j.epsl.2012.02.012. Retrieved 2012-08-21.
^ Bell, Trudy E. (November 6, 2006). Phillips, Tony (ed.). «Bizarre Lunar Orbits». Science@NASA. NASA. Retrieved 2017-09-08.
^ ^a ^b
A. Konopliv; S. Asmar; E. Carranza; W. Sjogren; D. Yuan (2001). «Recent gravity models as a result of the Lunar Prospector mission». Icarus. 50 (1): 1–18. Bibcode:2001Icar..150….1K. CiteSeerX 10.1.1.18.1930. doi:10.1006/icar.2000.6573.
^ Mazarico, E.; Lemoine, F. G.; Han, Shin-Chan; Smith, D. E. (2010). «GLGM-3: A degree-150 lunar gravity model from the historical tracking data of NASA Moon orbiters». Journal of Geophysical Research. 115 (E5): E05001, 1–14. Bibcode:2010JGRE..115.5001M. doi:10.1029/2009JE003472. ISSN 0148-0227.
^ Jianguo, Yan; Jinsong, Ping; Fei, Li; Jianfeng, Cao; Qian, Huang; Lihe, Fung (2010). «Chang’E-1 precision orbit determination and lunar gravity field solution». Advances in Space Research. 46 (1): 50–57. Bibcode:2010AdSpR..46…50J. doi:10.1016/j.asr.2010.03.002.
^ Matsumoto, K.; Goossens, S.; Ishihara, Y.; Liu, Q.; Kikuchi, F.; Iwata, T.; Namiki, N.; Noda, H.; Hanada, H.; et al. (2010). «An improved lunar gravity field model from SELENE and historical tracking data: Revealing the farside gravity features». Journal of Geophysical Research. 115 (E6): E06007, 1–20. Bibcode:2010JGRE..115.6007M. doi:10.1029/2009JE003499. ISSN 0148-0227.
^ Mazarico, E.; Lemoine, F. G.; Han, Shin-Chan; Smith, D. E. (2010). «GLGM-3: A degree-150 lunar gravity model from the historical tracking data of NASA Moon orbiters». Journal of Geophysical Research. 115 (E5): E05001, 1–14. Bibcode:2010JGRE..115.5001M. doi:10.1029/2009JE003472. ISSN 0148-0227.
^ Yan, Jianguo; Goossens, Sander; Matsumoto, Koji; Ping, Jinsong; Harada, Yuji; Iwata, Takahiro; Namiki, Noriyuki; Li, Fei; Tang, Geshi; et al. (2012). «CEGM02: An improved lunar gravity model using Chang’E-1 orbital tracking data». Planetary and Space Science. 62 (1): 1–9. Bibcode:2012P&SS…62….1Y. doi:10.1016/j.pss.2011.11.010.
^ Zuber, M. T.; Smith, D. E.; Neumann, G. A.; Goossens, S.; Andrews-Hanna, J. C.; Head, J. W.; Kiefer, W. S.; Asmar, S. W.; Konopliv, A. S.; et al. (2016). «Gravity field of the Orientale basin from the Gravity Recovery and Interior Laboratory Mission». Science. 354 (6311): 438–441. Bibcode:2016Sci…354..438Z. doi:10.1126/science.aag0519. ISSN 0036-8075. PMC 7462089. PMID 27789835.
^ Konopliv, Alex S.; Park, Ryan S.; Yuan, Dah-Ning; Asmar, Sami W.; Watkins, Michael M.; Williams, James G.; Fahnestock, Eugene; Kruizinga, Gerhard; Paik, Meegyeong; et al. (2013). «The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL Primary Mission». Journal of Geophysical Research: Planets. 118 (7): 1415–1434. Bibcode:2013JGRE..118.1415K. doi:10.1002/jgre.20097. hdl:1721.1/85858. S2CID 16559256.
^ ^a ^b ^c Lemoine, Frank G.; Goossens, Sander; Sabaka, Terence J.; Nicholas, Joseph B.; Mazarico, Erwan; Rowlands, David D.; Loomis, Bryant D.; Chinn, Douglas S.; Caprette, Douglas S.; Neumann, Gregory A.; Smith, David E. (2013). «High‒degree gravity models from GRAIL primary mission data». Journal of Geophysical Research: Planets. 118 (8): 1676–1698. Bibcode:2013JGRE..118.1676L. doi:10.1002/jgre.20118. ISSN 2169-9097.
^ ^a ^b ^c Konopliv, Alex S.; Park, Ryan S.; Yuan, Dah-Ning; Asmar, Sami W.; Watkins, Michael M.; Williams, James G.; Fahnestock, Eugene; Kruizinga, Gerhard; Paik, Meegyeong; Strekalov, Dmitry; Harvey, Nate (2014). «High-resolution lunar gravity fields from the GRAIL Primary and Extended Missions». Geophysical Research Letters. 41 (5): 1452–1458. Bibcode:2014GeoRL..41.1452K. doi:10.1002/2013GL059066.
^ Lemoine, Frank G.; Goossens, Sander; Sabaka, Terence J.; Nicholas, Joseph B.; Mazarico, Erwan; Rowlands, David D.; Loomis, Bryant D.; Chinn, Douglas S.; Neumann, Gregory A.; Smith, David E.; Zuber, Maria T. (2014). «GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data». Geophysical Research Letters. 41 (10): 3382–3389. Bibcode:2014GeoRL..41.3382L. doi:10.1002/2014GL060027. ISSN 0094-8276. PMC 4459205. PMID 26074638.
^ Goossens, Sander; et, al. (2016). «A global degree and order 1200 model of the lunar gravity field using GRAIL mission data» (PDF).{{cite web}}: CS1 maint: url-status (link)
^ Yan, Jianguo; Liu, Shanhong; Xiao, Chi; Ye, Mao; Cao, Jianfeng; Harada, Yuji; Li, Fei; Li, Xie; Barriot, Jean-Pierre (2020). «A degree-100 lunar gravity model from the Chang’e 5T1 mission». Astronomy & Astrophysics. 636: A45, 1–11. Bibcode:2020A&A…636A..45Y. doi:10.1051/0004-6361/201936802. ISSN 0004-6361. S2CID 216482920.
^ P. Muller; W. Sjogren (1968). «Mascons: Lunar mass concentrations». Science. 161 (3842): 680–84. Bibcode:1968Sci…161..680M. doi:10.1126/science.161.3842.680. PMID 17801458. S2CID 40110502.
^ Richard A. Kerr (12 April 2013). «The Mystery of Our Moon’s Gravitational Bumps Solved?». Science. 340 (6129): 138–39. doi:10.1126/science.340.6129.138-a. PMID 23580504.
^ Nine Planets
^ ^a ^b Williams, James G.; Konopliv, Alexander S.; Boggs, Dale H.; Park, Ryan S.; Yuan, Dah-Ning; Lemoine, Frank G.; Goossens, Sander; Mazarico, Erwan; Nimmo, Francis; Weber, Renee C.; Asmar, Sami W. (2014). «Lunar interior properties from the GRAIL mission». Journal of Geophysical Research: Planets. 119 (7): 1546–1578. Bibcode:2014JGRE..119.1546W. doi:10.1002/2013JE004559. S2CID 7045590.
^ Park, Ryan S.; Folkner, William M.; Williams, James G.; Boggs, Dale H. (2021). «The JPL Planetary and Lunar Ephemerides DE440 and DE441». The Astronomical Journal. 161 (3): 105. Bibcode:2021AJ….161..105P. doi:10.3847/1538-3881/abd414. ISSN 1538-3881. S2CID 233943954.
^ ^a ^b «China building «Artificial Moon» that simulates low gravity with magnets». Futurism.com. Recurrent Ventures. Retrieved 17 January 2022. Interestingly, the facility was partly inspired by previous research conducted by Russian physicist Andrew Geim in which he floated a frog with a magnet. The experiment earned Geim the Ig Nobel Prize in Physics, a satirical award given to unusual scientific research. It’s cool that a quirky experiment involving floating a frog could lead to something approaching an honest-to-God antigravity chamber.
^ ^a ^b Stephen Chen (12 January 2022). «China has built an artificial moon that simulates low-gravity conditions on Earth». South China Morning Post. Retrieved 17 January 2022. It is said to be the first of its kind and could play a key role in the country’s future lunar missions. Landscape is supported by a magnetic field and was inspired by experiments to levitate a frog.

Источник

Для определения значения радиуса Луны воспользуемся равенством: Mл / gл * Rл² = G (гравитационная постоянная) = Mз / gз * Rз², откуда выразим: Rл = √ (Mл * gз * Rз² / (gл * Mз)).

Значения постоянных: Мз (масса Земли) = 81Mл (масса Луны); gз — ускорение свободного падения на Земле (gз = 9,81 м/с²); Rз — радиус Земли (по условию Rз = 6370 км = 6370 * 10³ м); gл — ускорение свободного падения на Луне (по условию gл = 1,6 м/с²).

Расчет: Rл = √ (Mл * gз * Rз² / (gл * Mз)) = √ (Mл * 9,81 * (6370 * 10³) ² / (1,6 * 81Mл)) = 1752,6 * 10³ м = 1752,6 км.

Ответ: Радиус Луны, согласно расчету, составляет 1752,6 км.

Источник

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

УДК 531.51+523.34

Н.В. Островский

канд. техн. наук, ветеран труда г. Кирово-Чепецк, РФ E-mail: onv1@yandex.ru

О ГЕОМЕТРИИ ГРАВИТАЦИОННОГО ПОЛЯ ЛУНЫ

Аннотация

В статье представлены расчёты границ гравитационного поля Луны. Расчёты выполнены на основе решения гравитационной задачи трёх тел, ранее использованного для создания ряда динамических моделей. Гравитационное поле Луны представляет собой уширенный эллипсоид вращения, перицентр которого находится в соединении с Землёй. Полученные данные могут быть использованы при проектировании перелётных орбит Земля-Луна.

Ключевые слова

Гравитационная задача четырёх тел, гравитационное поле Луны, полёты к Луне.

В последние годы вновь стала актуальной тема экспедиций к Луне. Очевидно, что успех экспедиции и затраты на её осуществление зависят от точности расчёта перелётной орбиты, что требует знаний о гравитационном поле Луны. С 1958 г. состоялось 78 запусков космических аппаратов (КА) к Луне, значительная часть которых завершилась переходом КА на окололунную орбиту или посадкой на поверхность Луны [1]. Полученные данные слежения за движением КА позволили приступить к разработке моделей гравитационного поля Луны, но за прошедшие 60 лет проблема не нашла своего окончательного решения. Определение границ гравитационного поля Луны имеет ключевое значение при проектировании перелётной орбиты, т.к. на ней происходит смена небесного тела, которое является для КА центральным и, вместе с тем, происходит изменение углового момента (момента количества движения) КА. Важно подчеркнуть, что исключение углового момента из расчётных алгоритмов ведёт к ошибочным результатам [2].

Постановка задачи

Известно, что уравнение, описывающее закон тяготения Ньютона:

F = G-^-r2, где: (1)

F — сила тяготения,

G — универсальная гравитационная постоянная,

m1 и m2 — массы взаимодействующих тел,

r — расстояние между телами,

не пригодно для расчётов гравитационных взаимодействий в системах трёх и более тел.

Для решения данной проблемы ещё Лапласом было введено понятие сферы действия в связи с изучением движения комет при их сближении с планетами. При этом, под сферой действия понимается та область пространства, в которой планета выполняет роль центрального тела, сообщающего комете ускорение силы тяготения. Поверхность, ограничивающая сферу действия, определяют условием [3]:

a a

G,P,1 G ,S ,1

-=-, где: (2)

aG,S aG,P

aG,s — ускорение, которое Солнце сообщает комете в том случае, когда Солнце принимается за центральное тело;

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

аврл — возмущающее ускорение, вызываемое притяжением планеты;

ао,р- ускорение, которое планета сообщает комете в том случае, когда планета принимается за центральное тело;

а^,1 — возмущающее ускорение, вызываемое притяжением Солнца. Радиус сферы действия определяется уравнением:

, 1/5

т2

г 2 ^

А = r /j

Vi + 3cos2 ф

, где: (3)

Г1 — радиус-вектор планеты относительно Солнца

т -масса планеты в единицах масс Солнца;

ф — угол между направлениями из центра планеты на комету и на Солнце.

Для Земли, вычисленный по данному уравнению радиус сферы действия, изменяется в диапазоне от 7,92 до 9,40-108 м в зависимости от расстояния между Землей и Солнцем и выбранного направления. Таким образом, орбита Луна оказывается внутри сферы действия Земли, в то время как она находится вне сферы тяготения Земли, вычисленной по уравнению (1).

Сферу действия Луны можно также рассчитать по уравнению (3), подставив в него массу Луны, выраженную в массах Земли. Вычисленные значения радиуса сферы действия Луны находятся в диапазоне от 5,45 до 6,98 • 107 м в зависимости от направления радиус-вектора пробной точки и радиуса орбиты Луны.

Данный подход, однако, оказался не востребован при освоении космоса в связи с неточностями при расчётах ускорения силы тяготения.

Более точные результаты могут быть получены путём введения в уравнение Ньютона возмущающей функции, учитывающей воздействие внешних тел. Например, для спутника Земли возмущающая функция может иметь вид [4]:

R=GmM

Г.

с r

P2 CÖS^M 4

Gms

P2 CÖSa„, где: (4)

м V m J S V S J

тм и ms — массы Луны и Солнца, r — радиус-вектор спутника относительно Земли, гм и rs — расстояние от спутника до Луны и Солнца соответственно, P2 — полином Лежандра второй степени,

ам и as — угол между радиус-вектором спутника относительно Земли и радиус-векторами спутника относительно Луны и Солнца соответственно.

Аналогичный подход был использован и для описания гравитационного поля Луны. Первая модель Э.Л. Акима, опубликованная в 1966 г. содержала 11 коэффициентов [5], а модель M.P. Ananda, вышедшая в 1977 г., уже включала полиномы 20-го порядка [6]. Всего по состоянию на 1984 г. насчитывалось более 33 различных моделей гравитационного поля Луны [7].

По сути, все эти модели являются однотипными и аппроксимационными. По мере появления новых данных появляются и новые модели. Работа [8] содержит уравнение для вычисления гравитационного потенциала в окрестностях Луны для точки с координатами r, ф и X:

/ п

Л а п _____

V(r,p,Á) = ~Z — ZPm(sin^)(C„m cosтЛ + snm sinтЛ), где: (5)

V r У

m=9

r n=0

r, ф и X — радиус, широта и долгота, ц — гравитационная постоянная, а — средний радиус небесного тела,

Cnm и snm — полностью нормализованные коэффициенты Стокса, P™ (sin ф) — функция Лежандра степени n и порядка т.

Í 7 }

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

Но вопрос о границах гравитационного поля Луны ни в одной из работ не рассматривается. Это связано с тем, что модели создаются на основе наблюдений за движением искусственных спутников Луны, удалённость которых от поверхности Луны не превышает нескольких сот километров.

Поэтому для определения границ гравитационного поля Луны необходимо использовать иной подход.

Обобщённое решение задачи многих тел

В работе [9] было предложено обобщённое решение задачи трёх тел. Если мы имеем три тела с

т2 т3

массами т1, т2 и тз, то тело 1 будет притягиваться телом 2, когда->-. В противном случае на тело

Г3 Г3

’12 ’13

1 будет действовать сила со стороны тела 3. Величина силы тяготения при этом описывается уравнением:

F = Gm r

1 J2 и;

m3cosa

V 12

’13

, где: а — угол между Г12 и Г13.

(6)

Данный алгоритм был использован для построения моделей орбитального движения Луны и внешних спутников Юпитера, модели захвата Зёмлей внешнего тела, движущегося по гелиоцентрической орбите, расчёта приливных гравитационных эффектов [10-14].

В случае расчёта границ поля тяготения Луны мы имеем систему четырёх тел: Солнце (5), Земля (Е), Луна (М и пробная точка (Р) (см. рис. 1). Для определения направления силы тяготения, воздействующей

на пробную точку, мы должны сравнить три величины: т^’г^ , ЖЕ! Г^Е и тм /ГрМ .

P /

Рисунок 1 — Схема, описывающая взаимное расположение небесных тел и пробной точки

Для расчёта напряжённости гравитационного поля Луны (ускорения силы тяготения) при условии выполнения неравенства:

m m

«lM ^ «lE

3 3

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

г r

‘ PE

(7)

должно быть использовано уравнение:

ёы = GrPi

V pm

ы mS cosaS mEcosaE

, где:

а5 — угол между грм и гр5, аЕ — угол между грм и гре.

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

Результаты расчётов и их обсуждение

Расчёты показали, что равенство

определяющее границу гравитационного поля Луны,

достигается при значениях сравниваемых величин от 0,04 до 0,23 кг/м3, в то время как величина тз /Гр,8 в

окрестностях лунной орбиты составляет около 6 10-4 кг/м3. Поэтому положение Земли на орбите не влияет, в первом приближении, на границы гравитационного поля Луны. Вследствие этого на геометрию её гравитационного поля, опить-таки, в первом приближении, не влияет и фаза Луны, а влияет только расстояние между Луной и Землёй.

По форме гравитационное поле Луны напоминает эллипсоид вращения, хотя его сечение не в полной мере отвечает условию эллиптичности кривой. А именно, оно несколько уширено, так что отношение длины радиус-вектора пробной точки при угле 90° относительно радиус-вектора Луна-Земля к вычисленному значению фокального параметра эллипса находится в диапазоне от 1,024 (Луна в перигее) до 1,041 (Луна в апогее).

Размеры гравитационного поля Луны увеличиваются по мере её удаления от Земли. Если в перигее Луны большая полуось эллипсоида равна 8,85 107 м, а малая — 8,60-107 м (эксцентриситет 0,237), то в апогее большая полуось эллипсоида равна 9,90107 м, а малая — 9,63• 107 м (эксцентриситет 0,232). Перицентр эллипсоида находится в соединении с Землёю, а апоцентр — в оппозиции к ней (см. рис. 2).

Сопоставление с границами «сферы действия» Луны, найденными по уравнению (3), обнаруживает существенные различия. «Сфера действия» Луны также представляет собой эллипсоид, но Луна находится не в фокусе эллипса, а в его центре (см. рис. 3). Большая ось эллипса перпендикулярна радиус-вектору Луны относительно Земли. Размеры «сферы действия» значительно меньше. Соотношение радиусов изменяется от 0,8, когда пробная точка находится в соединении с Землёю, до 0,5, когда пробная точка находится в оппозиции к Земле.

Рисунок 2 — Зависимость радиуса гравитационного поля Луны от расстояния между Луной и Землёй и величины угла ЕМР (радиус в м, одно деление окружности — п/16).

Величина напряжённости гравитационного поля на его границе равна нулю, когда пробная точка находится в соединении с Землёю. Затем она начинает возрастать и достигает максимума при угле поворота

‘ У

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

относительно радиус-вектора Луна-Земля 135°. Далее следует минимум при угле поворота 180° (см. рис. 4). С увеличением размеров гравитационного поля Луны напряжённость поля на его границе уменьшается. Внутри гравитационной «сферы» напряжённость поля может быть вычислена по уравнению (8).

Рисунок 3 — Границы гравитационного поля и «сферы действия» Луны (Луна в перигее).

Заключение

Проведённые расчёты показали, что гравитационное поле Луны простирается на значительном расстоянии от небесного тела, а его границы постоянно меняются вследствие движения Луны по орбите.

Учёт границ гравитационного поля Луны должен существенно улучшить точность проектирования перелётных орбит Земля-Луна. Теоретически возможно найти некий функционал, описывающий границу гравитационного поля Луны, но более практичным представляется создание программного комплекса, позволяющего на основе эфемерид Земли и Луны вычислять напряжённость гравитационного поля Луны в любой точке и для любого момента времени. Точность вычислений напряжённости гравитационного поля будет определяться точностью используемых эфемерид и гравитационной постоянной Луны.

Рисунок 4 — Зависимости напряжённости гравитационного поля Луны на его границах от угла ЕМР.

-( ‘» )-

СИМВОЛ НАУКИ ISSN 2410-700X № 2/2019

Список использованной литературы:

1. Исследования Луны. // Интернет-сайт «Википедия». URL: https://m.wikipedia.org/wiki/Исследования_Луны (26.IX.2018).

2. Островский Н.В. Свойства эллиптических орбит. — М.: «Спутник+», 2018. — 48 с., с. 44.

3. Чеботарёв А.Г. Аналитические и численные методы небесной механики. — М.-Л.: Наука, 1965. — 367 с., с. 309.

4. Аксёнов Е.П. Теория движения искусственных спутников Земли. — М.: «Наука», ГРФМЛ, 1977. — 360 с., с. 212.

5. Аким Э.Л. Определение поля тяготения Луны по движению ИСЛ «Луна-10». // Доклады академии наук СССР, 1966, т. 170, с. 799-802.

6. Ananda M.P. Lunar gravity; a mass point model. // Journal Geophysics research, 1977, v. 82, p. 3049-3084.

7. Кислюк В.С. Эллипсоид инерции Луны. // Кинематика и физика небесных тел, 1985, № 1, с. 41-48.

8. Vilana E.C. Study of spacecraft orbits in the Gravity field of the moon. A dissertation submitted to the Department of Aerospace Engineering — Barselona: Universitaat Politecnica de Catalunya, 2012. — 96 p. [электронный ресурс]. URL: https://upcommons.upc.edu/bitstream/handle/2099.1/15241/Memoria.pdf (17.IX.2018).

9. Островский Н.В. Решение задачи трех тел на примере системы Солнце-Земля-Луна.//Материалы пятой Всероссийской научно-технической конференции «Современные проблемы математики и естествознания», Нижний Новгород, 18 апреля 2003. — Нижний Новгород: Нижегородский государственный технический университет, 2003, с. 4-5.

10. Nikolai V. Ostrovski. Physical model of the orbital movement of the Jupiter satellite Sinope.//Gamov Memorial International Conference dedicated to 100-th anniversary of George Gamov «Astrophysics after Gamov — theory and observations». Abstracts. Odessa: «Astroprint», 2004, p. 124-125.

11. Островский Н.В. Физическая модель движения спутника Юпитера Пасифе. //Вестник Удмуртского университета. Серия «Физика», 2005, № 4, с. 41-50.

12. Островский Н.В. Влияние Солнца на движение спутника Земли.//Вестник Тюменского государственного университета, 2005, № 4, с. 106-113.

13. Островский Н.В. Влияние Луны и Солнца на напряжённость гравитационного поля у поверхности неупругой Земли.// Омский научный вестник, 2006, № 10 (48), с. 5-8.

14. Ostrovskiy N.V. Modeling of the celestial body transition from heliocentric orbit to planet-centric.//Reports of International astronomical congress «Astrokazan-2011», Kazan, August 22-30. — Kazan: Kazan Federal University, 2011, p. 188-190.

}

Источник

Gravitational field[edit]

Mass of Moon[edit]

Theory[edit]

Gravity coefficients[edit]

Simulating lunar gravity[edit]

See also[edit]

References[edit]

Не пропустите также: