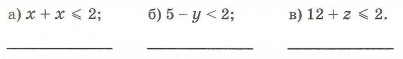Яра собрала в саду (216) яблок. Эти яблоки она решила разложить по корзинам, по (18) яблок в каждую корзину. Ей необходимо купить корзины. Разделить в уме (216) на (18) Яре сложно, но она может найти границы частного, то есть числа, между которыми находится правильный ответ.

При определении границ пользуются круглыми числами — числами, которые оканчиваются одним нулём или несколькими нулями.
Например, у числа (14) удобными круглыми соседями будут числа (10) и (20).
Чтобы Яре оценить частное чисел (216) и (18), нужно сделать следующие шаги.
1. Яра должна найти нижнюю границу частного: заменить делитель (18) бóльшим «круглым близким соседом» — (20), делимое (216) — мéньшим «круглым соседом», удобным для деления на (20) — (200).
2. Найти частное получившихся чисел: (200:20=10).
3. Теперь Яра должна найти верхнюю границу: заменить делитель (18) мéньшим «круглым близким соседом» — (10), делимое (216) — бóльшим «круглым соседом», удобным для деления на (10) — (300).
4. Найти частное получившихся чисел: (300:10=30).
5. Сделать вывод: частное находится в границах от (1)(0) до (3)(0). Значит, Яра должна купить не менее (10) и не более (30) корзин для яблок.
Это можно записать в виде двойного неравенства: (10<216:18<30).
Погрешность произведения
Пусть в результате измерений получено:
$$ x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x, y gt 0 $$
Найдём границы для произведения этих величин: z = xy
$$ {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow (x_0- Delta x)(y_0-Delta y) le xy le (x_0+ Delta x)(y_0+ Delta y) Rightarrow $$
$$ Rightarrow x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y+ Delta x Delta y) $$
(О правилах умножения двух неравенств, см. §36 данного справочника).
Абсолютные погрешности $Delta x ≪ x_0, Delta y≪y_0$ заметно меньше $x_0$ и $ y_0$, поэтому будем считать, что произведение $Delta x Delta y approx 0$, и им можно пренебречь. Получаем:
$$ x_0 y_0-( Delta xy_0+x_0 Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y) $$
$$ z = z_0 pm Delta z: z_0 = x_0 y_0, quad Delta z = Delta xy_0+x_0 Delta y $$
$$ δ_z = frac{Delta z}{z_0} = frac{Delta xy_0+x_0 Delta y}{x_0 y_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{xy} = δ_x+δ_y $$
При умножении приближенных величин их относительные погрешности складываются.
Погрешность степени
Пусть в результате измерений получено: $x = x_0 pm Delta x, x gt 0$
Тогда, для квадрата x из выражения для относительной погрешности произведения получаем: $δ_{x^2} = δ_x+δ_x = 2δ_x$.
Для куба: $δ_{x^3 } = δ_{x^2}+δ_x = 2δ_x+δ_x = 3δ_x$.
Для произвольной степени n:
$$ δ_{x^n} = n δ_x $$
При возведении приближенной величины в натуральную степень n, её относительная погрешность увеличивается в n раз.
Погрешность частного
Пусть в результате измерений получено:
$$x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x,y gt 0 $$
Найдём границы для частного этих величин: $z = frac{x}{y}$
$$ {left{ begin{array}{c} x_0- Delta x le x le x_0 + Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow {left{ begin{array}{c}x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0-Delta y} ge frac{1}{y} ge frac{1}{y_0+ Delta y} end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0+ Delta y} le frac{1}{y} le frac{1}{y_0- Delta y} end{array} right.} Rightarrow frac{x_0- Delta x}{y_0+ Delta y} le frac{x}{y} le frac{x_0+ Delta x}{y_0- Delta y} Rightarrow $$
$$ Rightarrow frac{ (x_0- Delta x)(y_0- Delta y)}{(y_0+ Delta y)(y_0- Delta y)} le frac{x}{y} le frac{(x_0+ Delta x)(y_0+ Delta y)}{(y_0- Delta y)(y_0+ Delta y)} Rightarrow $$
$$ Rightarrow frac{x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y)}{y_0^2- Delta y^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y+ Delta x Delta y)}{y_0^2- Delta y^2} $$
О правилах умножения двух неравенств и обращения положительных сторон, см. §36 данного справочника.
Считаем произведения и квадраты абсолютных погрешностей малыми величинами $Delta x Delta y approx 0, quad Delta y^2 approx 0$, которыми можно пренебречь. Получаем:
$$ frac{x_0 y_0-( Delta xy_0+x_0 Delta y)}{y_0^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y)}{y_0^2} $$
$$frac{x_0}{y_0} — left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) le frac{x}{y} le frac{x_0}{y_0} + left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) $$
$$ z = z_0 pm Delta z: z_0 = frac{x_0}{y_0}, Delta z = frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}$$
$$ δ_z = frac{Delta z}{z_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) : frac{x_0}{y_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) cdot frac{y_0}{x_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{frac{x}{y}} = δ_x+δ_y $$
При делении приближенных величин их относительные погрешности складываются.
Внимание!
Как при умножении, так и при делении приближённых величин, их относительные погрешности складываются.
Точность произведения или частного всегда меньше точности исходных величин.
Примеры
Пример 1. Точное значение выражения:
$$5,31 cdot 4,16+2,19 cdot 1,51 = 22,0896+3,3069 = 25,3965 $$
Считая все величины, входящие в выражение, приближёнными с абсолютной погрешностью $Delta$ x = 0,01, выясните, нужно ли округлять ответ.
Во сколько раз абсолютная погрешность результата больше абсолютной погрешности исходных данных? Во сколько раз относительная погрешность результата больше относительной погрешности сомножителя 5,31?
Обозначим a = 5,31, b = 4,16, c = 2,19, d = 1,51.
Относительные погрешности (округление с избытком):
$$δ_a = frac{0,01}{5,31} cdot 100 text{%} = 0,19 text{%}, quad δ_b = frac{0,01}{4,16} cdot 100 text{%} = 0,25 text{%} $$
$$δ_c = frac{0,01}{2,19} cdot 100 text{%} = 0,46 text{%}, quad δ_d = frac{0,01}{1,51} cdot 100 text{%} = 0,67 text{%} $$
Относительные погрешности произведений:
$$ δ_{ab} = δ_a+δ_b = 0,19 text{%} + 0,25 text{%} = 0,44 text{%} $$
$$ δ_{cd} = δ_c+δ_d = 0,46 text{%} +0,67 text{%} = 1,13 text{%} approx ↑ 1,2 text{%} $$
Абсолютные погрешности произведений:
$$ Delta_{ab} = δ_{ab} cdot ab = 0,0044 cdot 22,0896 approx 0,09719 approx ↑ 0,098 $$
$$ Delta_{cd} = δ_{cd} cdot cd = 0,012 cdot 3,3069 approx 0,03968 approx 0,040 $$
Оставляем в промежуточных оценках 2 значащие цифры для последующего округления. Абсолютная погрешность выражения:
$$ Delta_{ab+cd} = Delta_{ab} + Delta_{cd} = 0,098+0,040 = 0,138 approx ↑ 0,2 $$
Таким образом, ответ нужно округлить до десятых:
$$ 5,31 cdot 4,16+2,19 cdot 1,51 approx 25,4 ± 0,2 $$
Отношение абсолютной погрешности результата к погрешности исходных данных:
$ frac{0,2}{0,01} = 20$ — абсолютная погрешность увеличилась в 20 раз.
Относительная погрешность результата: $δ = frac{0,2}{25,4} cdot 100 text{%} approx 0,79 text{%} $
По отношению к $δ_a: frac{δ}{δ_a} = frac{0,79}{0,19} approx 4,2$ — относительная погрешность результата в 4,2 раза больше.
Пример 2. а) Границы приближенных величин $5 le x le 6,6 le y le 7$. Оцените сумму, разность, произведение и частное этих величин.
б) Считая x и y точными величинами, принимающими значения на заданных отрезках, найдите границы суммы, разности и произведения этих величин.
а) По условию:
$$ {left{ begin{array}{c} x_0-Delta x = 5 \ x_0+Delta x = 6 end{array} right.} Rightarrow {left{ begin{array}{c} 2x_0 = 5+6 = 11 \ 2 Delta x = 6-5 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} x_0 = 5,5 \ Delta x = 0,5 end{array} right.} Rightarrow δ_x = frac{0,5}{5,5} cdot 100 text{%} approx 9,1 text{%} $$
$$ {left{ begin{array}{c} y_0- Delta y = 6 \ y_0+ Delta y = 7 end{array} right.} Rightarrow {left{ begin{array}{c} 2y_0 = 6+7 = 13 \ 2 Delta y = 7-6 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} y_0 = 6,5 \ Delta y = 0,5 end{array} right.} Rightarrow δ_y = frac{0,5}{6,5} cdot 100 text{%} approx 7,7 text{%} $$
Абсолютная погрешность суммы: $Delta_{x+y} = Delta_x+Delta_y = 0,5+0,5 = 1$
$$ x+y = (5,5+6,5) pm 1 = 12 pm 1 $$
Границы суммы: $ 11 le x+y le 13$
Абсолютная погрешность разности: $Delta _{x-y} = Delta _x + Delta _y = 0,5+0,5 = 1$
$$ x-y = (5,5-6,5) pm 1 = -1 pm 1 $$
Границы разности: $-2 le x-y le 0$
Относительная погрешность произведения:
$$δ_{xy} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%}$$
Абсолютная погрешность произведения:
$$ Delta_{xy} = δ_{xy} cdot x_0 y_0 = 0,17 cdot 5,5 cdot 6,5 = 6,0775 approx ↑ 7 $$
$$ xy = (5,5 cdot 6,5) pm 7 approx 36 pm 7 $$
Границы произведения: $29 le xy le 43$
Относительная погрешность частного:
$$ δ_{x/y} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%} $$
Абсолютная погрешность частного:
$$ Delta_{frac{x}{y}} = δ_{frac{x}{y}} cdot frac{x_0}{y_0} = 0,17 cdot frac{5,5}{6,5} approx 0,14 approx ↑ 0,2 $$
$$ frac{x}{y} = left( frac{5,5}{6,5} right) pm 0,2 approx 0,8 pm 0,2 $$
Границы частного: $0,6 le frac{x}{y} le 1,0$
б) Для точных величин получаем следующие границы:
Границы суммы:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5+6 le x+y le 6+7 Rightarrow 11 le x+y le 13 $$
Границы разности:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ -7 le -y le -6 end{array} right.} Rightarrow 5-7 le x-y le 6-6 Rightarrow -2 le x-y le 0 $$
Границы произведения:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5 cdot 6 le xy le 6 cdot 7 Rightarrow 30 le xy le 42 $$
Границы частного:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ frac{1}{7} le frac{1}{y} le frac{1}{6} end{array} right.} Rightarrow frac{5}{7} le frac{x}{y} le 1 $$
Пример 3. В эксперименте по определению плотности вещества получен объём V = 9, 7 $pm$ 0,05 мл и масса m = 107 $pm$ 2 г. Найдите плотность.
Это свинец или железо?
Плотность:
$$ ρ = frac{m}{V}, ρ_0 = frac{m_0}{V_0} = frac{107 cdot 10^{-3} кг}{9,7 cdot 10^{-6} м^3} approx 11031 frac{кг}{м^3} $$
Относительные погрешности (округление с избытком):
$$ δ_V = frac{0,05}{9,7} cdot 100 text{%} approx 5,2 text{%}, δ_m = frac{2}{107} cdot 100 text{%} approx 1,9 text{%} $$
$$ δ_ρ = δ_V+δ_m = 5,2 text{%} +1,9 text{%} = 7,1 text{%} $$
Абсолютная погрешность для плотности (округление с избытком):
$$ Δ_ρ = δ_ρ cdot ρ_0 = 0,071 cdot 11031 approx 800 frac{кг}{м^3} $$
$$ ρ = 11000 pm 800 frac{кг}{м^3} $$
Это – свинец (табличное значение $ρ_{таб} = 11340 frac{кг}{м^3}$ ).
Инфоурок
›
Математика
›Другие методич. материалы›Памятка «Оценка суммы, разности, произведения, частного» 4 класс
Скачать материал
Скачать материал


- Сейчас обучается 1160 человек из 83 регионов


- Сейчас обучается 967 человек из 80 регионов


- Сейчас обучается 25 человек из 19 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 079 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
- 22.07.2019
- 593
- 8






- 04.06.2019
- 483
- 1


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Скачать материал
-
22.07.2019
6254
-
DOCX
124.5 кбайт -
85
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Гришаева Анастасия Алексеевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 4 года и 7 месяцев
- Подписчики: 7
- Всего просмотров: 25026
-
Всего материалов:
13
Определи, верно ли найдены границы для следующих частных:
а)
360 : 6 < 384 : 6 < 420 : 6 ДА, НЕТ
60 < 384 : 6 < 70
б)
24000 : 60 < 27612 : 59 < 30000 : 50 ДА, НЕТ
400 < 27612 : 59 < 600
в)
40000 : 80 < 40592 : 86 < 45000 : 90 ДА, НЕТ
500 < 40592 : 86 < 500
reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 9 урок. Оценка частного. Номер №2
Решение а
360 : 6 < 384 : 6 < 420 : 6
60 < 384 : 6 < 70
ДА, так как 60 < 64 < 70.
0
¯
384
0
36
¯
0
0
¯
24
00
24
¯
000
0
6
64
¯
Решение б
24000 : 60 < 27612 : 59 < 30000 : 50
400 < 27612 : 59 < 600
ДА, так как 400 < 468 < 600
0
¯
27612
0
236
¯
0
0
¯
401
00
354
¯
00
0
¯
472
000
472
¯
00000
0
59
468
¯
Решение в
40000 : 80 < 40592 : 86 < 45000 : 90
500 < 40592 : 86 < 500
НЕТ, так как 500 < 472 < 500 − не верно.
0
¯
40592
0
344
¯
0
0
¯
619
00
602
¯
00
0
¯
172
000
172
¯
00000
0
86
472
¯
Верно следующим образом:
36000 : 90 < 40592 : 86 < 48000 : 80
400 < 472 < 600
Урок 9. Оценка частного
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 9. Оценка частного
1. а) Как изменяется частное, если делимое увеличивается? Уменьшается?
б) Как изменяется частное, если делитель увеличивается? Уменьшается?
в) Расставь частные в порядке возрастания:
144 : 36, 180 : 18, 180 : 5, 72: 36, 144 :18.
Если одновременно заменить делимое меньшим числом, а делитель большим числом, то частное тем более уменьшится. А если заменить делимое большим числом, а делитель меньшим числом, то частное увеличится.
Эти свойства используются для нахождения границ частного:
Значит, частное 23 360:65 заключено между числами 300 и 400: 300 — его нижняя граница, а 400 — верхняя граница.
2. Определи, верно ли найдены границы для следующих частных:
а) 360 : 6 < 384 : 6 < 420 : 6 ДА, НЕТ
60 < 384 : 6 < 70
б) 24 000 : 60 < 27 612 : 59 < 30 000 : 50 ДА, НЕТ
400 < 27 612: 59 < 600
в) 40 000 : 80 < 40 592 : 86 < 45 000 : 90 ДА, НЕТ
500 < 40 592 : 86 < 500
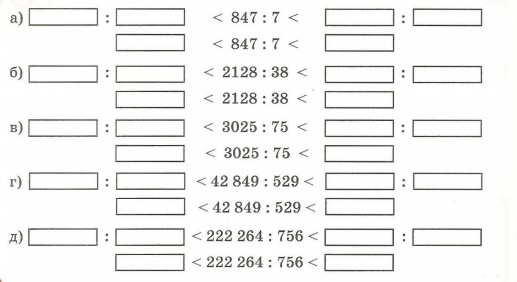
3. Сделай оценку следующих частных:
4. Докажи, что:
698 : 2 > 300
785 : 5 < 200
400 < 896 : 2 < 500
30 < 1645: 47 < 50
500 < 22 464 : 36 < 800
700 < 385 636 : 458 < 1000
5. В каких границах заключены частные:
423 : 9; 124 056 : 6; 22 848 : 56; 367 846 : 698?
6. Реши уравнения с комментированием по компонентам действий и сделай проверку:
а) 6 + m • 4 = 70; в) 30 — 200 : n = 25;
б) k : 5 + 8 = 27; г) t • 20 — 36 = 144.
7. Выполни действия:
а) (375 018 + 5678 • 924) :7- 15 192;
б) 4 280 185 + (89 040 ¦ 705 — 478 760): 8.
8. Запиши с помощью букв переместительное и сочетательное свойства сложения и умножения. Пользуясь ими, упрости выражения:
23 + а + 67 42 + b + 34 + 128 15 • с • 4 2 • d • 7 • 5 • 5 • 2
9. Продолжи ряд:
а) 15, 16, 18, 21, 25, … б) 4, 7, 13, 22, 34, …
10. Составь выражение и найди его значение. Придумай задачи с другими величинами, которые решаются так же.
а) За 4 часа теплоход прошел 136 км. Сколько километров он пройдет за 8 часов, двигаясь с той же скоростью?
б) Путь от одной станции до другой товарный поезд прошел за 9 часов, а пассажирский за 6 часов. Какова скорость пассажирского поезда, если скорость товарного поезда равна 40 км/ч?
в) Геологи 3 часа летели на вертолете со скоростью 95 км/ч, затем 2 часа ехали верхом со скоростью 12 км/ч. Какой путь проделали геологи за это время?
11. Найди для каждого неравенства множество его решении:
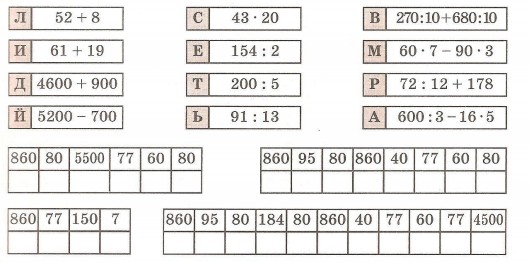
12. Расшифруй скороговорку;
13*. Раздели фигуры на 2 равные части ломаной линией, проходящей по сетке.
14*. В семье 4 детей, им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3?
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. — М.: Издательство «Ювента», 2005, — 64 с.: ил.
Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 4 класса скачать
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: