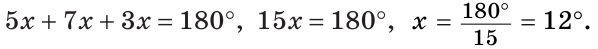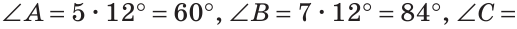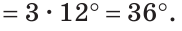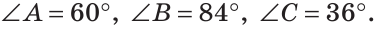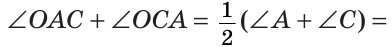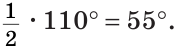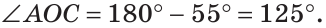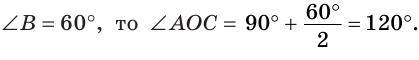Углы равностороннего треугольника
Чему равны углы равностороннего треугольника?
(свойство углов равностороннего треугольника)
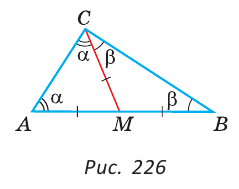
Все углы равностороннего треугольника равны по 60º.
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать .
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
Градусная мера угла
Время чтения: 14 минут
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
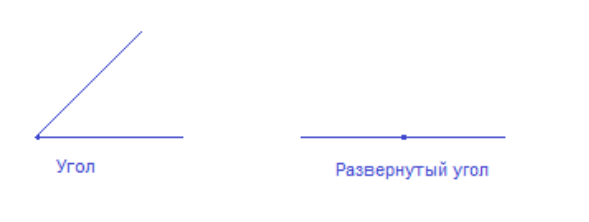
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac<1><180>] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
А для их измерения используется инструмент – транспортир.
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
Углы также различаются несколькими типами:
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
Пример 1. Задача с биссектрисой и развернутым углом.
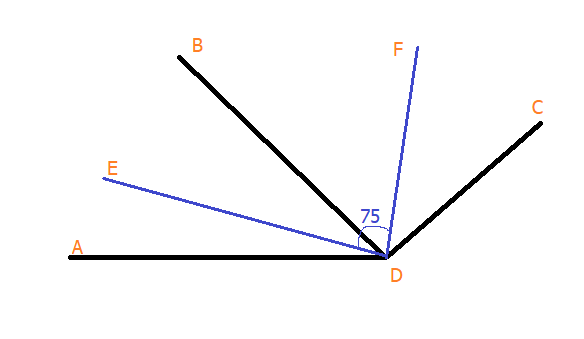
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Пример 2. Задача с биссектрисой и прямым углом.
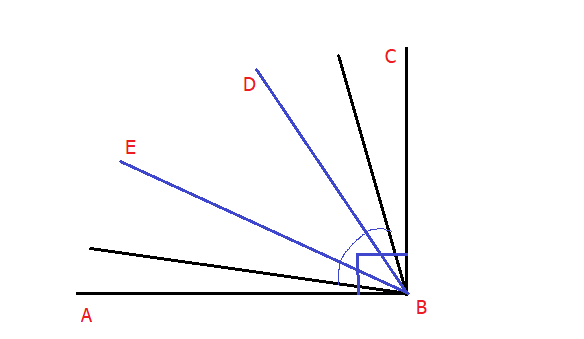
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
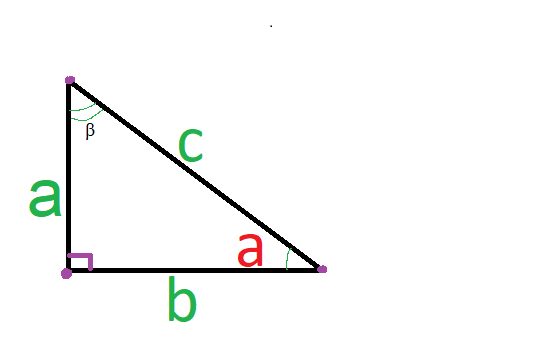
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.
Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
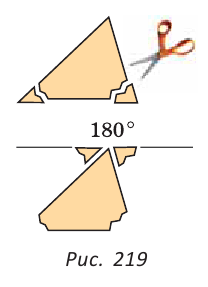
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
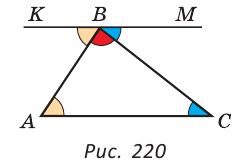
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 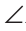





Следствия.
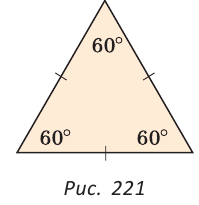
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
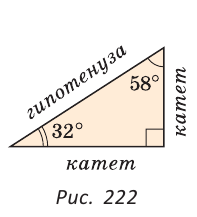
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
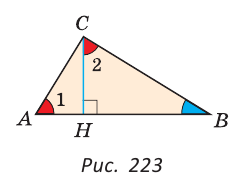
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то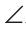
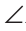
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
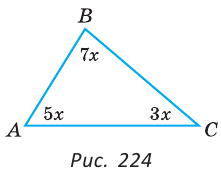
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 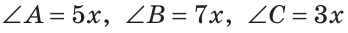
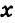
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
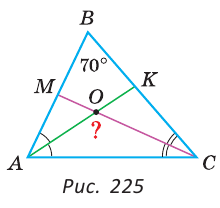
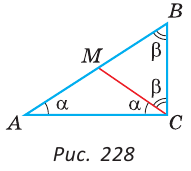
Пример:
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 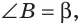
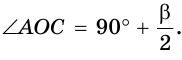
Пример:
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 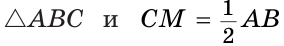
Докажем, что
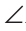

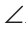






















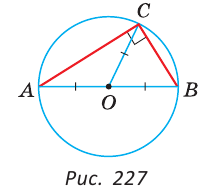
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://www.napishem.ru/spravochnik/matematika/gradusnaya-mera-ugla.html
http://www.evkova.org/summa-uglov-treugolnika
Правильный треугольник
Правильный треугольник — это такой треугольник у которого все три стороны равны и его три угла равны.
Правильный треугольник
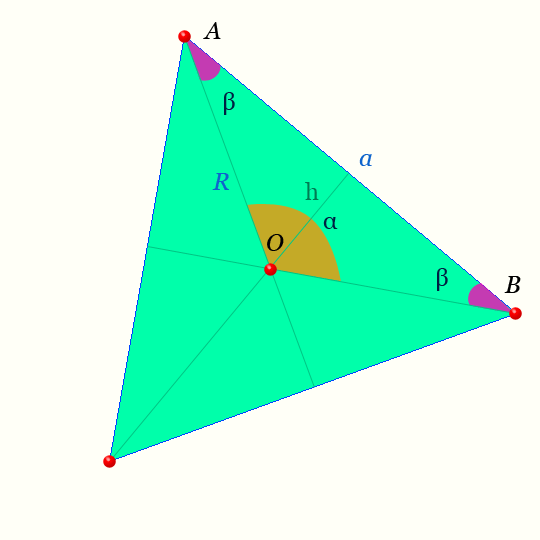
Центр правильного треугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного треугольника.
Обозначения на рисунке для правильного треугольника
| n=3 | число сторон и вершин правильного треугольника, | шт |
|---|---|---|
| α | центральный угол правильного треугольника, | радианы, ° |
| β | половина внутреннего угла правильного треугольника, | радианы, ° |
| γ | внутренний угол правильного треугольника, | радианы, ° |
| a | сторона правильного треугольника, | м |
| R | радиусы правильного треугольника, | м |
| p | полупериметр правильного треугольника, | м |
| L | периметр правильного треугольника, | м |
| h | апофемы правильного треугольника, | м |
Основные формулы для правильного треугольника
Периметр правильного треугольника
[ L = 3a ]
Полупериметр правильного треугольника
[ p = frac{3}{2}a ]
Центральный угол правильного треугольника в радианах
[ α = frac{2}{3}π ]
Центральный угол правильного треугольника в градусах
[ α = frac{360°}{3} = 120° ]
Половина внутреннего угла правильного треугольника в радианах
[ β = frac{1}{6}π ]
Половина внутреннего угла правильного треугольника в градусах
[ β = frac{180°}{6} = 30° ]
Внутренний угол правильного треугольника в радианах
[ γ = 2β = frac{π}{3} ]
Внутренний угол правильного треугольника в градусах
[ γ = frac{180°}{3} = 60° ]
Площадь правильного треугольника
[ S = ph = frac{3}{2}ha ]
Или учитывая формулу Площади равностороннего треугольника получим
[S=frac{sqrt{3}}{4}a^2]
Правильный треугольник |
стр. 267 |
|---|
Чему равны углы равностороннего треугольника?
Теорема
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.

AB=BC=AC
Доказать: ∠A=∠B=∠C=60º.
Доказательство:
Так как AB=BC, ∠A=∠C (как углы при основании равнобедренного треугольника).
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать.
Замечание.
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
В этой статье описаны все свойства, правила и определения равностороннего треугольника.
Математика — любимый предмет многих школьников, особенно тех, у которых получается решать задачи. Геометрия — это также интересная наука, но не все дети могут понять новый материал на уроке. Поэтому им приходится дорабатывать и доучивать дома. Давайте повторим правила равностороннего треугольника. Читайте ниже.
Все правила равностороннего треугольника: свойства
В самом слове «равносторонний» скрывается определение этой фигуры.
Определение равностороннего треугольника: Это треугольник, у которого все стороны равны друг другу.
Из-за того, что равносторонний треугольник – это в некотором роде равнобедренный треугольник, у него появляются признаки последнего. Например, в этих треугольниках биссектриса угла является еще медианой и высотой.
Вспомним: Биссектриса — луч, делящий угол пополам, медиана – луч, выпущенный из вершины, делящий противолежащую сторону пополам, а высота — это перпендикуляр, исходящий из вершины.
Вторым признаком равностороннего треугольника является то, что все его углы равны между собой и каждый из них имеет градусную меру в 60 градусов. Вывод об этом можно сделать из общего правила о сумме углов треугольника, равной 180 градусам. Следовательно, 180:3=60.
Следующее свойство: центром равностороннего треугольника, а также вписанной в него и описанной около него окружностей является точка пересечения всех его медиан (биссектрис).
Четвертое свойство: радиус описанной около равностороннего треугольника окружности превышает в два раза радиус вписанной окружности в эту фигуру. Убедиться в этом можно, посмотрев на чертеж. ОС является радиусом описанной около треугольника окружности, а ОВ1 — радиусом вписанной. Точка О — место пересечения медиан, значит, разделяет ее как 2:1. Из этого делаем вывод, что ОС = 2ОВ1.
Пятым свойством является то, что в этой геометрической фигуре легко посчитать составляющие элементы, если в условии указана длина одной стороны. При этом чаще всего используется теорема Пифагора.
Шестое свойство: площадь такого треугольника вычисляется по формуле S=(а^2*3) /4.
Седьмое свойство: радиусы окружности, описанной около треугольника, и окружности, вписанной в треугольник, соответственно равны
R = (a3) /3 и r = (a3) /6.
Рассмотрим примеры задач:
Пример 1:
Задача: Радиус окружности, вписанной в равносторонний треугольник равен 7 см. Найдите высоту треугольника.
Решение:
- Радиус вписанной окружности связан с последней формулой, следовательно, OM = (BC3) /6.
- BC = (6 * OM) /3 = (6*7) /3 = 143.
- AM = (BC3) /2; AM = (143*3) /2 = 21.
- Ответ: 21 см.
Эту задачу можно решить по-другому:
- Исходя из четвертого свойства, можно сделать вывод, что ОМ = 1/2 АМ.
- Следовательно, если ОМ равно 7, то АО равно 14, а АМ равно 21.
Пример 2:
Задача: Радиус описанной около треугольника окружности равен 8. Найдите высоту треугольника.
Решение:
- Пусть АВС – равносторонний треугольник.
- Как и в предыдущем примере, можно идти двумя путями: более простым – АО = 8 => ОМ =4. Тогда АМ = 12.
- И более длинным – чтобы найти АМ через формулу. АМ = (АС3) /2 = (83*3) /2 = 12.
- Ответ: 12.
Как видите, зная свойства и определение равностороннего треугольника, вы сможете решить любую задачу по геометрии по этой теме.
Видео: Геометрия Равносторонний треугольник
- Альфашкола
- Уроки по математике
- Планиметрия
- Равносторонний треугольник.
Равносторонний треугольник. — онлайн урок
Тема: Равносторонний треугольник 7 класс. В данном уроке дано определение равностороннего треугольника, определена градусная мера углов равностороннего треугольника, определены: длина высоты в равностороннем треугольнике, длина медианы в равностороннем треугольнике, длина биссектрисы в равностороннем треугольнике. Равносторонний треугольник и окружность: радиус вписанной в равносторонний треугольник окружности, радиус описанной вокруг равностороннего треугольника окружности. Рассмотрена формула нахождения площади равностороннего треугольника.
Отзывы:
Роман Михайлович очень хороший репетитор, внучка 9 лет очень довольна, занимается с интересом. Репетитор достоин уважения за терпеливость, умение общаться с детьми.
спасибо за урок! всё понравилось!
Великолепный преподаватель, знает подход к деткам. Очень увлекательные материалы.
Похожие уроки