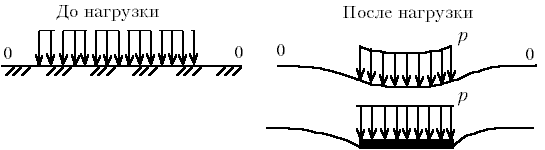Как найти градиент напора

М.5.1.
Что такое напор? Какова его размерность?

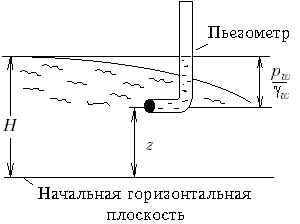
Полный
напор представляет собой расстояние,
измеряемое в единицах длины (метр) от
свободной поверхности воды в данной
точке до некоторой произвольной
горизонтальной плоскости, принятой за
начальную. Полный напор включает в себя
напор геометрический H_г,
пьезометрический H_п
и скоростной (скоростным напором мы
обычно пренебрегаем, так как он крайне
мал). Таким образом, мы получаем напор
H:

где 	давление в пьезометре в точке M;
	удельный вес воды (рис.М.5.1).

Рис.М.5.1.
Определение напора в грунтовом потоке

М.5.2.
Какое давление создает столб воды
высотой 1 м? Какой высоты столб воды
нужно взять, чтобы создать давление,
равное 1 кПа и 1 МПа?

Столб
воды высотой 1 м создает давление, равное
10 кПа. Чтобы создать давление 1 кПа,
требуется столб воды высотой 10 см, для
создания давления в 1 МПа требуется
столб воды 100 м.

Рис.М.5.3.
Определение напора и давления жидкости
в сосуде

М.5.3.
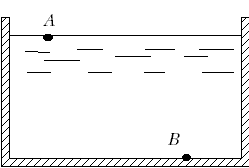
Одинаковы или различны напоры в сосуде
на поверхности воды и на дне сосуда?
Одинаковы или различны давления в воде
в этих точках?

Если
имеется сосуд с водой, то полные напоры
в точках A
и B
будут одинаковы (рис.М.5.3). В точке A
пьезометрический напор равен нулю и
полный напор совпадает с геометрическим.
Давления будут равными: в точке A

только атмосферному, в точке B

сумме атмосферного и веса столба жидкости
над ней.

М.5.4.
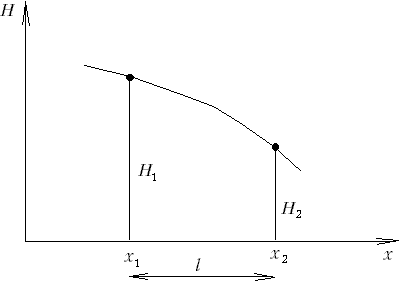
Что такое градиент напора? Какова его
размерность?

Градиент
напора i
равен падению напора на единицу длины:

Градиент
(уклон) 
величина безразмерная (рис.М.5.4).

Рис.М.5.4.
Определение градиента напора

М.5.5.
Запишите закон Дарси. Какова размерность
коэффициента фильтрации? От чего он
зависит? Что такое начальный градиент
фильтрации?

Закон
Дарси записывается так

то
есть скорость фильтрации пропорциональна
градиенту напора i
и коэффициенту фильтрации K_ф.
Коэффициент фильтрации зависит от вида
грунта, размера его пор (то есть от
линейного размера пор, но не пористости),
от температуры жидкости (меняется ее
вязкость).

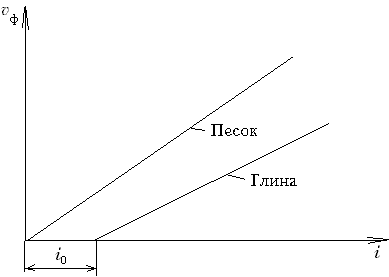
Начальный
градиент фильтрации 
величина градиента фильтрации в глинистых
грунтах, при котором начинается
практически ощутимая фильтрация
(рис.М.5.5). Закон Дарси с учетом начального
градиента фильтрации выражается
следующим образом:

при
;

при
.

Рис.М.5.5.
Зависимость скорости фильтрации от
градиента напора

М.5.6.
Что называется гидродинамическим
давлением и какова его размерность?

Гидродинамическим
давлением называется сила, передаваемая
перемещающимся потоком воды единице
объема грунта. Эта сила совпадает с
направлением движения воды и равна:

Гидродинамическое
давление имеет размерность объемной
силы кН/м³.

М.6. Распределение напряжений в грунтовых массивах

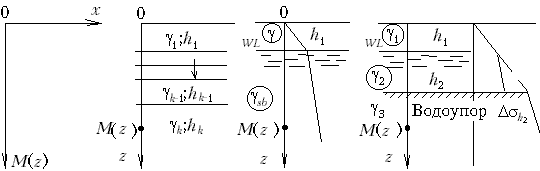
М.6.1.
Как вычислить вертикальные напряжения
в массиве грунта от его собственного
веса и чему они равны?

Вертикальное
напряжение от собственного веса грунта

_z
представляет собой вес столба грунта
над рассматриваемой точкой с площадью
поперечного сечения, равной единице.
Таким образом, если в точке M
на глубине z
грунт однородный, получаем 
_z
= 
_z,
если имеются различные слои (рис.М.6.1),
то

Рис.М.6.1.
Определение давления в грунте от его
собственного веса и наличия уровня
грунтовой воды

Удельный
вес грунта ниже горизонта воды принимается
с учетом действия выталкивающей силы
за счет взвешивания в воде, поэтому
получаем

Давление

_z
в водоупорном слое принимается с учетом
полного веса водонасыщенного грунта
(то есть выталкивающая сила не учитывается),
который расположен выше:

На
границе водоупора в эпюре 
z
имеет место скачок на величину
,
причем в данном случае.

М.6.2.
Следует ли учитывать деформации грунта
от его собственного веса и в каких
случаях?

Деформации
грунта от его собственного веса обычно
не учитываются, так как они давно
завершились. Однако в том случае, если
в силу обстоятельств изменяется структура
грунта, то сила собственного веса грунта
вызывает в нем дополнительные деформации
(например, при увлажнении лессового
грунта, изза которого растворяются
жесткие цементационные связи, или
оттаивания вечномерзлого грунта).

М.6.3.
Чему равны боковые напряжения от
собственного веса грунта? Что называется
коэффициентом бокового давления грунта
в условиях естественного залегания?
Может ли коэффициент бокового давления
грунта в условиях естественного залегания
быть более единицы?

Боковые
напряжения 
х
составляют обычно долю от вертикальных,
то есть 
_х=
₀
_z.
Коэффициент бокового давления грунта
в условиях его естественного залегания
₀
равен отношению бокового давления 
_x
к вертикальному 
_z.
(а не отношению приращений этих давлений),
то есть не следует путать ₀
и 
. Коэффициент ₀
может быть как больше, так и меньше
единицы.

М.6.4.
Как связаны между собой коэффициент
бокового давления грунта 
и коэффициент бокового давления в
условиях естественного залегания ₀?
От чего зависит величина₀?

Значение

может лишь совпадать с величиной _.
Для сыпучего грунта, у которого удельное
сцепление c
отсутствует, можно назвать следующие
пределы для _:

 
_
1/
.

Для
связного грунта эти пределы еще больше
и поэтому можно считать, что

то
есть практически коэффициент _
может быть любым. Величина _
зависит от условий образования массива
и тех геологических процессов, которые
протекали в течение длительного времени.
Опытное определение величины _
затруднительно. Часто считается, что
_=1,
так как все тела «текут» с определенным,
часто весьма малым коэффициентом
вязкости.

М.6.5.
Начертите эпюру распределения вертикальных
напряжений в массиве грунта от собственного
веса:

 если
сверху более легкий грунт;

 если
сверху более тяжелый грунт;

 при
наличии в слое уровня грунтовой воды;

 при
наличии водоупора;

см.также
ответы на вопрос М.6.1.

1. Если
сверху более легкий грунт, то график
сверху более крутой, в нижней 
более пологий.

2. При
более тяжелом грунте сверху в верхней
части график более пологий, в нижней 
более крутой.

3. При
наличии грунтовой воды, так как 
_sb<
, эпюра имеет вид такой же, как и в случае
2.

4.
На водоупоре имеет место скачок в эпюре
напряжений 
_z
(см. рис.М.6.1.).

М.6.6.
Что может являться доказательством
того, что с глубиной напряжения от
местной нагрузки, приложенной на
поверхности, рассеиваются?

То,
что поверхность опускается под действием
нагрузки не только в пределах загруженного
участка, но и рядом с ним (рис.М.6.6).

Рис.М.6.6.
Перемещение точек поверхности грунта
при приложении постоянной нагрузки

М.6.7.
Какие основные положения приняты в
теории упругости?

Основные
положения теории упругости следующие:

1. Тело
является сплошным и изотропным
(деформационные свойства в различных
направлениях одинаковы).

2. Тело
является упругим и со снятием нагрузки
все деформации исчезают.

3. Напряжения
в теле отсутствуют, если нет внешней
нагрузки.

4. Тело
является «бесконечно» прочным, то
есть в нем не возникает разрушений и
трещин, изменяющих напряженное состояние.

5. Связь
между напряжениями и деформациями
является линейной и описывается законом
Гука.

М.6.8.
Какие основные положения приняты в
теории линейнодеформируемых тел?

Для
того, чтобы можно было воспользоваться
решениями задач, имеющимися в теории
упругости, приняты следующие положения:

1. Грунт
состоит обычно из трех компонентов:
минерального скелета, воды и воздуха,
однако возможно его рассматривать как
квазисплошное тело, то есть тело, имеющее
свойства сплош
ного однородного тела,
в котором трещины и пустоты отсутствуют.
Грунт можно рассматривать как тело
изотропное, обладающее одинаковыми
деформационными свойствами в разных
направлениях.

2. Для
грунта характерно наличие остаточных
деформаций. При полном снятии нагрузки
все деформации не исчезают, а упругие
(то есть восстанавливающиеся) бывают
часто значительно менее неупругих
(остаточных) деформаций. Поэтому в теории
линейнодеформируемых тел рассматривается
только процесс нагрузки, а процесс
разгрузки, если в том есть необходимость,
рассматривается особо.

3. Считается,
что нагрузки на грунт не вызывают его
разрушения и далеки от предельных,
поэтому в грунтовом массиве не возникает
трещин, разрывов, срезов и т.д., то есть
не нарушается «квазисплошность».

4. Связь
между полными напряжениями и общими
деформациями принимается линейной.
Таким образом считается справедливым
закон Гука, связывающий напряжения и
деформации. Деформации считаются малыми.

М.6.9.
Чем теория линейнодеформируемых тел
отличается от теории упругости?

В
теории упругости рассматриваются только
упругие тела с восстанавливающими
деформациями, а в теории линейнодеформируемых
тел рассматриваются общие деформации,
включающие также остаточную деформацию.

М.6.10.
Какую пользу мы получаем от того, что
применяем теорию линейнодеформируемых
тел?

Поскольку
в теории упругости основная система
уравнений является линейной, это
позволяет суммировать отдельные решения
и интегрировать их. Такие сумма или
интеграл также удовлетворяют основной
системе дифференциальных уравнений
теории упругости и поэтому будут являться
искомыми решениями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

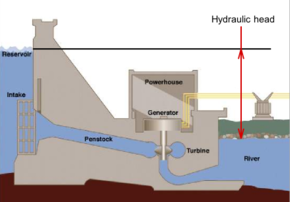
Available difference in hydraulic head across a hydroelectric dam, before head losses due to turbines, wall friction and turbulence

Fluid flows from the tank at the top to the basin at the bottom under the pressure of the hydraulic head.

Measuring hydraulic head in an artesian aquifer, where the water level is above the ground surface

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.^[1]^[2]

It is usually measured as a liquid surface elevation, expressed in units of length, at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer’s elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. The hydraulic head can be used to determine a hydraulic gradient between two or more points.

«Head» in fluid dynamics[edit]

In fluid dynamics, head is a concept that relates the energy in an incompressible fluid to the height of an equivalent static column of that fluid. From Bernoulli’s principle, the total energy at a given point in a fluid is the energy associated with the movement of the fluid, plus energy from static pressure in the fluid, plus energy from the height of the fluid relative to an arbitrary datum. Head is expressed in units of distance such as meters or feet. The force per unit volume on a fluid in a gravitational field is equal to ρg where ρ is the density of the fluid, and g is the gravitational acceleration. On Earth, additional height of fresh water adds a static pressure of about 9.8 kPa per meter (0.098 bar/m) or 0.433 psi per foot of water column height.

The static head of a pump is the maximum height (pressure) it can deliver. The capability of the pump at a certain RPM can be read from its Q-H curve (flow vs. height).

A common misconception is that the head equals the fluid’s energy per unit weight, while, in fact, the term with pressure does not represent any type of energy (in the Bernoulli equation for an incompressible fluid this term represents work of pressure forces). Head is useful in specifying centrifugal pumps because their pumping characteristics tend to be independent of the fluid’s density.

There are generally four types of head:

Velocity head is due to the bulk motion of a fluid (kinetic energy).

${displaystyle h_{v}={tfrac {1}{2}}rho v^{2}/rho g={frac {1}{2}}{frac {v^{2}}{g}}}$

Note that ${displaystyle rho gh_{v}}$ is equal to the dynamic pressure for irrotational flow.
Elevation head is due to the fluid’s weight, the gravitational force acting on a column of fluid. The elevation head is simply the elevation (h) of the fluid above an arbitrarily designated zero point:

${displaystyle h_{e}=rho gh/rho g}$
Pressure head is due to the static pressure, the internal molecular motion of a fluid that exerts a force on its container. It is equal to the pressure divided by the force/volume of the fluid in a gravitational field:

${displaystyle h_{p}=p/rho g}$
Resistance head (or friction head or Head Loss) is due to the frictional forces acting against a fluid’s motion by the container. For a continuous medium, this is described by Darcy’s law which relates volume flow rate (q) to the gradient of the hydraulic head through the hydraulic conductivity K:

while in a piped system head losses are described by the Hagen–Poiseuille equation and the Bernoulli Equation.

Components of hydraulic head[edit]

After free falling through a height in a vacuum from an initial velocity of 0, a mass will have reached a speed

where is the acceleration due to gravity. Rearranged as a head:

${displaystyle h={frac {v^{2}}{2g}}.}$

The term $frac{v^{2}}{2 g}$ is called the velocity head, expressed as a length measurement. In a flowing fluid, it represents the energy of the fluid due to its bulk motion.

The total hydraulic head of a fluid is composed of pressure head and elevation head.^[1]^[2] The pressure head is the equivalent gauge pressure of a column of water at the base of the piezometer, and the elevation head is the relative potential energy in terms of an elevation. The head equation, a simplified form of the Bernoulli principle for incompressible fluids, can be expressed as:

where

In an example with a 400 m deep piezometer, with an elevation of 1000 m, and a depth to water of 100 m: z = 600 m, ψ = 300 m, and h = 900 m.

The pressure head can be expressed as:

${displaystyle psi ={frac {P}{gamma }}={frac {P}{rho g}}}$

where
is the gauge pressure (Force per unit area, often Pa or psi),

Fresh water head[edit]

The pressure head is dependent on the density of water, which can vary depending on both the temperature and chemical composition (salinity, in particular). This means that the hydraulic head calculation is dependent on the density of the water within the piezometer. If one or more hydraulic head measurements are to be compared, they need to be standardized, usually to their fresh water head, which can be calculated as:

${displaystyle h_{mathrm {fw} }=psi {frac {rho }{rho _{mathrm {fw} }}}+z}$

where

Hydraulic gradient[edit]

The hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. For groundwater, it is also called the Darcy slope, since it determines the quantity of a Darcy flux or discharge. It also has applications in open-channel flow where it is also known as stream gradient and can be used to determine whether a reach is gaining or losing energy. A dimensionless hydraulic gradient can be calculated between two points with known head values as:

${displaystyle i={frac {dh}{dl}}={frac {h_{2}-h_{1}}{mathrm {length} }}}$

where

The hydraulic gradient can be expressed in vector notation, using the del operator. This requires a hydraulic head field, which can be practically obtained only from numerical models, such as MODFLOW for groundwater or standard step or HEC-RAS for open channels. In Cartesian coordinates, this can be expressed as:

${displaystyle nabla h=left({frac {partial h}{partial x}},{frac {partial h}{partial y}},{frac {partial h}{partial z}}right)={frac {partial h}{partial x}}mathbf {i} +{frac {partial h}{partial y}}mathbf {j} +{frac {partial h}{partial z}}mathbf {k} }$

This vector describes the direction of the groundwater flow, where negative values indicate flow along the dimension, and zero indicates ‘no flow’. As with any other example in physics, energy must flow from high to low, which is why the flow is in the negative gradient. This vector can be used in conjunction with Darcy’s law and a tensor of hydraulic conductivity to determine the flux of water in three dimensions.

Hydraulic head in groundwater[edit]

Relation between heads for a hydrostatic case and a downward flow case.

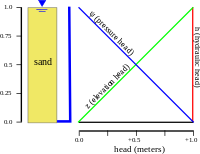
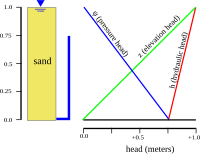
The distribution of hydraulic head through an aquifer determines where groundwater will flow. In a hydrostatic example (first figure), where the hydraulic head is constant, there is no flow. However, if there is a difference in hydraulic head from the top to bottom due to draining from the bottom (second figure), the water will flow downward, due to the difference in head, also called the hydraulic gradient.

Atmospheric pressure[edit]

Even though it is convention to use gauge pressure in the calculation of hydraulic head, it is more correct to use total pressure (gauge pressure + atmospheric pressure), since this is truly what drives groundwater flow. Often detailed observations of barometric pressure are not available at each well through time, so this is often disregarded (contributing to large errors at locations where hydraulic gradients are low or the angle between wells is acute.)

The effects of changes in atmospheric pressure upon water levels observed in wells has been known for many years. The effect is a direct one, an increase in atmospheric pressure is an increase in load on the water in the aquifer, which increases the depth to water (lowers the water level elevation). Pascal first qualitatively observed these effects in the 17th century, and they were more rigorously described by the soil physicist Edgar Buckingham (working for the United States Department of Agriculture (USDA)) using air flow models in 1907.

Head loss[edit]

In any real moving fluid, energy is dissipated due to friction; turbulence dissipates even more energy for high Reynolds number flows. This dissipation, called head loss, is divided into two main categories, «major losses» associated with energy loss per length of pipe, and «minor losses» associated with bends, fittings, valves, etc. The most common equation used to calculate major head losses is the Darcy–Weisbach equation. Older, more empirical approaches are the Hazen–Williams equation and the Prony equation.

For relatively short pipe systems, with a relatively large number of bends and fittings, minor losses can easily exceed major losses. In design, minor losses are usually estimated from tables using coefficients or a simpler and less accurate reduction of minor losses to equivalent length of pipe, a method often used for shortcut calculations of pneumatic conveying lines pressure drop.^[3]

Notes[edit]

^ ^a ^b Mulley, Raymond (2004), Flow of Industrial Fluids: Theory and Equations, CRC Press, ISBN 978-0849327674, 410 pages. See pp. 43–44.
^ ^a ^b Chanson, Hubert (2004), Hydraulics of Open Channel Flow: An Introduction, Butterworth–Heinemann, ISBN 978-0750659789, 650 pages. See p. 22.
^ «Pipe equivalent length (Pneumatic conveying)».

References[edit]

Bear, J. 1972. Dynamics of Fluids in Porous Media, Dover. ISBN 0-486-65675-6.
for other references which discuss hydraulic head in the context of hydrogeology, see that page’s further reading section

Источник

Основной закон фильтрации — закон Дарси — был установлен в 1856 г. Исторически закон был получен Анри Дарси экспериментально на основе анализа большого объема опытных данных путем наблюдений за расходом воды при движении через образец песка заданной длины и площади поперечного сечения, но может быть получен с помощью осреднения уравнений Навье-Стокса, описывающих течение в масштабе пор. Выражает зависимость скорости фильтрации флюида от градиента напора:

где k — коэффициент фильтрации [м/сут], численно равный скорости фильтрации при I = 1, а скорость фильтрации v представляет собой отношение расхода потока Q ко всей площади его поперечного сечения:

В этом случае v не является действительной скоростью фильтрации, поскольку при ее определении учитывается вся площадь сечения потока, а не площадь порового пространства, через которую реально движется вода. Значение скорости v позволяет легко сравнить между собой различные потоки. Действительная скорость фильтрации и связана со скоростью фильтрации соотношением

где n_a — активная пористость (трещиноватость).

Здесь v/k характеризует силы вязкости или сопротивления среды, а I — разность напоров, обуславливающая фильтрацию ПВ.

Определим расход потока:

где I — напорный градиент, определяемый отношением разницы гидростатических напоров (Н₁-Н₂) к длине участка L_1-2

Физический смысл коэффициента фильтрации:

Фильтрация под влиянием разности напоров

т.е. k — это расход потока через единичное сечение (1м²) при I = 1. Значения k для песков — 1-50 м/сут, супесей — 0,01-1,0, суглинков — 0001-0,01, глин — меньше 0,0001 м/сут.

Для вертикального потока (перетекания) из одного водоносного горизонта в другой через слой слабопроницаемых пород мощностью m_о и коэффициентом фильтрации k_о на участке территории длиной L и шириной В имеем:

где H₁ — уровень воды в пласте (1); H₂ — уровень воды в пласте (2).

Схема к расчету расхода перетекания через слой слабопроницаемых пород

Линейная связь между v и I на графике ниже, представлена прямой линией. Однако, поскольку этот закон является феноменологическим, он имеет пределы применимости — так называемые верхний и нижний пределы применимости.

В первом случае нарушение закона Дарси связано с возникновением турбулентности потока ПВ при больших скоростях фильтрации, которые возникают при значениях k>1000 м/сут и значительных градиентах потока (в закарстованных породах, вблизи шахтных стволов, открытых дрен, подземного контура плотин). Величина критической скорости v > 500 м/сут. Линейная зависимость нарушается, и справедливо выражение:

где a — коэффициент нелинейности фильтрации.

Во втором случае нарушение закона Дарси происходит в глинистых тонкодисперсных породах, где силы молекулярного взаимодействия между водой и породой вызывают дополнительные сопротивления движению жидкости. Существуют некоторые значения критического напорного градиента I₀, ниже которого движение подземных вод не происходит (v=0 при I ≤ I₀). При I > I₀ возникает течение подземных вод, причем коэффициент фильтрации изменяется в зависимости от I. При I > I₀ справедливо выражение

Графическое изображение обобщенного закона Дарси

1 — линейная зависимость; 2 — приближенная линейная зависимость (переходный режим фильтрации); 3-5 — обобщенные зависимости (3 — линейно-турбулентный режим фильтрации, 4 — линейно-вязкопластический режим фильтрации; 5 — с учетом молекулярных взаимодействий)

Источник

Подземные воды находятся в постоянном движении. Существует раздел гидрогеологии, изучающий закономерности движения подземных вод, который называется «Динамика подземных вод».

Законы движения подземных вод используются при гидрогеологичеких инженерных расчетах водозаборов, дренажей, определении притоков воды к строительным котлованам.

Подземные воды передвигаются в основном путем инфильтрации и фильтрации.

Под инфильтрацией понимают движение воды при частичном заполнении пор воздухом либо водяными парами.

При фильтрации движение воды происходит при полном заполнении пор(трещин) водой. Масса этой движущей воды создает фильтрационный поток.

Фильтрационные потоки различают по характеру движения (установившийся и неустановившийся), гидравлическому состоянию (безнапорные, напорные и напорно-безнапорные). Движение потоков в основном ламинарное (параллельным) , в крупных трещинах и пустотах может быть турбулентным (завихряющемся). В плане фильтрационные потоки можно рассматривать как плоские и радиальные (сходящиеся (например к колодцу) и расходящиеся).

Основной закон фильтрации подземных вод — Закон фильтрации Дарси

Движение подземных вод происходит при наличии разности гидравлических уровней (напоров). Воды двигаются от мест с высокими уровнями к местам с низкими уровнями.

Отношение разности напоров к длине пути фильтрации называется гидравлическим (напорным) градиентом. Чем градиент выше, тем больше скорость движения.

I = ΔH/l,

где ΔG = H1-H2 — разность напоров (H);

l — длина пути фильтрации.

Фильтрация в полностью водонасыщенных водах при ламинарном (параллельном, спокойном, без завихрений) движении воды подчиняется закону Дарси.

Q = КфFI,

где Q — расход воды (кол-во фильтрующей воды через поперечное сечение F в единицу времени);

К_ф — коэффициент фильтрации;

F — площадь поперечного сечения потока воды (водоносного пласта);

I — Гидравлический градиент.

Введем понятие скорость фильтрации (v) — отношение расхода воды к площади поперечного сечения потока (v = Q/F). Таким образом сформулировать закон Дарси можно как «Скорость фильтрации пропорциональна напорному градиенту»

v = К_фI

Коэффициент фильтрации можно таким образом можно выразить как скорость фильтрации при напорном градиенте равном единице.

Скорость фильтрации воды по представленной выше формуле не отвечает действительной скорости движения воды в породе. Это связано с тем что вода двигается не по всему сечению, а только через его часть, равную площади пор и трещин породы. Действительную скорость движения воды (v_д) определить можно как

v_д = v/n,

где n — пористость породы, выраженная в долях единицы.

Коэффициент фильтрации определяется в основном геометрией пор, а также свойствами самой воды и пр.

Точное значение коэффициента фильтрации определяют лабораторным путем, полевым путем и расчетным методом ( для песков и гравелистых пород)

Приближенная оценка для решения не требующих высокой точности задач (простые инженерные задачи) возможна по табличным данным.

Характеристика пород	Коэффициент фильтрации м/сутки
Очень хорошо проникаемые галечники с крупным песком	100 — 1000 и более
Хорошо проникаемые галечники и гравий с мелким песком, крупный песок, чистый среднезернистый песок,	100 — 10
Проницаемые галечники и графий с мелким песком, средензернистые и мелкозернистые пески	10 -1
Слабопроницаемые тонкозернистые пески, супеси	1 -0,1
Слабопроницаемые суглинки	0,1 -0,001
Глины, мергели, монолитные скальные породы	менее 0,001

Источник

М.6. Распределение напряжений в грунтовых массивах

«Head» in fluid dynamics[edit]

Components of hydraulic head[edit]

Fresh water head[edit]

Hydraulic gradient[edit]

Hydraulic head in groundwater[edit]

Atmospheric pressure[edit]

Head loss[edit]

See also[edit]

Notes[edit]

References[edit]

Фильтрация под влиянием разности напоров

Схема к расчету расхода перетекания через слой слабопроницаемых пород

Графическое изображение обобщенного закона Дарси

Не пропустите также: