Загрузить PDF
Загрузить PDF
Все прямоугольные треугольники имеют один прямой угол (90 градусов), а противоположная ему сторона называется гипотенузой.[1]
Гипотенуза — самая длинная сторона треугольника, и найти ее можно различными способами. В этой статье мы расскажем вам, как найти гипотенузу по теореме Пифагора (когда известны длины двух других сторон треугольника), по теореме синусов (когда известны длина катета и угол) и в некоторых частных случаях (часто такие задания встречаются на контрольных и тестах).
-
1
Теорема Пифагора связывает все стороны прямоугольного треугольника.[2]
Согласно данной теореме, в любом прямоугольном треугольнике с катетами «а» и «b» и гипотенузой «с»: a2 + b2 = c2.[3]
-
2
Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
- Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата.
-
3
Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла). Затем подставьте данные вам значения в формулу.
- Например, катеты треугольника равны 3 и 4. В этом случае а = 3, b = 4, а формула выглядит так: 32 + 42 = c2.
-
4
Возведите в квадрат значения катетов («a» и «b»). Для этого просто умножьте число само на себя:
- Если a = 3, то a2 = 3 x 3 = 9. Если b = 4, то b2 = 4 x 4 = 16.
- Подставьте эти значения в формулу: 9 + 16 = с2.
-
5
Сложите найденные квадраты катетов (a2 и b2), чтобы вычислить квадрат значения гипотенузы (с2).
- В нашем примере 9 + 16 = 25, поэтому с2 = 25.
-
6
Найдите квадратный корень с2. Используйте калькулятор, чтобы извлечь квадратный корень из найденного значения. Так вы вычислите гипотенузу треугольника.
- В нашем примере с2 = 25. Квадратный корень из 25 равен 5 (так как 5 х 5 = 25, поэтому √25 = 5). Это означает, что гипотенуза с = 5.
Реклама
-
1
Определение пифагоровой тройки. Пифагорова тройка — это три числа (длины трех сторон), которые удовлетворяют теореме Пифагора. Очень часто треугольники с такими сторонами приводятся в учебниках и на тестах. Если вы запомните первые несколько пифагоровых троек, вы сэкономите много времени на тестах или экзаменах, потому что сможете вычислить гипотенузу, просто взглянув на длины катетов.[4]
- Первая пифагорова тройка: 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Если дан треугольник с катетами 3 и 4, то вы можете с уверенностью заявить, что гипотенуза равна 5 (без необходимости делать какие-либо расчеты).
- Пифагоровы тройки работают даже в том случае, когда числа умножены или разделены на один коэффициент. Например, если катеты равны 6 и 8, гипотенуза равна 10 (62 + 82 = 102, 36 + 64 = 100). То же самое верно для 9-12-15 и даже для 1,5-2-2,5.
- Вторая пифагорова тройка: 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Также к этой тройке относятся, например, числа 10-24-26 и 2,5-6-6,5.
-
2
Равнобедренный прямоугольный треугольник. Это такой треугольник, углы которого равны 45,45 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:1:√2. Это означает, что гипотенуза в таком треугольнике равна произведению катета и квадратного корня из 2.
- Чтобы вычислить гипотенузу такого треугольника, просто умножьте длину любого катета на √2.[5]
- Это соотношение особенно удобно, когда в задачах вместо числовых значений даются переменные.
- Чтобы вычислить гипотенузу такого треугольника, просто умножьте длину любого катета на √2.[5]
-
3
Половина равностороннего прямоугольного треугольника. Это такой треугольник, углы которого равны 30,60 и 90 градусам. Соотношение между сторонами этого треугольника равно 1:√3:2 или х:х√3:2х. Чтобы найти гипотенузу в таком треугольнике выполните одно из следующих действий:[6]
- Если вам дан короткий катет (противолежащий углу в 30 градусов), просто умножьте длину этого катета на 2, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 8.
- Если вам дан длинный катет (противолежащий углу в 60 градусов), просто умножьте длину этого катета на 2/√3, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 4,62.
Реклама
-
1
Поймите, что означает «синус». Синус, косинус и тангенс угла — это основные тригонометрические функции, связывающие углы и стороны в прямоугольном треугольнике. Синус угла равен отношению противолежащей стороны к гипотенузе. Обозначается синус как sin.[7]
-
2
Научитесь вычислять синус. Чтобы вычислить синус, на калькуляторе найдите клавишу sin, нажмите ее, а затем введите значение угла. В некоторых калькуляторах сначала нужно нажать клавишу перехода к работе с функциями, а затем нажать клавишу sin. Поэтому поэкспериментируйте с калькулятором или проверьте его документацию.
- Чтобы найти синус угла в 80 градусов, нажмите «sin», «8», «0», «=» или нажмите «8», «0», «sin», «=» (ответ: -0,9939).
- Вы также можете найти онлайн-калькулятор, введя в поисковой системе «вычисление синуса» (без кавычек).[8]
-
3
Запомните теорему синусов. Теорема синусов является полезным инструментом для вычисления углов и сторон любого треугольника. В частности, она поможет вам найти гипотенузу прямоугольного треугольника, если вам дан катет и угол, отличный от прямого. Согласно теореме синусов, в любом треугольнике со сторонами a, b, c и углами A, B, C верно равенство a / sin A = b / sin B = c / sin С.[9]
- Теорема синусов применяется к любым треугольникам, а не только к прямоугольным (но только в прямоугольном треугольнике есть гипотенуза).
-
4
Обозначьте стороны треугольника через «а» (известный катет), «b» (неизвестный катет), «с» (гипотенуза). Затем обозначьте углы треугольника через «А» (напротив катета «а»), «В» (напротив катета «b»), «С» (напротив гипотенузы).
-
5
Найдите третий угол. Если вам дан один из острых углов прямоугольного треугольника (А или В), а второй угол всегда равен 90 градусам (С = 90), то третий угол вычисляется по формуле 180 — (90 + А) = B (помните, что сумма углов в любом треугольнике равна 180 градусам). При необходимости уравнение можно изменить и так: 180 — (90 + B) = A.
- Например, если угол A = 40 градусам, то B = 180 — (90 + 40) = 180 — 130 = 50 градусов.
-
6
На данном этапе вам известны значения всех трех углов и длина катета «а». Теперь вы можете подставить эти значения в формулу теоремы синусов, чтобы найти две другие стороны.
- В нашем примере допустим, что катет а = 10, а углы равны C = 90˚, A = 40˚, В = 50˚.
-
7
Подставьте данные и найденные значения в теорему синусов, чтобы найти гипотенузу: катет «а»/синус угла «A» = гипотенуза «с»/синус угла «С». При этом sin 90˚ = 1. Таким образом, уравнение упрощается до: а/sinA = с/1 или с = а/sinA.
-
8
Разделите длину катета «а» на синус угла «А», чтобы найти длину гипотенузы. Для этого сначала найдите синус угла, а затем выполните деление. Или вы можете воспользоваться калькулятором, введя 10/(sin40) или 10/(40sin) (не забудьте про скобки).
- В нашем примере sin 40 = 0,64278761, а с = 10/0,64278761 = 15,6.
Реклама
Об этой статье
Эту страницу просматривали 312 843 раза.
Была ли эта статья полезной?
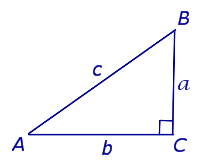
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Обратная теорема Пифагора:
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=<4>/<5>, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
http://poschitat.online/storony-pryamougolnogo-treugolnika
http://examer.ru/ege_po_matematike/teoriya/pryamougolnie_treugolniki
Известен катет AC и прилежащий угол a
Гипотенузу будем рассчитывать с помощью косинуса.
cos(a)=AC/AB
AB = AC / cos(a)
Как найти косинус угла ?
Решение
Гипотенуза AB = 17 / cos(30) = 19.6299092
Гипотенуза прямоугольного треугольника с катетом 17 и прилежащим углом 30 равна 19.6299092
Ссылка на результат
?n1=17&n2=30
Как известно, геометрия – непростая наука, требующая особой аккуратности и точности в решении задач. Многие выражения и формулы, которые мы впоследствии используем в более сложных вычислениях, изложены в учебниках по математике 6-7 класса. Чтобы сделать процесс изучения тригонометрических функций более простым и приятным, в этой статье мы рассмотрим несколько коротких способ вычисления гипотенузы прямоугольного треугольника.
Как найти гипотенузу по катетам?
Вспомним немного теории: прямоугольным треугольником называют плоскую фигуру, у которой есть три угла. Один из них имеет величину 90º, а стороны называют катетами и гипотенузой. Та сторона, которая противолежит прямому углу, и есть гипотенуза, а остальные две – это прилежащие катеты. Главная игра сторон проявляется в теореме Пифагора, согласно которой гипотенуза равняется сумме квадратов катетов. Однако это лишь кажется запутанным, ведь на самом деле все гораздо проще.
Свойства геометрической фигуры
Перед тем, как найти гипотенузу треугольника, необходимо разобраться, какие особенности имеет данная фигура. Рассмотрим главные из них:
- В прямоугольном треугольнике оба острых угла в сумме будут равны 90º.
- Катет, лежащий против угла в 30º, будет равен ½ от величины гипотенузы.
- Если катет равен ½ от значения гипотенузы, тогда второй угол будет иметь такую же величину – 30º.
Найти гипотенузу в прямоугольном треугольнике можно несколькими способами. Самым простым решением является вычисление через катеты. Допустим, вам известны значения катетов сторон А и В. Тогда на выручку приходит теорема Пифагора, повествующая нам, что если поставить каждую величину катета в квадрат и просуммировать полученные данные, мы узнаем чему равна гипотенуза. Таким образом, нам необходимо просто извлечь значение квадратного корня:
Например, если катет А = 3 см, а катет В = 4 см, тогда вычисление будет иметь следующий вид:
Как найти гипотенузу через угол?
Еще одним способом, который поможет узнать, чему равна гипотенуза в прямоугольном треугольнике, является вычисление через заданный угол. Для этого нам потребуется вывести величину через формулу синуса. Допустим, нам известна величина катета (А) и значение противолежащего угла (α). Тогда все решение заключается в одной формуле: С=А/sin(α).
Например, если длина катета 40 см, а угол составляет 45°, тогда длину гипотенузы можно вывести следующим образом:
40/sin(45°) = 40/0,71 = 56,33.
Определить искомую величину можно также через косинус заданного угла. Допустим, нам известно значение одного катета (В) и острого прилежащего угла (α). Тогда для решения задачи понадобится одна формула: С=В/ cos(α).
К примеру, если длина катета имеет значение 50 см, а угол составляет 45°, тогда гипотенузу можно вычислить следующим образом:
50/cos(45°) = 50/0,71 = 80,42.
Таким образом, мы рассмотрели основные способы как узнать гипотенузу в треугольнике. В ходе решения задания важно сконцентрировать внимание на имеющихся данных, тогда найти неизвестную величину будет достаточно просто. Необходимо знать всего пару формул и процесс решения задач станет простым и приятным.
Есть три варианта решения этой задачи. Первый — если в условиях задачи дано, что катеты равны (по сути, мы имеем прямоугольный равнобедренный треугольник). Второй — если еще дан какой-то угол (кроме угла в 45%, тогда мы имеем тот же равнобедренный треугольник и возвращаемся к первому варианту). И третий — когда известен один из катетов. Рассмотрим данные варианты подробнее.
Как найти равные катеты, при известной гипотенузе
- первый катет (обозначим его буквой «a») равен второму катету ((обозначим его буквой «b»): a=b;
- размер катетов;
В этом варианте решение задачи основывается на использовании теоремы Пифагора. Ее применяют к прямоугольным треугольникам и основной ее вариант звучит, как: «Квадрат гипотенузы равен сумме квадратов катетов». Так, как катеты у нас равны, то мы можем обозначать оба катета одним и тем же сиволом: a=b, значит — a=a.
- Подставляем наши условные обозначения в теорему (с учетом вышеизложенного):
c^2=a^2+a^2, - Далее максимально упрощаем формулу:
с^2=2*(a^2) — группируем,
с=√2*а — подносим обе части уравнения к квадратному кореню,
a=c/√2 — выносим искомое. - Подставлем данное значение гипотенузы и получаем решение:
a=x/√2
Как найти катеты, при известной гипотенузе и угле
- гипотенуза (обозначим ее буквой «c») равна х см: c=x;
- угол β равный q: β=q;
- размер катетов;
Для решения этой задачи необходимо использовать тригонометрические функции. Найболее популярны две из них:
- функция синуса — синус искомого угла равен отношению противолежащего катета к гипотенузе;
- функция косинуса — косинус искомого угла равен отношению прилежащего катета к гипотенузе;
Вы можете использовать любую. Я наведу пример с использованием первой. Пусть катеты у нас обозначаються символами «a» (прилежащий к углу) и «b» (противолежащий к углу). Соответственно наш угол лежит между катетом «a» и гипотенузой.
- Подставляем выбранные условные обозначения в формулу:
sinβ = b/c - Выводим катет:
b=c*sinβ - Подставляем наши данный и имеем один катет.
b=c*sinq
Второй катет можно найти воспользовавшись второй тригонометрической функцией, или же перейти к третьему варианту.
Как найти один катет, если известна гипотенуза и другой катет
- гипотенуза (обозначим ее буквой «c») равна х см: c=x;
- катет (обозначим его буквой «b») равен y см: b=y;
- размер другого катета (обозначим его буквой «a»);
В этом варианте решением задачи, как и в первом, является использование теоремы Пифагора.
- Подставляем наши условные обозначения в теорему:
c^2=a^2+b^2, - Выносим необходимый катет:
a^2=c^2-b^2 - Подносим обе части уравнения к квадратному кореню:
a=√(c^2-b^2) - Подставляем данные значения и имеем решение:
a=√(x^2-y^2)
Геометрия — не простая наука. Она требует к себе особого внимания и знания точных формул. Эта разновидность математики пришла к нам из Древней Греции и даже по прошествии нескольких тысяч лет она не теряет свою актуальность. Не стоит напрасно думать, что это бесполезный предмет, забивающий голову студентов и школьников. На самом деле геометрия применима во многих сферах жизни. Без нее знаний по геометрии не строится ни одно архитектурное сооружение, не создаются автомобили, космические корабли и самолеты. Сложные и не очень развязки дорог и колей — это все нуждается в геометрических расчетах. Да даже порой ремонт в своей комнате вы не сможете сделать без знания элементарных формул. Так что не стоит недооценивать всю важность этого предмета. Наиболее частые формулы, которые приходится использовать во многих решениях, мы изучаем еще в школе. Одна из них это нахождение гипотенузы в прямоугольном треугольнике. Чтобы разобраться в этом, читайте ниже.
Прежде чем приступить к практике, давайте начнем с основ и определим, что такое гипотенуза в прямоугольном треугольнике.
Гипотенуза — одна из сторон в прямоугольном треугольнике, которая находится напротив угла в 90 градусов (прямой угол) и всегда является самой длинной.
Существует несколько способов, как найти длину искомой гипотенузы в заданном прямоугольном треугольнике.
В случае, когда катеты нам уже известны- мы используем теорему Пифагора, где мы складываем сумму из квадратов двух катетов, что и будет равняться квадрату гипотенузы.
а и b -катеты, c- гипотенуза.
В нашем случае, для прямоугольного треугольника, соответственно, формула будет следующей:
Если подставить известные числа катетов а и b, пусть это будет а=3 а b=4, то с=√32+42 , то получим с=√25, с=5
Когда у нас известна длина лишь одного катета, то формулу можно преобразовать, чтобы найти длину второго. Выглядит это следующим образом:
В том случае, когда по условиям задачи у нас известен катет А и гипотенуза С, то можно рассчитать прямой угол треугольника, назовем его α.
Для этого воспользуемся формулой:
Пусть второй угол, который нам необходимо вычислить, будет β. Учитывая, что мы знаем сумма углов треугольника, которая составляет 180°, то: β= 180°-90°-α
В том случае, когда нам известны значения катетов, можно по формуле найти значение острого угла треугольника:
В зависимости от известных общепринятых значений, стороны прямоугольника можно найти по множеству разных формул. Приведем некоторые из них:
При решении задач с нахождением неизвестных в прямоугольном треугольнике, очень важно акцентировать внимание на уже известные вам значения и, исходя из этого, подставлять их в нужную формулу. Сразу запомнить их будет трудно, поэтому советуем вам сделать небольшую рукописную подсказку и вклеить в тетрадь.
Как видите, если вникнуть во все тонкости этой формулы, то можно без труда разобраться в этом. Рекомендуем попробовать решить несколько задач, основанных на данной формуле. После того, как увидите свой результат, вам станет ясно, поняли вы эту тему или нет. Постарайтесь не заучивать, а вникнуть в материал, это будет куда полезнее. Зазубренный материал забывается уже после первой контрольной, а эта формула вам будет встречаться достаточно часто, поэтому сначала поймите ее, а после заучивайте на память. Если эти рекомендации не дали положительного эффекта, то есть смысл в дополнительных занятиях этой темы. И помните: ученье свет, а не ученье тьма!
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Катетами называют называют две стороны прямоугольного треугольника, образующие прямой угол. Противоположная прямому углу самая длинная сторона треугольника именуется гипотенузой. Дабы обнаружить гипотенузу, необходимо знать длину катетов.
Инструкция
1.
Длины катетов и гипотенузы связаны соотношением, которое описывается теоремой Пифагора. Алгебраическая формулировка: “В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.”Формула Пифагора выглядит так:c2 = a2 + b2,где с — длина гипотенузы, a и b — длины катетов.
2.
Зная длины катетов, по теореме Пифагора дозволено обнаружить гипотенузу прямоугольного треугольника:c = ?(a2 + b2).
3.
Пример. Длина одного из катетов равна 3 см, длина иного — 4 см. Сумма их квадратов равна 25 см?:9 см? + 16 см? = 25 см?.Длина гипотенузы в нашем случае равна квадратному корню из 25 см? – 5 см. Стало быть, длина гипотенузы равняется 5 см.
Гипотенузой именуется сторона в прямоугольном треугольнике, которая находится наоборот угла в 90 градусов. Для того, дабы рассчитать его длину, довольно знать длину одного из катетов и величину одного из острых углов треугольника.
Инструкция
1.
При знаменитом катете и остром угле прямоугольного треугольника, то размер гипотенузы может быть равен отношению катета к косинусу/синусу этого угла, если данный угол является ему противолежащим/прилежащим:h = C1(либо C2)/sin?;h = С1(либо С2)/cos?.Пример: Пускай дан прямоугольный треугольник ABC с гипотенузой AB и прямым углом C. Пускай угол B равен 60 градусам, а угол A 30 градусам Длина катета BC 8 см. Нужно обнаружить длину гипотенузы AB. Для этого дозволено воспользоваться любым из предложенных выше методов:AB = BC/cos60 = 8 см.AB = BC/sin30 = 8 см.
Гипотенуза – самая длинная сторона прямоугольного треугольника
. Она расположена противоположно прямому углу. Метод нахождения гипотенузы прямоугольного треугольника
зависит от того, какими начальными данными вы владеете.
Инструкция
1.
Если вестимы катеты прямоугольного треугольника
, то длина гипотенузы прямоугольного треугольника
может быть обнаружена с подмогой теоремы Пифагора – квадрат длины гипотенузы равен сумме квадратов длин катетов:с2 = а2 + b2, где а и b – длины катетов прямоугольного треугольника
.
2.
Если вестим один из катетов и острый угол, то формула для нахождения гипотенузы будет зависеть от того, какой данный угол по отношению к вестимому катету – прилежащий (расположенный вблизи катета) либо противолежащий (расположенный наоборот него.В случае прилежащего угла, гипотенуза равна отношению катета на косинус этого угла: с = a/cos?;E угол противолежащий, гипотенуза равна отношению катета на синус угла: с = a/sin?.
Видео по теме
Гипотенузой называют сторону прямоугольного треугольника, лежащую наоборот прямого угла. Она является наибольшей стороной прямоугольного треугольника. Рассчитать ее дозволено по теореме Пифагора либо с поддержкой формул тригонометрических функций.
Инструкция
1.
Катетами называют стороны прямоугольного треугольника, прилежащие к прямому углу. На рисунке катеты обозначены как AB и BC. Пускай заданы длины обоих катетов. Обозначим их как |AB| и |BC|. Для того, дабы обнаружить длину гипотенузы |AC|, воспользуемся теоремой Пифагора. Согласно данной теореме сумма квадратов катетов равна квадрату гипотенузы, т.е. в обозначениях нашего рисунка |AB|^2 + |BC|^2 = |AC|^2. Из формулы получаем, что длина гипотенузы AC находится как |AC| = ?(|AB|^2 + |BC|^2) .
2.
Разглядим пример. Пускай заданы длины катетов |AB| = 13, |BC| = 21. По теореме Пифагора получаем, что |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610. Для того, дабы получить длину гипотенузы, нужно извлечь квадратный корень из суммы квадратов катетов, т.е. из числа 610: |AC| = ?610. Воспользовавшись таблицей квадратов целых чисел, выясняем, что число 610 не является полным квадратом какого-нибудь целого числа. Для того, дабы получить окончательное значение длины гипотенузы, испробуем перенести полный квадрат из под знака корня. Для этого разложим число 610 на множители. 610 = 2 * 5 * 61. По таблице примитивных чисел глядим, что 61 – число примитивное. Следственно последующее приведение числа?610 нереально. Получаем окончательный результат |AC| = ?610.Если бы квадрат гипотенузы был равен, к примеру, 675, тогда?675 = ?(3 * 25 * 9) = 5 * 3 * ?3 = 15 * ?3. В случае, если сходственное приведение допустимо, исполняйте обратную проверку – возведите итог в квадрат и сравните с начальным значением.
3.
Пускай нам знаменит один из катетов и прилежащий к нему угол. Для определенности пускай это будут катет |AB| и угол?. Тогда мы можем воспользоваться формулой для тригонометрической функции косинус – косинус угла равен отношению прилежащего катета к гипотенузе. Т.е. в наших обозначениях cos ? = |AB| / |AC|. Отсель получаем длину гипотенузы |AC| = |AB| / cos ?.Если же нам знамениты катет |BC| и угол?, то воспользуемся формулой для вычисления синуса угла – синус угла равен отношению противолежащего катета к гипотенузе: sin ? = |BC| / |AC|. Получаем, что длина гипотенузы находится как |AC| = |BC| / cos ?.
4.
Для наглядности разглядим пример. Пускай дана длина катета |AB| = 15. И угол? = 60°. Получаем |AC| = 15 / cos 60° = 15 / 0.5 = 30. Разглядим, как дозволено проверить свой итог с подмогой теоремы Пифагора. Для этого нам нужно посчитать длину второго катета |BC|. Воспользовавшись формулой для тангенса угла tg ? = |BC| / |AC|, получаем |BC| = |AB| * tg ? = 15 * tg 60° = 15 * ?3. Дальше применяем теорему Пифагора, получаем 15^2 + (15 * ?3)^2 = 30^2 => 225 + 675 = 900. Проверка исполнена.
Полезный совет
Рассчитав гипотенузу, исполняйте проверку – удовлетворяет ли полученное значение теореме Пифагора.
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см



































