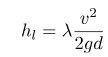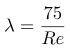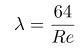Онлайн калькулятор позволяет определить величину гидравлического сопротивления и
потери напора на участке трубопровода. Расчет гидравлического сопротивления производится на
основе учебного пособия «Теоретические основы гидравлики и теплотехники».
Для определения потери напора используются формулы Дарси — Вейсбаха.
Результат вычислений потери напора по длине трубы может использоваться при
проектировании сетей и подборе насосных агрегатов.
Скачать
теоретические основы гидравлики и теплотехники
(pdf 1.5 Мб)
Гидравлическое сопротивление
Опубликовано 24 Июн 2018
Рубрика: Теплотехника | 36 комментариев

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.
Краткая теория.
В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.
Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
∆Р=ζ·ρ·w²/2, Па, где:
- ζ – безразмерный коэффициент местного сопротивления;
- ρ – объёмная плотность жидкости, кг/м3;
- w – скорость потока жидкости, м/с.
Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!
Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.
- В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:
∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:
- L – длина трубы, м;
- D – внутренний диаметр трубы, м;
- λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:
ζтр=λ·L/D
- Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:
∆Рм=ζм·ρ·w²/2, Па
Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
w=G/(ρ·π·D²/4), м/с, где:
- G – расход жидкости, кг/с;
- π – число Пи.
Тогда:
∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
Введем понятие гидравлических сопротивлений:
Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
∆Ртр=Sтр·G², Па;
∆Рм=Sм·G², Па.
Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м3/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.
Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.
Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
ai=(1/Si)0,5, (кг/с)/Па0,5.
Коэффициент гидравлического трения.
Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.
В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.
Обозначения в таблице:
- Re – число Рейнольдса;
- k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.
В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
Значения, полученные по этой формуле чрезвычайно близки значениям:
- функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10<Re<1500;
- функции λ=0,11·(68/Re+k/D)0,25 для зоны турбулентного характера потока при Re>4500;
- в диапазоне 1500<Re<4500 согласно анализу присутствует переходная зона.
В переходной зоне, согласно опытам Никурадзе, график функции λ=f(Re,D,k) имеет сложную форму. Он представляет собой две сопряженные обратные кривые, которые в свою очередь сопрягаются с одной стороны с кривой гладких труб (ламинарный поток), а с другой стороны с прямыми относительной шероховатости.
Данная зона до конца не изучена, поэтому желательно гидравлические режимы проектируемых систем рассчитывать без захода в эту область: 1500<Re<4500!
На следующем рисунке показаны графики функции λ=f(Re,D,k), построенные по вышеприведенной универсальной формуле. Характер кривых в переходной области соответствует графикам Никурадзе [2, 4].
Пользовательская функция в Excel КтрТрубаВода(Рвода,tвода,G,D,kэ) выполняет расчет коэффициента гидравлического трения λ по рассмотренной универсальной формуле. При этом везде далее kэ=k.
Внимание!
- В зоне переходного характера потока происходит смена знака наклона кривой λ, что может вызвать неработоспособность систем автоматического регулирования!
- ПФ КтрТрубаВода(Pвода,tвода,G,D,kэ) при турбулентном потоке существенно зависит от значения kэ – эквивалентной шероховатости внутренней поверхности трубы. В связи с этим следует обращать внимание на задание объективного значения kэ с учётом используемых при монтаже труб (см. [2] стр.78÷83).
Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.
Некоторые пояснения по аргументам пользовательских функций:
- ГСдиффузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходДиффузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСконфузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходКонфузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСотвод(Pвода,tвода,G,D0,R0,Угол,kэ) – свободные размеры;
- ГСотводГОСТ(Pвода,tвода,G,D,Угол,kэ) – стандартный отвод.
Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.
Для турбулентных течений длина начального участка должна быть не менее:
Lнач=(7,88·lg (Re) – 4,35)·D
Для ламинарных течений минимальная длина начального участка:
Lнач=B·Re·D
Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.
Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.
Литература:
- Черникин А.В. Обобщение расчета коэффициента гидравлического сопротивления трубопроводов // Наука и технология углеводородов. М.: 1998. №1. С. 21–23.
- И.Е. Идельчик, «Справочник по гидравлическим сопротивлениям». 3-е издание, переработанное и дополненное. Москва, «Машиностроение», 1992.
- А.Д. Альтшуль, «Гидравлические сопротивления», издание второе, переработанное и дополненное. Москва, «НЕДРА», 1982.
- Б.Н. Лобаев, д.т.н., профессор, «Расчёт трубопроводов систем водяного и парового отопления». Государственное издательство литературы по строительству и архитектуре. УССР, Киев, 1956.
Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Одной
из основных задач гидравлики является
определение гидравлического сопротивления
трубопроводной сети для того, чтобы
выбрать требуемый напор насосов, или
выбор диаметра трубопроводов,
обеспечивающих подачу требуемого
количества жидкости при располагаемом
напоре.
Сопротивление
трубопровода складывается из затрат
энергии на преодоление трения жидкости
о стенки трубы по всей ее длине и на
преодоление сопротивления в отдельных
местах потока, где наблюдается его
деформация (задвижка, поворот, резкое
сужение или расширение трубы и т. п.).
Первые потери называются линейными,
они распределяются по длине трубы
относительно равномерно и обозначаются
в виде потери располагаемой высоты hлин
или в виде потери давления рлин.
Вторые потери называются местными, они
концентрируются в отдельных местах, их
суммарный вклад в сопротивление
трубопровода равен сумме каждого из
местных сопротивлений, поэтому они
обозначаются hм
или рм.
Общую
величину потерь напора для участка
трубопровода, заключенного между двумя
сечениями, определяют как сумму потерь
напора по длине рассматриваемого участка
и всех местных потерь напора:
, (31.1)
. (31.1а)
Величину
линейных потерь определяют по формуле
Дарси-Вейсбаха
. (31.2)
Так
как
,
То
формулу Дарси-Вейсбаха можно представить
в виде
. (31.2а)
Здесь
ℓ
— длина трубы; d
– диаметр трубы;
—
коэффициент сопротивления трения или
коэффициент Дарси.
Местные
потери вычисляют по формуле
(31.3)
или
. (31.3а)
Здесь
— коэффициент местных потерь.
Формулы
(7.2а) и (7.3а) можно представить в виде
,
.
Величина
представляет собой число Эйлера, равное
отношению гидравлического сопротивления
к динамическому напору. Отсюда формулы
(7.2а) и (7.3а) принимают вид
, (31.4)
. (31.5)
В
формулах (7.2) и (7.3) потери напора зависят
от квадрата скорости, при этом в расчетах
используется средняя скорость потока,
определяемая как отношение секундного
расхода жидкости к площади поперечного
сечения трубы .
Однако
этот вывод справедлив только при
некоторых определенных условиях, так
как в общем случае коэффициенты
сопротивления
и
тоже зависят от скорости.
При
ламинарном течении средняя скорость
жидкости равна
.
Отсюда
следует
.
Сопоставляя
это выражение с формулой Дарси-Вейсбаха,
получим
.
Комплекс
есть критерий Рейнольдса, определяющий
режим течения жидкости. Окончательно
для ламинарного течения имеем
. (31.6)
Это
выражение называется формулой Пуазейля.
Хотя по формуле Дарси-Вейсбаха
сопротивление трубопровода пропорционально
скорости во второй степени, при ламинарном
течении коэффициент гидравлического
сопротивления обратно пропорционален
критерию Рейнольдса и, следовательно,
скорости. Поэтому в целом сопротивление
трубопровода оказывается пропорциональным
скорости в первой степени.
При
переходе к турбулентному течению влияние
скорости становится более существенным,
при этом заметное влияние начинает
оказывать шероховатость стенок трубы.
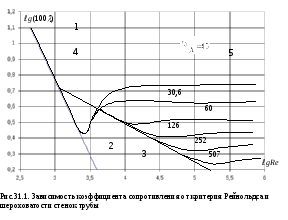
Экспериментальные
данные для
в зависимости от значений критерия
Рейнольдса и относительной шероховатости
были получены Никурадзе. В виде графика
в логарифмических координатах эти
зависимости представлены на рис.31.1. Всю
область чисел Рейнольдса можно разделить
на 5 характерных зон движения.
1.
Зона ламинарного течения при Re
<
2300 или lg
(Re)
< 3,36. Здесь коэффициент сопротивления
независимо от шероховатости стенок
соответствует формуле Пуазейля
.
Отсюда следует, что шероховатость стенок
не оказывает влияния на режим течения,
а потеря давления пропорциональна
скорости.
2.
Переходная зона при
или
.
Здесь ламинарный режим переходит в
турбулентный, коэффициент сопротивления
возрастает с увеличением числа Рейнольдса,
оставаясь одинаковым для различных
шероховатостей. Коэффициент сопротивления
для этого режима может быть найден по
формуле
. (31.7)
3.
Зона гидравлически гладких труб для
турбулентного режима. В логарифмических
координатах зависимость коэффициента
гидравлического сопротивления от
критерия Рейнольдса аппроксимируется
прямой линией и описывается формулой
Блазиуса
. (31.8)
-
Зона
шероховатых труб, в которой на
сопротивление влияет как скорость
потока, так и шероховатость стенки.
Отклонение от формулы Блазиуса наступает
тем раньше, чем выше шероховатость. При
этом с увеличением числа Re
коэффициент
сопротивления
возрастает, стремясь к некоторому
пределу. -
Зона
вполне шероховатых труб. Коэффициент
сопротивления практически не зависит
от критерия Рейнольдса, а гидравлические
потери пропорциональны квадрату
скорости. Коэффициент сопротивления
может быть рассчитан по формуле
Шифринсона
, (31.9)
где
— средняя высота выступов шероховатости.
Влияние
скорости и шероховатости на сопротивление
трубы объясняется следующим образом.
Допустим, на стенке трубы высота выступов
шероховатости равна .
При ламинарном течении в области 1
жидкость движется слоями, отсутствует
трение о стенки, гидравлическое
сопротивление трубы пропорционально
скорости потока, а коэффициент
сопротивления соответствует формуле
Пуазейля.
При
увеличении скорости выше критического
значения возникает турбулентность,
эффективная вязкость возрастает, но в
области 2 при относительно низких
скоростях на стенке сохраняется
ламинарный слой, перекрывающий выступы
шероховатости. Поэтому в этой области
шероховатость не влияет на гидравлическое
сопротивление.
Дальнейшее
увеличение скорости обеспечивает
поддержание устойчивого турбулентного
ядра внутри основного потока и наличие
пограничного слоя на стенке. Толщина
пограничного слоя уменьшается при
увеличении скорости. Здесь возможны
два режима течения, показанные на
рис.31.2.
Если
ламинарный слой, обволакивающий выступы
шероховатости, полностью их перекрывает,
(рис.31.2 а), то потери напора не будут
зависеть от степени шероховатости
стенок трубы: в этом случае жидкость
будет скользить по ламинарному слою,
вызывая трение жидкости о жидкость. И
хотя в целом режим движения турбулентный,
но выступы шероховатости погружены в
ламинарный слой, коэффициент
зависит только от числа Re,
его значение определяется по формуле
Блазиуса. Такая труба считается
гидравлически гладкой. Условие
существования этого режима определяется
соотношением л
.
С
увеличением скорости потока ламинарный
пограничный слой становится тоньше и
выступы шероховатости (рис.31.2 б) попадают
в турбулентное ядро. Они становятся
дополнительными очагами возмущения
потока, позади выступов создаются вихри,
на образование которых затрачивается
механическая энергия движения жидкости.
Такая труба считается гидравлически
шероховатыми. Условие существования
гидравлически шероховатых труб
определяется соотношением л
.
Понятия
гидравлически гладкой и шероховатой
поверхностей — относительные. Одна и та
же труба при малых числах Re
может быть гладкой, а при больших числах
Re
— шероховатой.
При
высокой скорости потока ламинарный
пограничный слой становится настолько
тонким, что в зоне 5 все трубы становятся
гидравлически шероховатыми, гидравлическое
сопротивление трубы становится
пропорциональным квадрату скорости, а
коэффициент
перестает зависеть от числа Re.
Наступает так называемая автомодельная
область течения. Величина
определяется по формуле Шифринсона в
зависимости от шероховатости трубы.
Местные
потери напора возникают в местах
установки кранов, задвижек, сужений,
расширений, поворотов трубопроводов.
Величина потерь рассчитывается по
формулам (31.3) или (31.3а):
,
.
Коэффициент
местных потерь
в общем случае зависит от формы местного
сопротивления, числа Re,
шероховатости поверхности, а для запорных
устройств также от степени их открытия.
Ввиду
большой сложности и разнообразия
происходящих в местных сопротивлениях
явлений коэффициенты
определяются экспериментально для
каждого типа сопротивления и приводятся
в справочниках.
Очень
часто диаметр трубопровода до местного
сопротивления и после него бывает
разным, поэтому и скорости потока при
этом разные. Поэтому при пользовании
справочниками необходимо обращать
внимание на то, к какому скоростному
напору, до или после сопротивления,
отнесен коэффициент .
Обычно его относят к скоростному напору
за сопротивлением.
Для
наиболее простых местных сопротивлений
значения
можно
оценить теоретически.
-
Внезапное
расширение потока. Поток с более высокой
скоростью v1
как бы сталкивается с более медленным
потоком, движущимся со скоростью v2.
Происходит неупругий удар, вследствие
чего возникают обратные течения и
частичное рассеивание энергии
высокоскоростного потока. Бернулли
получил выражение для определения
гидравлических потерь
. (31.10)
Уравнение
неразрывности потока несжимаемой
жидкости имеет вид
. (31.11)
Отсюда
. (31.12)
Подставляя
(7.12) в (7.10), получим

Сравнивая
(7.13) с (7.3), имеем

Можно
записать

откуда

-
Выход
из трубы в резервуар больших размеров.
В данном случае площадь сечения
резервуара много больше площади
подводящей трубы, поэтому можно принять.
Из (7.14) следует =1. -
Внезапное
сужение потока. В данном случае происходит
внезапное увеличение скорости без
удара, но на некотором расстоянии ниже
по течению наблюдается сужение струи
и затем переход к нормальному течению.
Коэффициент
зависит от соотношения
:
|
|
0,01 |
0,1 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
0,45 |
0,39 |
0,35 |
0,32 |
0,2 |
0,09 |
0 |
-
Постепенное
расширение потока в диффузоре. Диффузор
характеризуется двумя параметрами:
углом конусности
и степенью расширения n
= 2/1.
Основное влияние на конфигурацию потока
оказывает угол конусности. При малых
углах
< 4 — 5° течение в диффузоре происходит
безотрывно. Однако с увеличением
> 8 — 10° происходит более интенсивное
торможение потока, в пристеночном слое
силами вязкости поток полностью
затормаживается, а далее возникает
отрыв потока от стенки и появляются
обратные течения, приводящие к
значительным потерям энергии на
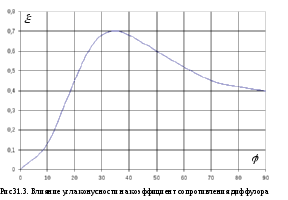
вихреобразование. Зависимость
коэффициента сопротивления от угла
конусности приведена на рис.31.3.
Максимум
сопротивления достигается при угле
=35,
причем в этом случае потери напора
значительно превышают потери при
внезапном расширении. Поэтому вместо
диффузоров с
>
20
выгоднее применять внезапное расширение
как переход к большему сечению.
Постепенное
сужение потока в виде конфузора приводит
к значительно меньшим потерям. При
плавном сопряжении конической части с
цилиндрической они практически равны
нулю.
.
Лекция
32.
Гидравлический
расчет трубопроводов
Классификация
трубопроводов
Трубопроводы
служат для перемещения разнообразных
жидкостей и газов. В зависимости от рода
перекачиваемой жидкости различают:
водопроводы, нефтепроводы, маслопроводы,
газопроводы и т.д.
В
зависимости от конфигурации различают
простые и сложные трубопроводы. Простым
называют трубопровод, не имеющий
разветвлений от точки забора до точки
потребления. Сложные трубопроводы
делятся на следующие виды:
1)
разветвленные;
2)
трубопроводы с параллельным соединением;
3)
кольцевые.
В
зависимости от длины и гидравлических
условий расчета трубопроводы разделяются
на длинные и короткие. Длинными считаются
трубопроводы, имеющие значительную
протяженность, в которых величина
местных потерь напора не превышает 10%
от потерь напора по длине. К длинным
трубопроводам относят наружные
водопроводные сети и водоводы, нефтепроводы
и т. д. При их расчете местные потери
отдельно не учитываются, а принимаются
равными 5…10% от линейных потерь.
У
коротких трубопроводов местные потери
составляют более 10% от линейных потерь.
Короткими трубопроводами являются
всасывающие линии насосных станций,
сифоны, самотечные линии водоприемников,
внутренние хозяйственно-питьевые
водопроводы и т. п. При их расчетах
обязательно учитывают потери напора в
каждом из местных сопротивлений.
При
проектировании трубопроводов задают
расход жидкости Q
и положения начального и конечного
пунктов трубопровода. Для сложного
трубопровода задают расходы на всех
участках трубопровода и положения всех
потребителей. Затем на плане наносят
трассировку трубопровода с указанием
высот и длины участков. Основной задачей
проекта является выбор диаметра
трубопровода d
и напора Н1
в начальной точке.
Эта
задача допускает множество решений,
так как при изменении диаметра d
изменяется и напор Н1:
с увеличением d
снижается потребный напор Н1.
Чаще
всего величину диаметра определяют из
экономических соображений. С увеличением
диаметра трубопровода возрастают
капитальные затраты на строительство
трубопровода, но снижаются эксплуатационные
затраты на перекачку жидкости.
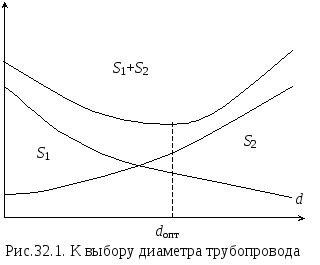
Для
нахождения экономически выгодного
диаметра выполняют несколько вариантов
расчетов с различными диаметрами труб
d
и строят графики зависимостей
и
,
где S1
– капитальные затраты, вычисленные с
учетом срока окупаемости; S2
– эксплуатационные расходы. Затем
наносят кривую суммарных затрат
.
Наиболее выгодным принимается диаметр,
при котором суммарные затраты минимальны.
Пример построения графика приведен на
рис.32.1.
В
ряде случаев решаются частные задачи:
1.
Определение потери напора
при заданном расходе Q
и размерах трубопровода.трубопроводу
диаметром
2.
Определение расхода Q
при заданном перепаде Н
и размерам трубопровода.
3.
Определение диаметра d
при заданных перепаде Н
и расходе Q.
Соседние файлы в папке ГГД
- #
- #
- #
Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:
Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.
Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.
Содержание
- Коэффициент гидравлического сопротивления
- Местные гидравлические сопротивления
- Видео о гидравлическом сопротивлении
Коэффициент гидравлического сопротивления
Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:
Δh= ΔP/(ρg)
где ρ — плотность среды, g — ускорение свободного падения.
В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.
Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.
hr = ξ υ2 / (2g)
где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).
Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.
Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.
В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.
Местные гидравлические сопротивления
Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.
Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.
ξвн. суж = 0,5(1- (F2/F1))
Значение коэффициента ξвн. суж от значения отношения (F2/F1)) можно найти в соответствующем справочнике по гидравлике.
Гидравлические потери при изменении направления трубопровода под некоторым углом
В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле
ξ поворот = 0,946sin(α/2) + 2.047sin(α/2)2
где α – угол поворота трубопровода.
Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.
Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:
ξвх = 0,505 + 0,303sin α + 0,223 sin α2
Местные гидравлические сопротивления задвижки
На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.
Гидравлическое сопротивление полностью открытой запорной арматуры равно
ξвентиля = от 2,9 до 4,5
Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.
Гидравлические потери диафрагмы
Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение.
Степень сужения и расширения струи зависит от ряда условий:
Для диафрагмы с острыми краями потери определяются по формуле:
ξдиафр = d02 / D02
Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.
ξвхода = 1
Видео о гидравлическом сопротивлении
На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)
Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.
Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу(chislo-reinoldsa)) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.
Вместе со статьей «Гидравлическое сопротивление» смотрят:

Ламинарный режим движения жидкости

Осевая сила насоса

Число Рейнольдса: опыты, формулы и режимы.
Расчет гидравлического сопротивления и его роль
Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги. А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление. Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.
Гидравлический расчёт выполняется с целью:
- Вычисления потерь давления на конкретных отрезках системы отопления;
- Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
- Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
- Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.
Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса. Только правильные расчёты помогут выбрать оптимальный вариант насоса. Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.
А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.
Коэффициент гидравлического сопротивления трубы
Это безмерная величина, показывающая, каковы потери удельной энергии.
Ламинарное перемещение рабочего потока
При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:
Где:
— потери давления по длине;
— коэффициент гидравлического сопротивления;
v – скорость движения рабочей среды;
g – ускорение силы тяжести;
d – диаметр трубопроводной магистрали.
Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.
Если Re меньше, чем 2300, то для расчёта применяется формула:
Для трубопроводов в форме круглого цилиндра:
Для трубопроводных коммуникаций с другим (не круглым) сечением:
Где А=57 – для квадратных труб.
Турбулентное течение рабочего потока
При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при
, то для расчёта применяется формула Блаузиуса:
В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.
Коэффициент местного сопротивления
Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:
Где:
– коэффициент местного сопротивления;
– потеря напора;
– отношение скорости потока к ускорению силы тяжести – скоростной поток.
При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:
, где
– энергия торможения.
Коэффициент гидравлического сопротивления различных труб
Для фитингов из ППР:
| Деталь | Обозначение | Примечание | Коэффициент |
|---|---|---|---|
| Муфта | 0,25 | ||
| Муфта переходная | Уменьшение на 1 размер | 0,40 | |
| Уменьшение на 2 размер | 0,50 | ||
| Уменьшение на 3 размер | 0,60 | ||
| Уменьшение на 4 размер | 0,70 | ||
| Угольник 90° | 1,20 | ||
| Угольник 45° | 0,50 | ||
| Тройник | Разделение потока | 1,20 | |
| Соединение потока | 0,80 | ||
| Крестовина | Соединение потока | 2,10 | |
| Разделение потока | 3,70 | ||
| Муфта комб. вн. рез. | 0,50 | ||
| Муфта комб. нар. рез | 0,70 | ||
| Угольник комб. вн. рез. | 1,40 | ||
| Угольник комб. нар. рез. | 1,60 | ||
| Тройник комб. вн. рез. | 1,40 — 1,80 | ||
| Вентиль | 20 мм | 9,50 | |
| 25 мм | 8,50 | ||
| 32 мм | 7,60 | ||
| 40 мм | 5,70 |
Для полиэтиленовых труб
| Труба | Расход, м3/час |
Скорость, м/с |
Потери напора в метрах, на 100 метров прямого трубопровода (м/100м) |
|---|---|---|---|
| Сталь новая 133×5 | 60 | 1,4 | 3,6 |
| Сталь старая 133×5 | 60 | 1,4 | 6,84 |
| ПЭ 100 110×6,6 (5ЭР 17)/td> | 60 | 2,26 | 4,1 |
| ПЭ 80 110×8,1 (ЗйР 13,6) | 60 | 2,41 | 4,8 |
| Сталь новая 245×6 | 400 | 2,6 | 4,3 |
| Сталь старая 245×6 | 400 | 2,6 | 7,0 |
| ПЭ 100 225×13,4 (50 В 17) | 400 | 3,6 | 4,0 |
| ПЭ 80 225×16,6 (ЗЭК 13,6) | 400 | 3,85 | 4,8 |
| Сталь новая 630×10 | 3000 | 2,85 | 1,33 |
| Сталь старая 630×10 | 3000 | 2,85 | 1,98 |
| ПЭ 100 560×33,2 (ЗЭК 17) | 3000 | 4,35 | 1,96 |
| ПЭ 80 560×41,2 (ЗЭК 13,6) | 3000 | 4,65 | 2,3 |
| Сталь новая 820×12 | 4000 | 2,23 | 0,6 |
| Сталь старая 820×12 | 4000 | 2,23 | 0,87 |
| ПЭ100 800×47,4 (ЗЭК 17) | 4000 | 2,85 | 0,59 |
| ПЭ 80 800×58,8 (ЗЭР 13,6) | 4000 | 3,0 | 0,69 |
Для бесшовных стальных труб
| Режим движения | Число Рейнольдса | Определения λ | |
|---|---|---|---|
| Ламинарный | |||
| Переходный | Проектирование трубопроводов не рекомендуется | ||
| Турбулентный | 1-я область |
||
| 2-я область |
|||
| 3-я область |
Для металлопластиковых труб
| Наименование | Символ | Коэффициент |
|---|---|---|
| Тройник разделения потока | 7,6 | |
| Тройник проходной | 4,2 | |
| Тройник противоположные потоки при разделении потока |
8,5 | |
| Тройник противоположные потоки при слиянии потока |
8,5 | |
| Угол 90° | 6,3 | |
| Дуга | 0,9 | |
| Редукционный переход | 6,3 | |
| Установочный уголок | 5,4 |
Трубы с низким коэффициентом гидравлического сопротивления
С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Система отлично подходит для систем горячего и холодного водоснабжения и отопления, как в частных, так и промышленных масштабах. Так же используется для транспортировки химических сред.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Трубопроводная система из инновационного материала fusiolen, специально разработанная для систем холодоснабжения, обогрева поверхностей, транспортировки агрессивных сред и сжатого воздуха, а также для систем геотермальной энергетики.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Вопросы, комментарии, отзывы
Здравствуйте! Помогите найти удельное сопротивление ПЭ труб SDR11 Д=400х36,3 ГОСТ 18599-2001
Уважаемая Ульяна! Информация направлена на Вашу почту!
Здравствуйте.
Помогите подобрать производительность насоса(давление ит.д) с учетом гидравлического сопротивления трубопроводов – результат: время перекачки 80 литров раствора NaOH плотностью 1,48 кг/л не должна быть выше 2 минут.
DN32, длина трубопровода 17м
Уважаемый Юрий! Информация направлена на Вашу почту.
Помогите рассчитать потерю давления на газопроводе с начальным диаметром dn80, через 0,1 м становиться dn32 и тянется 10 м
Уважаемый Андрей! Информация направлена на вашу почту!
Добрый день, помогите рассчитать сопротивление резиновых трубопроводов.
Уважаемый Николай! Информация направлена на Вашу почту.
Что такое м/100м (в потерях напора)?
Уважаемый Павел! Данная колонка с данными отображает потери напора в метрах, на 100 метров прямого трубопровода (м/100м).
Чтобы задать любой интересующий Вас вопрос, отправить запрос на расчет продукции или запросить необходимую документацию Вы можете воспользоваться специальной формой на сайте, отправить письмо по электронной почте или позвонить по телефону