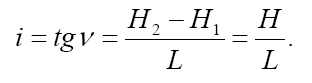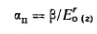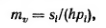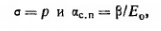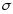Как найти гидравлический градиент

Закон
ламинарной фильтрации. Гидравлический
градиент.

Фильтрация
воды в грунтах представляет собой
сложный процесс. Действительно, поры в
разнозернистом грунте образуют извилистые
каналы переменного сечения, соединяющиеся
между собой в различных направлениях.
Следовательно, и траектории движения
воды в этих каналах будут крайне сложными.
В пылевато-глинистых грунтах пленки
связанной воды, окружающие глинистые
частицы и связанные с ними силами
электростатического притяжения, могут
образовывать пробки, перекрывающие
поровые каналы в некоторых сечениях и
затрудняющие движение свободной воды.
Действительная скорость движения воды
в разных сечениях грунта может быть
различной и, строго говоря, будет
неопределенной, поэтому математическое
описание фильтрации воды в грунте
связано со схематизацией этого процесса
и основывается на результатах
экспериментов.

Водопроницаемостью
называется
свойство водонасыщенного грунта под
действием разности напоров пропускать
через свои поры сплошной поток воды.
При этом под сплошным потоком воды
понимается ее неразрывное движение
(фильтрация) по всему сечению активных
пор грунта, т. е. той части пор, которая
не заполнена связанной водой.
Водопроницаемость грунтов зависит от
их пористости, гранулометрического и
минерального состава, градиента напора.

При
прочих равных условиях при физическом
строении с меньшим содержанием пор, и
при преобладании в составе частиц глины
водопроницаемость будет меньшей, нежели
у пористых и песчаных грунтов
соответственно. Нельзя недооценивать
данный показатель, т.к. в строительстве
он влияет на устойчивость земляных
сооружений и обуславливает скорость
уплотнения грунтов оснований, суффозию
грунта и оползневые явления (в т.ч. и на
сопротивление растяжению).

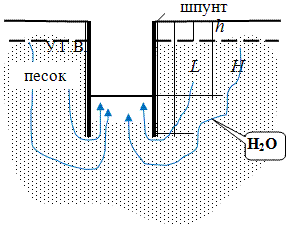
Рис
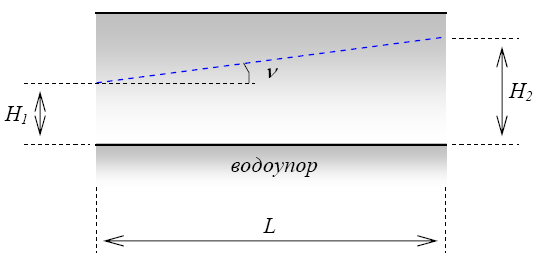
Напорные грунтовые воды. Здесь Н₁
и Н₂
– напоры; L – длина пути фильтрации; Н
= Н₂
— Н₁
– потеря напора или «действующий напор».

Если
линии токов воды (движения частиц в
потоке) нигде не пересекаются друг и
другом, то такое движение называется
ламинарным,
при наличии пересечений и завихрений
движение называется турбулентным.
В грунтах в большинстве случаев движение
воды будет ламинарным (опыты Пуазейля,
Дарси и другие).

Ламинарное
движение воды происходит с тем большей
скоростью, чем больше уклон поверхности
уровня грунтовых вод (так называемый
«гидравлический градиент»).

Гидравлический
градиент равен отношению потери напора
Н= Н₂—
Н₁
к длине пути фильтрации L:

Закон
ламинарной фильтрации (закон Дарси):
расход воды в единицу времени через
единицу площади поперечного сечения
грунта (скорость фильтрации) прямо
пропорционален гидравлическому градиенту
i:

v_ф
= k_ф
· i;

где
k_ф—
коэффициент фильтрации, равный скорости
фильтрации при градиенте i = 1 [см/сек,
см/год]. Коэффициент фильтрации зависит
от типа грунта и определяется
экспериментально.

Коэффициент
фильтрации.

Фильтрацией
называется движение свободногравитационной
воды в грунтах в различных направлениях
(горизонтально, вертикально вниз и
вверх) под воздействием гидравлического
градиента (уклона, равного потере напора
на пути движения) напора. Коэффициентом
фильтрации (k_f)
принято считать скорость фильтрации
при гидравлическом градиенте равном
единице. При этом скорость фильтрации
(V) прямо пропорциональна гидравлическому
градиенту (J). v = k_f
* i.

Зная
скорость фильтрации, не трудно дать
определение коэффициенту фильтрации:

k_ф
– коэффициент фильтрации – это скорость
фильтрации при i = 1 (см/сек; м/сут).

Коэффициент
фильтрации для различных грунтов имеет
значительный диапазон изменений, так
средние значения k_ф
для песков и глин может отличаться на
несколько порядков. k_ф._песок
= n 10^–2
см/сек, k_{ф.глина}=
n 10^–8
см/сек

Водопроницаемость
различных грунтов (по Н.Н.Маслову)

Грунты	k_ф, м/сут	Характеристика грунтов по водопроницаемости
Глины, монолитные скальные грунты	< 5 •10^-5	Практически водонепроницаемые
Суглинки, тяжелые супеси, нетрещиноватые песчаники	до 5 •10^-3	Весьма слабоводопроницаемые
Супеси, слаботрещиноватые глинистые сланцы, песчаники, известняки	до 0,5	Слабоводопроницаемые
Пески тонко- и мелкозернистые, трещиноватые скальные грунты	до 5	Водопроницаемые
Пески среднезернистые, скальные грунты повышенной трещиноватости	до 50	Хорошо водопроницаемые
Галечники, гравелистые пески, сильно трещиноватые скальные грунты	> 50	Сильноводопроницаемые

Коэффициент
фильтрации
образца грунта может быть определен с
помощью прибора, снабженного
пьезометрическими трубками. Если нужно
ориентировочно определить коэффициент
фильтрации в природных условиях, то
нужно взять образцы грунта (по возможности,
ненарушенной структуры) и испытать их.
Однако этот способ недостаточно надежен,
так как он может не дать характеристики
всей области в целом. Прибегают к полевым
способам определения коэффициента
фильтрации по
откачкам из скважины,
которые дают наиболее надежное значение
этой величины. При этом получается
некоторое среднее значение коэффициента
фильтрации для рассматриваемой области
движения. Коэффициент фильтрации зависит
от свойств грунта, величины и формы его
зерен, а также от жидкости, протекающей
в грунте, в частности от ее вязкости, а
следовательно, и температуры. Обычно
коэффициент фильтрации, определенный
тем или иным путем, относят к температуре
0°С или 10° С.

Н.
Е. Жуковский в 1888 г. обратил внимание на
зависимость коэффициента фильтрации
от атмосферного давления. Наблюдения
показывают, что высота грунтовых вод в
буровых скважинах уменьшается с
увеличением атмосферного давления и
увеличивается с его уменьшением,
Жуковский это объясняет тем, что при
падении давления упругие пузырьки
воздуха, находящиеся в водоносном слое
(они могут приноситься дождевыми водами),
расширяются и выталкивают грунтовые
воды. Уровень их в колодцах поднимается,
а ключи текут быстрее. При увеличении
давления будет обратная картина.

Но
и при постоянном давлении наличие в
грунтовой
водепузырьков воздуха изменяет
степень водопроницаемости грунта,
которая не остается постоянной при
производстве более или менее длительного
опыта. Переменность коэффициента
фильтрации во времени может обусловливаться
и другими физическими и химическими
процессами,— например выщелачиванием
растворимых солей, – а также биологическими
процессами в почве.

С.
А. Христиановичем дан метод изучения
движения грунтовых вод при нелинейных
законах фильтрации. Простейшая задача
– о притоке воды к колодцу – рассматривалась
рядом авторов, пришел к заключению, что
для большинства грунтов (рыхлых)
отклонения от стандартного закона Дарси
могут иметь место лишь в непосредственной
близости от скважины. При этом он
указывает, что обычно зона нарушения
закона Дарси является и зоной нарушения
естественного состояния грунта под
влиянием бурения и суффозионных (т. е.
связанных с выносом частиц) процессов,
происходящих при прокачке скважины.

В
трещиноватых породах, повидимому,
возможны более значительные отклонения
от линейного закона фильтрации.

Начальный
градиент в глинистых фунтах.

Зависимость
скорости фильтрации от гидравлического
градиента i. Для
водопроницаемых грунтов (пески, галечники)
зависимость прямая.

Скорость
движения воды в глинистых грунтах
невелика из-за внутреннего сопротивления,
создающегося из-за малых размеров пор
и водно-коллоидных пленок. В отличие от
песчаных, в глинистых грунтах фильтрация
возможна лишь при достижении определенного
градиента напора, способствующего
преодолению водой внутреннего
сопротивления.

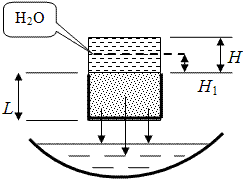
Для
глинистых грунтов в отличие от песков,
фильтрация начинается только при
определенном – начальном гидравлическом
градиенте i_н
(см. график)

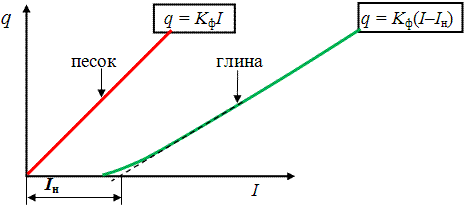
Рис.
Графики зависимости скорости фильтрации
от гидравлического градиента для
песчаного и глинистого грунтов.

Если
в глинистом грунте создается гидравлический
градиент меньше начальной величины,
фильтрации в грунте нет и такой грунт
является водоупором.

В
результате закон ламинарной фильтрации
для связных грунтов будет иметь вид: v_ф
= k_ф
· (i – i_н).

Фильтрационные
характеристики грунтов используются
при:

1
Расчёте дренажа.

2
Определении дебита источника подземного
водоснабжения.

3
Расчёте осадок сооружений (оснований)
во времени.

4
Искусственном понижение У.Г.В.

5
Расчёте шпунтового ограждения при
откопке котлованов, траншей.

Эффектное
и нейтральное давления в грунтовой
массе.

Грунты,
состоящие из отложений частиц разрушенных
горных пород и содержащие в порах воду
и воздух, образуют трехфазную систему,
в которой сочетаются три вида вещества
— твердого, жидкого и газообразного.
Если поры заняты только водой и коэффициент
влажности W=l,
то грунт будет представлять двухфазную
систему.

Свободная
вода, заполняющая поры грунта, которые
представляют собой как бы систему
сообщающихся сосудиков, подчиняется
законам гидростатики. Здесь каждая
частица грунта и воды подвергается
всестороннему сжатию, определяемому
глубиной их положения ниже горизонта
грунтовых вод. Гидростатическое давление
в водонасыщенном грунте называют
нейтральным,
или поровым.
Оно не вызывает деформаций грунта, так
как происходящее в условиях этого
давления объемное сжатие воды и твердых
грунтовых частиц чрезвычайно мало, и
им пренебрегают.

Частицы
грунтового скелета передают внешнюю
нагрузку от фундамента и собственного
веса нижележащим частицам. Это давление,
которое определяют с учетом взвешивающего
действия грунтовых вод на частицы и
фундамент, распространяется вниз и в
стороны по грунтовому скелету его
называют эффективным,
или
межчастичным.
Оно вызывает деформации частиц и
сложенного из них грунтового скелета,
а следовательно, и общую осадку грунтовой
толщи.

Сумму
этих двух давлений называют полным.
Для определения нагрузки от собственного
веса грунтового скелета, необходимо
знать объемный вес этого скелета; он
будет равен весу частиц, содержащихся
единице объема грунта, за вычетом веса
вытесненной ими воды. Действие
взвешивающего давления воды на сооружение
учитывают при наиболее низком уровне
ее стояния, так как нагрузка на основание
здесь будет наибольшей. Однако для
сооружений, подверженных действию
горизонтальных сил, важно произвести
поверочные расчеты их устойчивости на
сдвиг и при наиболее высоком положении
горизонта воды. В этом случае сопротивление
сил трения грунта сдвигу сооружения,
зависящее от величины нормального
давления на основание, будет меньше,
чем при каком-либо другом, более низком
положении уровня воды.

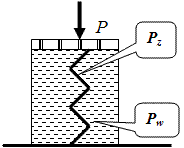
Рассматривая
грунтовую массу как двух фазную систему,
состоящую из скелета — минеральных
частиц и поровой воды, введем понятия:

Р_z
– эффективное
давление,
давление в скелете грунта (уплотняет и
упрочняет грунт).

Р_w–
нейтральное
давление,
давление в поровой воде (создает напор
в воде, вызывая ее фильтрацию).

В
любой момент времени в полностью
водонасыщенной грунтовой массе имеет
место соотношение Р = Р_z
+ Р_w
, где Р – полное
давление:

Р_z
– на представленной схеме моделируется
работой пружины, а Р_w–
давление, возникающие в воде.

Рис.
Модель грунтовой водонасыщенной массы.

В
первый момент времени передачи нагрузки
давления передаются на воду, затем в
работу включается скелет грунта
(пружина).

Тогда
можно записать:

при
t = 0; Р = Р_w

при
t = t1; Р = Р_w
+ Р_z

при
t = ∞; Р = Р_z
– это теоретически; практически для
того чтобы Р_w
≈0, требуется длительный период времени.

Следует
подчеркнуть, что осадка зданий, сооружений
может происходить и при Р = Р_z
за счет явлений ползучести скелета
грунта, т.е. достаточно длительно (см.
ниже приведённый график).

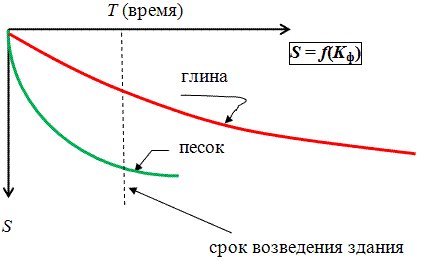
Рис.
График развития осадки сооружения во
времени для глинистого и песчаного
основания.

На
представленном графике видно, что за
период возведения здания осадка
сооружения на песчаном основании,
практически стабилизировалась. Осадка
же здания на глинистом грунте может
продолжаться довольно длительно и после
срока возведения сооружения (десятки
лет). В этом случае скорость протекания
осадки будет также зависеть от
фильтрационных особенностей глинистого
основания (теория фильтрационной
консолидации).

Тема
8. Зависимость между нормальным давлением
и сопротивлениям грунта сдвигу.
Сопротивление грунтов сдвигу, сыпучих
и связных грунтов Закон Кулона.
Сопротивление грунтов сдвигу связных
грунтов. Методы испытания связных
грунтов на сдвиг. Принцип линейной
деформируемости.

Зависимость
между нормальным давлением и сопротивлениям
грунта сдвигу.

При
изучении конструкционных материалов
под прочностью обычно понимают такое
предельное значение напряжения сжатия
или растяжения, после достижения которого
материал теряет свою сплошность, в нем
образуются трещины отрыва или сдвига
и он распадается на части или отдельные
куски. Этот процесс называют хрупким
разрушением.
Естественно, что хрупкое разрушение
материала может происходить и при
сложном напряженном состоянии, однако
оно всегда сопровождается образованием
трещин отрыва или сдвига. Такой характер
разрушения свойствен, например, образцам
прочных скальных грунтов.

В
некоторых случаях (битум, лед, образцы
мерзлых глинистых грунтов) предельные
нагрузки, характеризующие потерю
прочности, вызывают неограниченное
пластическое деформирование
материала без видимого нарушения
сплошности, переходящее
в течение.
Образцы таких материалов, нагружаемые
по схеме одноосного сжатия, приобретают
характерную бочкообразную форму.

Особенности
разрушения материалов (хрупкое или
пластическое) зависят не только от
преобладающих в них структурных связей,
но и от скорости нагружения. Многие
материалы, которым в обычных условиях
свойственно пластическое разрушение,
при быстром возрастании нагрузок могут
разрушаться хрупко.

Таким
образом, под прочностью в широком смысле
слова подразумевают свойства материала
сопротивляться разрушению или развитию
больших пластических деформаций,
приводящих к недопустимым искажениям
формы тела. До настоящего времени в
физике не разработана единая теория
прочности, и для различных материалов
используются те теории, которые показывают
наилучшее соответствие результатам
экспериментов.

Применительно
к песчаным грунтам еще в 1773 г. французским
ученым Ш. Кулоном было экспериментально
установлено, что их разрушение происходит
за счет сдвига одной части грунта по
другой. Сопротивление сдвигу песчаных
и крупнообломочных грунтов возникает
в основном в результате трения между
перемещающимися частицами и зацепления
их друг за друга. Сопротивление растяжению
в этих грунтах практически отсутствует,
поэтому часто песчаные и крупнообломочные
грунты называются сыпучими.

Такая
же концепция прочности (разрушение
за счет сдвига)
была позже распространена и на пылевато-
глинистые грунты. Однако процесс
разрушения в них развивается значительно
сложнее. Имеющиеся в них водно-коллоидные
и цементационные связи обеспечивают
пылевато-глянистым грунтам некоторое
сопротивление растяжению. Эти грунты
часто называют связными.

Сопротивление
сдвигу грунтов очень сильно зависит от
их плотности, влажности, гранулометрического
и минерального состава, напряженного
состояния. Характеристики сопротивления
сдвигу грунтов рассматриваются как
прочностные показатели и всегда
определяются экспериментально.

Сопротивление
сыпучих и связных грунтов сдвигу, закон
Кулона.

Сопротивление
сдвигу сыпучих грунтов

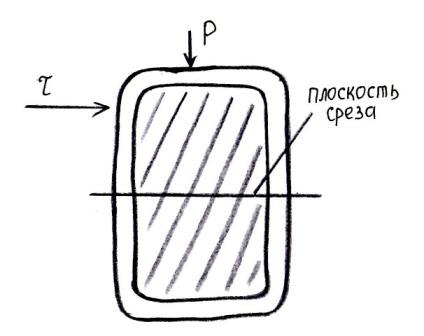
Если
образец песка 1 поместить в сдвиговой
прибор в виде кольца, разрезанного по
горизонтальной плоскости (рис. 2.9,а), то,
приложив силу N и постепенно увеличивая
силу Т, можно достигнуть среза (сдвига)
одной части образца по другой приблизительно
по линии, обозначенной пунктиром. Прибор
имеет нижнюю неподвижную обойму 4;
верхнюю подвижную обойму 3 и зубчатые
фильтрующие пластины сверху и снизу 2.

Если
мы проведем несколько таких опытов при
различном вертикальном напряжении σ
= N/A (где А — площадь образца в плоскости
среза), то получим, что чем больше σ,
тем больше предельное сопротивление
грунта сдвигу τ_u.
По данным экспериментов построим
зависимость предельного сопротивления
сыпучего грунта сдвигу τ_u
от давления (рис. 2.9,б). На основе
многочисленных опытов установлено
следующее: для несвязных (идеально
сыпучих) грунтов экспериментальные
точки в пределах обычных изменений
напряжений (до 0,5 МПа) оказываются на
прямой, выходящей из начала координат.

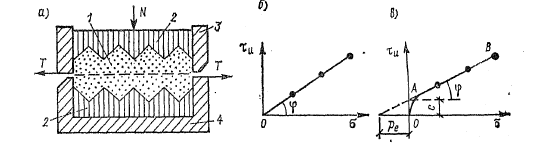
Рис.
2.9. Схема прибора для испытания грунта
па сдвиг (а) и графики сопротивления
сдвигу сыпучего (б) и связного (в) грунта

В
таком случае для любого нормального
напряжения

(2.20)

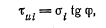
где
tg φ
– коэффициент внутреннего трения,
характеризующий трение грунта о грунт:
tgφ=f;
φ
—угол внутреннего трения.

Зависимость
(2.20) установлена Ш. Кулоном еще в 1773 г.
Она выражает закон сопротивления сыпучих
грунтов сдвигу, который формулируется
так: предельное
сопротивление сыпучих грунтов сдвигу
прямо пропорционально нормальному
напряжению.
Этот закон называется законом
Кулона.

Сопротивление
сдвигу связных грунтов

Глины,
суглинки и супеси обладают связностью,
интенсивность которой зависит от
влажности грунта и степени его
уплотненности. Как установлено,
приложенная к образцу водоиасыщенного
пылевато-глинистого грунта вертикальная
нагрузка в первый момент времени
передается на поровую воду. Лишь по мере
выдавливания ее из пор это давление
будет воздействовать на скелет грунта.
В связи с этим образец испытывают на
сдвиг после консолидации грунта, когда
все возникающее нормальное напряжение
уже передано на скелет грунта.

Для
сохранения природной структуры
пылевато-глинистого грунта фильтрующий
поршень и днище обычно делают плоскими
– без зубцов, показанных на рис. 2.9, а.
Если в таком приборе провести несколько
испытаний на сдвиг одного и того же
грунта, подвергая образцы воздействию
различных напряжений σ,
то получим в общем случае криволинейную
зависимость предельного сопротивления
грунта сдвигу τ_u
от σ
(рис.
2.9,в). Криволинейность зависимости
наиболее ощутима при малых значениях
σ.
При напряжениях в диапазоне 0,05 – 0,5 МПа
практически имеем прямую, описываемую
уравнением

(2.21)

где
с и φ
— параметры прямой.

Закон
сопротивления
пылевато-глинистых
грунтов сдвигу
формулируется так: предельное
сопротивление связных грунтов сдвигу
при завершенной их консолидации есть
функция первой ‘степени нормального
напряжения.

Следует
обратить внимание на то, что уравнение
(2.21) получено для образцов грунта,
находящихся в различном состоянии по
плотности, так как перед сдвигом они
подвергались уплотнению разным по
величине давлением. Очевидно, что каждый
образец при этом будет обладать своим
значением сцепления, т. е. сцепление
образцов одного и того же грунта,
уплотненных неодинаковым давлением,
различно. По этой причине угол наклона
прямой АВ на рис. 2.9, в, строго говоря, не
является углом внутреннего трения.
Однако в механике грунтов параметр с
принято называть удельным
сцеплением,
а φ
– углом
внутреннего трения.

Для
определения истинных значений сцепления
и угла внутреннего трения необходимо
испытывать образцы, находящиеся в одном
и том же состоянии по плотности. С этой
целью образцы грунта иногда испытывают
на сдвиг сразу же после приложения
нагрузки, не дожидаясь их консолидации.
Однако такое испытание не позволяет
учитывать упрочнение грунтов в связи
с их уплотнением в основании под действием
приложенной нагрузки.

Если
прямую АВ продлить влево до пересечения
с осью абсцисс, то она отсечет на ней
отрезок р_е
(рис 2.9, в). Величину р_е
часто называют давлением связности.
Используя это давление, параметр
сцепления (связности) грунта можно
представить в виде

откуда

Методы
испытания связных грунтов на сдвиг.

Для
определения сопротивления грунта сдвигу
сейчас существует довольно много
приборов:

в
лабораториях применяют:

односрезные
сдвиговые приборы

Поступательное
или вращательное смещение части образца
относительно другой части.

2х
срезные сдвиговые приборы,

приборы
3х осного сжатия (стабилометры)

Раздавливание
образца грунта в условиях трехостного
или одноостного сжатия. Подобные приборы
называются – одометр или стабилометр.

в
полевых условиях:

зондирование
(динамическое и статическое),

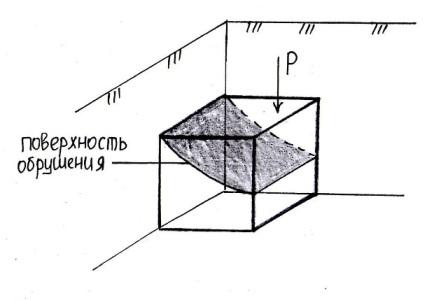
искусственное
обрушение откосов

Обрушение
или сдвиг призмы грунта в условиях
естественного залегания.

лопастные
испытания (крыльчатка)

Проворачивание
в грунте вдавленной крыльчатки.

метод
шарикового штампа.

Вдавливание
в грунт штампов определенного диаметра.

Принцип
линейной деформируемости.

Грунты,
как отмечалось ранее, представляют
собой сложнейшие минерально-дисперсные
образования, состоящие из разнообразных
взаимно связанных частиц, обладающих
различными механическими свойствами.

Применение
к грунтам общей теории напряжений,
разработанной для сплошных упругих
тел, требует особого рассмотрения. Так,
в любых дисперсных телах внешняя нагрузка
передастся от одной частицы к другой
лишь через точки контакта частиц,
которые в большинстве случаев
расположены незакономерно или по
некоторой структурной сетке.

Определение
напряжений в грунтах является значительно
более сложной задачей, чем в сплошных
телах.

При
действии внешней нагрузки отдельные
фазы (компоненты) грунтов по-разному
сопротивляются силовым воздействиям
и по-разному деформируются, что является
главнейшей особенностью
напряженно-деформированного состояния
грунтов.

При
общем рассмотрении необходимо изучить
напряженно-деформированное состояние
как грунта в целом, так и отдельных его
фаз во взаимодействии между собой.

Кроме
того, необходимо учитывать, что
деформируемость не только грунта в
целом, но и отдельных его фаз (например,
твердых частиц) зависит от времени
действия нагрузки вследствие явления
ползучести.

Рассмотрим
общий случай зависимости относительной
деформации ε от величины нормального
напряжения σ для грунта в целом. Такое
рассмотрение будет полностью справедливо
для начального и конечного состояний
грунта, когда отсутствует перераспределение
фаз в единице объема (например, когда
при уплотнении закончится выдавливание
воды из пор грунта). При рассмотрении
промежуточных состояний необходимо
учитывать процесс консолидации,
ползучесть скелета и пр.

При
анализе зависимости деформаций от
напряжений следует различать, по крайней
мере, два вида грунтов: сыпучие
и связные.

Для
сыпучих
грунтов
при однократном загружении всегда
возникают необратимые смешении и
повороты зерен грунта относительно
друг друга, что обусловливает постоянное
наличие остаточных деформаций.

Для
связных
грунтов на характер деформирования
существенно влияют структурные
связи, как жесткие, так и вязкие.

При
жестких
связях,
если величина нагрузки такова, что при
ее действии прочность связей не
нарушается, грунт будет деформироваться
как квазнтвердое тело.

При
вязких
(водно-коллоидных) связях
в грунтах некоторые связи начинают
разрушаться (или вязко течь) уже при
весьма небольших усилиях, другие—при
несколько больших и т.д., что и обусловливает
и у этих грунтов постоянное наличие при
разгрузке не только обратимых, но и
остаточных деформаций. Важно отметить,
что остаточные деформации часто во
много раз превосходят по величине
деформации обратимые.

Природные
связные грунты в большинстве случаев
имеют и жесткие и часто вязкие связи
различной прочности, поэтому процесс
деформирования их является весьма
сложным.

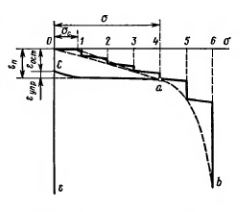
Рис.
Зависимость между деформациями е и
нормальными напряжениями о для грунта
при ступенчатом возрастании нагрузки

В
самом общем случае, как показывают
многочисленные исследования, зависимость
между деформациями и напряжениями для
грунтов, при значительных напряжениях,
будет нелинейной (рис., пунктирная кривая
Oab).

Эту
зависимость в общем виде можно представить
функцией

(2.35)

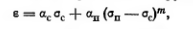
где
α_с
и α_n
– коэффициенты, определяемые опытом;
σ_с
– напряжение, не превосходящее начальной
прочности структурных связей (σ_с<р_стр);
(σ_п—σ_с)=σ
– действующее нормальное напряжение,
обусловливающее деформации грунта при
частичном или полком нарушении структурных
связей; m
— параметр нелинейности, также
определяемый опытным путем.

Можно
принять, что коэффициент α_с
обратно пропорционален модулю нормальной
упругости Е, т.е. α_с
= l/Е.

Что
касается коэффициента α_n,
то природа его значительно сложней.
Если рассматривать только стабилизированные
напряжения, то величина этого коэффициента
будет зависеть от модуля общей деформации
Е₀
грунт, который в общем случае может
входить в выражение в некоторой степени
r,
меньшей или равной единице, а также от
коэффициента β,
оценивающего способность бокового
расширения грунта, т. е. можно принять

где
параметр r≤1
также определяется опытным путем.

Если
рассматривать деформации грунта при
давлениях, больших структурной прочности
сжатия, то зависимости (2.35) можно придать
следующий вид:

(2.35′)

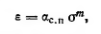
где
α_c_,_n
— некоторый общий коэффициент
пропорциональности, в простейшем случае
равный

Общая
зависимость (2.35′) даже в представленной
простой форме еще очень сложна для
применения на практике.

При
не очень больших изменениях внешних
давлений (порядка 0.3—0,5 МПа, а для плотных
и твердых грунтов и до 0,5—0,7 МПа) с
достаточной для практических целей
точностью зависимость между деформациями
ε
и напряжениями σ
может приниматься линейной (см. спрямленный
участок Оа на кривой рис.), что значительно
упрощает расчеты и не вносит в них
недопустимых погрешностей. Полагая в
выражении (2.35) значение параметра m=1
(что вполне допустимо при величине
напряжений, меньших практического
предела пропорциональности), между
общими деформациями и напряжением при
постоянстве модуля обшей деформации
будем иметь

(2.36)

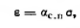
т.е.
при небольших изменениях напряжений к
грунтам с полным к тому основанием можно
применять теорию
линейно деформируемых тел.

Зависимость
между общими деформациями и напряжениями
линейна, то для определения напряжений
в грунтах полностью будут применимы
решения
теории упругости;
для определения же общих деформаций
грунтов необходимы добавочные условия
(например, зависимость изменения
коэффициента пористости от давления и
др.).

Изложенное
позволяет сформулировать для грунтов
так называемый принцип
линейной деформируемости,
а именно:

при
небольших изменениях давлений можно
рассматривать грунты как линейно
деформируемые тела, т.е. с достаточной
для практических целей точностью можно
принимать зависимость между общими
дефорнациями и напряжениями для грунтов
линейной.

Этот
принцип вытекает также и из рассмотренного
случая сжатия слоя грунта при сплошной
нагрузке (компрессии грунта) в диапазоне
давлений, при котором справедлив закон
уплотнения. Действительно, по формуле
(2.5′)

а
так как относительная деформация

то

(2.36^/)

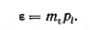
Сравнивая
далее выражение (2.36) с выражением (2.36^/)
и принимая во внимание, что в рассматриваемом
случае

получим

(2.37)

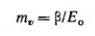
или

(2.37^/)

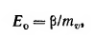
где
Е_о
— модуль общей деформации грунта,
определяемый по формуле
(2.27),

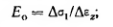
используя
результаты испытаний образцов грунта
на трехосное сжатие или данные полевых
опытов пробной нагрузкой.

Коэффициент
β,
как указывалось ранее, зависит от
коэффициента относительной поперечной
деформации грунта (аналогичного
коэффициенту Пуассона для упругих тел)
и приблизительно равен: для песков β
– 0,8; для супесей β=0,7;
для суглинков β=0,5
и для глин β=0,4.

Следует
отметить, что принцип
линейной деформируемости грунтов
(справедливый для грунтов средней
уплотненности при давлениях порядка
0,1—0,3 МПа и несколько более) является
одним из основных в современной механике
грунтов, так как на нем базируются почти
все инженерные расчеты напряжений и
деформаций естественных грунтовых
оснований. Для слабых же грунтов (при
несущей способности их меньше 0,1 МПа)
необходимо исходить из нелинейной
зависимости между деформациями и
напряжениями.

Тема
9. Определение напряжений в массиве
грунта. Распределение напряжений в
случае пространственной задачи от
действия одной или нескольких
сосредоточенных сил, действие равномерно
распределенной нагрузки; определение
сжимающих напряжений по методу угловых
точек; способ элементарного суммирования

Определение
напряжений в массиве грунта.

Вопрос
об определении напряжений в грунтовой
толще имеет особо
важное значение
для установления условии прочности и
устойчивости грунтов и определения их
деформаций (главным образом осадок) под
действием внешних сил и собственного
веса грунта.

В
настоящее время при решении вопроса о
распределении напряжений в грунтах в
механике грунтов применяют теорию
линейно деформируемых тел.
Для определения напряжений по этой
теории будут полностью справедливы
уравнения и зависимости теории упругости,
также базирующиеся на линейной зависимости
между напряжениями и деформациями в
упругой стадии (закон
Гука).
Для грунтов, однако, закон
Гука в общем случае будет неприменим,
так как при действии внешних сил в
грунтах при давлениях, больших структурной
прочности, возникают не только упругие,
но и значительно большей величины
остаточные деформации.

Тем
не менее, в определенных пределах и для
грунтов будет справедлива линейная
связь между напряжениями и общими
деформациями (не только упругими). Для
определении же общих
деформаций
(упругих и остаточных — уплотнения,
пластического течения, ползучести и
пр.) уравнений теории упругости будет
недостаточно. Здесь требуется учесть
добавочные условия, вытекающие из
физической природы грунтов как дисперсных
тел, а именно: их сжимаемость (компрессию),
ползучесть скелета и пр.

При
определении напряжений в массиве грунта
используются законы механики для
упругого
сплошного тела.
На сколько грунты удовлетворяют данным
требованиям?

Доказательство
применимости теории упругости к грунтам
(постулаты теории упругости).

а)
Деформации
пропорциональны напряжениям

На
отрезке ОА практически линейная
зависимость для грунтов (при малых
изменениях Р)

Штамп

б)Теория
упругости рассматривает тела упругие.

S_ост

S_упр.

В
грунтах наблюдаются большие остаточные
деформации S_ост.
Но для строителей существенно
одноразовое загружение основания,
т.е. здесь условие упругости применимо
(а в общем случае нет).

в)
Теория упругости рассматривает тела
сплошные.

Структура
грунта

при
передаче давления

_ср

 в
поре мало

в
точках контакта частиц

— огромно
(до 200 МПа)

В
расчетах допускается использовать
_ср.
— среднюю величину напряжений,
действующих по определенной площадке.

В
этом случае можно говорить о «сплошности»
грунтов.

г)Теория
упругости рассматривает тела изотропные

(Будем
считать с известными допущениями, что
грунт изотропное тело).

Источник

From Wikipedia, the free encyclopedia

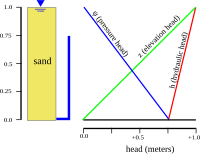
Available difference in hydraulic head across a hydroelectric dam, before head losses due to turbines, wall friction and turbulence

Fluid flows from the tank at the top to the basin at the bottom under the pressure of the hydraulic head.

Measuring hydraulic head in an artesian aquifer, where the water level is above the ground surface

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.^[1]^[2]

It is usually measured as a liquid surface elevation, expressed in units of length, at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer’s elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. The hydraulic head can be used to determine a hydraulic gradient between two or more points.

«Head» in fluid dynamics[edit]

In fluid dynamics, head is a concept that relates the energy in an incompressible fluid to the height of an equivalent static column of that fluid. From Bernoulli’s principle, the total energy at a given point in a fluid is the energy associated with the movement of the fluid, plus energy from static pressure in the fluid, plus energy from the height of the fluid relative to an arbitrary datum. Head is expressed in units of distance such as meters or feet. The force per unit volume on a fluid in a gravitational field is equal to ρg where ρ is the density of the fluid, and g is the gravitational acceleration. On Earth, additional height of fresh water adds a static pressure of about 9.8 kPa per meter (0.098 bar/m) or 0.433 psi per foot of water column height.

The static head of a pump is the maximum height (pressure) it can deliver. The capability of the pump at a certain RPM can be read from its Q-H curve (flow vs. height).

A common misconception is that the head equals the fluid’s energy per unit weight, while, in fact, the term with pressure does not represent any type of energy (in the Bernoulli equation for an incompressible fluid this term represents work of pressure forces). Head is useful in specifying centrifugal pumps because their pumping characteristics tend to be independent of the fluid’s density.

There are generally four types of head:

Velocity head is due to the bulk motion of a fluid (kinetic energy).

${displaystyle h_{v}={tfrac {1}{2}}rho v^{2}/rho g={frac {1}{2}}{frac {v^{2}}{g}}}$

Note that ${displaystyle rho gh_{v}}$ is equal to the dynamic pressure for irrotational flow.
Elevation head is due to the fluid’s weight, the gravitational force acting on a column of fluid. The elevation head is simply the elevation (h) of the fluid above an arbitrarily designated zero point:

${displaystyle h_{e}=rho gh/rho g}$
Pressure head is due to the static pressure, the internal molecular motion of a fluid that exerts a force on its container. It is equal to the pressure divided by the force/volume of the fluid in a gravitational field:

${displaystyle h_{p}=p/rho g}$
Resistance head (or friction head or Head Loss) is due to the frictional forces acting against a fluid’s motion by the container. For a continuous medium, this is described by Darcy’s law which relates volume flow rate (q) to the gradient of the hydraulic head through the hydraulic conductivity K:

while in a piped system head losses are described by the Hagen–Poiseuille equation and the Bernoulli Equation.

Components of hydraulic head[edit]

After free falling through a height in a vacuum from an initial velocity of 0, a mass will have reached a speed

where is the acceleration due to gravity. Rearranged as a head:

${displaystyle h={frac {v^{2}}{2g}}.}$

The term $frac{v^{2}}{2 g}$ is called the velocity head, expressed as a length measurement. In a flowing fluid, it represents the energy of the fluid due to its bulk motion.

The total hydraulic head of a fluid is composed of pressure head and elevation head.^[1]^[2] The pressure head is the equivalent gauge pressure of a column of water at the base of the piezometer, and the elevation head is the relative potential energy in terms of an elevation. The head equation, a simplified form of the Bernoulli principle for incompressible fluids, can be expressed as:

where

In an example with a 400 m deep piezometer, with an elevation of 1000 m, and a depth to water of 100 m: z = 600 m, ψ = 300 m, and h = 900 m.

The pressure head can be expressed as:

${displaystyle psi ={frac {P}{gamma }}={frac {P}{rho g}}}$

where
is the gauge pressure (Force per unit area, often Pa or psi),

Fresh water head[edit]

The pressure head is dependent on the density of water, which can vary depending on both the temperature and chemical composition (salinity, in particular). This means that the hydraulic head calculation is dependent on the density of the water within the piezometer. If one or more hydraulic head measurements are to be compared, they need to be standardized, usually to their fresh water head, which can be calculated as:

${displaystyle h_{mathrm {fw} }=psi {frac {rho }{rho _{mathrm {fw} }}}+z}$

where

Hydraulic gradient[edit]

The hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. For groundwater, it is also called the Darcy slope, since it determines the quantity of a Darcy flux or discharge. It also has applications in open-channel flow where it is also known as stream gradient and can be used to determine whether a reach is gaining or losing energy. A dimensionless hydraulic gradient can be calculated between two points with known head values as:

${displaystyle i={frac {dh}{dl}}={frac {h_{2}-h_{1}}{mathrm {length} }}}$

where

The hydraulic gradient can be expressed in vector notation, using the del operator. This requires a hydraulic head field, which can be practically obtained only from numerical models, such as MODFLOW for groundwater or standard step or HEC-RAS for open channels. In Cartesian coordinates, this can be expressed as:

${displaystyle nabla h=left({frac {partial h}{partial x}},{frac {partial h}{partial y}},{frac {partial h}{partial z}}right)={frac {partial h}{partial x}}mathbf {i} +{frac {partial h}{partial y}}mathbf {j} +{frac {partial h}{partial z}}mathbf {k} }$

This vector describes the direction of the groundwater flow, where negative values indicate flow along the dimension, and zero indicates ‘no flow’. As with any other example in physics, energy must flow from high to low, which is why the flow is in the negative gradient. This vector can be used in conjunction with Darcy’s law and a tensor of hydraulic conductivity to determine the flux of water in three dimensions.

Hydraulic head in groundwater[edit]

Relation between heads for a hydrostatic case and a downward flow case.

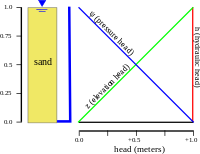
The distribution of hydraulic head through an aquifer determines where groundwater will flow. In a hydrostatic example (first figure), where the hydraulic head is constant, there is no flow. However, if there is a difference in hydraulic head from the top to bottom due to draining from the bottom (second figure), the water will flow downward, due to the difference in head, also called the hydraulic gradient.

Atmospheric pressure[edit]

Even though it is convention to use gauge pressure in the calculation of hydraulic head, it is more correct to use total pressure (gauge pressure + atmospheric pressure), since this is truly what drives groundwater flow. Often detailed observations of barometric pressure are not available at each well through time, so this is often disregarded (contributing to large errors at locations where hydraulic gradients are low or the angle between wells is acute.)

The effects of changes in atmospheric pressure upon water levels observed in wells has been known for many years. The effect is a direct one, an increase in atmospheric pressure is an increase in load on the water in the aquifer, which increases the depth to water (lowers the water level elevation). Pascal first qualitatively observed these effects in the 17th century, and they were more rigorously described by the soil physicist Edgar Buckingham (working for the United States Department of Agriculture (USDA)) using air flow models in 1907.

Head loss[edit]

In any real moving fluid, energy is dissipated due to friction; turbulence dissipates even more energy for high Reynolds number flows. This dissipation, called head loss, is divided into two main categories, «major losses» associated with energy loss per length of pipe, and «minor losses» associated with bends, fittings, valves, etc. The most common equation used to calculate major head losses is the Darcy–Weisbach equation. Older, more empirical approaches are the Hazen–Williams equation and the Prony equation.

For relatively short pipe systems, with a relatively large number of bends and fittings, minor losses can easily exceed major losses. In design, minor losses are usually estimated from tables using coefficients or a simpler and less accurate reduction of minor losses to equivalent length of pipe, a method often used for shortcut calculations of pneumatic conveying lines pressure drop.^[3]

Notes[edit]

^ ^a ^b Mulley, Raymond (2004), Flow of Industrial Fluids: Theory and Equations, CRC Press, ISBN 978-0849327674, 410 pages. See pp. 43–44.
^ ^a ^b Chanson, Hubert (2004), Hydraulics of Open Channel Flow: An Introduction, Butterworth–Heinemann, ISBN 978-0750659789, 650 pages. See p. 22.
^ «Pipe equivalent length (Pneumatic conveying)».

References[edit]

Bear, J. 1972. Dynamics of Fluids in Porous Media, Dover. ISBN 0-486-65675-6.
for other references which discuss hydraulic head in the context of hydrogeology, see that page’s further reading section

Источник

Подземные воды находятся в постоянном движении. Существует раздел гидрогеологии, изучающий закономерности движения подземных вод, который называется «Динамика подземных вод».

Законы движения подземных вод используются при гидрогеологичеких инженерных расчетах водозаборов, дренажей, определении притоков воды к строительным котлованам.

Подземные воды передвигаются в основном путем инфильтрации и фильтрации.

Под инфильтрацией понимают движение воды при частичном заполнении пор воздухом либо водяными парами.

При фильтрации движение воды происходит при полном заполнении пор(трещин) водой. Масса этой движущей воды создает фильтрационный поток.

Фильтрационные потоки различают по характеру движения (установившийся и неустановившийся), гидравлическому состоянию (безнапорные, напорные и напорно-безнапорные). Движение потоков в основном ламинарное (параллельным) , в крупных трещинах и пустотах может быть турбулентным (завихряющемся). В плане фильтрационные потоки можно рассматривать как плоские и радиальные (сходящиеся (например к колодцу) и расходящиеся).

Основной закон фильтрации подземных вод — Закон фильтрации Дарси

Движение подземных вод происходит при наличии разности гидравлических уровней (напоров). Воды двигаются от мест с высокими уровнями к местам с низкими уровнями.

Отношение разности напоров к длине пути фильтрации называется гидравлическим (напорным) градиентом. Чем градиент выше, тем больше скорость движения.

I = ΔH/l,

где ΔG = H1-H2 — разность напоров (H);

l — длина пути фильтрации.

Фильтрация в полностью водонасыщенных водах при ламинарном (параллельном, спокойном, без завихрений) движении воды подчиняется закону Дарси.

Q = КфFI,

где Q — расход воды (кол-во фильтрующей воды через поперечное сечение F в единицу времени);

К_ф — коэффициент фильтрации;

F — площадь поперечного сечения потока воды (водоносного пласта);

I — Гидравлический градиент.

Введем понятие скорость фильтрации (v) — отношение расхода воды к площади поперечного сечения потока (v = Q/F). Таким образом сформулировать закон Дарси можно как «Скорость фильтрации пропорциональна напорному градиенту»

v = К_фI

Коэффициент фильтрации можно таким образом можно выразить как скорость фильтрации при напорном градиенте равном единице.

Скорость фильтрации воды по представленной выше формуле не отвечает действительной скорости движения воды в породе. Это связано с тем что вода двигается не по всему сечению, а только через его часть, равную площади пор и трещин породы. Действительную скорость движения воды (v_д) определить можно как

v_д = v/n,

где n — пористость породы, выраженная в долях единицы.

Коэффициент фильтрации определяется в основном геометрией пор, а также свойствами самой воды и пр.

Точное значение коэффициента фильтрации определяют лабораторным путем, полевым путем и расчетным методом ( для песков и гравелистых пород)

Приближенная оценка для решения не требующих высокой точности задач (простые инженерные задачи) возможна по табличным данным.

Характеристика пород	Коэффициент фильтрации м/сутки
Очень хорошо проникаемые галечники с крупным песком	100 — 1000 и более
Хорошо проникаемые галечники и гравий с мелким песком, крупный песок, чистый среднезернистый песок,	100 — 10
Проницаемые галечники и графий с мелким песком, средензернистые и мелкозернистые пески	10 -1
Слабопроницаемые тонкозернистые пески, супеси	1 -0,1
Слабопроницаемые суглинки	0,1 -0,001
Глины, мергели, монолитные скальные породы	менее 0,001

Источник

Водопроницаемость грунтов

В строительстве фильтрационные свойства грунта (его водопроницаемость) связаны:

С инженерными задачами (фильтрация берегов в результате строительства плотин).
С вопросами временного понижения уровня грунтовых вод (У.Г.В.) для осушения котлованов.

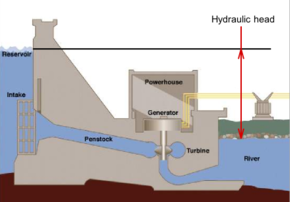
Для определения коэффициента фильтрации песчаных грунтов рассмотрим схему прибора,
используемого в условиях лаборатории.

Схема лабораторного метода определения коэффициента пористости песчаного грунта.

Лабораторный прибор для определения фильтрационных свойств грунтов представляет
собой сосуд с пористым днищем (см. схему), в который помещается песок. Сверху заливается
вода и измеряется ее расход (фильтрация через образец песка) с различными интервалами
времени.

Из законов гидравлики известно, что движение воды в грунтах в основном является
ламинарным и подчиняется закону «Дарси», при этом количество профильтровавшей
воды θ может быть определено следующим выражением:

Количество профильтровавшейся воды прямо пропорционально зависит от: времени фильтрации,
площади, коэффициента фильтрации и гидравлического градиента.

Обозначения принятые в формуле:

t – время;
F – площадь;
K_ф – коэффициент фильтрации;
I – гидравлический градиент.

—
определяется, как отношение напора (Н-Н₁) к пути фильтрации L.

Введем понятие скорости фильтрации, как количество профильтровавшийся жидкости в
единицу времени на единицу площади, или аналитически:

Зная скорость фильтрации, не трудно дать определение коэффициенту фильтрации:

K_ф– коэффициент фильтрации – это скорость фильтрации при
I = 1 (см/сек; м/сут).

Коэффициент фильтрации для различных грунтов имеет значительный диапазон изменений,
так средние значения K_ф для песков и глин может отличаться на несколько
порядков (см. ниже).

K_{ф.песок}= n 10^–2 см/сек

K_{ф.глина}= n 10^–8 см/сек

Для глинистых грунтов в отличие от песков, фильтрация начинается только при определенном
– начальном гидравлическом градиенте I_н (см. график)

Графики зависимости скорости фильтрации от гидравлического градиента для песчаного
и глинистого грунтов.

Если в глинистом грунте создается гидравлический градиент меньше начальной величины,
фильтрации в грунте нет и такой грунт является водоупором.

Фильтрационные характеристики грунтов используются при:

Расчёте дренажа.
Определении дебита источника подземного водоснабжения.
Расчёте осадок сооружений (оснований) во времени.
Искусственном понижение У.Г.В.
Расчёте шпунтового ограждения при откопке котлованов, траншей.

Рассмотрим в качестве примера откопку котлована в песчаном водонасыщенном
грунте.

Для решения данной геотехнической задачи обычно используется шпунтовое ограждение,
удерживающие стенки котлована в вертикальном состоянии. Шпунт не допускает проникновение
воды в котлован через стенки, однако вода будет поступать в такой котлован в обход
шпунта – через днище котлована (см. схему).

Количество поступающей воды в котлован
можно
уменьшить (обоснованно подобрать насос для водоотлива), только изменяя гидравлический
градиент
,
в нашем случае он определиться выражением
(см.
обозначения на представленном рисунке).

Схема устройства котлована в водонасыщенном песчаном грунте, с использованием шпунтового
ограждения.

Тогда из выражения
может
быть определена длина шпунта L, обеспечивающего минимальное поступление воды в котлован.

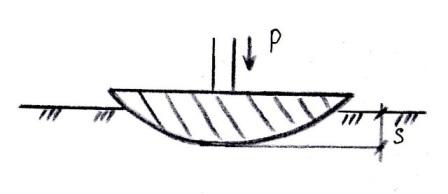
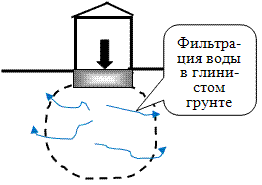
Другая геотехническая задача – определение возможности осадки возводимого сооружения
на водонасыщенных глинистых грунтах. Под фундаментом возводимого сооружения возникает
область напряженного состояния в которой, если гидравлический градиент превысит
значение начального гидравлического градиента для данных грунтов I >
I_н, то возникнет возможность фильтрации и будут развиваться осадки.

В случае значительных гидравлических градиентов в глинистом основании возникают
условия развития фильтрации, а, следовательно, осадок данного сооружения.

Если образовавшийся гидравлический градиент не превысит значение начального гидравлического
градиента для данных грунтов I < I_н, то фильтрации
в грунте не произойдет, а, следовательно, не возникнет и осадка данного сооружения
(используется теория фильтрационной консолидации).

Постоянный адрес этой главы:
www.buildcalc.ru/learning/soilmechanics/Open.aspx?id=Chapter4

Источник

Видео: Лекция_Проницаемость_Закон_Дарси_09_10_2018

Содержание

Что такое закон Дарси?
Уравнения закона Дарси
Дифференциальная форма закона Дарси
Расход, гидравлический градиент и проницаемость
1.- Расход Q
2.- Гидравлический градиент I
3.- Проницаемость K
Применение закона Дарси
Ограничения
Упражнение решено
Решение

Поток воды через две пористые среды обозначен черными стрелками. В среде 1 поток движется быстрее, чем в среде 2, так как скорость зависит от размера пустот и легкости сообщения между ними. Источник: Wikimedia Commons.

Что такое закон Дарси?

В закон Дарси представляет собой математическое соотношение, применимое к потоку текучей среды в проницаемой или пористой среде, например, к стеканию воды в песок.

Когда жидкость продвигается через пористую среду, ее гидростатическое давление изменяется, в частности, оно выше в точках, ближайших к источнику, и ниже в точках, ближайших к сливу. Таким образом, появляется понятие гидравлического градиента, физической величины, которая будет обозначаться буквой I.

С другой стороны, пористая среда характеризуется величиной, называемой гидравлическая проводимостьK. Очевидно, что существует взаимосвязь между пористостью, определяемой K, гидравлическим градиентом I и расходом на единицу площади поперечного сечения q.

Связь между ними была обнаружена французским инженером-гидротехником Генри Дарси (1803-1858), который отвечал за водоснабжение своего родного города: Дижона.

Закон Дарси был представлен в 1856 году в кропотливой работе, в которой физические величины, участвующие в законе, проведенные эксперименты и, в частности, устройство, называемое пермеаметр.

Уравнения закона Дарси

Закон Дарси показывает взаимосвязь между различными физическими величинами, которые описывают поток через пористую среду. Это указывает на то, что поток воды Q который движется через данную пористую среду прямо пропорционален пройденному поперечному сечению A и гидравлическому градиенту я:

Q ∝ A ∙ I

Константа пропорциональности — это проницаемость K пористой среды, также называемая гидравлическая проводимость. Таким образом, закон Дарси представлен как:

Q = K ∙ A ∙ I

Дифференциальная форма закона Дарси

Уравнение Дарси может быть выражено как дифференциальная зависимость между скоростью потока в каждой точке и локальным гидравлическим градиентом:

Поскольку гидравлический градиент является отрицательной величиной при вычислении в направлении потока, тогда необходимо умножить на отрицательную величину гидравлической проводимости, чтобы получить среднюю скорость потока q в каждом поперечном сечении.

Затем более подробно анализируются величины, представленные в законе Дарси.

Расход, гидравлический градиент и проницаемость

1.- Расход Q

Поток определяется как объем воды, который циркулирует через определенную площадь поперечного сечения в направлении потока за единицу времени:

Q = ΔV / Δt

В Международной системе единиц СИ расход измеряется в кубических метрах в секунду, но часто он также выражается в литрах в минуту или литрах в секунду.

Часто требуется расход на единицу площади q, который представляет собой отношение расхода Q к площади поперечного сечения:

д = Q / A

В SI q выражается в м / с, поэтому q представляет собой среднюю скорость жидкости в поперечном сечении трубы.

Важно отметить, что, хотя расход Q одинаков во всех секциях трубы, расход на единицу площади q или просто скорость потока выше в более узких секциях и ниже в более широких.

2.- Гидравлический градиент I

Когда жидкость циркулирует через пористую среду, гидростатическое давление уменьшается в том же направлении, что и поток.

Известно, что гидростатическое давление в определенной точке трубопровода пропорционально высоте h, отмеченной манометром с открытой трубкой в этом месте. Константа пропорциональности — это произведение плотности жидкости и ускорения свободного падения.

Таким образом, гидравлический градиент I определяется как частное между перепадом высот Δh столбцов двух манометров и ΔL, последняя величина представляет собой расстояние, разделяющее манометры (см. Рисунок ниже):

I = Δh / ΔL

Пермеаметр — устройство, изобретенное Генри Дарси для количественного определения потока воды через пористую среду. Источник: Ф. Сапата.

Это средний гидравлический градиент длины ΔL, безразмерная и отрицательная величина.

Если мы хотим найти гидравлический градиент в каждой точке трубопровода, мы берем предел для ΔL, стремящийся к нулю, в результате чего получаем производную функции гидравлического градиента относительно положения L вдоль потока:

3.- Проницаемость K

Проницаемость пористой среды или гидравлическая проводимость K — это отношение расхода Q и произведение площади поперечного сечения К гидравлическим градиентом я:

К = Q / A ∙ I

Гидравлическая проводимость имеет единицы скорости, метры за секунду в СИ.

Для K определена единица, называемая Дарсив честь Генри Дарси и определяется следующим образом:

А Дарси — проницаемость миллилитра жидкости с вязкостью один сантипуаз, движущейся на один сантиметр при перепаде давления в одну атмосферу через поперечное сечение одного квадратного сантиметра.

Применение закона Дарси

Основное применение закона Дарси — прогнозирование потока воды через водоносный горизонт перед бурением скважин.

Точно так же закон Дарси регулярно используется в сельскохозяйственной и гидрологической инженерии. Его также можно использовать в нефтяной промышленности для описания течения нефти и газа в пористой среде. Однако в этом случае K может изменяться в зависимости от того, является ли поток газом или нефтью, и не может зависеть исключительно и исключительно от проницаемого субстрата.

Ограничения

Закон Дарси предполагает, что гидравлическая проводимость K является надлежащей величиной среды, что верно во многих случаях. Однако иногда K зависит от динамической вязкости жидкости, которая, в свою очередь, может зависеть от расхода и температурных градиентов.

Предположение Дарси правдоподобно при рассмотрении потока грунтовых вод, где вязкость практически постоянна, поскольку на ее значение практически не влияет небольшая разница температур в водоносном горизонте.

В случаях течения нефти через пористую среду уравнение Дарси не может быть применено в том виде, в каком оно представлено здесь, а скорее внесены некоторые изменения, которые выходят за рамки цели данной статьи.

Упражнение решено

Определите гидравлическую проводимость пляжного песка с помощью лабораторного пермеаметра.

Предположим, что диаметр трубки пермеаметра составляет 20 см, а расстояние между двумя манометрами составляет 50 см. Также известно, что вода течет со скоростью 300 кубических дециметров в минуту, а разница в уровне между двумя датчиками составляет 25 см.

Решение

Расход Q составляет 300 кубических дециметров в минуту, но если выразить его в единицах международной системы, это будет выглядеть так:

Q = 300 х 10^-3 м³ / 60 с = 5 x 10^-3 м³ / с

Поперечное сечение площади A рассчитывается по формуле:

А = π ∙ R² = π ∙ (10 см)² = π ∙ (0,1 м)² = 0,314 м²

Гидравлический градиент I представляет собой частное между разницей манометрической высоты и расстоянием между манометрами:

I = 25 см / 50 см = 0,5

Согласно определению гидравлической проводимости K, приведенному выше:

К = Q / A ∙ I = (5 x 10^-3 м³ / с) / (0,314 м² ∙ 0,5) = 3,185 х 10^-2 м / с ≈ 2 м / мин.

Источник

«Head» in fluid dynamics[edit]

Components of hydraulic head[edit]

Fresh water head[edit]

Hydraulic gradient[edit]

Hydraulic head in groundwater[edit]

Atmospheric pressure[edit]

Head loss[edit]

See also[edit]

Notes[edit]

References[edit]

Водопроницаемость грунтов

Содержание

Что такое закон Дарси?

Уравнения закона Дарси

Дифференциальная форма закона Дарси

Расход, гидравлический градиент и проницаемость

1.- Расход Q

2.- Гидравлический градиент I

3.- Проницаемость K

Применение закона Дарси

Ограничения

Упражнение решено

Решение

Не пропустите также: