Как найти частоту
Частота характеризует собой циклические процессы колебаний или движение по окружности. Она равна количеству повторений процесса за единицу времени. Для ее измерения узнайте количество колебаний, которые произошли за некоторый промежуток времени. Иногда она измеряется более сложными способами. Если известен период повторений, ее можно просто рассчитать.
Вам понадобится
- — секундомер;
- — тестер;
- — калькулятор.
Инструкция
Наблюдая за колебаниями или другими повторяющимися движениями, отсчитайте некоторое их количество. Секундомером измерьте время, за которое произошли эти движения. Полным колебанием является возврат тела в исходную точку, как и полным оборотом. Для определения частоты ? поделите количество колебаний N на время t, за которое они произошли, измеренное в секундах. Например, если маятник за 20 секунд делал 30 колебаний, то частота равна ?=30/20=1,5 1/с (Герц). Если известен период колебаний (время одного колебания) найдите частоту ? поделив единицу на период Т (?=1/Т). Например, если период колебаний составляет 0,2 с, то частота этого колебания будет равна ?=1/0,2=5 Гц.
Для того чтобы определить частоту переменного тока возьмите тестер. Настройте его на измерение частоты специальным переключателем. Подключите прибор к цепи или источнику переменного тока, соблюдая осторожность. На экране тестера появится частота тока в сети. Например, в стандартной бытовой сети частота равна 50 Гц.
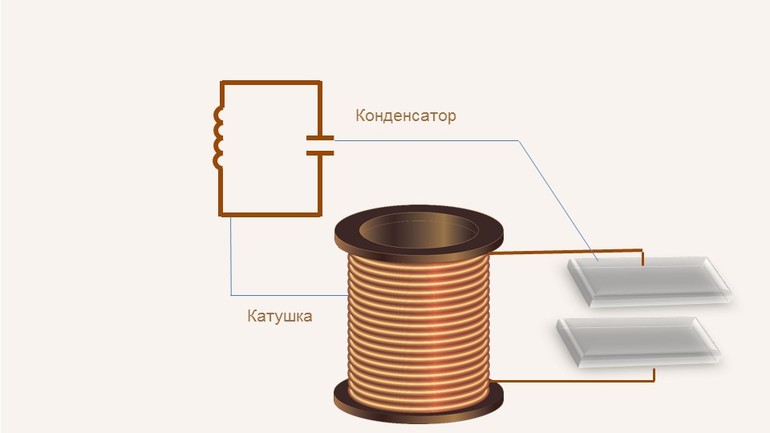
Чтобы измерить частоту колебательного контура, найдите индуктивность его катушки и емкость конденсатора, которые и составляют колебательный контур. Если они заранее неизвестны, подключите к ним тестер, настроенный, соответственно, на измерение индуктивности в Генри и электроемкости в Фарадах. Найдите частоту, используя формулу Томсона. Для этого число 2 умножьте на ??3,14 и корень квадратный из произведения индуктивности L и электроемкости C. Поделите число 1 на получившийся результат ?=1/(2•?•vL•C). Пример. Колебательный контур состоит и катушки индуктивностью 2 мГн и конденсатора электроемкостью 80 мкФ. Определите его частоту. Подставьте значения в формулу ?=1/(2•3,14•v2•10^(-3)•80•10^(-6))=1/(6.28•4•10^(-4))=0,04•10^4=400 Гц.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Свойства пружинного маятника
Определение 1
Идеальный пружинный маятник представляет собой пружину, массой которой можно пренебречь, с закрепленным на ней телом с точечной массой. При этом один или оба конца пружины закреплены, а силой трения можно пренебречь.
Такую конструкцию можно рассматривать лишь как математическую модель. Примерами реальных пружинных маятников (навитых из упругой проволоки цилиндрических спиралей) могут служить всевозможные устройства, гасящие колебания: амортизаторы, подвески, рессоры и т.п. Пружинные маятники, хотя и несколько иной конструкции (в виде плоских спиралей) используются в механических часах.
Свойства пружин зависят от вещества, из которого они изготовлены (как правило, это особая пружинная сталь), диаметра проволоки, формы ее сечения, диаметра цилиндра пружины, его длины. Эти показатели в совокупности обуславливают ключевую характеристику пружины — ее жесткость.
Пружина запасает энергию при продольном растяжении или сжатии за счет упругих деформаций в кристаллической решетке своего вещества.
Замечание 1
При слишком сильном растяжении или сжатии материал пружины теряет упругие свойства. Такая деформация называется пластической или остаточной.
Формула для расчета частоты колебаний
Если пружину с закрепленной на ней грузом, подвергнуть продольной упругой деформации, а затем отпустить, она начнет совершать возвратно-поступательные гармонические колебания, в ходе которых перемещение закрепленного на ней груза описывается формулой:
$x = A cdot cos(omega_0 cdot t + phi)$
Здесь $A$ — амплитуда колебаний, $phi$ — начальная фаза, $omega_0$ — собственная циклическая частота колебаний пружинного маятника, рассчитываемая как
$omega_0 = sqrt{frac{k}{m}}$ > $0$,
где:
- $k$ — жесткость пружины,
- $m$ — масса закрепленного на ней тела.
Циклическая частота отличается тем, что характеризует не количество полных циклов за единицу времени, а количество «пройденных» колеблющейся по гармоническому закону точкой радиан.
Период колебаний пружинного маятника вычисляется как
$T = 2 cdot pi cdot sqrt{frac{m}{k}}$.
Пример 1
Найти частоту и циклическую частоту пружинного маятника, период колебаний которого составляет 0,1 с.
Частоту можно найти как величину обратную к периоду:
$f = frac{1}{T}$
$f = frac{1}{0,1} = 10 Гц$
Циклическую частоту можно выразить как
$omega_0 = 2 cdot pi cdot f$
$omega_0 = 2 cdot 3,1415927 cdot 10 approx 62,831854 frac{рад}{с}$
Ответ: 10 герц и $approx$ 62,831854 радиан в секунду.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Примеры движения
Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.
В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:
- тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
- груза на нитке;
- электрического контура и других.
Амплитуда, период и частота
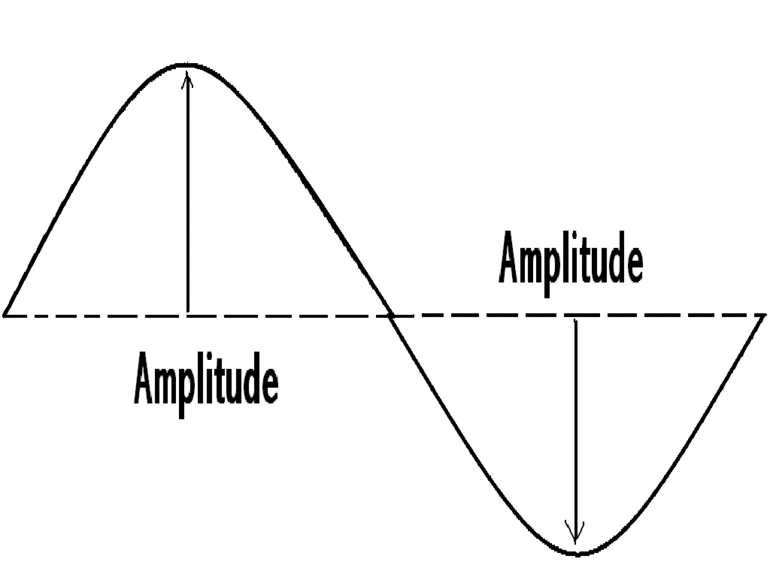
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:
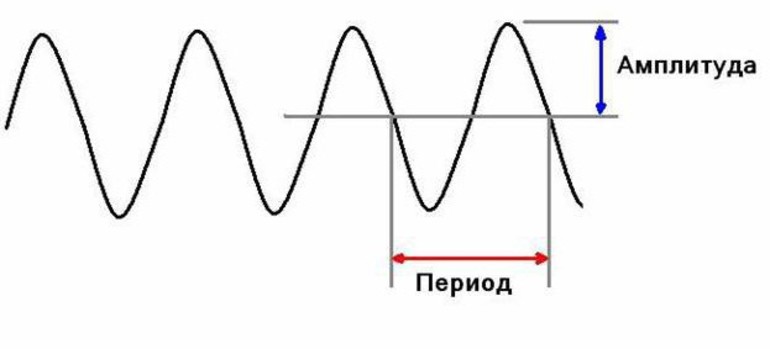
- Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
- Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
- Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
- Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.
Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.
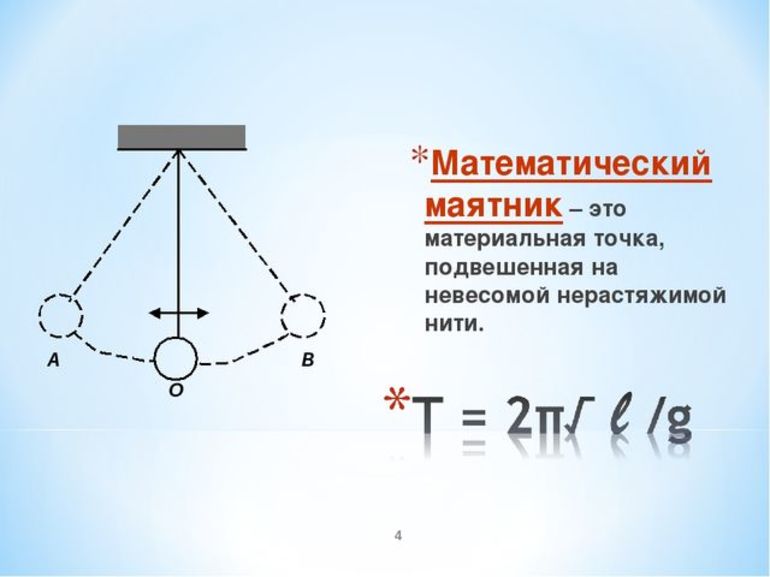
Математический маятник
Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.
Также нить должна быть невесомой и нерастяжимой.
Груз в этом случае считается материальной точкой.
При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:
α=x/l.
На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.
Период: T=2π /ω T=2π*sqrt (g/l)
Это формула Галилея, которая описывает движение математического маятника.
Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.
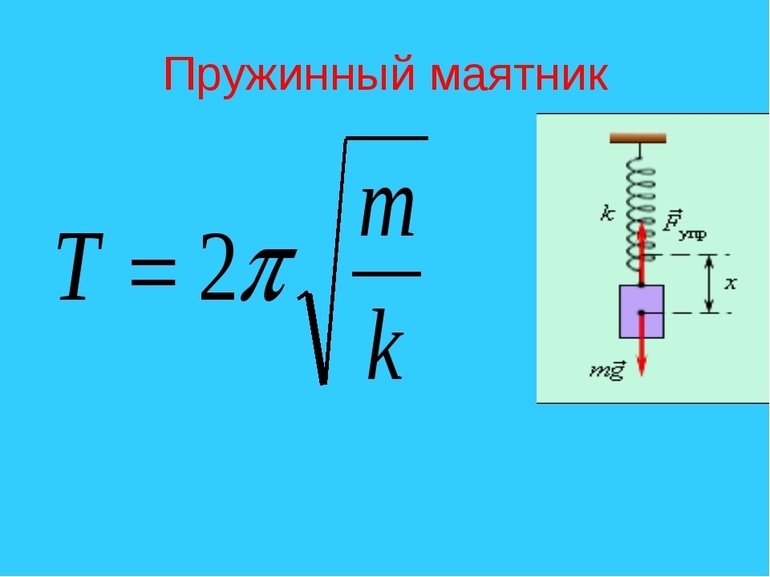
Пружинный маятник
Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.
Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:
F=-kx.
Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.
По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.
После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.
Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.
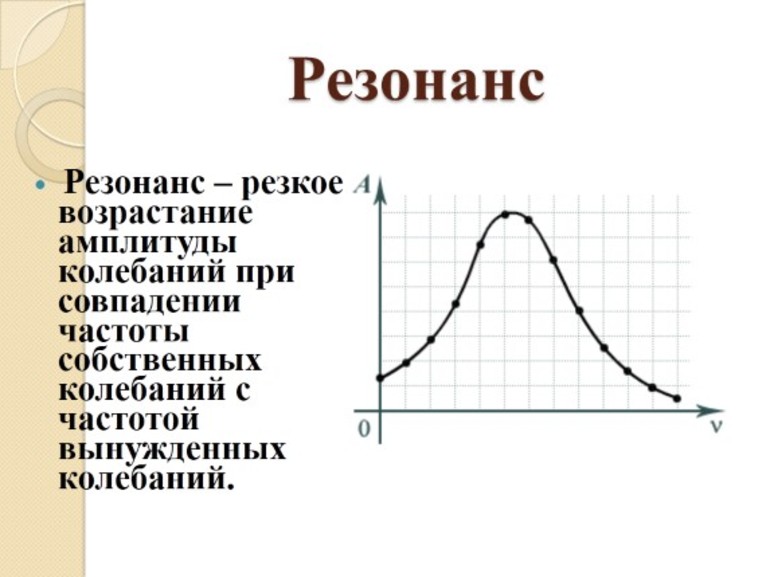
Явление резонанса
Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.
Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.
В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.
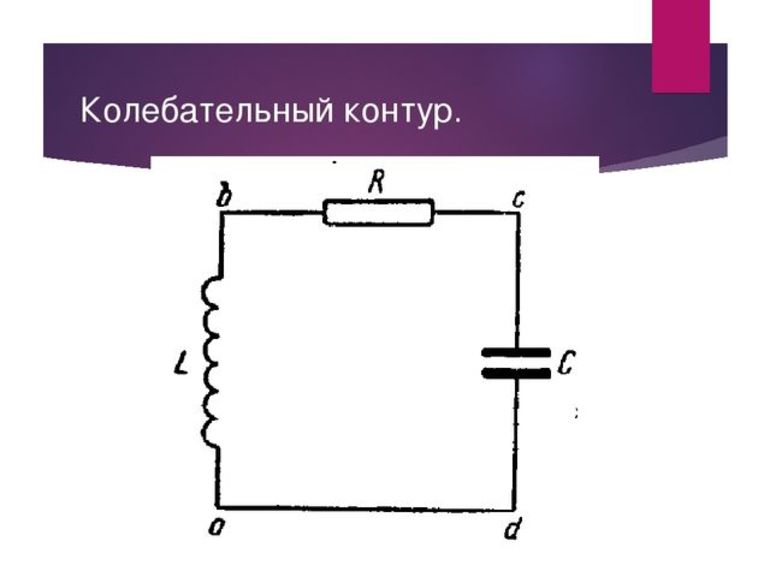
Колебательный контур
Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.
В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.
Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.
Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.
Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.
Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.
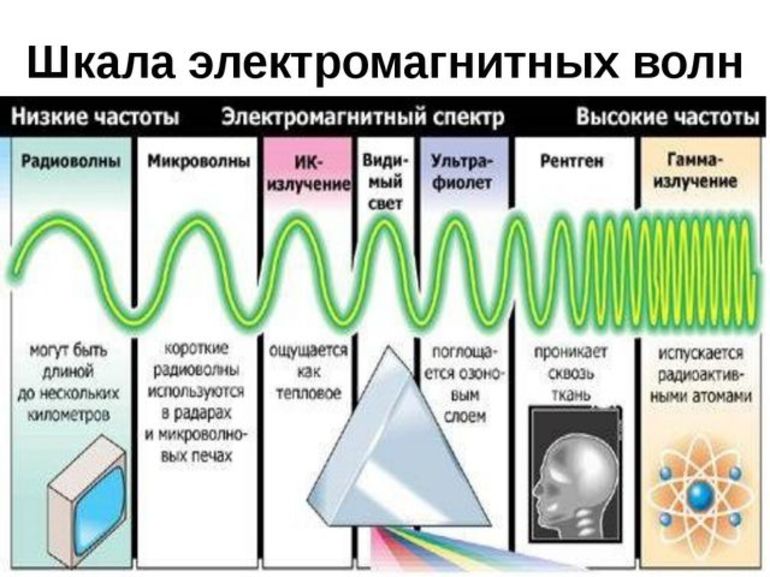
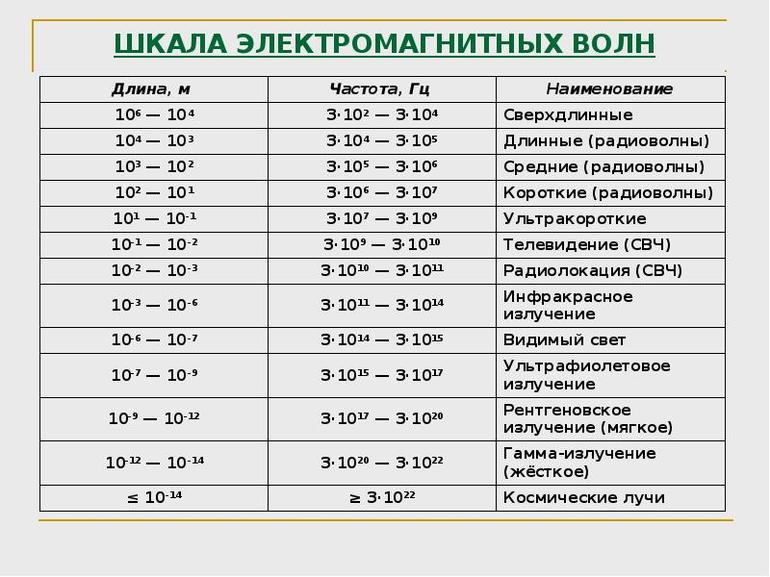
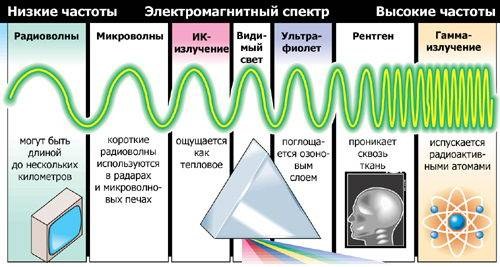
Звук и электромагнитные волны
Понятие частоты вводится и для звуковых и электромагнитных волн. Первые представляют собой колебания плотности среды. Вторые — изменение со временем напряженности магнитного и электрического полей.
От частоты звука зависит его тональность. Этим свойством пользуются для стандартизации описания музыки и создания музыкальных инструментов — каждой ноте соответствует своя частота.
До 16 Гц человеческое ухо не воспринимает, так же как и выше 20 КГЦ. Более высокие частоты используются в эхолокации, ультразвуковой диагностике.
Частота электромагнитных волн также определяет их способность взаимодействовать с человеческим организмом. Рентгеновское излучение проходит насквозь, при этом взаимодействуя с молекулами, вызывая их ионизацию. Ультразвук провоцирует процессы загара, фотосинтеза. Радиоволновое излучение практически не оказывает прямого воздействия, но хорошо подходит для передачи информации. В видимом диапазоне частота определяет цвет.
Есть также такая характеристика, как частота колебаний молекул. Она зависит от температуры тела и определяет его агрегатное состояние.
Таким образом, частота колебаний описывает большое количество процессов и оказывает воздействие на их характеристики.
Колебательное движение. Математический маятник
- Механические колебания
- Математический маятник
- Параметры колебаний математического маятника
- Задачи
- Лабораторная работа №4. Исследование колебаний математического маятника
п.1. Механические колебания
Кроме прямолинейного и криволинейного движения, с которыми мы уже познакомились, существует еще один вид механического движения – колебательный.
Механические колебания — это движения тел, которые в той или иной степени повторяются через определенные промежутки времени.
Примеры колебательных движений:
- движение маятника в часах;
- колебание автомобиля на рессорах;
- покачивание деревьев на ветру;
- раскачивание качели;
- сокращения сердца и легких;
- движение крыльев насекомых и птиц.
п.2. Математический маятник
Математическим маятником называют тело, подвешенное на длинной нерастяжимой нити, размеры которого значительно меньше длины нити.
Нить считается нерастяжимой и невесомой, а тело – материальной точкой на этой нити.
 |
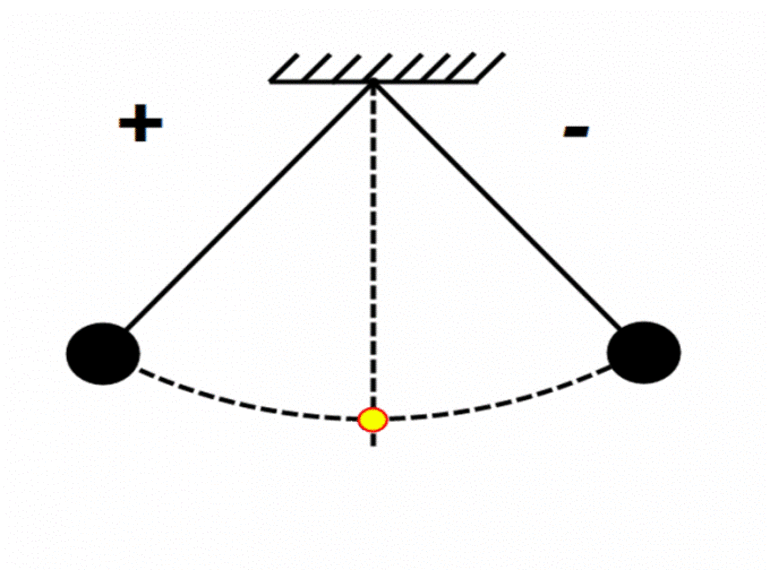
В положении равновесия тело (шарик) находится внизу. Отклонение от положения равновесия называют смещением тела, обозначают буквой x и измеряют в метрах (в СИ). Наибольшее смещение маятника от положения равновесия называют амплитудой колебаний, обозначают буквой A. В проекции на горизонтальную ось OX смещение изменяется в интервале (-Aleq xleq A). В положении равновесия x=0. Если маятник после смещения в положение 1, прошел положение равновесия 2, отклонился в положение 3, опять прошел положение 2, и вернулся в положение 1, говорят, что маятник совершил полное колебание. |
п.3. Параметры колебаний математического маятника
Период колебаний математического маятника – это время, за которое маятник совершает одно полное колебание. Период колебаний равен: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
На поверхности Земли (gapprox 9,8 м/с^2)
Частота колебаний математического маятника – это количество полных колебаний, которые маятник совершает за единицу времени: $$ f=frac 1T=frac{1}{2pi}sqrt{frac gL} $$
Период и частота колебаний – взаимно обратные величины
Период в СИ измеряют в секундах, частоту – в герцах: 1 Гц=1 c-1
Формула для периода колебаний справедлива для небольших отклонений маятника (на угол порядка 15-20° от положения равновесия).
п.4. Задачи
Задача 1. Маятник совершил 3 полных колебания за 9 с. Найдите период и частоту его колебаний. Чему равна длина нити, на которой подвешен маятник (ответ дайте в см, с округлением до целых)?
Дано:
(N=3)
(t=9 c)
__________________
(T, f, L-?)
Период колебаний: (T=frac tN)
Частота колебаний: (f=frac 1T=frac Nt)
Длина нити: $$ T=2pisqrt{frac Lg}Rightarrow sqrt{frac Lg}=frac{T}{2pi}Rightarrow frac Lg=left(frac{T}{2pi}right)^2Rightarrow L=gleft(frac{T}{2pi}right)^2 $$ Подставляем: begin{gather*} T=frac 93=3 (c)\ f=frac 13 (Гц)\ L=9,8cdotleft(frac{3}{2pi}right)^2approx 2,234 (м)approx 223 (см) end{gather*} Ответ: 3 с; 1/3 Гц; 223 см
Задача 2. Математический маятник колеблется с частотой 20?тиы кГц. Найдите период колебаний и число колебаний в минуту.
Дано:
(f=20 кГц=2cdot 10^4 Гц)
(t=1 мин=60 с)
__________________
(T, N-?)
Период колебаний: (T=frac 1f)
Частота колебаний за время (t: N=ft)
Подставляем: begin{gather*} T=frac{1}{2cdot 10^4}=0,5cdot 10^{-4} (c)=50cdot 10^{-6} (c)=50 (мкс)\ N=2cdot 10^4cdot 60=1,2cdot 10^6 end{gather*} Ответ: 50 мкс; 1,2·106
Задача 3. Расстояние от улья до цветочного поля 600 м. Пчела летит за нектаром со скоростью 8 м/с и машет крылышками с частотой 440 Гц. Возвращаясь в улей с нектаром, пчела летит со скоростью 5 м/с и машет крылышками с частотой 320 Гц. Найдите разность в количестве взмахов крылышками на пути туда и обратно.
Дано:
(s=600 м )
(v_1=8 м/с)
(f_1=440 Гц)
(v_2=5 м/с)
(f_2=320 Гц)
__________________
(triangle N-?)
Время полета из улья за нектаром (t_1=frac{s}{v_1})
Количество взмахов крылышками (N_1=f_1 t_1=f_1frac{s}{v_1})
Аналогично количество взмахов на пути назад (N_2=f_2frac{s}{v_2})
Найдем каждое из (N): begin{gather*} N_1=440cdotfrac{600}{8}=33000\ N_2=320cdotfrac{600}{5}=38400 end{gather*} На пути обратно пчела с грузом делает больше взмахов. Искомая разность: $$ triangle N=N_2-N_1=38400-33000=5400 $$ Ответ: 5400
Задача 4. Определите длину математического маятника с периодом колебаний 1с, если он находится: а) на Луне ((g_л=1,6 м/с^2)); б) на Марсе ((g_м=3,6 м/с^2)). Ответ запишите в см, с точностью до десятых.
Дано:
(T=1 с )
(g_л=1,6 м/с^2 )
(g_м=3,6 м/с^2)
__________________
(L_л, L_м-?)
Длина нити: begin{gather*} T=2pisqrt{frac Lg}Rightarrowsqrt{frac Lg} =frac{T}{2pi}Rightarrowfrac Lg=left( frac{T}{2pi}right)^2Rightarrow L = gleft(frac{T}{2pi}right)^2 end{gather*} На Луне: $$ L_л=1,6cdotleft(frac{1}{2pi}right)^2approx 0,0405 (м)approx 4,1 (см) $$ На Марсе: $$ L_м=3,6cdotleft(frac{1}{2pi}right)^2approx 0,0912 (м)approx 9,1 (см) $$ Ответ: 4,1 см; 9,1 см
п.5. Лабораторная работа №4. Исследование колебаний математического маятника
Цель работы
Исследовать, от каких величин зависит период колебаний математического маятника.
Теоретические сведения
При малых отклонениях (порядка 15-20° от вертикали) период колебаний математического маятника определяется формулой: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
Для работы принять (gapprox 9,80665 м/с^2).
При заданном периоде колебаний для длины маятника получаем: $$ L=gleft(frac{T}{2pi}right)^2 $$
Приборы и материалы
Два лабораторных грузика по 100 г, крепкая нить (1,5-2 м), линейка (30-50 см), штатив, секундомер.
Ход работы
1. Рассчитайте длину нитей, необходимых для создания маятников с периодами колебаний (T_1=1 с; T_2=2 с).
2. Закрепите один грузик на нити и подвесьте его на штативе так, чтобы длина подвеса была равна расчетной длине (L_1).
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний. Повторите опыт 5 раз. Проведите расчеты для определения периода колебаний (T_{1 эксп}) по методике, изложенной в лабораторной работе №2 (см. §4 данного справочника).
4. Теперь подвесьте грузик так, чтобы длина подвеса была равна расчетной длине (L_2). Повторите серию из 5 экспериментов и определите (T_{2 эксп}).
5. При длине подвеса (L_2) подвесьте к первому грузику второй. Повторите серию из 5 экспериментов и определите (T ‘). Сравните (T ‘) и (T_{2 эксп}).
6. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Расчет длины нитей begin{gather*} L=gleft(frac{T}{2pi}right)^2\ T_1=1 c, L_1=9,80665cdotleft(frac{1}{2pi}right)^2approx 0,248 (м)=24,8 (см)\ T_2=2 c, L_1=9,80665cdotleft(frac{2}{2pi}right)^2approx 0,9994 (м)=99,4 (см) end{gather*}
Определение (T_{1 эксп})
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1 c)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 9,7 | 10,2 | 9,8 | 9,9 | 10,3 | 50 |
| (triangle c) | 0,3 | 0,2 | 0,2 | 0,1 | 0,3 | 1 |
begin{gather*} t_{cp}=frac{50}{5}=10\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(10,0pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{1 эксп}=frac{1}{10}(t_0pmtriangle t), T_{1 эксп}=(1,00pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{1 эксп}}cdot 100text{%}=frac{0,02}{1}cdot 100text{%}=2,0text{%} $$
Определение (T_{2 эксп})
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 19,7 | 20,1 | 19,8 | 20,2 | 19,7 | 99,5 |
| (triangle c) | 0,2 | 0,2 | 0,1 | 0,3 | 0,2 | 1 |
begin{gather*} t_{cp}=frac{99,5}{5}=19,9\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,9pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{2 эксп}=frac{1}{10}(t_0pmtriangle t), T_{2 эксп}=(1,99pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{2 эксп}}cdot 100text{%}=frac{0,02}{1,99}cdot 100text{%}approx 1,0text{%} $$
Определение (T ‘) (с двумя грузиками)
Время 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 20,2 | 19,7 | 19,6 | 20,0 | 20,3 | 99,8 |
| (triangle c) | 0,24 | 0,26 | 0,36 | 0,04 | 0,34 | 1,24 |
begin{gather*} t_{cp}=frac{99,8}{5}=19,96\ triangle_{cp}=frac{1,24}{5}approx 0,25 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,25right}=0,25 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,96pm 0,25) c end{gather*} Период колебаний в 10 раз меньше: $$ T’=frac{1}{10}(t_0pmtriangle t), T’=(1,996pm 0,025) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T’}cdot 100text{%}=frac{0,025}{1,996}cdot 100text{%}approx 1,3text{%} $$
Полученные на опыте интервалы для (T_{2 эксп}) и (T’) (одинаковая длина нити (L_2) и разные массы грузиков – 100 г и 200 г соответственно): begin{gather*} 1,97leq T_{2 эксп}leq 2,01\ 1,971leq T’leq 2,021 end{gather*} Таким образом, (T_{2 эксп}approx T’), т.е. период колебаний математического маятника не зависит от массы груза.
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе с помощью расчетной формулы были определены длины нитей подвеса для маятников с периодами колебаний (T_1=1 с; T_2=2 с).
Полученный на опыте период колебаний для подвеса с (L_1=24,8 см) с грузиком 100 г равен $$ T_{1 эксп}=(1,00pm 0,02) c, delta=2,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 100 г равен $$ T_{2 эксп}=(1,99pm 0,02) c, delta=1,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 200 г равен $$ T’=(1,996pm 0,025) c, delta=1,3text{%} $$ Формула (T=2pisqrt{frac Lg}) данными экспериментами подтверждена.
Период колебаний математического маятника зависит от длины подвеса и не зависит от массы грузика на подвесе.
Цель первой части нашей работы: с помощью экспериментальной установки определить
период свободных колебаний математического маятника заданной длины.
Оборудование мы будем использовать из пятого комплекта, а
именно: штатив с муфтой и креплением для нити, груз с крючком, нить,
электронный секундомер, метровую линейку или мерную ленту, возможно вам
понадобится и транспортир.
Своеобразные движения, которые называются колебательными или
просто колебаниями, всем вам хорошо известны. Они широко распространены в
окружающем нас мире. Однако при всём разнообразии колебательных движений у всех
них есть одна важная особенность: через определённый промежуток времени
движение любого из этих тел повторяется.
Давайте вспомним, что процесс, при котором какая-либо
физическая величина, характеризующая этот процесс, последовательно изменяется
то в одну, то в другую сторону около своего положения равновесия называется
механическим колебанием. И если силы сопротивления будут отсутствовать, то
такое движение будет повторяться бесконечно долго, то есть колебания будут
являться свободными.
Свободно колеблющиеся тела всегда взаимодействуют с другими
телами и вместе с ними образуют систему тел. Так вот, совокупность тел, в
которой могут происходить колебательные процессы, мы с вами будем называть
механической колебательной системой.
Вы знаете, что для упрощённого рассмотрения тех или иных
явлений в науке часто пользуются идеальными моделями. Для колебательных систем
такими моделями являются маятники. В общем случае маятником называется
твёрдое тело, совершающее под действием приложенных сил колебания около
неподвижной точки или вокруг оси.
Существует несколько видов маятников. Но наиболее часто
встречающиеся, это пружинный маятник, представляющий собой груз,
прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной
или вертикальной оси.
И нитяной маятник — шарик, подвешенный на нити,
способный совершать колебательное движение.
Физической моделью обычного нитяного маятника является математический
маятник, с которым нам с вами и предстоит сегодня работать. (Математический
маятник — это материальная точка, подвешенная на конце невесомой нерастяжимой
нити.)
Теперь давайте вспомним, что любое колебательное движение
характеризуется амплитудой, частотой и периодом колебаний.
Амплитуда колебаний — это наибольшее смещение
колеблющегося тела от положения равновесия.
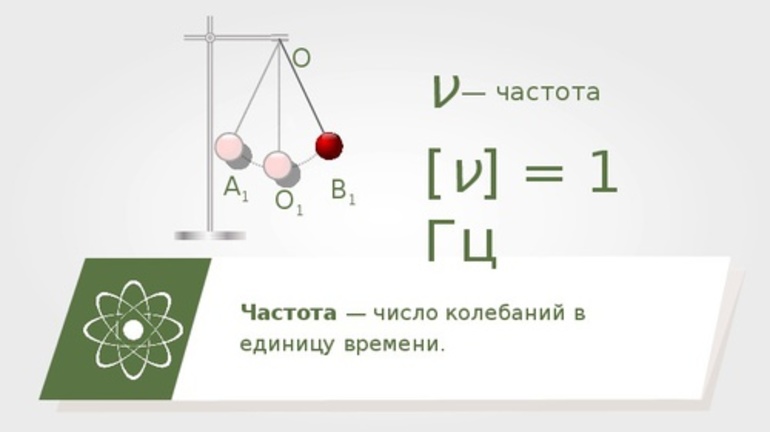
Частота
колебаний — это
число колебаний, совершаемых телом за единицу времени. Обозначается она
греческой буквой «Ню» (ν). А единицей её измерения в системе СИ является
герц [Гц]:
И, наконец, период
колебаний — это наименьший промежуток времени, через который полностью
повторяется состояние колебательной системы. Обозначается период большой буквой
«Тэ» (Т). Единица измерения — секунда [с]:
Именно период
колебаний мы с вами сейчас и будем искать. Итак, для начала давайте соберём
экспериментальную установку. Для этого закрепим перекладину в муфте у верхнего
края стержня штатива. Далее подвесим к перекладине с помощью нити один груз из
набора. Расстояние от точки повеса до центра груза, то есть длина маятника, по
условию задания должно быть равно 50 см. Если длины штатива не хватает и груз
лежит на поверхности стола, то штатив нужно разместите на столе так, чтобы
конец перекладины выступал за край поверхности стола. Электронный секундомер
переведём в ручной режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний — это время, за которое совершается
одно полное колебание. Он равен отношению промежутка времени, в течение
которого тело совершило N полных колебаний, к числу этих колебаний:
С формулой всё понятно, поэтому приступим непосредственно к
работе. Итак, отклоняем нить маятника на угол не более 10—15° (можно помочь
себе транспортиром). Затем отпускаем груз и даём маятнику совершить два — три
полных колебания, чтобы процесс колебаний стал установившимся. В момент
прохождения маятником крайнего положения запускаем секундомер. Теперь нам
остаётся только дождаться, пока маятник не совершит 30 полных колебаний. По окончании
последнего колебаний останавливаем секундомер.
Значение промежутка времени, за которое маятник совершил
заданное число колебаний, записываем в бланк ответов с учётом погрешности
измерения:
Сюда же записываем и количество колебаний, совершённых
маятником:
Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения промежутка
времени и числа полных колебаний:
Тогда в выводе напишем: период колебаний математического
маятника равен 1,42 с.
Во второй части работы мы с вами должны с помощью экспериментальной установки
определить частоту свободных колебаний математического маятника.
Оборудование мы будем использовать то же самое: штатив с
муфтой и креплением для нити, груз с крючком, нить, электронный секундомер,
метровую линейку или мерную ленту и транспортир.
Теория у нас остаётся та же. Только теперь мы с вами будем
находить число колебаний, которые маятник совершает за единицу времени, то есть
за одну секунду.
Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. К перекладине
подвесим наш маятник, длина которого по условию задания должна быть равна
одному метру (ещё раз напомним, что длину маятника мы измеряем от точки подвеса
до центра груза). Электронный секундомер переведём в ручной режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний — это время, за которое совершается
одно полное колебание:
А величина, обратная периоду, называется частотой
колебаний. Таким образом, она показывает, какое количество полных колебаний
совершается телом в единицу времени:
С формулами разобрались, поэтому приступим непосредственно к
самой работе. Итак, отклоняем нить маятника на угол не более 10—15° (можно
помочь себе транспортиром). Затем отпускаем груз и даём маятнику совершить два
— три полных колебания, чтобы процесс колебаний стал установившимся. В момент
прохождения маятником крайнего положения запускаем секундомер. Теперь нам
остаётся только дождаться, пока маятник не совершит 30 полных колебаний. По
окончании последнего колебаний останавливаем секундомер.
Значение промежутка времени, за которое маятник совершил
заданное число колебаний, записываем в бланк ответов с учётом погрешности
измерения:
Здесь же указываем и количество колебаний, совершённых
маятником:
Прямые измерения мы с вами завершили. Теперь определяем
частоту колебаний. Для этого подставляем в расчётную формулу значения числа
полных колебаний и промежутка времени, в течение которого эти колебания были
совершены:
В выводе можно написать, что частота колебаний
математического маятника составила примерно 0,49 Гц.