12.1. Простой
трубопровод постоянного сечения.
12.1.1.Общий вид
расчетного уравнения простого трубопровода
12.2.Простой
трубопровод между двумя резервуарами.
12.3. Простой
трубопровод при истечении в атмосферу.
12.4.Сифонный
трубопровод. Вакуум на участке
трубопровода.
12.5. Использование
приблизительных зависимостей при
расчете простого трубопровода.
Замена местных
сопротивлений.
12.6. Три задачи на
расчет простого трубопровода.
12.7 Графики напоров
12.1. Простой трубопровод постоянного
сечения
Трубопровод называют простым, если
жидкость транспортируется по нему от
питателя к приемнику без ответвлений
потока, но может иметь различные диаметры
и включать местные сопротивления.
Трубопроводы, содержащие
последовательные, параллельные соединения
и разветвления простых трубопроводов
называются сложными.
Жидкость движется по трубопроводу за
счет того, что энергия, имеющаяся в
начале трубопровода больше, чем в конце.
Энергии может быть обеспечена разностью
уровней жидкости, работой насоса или
давлением газа, например, за счет
применения гидроаккумуляторов.
Движение жидкости за счет разности
уровней (разности геометрических высот)
применяется в гидротехнике и водоснабжении.
В машиностроении движение жидкости
обеспечивается работой насоса и
гидроаккумуляторами. Гидроаккмуляторы
— емкости с разделителем с одной стороны
использующие давление газа или пружины
для создания запаса энергии с другой
стороны рабочую жидкость, заправленную
в гидроаккумулятор и находящуюся под
действием давления газа.
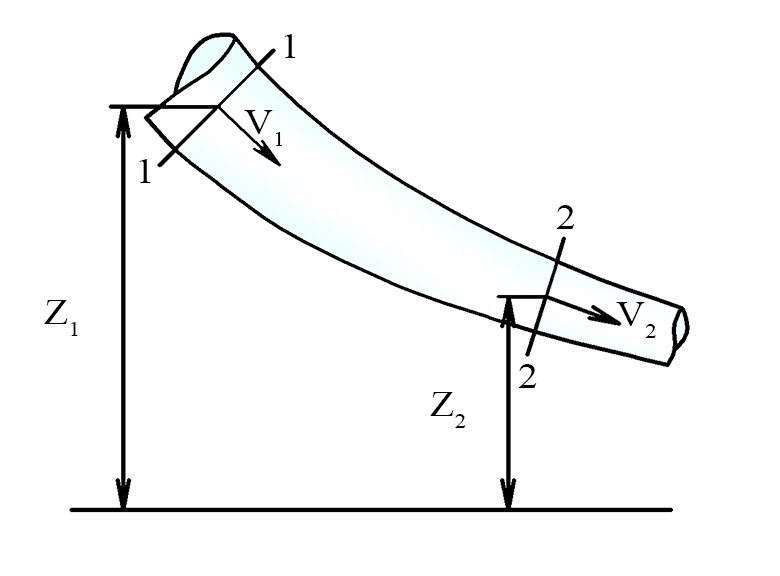
На рис.12.1 изображен простой трубопровод
постоянного сечения расположенный
произвольно в пространстве, состоящий
из нескольких участков с длиной li
и диаметромdiи содержащий местные сопротивления.
Запишем уравнение Бернулли для сечений
«1 – 1» и «2-2». Геометрические высоты:
z1иz2,
избыточные давления: Р1и Р2,
скорости:V1 иV2.ρ
(12.1)
Σh– сумма потерь на
трение по длине и в местных сопротивлениях,
а также потерь на входе и выходе из
трубопровода.
Гидростатическим напором называется
сумма геометрического и пьзометрического
напора в данном сечении трубопровода.
где z– геометрический
напор,— пьезометрический напор.
Разность гидростатических напоров
в в сечениях 1 и 2, называется располагаемым
напором — Нрасп,
если величина гидростатического
напора Нгст для
сечений 1 и 2 известна.
Если величина Нгст
не известна, разность гидростатических
напоров называется потребным напором
– Нпотр
и ее необходимо определить.
Таким образом, разность может быть
располагаемым или потребным напором,
в зависимости от наличия или отсутствия
исходных данных.
,
(12.2)
Используя разность гидростатических
напоров из уравнения баланса напоров
Бернулли, получаем общий вид
расчетного уравнения простого трубопровода
( 12.3 )
Это уравнение показывает, что имеющаяся
в нашем распоряжении потенциальная
энергиия в виде гидростатического
напора затрачивается на преодоление
разности скоростных напоров и потерь
в местных сопротивлениях и на трение
по длине.
Если площади питателя и приемника или
длины трубопроводов велики по сравнению
с сечением трубопровода, тогда скоростными
напорами можно пренебречь, уравнение
простого трубопровода принимает вид
(12.4)
В этом случае, потребный напор будет
равен сумме сопротивлений в трубопроводе.
Располагаемый напор будет затрачиваться
на преодоление гидравлических
сопротивлений.
Таким образом, уравнение простого
трубопровода позволяет решить две
задачи.
Первая: в случае известного располагаемого
напора определить сопротивления, которые
он может преодолеть.
Вторая: в случае известной суммы
сопротивлений определить располагаемый
напор.
Правая часть равенства (12.4) называется
характеристикой трубопровода. Уравнение
баланса напоров можно записать в виде
,
(12.4′)
где Σh– есть характеристика
трубопровода, которая является степенной
функцией расхода. ВеличинаК–
коэффициент сопротивления трубопровода,
а показатель степениmимеет значение, зависящее от режима
течения жидкости(ламинарный или
турбулентный).
Используя формулу (12.4′) можно построить
кривую потребного напора в координатах
Н=f(Q),
(рис.12.2), то есть зависимость напора от
расхода жидкости в трубопроводе.
Величина Нгст определяет положение
характеристики трубопровода относительно
начала координат Н-Q.
Соседние файлы в папке Лекции и семинары
- #
- #
- #
(кг/м3) – плотность
(н/м3) – удельный вес
ГИДРОСТАТИКА
р — давление или сжимающие напряжение (н/м2 = Па)
Свойства:
Давление всегда направлено к поверхности по внутренней нормали.
Действует одинаково по всем направлениям (не зависит от угла наклона площадки)
Основное уравнение гидростатики:
рА = ро + рв; рв = h·γ
рА – абсолютное давление;
ро – давление действующее на поверхность жидкости;
рв – весовое давление, т.е. давление столба жидкости.
рв = h·γ
h – глубина расположения точки;
γ – удельный вес жидкости.
При атмосферном давлении на поверхности:
рА = ра + ризб; ризб = hизб·γ
ра – атмосферное давление;
ризб – избыточное давление.
Выводы:
-
Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.
-
Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.
-
Можем измерять величину давления эквивалентной ему высотой столба жидкости.
р = h·γ, отсюда h = р/γ
Например давление величиной в 1 атм. р = 1 кгс/см2 соответствует
h = 10 м вод. столба
Сила давления жидкости на плоскую поверхность
Р = рсS = hсγS (н)
рс = hсγ – давление в центре тяжести при атмосферном давлении на поверхности
рс = hсγ + рМ, либо рс = hсγ – рВАК
hс – глубина расположения центра тяжести поверхности (м);
S – площадь поверхности (м2).
Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости
Удельная энергия (напор) Э = Е/G = Е/mg (м)
Z + hп = НГС = Э = const
Z – геометрический напор;
hп – пьезометрический напор;
НГС –гидростатический напор или полная удельная потенциальная энергия жидкости.
ГИДРОДИНАМИКА
Уравнение неразрывности
Q = V1ω1 = V2ω2 = const
Q – расход жидкости (м3/с);
V – средняя скорость потока (м/с);
Ω – площадь живого сечения потока (м2).
Vi = Q / ωi – средняя скорость потока
Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)
где z — геометрический напор, м;
P/γ — приведенная пьезометрическая высота (если Р — абсолютное давление) или пьезометрическая высота (если Р — избыточное давление), м;
V2/2g — скоростной напор, м.
— гидростатический напор,
удельная потенциальная энергия жидкости
НГС = Э – гидродинамический напор или полная удельная энергия
Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).
Σh = hпот = hℓ + hм – потери энергии при движении жидкости от 1 до 2 сечений (м);
α= ЕКД /ЕКУ – коэффициент кинетический энергии (коэффициент Кориолиса);
hℓ — потери по длине.
(м)
λ – коэффициент гидравлического трения f(Rе·Δ);
hм – потери на местных сопротивлениях.
(м)
РЕЖИМЫ ДВИЖЕНИЯ
Число (критерий) Рейнольдса
Для кругло-цилиндрических труб
(м)
RГ – гидравлический радиус;
ω – площадь живого сечения потока (м2);
Х – смоченный периметр.
Ламинарный режим: Rе < Rекр ≈ 2320
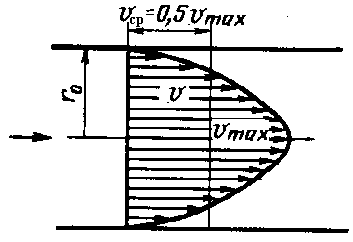
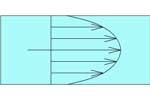
Эпюра скорости при ламинарном движении.
umax = 2V; α = 2; λ = f(Rе); λ = 64/Rе; hℓ = f (V1…1,4)
Турбулентный режим: Rе > Rекр
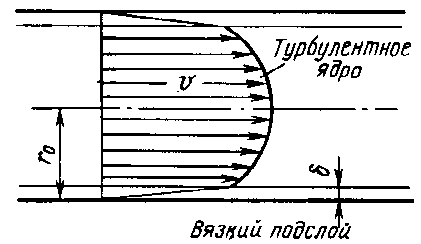
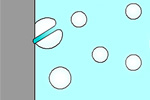
Профиль скорости при турбулентном движении
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)
u ≈ V; α = 1…1,4
В турбулентном режиме имеется три вида трения:
Гидравлически гладкие русла
λ = f(Rе) λ = 0,3164/Rе0,25
Смешанное трение
λ = f(Rе;Δ)
Шероховатое трение, квадратичная область турбулентного режима
λ = f (Δ); λ = 0,11(Δ /d)0,25
hℓ = f (V1,7…2)
СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
(м/с)
— коэффициент скорости
Но – действующий (расчетный напор (м)
Расход жидкости
(м3/с)
μ = φε – коэффициент расхода;
ω – площадь проходного (живого) сечения потока (м2);
Но – действующий напор (м).
7. Анализ основного уравнения гидростатики
Высоту напора принято называть пьезометрической высотой, или напором.
Согласно основному уравнению гидростатики,
p1+ ρghA= p2+ ρghH,
где ρ — плотность жидкости;
g — ускорение свободного падения.
p2, как правило, задается p2= pатм, поэтому, зная hА и hH, нетрудно определить искомую величину.
2. p1= p2= pатм. Совершенно очевидно, что из ρ = const, g = const следует, что hА= hH. Этот факт называют также законом сообщающихся сосудов.
3. p1< p2= pатм.
Между поверхностью жидкости в трубе и ее закрытым концом образуется вакуум. Такие приборы называют вакуумметры; их используют для измерения давлений, которые меньше атмосферного.
Высота, которая и является характеристикой изменения вакуума:
Вакуум измеряется в тех же единицах, что и давление.
Пьезометрический напор
Вернемся к основному гидростатическому уравнению. Здесь z — координата рассматриваемой точки, которая отсчитывается от плоскости XOY. В гидравлике плоскость XOY называется плоскостью сравнения.
Отсчитанную от этой плоскости координату z называют пооразному: геометрической высотой; высотой положения; геометрическим напором точки z.
В том же основном уравнении гидростатики величии на p/ρgh — также геометрическая высота, на которую поднимается жидкость в результате воздействия давления р. p/ρgh так же, как и геометрическая высота, измеряется в метрах. В случае, если через другой конец трубы на жидкость действует атмосферное давление то жидкость в трубе поднимается на высоту pизб/ρgh, которую называют вакуумметрической высотой.
Высоту, соответствующую давлению pвак, называют вакуумметрической.
В основном уравнении гидростатики сумма z + p/ρgh — гидростатический напор Н, различают также пьезометрический напор Hn , который соответствует атмосферному давлению pатм/ρgh:
Hn < H
2018-03-17
Уравнение Бернулли
Содержание:
- Уравнение Бернулли для потока идеальной жидкости
- Физический смысл уравнения Бернулли
- Уравнение Бернулли для потока реальной вязкой жидкости
- Иллюстрация уравнения Бернулли
- Уравнение Бернулли для горизонтальной трубы
- Алгоритм решения задач с помощью уравнения Бернулли
Основные уравнения гидродинамики — уравнение Бернулли и неразрывности позволяют установить взаимосвязь между параметрами плавно изменяющегося потока.
Уравнение Бернулли для потока идеальной жидкости
Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила — сила тяжести.
Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 — в конце.
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
- где z — геометрическая высота,
- p — давление в выбранном сечении,
- V — скорость жидкости в выбранном сечении,
- ρ — плотность жидкости,
- g — ускорение свободного падения.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор — величина постоянная.
- где z — геометрический напор,
- p/ρg — пьезометрический напор,
- z + p/ρg — статический напор,
- V2/2g — скоростной напор,
- z + p/ρg + V2/2g = Н — полный напор.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2
Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
- gz — удельная энергия положения,
- p/ρ — удельная энергия давления движущейся жидкости,
- V12/2 — удельная кинетическая энергия жидкости,
- gz + p/ρ + V2/2 = Hg — полная удельная энергия движущейся идеальной жидкости.
Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.
Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.
Уравнение Бернулли для потока реальной вязкой жидкости
Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:
Н1=Н2 + Δh1 — 2
z1 + p1/ρg + V12/2g = z2 + p2/ρg + V22/2g + Δh1 — 2
Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h1 — 2, вызванных гидравлическими сопротивлениями участка.
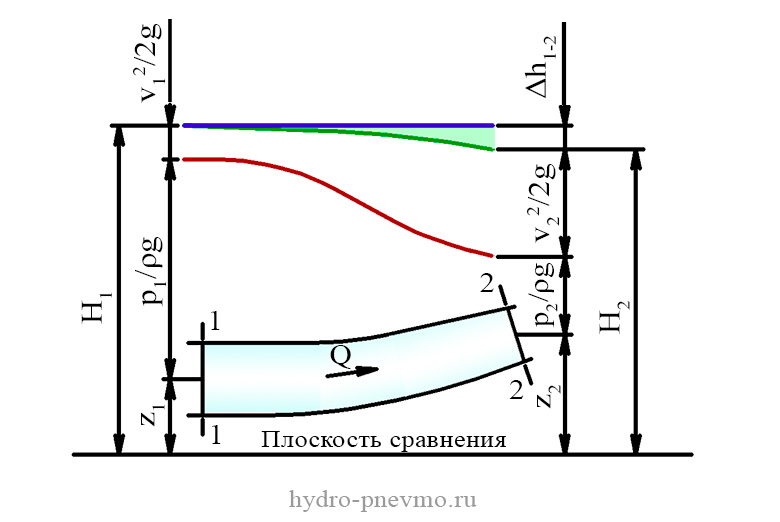
Иллюстрация уравнения Бернулли
Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.
Уравнение Бернулли для горизонтальной трубы
Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:
p1 + ρV12 = p2 + ρV22 + Δp1о
Алгоритм решения задач с помощью уравнения Бернулли
Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:
- Изобразить принципиальную гидравлическую схему системы
- Провести общую для всего потока плоскость сравнения. Лучше всего провести ее самой нижней точки системы, например на уровне оси самого нижнего трубопровода, или не уровне жилкости самого нижнего резервуара.
- Выбрать два (или несколько) живых сечения. Одно сечение выбирается в, том месте где параметры потока известны, другое там, где нужно определить неизвестные параметры (напрмер давление). Сечения следует выбирать только в тех местах где движение можно считать плавно изменяющимся. Нумеровать сечения следует в направлении движения жидкости.
- Записать уравенение Бернулли для выбранных сечений.
- При необходимости определить гидравлические потери напора на различных участка гидросистемы.
- Вычислить неизвестные параметры, используя уранение Бренулли.
Читайте также:
Все новости
Следовательно, гео.метрический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма трех высот напоров) — геометрической, пьезометрической и обусловленной скоростным напором — есть величина постоянная вдоль потока. В связи с этим линия полного напора будет параллельна плоскости сравнения (рис. 22.9). [c.280]
Можно сказать, что потенциальный напор (удельная потенциальная энергия) слагается из двух напоров геометрического напора (удельной энергии положения) и напора давления (удельной энергии давления). [c.47]
Как видно, полный напор представляет собой сумму двух напоров потенциального напора и скоростного (кинетического) напора = и Ц2д). Можно сказать также, что полный напор представляет собой сумму трех напоров геометрического z, напора давления р/у и скоростного напора и /(2д), причем сумма первых двух напоров равна удельной энергии потенциальной (УЭЛ). Энергетическое выражение полного напора можно представить следующей записью [c.101]
При элементарном рассмотрении этого явления гидравлика принимает, что вода при ударе уменьшает свою энергию на скоростной напор геометрической разности скоростей [c.28]
С другой стороны, равнодействующая Р реакции q полностью определяется гидродинамическим напором, геометрическими параметрами оболочки и длиной вышедшей из шахты части. С учетом [c.348]
Напор геометрический (нивелирный) 66 [c.620]
Мощность насосной установки определится по формуле (4-25), где Я — суммарный напор — геометрический Яг и затрачиваемый [c.199]
Статический напор газа в плоскости 3 равен нулю. В плоскости 4 за трубкой статический, динамический и геометрический напоры равны нулю, но имеется напор, затраченный на дар о неподвижный атмосферный воздух при, вытекании газа из тонкой трубки. Во всех положениях сумма напоров геометрического, пьезометрического, динамического и потерянного на сопротивления равна постоянной величине [c.17]
Наложение потоков 418 Напор геометрический 409 [c.619]
Нг — геометрический напор (геометрическая, геодезическая высота подъема), равный разности отметок нагнетания и всасывания к — сопротивления во всасывающем и напорном трубопроводах (исключая насос). [c.8]
Регенератор, изображенный на рис. 65, состоит из двух коН центрических втулок 2 я 4 я насадки 5. Эти детали изготовлены из материала с низкой теплопроводностью (нержавеющая сталь, титан, металлокерамика и т. п.) во избежание теплового замыкания , при котором теплота от нагревателя по втулкам регенератора непосредственно передается охладителю, увеличивая тем самым потери в цикле. Материал насадки должен иметь высокую теплоемкость, незначительную теплопроводность, высокую термостойкость, а также быть химически нейтральным к рабочему телу. С целью уменьшения температурного напора геометрическая форма насадки должна обладать наибольшей поверхностью теплообмена, приходящейся на единицу объема. Б то же время мертвые объемы регенератора и их гидравлическое сопротивление должны быть возможно малыми. [c.111]
Назовем уровни свободной поверхности жидкости в приемном и напорном резервуаре приемным и напорным уровнями, разность Яр высот напорного н приемного уровней — геометрическим напором насосной установки. [c.187]
| Рис. 2.31. Определение режима работы насоса на установку с отрицательным геометрическим напором | 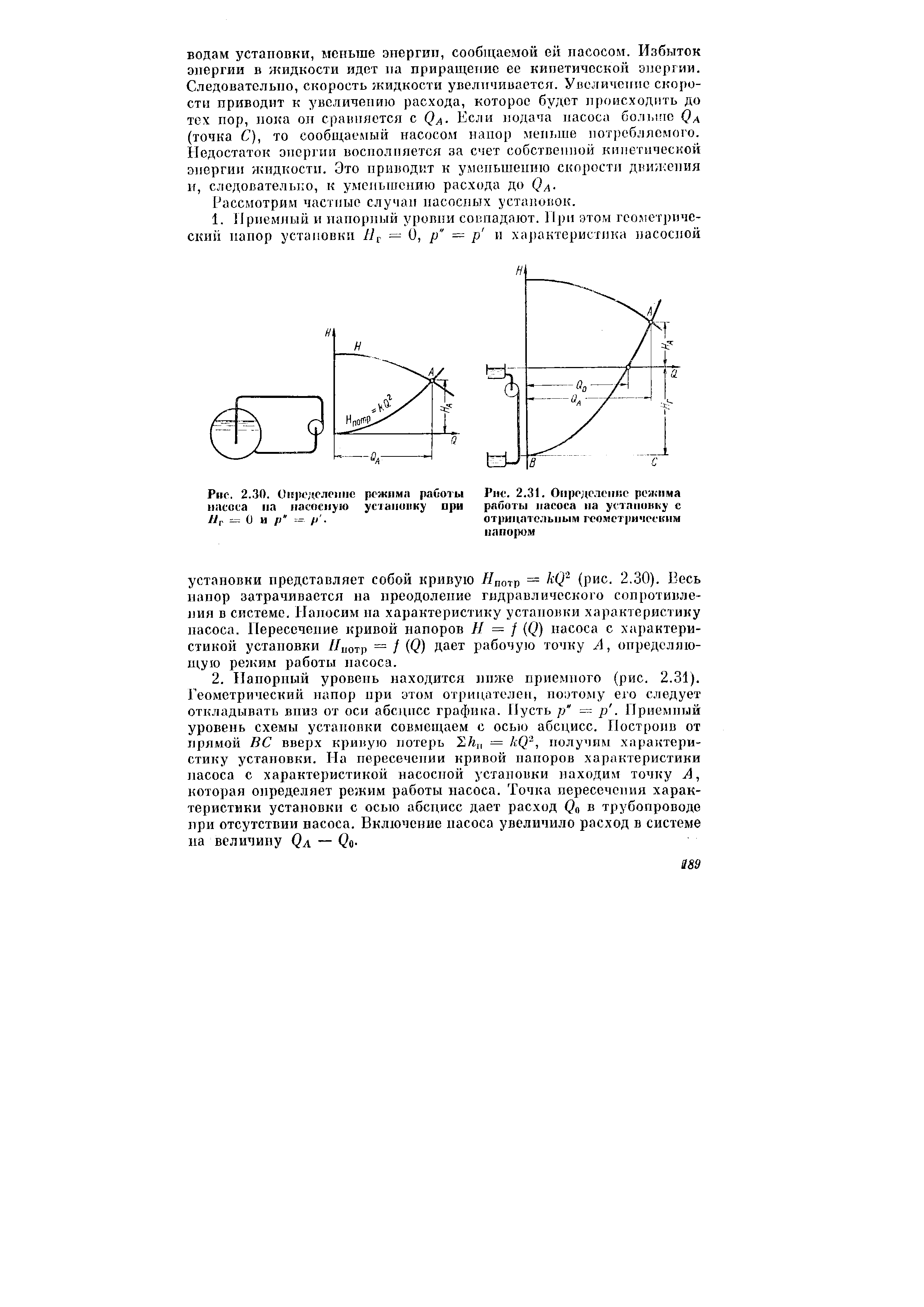 |
Истечение после сечения (2-2) происходит по типу водослива с широким порогом при геометрическом напоре Н. [c.225]
Часто при вычислении расхода водослива удобнее пользоваться вместо Яо значением геометрического напора Я, который можно замерить непосредственно. С этой целью перепишем (24-2) в таком виде [c.238]
При некоторых специальных расчетах необходимо знать значение геометрического напора [c.258]
Геометрический напор при этом будет Н = к» — Р1 = 2,2 м — 1 л( = 1,2 ж. [c.259]
О — вес (сила тяжести) g — ускорение свободного падения Я — геометрический напор Яд g — пьезометрический напор [c.5]
С геометрической точки зрения уравнение Д. Бернулли представляет собой уравнение напоров. Гидродинамический напор Яд [c.36]
В зависимости от соотношения толщины водосливной стенки и геометрического напора Н различают три типа водосливов [c.170]
Мощность нясосной установки определится по формуле (4-25), где И — суммарный напор — геометрический Яг и затрачиваемый на сопротивления во всасывающей Ясс и нагнетательной Янг линиях [c.203]
Рис. 2-9. йд — абсолютная пьезометр и-ческая высота (или абсолютный напор давления) Лизб — избыючная пьезометрическая высота или просто пьезометрическая высота (или избыточный напор давления) г — отметка (или напор геометрический) Яд—абсолютный потенциальный напор Я — избыточный потенциальный напор или просто потенциальный напор О— О — плоскость сравнения [c.33]
Координата г называется геометрической высотой. Воличт на /( os ) имеет линейную раз.мсрпость и называется пьезометрической высотой. Сумма Z — — р/ pg) называется гидростатическим напором. [c.18]
Итак, йля идеальной движущейся жидкости сумма трех напоров (высот) геометрического, пьезометрического и скоростного есть величина посто51нная вдоль струйки. [c.40]
Пьезометрическую высоту, стоящую в лозой части уравнения (1.138) назовем нотребныл напором // отр- Если же эта высота задана, то будем называть ее располагаемым напором Яраси- 1 ак видно из формулы, этот напор складывается из геометрической высоты Az = Z., — Zi, на которую нодиимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе. [c.119]
Теория подобия позволяет установить формулы пересчета пара- гетров лопастных насосов, определяющие зависимость подачи, напора, моментов сил и мощности геометрически подобных насосов, работающих па подобных режимах, от их размеров и частоты вращения. [c.176]
Характеристикой насосной установки называется зависимость потребного наиора от расхода жидкости. Геометрический напор Яг, давления р и р и, следовательно, статический нанор Нет от расхода [c.187]
Таким бразом, используя закономерности, описанные в разделах 4.1 и 4.2 гл. 4, для многокомпонентных свободно истекающих струйных течений определяются основные термогидрогазодинамические и технологические параметры, а также основные конструктивные размеры одно- и многосопловых эжекциониых аппаратов, которые обеспечивают процесс эжекции с максимальным КПД или с повышенным коэффициентом полного напора f, или с повышенным коэффициентом эжекции Uq. Для расчета требуются исходные сведения, включающие параметры высоконапорной среды давление Pg, температуру Tg, компонентный состав С,g, расход Fg при условии, если не задан радиус отверстия сопла г, по которому определяется этот расход параметры низконапорной среды давление Р , температуру Т , компонентный состав С/ , а также геометрические параметры струйного течения угол расширения пограничного слоя а и угол сужения потенциального ядра р кроме того, требуются величины коэффициентов для каждого компонента углеводородной смеси, которые входят в состав низконапорной или высоконапорной сред. [c.227]
Каждый водослив при пропуске различных расходов О работает под некоторым геометрическим напором Я, представляюшп.м разность отметок уровня верхнего бьефа и порога. При ЭТОЛ1 отметка уровня верхнего бьефа фиксируется там, где не заметен спад свобоД о1[ поверхности практически можно уровемт. верхнего бьефа фиксировать т[а расстоянии 1>ЗН. [c.237]
Геометрический напор Н может быть определен в предположении, что выходная часть водобойного колодца работает как затопленный водослив с широким порого.м. Способ определения величины Н был изложен в 24-23. [c.275]
Должно быть ясно, что геометрическая форма сетки движения определяется только границами фильтрационного потока (рис. 32-1), но не зависит ни от коэффициента фильтрации, ни от напора на, соо1ружен ии. В самом деле, если при тех лее границах заменим фильтрующий грунт грунтом с другим коэффициентом фультрации или нее изменим напор, скорость фильтрации и фильтрационный расход, конечно, изменятся, но частицы жидкости II при новых скоростях будут продолжать двигаться по прежни.м траекториям. Линии тока, следовательно, сохранят свою форму не изменится также и форма линий равного напора. Сохранится II общее наименование линий так, например, линия равного напора Ф = 0,ЗДо сохранит свое обозначение, так как она останется геометрическим местом точек с напором, равным 0,3 от нового напора. [c.324]
Среди многочисленных методов приближенного, пеаиалитического решения уравнения Лапласа большим распространением в гидротехнических расчетах пользуется метод графического решения, заключаюгцш шя в геометрическом построении ортогональной сетки линий равных напоров и линий тока, удовлетворяющих заданным граничным условиям задачи. [c.325]
Величины Z и pjy часто называют в гидравлике геометрической и пьезометрической высотами , тогда Я как сумма двух высот будет также высотой — ее называют гидростатическим напором. Согласно рис. 1.8, величина Я представляет собой ординату горизонтальной плоскости, именуемой плоскостью гидростатического напора. Эта плоскость расположена выше плоскости свободной поверхнс сти на высоту paly. [c.40]
c.35
]
Гидравлика (1982) — [
c.47
]
Гидравлика и гидропривод (1970) — [
c.46
]
Сборник задач по гидравлике и газодинамике для нефтяных вузов (1990) — [
c.54
]
Гидравлика (1984) — [
c.37
]
Метрология, специальные общетехнические вопросы Кн 1 (1962) — [
c.180
]
Технический справочник железнодорожника Том 1 (1951) — [
c.409
]
Гидравлика Изд.3 (1975) — [
c.37
]